Mat-lab常微分方程的求解实验报告
用MATLAB求解常微分方程实验报告

实验五 利用Matlab 求解常微分方程(组)的实验报告学院:数计学院 班级:1003班 姓名:黄晓丹 学号:1051020144一.实验目的:熟悉Matlab 软件中关于求解常微分方程的各种命令. 掌握利用Matlab 软件进行常微分方程的求解。
二.相关知识在MATLAB 中,由函数dsolve()解决常微分方程(组)的求解问题,其具体格式如下:X=dsolve(‘eqn1’,’eqn2’,…)函数dsolve 用来解符号常微分方程、方程组,如果没有初始条件,则求出通解,如果有初始条件,则求出特解.用字符串方程表示,自变量缺省值为t 。
导数用D 表示,2阶导数用D2表示,以此类推。
S 返回解析解。
在方程组情形,s 为一个符号结构。
[tout,yout]=ode45(‘yprime’,[t0,tf],y0) 采用变步长四阶Runge-Kutta 法和五阶Runge-Kutta-Felhberg 法求数值解,yprime 是用以表示f(t,y)的M 文件名,t0表示自变量的初始值,tf 表示自变量的终值,y0表示初始向量值。
输出向量tout 表示节点(t 0,t 1, …,t n )T ,输出矩阵yout 表示数值解,每一列对应y 的一个分量。
若无输出参数,则自动作出图形.三.实验内容:例1 求下列微分方程的解析解(1)(2)(3)方程(1)求解的MATLAB 代码为:>>clear;>>s=dsolve('Dy=a*y+b')结果为s =-b/a+exp(a*t)*C1方程(2)求解的MATLAB 代码为:>>clear;>>s=dsolve('D2y=sin(2*x)-y','y(0)=0','Dy(0)=1','x')>>simplify(s) %以最简形式显示s结果为s =(-1/6*cos(3*x)-1/2*cos(x))*sin(x)+(-1/2*sin(x)+1/6*sin(3*x))*cos(x)+5/3*sin(x)ans =-2/3*sin(x)*cos(x)+5/3*sin(x)方程(3)求解的MATLAB 代码为:b ay y +='1)0(',0)0(,)2sin(''==-=y y y x y 1)0(',1)0(',','==-=+=g f f g g g f f>>clear;>>s=dsolve('Df=f+g','Dg=g-f','f(0)=1','g(0)=1')>>simplify(s,f) %s 是一个结构>>simplify(s.g)结果为ans =exp(t)*cos(t)+exp(t)*sin(t)ans =-exp(t)*sin(t)+exp(t)*cos(t)例2 求解微分方程先求解析解,再求数值解,并进行比较。
常微分matlab实验报告

数学与信息科学系实训报告常微分方程初值问题数值解法及其MATLAB实现姓名:学号:专业:信息与计算科学年级:2010级指导教师:朱耀生完成时间:2013年11月25—2013年12月6实验目的:(1)研究满足给定方程的可微函数的数值方法(2)培养matlab编程和上机调试能力实验基本原理和内容:根据给定的初始条件,确定常微分方程惟一解的问题叫常微分方程初值问题。
大多数实际问题难以求得解析解,必须将微分问题离散化,用数值方法求其近似解。
一阶常微分方程的初值问题的提法是,求出函数,使满足条件(1)利用数值方法解问题(1)时,通常假定解存在且惟一,解函数及右端函数具有所需的光滑程度。
数值解法的基本思想是:先取自变量一系列离散点,把微分问题(1)离散化,求出离散问题的数值解,并以此作为微分问题解的近似。
例如取步长>0,以剖分区间[,],令=+,把微分方程离散化成一个差分方程。
以()表微分方程初值问题的解,以表差分问题的解,就是近似解的误差,称为全局误差。
因此,设计各种离散化模型,求出近似解,估计误差以及研究数值方法的稳定性和收敛性等构成了数值解法的基本内容1.欧拉法和后退欧拉法原理:function [x,y]=meuler(df,xspan,y0,h)%用途:改进欧拉公式解常微分方程y'=f(x,y), y(x0)=y0%格式:[xy]=meuler(df,a,b,y0,h) df为函数f(x,y), xspan为求解%区间[x0,xn], y0为初值y(x0), h为步长, [xy]返回节点和数值解矩阵x=xspan(1):h:xspan(2); y(1)=y0;for n=1:(length(x)-1)k1=feval(df,x(n),y(n));y(n+1)=y(n)+h*k1;k2=feval(df,x(n+1),y(n+1));y(n+1)=y(n)+h*(k1+k2)/2;end例题给定的初值问题y′=-y+x+2,0=<x=<1Y(0)=-1,取精确解y(x)=exp(-x)+x后退欧拉法,步长h=0.003, h=0.1求在节点k=1+0.1k (k=1,2,3……10)处的数值解若>>h=0.1;y=-1;x=1;for i=1:20k1=h*oulei_wf(x,y);k2=h*oulei_wf(x+h,y+k1);y=y+0.5*k1+0.5*k2x=x+h;z=ouleij_q(x)t=y-zendz = 4,z = 3.7000,y = -0.6150z = 1.4329, z =1.4329, t = -2.0479 z =3.7150, z =3.4435, y = -0.2571 z =1.5012, z =1.5012, t =-1.7583 z =3.4571, z = 3.2114, y =0.0763 z =1.5725, z =1.5725, t =-1.4962 z =3.2237, z = 3.0013, y =0.3876 z =1.6466, z =1.6466, t =-1.2590 z =3.0124,z =2.8112,y =0.6788z =1.7231,z =1.7231,t =-1.0444 z =2.8212,z = 2.6391,y =0.9518 z =1.8019,z =1.8019,t =-0.8501z = 2.6482,z =2.4834,y =1.2084z =1.8827,z =1.8827, t =-0.6743z =2.4916,z =2.3425, y =1.4501z =1.9653,z =1.9653, t =-0.5152实验结果的分析与研究1.对于欧拉法,步长越小,精度越高,而产生的误差越小。
matlab常微分方程的数值解法实验报告

实验四常微分方程的数值解法 指令:[t,y]=ode23(‘fun ’,tspan,yo) 2/3阶龙格库塔方法 [t,y]=ode45(‘fun ’,tspan,yo) 4/5阶龙格库塔方法 [t,y]=ode113(‘fun ’,tspan,yo) 高阶微分方程数值方法其中fun 是定义函数的文件名。
该函数fun 必须以为dx 输出量,以t,y 为输入量。
tspan=[t0 tfina]表示积分的起始值和终止值。
yo 是初始状态列向量。
考虑到初始条件有00d , (0)0,d d , (0)0.d SSI S S tI SI I I I tββμ⎧=-=>⎪⎪⎨⎪=-=≥⎪⎩ (5.24) 这就是Kermack 与McKendrick 的SIR 仓室模型. 方程(5.24)无法求出()S t 和()I t 的解析解.我们先做数值计算。
Matlab 代码为:function dy=rigid(t,y) dy=zeros(2,1); a=1; b=0.3;dy(1)=a*y(1).*y(2)-b*y(1); dy(2)=-a*y(1).*y(2);ts=0:.5:50; x0=[0.02,0.98];[T,Y]=ode45('rigid',ts,x0); %plot(T,Y(:,1),'-',T,Y(:,2),'*') plot(Y(:,2),Y(:,1),'b--') xlabel('s') ylabel('i')任务:1 画出i (t ),2分析各参数的影响例57:求解两点边值问题:0)5(,0)1(,32==='-''y y x y y x 。
(注意:相应的数值解法比较复杂)。
y=dsolve('x*D2y-3*Dy=x^2','y(1)=0,y(5)=0','x') ↙ y =-1/3*x^3+125/468+31/468*x^4例:用数值积分的方法求解下列微分方程 π21''2t y y -=+设初始时间t0=0;终止时间tf=3*pi ;初始条件0|',0|00====x x y y 。
matlab求微分方程的解 实验报告四
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,通系电1,力过根保管据护线生高0不产中仅工资2艺料22高试2可中卷以资配解料置决试技吊卷术顶要是层求指配,机置对组不电在规气进范设行高备继中进电资行保料空护试载高卷与中问带资题负料2荷试2,下卷而高总且中体可资配保料置障试时2卷,32调需3各控要类试在管验最路;大习对限题设度到备内位进来。行确在调保管整机路使组敷其高设在中过正资程常料1工试中况卷,下安要与全加过,强度并看工且25作尽52下可22都能护可地1关以缩于正小管常故路工障高作高中;中资对资料于料试继试卷电卷连保破接护坏管进范口行围处整,理核或高对者中定对资值某料,些试审异卷核常弯与高扁校中度对资固图料定纸试盒,卷位编工置写况.复进保杂行护设自层备动防与处腐装理跨置,接高尤地中其线资要弯料避曲试免半卷错径调误标试高方中等案资,,料要编试求5写、卷技重电保术要气护交设设装底备备置。4高调、动管中试电作线资高气,敷料中课并设3试资件且、技卷料中拒管术试试调绝路中验卷试动敷包方技作设含案术,技线以来术槽及避、系免管统不架启必等动要多方高项案中方;资式对料,整试为套卷解启突决动然高过停中程机语中。文高因电中此气资,课料电件试力中卷高管电中壁气资薄设料、备试接进卷口行保不调护严试装等工置问作调题并试,且技合进术理行,利过要用关求管运电线行力敷高保设中护技资装术料置。试做线卷到缆技准敷术确设指灵原导活则。。:对对在于于分调差线试动盒过保处程护,中装当高置不中高同资中电料资压试料回卷试路技卷交术调叉问试时题技,,术应作是采为指用调发金试电属人机隔员一板,变进需压行要器隔在组开事在处前发理掌生;握内同图部一纸故线资障槽料时内、,设需强备要电制进回造行路厂外须家部同出电时具源切高高断中中习资资题料料电试试源卷卷,试切线验除缆报从敷告而设与采完相用毕关高,技中要术资进资料行料试检,卷查并主和且要检了保测解护处现装理场置。设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
MATLAB实验4-微分方程求解分析

subplot(1,3,2);plot(sol.y(1,:));hold on;
subplot(1,3,3) plot(sol.y(2,:));
其中,x,f是n维向量,A是n阶矩阵。 k 为A的特征 根。称
max | Re(k ) | s min | Re(k ) |
为刚性比,s>10的方程可认为是刚性方程。
MATLAB中求解刚性方程的命令ode23s,ode15s等, 其用法与ode23,ode45相同。略。 2、延迟微分方程求解 延迟微分方程的一般形式为
(t ) f (t , x(t 1 ), x(t 2 ),, x(t n )) x
MATLAB提供了求解这类方程的隐式Runge-Kutta算 法dde23(), 可以直接求解延迟微分方程。该函数调 用格式为:
sol=dde23(f1,tau,f2,[t0,tf])
其中tau=[tau1,tau2,…,taun],f1为描述延 迟微分方程的 MATLAB语言函数,f2为描 述 t<=t0 时状态变量值的函数。该函数返 回的变量 sol 为结构体数据,其 sol.x 成员 变量为时间 t ,成员 sol.y 为各个时刻的源自 态向量构成的矩阵x。实验4
实验名称:微分方程求解 实验目的:熟悉并掌握常微分方程数值求解的基 本原理、方法;掌握常微分方程模型的MATLAB 解析解法与数值解法。
实验任务: 1、P139,习题6 2、P140,习题13.
附录一:基于MATLAB的微分方程求解
一、微分方程的解析运算
1、函数求导的解析运算
y=diff(fun,x)
则:
y=dsolve('D4y+10*D3y+35*D2y+50*Dy+24*y=uu','y( 0)=3','Dy(0)=2','D2y(0)=0','D3y(0)=0')
实验二MATLAB数值计算常微分方程的求解

实验二MATLAB数值计算常微分方程的求解引言:微分方程是描述物理问题和工程问题的重要工具,也是数学和工程学科中的重要课题。
解析方法可以求得一些简单微分方程的解析解,但对于复杂问题,常常无法得到解析解。
此时,数值求解方法成为一种有效的工具。
MATLAB是一个功能强大的数值计算软件,对于求解常微分方程组也提供了多种数值方法。
本实验将介绍MATLAB中求解常微分方程(组)的方法,并通过实例来演示这些方法的应用。
一、MATLAB的常微分方程(组)求解函数MATLAB提供了多种函数用于求解常微分方程(组),其中最常用的函数是ode45、ode23和ode15s。
这些函数采用不同的数值方法,精度和效率也不同。
下面分别对这些函数进行简单介绍:1. ode45函数:ode45函数采用了一种自适应的步长控制算法,可以在一个时间段内自动调整步长。
这个函数的语法是:[t,y] = ode45(odefun,tspan,y0,options)其中,odefun是一个函数句柄,表示待解的常微分方程组,tspan是求解区间,y0是初始条件,options是一个结构体,包含其他的参数和选项。
2. ode23函数:ode23函数也采用了自适应的步长控制算法,但相对于ode45,它是一个简化版本,只允许使用比较简单的问题。
这个函数的语法与ode45相似:[t,y] = ode23(odefun,tspan,y0,options)3. ode15s函数:ode15s函数采用了一种隐式数值方法,适用于比较刚性(stiff)的常微分方程。
这个函数的语法与前两个函数也相似:[t,y] = ode15s(odefun,tspan,y0,options)以上是MATLAB提供的三种解常微分方程(组)的函数,根据问题的特点和求解的需求选择相应的函数。
二、实例演示在本实验中,我们将通过一个实例来演示如何使用MATLAB解常微分方程组。
假设有一个简单的线性常微分方程组:dy1/dt = -2y1 + y2dy2/dt = y1 - 2y2给定初始条件为y1(0)=1,y2(0)=0,求在t=[0,5]时,y1和y2的解。
【免费下载】matlab求微分方程的解 实验报告四
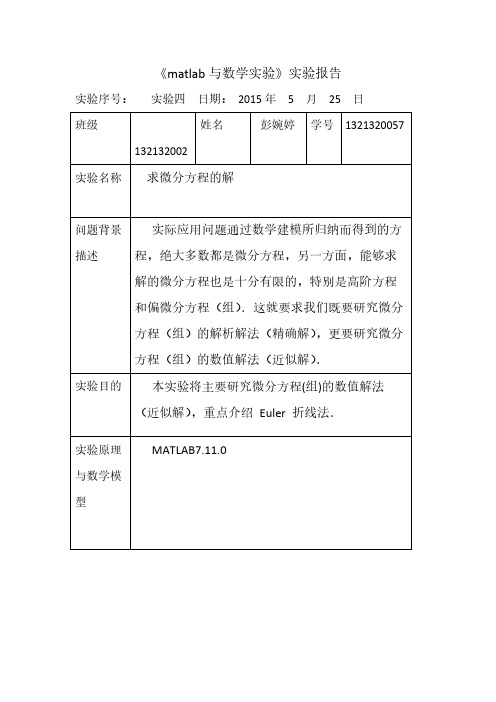
simplify(y)
答案: x =exp(2^(1/2)*t)/2 + 1/(2*exp(2^(1/2)*t)) -
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电,力根通保据过护生管高产线中工敷资艺设料高技试中术卷资,配料不置试仅技卷可术要以是求解指,决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高与中带资负料荷试下卷高问总中题体资,配料而置试且时卷可,调保需控障要试各在验类最;管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下,安与要全过加,度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高;试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中,核资或对料者定试对值卷某,弯些审扁异核度常与固高校定中对盒资图位料纸置试,.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置,弯高尤曲中其半资要径料避标试免高卷错等调误,试高要方中求案资技,料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高,术料课中并3中试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术,管以术来架及避等系免多统不项启必方动要式方高,案中为;资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资,管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装,工置合作调理并试利且技用进术管行,线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确:指灵在导活分。。线对对盒于于处调差,试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷,术调应问试采题技用,术金作是属为指隔调发板试电进人机行员一隔,变开需压处要器理在组;事在同前发一掌生线握内槽图部内 纸故,资障强料时电、,回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资,料料线试试缆卷卷敷试切设验除完报从毕告而,与采要相用进关高行技中检术资查资料和料试检,卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
实验三 常微分方程求解Matlab实验报告

北京理工大学珠海学院实验报告
ZHUHAI CAMPAUS OF BEIJING INSTITUTE OF TECHNOLOGY
班级2012电气2班学号xxxxxxxxx姓名陈冲指导教师张凯成绩
实验题目(实验三)常微分方程求解实验地点及时间JB501 2013/12/31(3-4节)
一、实验目的
1.掌握用程序语言来编辑函数。
2.学会用MATLAB编写RK4.m函数实现四阶Runge-kutta法。
二、实验环境
Matlab软件
三、实验内容
1、以书中第124页第11题为例编辑程序来实现计算结果。
2、使用MATLAB进行编写:
第一步:编写RK4.m函数,代码如下
第二步:利用上述函数编辑命令:(可见实验结果中的截图)
在此之前先建立一个名为ti124_11fun.m的M文件,代码如下
function z=ti124_11fun (x,y);
z=8-3*y;
再编代码:
得到结果y(0.4)=2.4654
四、实验题目
用四阶经典的龙格-库塔方法求解初值问题'83,(0)2
=-=,试取步长0.2
y y y
h=计算y的近似值,要求小数点后保留四位数字.
(0.4)
五、实验结果
五、总结
本次试验难度不大,只需注意符号别打错,实验过程无大问题。
………。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《数学实验》报告
实验名称Mat lab常微分方程的求解学院计算机与通信工程学院
专业班级计1103
姓名
学号
2013年6 月
一、【实验目的】
通过练习,熟悉Mat lab的求解常微分方程,函数文件的创建等。
了解Mat lab的命令窗口及其基本操作和常用命令。
通过练习,熟悉Mat lab的一些基本操作,掌握符号解法和数值解法,以及其中常用的方法。
二、【实验任务】
1、求解微分方程y'=xsin(x)/cos(y)。
2、用数值方法求解下列微分方程,用不同颜色和线形将y和y'画在同一个图形窗口里:
y''+ty'-y=1-2t,初始时间:t0=0;终止时间:t f=π;初始条件:y|t=0=0.1,y'|t=0=0.2。
三、【实验程序】
题一:
y= dsolve('Dy=x*sin(x)/cos(y)','x')
题二:
令:a=y,b=y'=a',b'=y''则:
a'=0*a+1*b+0;b'=1*a-t*b+(1-2*t);
[a';b']=[0 1;1 -t][a;b]+[0;1](1-2*t);
故化为一阶微分方程有:
x'=[0 1;1 -t]x+[0;1]u;其中:x'=[a';b'],u=(1-2*t)。
初始条件:当t=0时,a=0.1;b=0.2。
function xd = mainfun( t,x )
%UNTITLED Summary of this function goes here
% Detailed explanation goes here
u=1-2.*t;
xd=[0 1;1 -t]*x+[0;1]*u;
end
clf;
t0=0;
tf=pi;
x0t=[0.1;0.2];%初始条件
[t,x]=ode23('mainfun',[t0,tf],x0t) y=x(:,1);
Dy=x(:,2);
plot(t,y,'g--',t,Dy,'k-.')
xlabel('t轴'),ylabel('Y轴')
legend('原始函数y','一阶导数Dy')
四、【实验结果】
题一:
y =
asin(C3 + sin(x) - x*cos(x))
题二:
>> fun
t =
0.0145
0.0873
0.2014
0.3259
0.4621
0.6121
0.7778
0.9621
1.1482
1.2767
1.4053
1.5188
1.6706
1.8601
2.0891
2.3569
2.6546
2.9687
3.1416
x =
0.1000 0.2000
0.1030 0.2158
0.1214 0.2883
0.1598 0.3798
0.2116 0.4479
0.2756 0.4847
0.3485 0.4813
0.4245 0.4282
0.4939 0.3168
0.5388 0.1599
0.5513 0.0320
0.5466 -0.1069
0.5272 -0.2358
0.4780 -0.4127
0.3788 -0.6347
0.2037 -0.8952
-0.0742 -1.1797
-0.4677 -1.4646
-0.9691 -1.7290
-1.2793 -1.8586
五、【实验总结】
通过本次实验,熟悉了Mat lab的一些基本操作,通过练习,会求解常微分方程,并熟练掌握符号解法和数值解法,以及其中常用的方法,包括欧拉方法、梯形公式、龙格库塔方法等。
通过练习,熟悉Mat lab的语句的用法,要会把高阶微分方程,通过迭代和等效替代,化为一阶微分方程。
