微分方程实验报告(迎风-格式)信息科学
常微分方程 课程实习报告

福建农林大学计算机与信息学院(数学类课程)课程实习报告课程名称:常微分方程课程实习实习题目:常微分方程数值求解问题的实习姓名:上官火玉系:信息与计算科学专业:信息与计算科学年级:2008学号:081152048指导教师:陈永雪职称:讲师2010 年12 月 1 日福建农林大学计算机与信息学院数学类课程实习报告结果评定目录1. 实习的目的和任务 (1)2. 实习要求 (1)3. 实习地点 (1)4. 主要仪器设备 (1)5. 实习内容 (1)5.1 用不同格式对同一个初值问题的数值求解及其分析 (1)5.1.1求精确解 (1)5.1.2用欧拉法求解 (3)5.1.3用改进欧拉法求解 (5)5.1.4用4级4阶龙格—库塔法求解 (7)5.1.5 问题讨论与分析 (10)5.2 一个算法不同不长求解同一个初值问题及其分析 (12)6. 结束语 (13)参考文献 (13)常微分方程课程实习1.实习的目的和任务目的:通过课程实习能够应用MATLAB软来计算微分方程(组)的数值解;了解常微分方程数值解。
任务:通过具体的问题,利用MATLAB软件来计算问题的结果,分析问题的结论。
2.实习要求能够从案例的自然语言描述中,抽象出其中的数学模型;能够熟练应用所学的数值解计算方法;能够熟练使用MATLAB软件;对常微分方程数值解有所认识,包括对不同算法有所认识和对步长有所认识。
3.实习地点数学实验室4.主要仪器设备计算机、Microsoft Windows XPMatlab 6.55.实习内容5.1 用欧拉方法,改进欧拉方法,4阶龙格—库塔方法分别求下面微分方程的初值dy/dx=y+x+1 y(0)=1 x∈[0,2]5.1.1求精确解首先可以求得其精确解为:y=3*exp(x)-x-25.1.1 程序代码:>> x=0:0.1:2;>> y=3*exp(x)-x-2>> plot(x,y,'b*-');>> Data=[x',y']y =Columns 1 through 91.0000 1.2155 1.4642 1.74962.0755 2.44622.86643.3413 3.8766Columns 10 through 184.47885.1548 5.91256.76047.70798.76569.9451 11.2591 12.7218Columns 19 through 2114.3489 16.1577 18.1672Data =0 1.00000.1000 1.21550.2000 1.46420.3000 1.74960.4000 2.07550.5000 2.44620.6000 2.86640.7000 3.34130.8000 3.87660.9000 4.47881.0000 5.15481.1000 5.91251.2000 6.76041.3000 7.70791.4000 8.76561.5000 9.94511.6000 11.25911.7000 12.72181.8000 14.34891.9000 16.15772.0000 18.1672>>00.20.40.60.81 1.2 1.4 1.6 1.825.1.2 用欧拉法求解程序如下:建立函数文件cwfa1.mfunction [x,y]=cwfa1(fun,x_span,y0,h)x=x_span(1):h:x_span(2);y(1)=y0;for n=1:length(x)-1y(n+1)=y(n)+h*feval(fun,x(n),y(n)); endx=x';y=y';在MATLAB输入以下程序:>> clear all>> fun=inline(' y+x+1');>> [x,y]=cwfa1(fun,[0,2],1,0.1);>> [x,y]>> plot(x,y,'r*-')结果及其图象:ans =0 1.00000.1000 1.20000.2000 1.43000.3000 1.69300.4000 1.99230.5000 2.33150.6000 2.71470.7000 3.14620.8000 3.63080.9000 4.17381.0000 4.78121.1000 5.45941.2000 6.21531.3000 7.05681.4000 7.99251.5000 9.03171.6000 10.18491.7000 11.46341.8000 12.87981.9000 14.44772.0000 16.182500.20.40.60.81 1.2 1.4 1.6 1.825.1.3用改进欧拉法求解:程序如下:建立函数文件cwfa2.mfunction [x,y]=cwfa2(fun,x_span,y0,h)x=x_span(1):h:x_span(2);y(1)=y0;for n=1:length(x)-1k1=feval(fun,x(n),y(n));y(n+1)=y(n)+h*k1;k2=feval(fun,x(n+1),y(n+1));y(n+1)=y(n)+h*(k1+k2)/2;endx=x';y=y';在MATLAB输入以下程序:>> clear all>> fun=inline(' y+x+1');>> [x,y]=cwfa2(fun,[0,2],1,0.1); >> [x,y]>> plot(x,y,'r+-')结果及其图象:ans =0 1.00000.1000 1.21500.2000 1.46310.3000 1.74770.4000 2.07270.5000 2.44230.6000 2.86130.7000 3.33470.8000 3.86840.9000 4.46851.0000 5.14221.1000 5.89721.2000 6.74191.3000 7.68581.4000 8.73931.5000 9.91391.6000 11.22241.7000 12.67871.8000 14.29851.9000 16.09882.0000 18.0987>>00.20.40.60.81 1.2 1.4 1.6 1.825.1.4 用4阶龙格—库塔求解程序如下:建立函数文件cwfa3.mfunction [x,y]=cwfa3(fun,x_span,y0,h)x=x_span(1):h:x_span(2);y(1)=y0;for n=1:length(x)-1k1=feval(fun,x(n),y(n));k2=feval(fun,x(n)+h/2,y(n)+h/2*k1);k3=feval(fun,x(n)+h/2,y(n)+h/2*k2);k4=feval(fun,x(n+1),y(n)+h*k3);y(n+1)=y(n)+h*(k1+2*k2+2*k3+k4)/6;endx=x';y=y';在MATLAB输入以下程序:>> clear all;>> fun=inline(' y+x+1');>> [x,y]=cwfa3(fun,[0,2],1,0.1); >> [x,y]>> plot(x,y, 'b+-')结果及其图象:ans =0 1.00000.1000 1.21550.2000 1.46420.3000 1.74960.4000 2.07550.5000 2.44620.6000 2.86640.7000 3.34130.8000 3.87660.9000 4.47881.0000 5.15481.1000 5.91251.2000 6.76031.3000 7.70791.4000 8.76561.5000 9.94511.6000 11.25911.7000 12.72181.8000 14.34891.9000 16.15772.0000 18.1671>>00.20.40.60.81 1.2 1.4 1.6 1.825.1.5 问题讨论与分析由以上数值分析结果绘制表格:x=0:0.1:2;y1 = [1.0000 1.2155 1.4642 1.7496 2.0755 2.4462 2.8664 3.3413 3.8766 4.4788 5.1548 5.9125 6.7604 7.7079 8.7656 9.9451 11.2591 12.7218 14.3489 16.1577 18.1672];>> y1=[1.0000 1.2155 1.4642 1.7496 2.0755 2.4462 2.8664 3.3413 3.8766 4.4788 5.1548 5.9125 6.7604 7.7079 8.7656 9.9451 11.2591 12.7218 14.3489 16.1577 18.1672];>> y2=[1.0000 1.2000 1.4300 1.6930 1.9923 2.3315 2.7147 3.1462 3.6308 4.1738 4.7812 5.4594 6.2153 7.0568 7.9925 9.0317 10.1849 11.4634 12.8798 14.4477 16.1825];>> y3=[1.0000 1.2150 1.2192 1.4631 1.7477 2.0727 2.4423 2.8613 3.8684 4.4685 5.1422 5.8972 6.7419 7.6858 8.7393 9.9139 11.2224 12.6787 14.2985 16.0988 18.0987];>> y4=[1.0000 1.2155 1.4642 1.7496 2.0755 2.4462 2.8664 3.3413 3.8766 4.4788 5.1548 5.9125 6.7603 7.7079 8.7656 9.9451 11.2591 12.7218 14.3489 16.1577 18.1671 ];>> plot(x,y1,'r+-')>> hold on,plot(x,y2,'b-')>> plot(x,y1,'r+-')>> hold on,plot(x,y3,'b-')>> plot(x,y1,'r+-')>> hold on,plot(x,y4,'b-')00.20.40.60.81 1.2 1.4 1.6 1.8200.20.40.60.81 1.2 1.4 1.6 1.8200.20.40.60.81 1.2 1.4 1.6 1.82由上表和图可以看出欧拉法误差最大,而改进欧拉和龙格—库塔方法误差相对较小,并且龙格—库塔方法误差最小且大部分值都跟精确值相同。
常微分方程数值解实验报告

常微分方程数值解实验报告学院:数学与信息科学专业:信息与计算科学姓名:郑思义学号:201216524课程:常微分方程数值解实验一:常微分方程的数值解法1、分别用Euler 法、改进的Euler 法(预报校正格式)和S —K 法求解初值问题。
(h=0.1)并与真解作比较。
⎩⎨⎧=++-=10(1y')y x y 1.1实验代码:%欧拉法function [x,y]=naeuler(dyfun,xspan,y0,h)%dyfun 是常微分方程,xspan 是x 的取值范围,y0是初值,h 是步长 x=xspan(1):h:xspan(2); y(1)=y0;for n=1:length(x)-1y(n+1)=y(n)+h*feval(dyfun,x(n),y(n)); end%改进的欧拉法function [x,m,y]=naeuler2(dyfun,xspan,y0,h)%dyfun 是常微分方程,xspan 是x 的取值范围,y0是初值,h 是步长。
%返回值x 为x 取值,m 为预报解,y 为校正解 x=xspan(1):h:xspan(2); y(1)=y0;m=zeros(length(x)-1,1); for n=1:length(x)-1 k1=feval(dyfun,x(n),y(n)); y(n+1)=y(n)+h*k1; m(n)=y(n+1);k2=feval(dyfun,x(n+1),y(n+1)); y(n+1)=y(n)+h*(k1+k2)/2; end%四阶S —K 法function [x,y]=rk(dyfun,xspan,y0,h)%dyfun 是常微分方程,xspan 是x 的取值范围,y0是初值,h 是步长。
x=xspan(1):h:xspan(2); y(1)=y0;for n=1:length(x)-1 k1=feval(dyfun,x(n),y(n));k2=feval(dyfun,x(n)+h/2,y(n)+(h*k1)/2); k3=feval(dyfun,x(n)+h/2,y(n)+(h*k2)/2); k4=feval(dyfun,x(n)+h,y(n)+h*k3);y(n+1)=y(n)+(h/6)*(k1+2*k2+2*k3+k4);end%主程序x=[0:0.1:1];y=exp(-x)+x;dyfun=inline('-y+x+1');[x1,y1]=naeuler(dyfun,[0,1],1,0.1);[x2,m,y2]=naeuler2(dyfun,[0,1],1,0.1);[x3,y3]=rk(dyfun,[0,1],1,0.1);plot(x,y,'r',x1,y1,'+',x2,y2,'*',x3,y3,'o');xlabel('x');ylabel('y');legend('y为真解','y1为欧拉解','y2为改进欧拉解','y3为S—K解','Location','NorthWest');1.2实验结果:x 真解y 欧拉解y1 预报值m 校正值y2 S—K解y30.0 1.0000 1.0000 1.0000 1.00000.1 1.0048 1.0000 1.0000 1.0050 1.00480.2 1.0187 1.0100 1.0145 1.0190 1.01870.3 1.0408 1.0290 1.0371 1.0412 1.04080.4 1.0703 1.0561 1.0671 1.0708 1.07030.5 1.1065 1.0905 1.1037 1.1071 1.10650.6 1.1488 1.1314 1.1464 1.1494 1.14880.7 1.1966 1.1783 1.1945 1.1972 1.19660.8 1.2493 1.2305 1.2475 1.2500 1.24930.9 1.3066 1.2874 1.3050 1.3072 1.30661.0 1.3679 1.3487 1.3665 1.3685 1.36792、选取一种理论上收敛但是不稳定的算法对问题1进行计算,并与真解作比较。
常微分方程实验报告

常微分方程实验报告一、实验目的常微分方程是数学分析和实际应用中非常重要的一部分,本次实验的主要目的是通过实际操作和计算,深入理解常微分方程的概念、性质和求解方法,并能够将其应用到实际问题中,提高我们解决数学问题和实际应用问题的能力。
二、实验原理常微分方程是指含有一个自变量和一个未知函数及其导数的等式。
求解常微分方程的方法有很多,常见的有变量分离法、一阶线性方程的求解方法(如常数变易法)、恰当方程的求解方法(通过积分因子)等。
对于一阶常微分方程,形如\(y' + p(x)y = q(x)\)的方程,可以使用积分因子\(e^{\int p(x)dx}\)来求解。
对于可分离变量的方程,形如\(g(y)dy = f(x)dx\),可以通过分别积分求解。
三、实验内容(一)一阶常微分方程的求解1、求解方程\(y' + 2xy = 2x\)首先,计算积分因子\(e^{\int 2xdx} = e^{x^2}\),然后将方程两边乘以积分因子得到:\((ye^{x^2})'= 2xe^{x^2}\)两边积分可得\(ye^{x^2} = e^{x^2} + C\),解得\(y =1 + Ce^{x^2}\)2、求解方程\(xy' y = x^2\)将方程化为\(y' \frac{y}{x} = x\),这里\(p(x) =\frac{1}{x}\),积分因子为\(e^{\int \frac{1}{x}dx} =\frac{1}{x}\)。
方程两边乘以积分因子得到\((\frac{y}{x})'= 1\),积分可得\(\frac{y}{x} = x + C\),即\(y = x^2 + Cx\)(二)二阶常微分方程的求解1、求解方程\(y'' 2y' + y = 0\)特征方程为\(r^2 2r + 1 = 0\),解得\(r = 1\)(二重根),所以通解为\(y =(C_1 + C_2x)e^x\)2、求解方程\(y''+ 4y = 0\)特征方程为\(r^2 + 4 = 0\),解得\(r =\pm 2i\),所以通解为\(y = C_1\cos(2x) + C_2\sin(2x)\)(三)应用常微分方程解决实际问题1、考虑一个物体在受到与速度成正比的阻力作用下的运动,其运动方程为\(m\frac{dv}{dt} = kv\)(其中\(m\)为物体质量,\(k\)为阻力系数),求解速度\(v\)随时间\(t\)的变化。
微分方程数学实验报告

j=i;
elseiff(x)*f(a)>0
a=X(i);
j=i+1;
end
end
end
b=X(j);
k=k+பைடு நூலகம்;
e=b-a;
end
if(b-a)<d
w=a
else
w=(a+b)/(p-1)
end
k
运行结果:
(输入函数形式)fx=x-0.8
(输入二分法下限)a=0
(输入二分法上限)b=1
输入误差限d=0.001
d =
1.0000e-003
输入p分法的p值,p=10
p =
10
w =
0.7999
k =
4
4、实验总结
6、教师评语及评分
0.7969
x0 =
0.8047
x0 =
0.8008
x0 =
0.7988
x0 =
0.7998
(2)P分法
symsx;fun=input('(输入函数形式)fx=');
a=input('(输入二分法下限)a=');
b=input('(输入二分法上限)b=');
d=input('输入误差限d=')%二分法求根
p=input(‘输入p分法的p值,p=’)
f=inline(fun);%修改需要求解的inline函数的函数体
X=[1:p];
e=b-a;
k=0;
whilee>d
h=(b-a)/(p-1);
fori=0:p-1
X(i+1)=a+(h*i);
微分方程数值解法实验报告

微分方程数值解法实验报告2篇微分方程数值解法实验报告(一)在实际科学与工程问题中,我们经常会遇到微分方程的求解。
然而,许多微分方程往往没有解析解,这就需要我们利用数值方法来获得近似解。
本篇实验报告将介绍两种常见的微分方程数值解法:欧拉方法和改进的欧拉方法。
一、欧拉方法欧拉方法是最简单的微分方程数值解法之一。
其基本原理为离散化微分方程,将微分方程中的导数用差商代替。
设要求解的微分方程为dy/dx = f(x, y),步长为h,则可用以下公式进行递推计算:y_{n+1} = y_n +hf(x_n, y_n)二、算法实现为了对欧拉方法进行数值实验,我们以一阶线性常微分方程为例:dy/dx = x - y, y(0) = 1步骤如下:(1)选择合适的步长h和求解区间[a, b],这里我们取h=0.1,[a, b] = [0, 1];(2)初始化y_0 = 1;(3)利用欧拉方法递推计算y_{n+1} = y_n + 0.1(x_n - y_n);(4)重复步骤(3),直到x_n = 1。
三、实验结果与讨论我们通过上述步骤得到了在[0, 1]上的近似解y(x)。
下图展示了欧拉方法求解的结果。
从图中可以看出,欧拉方法得到的近似解与精确解有一定的偏差。
这是因为欧拉方法只是通过递推计算得到的近似解,并没有考虑到更高阶的误差。
所以在需要高精度解时,欧拉方法并不理想。
四、改进的欧拉方法针对欧拉方法的不足,我们可以考虑使用改进的欧拉方法(也称为改进的欧拉-柯西方法)。
它是通过利用前后两个步长欧拉方法得到的结果作为差商的中间项,从而提高了求解精度。
一阶线性常微分方程的改进欧拉方法可以表示为:y_{n+1} = y_n + h(f(x_n, y_n) + f(x_{n+1}, y_n + hf(x_n,y_n)))/2五、算法实现与结果展示将改进的欧拉方法应用于前述的一阶线性常微分方程,我们同样选择h=0.1,[a, b] = [0, 1]。
微分方程数值解实验报告

微分方程数值解实验报告实验目的:掌握微分方程数值解的基本方法,能够利用计算机编程求解微分方程。
实验原理:微分方程是自然科学与工程技术中常见的数学模型,它描述了变量之间的关系及其随时间、空间的变化规律。
解微分方程是研究和应用微分方程的基础,但有很多微分方程无法找到解析解,只能通过数值方法进行求解。
本实验采用欧拉方法和改进的欧拉方法求解微分方程的初值问题:$$\begin{cases}\frac{dy}{dt}=f(t,y)\\y(t_0)=y_0\end{cases}$$其中,$f(t,y)$是给定的函数,$y(t_0)=y_0$是已知的初值条件。
欧拉方法是最基本的数值解法,其步骤如下:1.给定$t_0$和$y_0$2.计算$t_{i+1}=t_i+h$,其中$h$是步长3. 计算$y_{i+1}=y_i+hf(t_i,y_i)$4.重复步骤2、3直到达到终止条件改进的欧拉方法是对欧拉方法进行改进,通过利用函数$y(t)$在$t+\frac{1}{2}h$处的斜率来更准确地估计$y_{i+1}$,其步骤如下:1.给定$t_0$和$y_0$2.计算$t_{i+1}=t_i+h$,其中$h$是步长3. 计算$y_*=y_i+\frac{1}{2}hf(t_i,y_i)$4. 计算$y_{i+1}=y_i+hf(t_i+\frac{1}{2}h,y_*)$5.重复步骤2、3、4直到达到终止条件实验步骤:1.编写程序实现欧拉方法和改进的欧拉方法2.给定微分方程和初值条件3.设置步长和终止条件4.利用欧拉方法和改进的欧拉方法求解微分方程5.比较不同步长下的数值解与解析解的误差6.绘制误差-步长曲线,分析数值解的精度和收敛性实验结果:以一阶常微分方程$y'=3ty+t$为例,给定初值$y(0)=1$,取步长$h=0.1$进行数值求解。
利用欧拉方法求解微分方程得到的数值解如下:\begin{array}{cccc}t & y_{\text{exact}} & y_{\text{Euler}} & \text{误差} \\ \hline0.0&1.000&1.000&0.000\\0.1&1.035&1.030&0.005\\0.2&1.104&1.108&0.004\\0.3&1.212&1.217&0.005\\0.4&1.360&1.364&0.004\\0.5&1.554&1.559&0.005\\0.6&1.805&1.810&0.005\\0.7&2.131&2.136&0.005\\0.8&2.554&2.560&0.006\\0.9&3.102&3.107&0.006\\1.0&3.807&3.812&0.005\\\end{array}利用改进的欧拉方法求解微分方程得到的数值解如下:\begin{array}{cccc}t & y_{\text{exact}} & y_{\text{Improved Euler}} & \text{误差} \\\hline0.0&1.000&1.000&0.000\\0.1&1.035&1.035&0.000\\0.2&1.104&1.103&0.001\\0.3&1.212&1.211&0.001\\0.4&1.360&1.358&0.002\\0.5&1.554&1.552&0.002\\0.6&1.805&1.802&0.003\\0.7&2.131&2.126&0.005\\0.8&2.554&2.545&0.009\\0.9&3.102&3.086&0.015\\1.0&3.807&3.774&0.032\\\end{array}误差-步长曲线如下:实验结论:通过对比欧拉方法和改进的欧拉方法的数值解与解析解的误差,可以发现改进的欧拉方法具有更高的精度和收敛性。
微分方程实验报告参考模板
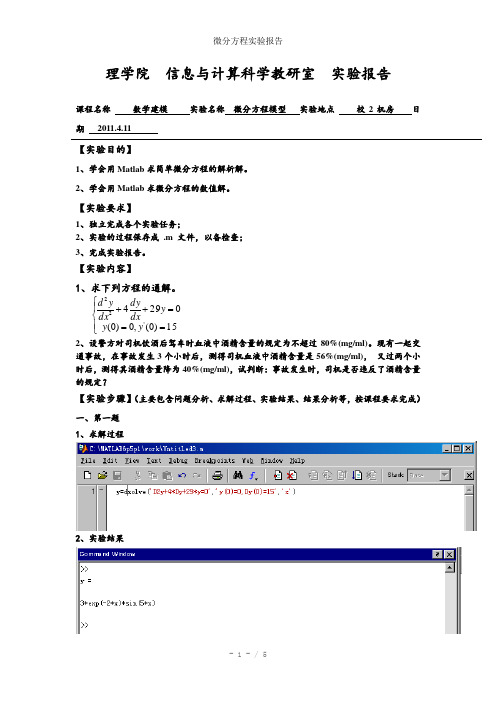
理学院 信息与计算科学教研室 实验报告课程名称 数学建模 实验名称 微分方程模型 实验地点 校2机房 日期 2011.4.11【实验目的】1、学会用Matlab 求简单微分方程的解析解。
2、学会用Matlab 求微分方程的数值解。
【实验要求】1、独立完成各个实验任务;2、实验的过程保存成 .m 文件,以备检查;3、完成实验报告。
【实验内容】1、求下列方程的通解。
2、设警方对司机饮酒后驾车时血液中酒精含量的规定为不超过80%(mg/ml)。
现有一起交通事故,在事故发生3个小时后,测得司机血液中酒精含量是56%(mg/ml), 又过两个小时后,测得其酒精含量降为40%(mg/ml),试判断:事故发生时,司机是否违反了酒精含量的规定?【实验步骤】(主要包含问题分析、求解过程、实验结果、结果分析等,按课程要求完成)一、第一题1、求解过程2、实验结果⎪⎩⎪⎨⎧===++15)0(,0)0(0294'22y y y dx dy dx y d二、第二题1、问题分析设在D时刻的酒精浓度为X,设t时刻的酒精浓度为X(t),在t到&t时刻内酒精浓度为X(t+&t)-X(t)-kX(t)kt;dx/dt=-kt通解:2、求解过程3、实验结果4、结果分析x(3)=c1*e^(-3k)=56x(5)=c1*e^(-5k)=40e^(2k)=7/5 k=0.17x0*e^(-3*0.17)=56 算得x0=93.2所以酒精含量超标了【实验小结】(主要包含实验心得等)因为有了前几次上机的经验,所以这次的实验没有那么盲目。
在做第一小题时,由于老师在课件上讲解过,所以我们很顺利的就完成了。
当拿到第二小题时,有了做第一题的基础,所以有了些须思路。
但是在做题的时候还是遇到了很多的问题,也包括一些小马虎的问题,例如少编写了一个分号或是括号等;在不断的编写,调试错误的过程中,最终把这两道题做了出来。
通过这次的实验,我对Matlab软件更加熟识,并学会了用Matlab求简单微分方程的解析解以及求微分方程的数值解。
微分方程数值方法实验报告

微分方程数值方法实验报告微分方程数值方法实验报告一、实验目的1、了解Euler法及梯形法的基本原理,能用其解决常微分方程初值问题,并把计算结果用图形表示出来。
2、理解4阶RK法基本计算步骤,能编程实现算法并解决相关常微分方程初值问题。
3、了解MATLAB主要功能和基本特征,熟悉MATLAB操作环境。
掌握MATLAB常用函数的使用以及图形处理。
二、实验题目对于初值问题u’=u,u(0)=1,在区间[0,1]上,用Euler法,梯形法及RK方法进行计算,取步长h=0.1,0.2,0.5,试比较(1)用同样步长,三种方法中哪一个精度最好;(2)对同一种方法一不同步长进行计算,哪一个结果最好。
三、实验内容1、步长为h=0.1时,用三种方法计算题目1)、MATLAB程序Euler法:>> a=0;b=1;h=0.1;N=(b-a)/h;y=zeros(N+1,1);y(1)=1;x=a:h:b;>> for i=2:N+1y(i)=y(i-1)+h*y(i-1);end求得:y = (1 1.1 1.21 1.331 1.4641 1.6105 1.7716 1.9487 2.1436 2.3579 2.5937)’梯形法:>> z=zeros(N+1,1);>> z(1)=1;>> for i=2:N+1v1=z(i-1);t=z(i-1)+h*v1;v2=t;z(i)=z(i-1)+h/2*(v1+v2);end1求得:z = (1 1.105 1.2205 1.3476 1.4873 1.641 1.8101 1.99622.2008 2.4258 2.6734)’RK法:>> w=zeros(N+1,1);>> w(1)=1;>> for i=2:N+1K1=w(i-1);K2=w(i-1)+K1*h/2;K3=w(i-1)+K2*h/2;K4=w(i-1)+K3*h;w(i)=w(i-1)+h*(K1+2*K2+2*K3+K4)/6;end求得:w =(1 1.1052 1.2214 1.3499 1.4918 1.6487 1.8221 2.01382.2255 2.4596 2.7183)’>> plot(x,y)>> hold on>> plot(x,z,':')>> plot(x,w,'--')>> plot(x,exp(x),'*')>> title('相同步长下三种方法与准确解的对比')>> legend('Euler法','梯形法','四阶RK法','准确解') 2)、图形对比相同步长下三种方法与准确解的对比2.82.62.42.221.81.6Euler法1.4梯形法四阶RK法1.2准确解1 00.10.20.30.40.50.60.70.80.9123)、结果分析由图得出三种方法中四阶RK法经确度最高,梯形法次之,Euler法精确度最差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本次实验,使我感觉到对流方程定解问题的难度相对于上次实验有点加大了。使用Lax-Wendroff格式来解决这个问题,我就知道了它的基本原理和一些基本的操作步骤,收获还是有的。
附Matlab程序代码:
首先定义函数
function f=IniU(x)
f=1+sin(2*pi*x);
然后
function u = peLaxW(a,dt,n,minx,maxx,M)
0.6909 1.2720 1.7492 1.9402 1.7721 1.3091 0.7280 0.2508
Columns 9 through 11
0.0598 0.2279 0.6909
实验结果分析:
通过调用程序计算 在 的近似解,由于n=11,当t=0.1时,M=5,调用u1= peLaxW(-2,0.02,11,0,1,5)计算得到t=0.1时的11个网格点对应的近似解。当t=0.5时,M=25, 故调用u2= peLaxW(-2,0.02,11,0,1,25)计算得到t=0.5时的11个网格点对应的近似解,它们的结果都是比较逼近的。并且在网格比小于等于1/2时,这个格式是比较稳定的。
Columns 9 through 11
0.9339 1.5258 1.9169
在Matlab命令窗口中输入命令:
u2 = peLaxW(-2,0.02,11,0,1,25)
运行程序得到实验结果为:
>> u2 = peLaxW(-2,0.02,11,0,1,25)
u2 =
Columns 1 through 8
format long;
h = (maxx-minx)/(n-1);
for j=1:(n+2*M)
u0(j) = IniU(minx+(j-M-1)*h);
end
u1 = u0;
for k=1:M
for i=k+1:n+2*M-k
u1(i) = dt*dt*a*a*(u0(i+1)-2*u0(i)+u0(i-1))/2/h/h - ...
其精确解为
采用Lax-Wendroff差分格式进行求解。
其数值差分格式为:
其中 为网格剖分的步长。
数值求解流程(图):
采用Matlab程序设计语言编程实现该问题的数值求解。取 轴方向的网格步长为 轴方向的网格步长为 , 为给定的常系数它的值为2。计算 在 的近似解。
首先定义函数
function f=IniU(x)
dt*a*(u0(i+1)-u0(i-1))/h/2+u0(i);
end
u0 = u1;
end
u = u1((M+1):(M+n));
format short;
指导教师评语:
签字:
年月日
THANKS !!!
致力为企业和个人提供合同协议,策划案计划书,学习课件等等
打造全网一站式需求
欢迎您的下载,资料仅供参考
湖南工程学院微分方程数值解法实验报告
专业班级
姓名
组别
同组实验人员
信息与计算科学10%%
实验日期
2011年11 月 21日
第2次实验
指导老师
杨继明
评分
实验名称
用Lax-Wendroff格式解对流方程的定解问题
实验目的熟悉掌握对流方程来自解问题的数值格式并程序实现实验原理与步骤:
考虑下列对流方程的定解问题:
f=1+sin(2*pi*x);
然后在Matlab命令窗口中输入命令:
u1= peLaxW(-2,0.02,11,0,1,5)
运行程序得到实验结果为:
>> u1= peLaxW(-2,0.02,11,0,1,5)
u1=
Columns 1 through 8
1.9169 1.9578 1.6328 1.0661 0.4742 0.0831 0.0422 0.3672
