一元二次方程解法练习题(四种方法)
(完整版)一元二次方程解法及其经典练习题
一元二次方程解法及其经典练习题方法一：直接开平方法（依据平方根的定义）平方根的定义：如果一个数 的平方等于a （ ），那么这个数 叫做a 的平方根即：如果 a x =2 那么 a x ±= 注意;x 可以是多项式一、 用直接开平方法解下列一元二次方程。
1.0142=-x 2、2)3(2=-x 3、()162812=-x 4．.25)1(412=+x5．(2x ＋1)2=(x －1)2． 6．(5－2x )2=9(x ＋3)2． 7．.063)4(22=--x方法二：配方法解一元二次方程1. 定义：把一个一元二次方程的左边配成一个 ，右边为一个 ，然后利用开平方数求解，这种解一元二次方程的方法叫做配方法。
2. 配方法解一元二次方程的步骤：（1） （2）（3） 4) (5)二、用配方法解下列一元二次方程。
1、.0662=--y y2、x x 4232=- 39642=-x x 、4、0542=--x x5、01322=-+x x6、07232=-+x x方法三：公式法1.定义：利用求根公式解一元二次方程的方法叫做公式法2.公式的推导：用配方法解方程ax 2＋bx ＋c = 0（a ≠0）解：二次项系数化为1，得 ，移项 ，得 ，配方, 得 ，方程左边写成平方式 ，∵a ≠0,∴4a 2 0,有以下三种情况：（1）当b 2-4ac>0时，=1x ， =2x（2）当b 2-4ac=0时，==21x x 。
（3）b 2-4ac<0时，方程根的情况为 。
3.由上可知，一元二次方程ax 2+bx+c=0（a ≠0）的根由方程的系数a 、b 、c 而定，因（1）式子ac b 42-叫做方程ax 2＋bx ＋c = 0（a ≠0）根的 ，通常用字母 “△” 表示。
当△ 0时， 方程ax 2+bx+c=0(a ≠0)有 实数根；当△ 0时， 方程ax 2+bx+c=0(a ≠0)有 实数根；当△ 0时， 方程ax 2+bx+c=0(a ≠0) 实数根。
一元二次方程知识点总结&练习
一元二次方程的解法【知识点归纳与总结】一、概念：一元二次方程的一般形式为：ax 2+bx+c=0, (a≠0)，它是只含一个未知数，并且未知数的最高次数是2的整式方程。
二、基本思路与方法: 解一元二次方程的基本思想方法是通过“降次”将它化为两个一元一次方程。
一元二次方程有四种解法：1、直接开平方法；2、配方法；3、公式法；4、因式分解法。
1 用直接开平方法解形如 (x-m)2=n (n≥0) 的方程，其解为x=m±.例1．解方程（1）75 (3x+1)2=7 （2）9x 2-24x+16=112．配方法：用配方法解方程ax 2+bx+c=0 (a≠0) 先将常数c 移到方程右边：ax 2+bx=-c 将二次项系数化为1：x 2+b a x=-ca方程两边分别加上一次项系数的一半的平方：x 2+b a x+(b 2a )2=-c a +(b2a)2方程左边成为一个完全平方式：(x+)2= 当b 2-4ac≥0时，x+=±∴ x= (这就是求根公式)例2．用配方法解方程 3x 2-4x-2=03．公式法：把一元二次方程化成一般形式，然后计算判别式△=b 2-4ac 的值，当b 2-4ac≥0时，把各项系数a, b, c 的值代入求根公式x=(b 2-4ac≥0)就可得到方程的根。
例3．用公式法解方程 2x 2-8x=-54．因式分解法：把方程变形为一边是零，把另一边的二次三项式分解成两个一次因式的积的形式，让两个一次因式分别等于零，得到两个一元一次方程，解这两个一元一次方程所得到的根，就是原方程的两个根。
这种解一元二次方程的方法叫做因式分解法。
例4．用因式分解法解下列方程：(1) (x+3)(x-6)=-8(2) 2x2+3x=0(3) 6x2+5x-50=0(4)x2-2(+)x+4=0小结：一般解一元二次方程，最常用的方法还是因式分解法，在应用因式分解法时，一般要先将方程写成一般形式，同时应使二次项系数化为正数。
初三一元二次方程的解法
一元二次方程的解法一、结构特殊的直接开平方法利用平方根的定义，直接开平方求一元二次方程的根的方法叫做直接开平方法．直接开平方法的理论依据是平方根的定义．形如2(0)x a a =≥或2()(0)ax b c c +=≥的方程可以直接运用“直接开平方法”求解．例1．解方程2256x =．解：∵2256x =，∴25616x =±=±．∴121616x x ==-，．例2．解方程2536x -=（）． 解：∵2536x -=（），∴56x -=±．∴12111x x ==-，． 有的方程可以通过整理，变形化为形如2(0)x a a =≥或2()(0)ax b c c +=≥的形式后，再采用直接开平方法来解．例3．解方程290x -=．解：∵290x -=，∴29x =．∴1233x x ==-，．例4．解方程21120x +-=（）． 解：∵21120x +-=（），∴2112x +=（）．∴123x +=±． ∴12231231x x =-=--，．通过以上例子，我们可以归纳出运用“直接开平方法”解一元二次方程的一般步骤： 1．将方程化为2(0)x a a =≥或2()(0)ax b c c +=≥的形式； 2．两边开平方，得x a =±或b cx a-±=． 这里要特别注意00a c ≥或≥的条件．若00a c <<或，则方程无实数根，只有当00a c ≥或≥时，方程才有实数根，而运用“直接开平方法”解应用题的关键是将方程化为2(0)x a a =≥或2()(0)ax b c c +=≥的形式．练习：用直接开平方法一元二次方程：1．9x 2-25＝0；2．(3x+2)2-4＝0； 4．(2x+3)2＝3(4x+3) ．二、法力无边的配方法把一个式子或一个式子的某一部分化成完全平方式或几个完全平方式的和、差形式，这种方法叫“配方法”．“直接开平方法”告我们根据完全平方公式2222a ab b a b ±+=±（）可以将一元二次方程化为形如2()(0)ax b c c +=≥的形式后求解，这就自然而然地导出了另一种解一元二次方程的解法 —— “配方法”．它的理论依据是完全平方公式2222a ab b a b ±+=±（）．例5．解方程2210x x +-=．解：方程两边都除以2，得21022x x +-=，移项，得2122x x +=， 配方，得2111216216x x ++=+，即219416x +=（）．开方，得12112x x ==-，．通过本例可以归纳出用“配方法”解一元二次方程的一般步骤： 1．方程两边同除以二次项系数，化二次项系数为1；2．移项，使方程左边为二次项和一次项，右边为常数项；3．配方，方程两边都加上一次项系数一半的平方，把原方程化为2()ax b c +=的形式； 4．若0c ≥，用“直接开平方法”解出；若0c <，则原方程无实数根即原方程无解． “配方法”是一种重要的数学方法，它不仅可应用于解一元二次方程，而且在数学的其它领域中也有着广泛的应用．练习：用配方法解一元二次方程：1．x 2-4x -3＝0； 2．6x 2+x ＝35；3．4x 2+4x+1＝7； 4．2x 2-3x -3＝0．三、神通广大的公式法公式法是解一元二次方程的一般方法，它是直接利用了“配方法”的结果，求根公式为224(40)2b b ac x b ac a-±-=-≥．例6．解方程28103x x +=．解：把该方程化为一般形式： 281030x x +-=．∵8103a b c ===-，，，22410483196b ac -=-⨯⨯-=（）， ∴2410196101422816b b ac x a -±--±-±===⨯．∴121342x x ==-，．通过本例可以看出，用公式法解一元二次方程的一般步骤是： 1．将方程化为一般形式：200ax bx c a ++=≠（）；2．正确确定a b c ，，的值；3．代入公式242b b acx a -±-=求解，若240b ac -≥则方程有实数根，若240b ac -<则方程无实数解即无解．练习：用公式法解一元二次方程：2．2x 2+7x -4＝0； 3 .2y 2 -y=5 4．3x 2+5(2x+1)=0四、简便易行的因式分解法因式分解法就是利用因式分解的手段，求出方程的解的方法，它是解一元二次方程的基本方法，它的理论依据是两个因式的积等于零的充分必要条件是这两个因式至少要有一个等于零，即0a b =，则00a b ==或，这种方法简便易行．是最常用的一种方法．例7．解方程23520x x --=．解：方程左边因式分解，得3120x x +-=（）（），∴31020x x +=-=，，∴12123x x =-=，．用因式分解法解一元二次方程的一般步骤是： 1．将方程的右边化为零；2．将方程的左边分解为两个一次因式的积； 3．令每个因式分别为零，得到两个一元一次方程； 4．解这两个一元一次方程，它们的解就是原方程的解．用因式分解法解一元二次方程的关键是： 1．要将方程右边化为零； 2．要熟练掌握因式分解的方法． 练习：用因式分解法解一元二次方程：1. )7(5)7(2+=+x x x2.223)(x 3)-(4x +=3．0822=--x x 4．06)23(2=---x x这四种方法既有区别又有联系．公式法比配方法简单，它直接由配方法导出的求根公式求解，但不如直接开平方法和因式分解法快捷，具体解方程时，要根据题目的特点，选择适当的方法求解．一般顺序为：先特殊后一般．直接开平方法→因式分解法→公式法．没有特别说明，一般不用配方法．遇到特殊结构或次数较高的方程，就需用到下面要讲的“换元法”．五、出奇制胜的换元法把一个数学式子或者其中的一部分看作一个整体，用一个中间变量去代替，从而达到繁为简，化难为易的目的，这种方法叫“换元法”，有些一元二次方程数式结构复杂，或次数较高，或字母个数过多，用常规的四种一元二次方程的解法计算既繁琐也困难，甚至根本无法求解，这时用“换元法”就会出奇制胜．例8．解方程25425430x x -+--=（）（）．解：设54x y -=，则原方程可化为2230y y +-=，130y y -+=（）（），1030y y -=+=或，∴13y y ==-或，即541543x x -=-=-或．∴12115x x ==，．例9． 解方程42440x x -+=．解：设2x y =，则原方程变为2440y y -+=，解之，得2y =．∴22x =，∴2x =±． 练习：用适当的方法解关于x 的方程1、095162=-+）（x 2、8)4(2=-x 3、8)32)(2(=++y y4、02x 3x 2=+-5、04x 3x 22=-+ 6、y 249y 162=+；7、0x 7)1x (52=-+ 8、（3 x-1）2-9x+3=4 9、（x-5）2+x 2=510、)7(5)7(2+=+x x x 11、01224=--x x 12、012222=--x x13、012)(8)(222=+---x x x x 14、02)32(3)32(2=++-+x xx x六、一元二次方程根的两个特性例1、先阅读，再填空解题：(1)方程：x 2-4x-12=0 的根是：x 1=6, x 2=-2，则x 1+x 2=4，x 1·x 2=-12； (2)方程2x 2-7x+3=0的根是：x 1=12, x 2=3，则x 1+x 2=72，x 1·x 2=32；(3)方程3x 2+6x-2=0的根是：x 1= , x 2= .则x 1+x 2= ，x 1·x 2= ； 根据以上（1）(2)(3)你能否猜出：如果关于x 的一元二次方程ax 2+bx+c=0（a ≠0且a 、b 、c 为常数）的两根为x 1、x 2，那么x 1+x 2、x 1x 2与系数a 、b 、c 有什么关系？请写出来你的猜想并说明理由。
一元二次方程解法练习题(四种方法)
一元二次方程解法练习题一、用直接开平方法解下列一元二次方程。
1、0142=-x2、2)3(2=-x3、()162812=-x二、 用配方法解下列一元二次方程。
1、.0662=--y y2、x x 4232=-3、9642=-x x三、 用公式解法解下列方程。
1、0822=--x x2、22314y y -=3、y y 32132=+4、01522=+-x x5、1842-=--x x6、02322=--x x四、 用因式分解法解下列一元二次方程。
1、x x 22=2、 x 2+4x -12=03、0862=+-x x4、03072=--x x五、用适当的方法解下列一元二次方程。
(选用你认为最简单的方法)1、()()513+=-x x x x2、x x 5322=-3、2260x y -+=4、01072=+-x x5、()()623=+-x x6、()()03342=-+-x x x7、()02152=--x 8、0432=-y y10、()()412=-+y y 11、()()1314-=-x x x 12、()025122=-+x13、22244a b ax x -=- 14、3631352=+x x 15、()()213=-+y y16、)0(0)(2≠=++-a b x b a ax 17、03)19(32=--+a x a x18、012=--x x 19 、02932=+-x x 20、02222=+-+a b ax x21、 22、030222=--x x 23、01752=+-x x24、1852-=-x x 25、3x 2+5(2x+1)=0 26、x x x 22)1)(1(=-+解答题：1、已知一元二次方程0132=-+-m x x .（1）若方程有两个不相等的实数根，求m 的取值范围.（2）若方程有两个相等的实数根，求此时方程的根2、已知方程2（m+1）x 2+4mx+3m=2，根据下列条件之一求m 的值．（1）方程有两个相等的实数根；（2）方程的一个根为0．3、无论m 为何值时，方程04222=---m mx x 总有两个不相等的实数根吗？给出答案并说明理由。
一元二次方程计算练习 (含答案)
一元二次方程计算练习1．解方程：（1）x2＝4x（因式分解法）；（2）2x2﹣4x﹣3＝0（公式法）．2．解下列方程：（1）x2﹣2x＝0；（2）x2﹣3x﹣4＝0．3．解方程：①x2﹣8x+12＝0；②x2﹣2x﹣8＝0．4．用适当的方法解下列方程：（1）x2﹣10x+16＝0；（2）2x（x﹣1）＝x﹣1．5．选用适当的方法解下列方程．（1）x2﹣4x﹣3＝0（2）5x（x+1）＝2（x+1）6．解方程（1）（x+1）2﹣25＝0（2）x2﹣4x﹣2＝07．（1）（x﹣1）2＝2（x﹣1）（2）2x2﹣5x﹣2＝08．解方程（1）x2﹣4x﹣4＝0（2）2（x+5）2＝x（x+5）9．解方程：（1）x2﹣6x﹣7＝0（2）（x+2）（x+3）＝110．解下列方程：（1）3x2﹣2x﹣1＝0（2）（x﹣1）2﹣16＝0 11．解方程：（1）2x2﹣16＝0；（2）2x2﹣3x﹣1＝0．12．解方程（1）（2x+3）2﹣81＝0；（2）y2﹣7y+6＝0．13．用合适的方法解下列方程．（1）x2﹣x﹣1＝0（2）2（x﹣1）2＝1﹣x．14．解方程：2x2+4x﹣3＝0．15．解方程：（1）x2+10x+9＝0（2）x2﹣x﹣＝0（3）3x2+6x﹣4＝0（4）4x2﹣6x﹣3＝0（5）x2+4x﹣9＝2x﹣11（6）x（x+4）＝8x+12．参考答案与试题解析1．解方程：（1）x2＝4x（因式分解法）；（2）2x2﹣4x﹣3＝0（公式法）．【分析】（1）根据因式分解的方法解方程即可；（2）根据公式法解方程即可．【解答】（1）x2＝4x，解：x2﹣4x＝0，x（x﹣4）＝0，∴x1＝0，x2＝4；（2）2x2﹣4x﹣3＝0，解：a＝2，b＝﹣4，c＝﹣3，代入求根公式，得：，∴，．【点评】此题考查了解一元二次方程﹣因式分解法、公式法，利用因式分解法解方程时，首先将方程右边化为0，左边化为积的形式，然后利用两数相乘积为0，两因式中至少有一个为0转化为两个一元一次方程来求解．2．解下列方程：（1）x2﹣2x＝0；（2）x2﹣3x﹣4＝0．【分析】（1）利用因式分解法把方程化为x＝0或x﹣2＝0，然后解一次方程即可；（2）利用因式分解法把方程化为x﹣4＝0或x+1＝0，然后解一次方程即可．【解答】解：（1）x（x﹣2）＝0，x＝0或x﹣2＝0，所以x1＝0，x2＝2；（2）（x﹣4）（x+1）＝0，x﹣4＝0或x+1＝0，所以x1＝4，x2＝﹣1．【点评】本题考查了解一元二次方程﹣因式分解法：因式分解法就是利用因式分解求出方程的解的方法，这种方法简便易用，是解一元二次方程最常用的方法．也考查了配方法解方程．3．解方程：①x2﹣8x+12＝0；②x2﹣2x﹣8＝0．【分析】利用因式分解法求解可得．【解答】解：①∵x2﹣8x+12＝0，∴（x﹣2）（x﹣6）＝0，则x﹣2＝0或x﹣6＝0，解得x＝2或x＝6；②∵x2﹣2x﹣8＝0，∴（x+2）（x﹣4）＝0，则x+2＝0或x﹣4＝0，解得x＝﹣2或x＝4．【点评】本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．4．用适当的方法解下列方程：（1）x2﹣10x+16＝0；（2）2x（x﹣1）＝x﹣1．【分析】（1）根据因式分解法节即可求出答案．（2）根据因式分解法即可求出答案．【解答】解：（1）∵x2﹣10x+16＝0，∴（x﹣2）（x﹣8）＝0，∴x＝2或x＝8．（2）∵2x（x﹣1）＝x﹣1，∴（x﹣1）（2x﹣1）＝0，∴x＝1或x＝．【点评】本题考查一元二次方程，解题的关键是熟练运用一元二次方程的解法，本题属于基础题型．5．选用适当的方法解下列方程．（1）x2﹣4x﹣3＝0（2）5x（x+1）＝2（x+1）【分析】（1）根据配方法即可求出答案．（2）根据因式分解法即可求出答案．【解答】解：（1）∵x2﹣4x﹣3＝0，∴x2﹣4x+4＝7，∴（x﹣2）2＝7，∴x1＝2+，x2＝2﹣．（2）∵5x（x+1）＝2（x+1），∴（5x﹣2）（x+1）＝0，∴x1＝，x2＝﹣1．【点评】本题考查一元二次方程，解题的关键是熟练运用一元二次方程的解法，本题属于基础题型．6．解方程（1）（x+1）2﹣25＝0（2）x2﹣4x﹣2＝0【分析】（1）利用直接开平方法解出方程；（2）先求出一元二次方程的判别式，再解出方程．【解答】解：（1）（x+1）2﹣25＝0，（x+1）2＝25，x+1＝±5，x＝±5﹣1，x1＝4，x2＝﹣6；（2）x2﹣4x﹣2＝0，∵a＝1，b＝﹣4，c＝﹣2，∴Δ＝b2﹣4ac＝（﹣4）2﹣4×1×（﹣2）＝24＞0，∴x＝＝2±，即x1＝2+，x2＝2﹣．【点评】本题考查的是一元二次方程的解法，掌握直接开平方法、公式法解一元二次方程的一般步骤是解题的关键．7．（1）（x﹣1）2＝2（x﹣1）（2）2x2﹣5x﹣2＝0【分析】（1）根据一元二次方程的解法即可求出答案．（2）根据一元二次方程的解法即可求出答案．【解答】解：（1）∵（x﹣1）2＝2（x﹣1），∴（x﹣1）2﹣2（x﹣1）＝0，∴（x﹣1）（x﹣1﹣2）＝0，∴x﹣1＝0或x﹣1﹣2＝0，∴x1＝1，x2＝3．（2）∵2x2﹣5x﹣2＝0，∴a＝2，b＝﹣5，c＝﹣2，∴△＝25﹣4×2×（﹣2）＝41＞0，∴x＝，∴x1＝，x2＝．【点评】本题考查一元二次方程，解题的关键是熟练运用一元二次方程的解法，本题属于基础题型．8．解方程（1）x2﹣4x﹣4＝0（2）2（x+5）2＝x（x+5）【分析】（1）根据配方法即可解方程；（2）根据因式分解法解方程即可．【解答】解：（1）x2﹣4x+4＝8（x﹣2）2＝8x﹣2＝∴x1＝2+2，x2＝2﹣2；（2）2（x+5）2﹣x（x+5）＝0（x+5）（2x+10﹣x）＝0x+5＝0或x+10＝0∴x1＝﹣5，x2＝﹣10．【点评】本题考查了因式分解法和配方法解一元二次方程，解决本题的关键是掌握因式分解法和配方法．9．解方程：（1）x2﹣6x﹣7＝0（2）（x+2）（x+3）＝1【分析】（1）利用因式分解法解方程；（2）先把方程化为一般式，然后利用求根公式法解方程．【解答】解：（1）（x﹣7）（x+1）＝0，x﹣7＝0或x+1＝0，所以x1＝7，x2＝﹣1；（2）x2+5x+5＝0，△＝52﹣4×5＝5，x＝，所以x1＝，x2＝．【点评】本题考查了解一元二次方程﹣因式分解法：因式分解法就是利用因式分解求出方程的解的方法，这种方法简便易用，是解一元二次方程最常用的方法．也考查了配方法．10．解下列方程：（1）3x2﹣2x﹣1＝0（2）（x﹣1）2﹣16＝0【分析】根据一元二次方程的解法即可求出答案．【解答】解：（1）∵3x2﹣2x﹣1＝0，∴（x﹣1）（3x+1）＝0，∴x＝1或x＝；（2）∵（x﹣1）2﹣16＝0，∴（x﹣1）2＝16，∴x﹣1＝±4，∴x＝5或x＝﹣3【点评】本题考查一元二次方程，解题的关键是熟练运用一元二次方程的解法，本题属于基础题型．11．解方程：（1）2x2﹣16＝0；（2）2x2﹣3x﹣1＝0．【分析】（1）根据直接开方法即可求出答案；（2）根据公式法即可求出答案．【解答】解：（1）∵2x2﹣16＝0，∴x2＝8，∴x＝±2，∴x1＝﹣2，x2＝2．（2）∵2x2﹣3x﹣1＝0，∴a＝2，b＝﹣3，c＝﹣1，∴△＝9﹣4×2×（﹣1）＝17＞0，∴x＝，∴x1＝，x2＝【点评】本题考查一元二次方程，解题的关键是熟练运用一元二次方程的解法，本题属于基础题型．12．解方程（1）（2x+3）2﹣81＝0；（2）y2﹣7y+6＝0．【分析】（1）先变形为（2x+3）2＝81，然后利用直接开平方法解方程；（2）利用因式分解法解方程．【解答】解：（1）（2x+3）2＝81，2x+3＝±9，所以x1＝3，x2＝﹣6；（2）（y﹣1）（y﹣6）＝0，y﹣1＝0或y﹣6＝0，所以y1＝1，y2＝6．【点评】本题考查了解一元二次方程﹣因式分解法：就是先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．也考查了直接开平方法解一元二次方程．13．用合适的方法解下列方程．（1）x2﹣x﹣1＝0（2）2（x﹣1）2＝1﹣x．【分析】（1）直接利用公式法解方程得出答案；（2）直接利用提取公因式法分解因式进而解方程得出答案．【解答】解：（1）x2﹣x﹣1＝0Δ＝b2﹣4ac＝1+4＝5＞0，则x＝，故x1＝，x2＝；（2）2（x﹣1）2＝1﹣x2（1﹣x）2＝1﹣x，则2（1﹣x）2﹣（1﹣x）＝0，故（1﹣x）[2（1﹣x）﹣1]＝0，解得：x1＝1，x2＝．【点评】此题主要考查了公式法以及因式分解法解方程，熟练掌握解方程的方法是解题关键．14．解方程：2x2+4x﹣3＝0．【分析】先计算判别式的值，然后根据求根公式解方程．【解答】解：△＝42﹣4×2×（﹣3）＝40＞0，x＝＝，所以x1＝，x2＝．【点评】本题考查了解一元二次方程﹣公式法：用求根公式解一元二次方程的方法是公式法．15．解方程：（1）x2+10x+9＝0（2）x2﹣x﹣＝0（3）3x2+6x﹣4＝0（4）4x2﹣6x﹣3＝0（5）x2+4x﹣9＝2x﹣11（6）x（x+4）＝8x+12．【分析】（1）先分解因式，即可得出两个一元一次方程，求出方程的解即可；（2）求出b2﹣4ac的值，代入公式求出即可；（3）求出b2﹣4ac的值，代入公式求出即可；（4）求出b2﹣4ac的值，代入公式求出即可；（5）求出b2﹣4ac的值，即可得出答案；（6）整理后分解因式，即可得出两个一元一次方程，求出方程的解即可．【解答】解：（1）x2+10x+9＝0，（x+1）（x+9）＝0，x+1＝0，x+9＝0，x1＝﹣1，x2＝﹣9；（2）x2﹣x﹣＝0，b2﹣4ac＝（﹣1）2﹣4×1×（﹣）＝8，x＝，x1＝，x2＝；（3）3x2+6x﹣4＝0，b2﹣4ac＝62﹣4×3×（﹣4）＝84，x＝，x1＝，x2＝；（4）4x2﹣6x﹣3＝0，b2﹣4ac＝（﹣6）2﹣4×4×（﹣3）＝84，x＝，x1＝，x2＝；（5）x2+4x﹣9＝2x﹣11，x2+2x+2＝0，b2﹣4ac＝22﹣4×1×2＜0，此方程无解；（6）x（x+4）＝8x+12，整理得：x2﹣4x﹣12＝0，（x﹣6）（x+2）＝0，x﹣6＝0，x+2＝0，x1＝6，x2＝﹣2．【点评】本题考查了解一元二次方程的应用，能选择适当的方法解一元二次方程是解此题的关键，难度适中．。
1.2一元二次方程的解法(四)(解析版)
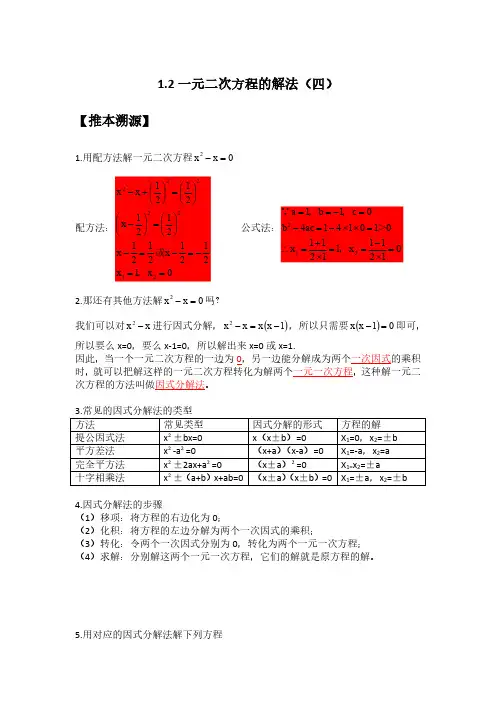
1.2一元二次方程的解法（四）【推本溯源】1.用配方法解一元二次方程0x x 2=-2.那还有其他方法解0x x 2=-吗？我们可以对x x 2-进行因式分解，()1x x x x 2-=-，所以只需要()01x x =-即可，所以要么x=0，要么x-1=0，所以解出来x=0或x=1.因此，当一个一元二次方程的一边为0，另一边能分解成为两个一次因式的乘积时，就可以把解这样的一元二次方程转化为解两个一元一次方程，这种解一元二次方程的方法叫做因式分解法。
3.常见的因式分解法的类型方法常见类型因式分解的形式方程的解提公因式法x ²±bx=0x （x ±b ）=0X 1=0，x 2=±b 平方差法x ²-a ²=0（x+a ）（x-a ）=0X 1=-a ，x 2=a 完全平方法x ²±2ax+a ²=0（x ±a ）²=0X 1=x 2=±a十字相乘法x ²±（a+b ）x+ab=0（x ±a ）（x ±b ）=0X 1=±a ，x 2=±b4.因式分解法的步骤（1）移项：将方程的右边化为0；（2）化积：将方程的左边分解为两个一次因式的乘积；（3）转化：令两个一次因式分别为0，转化为两个一元一次方程；（4）求解：分别解这两个一元一次方程，它们的解就是原方程的解。
5.用对应的因式分解法解下列方程（1）（提公因式法）x x 32=（2）()（平方差法）091x 2=-+4x 2x 21-==，（3）()（完全平方法））（011x 21x 2=+---0x x 21==（4）（十字相乘法）03x 2x 2=--1x 3x 21-==，【解惑】【摩拳擦掌】【答案】10【分析】根据给定的图找出其中的规律，列一元二次方程，求解即可．【详解】解：第1个图有7个棋子，第2个图有11个棋子，第3个图有17个棋子，第图有25个棋子，第5个图有35个棋子，⋯⋯第n 个图有215()()5n n n n ++=++个棋子，【详解】（1）解：260x x --=，()()320x x -+=，∴30x -=或20x +=，∴13x =，22x =-；（2）解∶()221180x --=，()219x -=，∴13x -=±，∴14x =，22x =-．【点睛】此题考查利用因式分解法和直接开平方法解一元二次方程，解题的关键是熟练掌握解一元二次方程的方法．10．（2023春·黑龙江哈尔滨·八年级校考期中）解下列方程：(1)2450x x +-=(2)()()22452x x -=-【答案】(1)11x =，25x =-(2)13x =，21x =【分析】（1）利用因式分解法解方程；（2）先移项得到()()224520x x ---=，然后利用因式分解法解方程．【详解】（1）2450x x +-=()()150x x -+=∴10x -=或50x +=∴解得11x =，25x =-；（2）22(4)(52)x x -=-()()224520x x ---=()()4524520x x x x --+-+-=【知不足】【详解】解：∵分式21x x x --的值为0，∴2010x x x ⎧-=⎨-≠⎩，解得0x =，故选A ．【点睛】本题主要考查了分式值为0的条件，熟知分式值为0的条件是分子为0，分母不为0是解题的关键．2．（2023·全国·九年级假期作业）若关于x 的一元二次方程()230x k x k +++=的一个根是2-，则另一个根是()A ．1B ．1-C ．3-D ．2【答案】A 【分析】将2x =-代入方程得：()4230k k -++=，解得：2k =-，再把2k =-代入原方程求解．【详解】解：将2x =-代入方程得：()4230k k -++=，解得：2k =-，∴原方程为：220x x +-=，则()2(1)0x x +-=，解得：2x =-或1x =，∴另一个根为1．故选：A ．【点睛】本题考查了一元二次方程的根，因式分解法解一元二次方程，属于基础题．3．（2023·辽宁沈阳·沈阳市第一二六中学校考三模）方程()()230x x -+=的解是（）A ．2x =B ．3x =-C ．12x =，23x =D ．12x =，23x =-【答案】D【分析】直接利用因式分解法解一元二次方程即可．【详解】解：()()230x x -+=，可得：20x -=或30x +=，【答案】27【分析】过C作CG得四边形ABCG为正方形，证明=，从而证明BE GF在直角梯形ABCD中， ∴∠=∠=︒，A B90=又90CGA，AB BC∠=︒∴四边形ABCG为正方形．键．【一览众山小】故选：D ．【点睛】本题考查了新定义，一元二次方程的解法，理解题意，得到方程并求解是解决本题的关键．3．（2022秋·广东茂名·八年级校联考期末）如图，直线:l y x m =-+交x 轴于点A ，交y 轴于点()0,3B ，点(),5P n 在直线l 上，已知M 是x 轴上的动点，当以A ，P ，M 为顶点的三角形是直角三角形时，点M 的坐标为（）A ．()2,0-B ．()5,0-C ．()2,0-或()7,0-D ．()2,0-或()5,0-【答案】C 【分析】根据题意求出A 、P 坐标，然后根据等腰直角三角形的性质进行分类讨论求解即可．【详解】解：由题意，将()0,3B 代入直线:l y x m =-+，得：3m =，∴直线:3l y x =-+，令0y =，得：3x =，则A 点坐标为()3,0A ，将(),5P n 代入3y x =-+，得：2n =-，∴P 点坐标为()2,5P -，∵3OA OB ==，90BOA ∠=︒，∴45BAO ∠=︒，设(),0M a ，①若90AMP ∠=︒，则 AMP 为等腰直角三角形，MP MA =，∵5MP =，3MA a =-，∴35a -=，解得：2a =-，∴M 点的坐标为()12,0M -；②若90APM ∠=︒，则此时，点A 和点M 关于点∴322a +=-，解得：③∵M 是x 轴上的动点，∴45PAM ∠=︒或135︒，不存在综上，满足条件的点M 的坐标为A ．(3,0)-B ．【答案】Dx A ．()4,4B ．【答案】D【分析】根据(0k y k x =≠()2,E x x +，代入解析式计算即可．k（1）四边形DCEB的面积为___________（2）k的值为___________；（3）若A，B两点的横坐标恰好是方程距离为___________．【答案】183/223∴1812232OAE S h ⨯==⨯⋅ =123【答案】8∵正方形ABCD 的边长为1∴33=1=88ABFE S ⨯四边形，设CF x =，则DH x =，则∴()1=2ABFE AE BF S +⨯四边形即()131128AE x +-⨯=根据图中棋子的排列规律解决下列问题：(1)第4个图中有__________颗棋子，第5个图中有(2)写出你猜想的第n个图中棋子的颗数（用含n【规律发现】请用含n的式子填空：(1)第n个图案中“”的个数为；12⨯★”的个数可表示为“”个，个，9个，12个，个，”的个数可表示为个，（舍去）或。
一元二次方程解法及其配套练习-精心--方法全面-例题经典
一元二次方程解法及其配套练习定义：只含有一个未知数（一元），并且未知数的最高次数是2（二次）的方程，叫做一元二次方程．一般地，任何一个关于x的一元二次方程，经过整理，都能化成如下形式ax2+bx+c=0（a≠0）．这种形式叫做一元二次方程的一般形式．一个一元二次方程经过整理化成ax2+bx+c=0（a≠0）后，其中ax2是二次项，a是二次项系数；bx 是一次项，b是一次项系数；c是常数项．解法一: ——直接开方法适用围：可解部分一元二次方程直接开平方法就是用直接开平方求解一元二次方程的方法。
用直接开平方法解形如(x-m)^2=n (n≥0)的方程，其解为x=m±√n我们已经讲了x2=9，根据平方根的意义，直接开平方得x=±3，如果x换元为2t+1，即（2t+1）2=9，我们也可以用直接开方法来解方程。
例1：解方程：(1)(2x-1) 2=5 (2)x 2+6x+9=2 (3)x 2-2x+4=-1分析：很清楚，x2+4x+4是一个完全平方公式，那么原方程就转化为（x+2）2=1．解：(2)由已知，得：（x+3）2=2直接开平方，得：x+3=即所以，方程的两根x1，x2例2．市政府计划2年将人均住房面积由现在的10m2提高到14.4m，求每年人均住房面积增长率．分析：设每年人均住房面积增长率为x．•一年后人均住房面积就应该是10+•10x=10（1+x）；二年后人均住房面积就应该是10（1+x）+10（1+x）x=10（1+x）2解：设每年人均住房面积增长率为x，则：10（1+x）2=14.4（1+x）2=1.44直接开平方，得1+x=±1.2即1+x=1.2，1+x=-1.2所以，方程的两根是x1=0.2=20%，x2=-2.2因为每年人均住房面积的增长率应为正的，因此，x2=-2.2应舍去．所以，每年人均住房面积增长率应为20%．例3．如图，在△ABC中，∠B=90°，点P从点B开始，沿AB边向点B以1cm/s•的速度移动，点Q从点B开始，沿BC边向点C以2cm/s的速度移动，如果AB=6cm，BC=12cm，•P、Q都从B点同C时出发，几秒后△PBQ的面积等于8cm2？解：设x秒后△PBQ的面积等于8cm2 则PB=x，BQ=2x依题意，得：12x·2x=8x2=8根据平方根的意义，得x=±即x1，x2可以验证，和都是方程12x·2x=8的两根，但是移动时间不能是负值．所以PBQ的面积等于8cm2．例4．某公司一月份营业额为1万元，第一季度总营业额为3.31万元，求该公司二、三月份营业额平均增长率是多少？分析：设该公司二、三月份营业额平均增长率为x，•那么二月份的营业额就应该是（1+x），三月份的营业额是在二月份的基础上再增长的，应是（1+x）2．解：设该公司二、三月份营业额平均增长率为x．那么1+（1+x）+（1+x）2=3.31把（1+x）当成一个数，配方得：（1+x+12）2=2.56，即（x+32）2=2．56x+32=±1.6，即x+32=1.6，x+32=-1.6方程的根为x1=10%，x2=-3.1因为增长率为正数，所以该公司二、三月份营业额平均增长率为10%．归纳小结：共同特点：把一个一元二次方程“降次”，转化为两个一元一次方程．•我们把这种思想称为“降次转化思想”．由应用直接开平方法解形如x2=p（p≥0），那么x=转化为应用直接开平方法解形如（mx+n）2=p（p≥0），那么mx+n=p＜0则方程无解配套练习题一、选择题1．若x2-4x+p=（x+q）2，那么p、q的值分别是（）．A．p=4，q=2 B．p=4，q=-2 C．p=-4，q=2 D．p=-4，q=-22．方程3x2+9=0的根为（）．A．3 B．-3 C．±3 D．无实数根3．用配方法解方程x2-23x+1=0正确的解法是（）．A．（x-13）2=89，x=13B．（x-13）2=-89，原方程无解C ．（x-23）2=59，x 1=23x 2 D ．（x-23）2=1，x 1=53，x 2=-13二、填空题1．若8x 2-16=0，则x 的值是_________．2．如果方程2（x-3）2=72，那么，这个一元二次方程的两根是________．3．如果a 、b 2-12b+36=0，那么ab 的值是_______．三、综合提高题1．解关于x 的方程（x+m ）2=n ．2．某农场要建一个长方形的养鸡场，鸡场的一边靠墙（墙长25m ），•另三边用木栏围成，木栏长40m ．（1）鸡场的面积能达到180m 2吗？能达到200m 吗？（2）鸡场的面积能达到210m 2吗？3．在一次手工制作中，某同学准备了一根长4米的铁丝，由于需要，现在要制成一个矩形方框，并且要使面积尽可能大，你能帮助这名同学制成方框，•并说明你制作的理由吗？解法二——配方法适用围：可解全部一元二次方程引例：要使一块矩形场地的长比宽多6m ，并且面积为16m 2,场地的长和宽各是多少？ 列出方程化简后得：x 2+6x-16=0 x 2+6x-16=0移项→x 2+6x=16两边加（6/2）2使左边配成x 2+2bx+b 2的形式 → x 2+6x+32=16+9左边写成平方形式 → （x+3）2=25 降次→x+3=±5 即 x+3=5或x+3=-5 解一次方程→x 1=2，x 2= -8可以验证：x 1=2，x 2= -8都是方程的根,但场地的宽不能使负值，所以场地的宽为2m ，常为8m. 像上面的解题方法，通过配成完全平方形式来解一元二次方程的方法，叫配方法． 可以看出，配方法是为了降次，把一个一元二次方程转化为两个一元一次方程来解．配方法解一元二次方程的一般步骤：(1)现将已知方程化为一般形式；（2）化二次项系数为1；（3）常数项移到右边； （4）方程两边都加上一次项系数的一半的平方，使左边配成一个完全平方式；（5）变形为(x+p)2=q 的形式，如果q ≥0，方程的根是x=-p ±√q ；如果q ＜0,方程无实根．用配方法解一元二次方程小口诀 二次系数化为一 常数要往右边移 一次系数一半方两边加上最相当例1．用配方法解下列关于x的方程（1）x2-8x+1=0 （2）x2-2x-12=0分析：（1）显然方程的左边不是一个完全平方式，因此，要按前面的方法化为完全平方式；（2）同上．解：略例2．如图，在Rt△ACB中，∠C=90°，AC=8m，CB=6m，点P、Q同时由A，B•两点出发分别沿AC、BC方向向点C匀速移动，它们的速度都是1m/s，•几秒后△PCQ•的面积为Rt△ACB面积的一半．分析：设x秒后△PCQ的面积为Rt△ABC面积的一半，△PCQ也是直角三角形．•根据已知列出等式．解：设x秒后△PCQ的面积为Rt△ACB面积的一半．根据题意，得：12（8-x）（6-x）=12×12×8×6整理，得：x2-14x+24=0（x-7）2=25即x1=12，x2=2x1=12，x2=2都是原方程的根，但x1=12不合题意，舍去．所以2秒后△PCQ的面积为Rt△ACB面积的一半．例3．解下列方程（1）2x2+1=3x （2）3x2-6x+4=0 （3）（1+x）2+2（1+x）-4=0分析：我们已经介绍了配方法，因此，我们解这些方程就可以用配方法来完成，即配一个含有x的完全平方．解：略例4．用配方法解方程（6x+7）2（3x+4）（x+1）=6分析：因为如果展开（6x+7）2，那么方程就变得很复杂，如果把（6x+7）看为一个数y，那么（6x+7）2=y2，其它的3x+4=12（6x+7）+12，x+1=16（6x+7）-16，因此，方程就转化为y•的方程，像这样的转化，我们把它称为换元法．解：设6x+7=y则3x+4=12y+12，x+1=16y-16依题意，得：y2（12y+12）（16y-16）=6去分母，得：y2（y+1）（y-1）=72 y2（y2-1）=72，y4-y2=72（y2-12）2=2894y2-12=±172y2=9或y2=-8（舍）∴y=±3当y=3时，6x+7=3 6x=-4 x=-2 3当y=-3时，6x+7=-3 6x=-10 x=-5 3所以，原方程的根为x1=-23，x2=-53CAQP例5. 求证:无论y 取何值时,代数式-3 y 2+8y-6恒小于0. 解：略配套练习题一、选择题1．配方法解方程2x 2-43x-2=0应把它先变形为（ ）． A ．（x-13）2=89 B ．（x-23）2=0C ．（x-13）2=89D ．（x-13）2=1092．下列方程中，一定有实数解的是（ ）．A ．x 2+1=0 B ．（2x+1）2=0 C ．（2x+1）2+3=0 D ．（12x-a ）2=a 3．已知x 2+y 2+z 2-2x+4y-6z+14=0，则x+y+z 的值是（ ）． A ．1 B ．2 C ．-1 D ．-24．将二次三项式x 2-4x+1配方后得（ ）．A ．（x-2）2+3B ．（x-2）2-3C ．（x+2）2+3D ．（x+2）2-35．已知x 2-8x+15=0，左边化成含有x 的完全平方形式，其中正确的是（ ）．A ．x 2-8x+（-4）2=31B ．x 2-8x+（-4）2=1C ．x 2+8x+42=1D ．x 2-4x+4=-116．如果mx 2+2（3-2m ）x+3m-2=0（m ≠0）的左边是一个关于x 的完全平方式，则m 等于（ ）． A ．1 B ．-1 C ．1或9 D ．-1或9二、填空题1．方程x 2+4x-5=0的解是________．2．代数式2221x x x ---的值为0，则x 的值为________．3．已知（x+y ）（x+y+2）-8=0，求x+y 的值，若设x+y=z ，则原方程可变为_______，所以求出z 的值即为x+y 的值，所以x+y 的值为______．4．如果x 2+4x-5=0，则x=_______．5．无论x 、y 取任何实数，多项式x 2+y 2-2x-4y+16的值总是_______数．6．如果16（x-y ）2+40（x-y ）+25=0，那么x 与y 的关系是________． 三、综合提高题1．用配方法解方程．（1）9y 2-18y-4=0 （2）x 2x2．已知三角形两边长分别为2和4，第三边是方程x 2-4x+3=0的解，求这个三角形的周长．3．如果x 2-4x+y 2，求（xy ）z的值．4．新华商场销售某种冰箱，每台进货价为2500•元，•市场调研表明：•当销售价为2900元时，平均每天能售出8台；而当销售价每降50元时，平均每天就能多售出4台，商场要想使这种冰箱的销售利润平均每天达5000元，每台冰箱的定价应为多少元？ 5．已知：x 2+4x+y 2-6y+13=0，求222x yx y-+的值．6．某商场销售一批名牌衬衫，平均每天可售出20件，每件赢利40元，•为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当降价措施，经调查发现，•如果每件衬衫每降价一元，商场平均每天可多售出2件． ①若商场平均每天赢利1200元，每件衬衫应降价多少元？②每件衬衫降价多少元时，商场平均每天赢利最多？请你设计销售方案．解法三——公式法适用围：可解全部一元二次方程首先，要通过Δ=b 2-4ac 的根的判别式来判断一元二次方程有几个根 1.当Δ=b 2-4ac<0时 x 无实数根（初中）2.当Δ=b 2-4ac=0时 x 有两个相同的实数根 即x1=x2 3.当Δ=b 2-4ac>0时 x 有两个不相同的实数根当判断完成后，若方程有根可根属于2、3两种情况方程有根则可根据公式：求根公式的推导用配方法解方程（1） ax 2－7x+3 =0 (2)a x 2+bx+3=0(3)如果这个一元二次方程是一般形式ax 2+bx+c=0（a ≠0），你能否用上面配方法的步骤求出它们的两根，请同学独立完成下面这个问题．问题：已知ax 2+bx+c=0（a ≠0），试推导它的两个根x 1=2b a -+，x 2=2b a--(这个方程一定有解吗?什么情况下有解？)分析：因为前面具体数字已做得很多，我们现在不妨把a 、b 、c•也当成一个具体数字，根据上面的解题步骤就可以一直推下去．解：移项，得：ax 2+bx=-c二次项系数化为1，得x 2+b a x=-c a 配方，得：x 2+b a x+（2b a ）2=-c a +（2b a）2 即（x+2b a）2=2244b aca -∵4a 2>0，4a2＞0,当b 2-4ac ≥0时2244b aca-≥0∴（x+2b a）2)2直接开平方，得：x+2ba = 即∴x 1x 2 由上可知，一元二次方程ax 2+bx+c=0（a ≠0）的根由方程的系数a 、b 、c 而定，因此：（1）解一元二次方程时，可以先将方程化为一般形式ax 2+bx+c=0，当b 2-4ac ≥0时，将a 、b 、c 代入式子(公式所出现的运算，恰好包括了所学过的六中运算，加、减、乘、除、乘方、开方，这体现了公式的统一性与和谐性。
(完整版)解一元二次方程练习题(配方法)(最新整理)
(7) 5x 2 －3x+2 =0
(8) 7x 2 －4x－3 =0
(9) -x 2 -x+12 =0
(10) x 2 －6x+9 =0
韦达定理：对于一元二次方程 ax2 bx c 0(a 0) ，如果方程有两个实数根 x1, x2 ，那么
x1
x2
b a
,
x1x2
c a
说明：（1）定理成立的条件 0
2．已知 x1，x2 是方程 2x2－7x＋4＝0 的两根，则 x1＋x2＝
，x1·x2＝
，
（x1－x2）2＝
1
3．已知方程 2x2－3x+k=0 的两根之差为 2 ，则 k=
;
2
4．若方程 x2+(a2－2)x－3=0 的两根是 1 和－3，则 a=
;
5．若关于 x 的方程 x2+2(m－1)x+4m2=0 有两个实数根，且这两个根互为倒数，那么 m 的值为
（2）注意公式重
x1
x2
b a
的负号与
b
的符号的区别
根系关系的三大用处
（1）计算对称式的值
例 若 x1, x2 是方程 x2 2x 2007 0 的两个根，试求下列各式的值：
(1) x12 x22 ；
(2) 1 1 ； x1 x2
(3) (x1 5)(x2 5) ；
(4) | x1 x2 | ．
25、 5x2 7x 1 0
26、 5x2 8x 1
27、 x2 2mx 3nx 3m2 mn 2n2 0
28、3x2+5(2x+1)=0
29、 (x 1)(x 1) 2 2x
30、 3x2 4x 1
解一元二次方程练习题(配方法)
解一元二次方程练习题(配方法)C . -2+/10D . 2-7109.不论X 、y 为什么实数，代数式x 2+y 2+2x-4y+7的值()10.用配方法解下列方程:2(1) 3X -5X =2. 11用配方法求解下列问题2(1)求2X -7X +2的最小值；(2)求-3X 2+5X +1的最大值。
1用适当的数填空: ①、X 2+6X+=(X+ )2; ②、X 2 — 5X+=(X — )2; 2 ③、X + X+ =(X+ )2; ④、X 2 — 9x+ =(X — )22. __________________________________________ 将二次三项式2X 2-3X -5进行配方，其结果为 ____________________ . 3. 已知4x 2-ax+1可变为(2x-b ) 2的形式，贝U ab= ________ . 4. 将一元二次方程X 2-2X -4=0用配方法化成(x+a ) 2=b 的形式为,?所以方程的根为5.若x 2+6x+m 2是一个完全平方式，则 m 的值是() D .以上都不对 6.用配方法将二次三项式a 2-4a+5变形，结果是( A . (a-2) 2+1 B . (a+2) 2-1 C . (a+2) 2+1A . 3B . -3C . ± 3D . (a-2) 2-1 7. 把方程X +3=4X 配方，得() 2 2 2 A . (X-2) =7 B . (X +2) 2=21 C . (X -2) 2=1 8. 用配方法解方程X 2+4X =10的根为()2 D . (X +2) 2=2 A .总不小于2 B .总不小于7 C .可为任何实数D .可能为负数2(2) X +8X =91 2)一 X -X -4=0(3) X 2+12X -15=0'元二次方程解法练习题一、用直接开平方法解下列一元二次方程。
1、4x2—1=02、（X -3）2=2 （X-1 f=524、81（x-2）2 =16用配方法解下列一元二次方程。
一元二次方程的解法练习
一元二次方程的解法练习例1、解下列方程：（1）9x 2－25 =0 ； （2）21（x +3）2 =8 ； （3）4（x －2）2－36 =0；例2、解下列方程：（1）（X －2）2 =（2X +3）2 ； （2）4（3X －1）2－9（3X +1）2 =0 。
例3、用配方法解下列方程：（1）x 2－12x －9964 =0 ； （2）2x 2 +3 =7x 。
例4、求证下列多项式的值恒大于零：（1）2x 2－4x + 7 ； （2）x 2 +2mx +2m 2 +1 。
例5、用公式法解下列方程：（1）－3x 2－5x +2 =0 ； （2）08121212=++x x 。
例6、已知y =2x 2 +7x －1，当x 为何值时，y 的值与4x + 1的值相等？x 为何值时，y 的值与x 2－19的值互为相反数？例7、已知三角形的两边长分别是1和2，第三边长是方程x 2－3x +2 =0的根，试求这个三角形的周长。
例8、已知关于x 的方程2x 2－kx +1 =0的一个解与方程4112=-+x x 的解相同。
（1）求k 的值； （2）求方程2k 2－kx +1 =0的另一个解。
例9、已知下列n （n 为正整数）个关于x 的一元二次方程：x 2－1 =0 （1）x 2 +x －2 =0 （2）x 2 +2x －3 =0 （3）……x 2 +（n －1）x －n =0 （n ）① 请求出上述一元二次方程（1）、（2）、（3）……（n ）的解；② 请你指出这n 个方程的根具有什么共同特点，写出一条即可。
例10、已知方程（a －x ）2－4（b －x ）（c －x ）=0，试说明：（1）此方程必有实数根；（2）若a 、b 、c 为△ABC 三边，方程有两个相等的实数根。
试确定△ABC 的形状。
同步练习1. 9)12(2=-x2. 42)2)(1(+=++x x x3. 3x 2–4x –1=04. 4x 2–8x +1=0（配方法）5. 0542=-+x x （配方法） 6. 025)2(10)2(2=++-+x x （因式分解法）7. 0672=+-x x (因式分解法) 8. )15(3)15(2-=-x x (因式分解法) 9. 0362=+-x x (配方法)10. 1)4(2=+x x (求根公式法) 11. 0)1(122=--+-kx k x x 12. 036252=-x13.0223)12(22=-+-+x x 14. 0)4()52(22=+--x x 15. 配方法x 2+4x -12=016. 公式法3x 2+5(2x+1)=0 17. 因式分解法3(x -5)2=2(5-x ) 18. 9)12(2=-x19. 0432=-+x x （配方法） 20. 3x 2+5(2x+1)=0（公式法） 21. ()()752652x x x +=+课下练习一、填空题1、方程x 2－3 = 0的根是 。
一元二次方程的四种解法
一元二次方程的四种解法教学目标1.理解一元二次方程及其有关概念2.会解一元二次方程,并能熟练运用四种方法去解教学重难点1.一元二次方程的判定，求根公式2.一元二次方程的解法与应用 课前练习： 1.方程()0132=+++mx xm m是关于x 的一元二次方程，则m 的值为 。
2.已知322-+y y 的值为2，则1242++y y 的值为 。
3.已知关于x 的一元二次方程()002≠=++a c bx ax 的系数满足b c a =+，则此方程必有一根为 。
4.关于x 的一元二次方程()04222=-++-a x x a 的一个根为0，则a 的值为 。
（1）基本思想方法：解一元二次方程就是通过“降次”将它化为两个一元一次方程。
（2）方法：①直接开方法；②因式分解法；③配方法；④公式法例1、解方程：;0822=-x ();0912=--x ()()2221619+=-x x11162492=+-x x例2. 下列方程无解的是（ ）A.12322-=+x xB.()022=-x C.x x -=+132 D.092=+x类型二、配方法 基本步骤 :1.先将常数c 移到方程右边2.将二次项系数化为13.方程两边分别加上一次项系数的一半的平方4.方程左边成为一个完全平方式：典型例题：例1、试用配方法说明322+-x x 的值恒大于0，47102-+-x x 的值恒小于0。
变式：若912322-+--=x x t ，则t 的最大值为 ，最小值为 。
例2、已知x 、y 为实数，求代数式74222+-++y x y x 的最小值。
例3、已知，x、y y x y x 0136422=+-++为实数，求yx 的值。
例4：已知010n 6-n m 2m 22=+++，求m 和n 的值。
例5：已知M=x+2，N=19-x 5x 5x -x 22+=+Q ，，其中x ＞2.（1）求证M ＜N ；（2）比较M 与Q 的大小。
一元二次方程的解法训练题
一元二次方程的解法训练题一、方程 x2 - 4x = 0 的解为？A. x = 0 或 x = 4B. x = 0 或 x = -4C. x = 2 或 x = -2D. x = 1 或 x = -4（答案）A。
解析：将方程 x2 - 4x = 0 提取公因子 x，得 x(x - 4) = 0，所以 x = 0 或 x - 4 = 0，解得 x = 0 或 x = 4。
二、方程 x2 + 6x + 9 = 0 的解为？A. x = 3B. x = -3C. x = 3 或 x = -3D. 无解（答案）B。
解析：方程 x2 + 6x + 9 = 0 可以写成 (x + 3)2 = 0，所以 x + 3 = 0，解得 x = -3，因为平方项等于0，所以只有一个解。
三、方程 x2 - 5x + 6 = 0 的解为？A. x = 2 或 x = 3B. x = -2 或 x = -3C. x = 2 或 x = -3D. x = -2 或 x = 3（答案）A。
解析：方程 x2 - 5x + 6 = 0 可以因式分解为 (x - 2)(x - 3) = 0，所以 x - 2 = 0 或 x - 3 = 0，解得 x = 2 或 x = 3。
四、方程 2x2 - 4x - 6 = 0 的解为？A. x = 1 或 x = -3B. x = -1 或 x = 3C. x = 2 或 x = -2D. x = 1 或 x = 3（答案）B。
解析：方程 2x2 - 4x - 6 = 0 可以先除以2简化为 x2 - 2x - 3 = 0，然后因式分解为 (x - 3)(x + 1) = 0，所以 x - 3 = 0 或 x + 1 = 0，解得 x = 3 或 x = -1。
五、方程 x2 - 2x - 8 = 0 的解为？A. x = 4 或 x = -2B. x = 4 或 x = 2C. x = -4 或 x = 2D. x = -4 或 x = -2（答案）A。
专题02 一元二次方程的4种解法(解析版)
专题02 一元二次方程的4种解法考点1：直接开方法；考点2：配方法；考点3：公式法；考点4：因式分解法。
1．方程（x +6）2﹣9＝0的两个根是（ ）A ．x 1＝3，x 2＝9B ．x 1＝﹣3，x 2＝9C ．x 1＝3，x 2＝﹣9D ．x 1＝﹣3，x 2＝﹣9解：∵（x +6）2﹣9＝0，∴（x +6）2＝9，则x +6＝±3，∴x 1＝﹣3，x 2＝﹣9，答案：D ．2．x 1、x 2是一元二次方程3（x ﹣1）2＝15的两个解，且x 1＜x 2，下列说法正确的是（ ）A ．x 1小于﹣1，x 2大于3B ．x 1小于﹣2，x 2大于3C ．x 1，x 2在﹣1和3之间D ．x 1，x 2都小于3解：∵x 1、x 2是一元二次方程3（x ﹣1）2＝15的两个解，且x 1＜x 2，∴（x ﹣1）2＝5，∴x ﹣1∴x 2＝13，x 1＝1−1，答案：A ．3．（易错题）若一元二次方程ax 2＝b （ab ＞0）的两根分别是m ﹣1和2m +3，则ba 的值为（ ）A ．16B ．259C ．25D ．259或25解：∵一元二次方程ax 2＝b 的两个根分别是m +1与2m ﹣13，且x =±∴m ﹣1+2m +3＝0，解得：m =−23，题型01 直接开方法即方程的根是：x 1=−53，x 2=53，∴b a =(±2=259，答案：B ．4．关于x 的一元二次方程x 2＝a 的两个根分别是2m ﹣1与m ﹣5，则m ＝ 2 ．解：根据题意得2m ﹣1+m ﹣5＝0，解得m ＝2，答案：2．5．关于x 的方程（2x +5）2＝m +1无实数解，则m 的取值范围 m ＜﹣1 ．解：∵关于x 的方程（2x +5）2＝m +1无实数解，∴m +1＜0，解得m ＜﹣1．答案：m ＜﹣1．6．对于解一元二次方程（x +3）2＝4，通过降次转化为两个一元一次方程，其中一个一元一次方程是x +3＝2，则另一个一元一次方程是 x +3＝﹣2 ．解：（x +3）2＝4，∴x +3＝±2，∴x +3＝2或x +3＝﹣2，答案：x +3＝﹣2．7．解方程：（1）x 2﹣81＝0；（2）4（x ﹣1）2＝9．解：（1）x 2﹣81＝0，x 2＝81，∴x ＝±9，∴x 1＝9，x 2＝﹣9；（2）4（x ﹣1）2＝9，（x ﹣1）2=94，∴x ﹣1＝±32，∴x 1=52，x 2=−12．8．一元二次方程y 2﹣y −34=0配方后可化为（ ）A ．（y +12）2＝1B ．（y −12）2＝1C ．（y +12）2=34D ．（y −12）2=34解：y 2﹣y −34=0y 2﹣y =34y 2﹣y +14=1（y −12）2＝1答案：B ．9．将代数式x 2﹣10x +5配方后，发现它的最小值为（ ）A ．﹣30B ．﹣20C ．﹣5D ．0解：x 2﹣10x +5＝x 2﹣10x +25﹣20＝（x ﹣5）2﹣20，当x ＝5时，代数式的最小值为﹣20，答案：B ．10．（易错题）设a 、b 是两个整数，若定义一种运算“△”，a △b ＝a 2+b 2+ab ，则方程（x +2）△x ＝1的实数根是（ ）A ．x 1＝x 2＝1B ．x 1＝0，x 2＝1C ．x 1＝x 2＝﹣1D ．x 1＝1，x 2＝﹣2解：∵a △b ＝a 2+b 2+ab ，∴（x +2）△x ＝（x +2）2+x 2+x （x +2）＝1，整理得：x 2+2x +1＝0，即（x +1）2＝0，解得：x 1＝x 2＝﹣1．答案：C ．11．把方程x 2﹣2＝4x 用配方法化为（x +m ）2＝n 的形式，则mn 的值是 ﹣12 ．题型02 配方法解：∵x2﹣2＝4x，∴x2﹣4x＝2，∴x2﹣4x+4＝2+4，∴（x﹣2）2＝6，∴m＝﹣2，n＝6，∴mn＝﹣12，答案：﹣1212．方程x2﹣2x﹣1＝0的解是 x1＝1+解：∵x2﹣2x﹣1＝0，∴x2﹣2x＝1，∴x2﹣2x+1＝2，∴（x﹣1）2＝2，∴x＝1∴原方程的解为：x1＝1+x2＝1答案：x1＝1+x2＝113．小明设计了一个魔术盒，当任意实数对（a，b）进入其中，会得到一个新的实数a2﹣2b+3．若将实数（x，﹣2x）放入其中，得到﹣1，则x＝ ﹣2 ．解：根据题意得x2﹣2•（﹣2x）+3＝﹣1，整理得x2+4x+4＝0，（x+2）2＝0，所以x1＝x2＝﹣2．答案：﹣2．14．（易错题）嘉淇同学用配方法推导一元二次方程ax2+bx+c＝0（a≠0）的求根公式时，对于b2﹣4ac＞0的情况，她是这样做的：由于a≠0，方程ax2+bx+c＝0变形为：x2+bax=−ca，…第一步x2+bax+（b2a）2=−ca+（b2a）2，…第二步（x +b 2a ）2=b 2−4ac 4a 2，…第三步x +b 2a =b 2﹣4ac ＞0），…第四步x =2a ，…第五步嘉淇的解法从第 四 步开始出现错误；事实上，当b 2﹣4ac ＞0时，方程ax 2+bx +c ＝0（a ≠O ）的求根公式是 x =−b 2a ．用配方法解方程：x 2﹣2x ﹣24＝0．解：在第四步中，开方应该是x +b 2a =x =答案：四；x用配方法解方程：x 2﹣2x ﹣24＝0解：移项，得x 2﹣2x ＝24，配方，得x 2﹣2x +1＝24+1，即（x ﹣1）2＝25，开方得x ﹣1＝±5，∴x 1＝6，x 2＝﹣4．15．一元二次方程x 2+4x ﹣8＝0的解是（ ）A ．x 1＝x 2＝2﹣B ．x 1＝x 2＝2﹣C ．x 1＝﹣x 2＝﹣2﹣D ．x 1＝﹣x 2＝﹣2﹣解：∵a ＝1，b ＝4，c ＝﹣8，∴Δ＝42﹣4×1×（﹣8）＝48＞0，则x −2±∴x 1＝﹣x 2＝﹣2﹣题型03 公式法答案：D ．16．已知a 是一元二次方程x 2﹣x ﹣1＝0较大的根，则下面对a 的估计正确的是（ ）A ．0＜a ＜1B ．1＜a ＜1.5C ．1.5＜a ＜2D ．2＜a ＜3解：解方程x 2﹣x ﹣1＝0得：x =∵a 是方程x 2﹣x ﹣1＝0较大的根，∴a∵23，∴3＜1+4，∴32＜2，答案：C ．17．若实数a ，b 满足a 2+ab ﹣b 2＝0，则a b = ．解：a 2+ab ﹣b 2＝0△＝b 2+4b 2＝5b 2．a =−b 2=∴a b =18．（易错题）对任意的两实数a ，b ，用min （a ，b ）表示其中较小的数，如min （2，﹣4）＝﹣4，则方程x •min（2，2x ﹣1）＝x +1的解是 x =或x = ．解：①若2＜2x ﹣1，即x ＞1.5时，x +1＝2x ，解得x ＝1（舍）；②若2x ﹣1≤2，即x ≤1.5时，x （2x ﹣1）＝x +1，解得x x答案：x=x=19．关于x的一元二次方程为（m﹣1）x2﹣2mx+m+1＝0．（1）求出方程的根；（2）m为何整数时，此方程的两个根都为正整数？解：（1）根据题意，得m≠1．∵a＝m﹣1，b＝﹣2m，c＝m+1，∴Δ＝b2﹣4ac＝（﹣2m）2﹣4（m﹣1）（m+1）＝4，则x1=2m22(m−1)=m1m−1，x2＝1；（2）由（1）知，x1=m1m−1=1+2m−1，∵方程的两个根都为正整数，∴2m−1是正整数，∴m﹣1＝1或m﹣1＝2，解得m＝2或3．即m为2或3时，此方程的两个根都为正整数．20．方程x2﹣x＝56的根是（ ）A．x1＝7，x2＝8B．x1＝7，x2＝﹣8 C．x1＝﹣7，x2＝8D．x1＝﹣7，x2＝﹣8解：∵x2﹣x＝56，∴x2﹣x﹣56＝0，则（x﹣8）（x+7）＝0，∴x﹣8＝0或x+7＝0，解得x1＝﹣7，x2＝8，答案：C．21．一元二次方程x（x﹣2）＝x﹣2的解是（ ）题型04 因式分解法A．x1＝x2＝0B．x1＝x2＝1C．x1＝0，x2＝2D．x1＝1，x2＝2解：x（x﹣2）＝x﹣2，移项，得x（x﹣2）﹣（x﹣2）＝0，提公因式，得（x﹣2）（x﹣1）＝0，∴x﹣2＝0或x﹣1＝0，解得x1＝2，x2＝1．答案：D．22．一个等腰三角形的两条边长分别是方程x2﹣7x+10＝0的两根，则该等腰三角形的周长是（ ）A．12B．9C．13D．12或9解：x2﹣7x+10＝0，（x﹣2）（x﹣5）＝0，x﹣2＝0，x﹣5＝0，x1＝2，x2＝5，①等腰三角形的三边是2，2，5∵2+2＜5，∴不符合三角形三边关系定理，此时不符合题意；②等腰三角形的三边是2，5，5，此时符合三角形三边关系定理，三角形的周长是2+5+5＝12；即等腰三角形的周长是12．答案：A．23．方程2x2+1＝3x的解为 x1＝1，x2=12 ．解：2x2+1＝3x，2x2﹣3x+1＝0，（x﹣1）（2x﹣1）＝0，解得：x1＝1，x2=1 2．答案：x1＝1，x2=1 2．24．（易错题）菱形的一条对角线长为8，其边长是方程x2﹣9x+20＝0的一个根，则该菱形的周长为 20 ．解：如图所示：∵四边形ABCD是菱形，∴AB＝BC＝CD＝AD，∵x2﹣9x+20＝0，因式分解得：（x﹣4）（x﹣5）＝0，解得：x＝4或x＝5，分两种情况：①当AB＝AD＝4时，4+4＝8，不能构成三角形；②当AB＝AD＝5时，5+5＞8，∴菱形ABCD的周长＝4AB＝20．答案：20．25．（易错题）对于实数a，b，定义运算“◎”如下：a◎b＝（a+b）2﹣（a﹣b）2．若（m+2）◎（m﹣3）＝24，则m＝ ﹣3或4 ．解：根据题意得[（m+2）+（m﹣3）]2﹣[（m+2）﹣（m﹣3）]2＝24，（2m﹣1）2﹣49＝0，（2m﹣1+7）（2m﹣1﹣7）＝0，2m﹣1+7＝0或2m﹣1﹣7＝0，所以m1＝﹣3，m2＝4．答案：﹣3或4．26．解方程（1）2x2﹣3x﹣2＝0；（2）x（2x+3）﹣2x﹣3＝0．解：（1）（2x+1）（x﹣2）＝0，2x+1＝0或x﹣2＝0，所以x1=−12，x2＝2；（2）x（2x+3）﹣（2x+3）＝0，（2x+3）（x﹣1）＝0，2x+3＝0或x﹣1＝0，所以x1=−32，x2＝1．。
(完整版)解一元二次方程练习题(配方法、公式法)
解一元二次方程练习题(配方法)配方法的理论根据是完全平方公式222)(2b a b ab a +=+±，把公式中的a 看做未知数x ，并用x 代替，则有222)(2b x b bx x ±=+±。
配方法的步骤：先把常数项移到方程的右边，再把二次项的系数化为1，再同时加上1次项的系数的一半的平方，最后配成完全平方公式1．用适当的数填空：①、x 2+6x+ =（x+ ）2 ②、x 2－5x+ =（x － ）2；③、x 2+ x+ =（x+ ）2 ④、x 2－9x+ =（x － ）22．将二次三项式2x 2-3x-5进行配方，其结果为_________．3．已知4x 2-ax+1可变为（2x-b ）2的形式，则ab=_______．4．将x 2-2x-4=0用配方法化成（x+a ）2=b 的形式为___ ____，•所以方程的根为_________．5．若x 2+6x+m 2是一个完全平方式，则m 的值是6．用配方法将二次三项式a 2-4a+5变形，结果是7．把方程x 2+3=4x 配方，得8．用配方法解方程x 2+4x=10的根为9．用配方法解下列方程：（1）3x 2-5x=2． （2）x 2+8x=9（3）x 2+12x-15=0 （4）41 x 2-x-4=010.用配方法求解下列问题（1）求2x 2-7x+2的最小值 ； （2）求-3x 2+5x+1的最大值。
解一元二次方程练习题(公式法)公式法是用求根公式解一元二次方程的解的方法，它是解一元二次方程的一般方法。
一元二次方程)0(02≠=++a c bx ax 的求根公式：)04(2422≥--±-=ac b aac b b x 公式法的步骤：就把一元二次方程的各系数分别代入，这里二次项的系数为a ，一次项的系数为b ，常数项的系数为c一、填空题1．一般地，对于一元二次方程ax 2+bx+c=0（a≠0），当b 2-4ac≥0时，它的根是__ ___ 当b-4ac<0时，方程___ ______．2．方程ax 2+bx+c=0（a≠0）有两个相等的实数根，则有____ ____ ，•若有两个不相等的实数根，则有_____ ____，若方程无解，则有__________．3．用公式法解方程x 2 = -8x-15，其中b 2-4ac= _______，x 1=_____，x 2=________．4．已知一个矩形的长比宽多2cm ，其面积为8cm 2，则此长方形的周长为________．5．用公式法解方程4y 2=12y+3，得到6．不解方程，判断方程：①x 2+3x+7=0；②x 2+4=0；③x 2+x-1=0中，有实数根的方程有 个 7．当x=_____ __时，代数式13x +与2214x x +-的值互为相反数． 8．若方程x-4x+a=0的两根之差为0，则a 的值为________．二、利用公式法解下列方程（1）220x -+= （2） 012632=--x x （3）x=4x 2+2（4）－3x 2＋22x －24＝0 （5）2x （x －3）=x －3 （6） 3x 2+5(2x+1)=0（7）(x+1)(x+8)=-12 （8）2(x －3) 2＝x 2－9 （9）－3x 2＋22x －24＝0解一元二次方程练习题(因式分解法)因式分解法就是利用因式分解的手段，求出方程的解的方法，这种方法简单易行，是解一元二次方程最常用的方法。
(完整word版)九年级数学一元二次方程(带答案)(良心出品必属精品)
第二章一元二次方程第1讲一元二次方程概念及解法【知识要点】:知识结构网络一元二次方程的四种解法直接开平方法、因式分解法、配方法、公式法1. 直接开平方法是解一元二次方程的常用方法之一，适用于方程经过适当整理后，可化为x2 =bb -0或x a 2二b的形式的方程求解。
当b 一0时，可两边开平方求得方程的解；当b：：： 0时, 方程无实数根。
2. 因式分解法解方程的步骤：（1）将方程一边化为0；（2）将方程另一边分解为两个一次因式的乘积；（3）令每个一次因式等于0,得到两个一元一次方程后求解，它们的解就是原一元二次方程的解。
3. 配方法解一元二次方程的步骤为：（1）化二次项系数为1（2）移项，使方程左边为二次项和一次项，右边为常数项。
（3）方程两边都加上一次项系数的一半的平方（4）原方程变为（x m）^ n 的形式（5）如果右边是非负数，就可用直接开平方法求出方程的解。
4. 公式法解一元二次方程的基本步骤：（1）将方程化为一般形式ax2 bx 0，确定a、b、c的..b b2- 4ac 值；（2）计算b2-4ac的值并判别其符号；（3）若b2-4ac — 0，则利用公式x二」b—4ac求2a 方程的解，若b2 -4ac ：：： 0，则方程无实数解。
【典型例题】(1) 6x 2 —7x —3=0 (用因式分解法)解：(3x1)( 2x - 3) = 0 • 3x 1 二 0 或 2x _3=0 1 3 x 1, x 2 = — 3 2 (2) 3x 2 = 4x 1 （用公式法）解：3x 2 — 4x — 1 = 0.-：=(一4)2 - 4 X 3 X ( _1) = 28 . 0解:手）—2= 3 2, -5 2【经典练习】、直接开方法二、配方法注：（1） 2x 2 -、2x -30 = 0 二、公式法1. 用求根公式法解下列方程(1) x 2 2x —2 =0; -(-4) ± ,28 2 ± ,7(3) 2x -2x-30 0 （用配方法） ,2 x (-2)2 4 二 15 ( (1) (x 1)2 二(1 -2x)(2) (x a)2 = b.2121 (2) 3x2 = 4x 1解：2(2) 2y 8y _1 =0 ;解：2 1⑶2x -3x 0 ;8解：(4) 3y2 -2y =1 ;解：(5) 2x2 5x -1 =0 ;解：2 —(6) x 2..5x 3=0 ;解：(7) 3x2 -4x 5 =0 ;解：(7)方程无实数根；(8) 、2x2 4 3x - 2 .2 =0 ;解：(9) 0.02x2 - 0.03x =0.35 ;解：(9)先在方程两边同乘以100,化为整数系数，再代入求根公式, (10) (1 2、3)x —x2二、、3(1 、3)解：。
一元二次方程解法
一元二次方程的解法一例题：1. 解下列方程：（1）()922=+x （2）()05122=+--y （3)()322212=+t (4)()0412=+-x2. 用开平方法解下列方程：（1）022=-x （2）()361642=-x3. 用配方法解关于x 的方程02=++n mx x ，此方程可变形为（ ） A. 44222m n m x -=⎪⎭⎫ ⎝⎛+ B. 44222n m m x -=⎪⎭⎫ ⎝⎛+ C. 24222n m m x -=⎪⎭⎫ ⎝⎛+ D. 24222m n m x -=⎪⎭⎫ ⎝⎛+ 4. 用配方法解方程：0222=-+x x练习：1. 方程0742=-x 的解是（ ）A. 47=xB. 47±=x C. 27±=x D. 47±=x 2. 一元二次方程()212=-x 的解是（ ）A. 21,2121+-=--=x xB. 21,2121+=-=x xC. 1,321-==x xD. 3,121-==x x3. 已知关于x 的一元二次方程()n m x =+2有实数根，则（ ） A. 0>n B. 0≥n C. 0≠n D. 为任何实数n4. 如果04412=+-xx ，那么x 2的值是（ ） A. -1 B. 1 C. 2 D. 1或25. 请写出一个两根互为相反数的一元二次方程_________6. 在下列各空白处填上适当的数，使等式成立。
（1）++x x 122______=()2____+x （2）++x x 312______=()2___+x （3）223191___⎪⎭⎫ ⎝⎛-=+-x x x 7. 若0>n ，对所有x ，式子()223369n x mx x +=++成立，则=-n m ________ 8. 解下列方程：（1）02522=⎪⎭⎫ ⎝⎛-x （2）()6232=-x （3）()01342=-+x （4）()()22431-=-x x9. 用配方法证明对于任意实数x ，二次三项式25222-+-x x 的值恒大于零。
解一元二次方程练习题(四种解法)
一 直接开方法
类型
I： ax2
=
b
x2
=
b a
b a
0
x
=
b (结果要分母有理化)
a
类型 II： a2 = b2 a = b或a = −b
（1） x2 = 9
（2） 4x2 = 25
（3） ( x +1)2 = 16
（4） 4(2x −1)2 = 81
一元二次方程的解法专题训练
三 公式法
x = −b b2 − 4ac 2a
步骤： 第一步：写成一般式； 第二步：找出 a，b，c；
第三步：计算 = b2 − 4ac ；
第四步：若△≥0，则代入公式；若△≥0，则原方程无实数解；
（1） x2 + 2x −1 = 0
（2） 2x2 + 4x = 1
（7） 300x2 − 40x +1 = 0
（8） ( x − 3)( x + 2) = 6
一元二次方程的解法专题训练
综合练习
（1） x2 − 6x + 8 = 0
（2） x2 − 4x = 1
（3） x2 −12x + 20 = 0
（4） x2 − 40x + 300 = 0
（5） x2 −100x + 2400 = 0
（5） (2x +1)2 = ( x − 3)2
（6） 250( x +1)2 = 360
（7）100(1− x)2 = 81
（8） 440( x +1)2 = 633.6
（9） −2( x − 4)2 + 9 = 5
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一元二次方程解法练习题 姓名
一、用直接开平方法解下列一元二次方程。
1、0142=-x
2、2)3(2=-x
3、()162812
=-x
二、 用配方法解下列一元二次方程。
1、.0662=--y y
2、x x 4232=-
3、9642=-x x
4、0542=--x x
5、01322=-+x x
6、07232=-+x x
三、 用公式解法解下列方程。
1、0822=--x x
2、223
14y y -=
3、y y 32132=+
4、01522=+-x x
5、1842-=--x x
6、02322=--x x
四、 用因式分解法解下列一元二次方程。
1、x x 22=
2、0)32()1(22=--+x x
3、0862=+-x x
4、22)2(25)3(4-=+x x
5、0)21()21(2=--+x x
6、0)23()32(2=-+-x x
五、用适当的方法解下列一元二次方程。
(选用你认为最简单的方法)
1、()()513+=-x x x x
2、x x 5322=-
3、2
260x y -+=
4、01072=+-x x
5、()()623=+-x x
6、()()03342
=-+-x x x
7、()02152
=--x 8、0432=-y y 9、03072=--x x
10、()()412=-+y y 11、()()1314-=-x x x 12、()025122
=-+x
13、22244a b ax x -=- 14、3631352=+x x 15、()()213=-+y y
16、)
0(0)(2≠=++-a b x b a ax 17、03)19(32=--+a x a x
18、012=--x x
19 、02932=+-x x 20、02222=+-+a b ax x
21、 x 2+4x -12=0
22、030222=--x x 23、01752=+-x x
24、1852-=-x x 25、3x 2+5(2x+1)=0 26、x x x 22)1)(1(=-+
解答题：
1、已知一元二次方程0132=-+-m x x .
（1）若方程有两个不相等的实数根，求m 的取值范围.
（2）若方程有两个相等的实数根，求此时方程的根
2、已知方程2（m+1）x 2+4mx+3m=2，根据下列条件之一求m 的值．
（1）方程有两个相等的实数根；（2）方程的一个根为0．
3、无论m 为何值时，方程04222=---m mx x 总有两个不相等的实数根吗？给出答案并说明理由。