变截面板簧刚度设计与计算
汽车钢板弹簧设计计算1

#DIV/0! #DIV/0! #DIV/0!! #DIV/0! #DIV/0! #DIV/0!
#DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! 0 #DIV/0! #DIV/0! #DIV/0! #DIV/0!
1
14)(1-μi-1)↑3Ki 12)*13)
15)Bi 14)+1 16)ξi=Bi-αi-2*Ci-2 n=6,ξn=ξ6
2.钢板弹簧总成刚 度C=6EIn/ln↑3/ξ
n (N/mm)
1)刚度差(C实-C 理)/C实*100 (%) 2)钢板弹簧总成挠 度fc=2*Pn/C (mm) 3)钢板弹簧的固有 频率N (Hz)=16/fc ↑0.5 (1.3~2.3Hz)
0
#DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! 0 #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0!
0 -0.1889 -0.13115 #DIV/0! #DIV/0! #DIV/0! #DIV/0!
47 #DIV/0!
#DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0!
45
#DIV/0! ###### ###### #DIV/0!
2.065591 #DIV/0! #DIV/0! #DIV/0! #DIV/0!
#DIV/0! #DIV/0! #DIV/0!
4.A(L/2,(n0-1)h↑ 3),B(S/2,nh↑3)两 点直线方程: (x-x1)/(x1x2)=(y-y1)/ (y1-y2) 即:x=ay+b x1=L/2 x2=S/2 a=(x1-x2)/(y1y2) b=x1-(x1-x2) *y1/(y1-y2) 5.求各片的弦长Li (xi)圆整为尾数为 1)最短片L1 L2 (单边) L3 L4 L5 L6 L7 L8 L9 L10 L11 L12 L13 L14 L15 n=6,Ln=L6
少片变截面钢板弹簧的设计计算

少片变截面钢板弹簧的设计计算钢板弹簧是一种常见的机械弹簧,在各种机械和设备中得到广泛应用。
它由在轴线方向上并排排列的一系列弯曲的钢板组成,呈螺旋状。
当外力作用于弹簧时,它会发生形变,具有很好的弹性回复能力,是一种具有重要机械性能的弹簧。
一、设计计算1、弹簧基本要素弹簧基本要素包括钢带材料、外直径、内直径、圈数、导程、自由长度和加工工艺。
其中材料是决定弹簧机械性能的关键要素。
通常钢板弹簧采用碳素钢、合金钢等材料,其弹性模量会随材料强度的提高而增大。
2、弹簧设计弹簧的设计需要考虑弹簧的工作条件,计算外力的大小、方向、作用点等,从而确定弹簧材料的选择、外径、圈数等要素。
弹簧设计需要考虑以下几个方面:(1)弹簧的工作负荷:根据机械设备的工作条件和要求确定弹簧承受的最大负荷,以此作为设计的起点。
(2)弹簧的外径和内径:根据弹簧材料、工作负荷和工作环境等要素来确定弹簧的外径和内径大小。
(3)弹簧的圈数和导程:弹簧的圈数和导程直接决定了其刚度和变形量,需要根据实际需求来设计,避免过强或过松。
(4)弹簧自由长度:弹簧自由长度也会影响到其机械性能,需要根据实际工作环境来确定。
二、样例下面以一种常见的钢板弹簧为例,介绍其设计和计算过程。
1、材料选择假设需要设计一种碳素钢的钢板弹簧,采用SWO-A钢带材,其具有以下机械性能:屈服强度:235MPa弹性模量:210GPa泊松比:0.3材料密度:7.85g/cm³2、外径和内径的确定假设弹簧的最大工作负荷为500N,弹簧碳素钢钢带的工作应力取90%时,最大弹簧应变量ρs应该小于σ/2E,即(υ-Dw)/Dw≥0.08。
可根据此公式,确定外径Dw=20mm。
根据设计要求,弹簧的圈数为8,导程为3mm。
当弹簧材料确定且弹簧固定长度生成后,利用弹簧方程(Fs=kρs)推导,得到弹簧直径Di=17.9mm。
3、根据内径、外径和圈数确定性能参数内直径ID=Di-2t,弹簧导程l0=π(Di+Dw)/2,自由长度L0=l0*(n-1)+2*ra+ra-ra*υ/Dw。
基于接触摩擦的少片变截面钢板弹簧的刚度分析_唐应时

nc ⎡ = ⎢t N N s
s=1 ⎣
+ tT
l l
⎜⎜⎝⎛Ts
+
gN l
N 0 ⎟⎟⎠⎞⎥⎦⎤ 。
(8)
其中:gN≤0;D 为所有等效节点位移组成的向量。 2.3 少片变截面钢板弹簧的接触定义
图 4 所示为隐藏掉实体单元的接触面单元。整个 钢板弹簧总成共定义了 3 个接触对,每一对包含 1 个 目标面和 1 个接触面,定义凹面为目标面,凸面为接
程:
δd
T s
g
⎡ ⎢t
N
N
s
⎣
+ tT
l l
⎜⎜⎝⎛Ts
+
gN l
N 0 ⎟⎟⎠⎞⎥⎦⎤ 。
(6)
其中:gN≤0;l
为接触发生前目标段的长度;
δd
T s
为
3
节点接触对的位移向量;
δd
T s
=(us,
vs,
u1,
v1,
u2,
v2);
tN, tT 为接触面上的法向和切向接触力;Ns={0, 1, 0,
可以看出在加载过程中钢板弹簧的负载和挠度基本上是线性变化的而弹簧的静态刚度没有发生明显变化符合该型号钢板弹簧的设计要求39030荷步的刚度平均值为4068钢板弹簧的负载挠度静态刚度和最大应力tableloaddeflectionstaticstiffnessmaximumstresstaperleafspring载荷步少片变截面钢板弹簧的试验分析在进行弹簧特性试验时用夹紧机构对钢板弹簧的卷耳进行夹紧支承
TANG Ying-shi1, CHAI Tian1, HE Jin-jun1, SU Jia-li1, LI En-bao2
浅析变截面少片簧计算

浅析变截面少片簧计算汤玉平李细平江照亮(三一重工股份有限公司邮编410010)摘要:少片簧具备很多优点,质量轻,摩擦小噪音低,同时还能改善车轮和路面的附着性能等。
所以在汽车领域少片簧的应用已经越来越广泛。
但是少片簧如果设计不当,也很容易出现致命的故障。
所以少片簧的设计计算尤为重要。
关键词:汽车少片簧优点计算引言:要想变截面少片簧在各截面处的应力相等,断面形式从理论上来讲,板簧各点厚度沿长度方向必须做成抛物线型式。
这种抛物线型式板簧是理想的等强度梁,板簧各点应力分布最合理。
材料利用率很高。
但由于抛物线型式板簧根部不便装夹,端部不便卷耳,图1所示实际中不能使用。
图1抛物线形叶片板簧抛物线板簧基于上缺点,所以一般在抛物线板簧的基础加以改进,在根部做成等厚平直段,考虑到端部承受剪切力、端部卷耳及其加工性,不但卷耳片做成等厚平直段,而且其他簧片也作成等厚平直段,如图2所示。
图2 改进后的抛物线形叶片板簧经改进后,虽根部和端部得到了加强,但整个抛物线段都是高应力危险区,对材料和加工缺陷敏感性大,所以实际上目前使用的最普遍的是锥形段均采用同抛物线相切的直线形来代替抛物线形。
同时为了降低中心孔部位的应力和提高端部卷耳的强度,一般都采用如图3所示断面的板簧。
图3 根部和端部同时加强的变截面板簧为了适合长跨度产品的需要,可采用图4所示断面的板簧图4 长跨度加强型变截面板簧1、少片簧的计算1.1 已经条件在进行钢板弹簧计算之前,应当知道下列初始条件,轴(桥)负荷G 1、簧下部分荷重G 2、U 型螺栓距、板簧宽度、板簧跨度、板簧材料等。
1.2 少片簧厚度的计算本文将从等应力梁的角度,对少片簧的计算做初步的探讨。
图4所示 变截面簧,根部满足安装应做成等厚平直段,同时满足U 形螺栓夹紧处的工作应力cσ(cσ<[σ])。
则其厚度为h 22h =1)式中: Pi ——板簧端部载荷 l ——板簧伸直长度之半 B ——板簧宽度 S ——U 形螺栓中心距板簧端部为了主片承载也需要做成等厚平直段,板簧连接处应做成圆角过渡。
汽车变截面钢板弹簧的设计计算

汽车变截面钢板弹簧的设计计算东风汽车工程研究院 陈耀明 2006年5月前 言少片变截面钢板弹簧在我国已有多年的制造和使用经验,特别是大、中型客车,采用者相当广泛。
然而,涉及变截面簧的设计计算方法,虽然二十几年前悬架专委会曾做过一些介绍,但资料零散、重复、不完整,尤其是比较常用的加强型变截面簧,资料反而欠缺。
撰写本文的目的,就是为悬架设计者提供变截面簧的比较完整的设计计算资料,主要是刚度计算公式和应力分布计算方法。
变截面簧轮廓线包括梯形和抛物线形两大类,每类又含有根部、端部加厚,或只有根部加厚,或都不加厚等几种变型。
这样,可以说几乎所有的变截面簧轮廓线都可在本文找到计算公式。
此外,本文还介绍了各种轮廓线的选型原则以及若干设计经验等,可供设计人员参考。
附录中列出已有资料中的一些计算公式,并证明了它们和本文公式的一致性。
本文的式(1)~(3)引自日本资料“自动车用重型钢板弹簧”,其它公式(6)~(15)是笔者近期重新推导出来的。
当然,有一些和过去推导出来的公式完全一致。
一、 纵截面为梯形的变截面弹簧这种弹簧的轧锥部分(3l ~4l 段)为梯形,而根部和端部都将厚度增大,称为加强型变截面簧,见图1。
图1为四分之一椭圆钢板弹簧,其刚度计算公式为:654321αααααα+++++=EK ----------------(1)若对称地扩展成为半椭圆钢板弹簧,其总刚度为:6543212αααααα+++++=EK ----------------(2)若弹簧由若干等长、相同轮廓线的叠片所组成,则其合成的总成刚度为:6543212αααααα+++++=nEK ----------------(3)式中 )/(10058.225mm N E ×=为弹性模数n 弹簧片数,单片弹簧1=n313114bt l =α⎥⎦⎤⎢⎣⎡++−+−+−−=1221112121221122212211132ln 223)(22212t t t Al t t l A t Al t t l A t Al t bA α )(43233323l l bt −=α ⎥⎦⎤⎢⎣⎡++−+−+−−=2322322223233223232223234ln 223)(22212t t t Bl t t l B t Bl t t l B t Bl t bB α ⎥⎦⎤⎢⎣⎡++−+−+−−=3423432324244324242234335ln 223)(22212t t t Cl t t l C t Cl t t l C t Cl t bC α )(43536346l l bt −=α而 1212l l t t A −−=3423l l t t B −−=4534l l t t C −−=其中 b 弹簧宽度实际应用中,有些弹簧的轮廓线有所简化,见图2,其刚度计算式也有所变化: 1、增厚转折点急剧变化,2型。
少片变截面弹簧的计算
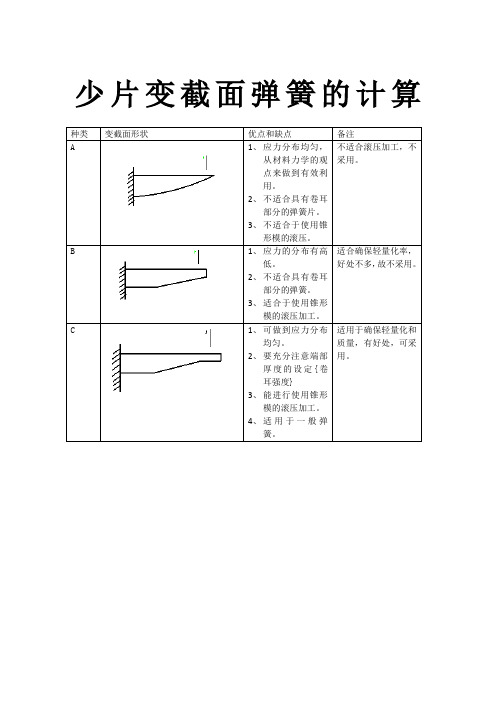
少片变截面弹簧的计算种类变截面形状优点和缺点备注A1、应力分布均匀,从材料力学的观点来做到有效利用。
2、不适合具有卷耳部分的弹簧片。
3、不适合于使用锥形模的滚压。
不适合滚压加工,不采用。
B1、应力的分布有高低。
2、不适合具有卷耳部分的弹簧。
3、适合于使用锥形模的滚压加工。
适合确保轻量化率,好处不多,故不采用。
C1、可做到应力分布均匀。
2、要充分注意端部厚度的设定{卷耳强度}3、能进行使用锥形模的滚压加工。
4、适用于一般弹簧。
适用于确保轻量化和质量,有好处,可采用。
D 1、以减轻C形中心孔部分应力为圆进行改良的。
2、能进行使用锥形模的滚压加工。
适合于小车型车辆用簧。
对确保质量有好处,可采用。
—1—种类变截面形状优点和缺点备注E1、为提高C形卷耳部分的强度,进行了改良。
2、能进行使用锥形模对确保质量有好处,可采用。
3、适用与中型车和大型车{前轴}的弹簧。
F1、是通过把D和E的形态结合在一起,有效地利用材料的形状。
对轻型化确保质量有好处,可采用。
G1、为适合长跨度产品,把F形状的加以改良的,是最有效地利用材料的形状。
2、能进行使用锥形模的滚压加工。
对轻量化有好处,可采用。
少片变截面弹簧的优点:1、应力分布均匀,接近于等应力梁,片数1—4片。
特殊工艺处理而提高其设计应力,从而使边界面弹簧轻量化,同等截面相比可减轻重量30—40%左右。
2、总成簧片在承载时,除端部传力处接触和中部骑马螺栓夹紧部位接触外,无片间接触现象,从而减少摩擦,使动刚度大力降低,提高乘坐舒适性。
3、由于片间接触区大为减少,基本上消除了由于片间接触摩擦磨损引起的使弹簧片早期损坏的疲劳源的产生,从而提高了疲劳寿命。
4、在总成中间平直等厚度的弹簧片,同上下保护垫板之间和簧片之间,插入塑料片或软金属垫片,这样就消除了弹簧总成工作时在中间平直等厚度段片间的直接挤压、摩擦,从而提高寿命。
5、采用喷完处理,中心孔挤压工艺和防锈性能,较好地油漆,这样也提高了疲劳寿命。
EQ153系列钢板弹簧刚度计算

钢板弹簧EQ153-G-F的自由刚度K=216.7N/mm,夹紧刚度(K)=238.5N/mm(夹紧距108mm)总成弧高150±6mm(2).EQ153H1-F前钢板弹簧自由刚度计算(片厚15,60Si2Mn)钢板弹簧EQ153H1-F的自由刚度K=369.8N/mm,夹紧刚度(K)=410N/mm(夹紧距108mm)总成弧高140±5mm钢板弹簧EQ153H-F的自由刚度K=413.9N/mm,夹紧刚度(K)=455.5N/mm(夹紧距108mm)总成弧高145±5mm(4).EQ153K前钢板弹簧自由刚度计算(片厚13,55CrMnA)钢板弹簧EQ153K的自由刚度K=319.1N/mm,夹紧刚度(K)=356.2N/mm(夹紧距108mm)总成弧高150±3mm55CrMnA)(与EQ153K有啥区别?)钢板弹簧EQ153K-F的自由刚度K=319.1N/mm,夹紧刚度(K)=356.2N/mm(夹紧距108mm)总成弧高150±3mm(6).EQ153D后钢板弹簧自由刚度计算(片厚16,60Si2Mn)钢板弹簧EQ153D的自由刚度K=575.7N/mm,夹紧刚度(K)=690.4N/mm(夹紧距188mm)总成弧高165±6mm钢板弹簧EQ153H的自由刚度K=574.7N/mm,夹紧刚度(K)=689N/mm(夹紧距188mm)总成弧高165±6mm(仅比EQ153D少块斜铁)(8).EQ153K后钢板弹簧自由刚度计算(片厚18, 55CrMnA,片宽100)钢板弹簧EQ153K的自由刚度K=820.2N/mm,夹紧刚度(K)=?N/mm(夹紧距?mm)总成弧高100±8mm钢板弹簧EQ153TH的自由刚度K=750.4N/mm,夹紧刚度(K)=900N/mm(夹紧距188mm)总成弧高155±6mm(10).EQ153TH1后钢板弹簧自由刚度计算(片厚18, 60Si2Mn)钢板弹簧EQ153TH1的自由刚度K=758.3N/mm,夹紧刚度(K)=909N/mm(夹紧距188mm)总成弧高155±6mm(与EQ153TH相比,仅多块斜铁)片宽100)钢板弹簧EQ153K的自由刚度K=438.3N/mm,夹紧刚度(K)=?N/mm(作用长度?mm,夹紧距?mm)总成弧高100±8mm钢板弹簧EQ153D的自由刚度K=463.8N/mm,夹紧刚度(K)=850N/mm(作用长度1140mm,夹紧距188mm)总成弧高70±6mm钢板弹簧EQ153H的自由刚度K=471.7N/mm,夹紧刚度(K)=820.5N/mm(作用长度1150mm,夹紧距188mm)总成弧高70±6mm(14).EQ153TH副钢板弹簧自由刚度计算(片厚16, 60Si2Mn)钢板弹簧EQ153TH的自由刚度K=801N/mm,夹紧刚度(K)=1468N/mm(作用长度1140mm,夹紧距188mm)总成弧高70±6mm。
梯形变截面板簧片简易设计方法_整理材料

梯形变截面板簧片的简易设计方法在少片簧设计中,为了节约材料,减轻自重,各板簧片尽可能做成等应力梁,使材料得到充分利用。
抛物线形板簧片属于等应力梁,但制作工艺要求较高,不易控制。
传统的少片簧板簧片采用梯形变截面结构,如果要少片簧设计的最轻,板簧材料得到充分利用,梯形变截面板簧片要设计的尽可能接近等应力梁。
目前梯形变截面板簧片的设计通常有两种方法,一种为试凑法,即根据经验初步选取尺寸参数,然后代入公式验算,经过反复计算,直到选择到最优的参数,这种设计方法不容易获得最佳设计方案,且费工时;另一种为最优化数学方法,将梯形弹簧的各设计参数做为变量,建立一系列函数方程,以理论质量最小作为目标函数,根据各约束要求,求解各参数,该方法虽然能得到最佳方案,但需要进行大量的计算,费工费时。
半 l ,线段NA 等于板簧片厚度h ;若将该梯形变截面板簧片设计的质量最轻,使之接近等应力梁,则线段BC 愈接近曲线OB ,此时梯形NABCO 的面积最小。
建立如下数学建模:由于OA 曲线为抛物线规律变化,则有:5.0⎪⎭⎫⎝⎛=l x h y (1)假设E 点坐标为(x 1,y 1)对(1)式E 点(x 1,y 1)求导可得,E 点的斜率k 为: ⋅=lx h k 12 (2)假设线段OC 长度为OC 则线段BC 的方程为:OC kx y += (3)又线段BC 过E 点(x 1,y 1),111kx y OC -=将(1)式、(2)式带入可得:115.01112x lx hl x h kx y OC -⎪⎭⎫ ⎝⎛=-= =lx h 12 (4) 线段CF 长度:lx h h OC h CF 21-=⋅-= (5)线段l 2长度:1122x l x kCFl -=⋅=(6) 三角形CBF 的面积S 为221l CF S = (7)将(5)式、(6) 式带入(7) 式整理得:()1112221x l x lx hh S -⎪⎪⎭⎫⎝⎛-==lx hx hx l x h 11114+- 若三角形S 面积最大,则梯形NABCO 面积最小,线段ABC 就愈接近抛物线,此时以截面为梯形NABCO 的板簧片就愈接近等应力梁。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
变截面板簧具有重量轻 , 寿命高, 减振性能 好 , 具有应力分布最合理 , 材料利用最充分的优 点 , 是一种最理想的汽车钢板弹簧结构形式 , 得 到了越来越广泛的应用。 而刚度是设计变截面汽 车钢板弹簧最重要的设计参数之一 , 变截面板簧 如图1所示。
H= Kp
L- X
K p : 抛物线常数; X : 板簧任意一点处距板簧中心长度 根据 莫尔定 理, 当板 簧端部 受到 作用 力 P 时, 其端部产生变形为 。 = 式中 : M ( X ) : 作用力 P 在 X 处产生的弯矩 , M( X ) = P ( L - X ) ; M ( 0) : 表示单位力 P = 1 作用下, 在 X 处产生 的弯矩, M ( 0) = ( L - X ) ; E : 弹簧材料的弹性模量,
3
3
B Kp 3
(L- X )3 12
4P ( G ( 1) + G ( 2) + G ( 3) + G ( 4) + G ( 5) + G ( 6) ) EB P EB 所以 , 刚度 G = = 4 G (i) 单片板簧刚度 : GD = 2 G GZ = 2N G 计算实例 :
由 N 片组成两端 对称的板簧 总成刚度 数:
=
t
= 0. 61m m 即可。 由式 ( 4) 算出第三个上辊
6
的压 弯量
=
w6
+ (
w5
+
w7
) / 2= 0. 9 + ( 2+
0. 61) / 2= 2. 2mm 。 第四个上辊压弯量为 8 = 2 t = 1. 22m m 。 考虑断面 高度公差± 0. 5mm 的影响, 取
2
=
4
= 4. 5m m,
3 3 3
L - D ( 0) h3 ( 0) 3 3 8( D ( 1) - D ( 2) ) ( h ( 1) + h( 2) ) 3 2 3/ 2 2( D 3/ ( 2) - D ( 3) ) 3 KP 3 D3 ( 3) - D ( 4) 3 h( 3 ) 3 8( D 3 ( 4) - D ( 5) ) 3 ( h ( 4) + h( 5) ) 3 D ( 5) h3 ( 5) ( 5) ( 6)
P(L- X )2 dx + EI ( 3)
2 L L
( 6) ( 5)
∫
( 4) ( 3)
L L
P(L- X )2 dx + EI ( 4)
2
∫
( 5) ( 4)
L L
令: G ( 1) = G ( 2) =
P(L- X ) EI ( 5) dx +
- X) ∫P ( L dx EI
( 6)
( 2) G ( 3) = G ( 4) = G ( 5) = G ( 6) = =
= B [ h( 1) + h ( 2) ] / 96 I ( 3) 为 L ( 2) ~ L ( 3) 段内的惯性矩 , 该段为抛物 线段, 所以 I ( 3) = 同理: I ( 4) = B h ( 5) / 12 I ( 5) = B ( h( 4) + h ( 5) ) / 96 I ( 6) = B h ( 5) / 12 将 I ( 1) ~ I ( 6) 代入 ( 2) 式积分得: 4P 3 3 3 [ ( L - L ( 0) ) - ( L - L ( 1) ) ] + EB h( 0) 32P 3 3 [ ( L - L ( 1) ) - ( L - L ( 2) ) ] + E B ( h ( 1) + h( 2) ) 3 = 8P 4P [ ( L - L ( 2) ) 3/ 2- ( L - L ( 3) ) 3/ 2 ] + [( L E BK P 3 EB h3 ( 3) 32P - L ( 3) ) 3 - ( L - L ( 4) ) 3 ] + [( L E B ( h ( 4) + h( 5) ) 3 4P 3 3 [ ( L - L ( 5) ) 3] ( 3) L ( 4) ) - ( L - L ( 5) ) ] + EB h3 ( 5) 令 : D ( i) = L - L ( i) 所以: D ( 0) = L - L ( 0) D ( 1) = L - L ( 1) D ( 2) = L - L ( 2) D ( 3) = L - L ( 3) D ( 4) = L - L ( 4) D ( 5) = L - L ( 5) D ( 6) = L - L ( 6) 则 ( 3) 式变为 : 3 3 3 3 4P L - D ( 0) 8( D ( 1) - D ( 2) = [ + + 3 EB h ( 0) ( h( 1 ) + h ( 2) ) 3 3/ 2 3/ 2 3 3 3 3 3 2( D ( 2) - D ( 3) D ( 3) - D ( 4) 8( D ( 4) - D ( 5) D ( 5) + + 3 3 3+ 3 ] KP h( 3) ( h ( 4) + h( 5) ) h( 5) ( 4)
( 北京科技大学 100083)
摘要 根 据材料力学理论 , 运用数学力 学方法 , 精确 推导出了变截面板 簧的刚度设计 与计算公式 , 为变 截面板簧的设计提供了依据。 这种板簧应用于各种矿用、 民用汽车行业中。 关键词 变截面板簧 刚度 设计计算
Calculation and Design of Taper Leaf Spring Stif fness
G =
EB = 37. 5 N/ m m 4 K ( i) GD 1= 2G = 75 N/ m m 第一片简图( 如图2 所示) :
图 2 6700后簧第一片
( 转第6 页) — 31 —
总 第 113 期 冶 金 设 备 1999年 2 月第 1期
其中: I ( 1) 为 L ( 0) ~L ( 1) 段内的惯性矩 I ( 1) = B h ( 0) / 12 I ( 2) 为 L ( 1) ~ L ( 2ቤተ መጻሕፍቲ ባይዱ 段内的惯性矩, 该段长度较 短 , 可取近似计算
3 I ( 2) = B [ ( h( 1) + h ( 2) ) / 2 ] / 12 3
5 E = 2. 1× 10 M pa ;
∫MEI M dx
(X) 0 0 (x )
L
( 1)
图 1 变截面板簧示意图
图中各符号表示意义如下: h( 0) ~ h( 6) : 板簧各段接点处厚度值 m m; L mm ; P : 作用于板簧端部的载荷 kN; L : 板簧半跨长度 m m; 图中 AB 段为抛物线段 , 其抛物线方程为 — 30 —
L L
2
( 2)
dx +
总第 113 期 T ot al N o . 113 冶 金 设 备 1999年 2 月第 1期 Februar y 1999 M ET A L LU RGI CA L EQ U IP M ENT
∫
( 3) ( 2)
L L
( 0)
~ L ( 6) : 板簧各段接点处距板簧中心长度
I ( X ) : 到中心距离为 X 处的惯性距 ,
3 I ( X ) = B h( X ) / 12;
由( 1) 式得 : P(L- X ) = L ( 0) EI ( 1) dx +
∫
( 1)
L
2
L- X) ∫ P( E I
( 2) ( 1)
总第 113 期 T ot al N o . 113 冶 金 设 备 1999年 2 月第 1期 Februar y 1999 M ET A L LU RGI CA L EQ U IP M ENT
新设备 新技术 新工艺
变截面板簧刚度设计与计算
薛彪 孙乐殿 刘日春
( 接第31页) 第二、 三、 四片简图 ( 如图3所示) :
#
量受人为因素影响较大 , 前六个辊的压弯量可以 基本相同, 也可以特殊加大 某个辊的压弯。 容易 咬入的工件, 第二辊的压弯 可以加大, 甚至大于 第四辊。 当第六辊也用大压 弯时, 第七辊必将随 之产 生较大压 弯, 工 件走出 第八辊 后得 不到矫 直 , 因此必须减小第八辊的 压弯量, 甚至不予压
6
= 2. 7mm ,
8
= 1. 7mm 。 文
献 [ 2] 用大变形压弯时所纪录的实测压弯量仍有 一定的对比价值, 现列于表 5中。 鉴于大变形压弯
表 5 8× 1300mm 矫直机矫 56 工字钢时 大变形压弯量的对比表 ( 单位 : mm) 辊号 2 4 6 8 指示值 12. 2 8 7. 5 0 弹跳值 4. 15 3. 79 2. 99 1. 67 真实值 8. 05 4. 21 4. 51 - 1. 67 理论值 4. 5 4. 5 2. 7 1. 7 误差值 - 3. 55 + 0. 29 - 1. 81 + 3. 37
参考文 献 [ 1] 崔甫 . 《 矫 直理论 与参数 计算》 ( 第 二版 ) . 机械工 业出 版社 , 1994 [ 2] 沈 久珩 . 《 1300轨 梁矫直 机辊 轴悬臂 刚度 测试分 析及 真 实压下 量的确 定》 . 中国 金属学 会矫直 学术会 议论 文 , 1986 [ 3] 邹家祥 , 施东成 . 《 轧钢机械理 论与结构 设计》 ( 下) . 冶 金工业出版社 , 1993 [ 4] 钦 明浩等 . “ 精 密矫直 机中轴 类零件 矫直 工艺理 论研 究” .《 机械工程学报》 , 1997. 4 ( 1998 年 10 月 12 日收稿 )
以 6700 后簧为 例该簧由 4 片组成 , 宽度 B = 76mm , 半 跨长 L = 700mm , 抛 物 线 系 数 Kp = 0. 68, 计算其总成刚度: 第一片刚度计算( 见表1) :
