弹簧刚度计算-新
弹簧刚度
弹簧刚度科技名词定义中文名称：弹簧刚度英文名称：stiffness of spring定义：产生单位变形量的弹簧载荷。
应用学科：机械工程（一级学科）；机械零件（二级学科）；弹簧（三级学科）以上内容由全国科学技术名词审定委员会审定公布1、弹簧的刚度是载荷增量dF与变形增量dλ之比，即产生单位变形所需的载荷，弹簧的刚度计算公式为F'=dF/dλ。
特性线为渐增型的弹簧，刚度随着载荷的增加而增大；而渐减型的弹簧，刚度随着载荷的增加而减少。
至于直线型的弹簧，刚度则不随载荷变化而变化，即F'=dF/dλ=F/λ=常数。
因此，对于具有直线型特性线的弹簧，其刚度也成为弹簧常数。
2、单位力使弹簧所产生的变形，即刚度的倒数称为弹簧的柔度。
3、计算：弹簧刚度是指使弹簧产生单位变形的载荷，用C和CT分别表示拉（压）弹簧的刚度与扭转弹簧的刚度，其表达式如下：对于拉压弹簧其中：F --- 弹簧轴向拉（压）力；λ --- 弹簧轴向伸长量或压缩量；对于扭转弹簧T --- 扭转弹簧的扭矩；Φ--- 扭转弹簧的扭转角。
[1]20.3.2 弹簧刚度1、定义：弹簧刚度是指使弹簧产生单位变形的载荷，用K和K T分别表示拉（压）弹簧的刚度与扭转弹簧的刚度，其表达式如下：对于拉压弹簧对于扭转弹簧其中：F --- 弹簧轴向拉（压）力；λ--- 弹簧轴向伸长量或压缩量；T --- 扭转弹簧的扭矩；ø--- 扭转弹簧的扭转角。
2、弹簧刚度与弹簧特性的关系图a）所示的直线型弹簧，其刚度为一常数。
这种弹簧的特性曲线越陡，弹簧刚度相应愈大，即弹簧愈硬；反之则愈软。
图b）所示的弹簧特性曲线为刚度渐增型，即弹簧随变形量的增大其刚度越大，且在最大或冲击载荷作用时，仍具有较好的缓冲减振性能，故多使用弹簧特性曲线具有该型曲线的走向。
图c）所示弹簧特性曲线为刚度渐减型，即弹簧刚度随变形的增大而越小。
为了在冲击动能一定时，获得较小冲击力，则应使用具有刚度渐减型特性曲线的弹簧为宜。
弹簧弹力简单计算
弹簧刚度查手册，弹力计算公式弹簧刚度自行计算，弹力计算公式
公式F=K*s=(Kd/n)*s公式F=K*s=((G*d4)/(8*D3*n))*s F:压簧弹力（N）F:压簧弹力（N）
K：弹簧整体刚度（N/mm）K：弹簧整体刚度（N/mm）
s：弹簧压缩距离（mm）s：弹簧压缩距离（mm）
K=Kd/n K=(G*d4)/(8*D3*n)
Kd:弹簧一圈刚度（N/mm）G:弹簧材料切变模量（GPa）
n:弹簧有效圈数1GPa=1000MP2)
d:弹簧丝径（
D:弹簧中径（mm）
n:弹簧有效圈数
G值查《机械设计手册（
教育出版社2009年1月第2版）P313，表1
不锈钢材质：1Cr18Ni9
自行计算，弹力计算公式
((G*d4)/(8*D3*n))*s
弹力（N）
K：弹簧整体刚度（N/mm）
s：弹簧压缩距离（mm）
4)/(8*D3*n)
材料切变模量（GPa）
000MPa=1000*(N/mm2)
丝径（mm）
D:弹簧中径（mm）
n:弹簧有效圈数
手册（第2版）吴宗泽 高志 主编》（高等版社2009年1月第2版）P313，表14-2 弹簧常用材料18Ni9Ti。
弹簧刚度计算
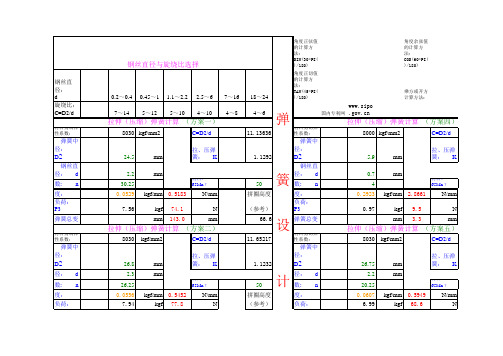
最大工作 负荷下间 距
材料剪切 弹性系 数： G
弹簧中 径：
D2
钢丝直 径： d
有效圈 数: n
弹簧刚 度： P允` 许极限 负荷： P3 极限负荷 弹簧总变 形量： f3
←δ1
（适用于
压缩弹
簧，指弹
簧钢丝间
δ1
0.11 mm 隙）
CM8（计算弹簧刚度及有关参数）
kgf/mm
8030
2
旋绕比： C=D2/d
YII型 L型（不 加钩环尺
寸）
当b＞3 时，弹簧 须套在心 轴上使用
。
b≤3 b≤3
b≤3
2.12 1.86
0.91
F1
7.00 mm
F2
9.00 mm
F3
16.00 mm
H1 H-F1 mm
H2 H-F2 mm
H3 H-F3 mm
tgα
0.10
定设计计算）
t
7.07 mm
H
YII型 H L型（不 加钩环尺
N
mm
圆柱簧（计算弹簧刚度及有关参数）
kgf/mm
8030
2
旋绕比： C=D2/d
20.5 mm
拉、压弹 簧： K
3.5 mm
mm
N
p'
00
0
0 0.00 ######
10 4.2 4.1 4.2 4.17 ######
75 拼圈高度 （参考）
20 8.4 30 12.6
8.3 12.6
8.4 8.37 ###### 12.7 12.63 ######
f3
3.07 mm （长）度
极限负荷
下高
弹簧刚度公式
弹簧刚度公式
弹簧刚度是指弹簧在受力作用下所发生的位移与力的比值，它是
描述弹簧硬度的重要指标。
弹簧刚度的公式通常是f=kx，其中f表示
所施加的力，k表示弹簧的刚度系数，x表示弹簧所发生的位移。
而弹
簧刚度的计算方式则与材质、形状、尺寸、加工工艺等相关因素密切
相关。
在实际生产过程中，弹簧刚度的计算和应用非常重要。
对于需要
反弹或拉伸的部件，例如汽车悬挂系统、圆珠笔弹簧等等，弹簧刚度
的准确计算可以确保零部件的性能和长期使用性。
同时，弹簧刚度的
调整和优化还能提高生产效率、降低成本，带来更高的经济效益。
在实际应用中，弹簧刚度的值不仅受到弹簧的形状和材料的影响，还受到所施加力的方式、温度、湿度等多种因素的影响。
对于不同类
型的弹簧，我们需要根据具体情况来选择最合适的刚度系数。
对于一
些特殊用途的弹簧，例如高品质音箱的振膜弹簧、航空航天中的高强
度弹簧等，需要进行更为精细的计算和设计，以确保其性能符合最高
标准。
总的来说，弹簧刚度作为弹簧的重要指标之一，对于各种实际应
用场景具有重要意义。
在实际生产中，需要结合具体情况，根据弹簧
刚度公式进行计算和设计，达到理想的效果。
这有助于提高生产效率、降低成本，同时保证产品的质量和性能。
同时还能在提高生产经济效
益的同时，满足客户的需求，为企业创造更多的经济价值。
弹簧进度系数公式
弹簧进度系数公式
弹簧进度系数公式指的是弹簧刚度的计算公式。
弹簧刚度表示单位长度或单位位移下弹簧恢复力的大小。
弹簧进度系数公式可以表示为：
C = (Gd^4)/(8Na^3)
其中：
C表示弹簧进度系数（也称为刚度系数或刚度常数）
G表示材料的剪切模量（也称为剪切刚度）
d表示弹簧线径（即弹簧直径）
N表示弹簧的总匝数
a表示弹簧杆的平均半径（即弹簧线径d加上弹簧线圈直径D 的一半的平均值）
这个公式可以用于计算弹簧的刚度系数，从而进一步计算弹簧的力学性能和设计要求。
弹簧刚度计算公式 推导
弹簧刚度计算公式推导摘要：1.弹簧刚度的定义与意义2.弹簧刚度计算公式的推导3.弹簧刚度计算公式的应用4.弹簧刚度在工程中的重要性正文：一、弹簧刚度的定义与意义弹簧刚度是指弹簧在受到外力作用时，其变形量与所受外力之比。
具体来说，就是单位变形所需的载荷。
弹簧刚度是弹簧的一个重要特性，它直接影响弹簧在实际应用中的性能和效果。
在工程中，弹簧刚度要求严格，因为刚度不足或过大都会导致弹簧性能不佳，影响设备的运行和使用寿命。
二、弹簧刚度计算公式的推导弹簧刚度计算公式是f"df/d，其中f 表示载荷增量，d 表示变形增量。
这个公式是从弹簧的工作原理和力学原理推导得出的。
弹簧刚度与弹簧的材料、尺寸、形状等因素有关。
在实际应用中，弹簧刚度的计算需要考虑这些因素，以确保弹簧的性能和使用效果。
三、弹簧刚度计算公式的应用弹簧刚度计算公式在工程中具有广泛的应用。
在设计弹簧时，工程师需要根据弹簧的工作环境和性能要求，确定弹簧的材料、尺寸和形状，然后利用刚度计算公式计算弹簧的刚度，以确保弹簧在实际应用中具有良好的性能。
在制造和使用弹簧时，工程师也需要根据弹簧的刚度要求，进行质量检测和性能测试，确保弹簧的质量和使用效果。
四、弹簧刚度在工程中的重要性弹簧刚度在工程中具有重要意义。
它直接影响弹簧的性能、使用寿命和设备的运行效果。
在工程设计中，工程师需要根据弹簧的工作环境和性能要求，合理选择弹簧的材料、尺寸和形状，以确保弹簧具有良好的刚度性能。
在制造和使用过程中，工程师也需要根据弹簧的刚度要求，进行质量检测和性能测试，确保弹簧的质量和使用效果。
弹簧刚度计算
50
簧 径：有效圈d 数:弹簧刚n
0.7
mm
4
材料： 65Mnτ
拼圈高度
度允：许极限
0.2923 kgf/mm 2.8661
N/mm
负荷：
（参考）
P极3限负荷
0.97
kgf 9.5
N
设 9.0
弹簧总变
11.65217
材料剪切弹 性系数：
mm 3.3
mm
拉伸（压缩）弹簧计算 （方旋案绕比五：）
8030 kgf/mm2
钢丝直 径： d 旋绕比： C=D2/d
材料剪切弹 性系数：
弹簧中 径：
D2
钢丝直 径：有效圈d 数:弹簧刚n 度允： 许极限 负荷： P极3限负荷 弹簧总变
材料剪切弹 性系数：
弹簧中 径：
D2钢丝直
径：有效圈d 数:弹簧刚n 度允： 许极限 负荷：
钢丝直径与旋绕比选择
0.2～0.4 0.45～1 1.1～2.2 2.5～6 7～16
2
42.0 6.4211
94
5
6
5
56.5 15.2727
25
3
3
3
11.5 7.6000
注：H、d、n、b为可变参数，圈数n按4舍5入方法计算。
8^2=64
64^(1/3)=4
方案四）
8.428571
1.1739
方案五）
50 拼圈高度 （参考）
3.5
12.15909
1.1178
50 拼圈高度 （参考）
b≤3 b≤3
0.93 0.34
钢丝直径 弹簧中径
工作圈数
最小工作
负荷下变
n1
弹簧总刚度
弹簧总刚度"弹簧总刚度" 是一个工程力学和弹性力学领域的概念，通常涉及到弹簧的设计和性能分析。
弹簧总刚度表示弹簧在受力时的整体刚度，是弹簧系统对外界加载的响应的一个重要参数。
以下是关于弹簧总刚度的一些基本概念和相关信息：1. 弹簧总刚度的定义弹簧总刚度是指弹簧在受到一定的外力或位移作用时，所表现出的整体刚度。
刚度通常用弹性系数（弹性常数）来表示，它是弹簧的材料和几何特性的函数。
2. 弹簧总刚度的计算弹簧总刚度的计算涉及到弹簧的材料、几何形状、工作原理等多个因素。
对于一些简单的情况，弹簧总刚度可以通过胡克定律（Hooke's Law）计算，即刚度等于受力与位移的比值：是弹簧总刚度（弹性系数）。
是作用在弹簧上的力。
是由于受力而发生的弹簧的位移。
对于复杂的弹簧系统，可能需要考虑弹簧的材料特性、弯曲形状、叠加效应等因素，使用更复杂的数学模型和方法进行计算。
3. 弹簧总刚度与刚度的变化弹簧总刚度可能会受到温度、疲劳、变形等因素的影响而发生变化。
在一些情况下，这些因素可能导致弹簧的刚度减小，甚至失去其弹性性能。
因此，在设计和使用弹簧系统时，需要考虑这些因素，以确保系统的性能和可靠性。
4. 工程应用弹簧总刚度的概念在各种工程应用中都有重要的作用，如机械工程、汽车工程、建筑工程等。
在这些领域，弹簧总刚度的准确计算和控制对于系统的正常运行和性能至关重要。
总结弹簧总刚度是描述弹簧系统刚性的重要参数，对于设计和分析弹簧系统的性能至关重要。
在实际应用中，需要考虑多种因素，使用适当的数学模型和方法来计算和控制弹簧总刚度，以确保系统的可靠性和稳定性。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
75 拼圈高度 （参考）
允许极限负荷： P3
kgf/mm 0.3943 #DIV/0! kgf
0.0402 f3
N/mm N mm
N 0.00 4.17 8.37 12.63 16.90 21.10
p' ###### ###### ###### ###### ###### ###### ######
拉伸（压缩）弹簧计算 （方案三）
弹簧中径： 钢丝直径： 有效圈数: 弹簧刚度： D2 d n P` 拉、压弹簧：
拉伸（压缩）弹簧计算 （方案六）
8140 kgf/mm2 26.75 2.2 20.25 0.0615 6.99 f3 kgf/mm 0.6030 kgf 68.6 mm 113.7 mm mm
62.2
第四步（方案确定设计计算） 60.00 kgf/mm2 节距 75.00 kgf/mm2 自由高度或长度: YI型 8030 kgf/mm2 5.7500 L型（不加钩环尺寸） 1.2649 压缩弹簧稳定性指标: YI型 4.00 mm 23.00 mm L型（不加钩环尺寸） 6.00 当b＞3时，弹簧须套在心轴上使
CM8（计算弹簧刚度及有关参数） 材料剪切弹性系数： G 8030 kgf/mm2 旋绕比： C=D2/d 12.18182 弹簧中径： D2 26.8 mm 拉、压弹簧： K 1.1176 钢丝直径： d 2.2 mm
有效圈数: 弹簧刚度： n P` 28.25 0.0432 10.47 f3
材料：65Mnτ (kgf/mm2)
角度正弦值的计算方法：SIN(30*PI()/180) 角度正切值的计算方法：TAN(45*PI()/180)
角度余弦值的计算方法：COS(60*PI()/180) 乘方或开方计算方法:
拉伸（压缩）弹簧计算 （方案一）
材料剪切弹性系数： G
弹 簧 设 计 验 算
国内专利网
材料：65Mnτ (kgf/mm2)
弹簧中径： 钢丝直径： 有效圈数: 弹簧刚度：
D2 d n P`
拉、压弹簧：
材料：65Mnτ (kgf/mm2)
N/mm N mm
N/mm N mm
允许极限负荷： P3
允许极限负荷： P3 极限负荷弹簧总变形量：
极限负荷弹簧总变形量：
拉伸（压缩）弹簧设计计算步骤
8000 kgf/mm2 5.9 0.7 4 0.2923 0.97 f3 kgf/mm 2.8661 kgf mm 9.5 3.3 mm mm
旋绕比：
C=D2/d K
弹簧中径： 钢丝直径： 有效圈数: 弹簧刚度：
D2 d n P`
拉、压弹簧：
弹簧中径： 钢丝直径： 有效圈数: 弹簧刚度：
D2 d n P`
钢丝直径与旋绕比选择
钢丝直径： 旋绕比： d C=D2/d 0.2～0.4 7～14 0.45～1 5～12 1.1～2.2 5～10 2.5～6 4～10 旋绕比： 7～16 4～8 C=D2/d K 18～24 4～6 7 1.2129 50 拼圈高度 （参考） 16.0 C=D2/d 11.65217 K 1.1232 50 拼圈高度 （参考） 60.4 C=D2/d K 11.25 1.1278 50 拼圈高度 （参考） 65.4
极限负荷弹簧总变形量：
圆柱簧（计算弹簧刚度及有关参数） 材料剪切弹性系数： G 8030 kgf/mm2 旋绕比： C=D2/d 5.857143 弹簧中径： D2 20.5 mm 拉、压弹簧： K 1.2594 钢丝直径： d 3.5 mm
有效圈数: 弹簧刚度： n 1.5 48.91 f3
材料：65Mnτ (kgf/mm2)
弹簧中径： 钢丝直径： 有效圈数: 弹簧刚度： D2 d n P` 拉、压弹簧：
拉伸（压缩）弹簧计算 （方案五）
8030 kgf/mm2 26.75 2.2 20.25 0.0607 6.99 f3 kgf/mm 0.5949 kgf 68.6 mm 115.3 mm mm
材料：65Mnτ (kgf/mm2)
弹簧材料：60Si2Mn 弹簧材料：60Si2Mn 弹簧剪切弹性系数 弹簧指数： 曲度系数 钢丝直径 弹簧中径 工作圈数 总圈数 最小工作负荷 最大工作负荷 允许极限负荷 极限负荷单圈变形量 弹簧钢丝间距 弹簧刚度 最大工作负荷下间距 C=D2/d
第二步（验算弹簧工作圈数及有关参数） [τ ] 60.00 kgf/mm2 节距 τ 75.00 kgf/mm2 自由高度或长度: YI型 G 8030 kgf/mm2 C 5.7500 L型（不加钩环尺寸） K 1.2649 压缩弹簧稳定性指标: YI型 d 4.00 mm D2 23.00 mm L型（不加钩环尺寸） n 5.21 当b＞3时，弹簧须套在心轴上使 n1 7.21 最小工作负荷下变形量 P1 26.60 kgf 最大工作负荷下变形量 P2 34.70 kgf 极限负荷下变形量 P3 64.79 kgf 最小工作负荷下高（长）度 f3 3.07 mm 最大工作负荷下高（长）度 δ 3.07 mm 极限负荷下高（长）度 P` 4.0500 kgf/mm 螺旋角 δ 1 1.42 mm ←δ 1（适用于压缩弹簧，指
允许极限负荷： P3
kgf/mm 0.4225 kgf 102.7
243.1
N/mm N mm
极限负荷弹簧总变形量：
62.2 mm 0 0 0 0 10 4.2 4.1 4.2 20 8.4 8.3 8.4 30 12.6 12.6 12.7 40 16.9 16.9 16.9 50 21.1 21.1 21.1 d=2.2 D=28.8 n=22.75
有效圈数: 弹簧刚度： n P` 28.25 0.0431 10.47 f3
材料：65Mnτ (kgf/mm2)
75 拼圈高度 （参考）
8.00 最小工作负荷下变形量 26.60 kgf 最大工作负荷下变形量 34.70 kgf 极限负荷下变形量 64.79 kgf 最小工作负荷下高（长）度 3.07 mm 最大工作负荷下高（长）度 3.07 mm 极限负荷下高（长）度 3.5199 kgf/mm 螺旋角 1.42 mm ←δ 1（适用于压缩弹簧，指
拉、压弹簧：
材料：65Mnτ (kgf/mm2)
材料：65Mnτ (kgf/mm2)
N/mm N mm 旋绕比：
N/mm N mm 旋绕比： C=D2/d K
允许极限负荷： P3
允许极限负荷： P3 极限负荷弹簧总变形量：
材料剪切弹性系数： G
极限负荷弹簧总变形量：
材料剪切弹性系数： G
拉伸（压缩）弹簧计算 （方案二）
75 拼圈高度 （参考）
P` 11.6559
允许极限负荷： P3
kgf/mm 114.305 kgf 479.6
4.2
N/mm N mm
0
20
40
60极限Βιβλιοθήκη 荷弹簧总变形量：5.3计算方法：COS(60*PI()/180) 8^2=64 64^(1/3)=4
方案四）
C=D2/d 8.428571 K 1.1739 50 拼圈高度 （参考） 3.5 C=D2/d 12.15909 K 1.1178 50 拼圈高度 （参考） 44.6 C=D2/d 12.15909 K 1.1178 50 拼圈高度 （参考） 44.6
弹簧材料：60Si2Mn 弹簧材料：60Si2Mn 弹簧剪切弹性系数 弹簧指数： 曲度系数 钢丝直径 弹簧中径 工作圈数 C=D2/d
[τ ] τ G C K d D2 n
75 拼圈高度 （参考）
允许极限负荷： P3
kgf/mm 0.4240 kgf 102.7
242.2
N/mm N mm
极限负荷弹簧总变形量：
25.00 20.00 15.00 10.00 5.00
0.00
系列1
截锥簧（计算弹簧刚度及有关参数） 材料剪切弹性系数： G 8000 kgf/mm2 旋绕比： C=D2/d 弹簧小中径： d2 1.9 mm 弹簧大中径： D2 2.4 mm 拉、压弹簧： K 钢丝直径： d 0.3 mm
有效圈数: 弹簧刚度： n P` 2.5
压缩弹簧稳定性指标: YI b≤ 型 3
型（不加钩环尺寸）
7.07 48.86 42.86 20.86 2.12 1.86 0.91 7.00 9.00 16.00 H-F1 H-F2 H-F3 0.10
mm mm mm mm
＞3时，弹簧须套在心轴上使用。
最小工作负荷下变形量 F1 F3
最大工作负荷下变形量 F2
弹簧中径： 钢丝直径： 有效圈数: 弹簧刚度：
D2 d n P`
拉、压弹簧：
材料：65Mnτ (kgf/mm2)
N/mm N mm 旋绕比：
N/mm N mm 旋绕比： C=D2/d K
允许极限负荷： P3
允许极限负荷： P3 极限负荷弹簧总变形量：
材料剪切弹性系数： G
极限负荷弹簧总变形量：
材料剪切弹性系数： G
拉伸（压缩）弹簧计算 （方案四）
材料剪切弹性系数： G
8030 kgf/mm2 7 1 16 0.1829 2.31 f3 8030 26.8 2.3 26.25 0.0556 7.94 f3 8030 27 2.4 27.25 0.0621 8.91 f3 kgf/mm 0.6089 kgf 87.4 mm 143.6 kgf/mm 0.5452 kgf 77.8 mm 142.8 kgf/mm2 mm mm kgf/mm 1.7936 kgf mm kgf/mm2 mm mm 22.7 12.6 mm mm
旋绕比：
拉、压弹簧：
材料：65Mnτ (kgf/mm2)