东南大学2013射频集成电路作业答案
2015年(秋)RFIC习题_参考答案
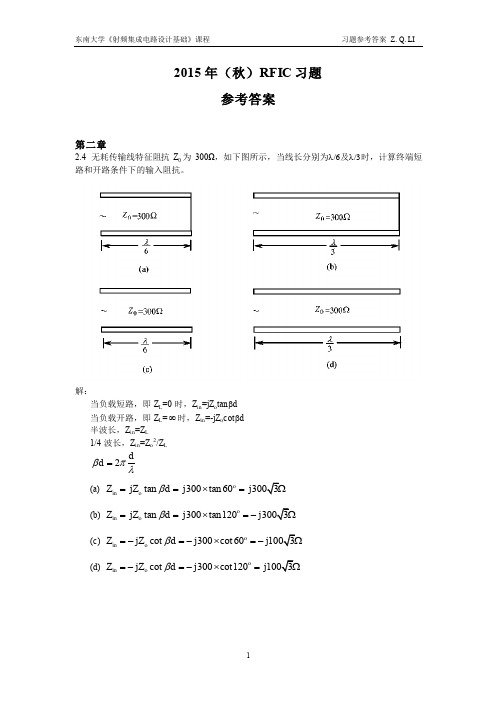
d avg
假设 R s 完全由趋肤效应所引起。
9
东南大学《射频集成电路设计基础》课程
习题参考答案 Z. Q. LI
解:
第五章
5.1 试比较本章介绍的几种接收机结构的优缺点。 答:见教材。 5.2 比较超外差接收机、 零中频接收机和低中频接收机在解决镜像抑制问题时所采用方法的 异同。 答:见教材。 5.11 某一超外差接收机射频部分各模块间相互匹配,它们的增益、噪声、输出三阶互调点 如下图所示,求: (1) (2) (3) 系统总的增益。 系统总的噪声系数。 计算级联后,各模块输入端的 IIP3,各模块输出端的 OIP3。
o
(d) Zin jZo cot d j 300 cot120 j100 3
o
1
东南大学《射频集成电路设计基础》课程
习题参考答案 Z. Q. LI
2.5 求出下图所示各电路的输入端反射系数 Γin 及输入阻抗 Zin 。
解:
Γ IN = Z IN Z 0 Z IN Z 0
东南大学《射频集成电路设计基础》课程
习题参考答案 Z. Q. LI
(1)系统总增益:Gtotal =-5+10-2-5-2+20+4-6+50=64dB (2)系统总噪声系数:使用 FRIIS 公式计算(注意公式中的变量均为非 dB 值)。
Ftotal F1 F 1 F2 1 F3 1 nn1 GA1 GA1GA2 i 1 GAi
混频器1 双工滤波器 混频器2 I中频滤 波器
LNA
镜频滤 波器
中放
II中频滤 波器
中放
Gain NF OIP3
L=5
10 2
《射频通信电路》习题和解答

《射频通信电路》习题和解答习题1:1、1本书使用得射频概念所指得频率范围就是多少?解:本书采用得射频范围就是30MHz~4GHz1、2列举一些工作在射频范围内得电子系统、根据表1-1判断其工作波段、并估算相应射频信号得波长。
解:广播工作在甚高频(VHF)其波长在10~1m等1、3从成都到上海得距离约为1700km。
如果要把50Hz得交流电从成都输送到上海、请问两地交流电得相位差就是多少?解:1、4射频通信系统得主要优势就是什么?解:1、射频得频率更高、可以利用更宽得频带与更高得信息容量2、射频电路中电容与电感得尺寸缩小、通信设备得体积进一步减小3、射频通信可以提供更多得可用频谱、解决频率资源紧张得问题4、通信信道得间隙增大、减小信道得相互干扰等等1、5GSM与CDMA都就是移动通信得标准、请写出GSM与CD MA得英文全称与中文含意。
(提示:可以在互联网上搜索。
) 解:GSM就是GlobalSystem for Mobile munications得缩写、意为全球移动通信系统。
CDMA英文全称就是Code Division Multiple Address,意为码分多址。
1、6有一个C=10pF得电容器、引脚得分布电感为L=2nH。
请问当频率f为多少时、电容器开始呈现感抗。
解:既当f=1、125GHz时、电容器为0阻抗、f继续增大时、电容器呈现感抗。
1、7 一个L=10nF得电容器、引脚得分布电容为C=1pF。
请问当频率f为多少时、电感器开始呈现容抗。
解:思路同上、当频率f小于1、59 GHz时、电感器呈现感抗。
1、81)试证明(1、2)式。
2)如果导体横截面为矩形、边长分别为a与b、请给出射频电阻RRF与直流电阻R DC得关系。
解:,s对于同一个导体就是一个常量当直流时、横截面积当交流时、横截面积得:2)直流时、横截面积当交流时、横截面积得:1、9已知铜得电导率为、铝得电导率为、金得电导率为。
东南大学2013射频集成电路作业答案
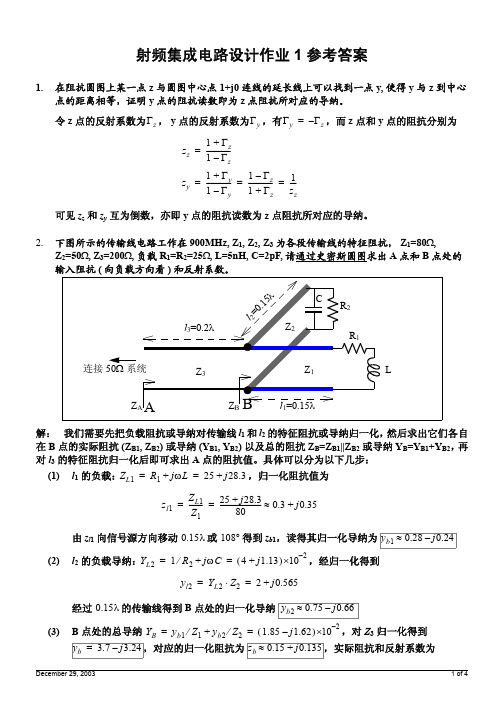
(2) 计算电感值
已知 µ = µ0 = 4π×10–7 H/m , n = 6 , c1 = 1.27 , c2 = 2.07 , c3 = 0.18 , c4 = 0.13 , 需要
求电感内径 : din = dout – 2[nw + (n – 1)s] = 68µm , 由此求得 davg = 184µm , ρ = 0.63 ;
-80
-100
0.1
0.41
-90
0.11
0.13
0.12
0.4
0.39
0.37
0.38
射频集成电路设计作业 1 参考答案
2 of 4
3. 对于图示阻抗变换电路,
C1
C1 Cs
C2
R2
Rs
Ceq
Cp
Rp
Rs
(1)
试证明近似式
Rp
≈
C-----1--C-+---1--C-----2
2
R2
成立并说明其成立的条件。
当 Q=4 时,Q2
=
1.803 ,
C2
=
6.380pF , C1
=
6.846pF ,
C-----1--C-+---1--C-----2
2
=
3.732 < R-R---p2-
当 Q=40 时,Q2
=
19.98 ,
C2
=
70.700pF ,
C1
=
70.735 pF ,
-C----1--C-+---1--C-----2
Rp ≈ ω-----2--1-C----e2--q- ω-----2---CR----222---R----22-
射频与通信集成电路设计习题参考答案

RL (1 Q2 ) RS
Q RS 1 50 1 0.816
RL
30
X Lp
X L' (1
1 Q2
)
QRL (1
1 Q2
)
61.24
Q L ' L ' QRL
RL
L QRL 15 0.81630 15 0.63nH 2π 2.4109
LP
X Lp
61.24 2π 2.4109
Qn=2 4.58nH
2.91nH
1.53pF
(b)
(b)
Qn=2
2.44nH
2.61pF
3.76pF
Qn=2
1.79pF
1.69nH
2.22nH
6
东南大学《射频集成电路设计基础》课程
(二)计算法 1)L 型匹配网络计算
L
j15
L’
LP
C
0(RL)
C
习题参考答案 Z. Q. LI RL(1+Q2)
(a)
(b)
L=0.64nH C=1.09pF
C=1.67pF L=4.06nH
5
东南大学《射频集成电路设计基础》课程
2)具有最大节点品质因数为 2 的 T 型匹配网络
习题参考答案 Z. Q. LI
Qn=2 947.6fF
890.9fF
2.9nH
(a) 3)具有最大节点品质因数为 2 的型匹配网络 (a)
(d) ZIN 2Zo ,
1 ΓIN = 3
2.7 请将下图中 Smith 圆图上的曲线与它们的性质对应起来,并填入到下表中。
曲线性质
曲线编号
某频率点上的 LC 网络阻抗匹配
东南大学历年电路试卷2010~2011期中A(答案)

t
15 5e 10 tV
9
t 0
六、图示电路中,已知 U=8V。求: (1) R 为何值时它消耗的功率为最大?并求出此功率。 (2) 求 R=12Ω时电流 I 和 I1 的值
I1 + U - U - + U - 16Ω 16Ω + U - 8Ω 16Ω + U - 8Ω 16Ω + U - 8Ω 16Ω + 8Ω 16Ω I R
i1 4A R S 10i1
i L
九、叙述并证明戴维宁定理。
共5页 第5页
共5页
第1页
i1 2 i1 2 A 20 20i 20i 10 10 I i 1A 2 3 2 7i1 20i2 7 20 3i3 4 i3 1A I 1A I i1 i2 CCVS 的功率为 P 10I i2 10 11 10W
Ix -
2Ω
U
2Ω 1.5U
共5页 第2页
五、在 t=0 时刻,图中开关闭合,求电流 i(t)及电容的电压 u(t)。
t=0
5W
i
+ 20V -
2A
5W
+
u
- 400pF
解:开关闭合前,电容断V
所以
u0 u0 10V
开关闭合无限长时间后,电容断路处理,则
共5页 第3页
解:反复利用电源的等效变换,可得到除 R 之外的电路其它部分的戴维宁等效电路为:
8Ω + 8V -
所以当 R=8Ω时,其消耗的功率最大,此功率为 (2)当 R=12Ω时,易求 I=8/(12+8)=0.4A 反复倒退计算,得 I1=0.0125A 七、求图中电阻能获得的最大功率。
2013东大真题解答

图 1 题二电路图
= 解:Ru0/r/(ss)C10
−uc(s) R1+sC11
T(s) = − (R0C0s+1)(R1C1s+1)
R0C1s
三、(共 20 分)已知控制系统结构图如图 2 所示,其中������������(������)的单位脉冲响应为������������ − ������������������−������。 试分析内反馈������������的存在对系统稳定性以及系统稳态误差的影响。
继电器特性描述函数:������(������) = ������������ √������ − (������)������ ,������ ≥ ������。
������������
������
图 4 题七系统结构图
解:W (s)
3
, W ( j)
j3
s(0.8s 1)(s 1)
(s + 2)[(s + 2)(s + 5) − (s − 1)(2s + 10 + s + 2)] = 0 ������1 = −2,为两个开环极点 ������2 + ������ − 11 = 0
������ = −1±√1+44 = −1±6.7,
2
2
������2 = 2.85(舍去),������3 = −3.85——分离点
−1]Βιβλιοθήκη Kz−1(0.368 + 0.264Zz−1) = (1 − 0.368z−1)[1 + (K − 1)z−1]
所以,Wk(Z)
=
Z
[1]
s
∙
Wk1(Z)
射频集成电路与系统 RFIC习题_参考答案

L=0.64nH
C=1.09pF
( b)
C=1.67pF
L=4.06nH
5
东南大学《射频集成电路设计基础》课程
习题参考答案 Z. Q. LI
2)具有最大节点品质因数为 2 的 T 型匹配网络
Qn=2 947.6fF 890.9fF
4.58nH
Qn=2 2.91nH
2.9nH
1.53pF
(a) 3)具有最大节点品质因数为 2 的型匹配网络 (a)
d 2
d
o
(a) Zin jZo tan d j300 tan 60 j300 3 (b) Zin jZo tan d j300 tan120 j300 3
o
(c) Zin jZo cot d j 300 cot 60 j100 3
(b)
Qn=2 2.44nH
2.61pF
3.76pF
(b)
Qn=2 1.79pF
1.69nH
2.22nH
6
东南大学《射频集成电路设计基础》课程
习题参考答案 Z. Q. LI
(二)计算法 1)L 型匹配网络计算
L j15 0(RL)
L’ C
C
LP
RL(1+Q2)
RL (1 Q2 ) RS
东南大学《射频集成电路设计基础》课程
习题参考答案 Z. Q. LI
2012 年(春) RFIC 习题 参考答案
第二章
2.4 无耗传输线特征阻抗 Z0 为 300Ω,如下图所示,当线长分别为及时,计算终端短 路和开路条件下的输入阻抗。
解: 当负载短路,即 ZL =0 时,Zin =jZo tand 当负载开路,即 ZL = 时,Zin =-jZo cotd 半波长,Zin =ZL 1/4 波长,Zin =Zo 2 /ZL
射频电路基础复习题答案

一、选择1.传输线输入阻抗是指传输线上该点的( B )A.入射电压与电流比B.电压与电流之比C.入射电压波之比D.入射电流波之比2.传输线的无色散是指(C )与频率无关。
A.波的速度B.波的能量流动的速度C.波的相速D.波的群速3.当传输线处于行波工作状态时,传输线的反射系数为(C )。
A.1 B.-1 C.0 D.无法判断4.下面哪一种不能构成纯驻波状态的传输条件是(D )。
A.Z L=0 B.Z L=∞C.Z L=jX .Z L= Z05.驻波系数ρ的取值范围是(D )。
A.ρ=1 B.0≤ρ≤1 C.0≤ρ<1 D.1≤ρ<∞6.在史密斯圆图中坐标原点表示(C )。
A.开路点B.短路点C.匹配点D.无法判断7.均匀无耗传输线终端开路时对应于史密斯圆图的(A )。
A.右端点B.左端点C.原点D.上顶点8.无耗均匀传输线的特性阻抗为50Ω,终端负载阻抗为32 Ω,距离终端λ/4处的输入阻抗为(D )Ω。
A.50 B.32 C.40 D.78.1259.当终端反射系数为0.2时,传输线的驻波比为(B )。
A.2 B.1.5 C.0.67 D.无法判断10.微带传输线传输的电磁波是( B )。
A.TEM波B.准TEM波C.TE波D.TM波二、判断题11.无耗均匀传输线上各点的电压反射系数幅值都相等。
对12.已知无耗均匀传输线的负载,求距负载一段距离的输入阻抗,在利用史密斯圆图时,找到负载的归一化电抗,再顺时针旋转对应的电长度得到。
错13.当均匀无耗传输线终端接感性负载时,传输线工作在行驻波工作状态下。
错14.在史密斯圆图上左半实轴部分是电压的波节点。
对15.为了消除传输线上的反射,通常要在传输线的终端进行阻抗匹配。
对16.微带线可以作为传输线,用在大功率传输系统中。
错17.在无耗互易二端口网络中,S12=S21。
对18.二端口转移参量都是有单位的参量,都可以表示明确的物理意义。
错19.均匀无耗传输线工作在行波状态时,沿线各点的电压和电流均不变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)
以上推导均假设串并转换过程中电路 Q 值足够大,转换前后的电阻值之间仅为 Q2 的关系 而电容值保持不变。 C1 Cs 1 - ,Q = ω C R = -----------------1 - 及 C = -----------------由 Q 2 = ω C 2 R 2 = --------------可得 p p eq ω Cs Rs ω C eq R s C1 + Cs C s 1 -C 1 + Cs 1 - = --------------1- -----------------Q = -----------------= Q 2 1 + ----- ,因为 C s = C 2 1 + -----, 2 ω Cs Rs C1 ω C eq R s C1 Q2
C 1 + C 2 2 Rp - = 3.732 < ----当 Q=4 时,Q 2 = 1.803 , C 2 = 6.380pF , C 1 = 6.846pF , ----------------- C1 R2 C 1 + C 2 2 Rp - = 3.998 ≈ ----当 Q=40 时,Q 2 = 19.98 , C 2 = 70.700pF , C 1 = 70.735 pF , ----------------- C1 R2 由此验证了第一小题所给出公式在不同 Q 值情况下的近似程度。 4. 一个平面螺旋电感由 6 圈金属构成 , 总面积 300×300µm2 ( 如图所示 )。金属宽 16µm, 间距 4µm,厚 1µm,趋肤深度 δ 约 2µm ;主线圈与下层引出线之间相距 1µm、与衬底相距 5µm, 绝缘层介电常数 εox=3.9×8.854×10−18 F/µm,衬底等效的 Gsub=10−7 S/µm2, Csub=7×10−3 fF/µm2,
2 C2 QQ 2 – Q 2 C2 1 - 1 + ------ ,经过整理后即得 ----- = ----------------------Q = Q 2 1 + ----2 2 C1 C1 Q2 1 + Q2
(3)
在已知 ω, Q, R2 和 Rp 的情况下,可以先求出 Q2,由 Q2 解得 C2,再根据上一小题的结论 Rp R2 得到 C1 值。因为 R s = --------------- = --------------- , Q2 = 2 1 + Q2 1 + Q2 R2 Q2 ----- ( 1 + Q 2 ) – 1 , C 2 = ---------。 Rp ω R2
射频集成电路设计作业 1 参考答案
1. 在阻抗圆图上某一点 z 与圆图中心点 1+j0 连线的延长线上可以找到一点 y, 使得 y 与 z 到中心 点的距离相等,证明 y 点的阻抗读数即为 z 点阻抗所对应的导纳。 令 z 点的反射系数为 Γ z , y 点的反射系数为 Γ y ,有 Γ y = – Γ z ,而 z 点和 y 点的阻抗分别为 1 + Γz z z = -------------1 – Γz 1 + Γy 1 – Γz 1 - = -------------= --z y = -------------1 – Γy 1 + Γz zz 可见 zz 和 zy 互为倒数,亦即 y 点的阻抗读数为 z 点阻抗所对应的导纳。 2. 下图所示的传输线电路工作在 900MHz, Z1, Z2, Z3 为各段传输线的特征阻抗, Z1=80Ω, Z2=50Ω, Z3=200Ω, 负载 R1=R2=25Ω, L=5nH, C=2pF, 请通过史密斯圆图求出 A 点和 B 点处的 输入阻抗 ( 向负载方向看 ) 和反射系数。
December 29, 2003 1 of 4
–2
–2
zb – 1 - ≈ – 0.72 + j 0.2 ≈ 0.74 ∠164 ° Z B = z b ⋅ Z 3 = 30 + j 27 Ω ,Γ B = ------------zb + 1 (4) yb 经过 0.2 λ 后得到 A 点处的归一化导纳 ya,对应的归一化阻抗 z a ≈ 2.8 + j 3.22 ,于是 A 点处的阻抗和反射系数 ( 对应于 50 Ω 系统 ) 为 Z A – 50 - ≈ 0.92 + j 0.08 ≈ 0.93 ∠5.1 ° Z A = z a ⋅ Z 3 = 560 + j 644 Ω ,Γ A = ----------------Z A + 50 ZA 的精确值为 Z A = 554.4 + j 644.1 Ω,可见使用圆图可以达到很高的精确度。 附 : 各点标于圆图上
50
RESISTANCE COMPONENT (R/Zo), OR CONDUCTANCE COMPONENT (G/Yo) 0.2
50
20
0
0.
8
0.
0.
6
6
zb
0.2
0. 8
0.4
0. 43 0. -1 07 30
0.
4
40
0.
0. 2
6 0. 0.15 λ
0. 8
3.
0
3
21 0. 29 0. 30
0.1
0.
6
8 0.
yb
5.0
0.
3
5
0.
6
0.7
1.
1.4
0.8
1.2
0.9
1.0
射频集成电路设计作业 1 参考答案
0.
0.
33
17 60 -
1.
6
0.
32 18 0. 0 -5
8
0 2.
0.
0.
34
16
-70
5 0.3 5 0.1
0.36
0.14 -80
0.37
0.13
0.2
-90
0.12
0.38
0.
3
4.
0
zl1
1.
ቤተ መጻሕፍቲ ባይዱ
0
0.25 0.26 0.24 0.27 0.23 0.25 0.24 0.26 0.2 0. 2 7 2 2 . 3 8 0 LECTION COEFFICIENT IN 0.2 DEGR F REF 0.2 8 EES LE O 0.2 0 ANG -20 2 2
zb 1 yl2
OR
0.4
,
1.
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.2
1.4
1.6
1.8
2.0
3.0
4.0
5.0
10
20
0.0
0.0 180
0.49 0.48 AD <— O L D 7 R 0.4 TOWA -170 THS ENG 60 6 L 4 E 1 V 0. A W /Yo) <— (-jB 45 NCE 50 A . 1 T 0 EP 05 SC 0. SU E V 4 I 4 CT 0. 06 140 DU IN 0. OR ), Zo
0.
43 0. 0 13
1.
0.
07
6 0.
0. 2 4 0 0. 12
0.7
08
E IV IT AC P CA
) B/Yo (+j NCE A T EP SC SU
1.4
4 0.
110
0.1 5 0.3 5 70
0. 0.
16
34
60
8
0. 1 0. 7 33
0.
0.2
0.
18
2.
50
5
0
32
0. 19 0. 31
15
C Z2
λ
l3=0.2λ
l2 = 0.
R2 R1
连接 50Ω 系统 ZA A
Z3 ZB
Z1
L
B
l1=0.15λ
然后求出它们各自 解: 我们需要先把负载阻抗或导纳对传输线 l1 和 l2 的特征阻抗或导纳归一化, 在 B 点的实际阻抗 (ZB1, ZB2) 或导纳 (YB1, YB2) 以及总的阻抗 ZB=ZB1||ZB2 或导纳 YB=YB1+YB2, 再 对 l3 的特征阻抗归一化后即可求出 A 点的阻抗值。具体可以分为以下几步: (1) l1 的负载:Z L 1 = R 1 + j ω L = 25 + j 28.3 ,归一化阻抗值为 ZL1 25 + j 28.3 z l 1 = ------- = ------------------------ ≈ 0.3 + j 0.35 80 Z1 由 zl1 向信号源方向移动 0.15 λ 或 108 ° 得到 zb1,读得其归一化导纳为 y b 1 ≈ 0.28 – j 0.24 (2) l2 的负载导纳:Y L 2 = 1 ⁄ R 2 + j ω C = ( 4 + j 1.13 ) ×10 ,经归一化得到 y l 2 = Y L 2 ⋅ Z 2 = 2 + j 0.565 经过 0.15 λ 的传输线得到 B 点处的归一化导纳 y b 2 ≈ 0.75 – j 0.66 (3) B 点处的总导纳 Y B = y b 1 ⁄ Z 1 + y b 2 ⁄ Z 2 = ( 1.85 – j 1.62 ) ×10 ,对 Z3 归一化得到 y b = 3.7 – j 3.24 ,对应的归一化阻抗为 z b ≈ 0.15 + j 0.135 ,实际阻抗和反射系数为
µ n 2 d avg c 1 c 2 - ln ---- + c3 ρ + c4 ρ 2 L = ------------------------ ρ 2
