一矩形波导内的TE电磁波
电磁波与天线---矩形波导

mπ 当x=0时,A2=0.当x=a时, k x = a 同理可得, nπ 当y=0时,B2=0,当y=b时, y = k b
最后得: 最后得
mπ x nπ y − j β z H z = H 0 cos e cos a b
ˆ ax ∂ ∂x Hx ˆ ay ∂ ∂y Hy
(9) ( n = 0 ,1, 2 , L )
(1) TE10 模的场结构
• 在(10)式中,令 m=1, n=0, 并注意到 )式中, • 那么, 那么,
mπ 2 nπ 2 π 2 kc = ( ) +( ) =( ) a b a
2
H z = H 0 cos( x)e− j β z a π a H x = j β H 0 sin( x)e − j β z π a a π E y = − jωµ H 0 sin( x)e − j β z π a
−
∂H
y
= jω ε E
x
同理,可得 在直角坐标系中展开可得 在直角坐标系中展开可得: 同理,可得E在直角坐标系中展开可得:
解式中的变量Z因 解式中的变量 因 − jβ z 为e ,所以上面 的两式可以对Z的偏 的两式可以对 的偏 导数化解。 导数化解。我们仅 对其中的4个式子进 对其中的 个式子进 行化解
2 2
∇ H =0
利用公式:∇×(∇×H) =∇∇•H)−∇ H (
2
• 得:
∇ H + ω µε H = ∇ H + k H = 0
2
2
2
2
• 式中: • 同理
k = ω µε
2
∇ E+k E =0
2 2
• 导波系统中,我们用直角坐标系,在 直角坐标系中,我们以E为例分解:
矩形波导te模式

矩形波导te模式
摘要:
1.矩形波导的基本概念
2.矩形波导中的TE 模式
3.TE 模式的特点和应用
正文:
一、矩形波导的基本概念
矩形波导(Rectangular Waveguide)是一种用于传输电磁波的结构,其内部可以存在多种不同的电磁波模式。
矩形波导的结构主要由两个平行的金属壁和其间的介质构成。
根据波长的不同,矩形波导可以传输不同的模式,如TE 模式和TM 模式。
二、矩形波导中的TE 模式
TE 模式(Transverse Electric Mode)是矩形波导中一种常见的电磁波模式。
在TE 模式中,电场的纵向分量在传播方向上为零,而横向分量存在。
这种模式的电磁波在矩形波导内部沿着宽度方向传播,而电场的能量主要集中在波导的底部。
三、TE 模式的特点和应用
TE 模式具有以下特点:
1.在矩形波导内部,TE 模式具有稳定的传播特性。
2.TE 模式的能量集中在波导的底部,这使得它在实际应用中具有较高的传输效率。
3.TE 模式与TM 模式相比,具有更低的损耗和更远的传输距离。
TE 模式在实际应用中具有广泛的应用,如:
1.无线通信:TE 模式可用于微波通信系统、卫星通信系统等。
2.天线技术:TE 模式在天线设计中有着广泛的应用,如矩形微带天线、印制天线等。
3.雷达技术:TE 模式在雷达系统中具有重要的应用价值,如在合成孔径雷达(SAR)中,TE 模式可用于获取目标的纵向信息。
总之,矩形波导中的TE 模式具有稳定的传播特性、较高的传输效率以及广泛的应用前景。
矩形波导的模式(3篇)

第1篇一、矩形波导的模式分类矩形波导中的电磁波模式主要分为TE(横电磁波)模式和TM(纵电磁波)模式。
1. TE模式TE模式是指电场只在波导的横向(垂直于传播方向)分量存在,而磁场则在纵向(沿传播方向)分量存在。
根据电场和磁场在波导横截面上的分布,TE模式又可以分为TE10、TE20、TE01等模式。
(1)TE10模式:TE10模式是矩形波导中最基本、最常用的模式。
其电场分布呈矩形,磁场分布呈椭圆。
TE10模式的截止频率最高,适用于高频传输。
(2)TE20模式:TE20模式的电场分布呈矩形,磁场分布呈圆形。
其截止频率低于TE10模式,适用于中频传输。
(3)TE01模式:TE01模式的电场分布呈矩形,磁场分布呈椭圆。
其截止频率最低,适用于低频传输。
2. TM模式TM模式是指磁场只在波导的横向分量存在,而电场则在纵向分量存在。
根据电场和磁场在波导横截面上的分布,TM模式又可以分为TM01、TM11、TM21等模式。
(1)TM01模式:TM01模式的电场分布呈矩形,磁场分布呈圆形。
其截止频率最高,适用于高频传输。
(2)TM11模式:TM11模式的电场分布呈矩形,磁场分布呈椭圆。
其截止频率低于TM01模式,适用于中频传输。
(3)TM21模式:TM21模式的电场分布呈矩形,磁场分布呈圆形。
其截止频率最低,适用于低频传输。
二、矩形波导的模式特性1. 截止频率截止频率是矩形波导中一个重要的参数,它决定了电磁波在波导中能否有效传输。
不同模式的截止频率不同,其中TE10模式的截止频率最高,适用于高频传输。
2. 相速度相速度是指电磁波在波导中传播的速度。
不同模式的相速度不同,TE模式的相速度比TM模式快。
3. 模式损耗模式损耗是指电磁波在波导中传播时,由于波导壁的吸收和辐射等原因,能量逐渐衰减的现象。
不同模式的损耗不同,TE模式的损耗比TM模式小。
4. 传输特性矩形波导中不同模式的传输特性不同,如TE模式的传输特性较好,适用于高频传输;TM模式的传输特性较差,适用于低频传输。
微波技术矩形波导中电磁波的通解要点

微波技术矩形波导中电磁波的通解要点矩形波导是一种常见的微波传输线结构,具有广泛的应用,如微波通信、雷达系统和微波功率传输等。
在矩形波导中,电磁波的传播可以通过求解波动方程得到其通解。
下面将介绍矩形波导中电磁波的通解的要点。
矩形波导中的电磁波动方程是由Maxwell方程组给出的。
在无源情况下,即没有电流密度和电荷密度,Maxwell方程组可以简化为两个波动方程,即:(1)对电场E的波动方程:∇^2E+k^2E=0(2)对磁场H的波动方程:∇^2H+k^2H=0其中,k为波数,k=ω/c,ω为角频率,c为光速,∇^2为Laplace 算子。
为了求解上述波动方程,我们需要确定边界条件。
(1)边界条件:矩形波导具有无限大的边界,因此我们可以选择适当的坐标系来求解波动方程。
一种常见的坐标系选择是矩形坐标系,其中坐标轴沿着波导的边界方向。
在矩形波导的壁面上,电场E和磁场H应满足如下边界条件:a)电场E与波导壁面垂直,即E·n=0,其中n为壁面的法向量;b)磁场H与波导壁面平行,即H·n=0。
(2)模态理论:矩形波导中的电磁波存在多个模式,每个模式由一组特定的场分布和频率特征确定。
每个模式都对应于特定的截止频率,超过这个频率时将不能在波导中传播。
对于矩形波导,存在两个基本的模式,即TE (Transverse Electric)模式和TM (Transverse Magnetic)模式。
TE模式是指电场E的一部分为零,也就是垂直于波导壁面的电场分量为零。
TE模式有多种类型,根据电场分布情况的不同而命名。
例如,TE10模式表示只有横向电场分量的模式,而TE20模式表示有两个横向电场分量的模式。
TM模式是指磁场H的一部分为零,也就是垂直于波导壁面的磁场分量为零。
TM模式也有多种类型,根据磁场分布情况的不同而命名。
例如,TM11模式表示只有横向磁场分量的模式,而TM30模式表示有三个横向磁场分量的模式。
《矩形波导TE波》PPT课件

2021/8/17
17
二、TE10波的功率和容量
图 13-5 尖端效应影响耐功率
2021/8/17
18
三、TE10波内壁电流
在电磁理论中已经讲过波导管壁的传导电流分
布是由管内磁场的切向分J 量s 所n 决H 定r 。
(13-8)
Js
Ht
n
图 13-6 波导管内壁电流
2021/8/17
19
三、TE10波内壁电流
目前的雷达战中,对提高峰值功率容量极为重视。
因为在一定意义上,功率就是作用距离,所以增加传
输线功率容量相当重要。
气体击空的实质是场拉出游离电子在撞到气体分子
之前已具有足够的动能,再次打出电子,形成连锁反
应,以致击穿。如果在概念上,我们加大气体密度,
就不会出现很大动能的电子,所以加大气压和降低温
度是增加耐压功率的常用办法。
是一个问题的两个方面:增加功率是为了使通讯雷
达“看”远,减小衰减是为了保证功率不受损失,
一个“增产”,一个“节支”,相互依存,缺一不
可。
一般认为波导空间(Air Space)是无耗的,所谓
衰减是指电流的壁损耗。假定P0是理想导体波导的
传输功率,则
P P0 e 2 az
P z
2aP0 e 2az
2021/8/17
2
波型阻抗
1
2021/8/17
1
2a
2
5
一、TE10波的另一种表示
我们在上面给出的TE10波表达式,是以Hz为领矢
矢量的。然而,在实用上也常有用Ey作领矢矢量,即
设
Ey E0sinaxejz
(13-1)
利用Maxwell方程
矩形波导中电磁波截止波长的计算(1)(1)

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载矩形波导中电磁波截止波长的计算(1)(1)地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容矩形波导中电磁波截止波长的计算周和伟物理与电子信息工程学院 07物理学 07234030[摘要]:本文从麦克斯韦方程组出发,从理论上推导了电磁场遵循的波动方程和时谐电磁波遵循的波动方程;根据边值关系从理论上求出了时谐电磁波在矩形波导中的解,并对矩形波导管中传播的电磁波波解进行了讨论;计算了不同尺寸的矩形波导管的截止波长,截止波长大多属于厘米量级,说明波导管只适用于传播微波。
[关键词]:矩形波导电磁波截止波长1 绪言波导是一种用来约束或引导电磁波传输的装置,矩形波导是指横截面是矩形的波导,一般是中空的金属管。
也有其他形式的波导装置,如介质棒或由导电材料和介质材料组成的混合构件[1]。
因此,在广义的定义下,波导不仅是指矩形中空金属管,同时也包括其他波导形式如矩形介质波导等,还包括双导线、同轴线、带状线、微带和镜像线、单根表面波传输线等。
根据波导横截面的形状不同还有其他形状波导,如圆波导等。
尽管已存在很多不同波导形式,且新的形式还不断出现,但直到目前,在实际应用中矩形波导是一种最主要的波导形式。
由于无线信号传输媒介,具有传输频带宽、传输损耗小、可靠性高、抗干扰能力强等特点,因此波导技术在电子技术领域运用非常广泛,主要用于铁氧体结环形器,窄壁缝隙天线阵[2],速调管矩形波导窗,高精度矩形弯铜波导管加工研究【3】等器件设备的制造生产,以及在地铁信号系统中的应用都很广泛。
为了加深对波导传输特性的理解,本文从麦克斯韦方程组出发,推导了电磁场遵循的波动方程和时谐电磁波遵循的波动方程;根据边值关系从理论上求出了时谐电磁波在矩形波导中的解,并对矩形波导管中传播的电磁波波解进行了讨论;计算了不同尺寸的矩形波导管的截止波长,发现其截止波长都在厘米量级,说明波导管只适用于传播微波。
《电磁场与微波技术教学课件》2.2 矩形波导
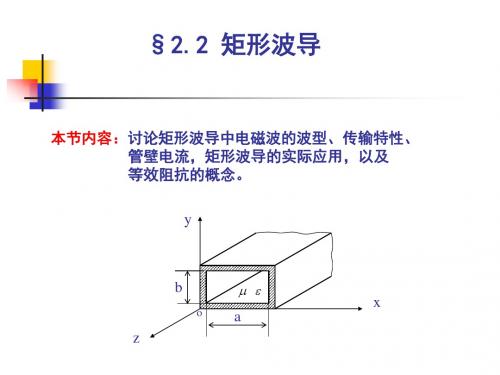
n m n j z H y 2 H0 cos x sin y e b a b Kc
n m n j z Ex j 2 H 0 cos x sin y e b a b Kc
* (5)由 S E H ,在z向有实功率,传输能量;在横向是虚功率,
只存储能量。
§2.2 矩形波导
2.截止波长和简并波形 截止波数:
n 2 2 2 m Kc Kx Ky a b
2 2
m n Kc a b
§2.2 矩形波导
通解也可以写成下面的形式 X A cos( K x x x ) (2-70) Y B cos( K y y y ) (2-71)
A、φx、 B、 φy 、Kx、Ky为待定常数 (6个) 当考虑纵向行波传输规律时,电场强度可写成
Ez ( x, y, z) X ( x)Y ( y)Z ( z) E0 cos(Kx x x ) cos(K y y y )e jz (2-72)
内表面上的切向磁场强度 横向磁场决定纵向电流; 纵向磁场决定横向电流
§2.2 矩形波导
H10波各波导壁上的面电流密度为:
在x=0窄壁上
ˆz ˆH 0 cos(t z) J y ˆH z y J S n H x
在x=a窄壁上
ˆz ˆH 0 cos cos(t z) J y ˆH z y J S n H x
m, n 0
§2.2 矩形波导
分析: (1) m、n为自然数,分别表示常量沿x轴和y轴出现的 半周期数; (2) 不同的m、n对应一种波型TEmn,m、n不能同时为零, 但有一个可以取零。 最低次波型为TE10(a>b)或TE01 (a<b)。
矩形波导中电磁波的传播模式

矩形波导中电磁波的传播模式矩形波导是一种常见的波导结构,它由四个边界构成,上下为金属板,左右为无限长的平行金属条。
矩形波导中存在多种电磁波的传播模式,如TE模式、TM模式和TEM模式等。
下面将分别介绍这些模式的特点和传播方式。
1. TE模式(Transverse Electric mode)在TE模式中,电磁场的电场的矢量只存在于横向方向,并且垂直于波导的传播方向。
在该模式中,磁场的矢量沿着波导的传播方向。
这意味着在TE模式下,波导内部的电场是零,而磁场是非零的。
因此,TE模式也被称为横电模。
TE模式可进一步分为多种亚模式,如TE10、TE20等。
其中,TE10模式是最低频的模式,在矩形波导中最常用。
TE10模式中,电磁波沿短边传播,且边界条件要求电场分量为零。
其传播速度取决于矩形波导的长边尺寸和频率。
当频率低于截止频率时,该模式不再存在。
2. TM模式(Transverse Magnetic mode)在TM模式中,电场的矢量只存在于横向方向,并且垂直于波导的传播方向。
而磁场的矢量沿着波导的传播方向。
因此,在TM模式下,波导内部的磁场是零,而电场是非零的。
所以,TM模式也被称为横磁模。
TM模式同样可以分为多种亚模式,如TM11、TM21等。
其中,TM11模式也是最常见的模式,在矩形波导中使用较为广泛。
在TM11模式中,磁场沿短边传播,且边界条件要求磁场分量为零。
和TE10模式类似,其传播速度也取决于波导的尺寸和频率,当频率低于截止频率时,该模式也不再存在。
3. TEM模式(Transverse Electro-Magnetic mode)在TEM模式中,电场和磁场的矢量都存在于横向方向,并且垂直于波导的传播方向。
在TEM模式下,波导内部的电场和磁场都是非零的。
由于在波导内部,电场和磁场都存在,而且正交分布,所以也被称为横电磁模。
TEM模式是矩形波导中的基本模式,同时也是最简单的模式。
在TEM模式中,电磁波的传播速度与真空中的光速相同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
则有
f
1 (x)
2
f (x) x2
1 g( y)
2g(y) y2
k c2
0
分离变量
f
1 (x)
d
2 f (x) dx 2
k
2 x
1 g( y)
d 2g(y) d y2
k
2 y
其中
k
2 x
k
2 y
k
2 c
2
k2
写成标准形式
d
2 f (x) dx 2
k
2 x
f
第九章课后习题
• 9.1; 9.2;9.3;9.4;9.5;9.8;9.9;9.10; 9.11;9.15;9.20;9.23
①无界媒质中 麦克斯韦方程的解 波导中 麦克斯韦方程的解
均匀平面电磁波 导行电磁波
②波导
广义:用来导引电磁波进行定向传输的装置。
{习惯上
按结构分: 平行双线传输线、同轴线、带线和微带线等
j E0y
H0y x
H0x y
j E0z
E0z y
E0y
j H 0x
E0x
E0z x
j H0y
E0y x
E0x y
j H 0z
电磁场共有六个分量,但其中四个横向分量可以用两个纵向分量导出
因此可以得到由纵向分量 E0z H 0z 表示的横向分量表达式
E0x ( y 0) 0
①
E0x ( y b) 0
②
E0y (x 0) 0
③
E0y (x a) 0
2H0z y2
( 2
k 2 )H0z
0
令
k
2 c
2
k2
,
2 t
2 x2
2 y2
则以上两式可以写成
2 t
E0
z
k
2 c
E0
z
0
2 t
H
0
z
k
2 c
H
0z
0
求解这两个纵向分量的方程,就可以得到波导中的电磁场解。
2、波导中电磁波解的分类
① kc 0 E0z 0 , H0z 0 E0z 0 , H0z 0 E0z 0 , H0z 0
h1 u1
Ez
j H
z
1 1 1
H u1
Hu2
kc2
h1
1
h2
u1 u2
h2 u2
1 1
h1 u1
Hz
j
Ez
在直角坐标系中, h1 h2 1 u1 x, u2 y
在圆柱坐标系中, h1 1
h r
u1
u2
电场、磁场都满足齐次亥姆霍兹方程
2E k2E 0
2H k2H 0
由此可求得电磁场纵向分量满足以下方程
2E0z x2
2E0z y2
( 2
k 2 )E0z
0
2H0z x2
横电波或TE波,也称为磁波或H波 横磁波或TM波,也称为电波或E波 TE波和TM波的组合叠加
② kc 0 只有当 E0z H0z 0 时,才可能有不等于零的横向场分量 导行电磁波的电场分量和磁场分量都垂直于传播方向, 故称为横电磁波或TEM波 。
§9.2 矩形波导管中的电磁波
矩形波导管轴线与 z 轴方向一致, y
其中 k 2 2
可见,若求得了E0z和 H 0z,则电磁场的各分量就可求得。
在广义坐标系下,电磁场的横向电磁分量可由纵向电磁分量来 导出,写成矩阵的形式为
1
Eu1
Eu2
kc2
h1
1
h2
u1 u2
11
h2 u2
1 1
内壁坐标分别为
b
x0 , xa , y0 , yb
假设波导管材料为理想导体,
内部为理想介质。
z
一. 矩形波导内的 TE 电磁波
, , =0
ax 图9-1 矩形波导管
因为 E0z 0 , H0z 0 ,所以只需求解方程
2 t
H
0
z
k
2 c
H
0
z
0
可利用分离变量法求解,令 H0z f (x) g( y)
E0x
2
1 k2
(
E0z x
பைடு நூலகம்
j H 0z ) y
E0y
2
1 k2
(
E0z y
j H 0z ) x
H0x
2
1 k2
( j
E0z y
H0z ) x
H0y
2
1 k2
( j
E0z x
H0z ) y
(x)
0
d
2 g( y) dy 2
k
2 y
g( y)
0
两方程的解分别为 f (x) Asin kx x B cos kx x
g( y) C sin ky y D cos ky y
所以 H 0z ( Asin kx x B cos kx x)(C sin k y y D cos k y y)
利用横向分量与纵向分量的关系可得两个磁场分量
E0x
j
k
2 c
k y (Asin k x x
B cos k x x)(C cos k y y
D sin k y y)
E0 y
j
kc2
k
x
(
A cos
k
x
x
B
sin
k
x
x)(C
sin
k
y
y
D
cos
k
y
y)
在波导壁上,电场切向分量满足零边界条件,即
③电磁波在媒质中沿导体向方向传播。
此时电磁场的复矢量为:
E E0 (x, y) e z (xˆE0x yˆE0 y zˆE0z )e z H H 0 (x, y) e z (xˆH 0x yˆ H 0 y zˆH 0z )e z
称为导行电磁波的传播常数
按横截面形状分: 矩形波导、圆形波导和椭圆波导等
按使用频段分:
介质波导和光纤
③导行电磁波问题仍然是电磁场的边值问题,即求解满足 波导边界条件的波动方程,然后分析沿波导的传播特性。
§9.1 导行波的电磁场
1、均匀波导中的 E, H
假定 ①由理想导体构成的导波装置沿z方向均匀;
②并且置于线性、均匀、各向同性的理想媒质中;
将这两个表达式代入理想媒质无源区域的麦克斯韦方程中,即
H j E
E j H
H 0
E 0
考虑到各分量都有 / z 的关系,则在直角坐标系中有
H0z y
H0y
j
E0x
H 0x
H0z x
