利用Matlab实现矩形波导电磁场分布图的绘制

;0001/ob=b ;0001/oa=a 图构结场的刻时 t t% 度精样采 d% 长波导波为取里这向方输传 c% 寸尺导波 b a% 长波止截模 01ET cl% 长波导波 gl% 长波/率频作工 0l f% 米毫为入输米为位单算计有所构结场导波形矩画% )t,f,0H,d,ob,oa(1tcrtsevawtcer noitcnuf niam% ;)30.0,9^01*48.9,1,6,61.01,68.22(1tcrtsevawtcer 单清序程附.C 2图
;))1y(ezis(sorez=yh ;)B*.1z-t*w(soc*.)1x*.a/.ip(soc*.0H=zh ;ip/.)1z*.B-t*w(nis*.)1x*.a/.ip(nis*.0H*.a*.B-=xh ;)1z,1y,1x(hsem% ;)z,y,x(dirghsem=]1z,1y,1x[ ;c:d/c:0=z ;b:d/b:0=y ;a:d/a:0=x ;)8^01*3(/B=w ;gl/ip*2=B ;gl=c ;)5.0^)2^)cl/0l(-1((/0l=gl ;flc esle ;nruter )cl>0l(fi ;)7-(^01*ip*4=u ;f/8^01*3=0l 率频止截 01ET% ;a*2=cl
��
�1-1�
�下如量参各中式上
�下如示表导推可量分场磁电其。a*2 为长波止截的模 01ET�b*a 为寸尺导波属金设。模 01ET 为模主的输传中导波形矩 .A 。定给部外由均刻时及率频作工、寸尺导波。图布分场磁电的模 01ET 模主的导波形矩属金刻时意任出磁电导波形矩现实 baltaM 用利
图果效布分线力磁力电的维三 .C
。加叠像图许允不。布分场电制绘�数函 3reviuq 用 .4 。加叠像图许允。布分场磁制绘�数函 3reviuq 用 .3 。量分的场磁、场电到得算计�1-1�式公照按。点标坐的场磁和场电定确别分�度精图绘的定给部外由 .2 。量参到得算计式�2-1�照参率频作工、寸尺导波的定给部外由 .1 �骤步的线力磁电画 baltaM 用 .B �2-1�

matlab矩形波

matlab矩形波Matlab矩形波是一种经典的信号模型，通常用于数字信号处理和模拟电路设计中。

本文将从简单到复杂，逐步讲解如何在Matlab中生成矩形波，并探讨其一些简单的应用。

这里先定义矩形波的数学表达式：$rect(x)= \begin{cases} 1, &|x| < \frac{1}{2} \\ 0, &\text{其他} \end{cases}$，其中$x$为自变量。

可以看到，矩形波在以$\frac{1}{2}$为半长的区间内取值为1，其他地方取值为0。

在Matlab中，我们可以使用以下代码生成矩形波：```matlabt = -5:0.01:5; %定义自变量t的取值范围y = rect(t); %用自定义的rect函数生成对应的矩形波yplot(t,y); %用plot函数将t和y作图xlabel('t'); ylabel('y');title('矩形波'); %添加横轴和纵轴标签，以及图像标题```这段代码中用到了自定义的rect函数，它的具体实现如下：```matlabfunction y = rect(x)y = zeros(size(x));y(abs(x) < 0.5) = 1;end```该函数接受一个实参$x$，返回与之对应的矩形波$y$。

在函数中，首先用zeros函数创建一个与$x$相同大小的全零数组$y$。

然后根据矩形波的数学表达式，将$|x|$小于0.5的元素赋值为1。

最后返回数组$y$。

通过上述代码，在Matlab中就可以生成矩形波，并将其可视化。

下面我们将扩展其一些简单应用。

首先是频率分析。

在信号处理中，我们通常需要分析信号的频域特性。

对于矩形波来说，它的频域分布非常特殊，其频谱呈现出周期性衰减的形式。

在Matlab中，可以使用以下代码绘制矩形波的频谱图：```matlabFs = 100; %定义采样频率为100HzT = 1/Fs; %定义采样周期L = 1000; %定义采样点数t = (0:L-1)*T; %定义采样时间序列y = rect(t); %用自定义的rect函数生成矩形波yY = fft(y); %对y进行傅里叶变换，得到YP2 = abs(Y/L); %计算单侧频谱的幅度P1 = P2(1:L/2+1); %仅保留正半轴部分P1(2:end-1) = 2*P1(2:end-1); %将幅值乘2，除去直流分量和Nyquist频率f = Fs*(0:(L/2))/L; %定义频率向量plot(f,P1); %用plot函数将f和P1作图xlabel('f (Hz)'); ylabel('|P1(f)|');title('单侧幅度谱'); %添加横轴和纵轴标签，以及图像标题```这段代码首先定义了采样频率、采样周期、采样点数和时间序列$t$。

利用Matlab模拟矩形恒定电流线圈的磁场分布

利用Matlab模拟矩形恒定电流线圈的磁场分布作者：孙海倍来源：《科技风》2019年第01期摘要：随着计算机科学的发展，计算机仿真模拟无论在科学研究还是工业设计中已经成为一种不可或缺的实验手段。

本文利用Matlab软件数值模拟了一个通有恒定电流的矩形电流线圈在空间中产生的磁感应强度分布，并讨论了磁场的均匀性质。

关键词：计算机仿真；Matlab；矩形线圈；磁场一、计算机仿真的发展与应用近几年来，随着计算机技术的快速发展，计算机仿真模拟已经渗透到了包括城市规划、工业设计、科学研究以及金融交易中的每一环节。

[1]交通拥堵一个一直以来困扰着人们，它极大地影响了人们的生活和出行效率。

而现在许多城市已经建立了智能的城市交通控制系统，它利用道路上的各个检测采集系统收集道路、交叉口上的车流量和拥堵信息，利用计算机程序实时地计算、分析，通过调节各个路口处的交通信号灯时间长度，获得最佳的控制方案、最大限度地保证城市交通的流畅和通行效率。

计算机仿真可以在工业制造中，[2]工程师已经可以利用计算机程序结合系统地计算方法（如有限元、有限体积等）来建立工业制品的三维结构图，再过赋予其材质参数，从而分析部件的形状、尺寸、结构等各种物理特性，同时可以模拟部件在不同环境条件下的受力载荷和工作状态，不仅可以有效地分析、评估执产品的可靠性和实用性，同时也降低了应为频繁进行实验带来的巨大成本开销。

在控制调度领域中[3]（如公交系统、生产线、应急救灾系统等），我们可以利用程序算法可以实现资源系统的实时调度、预测维护、以及监控控制等过程，进一步提高我们对复杂系统的控制响应速度和调度效率。

而在电器控制领域[4]，我们可以利用计算机程序和算法实现有效的电机实时控制，以提高能源的利用效率。

可以看到，當前计算机仿真已经融入到了科学研究和工业制造设计中的每一个领域，它正在渐成为当代科学研究中不可或缺的方法。

MATLAB是美国Mathworks开发的一款商业的高性能数值计算软件。

7.2.1矩形波导中的场分布

Em sin a
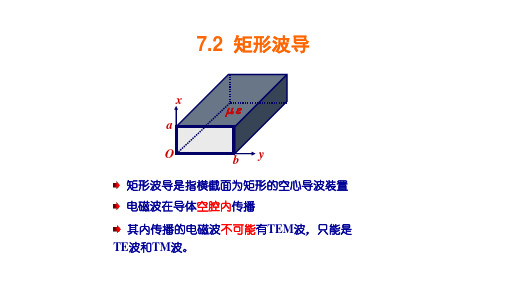
n z x sin y e b
由纵向场法，可得： m m n z Ex k 2 a Em cos a x sin b y e c E n E sin m x cos n y e z y m kc2 b a b m n z H x j n Em sin x cos y e 2 kc b a b m m n z H y j 2 Em cos x sin ye kc a a b
再加上边界条件
Ez |x 0 0 Ez |x a 0 E z | y 0 0 E z | y b 0
可以解得:
m k x a f ( x) A sin m x a
故
n k y b g ( y ) C sin n y b
两个常微分方程的通解为：f ( x)
A sin k x x B cos k x x,
g ( y ) C sin k y y D cos k y y
4
f ( x) A sin k x x B cos k x x, g ( y ) C sin k y y D cos k y y
③ 由于对相同的 m 和 n ， TMmn 模和 TEmn 模的截止波数 kcmn 相同，
这种情况称为模式的简并； ④ 对于 TEmn 模，其 m 和 n 可以为 0 ，但不能同时为 0 ；而对于 TMmn 模，其m 和n不能为0，即不存在TM0n 模和TMm0模。
7
振幅Em=AC，其大小由激励源强度决定。

利用Matlab实现矩形波导电磁场分布图的绘制

利用Matlab实现矩形波导电磁场分布图的绘制（附源程序）通过Matlab计算并绘出任意时刻金属矩形波导的主模TE10模的电磁场分布图。

波导尺寸、工作频率及时刻均由外部给定。

A.矩形波导中传输的主模为TE10模。

设金属波导尺寸为a*b，TE10模的截止波长为2*a。

其电磁场分量可推导表示如下：上式中各参量如下，（1-1）B.用Matlab画电磁力线的步骤：1.由外部给定的波导尺寸、工作频率参照（1-2）式计算得到参量。

2.由外部给定的绘图精度，分别确定电场和磁场的坐标点。

按照公式（1-1）计算得到电场、磁场的分量。

3.用quiver3函数，绘制磁场分布。

允许图像叠加。

4.用quiver3函数，绘制电场分布。

不允许图像叠加。

C.三维的电力磁力线分布效果图cH（1-2）图1图2C.附程序清单rectwavestrct1(22.86,10.16,6,1,9.84*10^9,0.03);%mainfunction rectwavestrct1(ao,bo,d,H0,f,t)%画矩形波导场结构所有计算单位为米输入为毫米%f l0工作频率/波长%lg波导波长%lcTE10模截止波长%a b波导尺寸%c传输方向这里取为波导波长%d采样精度%tt时刻的场结构图a=ao/1000;b=bo/1000;lc=2*a;%TE10截止频率l0=3*10^8/f;u=4*pi*10^(-7);if(l0>lc)return;elseclf;lg=l0/((1-(l0/lc)^2)^0.5);c=lg;B=2*pi/lg;w=B/(3*10^8);x=0:a/d:a;y=0:b/d:b;z=0:c/d:c;[x1,y1,z1]=meshgrid(x,y,z);%mesh(x1,y1,z1);hx=-B.*a.*H0.*sin(pi./a.*x1).*sin(w*t-B.*z1)./pi; hz=H0.*cos(pi./a.*x1).*cos(w*t-z1.*B);hy=zeros(size(y1));quiver3(z1,x1,y1,hz,hx,hy,'b');hold on;x2=x1-0.001;y2=y1-0.001;z2=z1-0.001;ex=zeros(size(x2));ey=w.*u.*a.*H0.*sin(pi./a.*x2).*sin(w*t-B.*z2)./pi;ez=zeros(size(z2));quiver3(z2,x2,y2,ez,ex,ey,'r');xlabel('传输方向');ylabel('波导宽边a');zlabel('波导窄边b');hold off;end%------------------------------------------------------------------End Code----------------------------------。

利用Matlab模拟矩形恒定电流线圈的磁场分布

利用Matlab模拟矩形恒定电流线圈的磁场分布龙源期刊网/doc/303506916.html, 利用Matlab模拟矩形恒定电流线圈的磁场分布作者：孙海倍来源：《科技风》2019年第01期摘要：随着计算机科学的发展，计算机仿真模拟无论在科学研究还是工业设计中已经成为一种不可或缺的实验手段。

本文利用Matlab 软件数值模拟了一个通有恒定电流的矩形电流线圈在空间中产生的磁感应强度分布，并讨论了磁场的均匀性质。

关键词：计算机仿真；Matlab；矩形线圈；磁场一、计算机仿真的发展与应用近几年来，随着计算机技术的快速发展，计算机仿真模拟已经渗透到了包括城市规划、工业设计、科学研究以及金融交易中的每一环节。

[1]交通拥堵一个一直以来困扰着人们，它极大地影响了人们的生活和出行效率。

而现在许多城市已经建立了智能的城市交通控制系统，它利用道路上的各个检测采集系统收集道路、交叉口上的车流量和拥堵信息，利用计算机程序实时地计算、分析，通过调节各个路口处的交通信号灯时间长度，获得最佳的控制方案、最大限度地保证城市交通的流畅和通行效率。

计算机仿真可以在工业制造中，[2]工程师已经可以利用计算机程序结合系统地计算方法（如有限元、有限体积等）来建立工业制品的三维结构图，再过赋予其材质参数，从而分析部件的形状、尺寸、结构等各种物理特性，同时可以模拟部件在不同环境条件下的受力载荷和工作状态，不仅可以有效地分析、评估执产品的可靠性和实用性，同时也降低了应为频繁进行实验带来的巨大成本开销。

在控制调度领域中[3]（如公交系统、生产线、应急救灾系统等），我们可以利用程序算法可以实现资源系统的实时调度、预测维护、以及监控控制等过程，进一步提高我们对复杂系统的控制响应速度和调度效率。

而在电器控制领域[4]，我们可以利用计算机程序和算法实现有效的电机实时控制，以提高能源的利用效率。

可以看到，當前计算机仿真已经融入到了科学研究和工业制造设计中的每一个领域，它正在渐成为当代科学研究中不可或缺的方法。

电磁场的Matlab仿真.

电磁场的Matlab仿真.Matlab 与电磁场模拟⼀单电荷的场分布：单电荷的外部电位计算公式：qφ=4πε0r等位线就是连接距离电荷等距离的点，在图上表⽰就是⼀圈⼀圈的圆，⽽电⼒线就是由点向外辐射的线。

MATLAB 程序：theta=[0:.01:2*pi]'; r=0:10;x=sin(theta*r; y=cos(theta*r; plot(x,y,'b' x=linspace(-5,5,100; for theta=[-pi/4 0 pi/4] y=x*tan(theta; hold on ; plot(x,y; end grid on 单电荷的等位线和电⼒线分布图：⼆多个点电荷的电场情况：模拟⼀对同号点电荷的静电场设有两个同号点电荷, 其带电量分别为 +Q1和+Q2(Q1、Q2>0 距离为 2a 则两电荷在点P(x, y处产⽣的电势为:由电场强度可得E = -?U, 在xOy 平⾯上, 电场强度的公式为:为了简单起见, 对电势U 做如下变换:。

Matlab 程序：q=1; xm=2.5; ym=2;x=linspace(-xm,xm; y=linspace(-ym,ym; [X,Y]=meshgrid(x,y;R1=sqrt((X+1.^2+Y.^2; R2=sqrt((X-1.^2+Y.^2; U=1./R1+q./R2; u=1:0.5:4; figure contour(X,Y,U,u grid onlegend(num2str(u' hold onplot([-xm;xm],[0;0] plot([0;0],[-ym;ym]plot(-1,0,'o' , 'MarkerSize' ,12 plot(1,0,'o' , 'MarkerSize' ,12 [DX,DY] = gradient(U; quiver(X,Y,-DX,-DY; surf(X,Y,U;同号电荷的静电场图像为：50403020100-22同理，将程序稍作修改，便可以得到异号电荷的静电场图像：403020100-10-20-30-4022.5三、线电荷产⽣的电位：设电荷均匀分布在从z=-L到z=L,通过原点的线段上，其密度为q(单位C/m,求在xy 平⾯上的电位分布。

基于matlab的电磁场分析

1.基于matlab－PDE Toolbox的泊松（拉普拉斯）方程求解在二维电磁场的有限元法计算中，用矩阵方程编制的计算程序长、大，而又复杂，且输入数据要化费很大的劳动。

而MATLAB是一种以矩阵运算为基础的交互式语言，它是采用有限元法来求解偏微分方程的。

因此在计算中，我们选用MATLAB提供的一个用户图形界面（GUI）的偏微分方程工具箱（PDE Toolbox）进行数值求解，采用的是三角形网格自动剖分。

下面举例说明。

【例1－1】横截面为矩形的无限长槽由3块接地导体板构成，如图3－3所示，槽的盖板接直流电压100V，求矩形槽的电位分布。

解：这是二维平面场问题。

由于电位函数和电场强度之间关系为利用麦克斯韦方程和关系式，得到泊松方程式中，为介电常数，为体电荷密度。

由于所求区域内体电荷密度，得到拉普拉斯方程：其边界满足狄里赫利（Didchlet）条件：，，本题运用MATLAB的偏微分方程工具箱（PDE Toolbox）进行数值求解。

在命令窗口中输入命令pdetool，打开PDE图形用户界面，计算步骤为：（1）网格设置：选择菜单Options下的Grid和Grid Spacing…，将X-axis linear Spacings设置为［-1.5：0.2：1.5］，Y-axis linear Spacings取Auto。

（2）区域设置：选择菜单Draw下的Rectangle／Square或按，画矩形。

（3）应用模式设置：在工具条中单击Generic Scalar下拉列表框，选Electrostatics（静电学）应用模式。

（4）输入边界条件：进入Boundary Mode或按，输入：1、左边界：狄里赫利（Diriehlet）条件：h＝1，r＝0。

2、右边界：狄里赫利（Dirichlet）条件：h＝1，r＝0。

3、上边界：狄里赫利（Dirichlet）条件：h＝1，r＝100。

4、下边界：狄里赫利（Dirichlet）条件：h＝1，r＝0。

电磁波仿真实验

电磁波仿真实验实验内容1．本次实验介绍了matlab的安装过程2．初步对于MATLAB有了基本的认识与了解3．熟悉MATLAB软件的基本操作有时，为了使图形具有可读性，需要在所绘制的图形中，加上一些网格线来反映信号的幅度大小。

在MATLAB中使用grid函数可实现在图形中加网格线。

gridon%在图形中加网格线gridoff%取消图形中的网格线holdon%图形显示窗口原来的图像保持holdoff%关闭图形保持功能figure%打开新的显示窗口MATLAB的工作环境主要由工具栏、文件路径，当前文件夹，命令窗口以及工作变量区构成（由于设置不同，软件中也会显示历史窗口，记录的是在命令窗口的历史输入），如图1所示。

工具栏也就是如下图所示的部分，它是用来对软件进行一系列操作的区域。

命令窗口是进行一系列命令输入的地方，当有指令输入并按下Enter 键时，软件会自动执行该条指令，并执行出该命令的结果。

文件路径是当前文件夹的地址，在该区域可以实现文件路径的切换。

当前文件夹是显示当前文件路径下所有文件的窗口，可以在此双击打开所需要的.m等不同格式的文件。

工作变量区是存放所执行程序中涉及到的所有变量值的空间，可以在该区域双击某变量查看该变量具体表示情况。

MATLAB使用中的部分注意事项如下：1、变量不需要先定义，随时用随时起名字即可；2、用文本编辑器编写的程序、函数的文件扩展名均为“.m”；3、程序文件在起名字时要注意不能用数字和中文作为文件名；4、函数文件在保存时会自动以定义的函数名作为其文件名，不允许修改，否则函数无法运行；5、变量和常量的标识符中的第一个字符必须是英文字符；6、MATLAB变量区分大小写；7、如果不想在命令行窗口输出运行结果，只需在代码后面加上分号即可；8、plot是绘图的意思，ub是子的意思。

ubplot(m,n,p)表示生成m某n个子图，当前激活第p个子图；9、程序某=input(‘Typeinignal某(t)incloedform:’)，表示接收键盘输入值并赋值给某。

matlab电磁场

matlab电磁场
Matlab是一种强大的数学软件，可以用来模拟电磁场的分布。

使用Matlab模拟电磁场分布时，需要使用相关的工具箱来进行计算和绘图。

下面将介绍如何使用Matlab模拟电磁场分布。

1. 安装Matlab及相关工具箱
首先需要在计算机上安装Matlab软件，并安装相应的工具箱。

其中，电磁场分布模拟需要使用的工具箱包括电磁场仿真工具箱、数值方法
工具箱和曲面拟合工具箱等。

2. 建立电磁场模型
在Matlab中建立电磁场模型时，需要先定义所要模拟的物理场问题。

例如，可以定义三维空间内的坐标系、电荷分布、电流分布等。

通过
输入这些参数，可以建立电磁场的数学模型。

3. 进行电磁场仿真计算
在建立好电磁场模型后，就可以进行仿真计算了。

Matlab提供了快速、高精度的数值方法工具箱，可以用来计算电场、磁场、电流密度等参
数的分布情况。

在进行仿真计算时，可以通过调整不同的参数，来得
到不同的电磁场分布结果。

4. 绘制电磁场分布图
在得到电磁场仿真计算结果后，还需要将其以图形化的方式展示出来。

Matlab中提供了丰富的绘图函数，可以将电磁场的分布情况绘制成三维图形或二维图形，并对其进行动画效果展示。

综上所述，使用Matlab来模拟电磁场分布可以帮助分析电磁场的分
布情况，为电磁场应用领域提供有力的支持。

基于matlab的电磁场图示化教学

目录摘要 (1)关键词 (1)Abstract (1)Key Words (1)引言 (2)1 Matlab的图示化技术 (3)1.1 几个常用的绘图指令 (3)1.2 具有两个纵坐标标度的图形 (3)1.3 三维曲线 (4)2 Matlab在静电场图示化中的应用 (4)2.1 基本原理 (4)2.2 等量同号点电荷的电场线的绘制 (5)2.3 静电场中的导体 (8)3 Matlab在恒定磁场图示化中的应用 (9)3.1 电偶极子电磁场的Matlab图示与应用 (9)3.2 两根载流长直导线在电磁场中的Matlab图示 (11)3.3 运动的带电粒子在均匀电磁场中的Matlab图示 (13)3.4 电磁波的Matlab图示 (15)4 Matlab在时变电磁场仿真分析中的应用 (16)4.1 Matlab图示化分析均匀平面波在理想介质中的传播 (16)4.2 Matlab图示化分析矩形波导的场量分布 (19)5 结语 (25)致 (26)参考文献 (26)基于Matlab的电磁场图示化教学自动化王丽洁指导教师王庆兰摘要：Matlab是由美国Mathworks公司发布的主要面对科学计算、可视化以及交互式程序设计的高科技计算环境。

Matlab具有丰富的计算功能和科学计算数据的可视化能力，特别是应用偏微分方程工具箱在大学物理电磁学等各类物理场的数值仿真中具有无比的优势。

本文将主要介绍Matlab在静电场图示化中的应用、Matlab在恒定磁场图示化中的应用以及Matlab在时变电磁场仿真分析中的应用。

利用Matlab的图示化技术、利用Matlab分析电磁学，能够更为方便的实现电磁场图示化教学，能使复杂的问题大大简化，对阐述相关原理能起到很大的作用。

关键词：Matlab 图示化教学电磁场时变电磁场The electromagnetic field of graphical teaching based onMatlabStudent majoring in automation Wang LijieT utor Wang QinglanAbstract：Matlab is published by the United States, the main face of the company Mathworks scientific computing, visualization and interactive program designed for high-tech computing environment. Matlab has a computing functions and rich scientific computing visualization capability of data, especially the application of partial differential equation toolbox has incomparable advantages in numerical simulation of university physics electromagnetism and other types of physical field. Mainly introduces the application of Matlab in electrostatic field, the graphic in Matlab in a constant magnetic field of graphical applications and Matlab application of electromagnetic simulation in the analysis of time. Using Matlab graphic technology, using the Matlab analysis of electromagnetism, can more convenient teaching, the implementation of the electromagnetic field shown can greatly simplify the complex problems, the paper related principle can play a big role.Key Words:Matlab; graphic teaching; electromagnetic field; time-varying electromagnetic field引言在工科物理教学中，物理实验极其重要，一般院校都将其列为一门单独的课程，它担负着学生的基本实验技能训练的任务，通过一系列的实验、学习，学生可在一定程度上掌握前人对一些物理量的典型测量方法和实验技术，并在以后的实验工作中有所借鉴，能够在这些基础上有所创新。

基于Matlab的矩形载流线框磁场分布特征的仿真分析

ＴＨＥＳＩＭＵＬＡＴＩｏＮＡＮＡＬＹＳＩＳｏＦＴＨＥＭＡＧＮＥＴＩＣ．ＦＩＥＬＤＰＲＯＤＵＣＥＤＢＹＲＥＣＴＡＮＧＵＬＡＲＣＯＩＬＢＡＳＥＤｏＮＭＡＴＬＡＢ
ＷａｎｇＫｅｘｉｎ
（ＳｃｈｏｏｌｏｆＬｉｆｅＳｃｉｅｎｃｅａｎｄＥｎｇｉｎｅｅｒｉｎｇ，ＬａｎｚｈｏｕＵｎｉｖｅｒｓｉｔｙｏｆＴｅｃｈｎｏｌｏｇｙ，Ｌａｎｚｈｏｕ，Ｇａｎｓｕ７３００５０）
原理推导出空间某点处磁感应强度的计算公式，再利用Ｍａｔｌａｂ软件编制程序，通过循环求和实现磁场的数值计算．在此基础上，以单匝矩形载流线框为对象，数值计算了其
空间磁场分布，绘出了多种条件下磁场的分布图像，进而通过对比分析得到了磁场的
由于矩形磁系应用十分广泛67本文针对矩形载流线框的特殊结构以毕奥萨伐尔定律为基础结合磁场的叠加原理通过将矩形载流线框分割成无数电流微元再将微元磁场叠加求和得到空间任意场点处磁场的计算公式并利用matlab软件编程实现磁场的数值计算进而绘制出一定条件下的磁场601物理与工程vol26no62016分布图从而直观地获得矩形线框磁场的空间分布特征
ｕｉｒｎｇｗｉｔｈＭａｔｌａｂｓｏｆｔｗａｒｅｔｈｒｏｕｇｈｃｙｃｌｉｃｓｕｍｍｉｎｇ．Ｂａｓｅｄｏｎｔｈｅａｂｏｖｅｗｏｒｋｓ，ｔｈｅｍａｇｎｅｔｉｃ

利用MATLAB图形技术实现电磁波的可视化

9&- ;$&( 6<=’1&0’ )7 %&’(&) <=+>?@A 2.A?BC/C<7D+E ./.A2=C3+<B.2@A -+F. 2=+BE@2E @B E>+A.D @2E 3C2@CB @E E@3G/+2.H @B 2?@E >+>.=6 ’?@E >=CA.EE +=. ?./>IG/ IC= E2GH.B2E 2C AC3>=.?.BH +BH 3+E2.= 2?. EGJK.A2 CI ./.A2=C3+<B.2@A I@./H +BH ./.A2=C: 3+<B.2@A -+F.6 >+5?-1@ %&’(&) L=+>?@A ’.A?BC/C<7 0/.A2=C3+<B.2@A M@./H 0/.A2=C3+<B.2@A N+F.
!"" # 年 ! 月
电
脑
学
习
第 $ 期
利用 %&’(&) 图形技术实现电磁波的可视化
0 1!
2 3
利用 %&’(&) 图形技术的特点，动态模拟了电磁波在空间传播时的状态，有助于学生对电磁场与电磁波课程的理解与掌握。
456
%&’(&)
图形技术
电磁场理论
电磁波
!"#$%&’"() ’*+ ,-’"-( -. /%+0’1-#&)(+’"0 2&3+ 45 ,67864 91&:*"0 7+0*(-%-)5

matlab 矩形波

MATLAB矩形波简介矩形波是一种周期性的信号，其波形由一系列等宽的方波组成。

在MATLAB中，我们可以使用各种方法来生成和处理矩形波信号。

本文将介绍如何使用MATLAB生成矩形波信号、修改其参数以及进行频谱分析。

生成矩形波信号在MATLAB中，我们可以使用square函数来生成矩形波信号。

该函数的基本语法如下：y = square(t, duty)其中，t是时间变量，表示要生成的信号的时间范围；duty是占空比，表示方波高电平持续时间与周期的比例。

下面是一个简单的示例代码，演示了如何生成一个周期为2秒、占空比为0.5的矩形波信号：t = 0:0.01:10; % 时间范围从0到10秒，步长为0.01秒duty = 0.5; % 占空比为0.5y = square(t, duty); % 生成矩形波信号plot(t, y); % 绘制波形图xlabel('Time (s)'); % X轴标签ylabel('Amplitude'); % Y轴标签title('Square Wave'); % 图片标题grid on; % 显示网格运行以上代码，将会生成一个周期为2秒、占空比为0.5的矩形波信号的波形图。

修改矩形波参数除了基本的时间范围和占空比之外，我们还可以通过修改其他参数来改变矩形波信号的特性。

频率和周期矩形波信号的频率是指单位时间内周期的个数，频率的倒数即为周期。

在MATLAB 中，我们可以通过修改时间变量的步长来改变频率和周期。

例如，如果我们将上面示例代码中的步长由0.01秒改为0.1秒，则生成的矩形波信号将具有更低的频率和更长的周期。

占空比矩形波信号的占空比是指方波高电平持续时间与周期之间的比例。

在上面示例代码中，我们将占空比设置为0.5，即高电平持续时间等于低电平持续时间。

如果我们将占空比设置为0.2，则方波高电平持续时间仅为低电平持续时间的五分之一。

矩形导波和圆波导场分布 matlab

矩形导波和圆波导是电磁波传播领域常见的两种波导结构。

它们在无线通信、微波技术、雷达系统等领域具有重要应用价值。

Matlab是一种强大的科学计算软件，可以用于分析和模拟电磁波在矩形导波和圆波导中的场分布。

本文将针对矩形导波和圆波导场分布的Matlab分析和模拟进行详细介绍。

1. 矩形导波场分布的Matlab分析和模拟矩形导波是一种矩形截面的波导结构，常见于微波器件和天线系统中。

在Matlab中，可以通过Maxwell方程组的数值解来分析矩形导波中的场分布。

通过设定矩形导波的几何尺寸和工作频率，可以利用Matlab进行电磁场的模拟和分析，得到矩形导波中的电场和磁场分布图，并进一步分析波导内的功率传输和传输损耗。

这对于设计和优化微波器件和天线系统具有重要的意义。

2. 圆波导场分布的Matlab分析和模拟圆波导是一种圆形截面的波导结构，常见于雷达系统和天线阵列中。

在Matlab中，同样可以利用Maxwell方程组的数值解来分析圆波导中的场分布。

通过设定圆波导的几何尺寸和工作频率，利用Matlab进行电磁场的模拟和分析，同样可以得到圆波导中的电场和磁场分布图，并进一步分析波导内的功率传输和传输损耗。

这对于设计和优化雷达系统和天线阵列具有重要的意义。

3. Matlab在矩形导波和圆波导场分布分析中的应用Matlab是一种功能强大、灵活多样的科学计算软件，它在电磁场分析和模拟领域具有广泛的应用。

在矩形导波和圆波导场分布分析中，Matlab可以提供丰富的数学工具和绘图函数，方便工程师和研究人员进行电磁场的模拟和分析工作。

通过Matlab，可以直观地观察到矩形导波和圆波导中的场分布特性，为工程设计和研究提供重要的参考依据。

4. 结语矩形导波和圆波导是电磁波传播领域重要的波导结构，它们在无线通信、微波技术、雷达系统等领域具有广泛的应用。

通过Matlab对矩形导波和圆波导场分布进行分析和模拟，可以帮助工程师和研究人员更好地理解电磁场在波导中的传播规律，为相关领域的设计和优化提供有力的支持。

矩形波导matlab求解

矩形波导matlab求解题目：1、已知宽度为50mm, 高度为34mm的矩形波导管，长度为5m。

忽略边缘效应，该波导管中的场满足方程：220m, n为波沿x轴和y轴的模式画出：1. m=1,n=02. m=2, n=3 时波导管中的场分布1、求解定解问题2、用Matlab（C语言/Java, etc.）编程，画出求解区域中的场二维分布图，横坐标为x轴/y轴/z轴，纵坐标为电位值2x k 2yk1.求解方程对于TM 波，Hz=0,Ez 满足如下关系： Ez=Eoz(x, y)e(-j βz)在直角坐标系中,上式可写作0),(),()(22222=+∂∂+∂∂y x E k y x E yx oz c oz 应用分离变量法, 令Eoz(x, y)=X(x)Y(y) 代入上式, 并除以X(x)Y(y), 得：22222)()(1)()(1ck dy y Y d y Y dx x X d x X =---要使上式成立, 上式左边每项必须均为常数, 设分和可得 0)()(222=+x X k dxx X d x 0)()(222=+y Y k dyy Y d y +2x k 22cy k k =于是, Eoz(x, y)的通解为：Eoz(x,y)=(A1coskxx+A2sinkxx)(B1coskyy+B2sinkyy)其中, A1A2B1B2为待定系数, 由边界条件确定。

Ez 应满足的边界条件为：0||0====a x x Ez Ez||0====b y y Ez Ez代入可得02=A 02=B am K xπ=bn K yπ=于是方程的基本解为zj mn z j z ey bn x a m E e y b n x a m B A E ββππππ--==)sin()sin()sin()sin(11zj mn c Xe y bn x a m E a m k j E βπππβ--=)sin()cos(2zj mn c ye y bn x a m E b m k j E βπππβ--=)cos()sin(2z j mn c Xe y bn x a m E b m k jw H βπππε-=)cos()sin(2zj mn c ye y bn x a m E a m k jw H βπππε-=)sin()cos(-20=Hz截止波长λc=2*pi/(((m*pi/a)^2+(n*pi/b)^2)^0.5)截止频率fc=c/λc 无尽空间中波长λ0=3*10^8/f （f 为工作频率）波导波长λg=l0/((1-(3*10^8/(lc*f))^2)^0.5) 相位常数B=2*pi/lg w=B*(3*10^8)由激励源强度决定可得TM 波其他横向用matlab 画出场分布在matlab 中新建m 文件mnEfunction n(ao,bo,d,Emn,f,m,n,t)%画矩形波导场结构所有计算单位为米 a0,b0输入为毫米%f工作频率/波长%lg 波导波长%lc TM11模截止波长%a b 波导尺寸%d 采样精度%t t时刻的场结构图a=ao/1000;b=bo/1000;lc=2*pi/(((m*pi/a)^2+(n*pi/b)^2)^0.5);l0=3*10^8/f;u=1/(36*pi)*10^(-9);lg=l0/((1-(3*10^8/(lc*f))^2)^0.5);c=lg;B=2*pi/lg;w=B*(3*10^8);x=0:a/d:a;y=0:b/d:b;z=0:c/d:c;[x1,y1,z1]=meshgrid(x,y,z);Ex=B./((m*pi./a)^2+(n*pi./b)^2).*(m*pi./a).*Emn.*cos(m*pi ./a.*x1).*sin(n*pi./b.*y1).*sin(w*t-B.*z1);Ey=B./((m*pi./a)^2+(n*pi./b)^2).*(n*pi./b).*Emn.*sin(m*pi ./a.*x1).*cos(n*pi./b.*y1).*sin(w*t-B.*z1);Ez=Emn.*sin(m*pi./a.*x1).*sin(n*pi./b.*y1).*cos(w*t-z1.*B );quiver3(z1,x1,y1,Ez,Ex,Ey,'b');hold on;x2=x1-0.05;y2=y1-0.05;z2=z1-0.05;Hz=zeros(size(z2));Hy=-w.*u./((m*pi./a)^2+(n*pi./b)^2).*(m*pi./a).*Emn.*cos( m*pi./a.*x2).*sin(n*pi./b.*y2).*sin(w*t-B.*z2);Hx=-w.*u./((m*pi./a)^2+(n*pi./b)^2).*(n*pi./b).*Emn.*sin( m*pi./a.*x2).*cos(n*pi./b.*y2).*sin(w*t-B.*z2);quiver3(z2,x2,y2,Hz,Hx,Hy,'r'); xlabel('传输方向');ylabel('波导宽边a');zlabel('波导窄边b');hold off;End当m=1,n=1时在命令框输入n(50,34,10,1,5.5*10^9,1,1,0)场分布如图当m=2,n=3时输入如下命令n(50,34,10,1,5*10^10,2,3,0)。

基于Matlab的电磁场图示化教学概要

目录摘要 (1)关键词 (1)Abstract (1)Key Words (1)引言 (2)1 Matlab的图示化技术 (2)1.1 几个常用的绘图指令 (2)1.2 具有两个纵坐标标度的图形 (2)1.3 三维曲线 (3)2 Matlab在静电场图示化中的应用 (3)2.1 基本原理 (3)2.2 等量同号点电荷的电场线的绘制 (4)2.3 静电场中的导体 (6)3 Matlab在恒定磁场图示化中的应用 (6)3.1 电偶极子电磁场的Matlab图示与应用 (6)3.2 两根载流长直导线在电磁场中的Matlab图示 (8)3.3 运动的带电粒子在均匀电磁场中的Matlab图示 (9)3.4 电磁波的Matlab图示 (11)4 Matlab在时变电磁场仿真分析中的应用 (12)4.1 Matlab图示化分析均匀平面波在理想介质中的传播 (12)4.2 Matlab图示化分析矩形波导的场量分布 (14)5 结语 (19)致谢 (19)参考文献 (20)基于Matlab的电磁场图示化教学自动化王丽洁指导教师王庆兰摘要：Matlab是由美国Mathworks公司发布的主要面对科学计算、可视化以及交互式程序设计的高科技计算环境。

Matlab具有丰富的计算功能和科学计算数据的可视化能力，特别是应用偏微分方程工具箱在大学物理电磁学等各类物理场的数值仿真中具有无比的优势。

本文将主要介绍Matlab在静电场图示化中的应用、Matlab在恒定磁场图示化中的应用以及Matlab在时变电磁场仿真分析中的应用。

利用Matlab的图示化技术、利用Matlab分析电磁学，能够更为方便的实现电磁场图示化教学，能使复杂的问题大大简化，对阐述相关原理能起到很大的作用。

关键词：Matlab 图示化教学电磁场时变电磁场The electromagnetic field of graphical teaching based on MatlabStudent majoring in automation Wang LijieTutor Wang QinglanAbstract：Matlab is published by the United States, the main face of the company Mathworks scientific computing, visualization and interactive program designed for high-tech computing environment. Matlab has a computing functions and rich scientific computing visualization capability of data, especially the application of partial differential equation toolbox has incomparable advantages in numerical simulation of university physics electromagnetism and other types of physical field. Mainly introduces the application of Matlab in electrostatic field, the graphic in Matlab in a constant magnetic field of graphical applications and Matlab application of electromagnetic simulation in the analysis of time. Using Matlab graphic technology, using the Matlab analysis of electromagnetism, can more convenient teaching, the implementation of the electromagnetic field shown can greatly simplify the complex problems, the paper related principle can play a big role.Key Words:Matlab; graphic teaching; electromagnetic field; time-varying electromagnetic field引言在工科物理教学中，物理实验极其重要，一般院校都将其列为一门单独的课程，它担负着学生的基本实验技能训练的任务，通过一系列的实验、学习，学生可在一定程度上掌握前人对一些物理量的典型测量方法和实验技术，并在以后的实验工作中有所借鉴，能够在这些基础上有所创新。

矩形谐振腔电磁场的FDTD分析和Matlab仿真

矩形谐振腔电磁场的FDTD分析和Matlab仿真矩形谐振腔电磁场的FDTD分析和Matlab仿真摘要：目前，电磁场的时域计算方法越来越引人注目。

这种方法已经广泛应用到各种电磁问题的分析之中。

而将Matlab 作为一种仿真工具，用于时域有限差分法，可以简化编程，使研究者重心放在FDTD 本身上，而不必在编程上花费过多的时间。

本课题通过用FDTD方法计算矩形谐振腔电磁场分布，并用Matlab 进行仿真。

关键词：时域有限差分法，Matlab 仿真，矩形谐振腔1. 引言时域有限差分法（Finite-Dfference Time-Domain Method ）是求解电磁问题的一种数值技术，是在1966年由K.S.Yee第一次提出的。

FDTD法直接将有限差分式代替麦克斯韦时域场旋度方程中的微分式，得到关于场分量的有限差分式，用具有相同电参量的空间网格去模拟被研究体，选取合适的场始值和计算空间的边界条件，可以得到包括时间变量的麦克斯韦方程的四维数值解，通过傅里叶变换可求得三维空间的频域解。

时域有限差分法突出的优点是所需的存储量及计算时间与N成正比，使得很多复杂的电磁场计算问题成为可能，用时域有限差分法容易模拟各种复杂的结构，使得用其他方法不能解决的问题有了新的处理方法。

本文主要讨论如何用Matlab语言来编写FDTD勺吸收边界条件以及编程时应注意的问题。

2时域有限差分法的基本理论2.1 时域有限差分法的简介1966 年K.S.Yee 首次提出了一种电磁场数值计算的新方法——时域有限差分（Finite-Dfferenee Time-Domain Method）方法。

对电磁场E、H分量在时间和空间上采取交替抽样的离散方式，每一个E （或H）场分量四周有四个H （或E）场分量环绕，应用这种离散方式将含时间变量的麦克斯韦旋度方程转化为一组差分方程，并在时间轴上逐步推进地求解空间电磁场。

Yee提出的这种抽样方式后来被称为Yee元胞。

利用MATLAB计算电磁场有关分布

电磁场实验报告实验一模拟电偶极子的电场和等位线学院：电气工程及其自动化班级：学号：姓名:实验目的： 1、了解并掌握 MATLAB 软件，熟练运用 MATLAB 语言进行数值运算。

2、熟练掌握电偶极子所激发出的静电场的基本性质 3、掌握等位线与电力线的绘制方法实验要求： 1、通过编程，完成练习中的每个问题，熟练掌握 MATLAB 的基本操作。

2、请将原程序以及运行结果写成 word 文档以方便检查实验内容：一、相关概念回顾对于下图两个点电荷形成的电场两个电荷共同产生的电位为：  pq 4π 0(1 r11 r2)q 4π 0r2  r1 r1r2其中距离分别为 r1  (x  q1x)2  ( y  q1y)2 ， r2  (x  q2x)2  ( y  q2 y)2 电场强度与电位的关系是 E p  等位线函数为: (x, y, z)  C电力线函数为： Ex  Ey dx dy二、实验步骤 1、打开 MATLAB 软件，新建命令文档并保存，并在文档中输入程序。

2、输入点电荷 q1 的坐标（q1x，q1y）, 以及 q1 所带的电量。

调用 input 函数。

如果不知道该函数的使用方法可在 MATLAB 命令行处键入 doc input。

3、输入点电荷 q1 的坐标（q1x，q1y）, 以及 q1 所带的电量。

4、定义比例常系数 1  9e9 ，命令为 k=9e9。

4π 05、定义研究的坐标系范围为 x 5,5, y 5,5,步长值为 0.1。

6、将x,y两组向量转化为二维坐标的网点结构，函数为meshgrid。

命令为 [X,Y]=meshgrid(x,y)，如果不知道该函数的使用方法可在MATLAB命令行处键入 doc meshgrid。

7、计算任意一点与点电荷之间的距离 r，公式为 r1  (x  q1x)2  ( y  q1y)2 ，r2  (x  q2x)2  ( y  q2 y)2q 11 V (  ) 8、计算由 q1,q2 两个点电荷共同产生的电势 4π0 r1 r2 9、注意，由于在 q1 和 q2 位置处计算电势函数为无穷大或者无穷小，因此要把这两点去掉掉，以方便下面绘制等势线。