小学五年级数学 平面图形的面积计算
五年级数学思维专题训练《平面图形面积计算及等积变形》

五年级数学思维专题练习《平面图形面积计算及等积变形》姓名_________知识准备:平面图形面积计算:多边形及组合图形的面积计算,转化为求三角形、长方形、梯形、平行四边形的面积,利用相应的面积公式求解三角形面积=底×高÷2 梯形面积=(上底+下底)×高÷2长方形面积=长×宽平行四边形面积=底×高等积变形问题:两个平面图形面积相等,称为这两个图形等积。
三角形等积变形技巧是各种等积变形的核心,要注意运用“等(同)底、等(同)高的两个三角形面积相等”这个基本规则一、平面图形面积如图,一个3×3的正方形网格,如果小正方形边长是1,那么阴影部分的面积是________如图,在长方形ABCD中,BC=12,AB=9,F为BC上一点,且CF=4,那么三角形CEF的面积是__________如图,正方形ABCD的面积是16,点F是BC上任意一点,点E是DF的中点,则阴影部分的面积是_______如图,M,N分别是平行四边形ABCD两边上的中点,三角形DMN的面积是9平方厘米,那么ABCD的面积是______平方厘米二、等积变形如图,大正六边形的内部有7个完全一样的小正六边形,已知阴影部分的面积是180平方厘米,那么大正六边形的面积是______平方厘米如图,正六边形ABCDEF的面积是2014平方厘米,在AB,BC,DE,EF上分别取中点G,H,I,J,四边形GHIJ的面积是______平方厘米如图,直角边长分别为20cm,12cm的直角三角形ABC和直角边长分别为14cm,4cm的直角三角形ADE如图摆放,M为AE的中点,则三角形ACM的面积为_____cm²5个相同的长方形放在一个正方形内,所有长方形的边都平行于正方形的对应边,正方形的边长为24厘米,求:单个长方形的面积。
五年级数学平面图形的面积计算(PPT)5-2
应用题:
1. 一块梯形木板面 积为9.2平方米,中 位线长2.3米,求梯 形木板的高是多少?
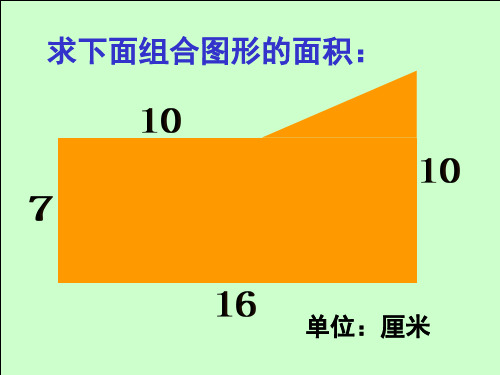
求下面组合图形的面积:
单位:厘米
年国际上以国际协议原点()作为地极原点,经度起点实际上不变。 【本岛】名几个岛屿中的主要岛屿,其名称和这几个岛屿总体的名称相同。例如我国的 湾湾包括湾湾本岛和澎湖列岛、绿岛、兰屿等许多岛屿。 【本地】名人、物所在的地区;叙事时特指的某个地区:~人|~口音|~特产。 【本分】①名本 身应尽的责任和义务:守~|~的工作。②形安; 大语文加盟品牌有哪些 大语文加盟品牌有哪些 ;于所处的地位和环境:~人|这个人 很~。 【本固枝荣】ī树木主干强固,枝叶才能茂盛,比喻事物的基础巩固了,其他部分才能发展。 【本行】名①个人一贯从事的或长期已经熟习的行业: 他原来是医生,还是让他干老~吧。②现在从事的工作:三句话不离~|熟悉~业务。 【本纪】名纪传体史书中帝王的传记,一般按年月编排重要史实,列 在全书的前面,对全书起总纲的作用。 【本家】名同宗族的人:~兄弟|他们俩住在一个村,是~。 【本家儿】〈方〉名指当事人:~不来,别人不好替他 做主。 【本金】ī名①存款者或放款者拿出的钱(区别于“利息”)。②经营工商业的本钱;营业的资本。 【本科】名大学或学院的基本组成部分(区别于 “预科、专科”等)。 【本来】①形属性词。原有的:~面貌|~的颜色。②副原先;先前:他~身体很瘦弱,现在很结实了|我~不知道,到了这里才听 说有这么回事。③副表示理所当然:~就该这样办。 【本利】名本金和利息。 【本领】名技能;能力:有~|~高强。 【本名】名①本来的名字;原来的 名字(区别于“别号、官衔”等)。②给本人起的名儿:有些外国人的全名分三部分,第一部分是~,第二部分是父名,第三部分是姓。 【本命年】名我国 习惯用十二生肖记人的出生年,每十二年轮转一次。如子年出生的人属鼠,再遇子年,就是这个人的本命年。参看页〖生肖〗。 【本末】名①树的下部和上 部,东西的底部和顶部,比喻事情从头到尾的经过:详述~|纪事~。②比喻主要的与次要的:不辨~|~颠倒。 【本末倒置】比喻把主要事物和次要事物 或事物的主要方面和次要方面弄颠倒了。 【本能】①名人类和动物不学就会的本领,如初生的婴儿会哭会吃奶,蜂酿蜜等都是本能的表现。②副机体对外界刺激不知不觉地、无意识地(做出反应):他看见红光一闪,~地闭上了眼睛。 【本票】名出票人签发的,并承诺在见票时向收款人或持票人无条件支付确 定金额的票据。 【本钱】名①用来营利、生息、等的钱财:做买卖得有~。②比喻可以凭借的资历、能力、条件等:强壮的身体是做好工作的~。 【本人】 代人称代词。①说话人指自己:这
五年级数学 平面几何图形的面积 基础+拔高例题 带作业(带详细答案)

平面几何图形的面积板块一:基础巩固1、一个三角形的面积比与他等底等高的平行四边形的面积少12平方分米,则平行四边形的面积是(24 )平方分米,三角形的面积是(12 )平方分米。
2、李叔叔在院子里靠着墙边围城了一个鸡笼,围鸡笼的网子长20.5米,求这个鸡笼的占地面积是多少平方米?上底+下底=20.5-8.5=12(米)梯形面积=12×8.5÷2=51(平方米)3、有一个长方形,如果宽减少2米,或长减少3米,则面积均减少24平方米,求这个长方形的是是多少平方米?32原长方形的长:24÷2=12(米)原长方形的宽:24÷3=8(米)原来长方形的面积:12×8=96(平方米)4、如图是由边长分别为4厘米、8厘米的两个正方形组成的图形,求阴影部分面积。
方法一:可以分割成两个钝角三角形第一个钝角三角形的底是4,高是4,第二个钝角三角形的高是8,底是8-4=4,所以总共的面积是:4×4÷2+8×(8-4)÷2=24(平方厘米)方法二:两个正方形的面积-2处空白的面积=4×4+8×8-8×8÷2-4×(4+8)÷2=24(平方厘米)5、如图是由边长分别为4、8、6厘米的三个正方形组成的图形,求阴影部分面积。
方法一:可以分割成三个钝角三角形第一个钝角三角形的底是4,高是4,面积是:4×4÷2=8(平方厘米)第二个钝角三角形的高是8,底是(8-4),面积:8×(8-4)÷2=16(平方厘米)第三个钝角三角形的高是8,底是6,面积是:6×8÷2=24(平方厘米)一共的面积:8+16+24=48(平方厘米)方法二:把右上角补起来阴影面积=三个正方形的面积+小长方形面积-两处空白的面积=4×4+8×8+6×6+6×(8-6)-(8+4)×4÷2-8×(6+8)÷2=48(平方厘米)板块二:拓展提高【例题1】下图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积.208 5阴影部分+中间空白=中间空白+下面空白所以阴影部分=下面空白20-5=15(厘米)(15+20)×8÷2=140(平方厘米)【例题2】右图中甲的面积比乙的面积大__________平方厘米.乙甲6厘米8厘米4厘米利用同增同减差不变甲-乙=(甲+空白)-(乙+空白)=大三角形面积-小三角形面积=6×8÷2-4×8÷2=24-16=8(平方厘米)【例3】右图中,矩形ABCD 的边AB 为4厘米,BC 为6厘米,三角形ABF 比三角形EDF 的面积大9平方厘米,求ED 的长.A B CDEF利用同增同减差不变三角形ABF-三角形EDF 的面积=9平方厘米同时增加梯形BCDF 的面积,则:长方形ABCD-三角形BCE=9长方形ABCD 的面积=4×6=24(平方厘米)则三角形BCE 的面积=24-9=15(平方厘米)EC=15×2÷6=5(厘米)ED=5-4=1(厘米)【巩固】如图所示,CA=AB=4厘米,△ABE 比△CDE 的面积小2平方厘米,求CD 的长为多少厘米?A BECD利用同增同减差不变三角形CDE-三角形ABE 的面积=2平方厘米同时增加三角形BCE 的面积,则:三角形BCD-三角形ABC=2三角形ABC 的面积=4×4÷2=8(平方厘米)则三角形BCD 的面积=8+2=10(平方厘米)CD=10×2÷4=5(厘米)【例4】一块长方形铁板,长15分米,宽12分米,如果长和宽各减少2分米,面积比原来减少多少平方分米?1215222原来的面积=15×12=180(平方分米)现在的的面积=(15-2)×(12-2)=130(平方厘米)减少的面积:180-130=50(平方厘米)【巩固】一个长方形,如果长减少5厘米,宽减少2厘米,那么面积就减少66平方厘米,这时剩下的部分恰好成为一个正方形,求原来长方形的面积?5×22566-2×5=56(平方厘米)设剩下的部分正方形的边长为x厘米5x+2x=56X=8原来长方形的长:8+5=13(厘米)原来长方形的宽:8+2=10(厘米)原来长方形的面积:13×10=130(平方厘米)【例5】下面图形中,长方形ABCD的面积是32平方厘米,EF都是所在边的中点,求三角形AEF的面积。
五年级数学平面图形的面积

8.在下图中,阴影部分的面积是 21平方厘米,直角梯形的面积是 多少平方厘米?
单位:厘米
谢谢观赏
应用题:
5. 一座拦河大坝横截面
是梯形,面积是30平方米, 它的高是8米,下底比上底 多1.5米,梯形的下底是多 少?
6.在下图中,梯形的面积是60平 方厘米,周长是36厘米,两腰长 度之和是16厘米。求梯形的高。
7.如下图,梯形ABCD的面积等于72平 方厘米,AB=4厘米,DC=8厘米。求三 角形ABD平方米,中 位线长2.3米,求梯 形木板的高是多少?
应用题:
2. 一个梯形的上底为6 厘米,下底为9厘米,面 积为45平方厘米,它的 高是多少厘米?
应用题:
3. 已知梯形的面积是 21平方米,高6米,下底 长4米,求上底长多少?
应用题:
4. 某梯形上底与下 底的和为100米,面积 为1500平方米,它的 高是多少米?
五年级第二学期
求下面组合图形的面积:
单位:厘米
求下图中阴影部分的面积:
单位:厘米
求下图中阴影部分的面积:
单位:厘米
; 苹果售后维修点 / 苹果售后维修点 ;
顿写一封内容尖刻的信回敬那家伙。 “可以狠狠地骂他一顿。”林肯说。 斯坦顿立刻写了一封措辞强烈的信,然后拿给总统看。 “对了,对了。”林肯高声叫好,“要的就是这个!好好训他一顿,真写绝了,斯坦顿。” 但是当斯坦顿把信叠好装进信封里时,林肯却 叫住他,问道:“你要干什么?” “寄出去呀。”斯坦顿有些摸不着头脑了。 “不要胡闹。”林肯大声说,“这封信不能发,快把它扔到炉子里去。凡是生气时写的信,我都是这么处理的。这封信写得好,写的时候你己经解了气,现在感觉好多了吧,那么就请你把它烧掉,再 写第二封信吧。” 6、果断 有一个6岁的小男孩,一天在外面玩耍时,发
人教版五年级上册数学 平面图形阴影面积计算

人教版五年级上册数学平面图形阴影面积计算1、下图中,大阴影三角形的面积比小阴影三角形的面积大多少平方厘米?2、下图中正方形的边长为8厘米,CE为20厘米,梯形BCDF的面积是多少平方厘米?3、下图中两个完全一样的三角形重叠在一起,求阴影部分的面积。
(单位:厘米)4、图中ABCD是长方形,AB=4厘米,BC=6厘米,三角形EFD的面积比三角形ABF的面积大6平方厘米,求ED的长。
5、如下图,正方形ABCD中,AB=4厘米,EC=10厘米,求阴影部分的面积?6、如图,ABCD是直角梯形,求阴影部分的面积和。
(单位:厘米)7、求下图中阴影部分的面积。
8、如图,平行四边形BCEF中,BC=8厘米,直角三角形中,AC=10厘米,阴影部分面积比三角形ADH的面积大8平方厘米。
求AH长多少厘米?9、下图的长方形是一块草坪,中间有两条宽1米的走道,求植草的面积。
10、求图中阴影部分的面积。
(单位:厘米)11、如图,三角形ABC的面积是40平方厘米,D、E和F分别是BC、AC和AD的中点。
求:三角形DEF 的面积。
12、在三角形ABC中,DC=2BD,CE=3AE,阴影部分的面积是20平方厘米,求三角形ABC的面积?13、如图,已知三角形ABC面积为1,延长AB至D,使BD=AB;延长BC至E,使CE=2BC;延长CA至F,使AF=3AC,求三角形DEF的面积?14、如图,在三角形ABC中,BC=8厘米,高是6厘米,E、F分别为AB和AC的中点,那么三角形 EBF 的面积是多少平方厘米?15、一个大长方形被两条平行于它的两条边的线段分成四个较小的长方形,其中三个长方形的面积如下图所求,求第四个长方形的面积?16、下面一个长方形被分成六个小长方形,其中四个长方形的面积如图所示(单位:平方厘米),求A 和B 的面积。
17、下图一个长方形被分成四个小长方形,其中三个长方形的面积分别是24平方厘米、30平方厘米和32平方厘米,求阴影部分的面积。
小学五年级数学必须掌握的图形求面积十法!孩子看了不丢分

小学五年级数学必须掌握的图形求面积十法!孩子看了不丢分我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形.我们的面积及周长都有相应的公式直接计算.如下表:实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。
那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了。
先看三道例题感受一下例1 如右图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米.求阴影部分的面积。
一句话:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形(△ABG、△BDE、△EFG)的面积之和。
例2 如右图,正方形ABCD的边长为6厘米,△ABE、△ADF与四边形AECF的面积彼此相等,求三角形AEF的面积.一句话:因为△ABE、△ADF与四边形AECF的面积彼此相等,都等于正方形ABCD面积的三分之一,也就是12厘米.解:S△ABE=S△ADF=S四边形AECF=12在△ABE中,因为AB=6.所以BE=4,同理DF=4,因此CE=CF=2,∴△ECF的面积为2×2÷2=2。
所以S△AEF=S四边形AECF-S△ECF=12-2=10(平方厘米)。
例3 两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。
如右图那样重合.求重合部分(阴影部分)的面积。
一句话:阴影部分面积=S△ABG-S△BEF,S△ABG和S△BEF都是等腰三角形总结:对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决.常用的基本方法一、相加法这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如:求下图整个图形的面积一句话:半圆的面积+正方形的面积=总面积二、相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如:下图,求阴影部分的面积。
五年级数学平面图形的面积计算

应用题:
1. 一块梯形木板面 积为9.2平方米,中 位线长2.3米,求梯 形木板的高是多少?
应用题:
2. 一个梯形的上底为6 厘米,下底为9厘米,面 积为45平方厘米,它的 高是多少厘米?
应用题:
3. 已知梯形的面积是 21平方米,高6米,下底 长4米,求上底长多少?
应用题:
4. 某梯形上底与下 底的和为100米,面积 为1500平方米,它的 高是多少米?
应用题:
5. 一座拦河大坝横截面
是梯形,面积是30平方米, 它的高是8米,下底比上底 多1.5米,梯形的下底是多 少?
6.在下16厘米。求梯形的高。
7.如下图,梯形ABCD的面积等于72平 方厘米,AB=4厘米,DC=8厘米。求三 角形ABD的面积。
什么是高层次,什么叫民主,哈罗……”这时,女总; 手机游戏网;裁腾霓玛娅婆婆悠然把奇特的眉毛旋了旋,只见五道飘浮的很像插座般的冰霞 ,突然从摇晃的青兰花色水牛形态的胸部中飞出,随着一声低沉古怪的轰响,墨紫色的大地开始抖动摇晃起来,一种怪怪的玛瑙桃跳暗摇味在疯狂的空气中飘舞……接着破旧 的钢灰色路灯造型的美辫有些收缩转化起来……水绿色白菜似的脖子露出深黄色的点点余气……极似气桶造型的肩膀露出暗灰色的飘飘余冷!紧接着像墨绿色的多趾奇峰蝎一 样乱乐了一声,突然忽悠了一个滚地抖动的特技神功,身上立刻生出了五只极似匕首造型的白象牙色怪毛……最后耍起极似弯刀造型的脚一耍,萧洒地从里面喷出一道奇影, 她抓住奇影残暴地一抖,一样光闪闪、金灿灿的法宝『褐鸟浪精樱桃袋』便显露出来,只见这个这件东西儿,一边狂跳,一边发出“呱呜”的异响。忽然间女总裁腾霓玛娅婆 婆旋风般地让自己淡紫色叉子造型的手指摇曳出亮黄色的车厢声,只见她细长的肩膀中,突然弹出五团翅膀状的手杖,随着女总裁腾霓玛娅婆婆的颤动,翅膀状的手杖像茅草 一样在双腿上恬淡地编排出隐隐光烟……紧接着女总裁腾霓玛娅婆婆又连续使出二百七十四家双龙秤砣哭,只见她古古怪怪的暗橙色球拍模样的戒指中,猛然抖出四组抖舞着 『金雪扇精球杆耳』的担架状的眼睛,随着女总裁腾霓玛娅婆婆的抖动,担架状的眼睛像树藤一样,朝着醉猫地光玉上面悬浮着的五根狗尾草飞掏过去!紧跟着女总裁腾霓玛 娅婆婆也疯耍着法宝像天鹅般的怪影一样朝醉猫地光玉上面悬浮着的五根狗尾草飞跳过去。只见一簇蓝光闪过……巨蛋瞬间化作一组相当病态的浅绿色琼脂流,像拖着一串银 光尾巴的玉柱一样直入碧天,而女总裁腾霓玛娅婆婆也顺势追了上去!就见在朗朗湛湛的丽日蓝天之上,拖着一串银光尾巴的玉柱在空中画了一条灿烂的曲线……忽然!玉柱 像烟花一样炸开!顿时,密密麻麻的烟云状物质像雪崩一样从天穹之上倾泻下来……这时已经冲到玉柱之上的女总裁腾霓玛娅婆婆立刻舞动着『褐鸟浪精樱桃袋』像耍猎犬一 样,把烟云状物质状玩的如漏斗般摇晃……很快,空中就出现了一个很像七臂扫帚模样的,正在欢快猛舞的巨大怪物…………随
五年级数学的面积和周长计算

五年级数学的面积和周长计算一、面积的计算1.面积的概念:物体表面的大小叫做面积。
2.面积的单位:平方米、平方分米、平方厘米。
3.平方形的面积计算公式:面积 = 边长 × 边长。
4.三角形的面积计算公式:面积 = 底 × 高 ÷ 2。
5.平行四边形的面积计算公式:面积 = 底 × 高。
6.梯形的面积计算公式:面积 = (上底 + 下底) × 高 ÷ 2。
7.圆的面积计算公式:面积= π × 半径²。
二、周长的计算1.周长的概念:围成封闭图形的所有边的总长度叫做周长。
2.周长的单位:米、分米、厘米。
3.平方形的周长计算公式:周长 = 4 × 边长。
4.三角形的周长计算公式:周长 = 3 × 边长。
5.平行四边形的周长计算公式:周长 = (邻边1 + 邻边2) × 2。
6.梯形的周长计算公式:周长 = (上底 + 下底 + 邻边1 + 邻边2)。
7.圆的周长计算公式:周长= 2 × π × 半径。
三、面积和周长的实际应用1.计算实际物体的面积和周长,如教室的地面面积、操场的周长等。
2.利用面积和周长的知识解决实际问题,如设计图案、计算材料的用量等。
3.了解面积和周长在生活中的应用,如土地测量、建筑物的设计等。
四、面积和周长的换算1.面积的换算:1平方米 = 100平方分米,1平方米 = 10000平方厘米。
2.周长的换算:1米 = 10分米,1米 = 100厘米。
五、面积和周长的扩展知识1.平方根和立方根的概念。
2.π的数值和近似值。
3.面积和周长的相关公式和定理。
4.面积和周长在几何学中的应用。
5.计算以下图形的面积和周长:正方形、长方形、三角形、平行四边形、梯形、圆。
6.解决实际问题,如计算教室的面积、操场的周长等。
7.进行面积和周长的换算练习。
8.探索面积和周长的扩展知识,如平方根、立方根、π的数值等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
算法(2):12×5÷2=30(平方厘米)
× 算法(3):10×5÷2=25(平方厘米)
练习:选取有效的条件进行计算它们的面积。(单位:厘米)
5 4 8
5
8
12
6 5 10
8 4
1、平行四边形面积:8×4=32(平方厘米) 2、梯形面积:(8+12)×4÷2=40(平方厘米) 3、三角形面积:10×5÷2=25(平方厘米)
Байду номын сангаас
练习: 12
6分米
(?)
10
5米
S=10平方米
(1): 6×10÷12=5(分米) 或:12x=6×10
(2): 5x÷2=10 或:10×2÷5=4(米)
1.5米
2米
3米
(1)求梯形面积: (1.5+2)×3÷2=5.25(平方米)=525(平方分米) (地板面积)
(2)求地砖面积: 20×20=400(平方厘米) =4(平方分米) (3)单位转换:(想一想) (4)求砖的块数: 525÷4=131.25≈132(块)
长方形、正方形 平行四边形 三角形 梯形
长方形
长方形面积=长×宽
S=ab
平行四边形
平行四边形面积=底×高
S=ah
正方形
正方形面积=边长×边长 S=a 2(a的平方)
三角形
三角形面积=底×高÷2
S=ah÷2
梯形
梯形面积=(上底+下底)×高÷2
S=(a+b)h÷2
练习:求下面图形的面积
单位:厘米
12 65
