工程光学2019第二章平面光学系统
合集下载
工程光学第二章
高斯公式
1 1 1 l l f
y l yl
牛顿与高斯公式的转换: x l f ......x l f
当系统确定时，f
可根据公式，改变 x(l) 可得到不同β， 或β按要求，可计算出相应的 x(l) .
例:有一理想光组,其焦距为 f f 75mm
其前方150mm处有一物高为20mm的物体,
求像的位置和大小.若要求 0.5x 问物体应位于何处?
解:
1)根据 1 1 1 l l f
Q Q' B y
A
F
H H'
F
A'
l 150mm
-y'
f 75mm
R
R'
-x
-f
f'
B' x'
l 150mm
-l
l 1 l
一个理想光学系统可以用其基点（面）来表示，而 不需考虑其具体结构如何。
O
B O2
O1 A
A'
O' B' O'2
M
图2-3 两对共轭面已知的情况
O
B
A
O3
O1 O2
O'
A'
B'
M
图2-4 一对共轭面及两对共轭点已知的情况
第二节 理想光学系统的基点和基面
一.焦点与焦平面
1.像方焦点与像方焦平面（对应 L＝－∞）
l x f 902.605mm
以O1为原点! 以H 为原点!
x f 8.2055mm l x f 90.2605mm
L=-∞ F'
工程光学2019第二章平面光学系统精品文档
第二章 平面光学系统
2019/10/18
1
§2-1 平面镜的成像性质
一、物像的坐标关系
P
y
z
O
x
y'
z'
O’
x'
Q
2019/10/18
Z Y X
食
指
大代
拇表
中 指 代
指 代 表
轴
表轴
轴
2
物像坐标系：坐标关系符合左手的称为左手系 ； 坐标关系符合右手的称为右手系。
物像关系分类： 镜像：物为左（右）手系，像为右（左）手系.
O1
双平面镜的2θ 原则
O2
I2
I2
q
N
β =2θ
q
M
β≤90
b
2019/10/18
P
9
P光1，线PA2O为1两经个两平个面平镜面。镜假反设射两后者，间沿的着夹O2角B的为方θ，向入射射出 ，间个内的延角夹长之角AO和为1和的β，O关2由B系相△交O1于O2一M点根M据，外设角入等射于和不出相射邻光的线两 两平面镜的法线相交于一点N，由△O1O2N得 将以上关系代入上面β的公式，得到 以上关系和I角的大小无关。
这种复合棱镜的用途也是 倒像作用。
2019/10/18
49
(a)阿贝棱镜
y
z x
z′ x ′ y′
2019/10/18
50
y
x
z
y′
x′ z′
（b）别汉棱镜
2019/10/18
51
（c）分光棱镜
2019/10/18
52
（d）分色棱镜
2019/10/18
53
（e）转像棱镜
2019/10/18
1
§2-1 平面镜的成像性质
一、物像的坐标关系
P
y
z
O
x
y'
z'
O’
x'
Q
2019/10/18
Z Y X
食
指
大代
拇表
中 指 代
指 代 表
轴
表轴
轴
2
物像坐标系：坐标关系符合左手的称为左手系 ； 坐标关系符合右手的称为右手系。
物像关系分类： 镜像：物为左（右）手系，像为右（左）手系.
O1
双平面镜的2θ 原则
O2
I2
I2
q
N
β =2θ
q
M
β≤90
b
2019/10/18
P
9
P光1，线PA2O为1两经个两平个面平镜面。镜假反设射两后者，间沿的着夹O2角B的为方θ，向入射射出 ，间个内的延角夹长之角AO和为1和的β，O关2由B系相△交O1于O2一M点根M据，外设角入等射于和不出相射邻光的线两 两平面镜的法线相交于一点N，由△O1O2N得 将以上关系代入上面β的公式，得到 以上关系和I角的大小无关。
这种复合棱镜的用途也是 倒像作用。
2019/10/18
49
(a)阿贝棱镜
y
z x
z′ x ′ y′
2019/10/18
50
y
x
z
y′
x′ z′
（b）别汉棱镜
2019/10/18
51
（c）分光棱镜
2019/10/18
52
（d）分色棱镜
2019/10/18
53
（e）转像棱镜
工程光学习题参考答案第二章理想光学系统
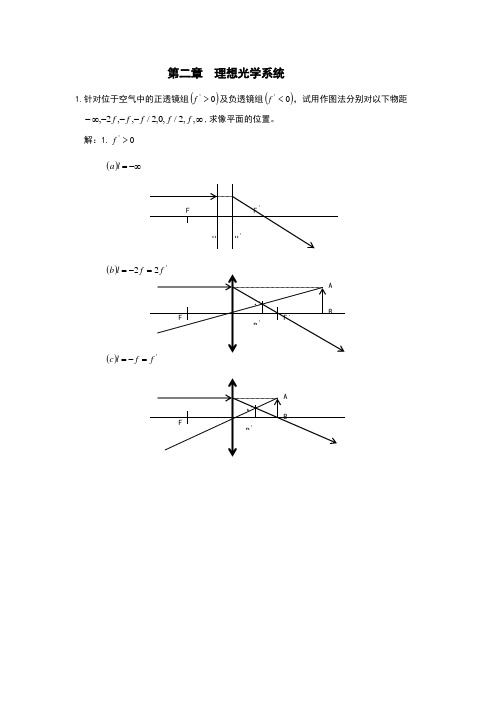
第二章 理想光学系统1.针对位于空气中的正透镜组()0'>f 及负透镜组()0'<f ，试用作图法分别对以下物距 ∞---∞-,,2/,0,2/,,2,f f f f f ,求像平面的位置。
解：1.0'>f ()-∞=l a()'2f l b -=()f f l c =-=()/f l d -=()0=l e()/f l f =')(f f l g -=='22)(f f l h -==+∞=l i )(2.0'<f -∞=l a )(l b )(=l c =)(/)(f l d -=0 el(=)f=l2/ (f)()fg=l(=h)ll i)(+∞=2. 已知照相物镜的焦距f’＝75mm,被摄景物位于（以F 点为坐标原点）=x ,2,4,6,8,10,m m m m m -----∝-处，试求照相底片应分别放在离物镜的像方焦面多远的地方。
解： （1）x= -∝ ，xx ′=ff ′ 得到：x ′=0 （2）x ′= （3）x ′= （4）x ′= （5）x ′=（6）x ′=3.设一系统位于空气中，垂轴放大率*-=10β，由物面到像面的距离（共轭距离）为7200mm ， 物镜两焦点间距离为1140mm 。
求该物镜焦距，并绘出基点位置图。
解:∵ 系统位于空气中，f f -='10''-===ll y y β 由已知条件：1140)('=+-+x f f7200)('=+-+x l l解得：mm f 600'= mm x 60-=4.已知一个透镜把物体放大*-3投影到屏幕上，当透镜向物体移近18mm 时，物体将被放大*-4，试求透镜的焦距，并用图解法校核之。
解：方法一：31'11-==l l β ⇒ ()183321'1--=-=l l l ①42'22-==l l β ⇒ 2'24l l -= ② 1821+-=-l l ⇒ 1821-=l l ③ '/1/1/11'1f l l =-'/1/1/12'2f l l =-将①②③代入④中得 mm l 2702-= mm l 1080'2-= ∴ mm f 216'=方法二： 311-=-=x fβ 422-=-=x fβ ⇒ mm f 216-= 1812=-x x方法三： 12)4)(3(21''=--==∆∆=ββαnn x x2161812'-=⨯=∆x''fx -=β143''''2'121=+-=∆=+-=-∴fx fx x ββ mm x f 216''=∆=∴5.一个薄透镜对某一物体成实像，放大率为⨯-1,今以另一个薄透镜紧贴在第一个透镜上，则见像向透镜方向移动，放大率为原先的3/4倍，求两块透镜的焦距为多少 解：⇒ 2'21'1/1/1/1/1l l l l -=- ④6.有一正薄透镜对某一物成倒立的实像，像高为物高的一半，今将物面向物体移近100mm ， 则所得像与物同大小，求该正透镜组的焦距。
工程光学课件第02章
第一节 理想光学系统与共线成像理论
理想光学系统理论是在1841年由高斯提出来的，所以理想 光学系统理论又被称为“高斯光学”。 理想光学系统中，任何一个物点发出的光线在系统的作用 下所有的出射光线仍然相交于一点。每个物点对应于唯一的 一个像点，这种物像对应关系叫做“共轭”。
物空间 像空间 点 直线 平面 共轭
F'：像方焦点，过F'垂直于光轴的平面为像方焦平面， 这个焦平面是与无限远处垂直于光轴的物平面共轭的 像平面。
第二节 理想光学系统的基点与基面
H'：像方主点，过H'垂直于 光轴的平面为像方主平面。
从像方主点H'到像方焦点 的距离为像方焦距f' 无限远轴外物点发出一束 平行光线，通过光学系统 后交于像方焦平面上一点。
A
F
H
H′ F′
A A′
H
H′ F′
A′
F
A F
H
H′ F′
A A′ F
H
H′ F′
A′
第三节
理想光学系统的物像关系
（三）轴上点经过两个光组的图解法求像
第三节
练习：作图求像
A
理想光学系统的物像关系
A
H′ H F H′ F′
A′
H
F′
A′
F
A′ A
H
H′ F′
A A′
F F′ H H′ F
第三节
理想光学系统的物像关系
用作图法求以下双光组等效系统的基点、基面
F1
H1
H1’ F1’ F2 H2
F2’ H2’
d Q H F Q’
F1
H1
H1’ F1’ F2 H2
F2’ H2’
工程光学设计 第2章 第二讲
B
垂轴色差 yF C yZF yZC
垂轴色差
A
C
D
y Z C
F yZF yZD
B
垂轴色差
yF C yZF yZC
❖ 3 二级光谱
d(sini sin m ) m
第二章 像差理论
2.3 薄透镜的初级像差理 论
2.3 薄透镜的初级像差理论
一. 薄透镜的初级像差普遍公式
球差和数 S hni(i u)(i i)
四 畸变
无畸变
正畸变
负畸变
负畸变
（a） 光阑位于透镜之前产生负畸变
正畸变
（a） 光阑位于透镜之后产生正畸变
❖ 线畸
yz yz y
q yz 100 %
y
五 色差
1 轴向色差
O1 O2
1 23
兰（F） 绿（D） 红（C）
l
′
F
AF′
AC′
-△l
′
FC
l
′
C
2 垂轴色差
A
F
D
C yZ C yZD yZF
四 反射光学系统和平面光学系统的像 差理论
❖ 1 平面反射镜像差
- i′ -i
-u
u′
2 加工或装配误差产生像差
仪器的主光轴
五 球面反射镜的像差
像点
球心
u=0
-i
- i′ - u′
h
r
光阑在反射镜球心
l
lp
球心
阑
光阑在反射镜顶点
l 球心 ip
lp 阑
六 棱镜或平面平行板的像差
光阑
- i1
正透镜
A
A0′ A′
负透镜
工程光学2
例：三片型照相物镜, 若要求此物镜成像-1/10x, 问 物平面应放在什么位置。
由多个光组组成的理想光学系统的成像
1、光组：一个光学系统可由一个或几个部件组成, 每个部件可以由一个或几个透镜组成, 这些部件被 称为光组。 2、光组间的过渡公式：
理想光学系统两焦距之间的关系
物方焦距和像方焦距之间的关系式
高斯公式
说明几点： 垂轴放大率β与物体的位置有关，某一垂轴放大率 只对应一个物体位置； 对于同一共轭面，β是常数，因此平面物与其像相 似； 理想光学系统的成像性质主要表现在像的位置、大 小、虚实、正倒上，利用上述公式可描述任意位置 物体的成像问题； 工程实际中有一类问题是寻求物体放于什么位置， 可以满足合适的倍率。
特点：这种组合光组的焦距f’大于光组的筒长 应用：长焦距镜头的设计。
。
例2．反远距型光组
一光组由两个薄光组组合而成。第一个薄光组的焦距f1’=35mm，第二个薄光组的焦距f2’＝25mm，两薄光组之间的 间隔d＝15mm。求合成焦距f’并比较工作距lF’与f’的长短。
特点：这个组合光组的工作距比焦距f’要长。
⑤焦点位置公式：
主平面位置公式：
多光组组合计算
一个基于计算来求组合系统的方法。 方法：追迹一条投射高度为h1的平行于光轴的光线， 只要计算出最后的出射光线与光轴的夹角(孔径 角) , 则
过渡公式的推导： 对任意一个单独的光组来说, 将高斯公式两边同乘以共轭点 的光线在其上的投射高度h有 因有 , , 所以
（5）正弯月形透镜的主面位于相应折射面远离球 面曲率中心一侧；负弯月形透镜的主面位于相应折 射面靠近曲率中心的一侧。这两种弯月形透镜的主 面可能有一个主面位于空气中，或两个主面同时位 于空气中，由两个曲率半径和厚度的数值决定。 (6)忽略厚度不计的透镜称为薄透镜。 当d→0时，有下式成立：
(工程光学教学课件)第2章 高斯光学系统
上两对共轭点的位置，则系统的成像特性确定，其它物点的像点均可由 这些已知共轭点和面来表示<已知物像求光瞳或反之>。
共线成像理论小结
➢ 点对点；直线对直线；点在线上； ➢ 平面对平面；同心光束对应同心光束。
B A•
D•
p
C
理想光 学系统
p
C
• D
B
•A
§2-2 理想光学系统的基点与基面
这里我们定义一些特殊的共轭点和共轭面作为理想光学系统的基点和基面。
一、垂轴放大率
上节已经推导出了系统垂轴放大率的表达式，即：
y f x
y x f
nl nn时 l
1 1 1 l l f
放大率公式
由牛顿公式得： x= f f /x
两边同加上f ，得： x + f = f f / x+f = f /x (x + f)
由于x + f = l，x + f = l，代入上式，得： f /x = l / l
根据牛顿形式的放大率公式，有：
= -f / x = -(f /x)(f /f ) = -(f /f )(l/l)
物空间平行于光轴的光线光学系统或平行或与光轴相交。我们先考虑与 光轴相交的情况。
一、理想光学系统的焦点与焦面
A
A
(物方焦点) F 第一焦点 前焦点
物方焦平面
无穷远物点 与 F 共轭
注意： F 与 F 不是一对共轭点
F(像方焦点) 第二焦点 后焦点
像方焦平面
F 与 无穷远像点 共轭
轴外物体的成像光束
➢平行入射过焦(面上的)点； ➢通过焦(面上的)点变平行； ➢通过节(主)点光线不改变方向。 作图求解物像关系时，可任选其中二根光线直接作图或作为辅助光线。 注意点：光线在主面上等高的地方改变方向。
共线成像理论小结
➢ 点对点；直线对直线；点在线上； ➢ 平面对平面；同心光束对应同心光束。
B A•
D•
p
C
理想光 学系统
p
C
• D
B
•A
§2-2 理想光学系统的基点与基面
这里我们定义一些特殊的共轭点和共轭面作为理想光学系统的基点和基面。
一、垂轴放大率
上节已经推导出了系统垂轴放大率的表达式，即：
y f x
y x f
nl nn时 l
1 1 1 l l f
放大率公式
由牛顿公式得： x= f f /x
两边同加上f ，得： x + f = f f / x+f = f /x (x + f)
由于x + f = l，x + f = l，代入上式，得： f /x = l / l
根据牛顿形式的放大率公式，有：
= -f / x = -(f /x)(f /f ) = -(f /f )(l/l)
物空间平行于光轴的光线光学系统或平行或与光轴相交。我们先考虑与 光轴相交的情况。
一、理想光学系统的焦点与焦面
A
A
(物方焦点) F 第一焦点 前焦点
物方焦平面
无穷远物点 与 F 共轭
注意： F 与 F 不是一对共轭点
F(像方焦点) 第二焦点 后焦点
像方焦平面
F 与 无穷远像点 共轭
轴外物体的成像光束
➢平行入射过焦(面上的)点； ➢通过焦(面上的)点变平行； ➢通过节(主)点光线不改变方向。 作图求解物像关系时，可任选其中二根光线直接作图或作为辅助光线。 注意点：光线在主面上等高的地方改变方向。
哈工大《工程光学》课件
※ 入射光线AE与光轴的夹角为物方倾斜角也叫物方 孔径角，用U 表示。
Engineering Optics
授课：任秀云
n
E n’
A
-U
h
C U’
A’
O r
-L
L’
折射光线EA’ 由以下参量确定：
※像方截距：顶点O到折射光线与光轴交点，用L’表示。
※像方倾斜角：折射光线EA’ 与光轴的夹角，也叫像方 孔径角，用U’ 表示。
（5）r = -40mm, L = -100mm, U = -10°, L’= -200mm
Engineering Optics
授课：任秀云
2.1.3 单折射球面成像的光路计算
一、实际光路的计算公式（追迹公式或大L公式）：
nE
n’
A
-U
C O
r
-L
当结构参数 r , n , n’ 给定时，只要知道 L 和 U ，就可求L’ 和 U’
光轴 为起始边。
B
y -U
A
-L
E I
h
I’
φ
C
U’
A’
O
r
-y’ B’
L’
Engineering Optics
授课：任秀云
×
×
√
×
L = 100mm, U = 30°
Engineering Optics
授课：任秀云
同学们一定要记住上面 的符号规则！
Engineering Optics
授课：任秀云
Engineering Optics
n
授课：任秀云
I
E
n’
-U A
-L
φC
O
r
Engineering Optics
授课：任秀云
n
E n’
A
-U
h
C U’
A’
O r
-L
L’
折射光线EA’ 由以下参量确定：
※像方截距：顶点O到折射光线与光轴交点，用L’表示。
※像方倾斜角：折射光线EA’ 与光轴的夹角，也叫像方 孔径角，用U’ 表示。
（5）r = -40mm, L = -100mm, U = -10°, L’= -200mm
Engineering Optics
授课：任秀云
2.1.3 单折射球面成像的光路计算
一、实际光路的计算公式（追迹公式或大L公式）：
nE
n’
A
-U
C O
r
-L
当结构参数 r , n , n’ 给定时，只要知道 L 和 U ，就可求L’ 和 U’
光轴 为起始边。
B
y -U
A
-L
E I
h
I’
φ
C
U’
A’
O
r
-y’ B’
L’
Engineering Optics
授课：任秀云
×
×
√
×
L = 100mm, U = 30°
Engineering Optics
授课：任秀云
同学们一定要记住上面 的符号规则！
Engineering Optics
授课：任秀云
Engineering Optics
n
授课：任秀云
I
E
n’
-U A
-L
φC
O
r
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
l' d1 1 n
因此，物点以近轴光经平行平面板成像是完 善的。
2020/6/25
20
三、侧向位移Z大小：
平行平面板的厚度为d，由 ΔABD和ABC得
Z A sB i I1 n I1 '
d AB
co s I1'
2020/6/25
21
Z d sinI1 I1'
c os I1 '
d 1
c os I1 n2 sin 2
I1
sin
I1
光线移动的距离随入射 角的不同而不同
同样也随平板的厚度不 同而变化
2020/6/25
22
如果是在近轴区，上式可以写为
zdi1i1'd11 ni1
如果d、n是常数，因此 z 和 i1成正比。
平行平面板的这一性质使它在测微机构的读数 系统中得到应用。
15
所以 ： I1 I2' = U1U2'（2-5）
tgU2 ' tgU1
1
b1 1
，
，
b 2 1
（2-6）
A′ 1(A2)
n1=1
I1
U1′ A
U1 A′ 2 L′
L1 L′1
L2
D I1′I2 GU′ 2
O1
n2=n′1=n
d L′2
I′ 2 E F n′ 2= 1
O2
图
表明，平行平板不会使物体放大或缩小，对光束既不发散也不
物像关系 一致像：物为左（右）手系，像为左（右）手系。 其中，物像坐标方向完成相同的称为完全一致像。除光轴外，
其它两个坐标反向的称为倒的一致像。
2020/6/25
3
二 平面镜的成像性质
A B
POQFra bibliotekA’2020/6/25
实物成虚像
4
A’
P
A
2020/6/25
Q
虚物成实像
5
（一）单平面镜的成像特性
成完善像。即：若入射光束为单心光束，出射光束也为单心
光束，一物点成唯一像点；
实物成虚像，虚物成实像。虚实相反。
物和像大小相等，正立，对称，反像。
凡一次镜面反射或奇次 镜面反射像被 称为镜像； 偶次反射成一致像。
镜像
2020/6/25
6
（二）平面镜的旋转效应
1.单平面镜的旋转效应
∠A’OA”=2∠POP’
2020/6/25
7
2.双平面镜 的旋转效应
对于夹角为α的双平面镜系统 ： α =0 时，像有无数个，分 布如右； α = π时，单平面镜 ，像有一个 ；α为任意角时 成像若干个。
2020/6/25
8
P
AP
I1
I1
O1
双平面镜的2θ原则
O2
I2
I2
q
N
β=2θ
q
M
β≤90
b
2020/6/25
P
9
会聚，表明它是一个无焦元件，在光学系统中对光焦度无贡献。
同时还表明，物体经平板成正立像，物像始终位于平板的同侧，
且虚实相反。
2020/6/25
16
结论
平行平面板的出射光线BS′ 和 入射光线SA是平行，即不改变 光线方向。
平行平板不会使物体放大或缩小，对光束既 不发散也不会聚，表明它是一个无焦元件， 在光学系统中对光焦度无贡献。
P光1，线PA2O为1两经个两平个面平镜面。镜假反设射两后者，间沿的着夹O2角B的为方θ，向入射射出 ，间个内的延角夹长之角AO和为1和的β，O关2由B系相△交O1于O2一M点根M据，外设角入等射于和不出相射邻光的线两 两平面镜的法线相交于一点N，由△O1O2N得 将以上关系代入上面β的公式，得到 以上关系和I角的大小无关。
2020/6/25
23
四、平行平板的应用
1.如分划板、显微镜载物台上的载波片和盖玻片、 滤光片和滤色片、补偿平板及保护玻璃片等。
2020/6/25
24
四、平行平板的应用
2.平行平面板在测微机构的读数系统中得到应用 ---平板测微器
zdi1i1'd11n
通过分划板的刻线与A‘A“重合，可测小角α。
物体经平板成正立像，物像始终位于平板的同 侧，且虚实相反。
2020/6/25
17
二、光线在光轴方向上有一轴向 位移ΔL′大小：
设入射光线为同心光束并会聚于E 点（为虚物点）
L 'B FFK dAF1ctgI
AFdtg1'I
L'
d1
tgI1' tgI1
2020/6/25
18
L'
d1
tgI1' tgI1
2020/6/25
25
§2-4 反射棱镜
2020/6/25
26
一、基本概念
定义：把多个反射面集成在同 一块光学材料上的光学元件。
棱镜的光轴：光学系统的 光轴在棱镜中的部分。 ABC---棱镜光轴
A
2020/6/25
光轴长度：棱镜光轴 的几何长度；
AB+BC=L 棱镜光轴 长度
第二章 平面光学系统
2020/6/25
1
§2-1 平面镜的成像性质
一、物像的坐标关系
P
y
z
O
x
y'
z'
O’
x'
Q
2020/6/25
Z Y X
食
指
大代
拇表
中 指 代
指 代 表
轴
表轴
轴
2
物像坐标系：坐标关系符合左手的称为左手系 ； 坐标关系符合右手的称为右手系。
物像关系分类： 镜像：物为左（右）手系，像为右（左）手系. 其中：上下方向不变的称为正镜像。上下变化的为倒 镜像。
公式表明：ΔL′因不同的I1值不同而不同。 即从具有不同入射角的各条光线经平行平面板折射后，具
有不同的轴向位移量。
结论：同心光束经平行平面板后变为非同心光束，成像 是不完善的。
平行平面板的厚度d 愈大，成像不完善程度也愈大。
2020/6/25
19
如入射光束孔径很小，即为近轴光束成像， 则因I1角很小，
2020/6/25
10
双平面镜具有以下成像性质：
二次反射像与原物坐标系相同，成一致像 。 位于主截面（两平面镜的公共垂直面）内 的光线，不论入射光线方向如何，出射光 线的转角永远等于两平面镜夹角的两倍。
2020/6/25
11
三、平面镜的应用
1. 成像作用 2.光放大作用---光学杠杆
M
L1
A'
F'
元件称为平行平面板。
常见的如：标尺、刻有标志的分划板、 补偿板、滤光镜、保护玻璃等等
2020/6/25
14
一、平行平面板的成像特性 应用折射定律
siIn 1nsiIn 1'
nsiIn 2siIn 2'
平板的两面是平行的
I1' I2
sin I2'sin I1
I2' I1 U2' U1
2020/6/25
A
H H'
M -f
b)
由于转角 很小，此装置的位移量放大倍数为：
P
a
测杆 P
MAxAfat gt2 g2af
2020/6/25
12
3. 转折光轴:使光轴转到某一特定角以及缩小仪
器的体积。
出射光线不稳定
五角棱镜两反射面的夹角一定 则出射光线稳定
2020/6/25
13
§2-2 平行平板的成像
由两个相互平行的折射平面构成的光学
因此，物点以近轴光经平行平面板成像是完 善的。
2020/6/25
20
三、侧向位移Z大小：
平行平面板的厚度为d，由 ΔABD和ABC得
Z A sB i I1 n I1 '
d AB
co s I1'
2020/6/25
21
Z d sinI1 I1'
c os I1 '
d 1
c os I1 n2 sin 2
I1
sin
I1
光线移动的距离随入射 角的不同而不同
同样也随平板的厚度不 同而变化
2020/6/25
22
如果是在近轴区，上式可以写为
zdi1i1'd11 ni1
如果d、n是常数，因此 z 和 i1成正比。
平行平面板的这一性质使它在测微机构的读数 系统中得到应用。
15
所以 ： I1 I2' = U1U2'（2-5）
tgU2 ' tgU1
1
b1 1
，
，
b 2 1
（2-6）
A′ 1(A2)
n1=1
I1
U1′ A
U1 A′ 2 L′
L1 L′1
L2
D I1′I2 GU′ 2
O1
n2=n′1=n
d L′2
I′ 2 E F n′ 2= 1
O2
图
表明，平行平板不会使物体放大或缩小，对光束既不发散也不
物像关系 一致像：物为左（右）手系，像为左（右）手系。 其中，物像坐标方向完成相同的称为完全一致像。除光轴外，
其它两个坐标反向的称为倒的一致像。
2020/6/25
3
二 平面镜的成像性质
A B
POQFra bibliotekA’2020/6/25
实物成虚像
4
A’
P
A
2020/6/25
Q
虚物成实像
5
（一）单平面镜的成像特性
成完善像。即：若入射光束为单心光束，出射光束也为单心
光束，一物点成唯一像点；
实物成虚像，虚物成实像。虚实相反。
物和像大小相等，正立，对称，反像。
凡一次镜面反射或奇次 镜面反射像被 称为镜像； 偶次反射成一致像。
镜像
2020/6/25
6
（二）平面镜的旋转效应
1.单平面镜的旋转效应
∠A’OA”=2∠POP’
2020/6/25
7
2.双平面镜 的旋转效应
对于夹角为α的双平面镜系统 ： α =0 时，像有无数个，分 布如右； α = π时，单平面镜 ，像有一个 ；α为任意角时 成像若干个。
2020/6/25
8
P
AP
I1
I1
O1
双平面镜的2θ原则
O2
I2
I2
q
N
β=2θ
q
M
β≤90
b
2020/6/25
P
9
会聚，表明它是一个无焦元件，在光学系统中对光焦度无贡献。
同时还表明，物体经平板成正立像，物像始终位于平板的同侧，
且虚实相反。
2020/6/25
16
结论
平行平面板的出射光线BS′ 和 入射光线SA是平行，即不改变 光线方向。
平行平板不会使物体放大或缩小，对光束既 不发散也不会聚，表明它是一个无焦元件， 在光学系统中对光焦度无贡献。
P光1，线PA2O为1两经个两平个面平镜面。镜假反设射两后者，间沿的着夹O2角B的为方θ，向入射射出 ，间个内的延角夹长之角AO和为1和的β，O关2由B系相△交O1于O2一M点根M据，外设角入等射于和不出相射邻光的线两 两平面镜的法线相交于一点N，由△O1O2N得 将以上关系代入上面β的公式，得到 以上关系和I角的大小无关。
2020/6/25
23
四、平行平板的应用
1.如分划板、显微镜载物台上的载波片和盖玻片、 滤光片和滤色片、补偿平板及保护玻璃片等。
2020/6/25
24
四、平行平板的应用
2.平行平面板在测微机构的读数系统中得到应用 ---平板测微器
zdi1i1'd11n
通过分划板的刻线与A‘A“重合，可测小角α。
物体经平板成正立像，物像始终位于平板的同 侧，且虚实相反。
2020/6/25
17
二、光线在光轴方向上有一轴向 位移ΔL′大小：
设入射光线为同心光束并会聚于E 点（为虚物点）
L 'B FFK dAF1ctgI
AFdtg1'I
L'
d1
tgI1' tgI1
2020/6/25
18
L'
d1
tgI1' tgI1
2020/6/25
25
§2-4 反射棱镜
2020/6/25
26
一、基本概念
定义：把多个反射面集成在同 一块光学材料上的光学元件。
棱镜的光轴：光学系统的 光轴在棱镜中的部分。 ABC---棱镜光轴
A
2020/6/25
光轴长度：棱镜光轴 的几何长度；
AB+BC=L 棱镜光轴 长度
第二章 平面光学系统
2020/6/25
1
§2-1 平面镜的成像性质
一、物像的坐标关系
P
y
z
O
x
y'
z'
O’
x'
Q
2020/6/25
Z Y X
食
指
大代
拇表
中 指 代
指 代 表
轴
表轴
轴
2
物像坐标系：坐标关系符合左手的称为左手系 ； 坐标关系符合右手的称为右手系。
物像关系分类： 镜像：物为左（右）手系，像为右（左）手系. 其中：上下方向不变的称为正镜像。上下变化的为倒 镜像。
公式表明：ΔL′因不同的I1值不同而不同。 即从具有不同入射角的各条光线经平行平面板折射后，具
有不同的轴向位移量。
结论：同心光束经平行平面板后变为非同心光束，成像 是不完善的。
平行平面板的厚度d 愈大，成像不完善程度也愈大。
2020/6/25
19
如入射光束孔径很小，即为近轴光束成像， 则因I1角很小，
2020/6/25
10
双平面镜具有以下成像性质：
二次反射像与原物坐标系相同，成一致像 。 位于主截面（两平面镜的公共垂直面）内 的光线，不论入射光线方向如何，出射光 线的转角永远等于两平面镜夹角的两倍。
2020/6/25
11
三、平面镜的应用
1. 成像作用 2.光放大作用---光学杠杆
M
L1
A'
F'
元件称为平行平面板。
常见的如：标尺、刻有标志的分划板、 补偿板、滤光镜、保护玻璃等等
2020/6/25
14
一、平行平面板的成像特性 应用折射定律
siIn 1nsiIn 1'
nsiIn 2siIn 2'
平板的两面是平行的
I1' I2
sin I2'sin I1
I2' I1 U2' U1
2020/6/25
A
H H'
M -f
b)
由于转角 很小，此装置的位移量放大倍数为：
P
a
测杆 P
MAxAfat gt2 g2af
2020/6/25
12
3. 转折光轴:使光轴转到某一特定角以及缩小仪
器的体积。
出射光线不稳定
五角棱镜两反射面的夹角一定 则出射光线稳定
2020/6/25
13
§2-2 平行平板的成像
由两个相互平行的折射平面构成的光学