工程光学习题解答--第二章-理想光学系统
工程光学第二章

高斯公式
1 1 1 l l f
y l yl
牛顿与高斯公式的转换: x l f ......x l f
当系统确定时,f
可根据公式,改变 x(l) 可得到不同β, 或β按要求,可计算出相应的 x(l) .
例:有一理想光组,其焦距为 f f 75mm
其前方150mm处有一物高为20mm的物体,
求像的位置和大小.若要求 0.5x 问物体应位于何处?
解:
1)根据 1 1 1 l l f
Q Q' B y
A
F
H H'
F
A'
l 150mm
-y'
f 75mm
R
R'
-x
-f
f'
B' x'
l 150mm
-l
l 1 l
一个理想光学系统可以用其基点(面)来表示,而 不需考虑其具体结构如何。
O
B O2
O1 A
A'
O' B' O'2
M
图2-3 两对共轭面已知的情况
O
B
A
O3
O1 O2
O'
A'
B'
M
图2-4 一对共轭面及两对共轭点已知的情况
第二节 理想光学系统的基点和基面
一.焦点与焦平面
1.像方焦点与像方焦平面(对应 L=-∞)
l x f 902.605mm
以O1为原点! 以H 为原点!
x f 8.2055mm l x f 90.2605mm
L=-∞ F'
工程光学,郁道银,第二章 习题及答案

第二章习题及答案1、已知照相物镜的焦距f’=75mm,被摄景物位于(以F 点为坐标原点)x=-∞、-10m、-8m、-6m、-4m、-2m 处,试求照相底片应分别放在离物镜的像方焦面多远的地方。
解:(1)xx′=ff′,x= -∝得到:x′=0(2)x= -10 ,x′=0.5625(3)x= -8 ,x′=0.703(4)x= -6 ,x′=0.937(5)x= -4 ,x′=1.4(6)x= -2 ,x′=2.812、已知一个透镜把物体放大-3x 投影在屏幕上,当透镜向物体移近18mm 时,物体将被放大-4x 试求透镜的焦距,并用图解法校核之。
解:3.一个薄透镜对某一物体成实像,放大率为-1x,今以另一个薄透镜紧贴在第一个透镜上,则见像向透镜方向移动20mm,放大率为原先的3/4 倍,求两块透镜的焦距为多少?解:4.有一正薄透镜对某一物成倒立的实像,像高为物高的一半,今将物面向透镜移近100mm,则所得像与物同大小,求该正透镜组的焦距。
解:5.希望得到一个对无限远成像的长焦距物镜,焦距=1200mm,由物镜顶点到像面的距离L=700 mm,由系统最后一面到像平面的距离(工作距)为,按最简单结构的薄透镜系统考虑,求系统结构,并画出光路图。
解:6.一短焦距物镜,已知其焦距为35 mm,筒长L=65 mm,工作距,按最简单结构的薄透镜系统考虑,求系统结构。
解:7.已知一透镜求其焦距、光焦度。
解:8.一薄透镜组焦距为100 mm,和另一焦距为50 mm 的薄透镜组合,其组合焦距仍为100 mm,问两薄透镜的相对位置。
解:9.长60 mm,折射率为1.5 的玻璃棒,在其两端磨成曲率半径为10 mm 的凸球面,试求其焦距。
解:10.一束平行光垂直入射到平凸透镜上,会聚于透镜后480 mm 处,如在此透镜凸面上镀银,则平行光会聚于透镜前80 mm 处,求透镜折射率和凸面曲率半径。
解:。
工程光学习题解答

第一章习题1、已知真空中的光速c=3 m/s,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s,当光在冕牌玻璃中,n=1.51时,v=1.99 m/s,当光在火石玻璃中,n=1.65时,v=1.82 m/s,当光在加拿大树胶中,n=1.526时,v=1.97 m/s,当光在金刚石中,n=2.417时,v=1.24 m/s。
2、一物体经针孔相机在屏上成一60mm大小的像,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm。
3、一厚度为200mm的平行平板玻璃(设n=1.5),下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:令纸片最小半径为x,则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=1.5,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm,所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有:n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上,求其会聚点的位置。
工程光学第二版习题答案(李湘宁_贾志宏)

丝,问其通过球面的共轭像在何处?当入射高度
h=10mm,实际光线的像方截距为多少?与高斯像面的距离
为多少?
解:
8、一球面镜半径 r=-100mm, 求 = 0 , -0.1 , -0.2 , -1 ,1 , 5, 10,∝时的物距像距。
第 4 页 共 29 页
解:( 1)
东北石油大学测控 09 级工程光学期末复习资料
解:
100mm,则所得像与物
6.希望得到一个对无限远成像的长焦距物镜,焦距 系统最后一面到像平面的距离 (工作距) 为 并画出光路图。
解:
=1200mm,由物镜顶点到像面的距离 L=700 mm,由 ,按最简单结构的薄透镜系统考虑, 求系统结构,
7.一短焦距物镜,已知其焦距为 系统结构。
35 mm,筒长 L=65 mm,工作距 , 按最简单结构的薄透镜系统考虑,求
3.一光学系统由一透镜和平面镜组成,如图
3-29 所示,平面镜 MM与透镜光轴垂直交于 D 点,透镜前方
离平面镜 600 mm有一物体 AB,经透镜和平面镜后,所成虚像
至平面镜的距离为 150 mm,且像高为
物高的一半,试分析透镜焦距的正负,确定透镜的位置和焦距,并画出光路图。
解:平面镜成 β =1 的像,且分别在镜子两侧,物像虚实相反 级工程光学期末复习资料
第六章习题
1.如果一个光学系统的初级子午彗差等于焦宽(),则
应等于多少?
解:
2.如果一个光学系统的初级球差等于焦深
(),则
应为多少? 解:
3. 设计一双胶合消色差望远物镜,
和火石玻璃 F2(
,
面的曲率半径。
解:
,采用冕牌玻璃 K9 (
解:设一个气泡在中心处,另一个在第二面和中心之间。
工程光学习题解答--第二章-理想光学系统
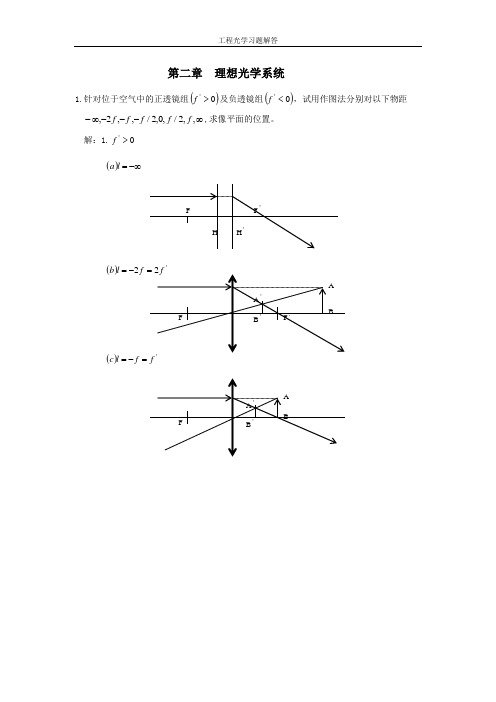
第二章 理想光学系统1.针对位于空气中的正透镜组()0'>f 及负透镜组()0'<f ,试用作图法分别对以下物距 ∞---∞-,,2/,0,2/,,2,f f f f f ,求像平面的位置。
解:1.0'>f ()-∞=l a()'2f l b -=()f f l c=-=()/f l d -=()0=l e()/f lf =')(f f l g -=='22)(f f l h -==+∞=l i )(2.0'<f -∞=l a )(l b )(=l c =)(/)(f l d -=0 el(=)f=l2/ (f)()fg=l(=h)ll i)(+∞=2. 已知照相物镜的焦距f’=75mm,被摄景物位于(以F 点为坐标原点)=x ,2,4,6,8,10,m m m m m -----∝-处,试求照相底片应分别放在离物镜的像方焦面多远的地方。
解: (1)x= -∝ ,xx ′=ff ′ 得到:x ′=0 (2)x ′=0.5625 (3)x ′=0.703 (4)x ′=0.937 (5)x ′=1.4(6)x ′=2.813.设一系统位于空气中,垂轴放大率*-=10β,由物面到像面的距离(共轭距离)为7200mm , 物镜两焦点间距离为1140mm 。
求该物镜焦距,并绘出基点位置图。
解:∵ 系统位于空气中,f f -='10''-===ll y y β 由已知条件:1140)('=+-+x f f7200)('=+-+x l l解得:mm f 600'= mm x 60-=4.已知一个透镜把物体放大*-3投影到屏幕上,当透镜向物体移近18mm 时,物体将被放大*-4,试求透镜的焦距,并用图解法校核之。
解:方法一:31'11-==l l β ⇒ ()183321'1--=-=l l l ①42'22-==l l β ⇒ 2'24l l -= ② 1821+-=-l l ⇒ 1821-=l l ③ '/1/1/11'1f l l =-'/1/1/12'2f l l =-将①②③代入④中得 mm l 2702-= mm l 1080'2-= ∴ mm f 216'=方法二: 311-=-=x fβ 422-=-=x fβ ⇒ mm f 216-= 1812=-x x方法三: 12)4)(3(21''=--==∆∆=ββαnn x x2161812'-=⨯=∆x''fx -=β143''''2'121=+-=∆=+-=-∴fx fx x ββ mm x f 216''=∆=∴5.一个薄透镜对某一物体成实像,放大率为⨯-1,今以另一个薄透镜紧贴在第一个透镜上,则见像向透镜方向移动,放大率为原先的3/4倍,求两块透镜的焦距为多少? 解:⇒ 2'21'1/1/1/1/1l l l l -=- ④6.有一正薄透镜对某一物成倒立的实像,像高为物高的一半,今将物面向物体移近100mm , 则所得像与物同大小,求该正透镜组的焦距。
工程光学(知识讲座)

工程光学第二章理想光学系统1、一个折射率为1.52的双凸薄透镜,其中一个折射面的曲率半径是另一个折射面的2倍,且其焦距为5cm,则这两个折射面的曲率半径分别是〔7.8〕cm和〔-3.9〕cm。
2、一个薄透镜折射率为1.5,光焦度500D。
将它浸入某液体,光焦度变成-1.00D,则此液体的折射率为〔1.502〕。
3、反远距型光组由〔一个负透镜和一个正透镜〕组成,其特点是〔工作距大于组合焦距〕。
4、远摄型光组由一个〔正透镜〕和一个〔负透镜〕组成,其主要特点是〔焦距大于筒长〕,因此该组合系统常用在〔长焦距镜头〕的设计中。
第三章平面与平面系统1、反射棱镜在光学系统中的主要作用有〔折叠光路〕、〔转折光路〕和转像、倒像等,在光路中可等效为平行平板加〔平面反射镜〕。
2、某种波长的光入射到顶角为60°的折射棱镜,测得最小偏向角为42°15′,则该种玻璃对于入射波长的折射率为〔1.557〕。
3、唯一能完善成像的光学元器件是〔平面反射镜〕,利用其旋转特性可制作光学杠杆进行放大测量;利用双光楔也可以实现〔微小角度和微小位移〕的测量,主要有〔双光楔旋转测微〕和〔双光楔移动测微〕两种形式。
4、用于制作光学元件的光学材料包括光学玻璃,〔光学晶体〕和〔光学塑料〕三类。
选用光学玻璃时的两个重要参数是〔折射率〕和〔阿贝常数〕。
5、一个右手坐标的虚物,经一个直角屋脊棱镜反射后,成〔右手〕坐标的〔虚〕像。
第四章光学系统中的光束限制1、限制轴上物点成像光束宽度的光阑是〔孔径光阑〕,而〔渐晕光阑〕在其基础上进一步限制轴外物点的成像光束宽度。
2、为减少测量误差,测量仪器一般采用〔物方远心〕光路。
3、测量显微镜的孔径光阑放置在〔物镜后焦平面上〕,视场光阑放置在〔一次实像面处〕,如果用1/2″的CCD接收图像并用14″的监视器观察图像,要求系统放大倍率为140倍,则显微镜的放大倍率是〔5倍〕。
第五章光线的光路计算及像差理论1、实际像与〔理想像〕之间的差异称为像差,包括单色像差和色差两大类。
工程光学第二章练习参考答案
f 2' ' f1 f 2'
D2 20 x 0.714286 tg 2 ' 2 0.09920635 f1 108
5.66557
2 11.331
渐晕50%视场
ω
F1’ F2
D2 20 tg 2' 2 0.07936508 f1 108
8
(2)
100
f o' f e' 100 ' fo f' 8 e
f o' 88.89mm ' f e 11.11mm
第七章 (3)
6
-l=-100
l’
1 1 1 l ' 100 11.11 l ' 12.5mm
第七章 (4)
l1 90, l1 ' 270
第二章
4
l1 90,
l1 ' 270
1 1 1 l1 ' l1 f ' f ' 67.5 1 1 1 270 90 f '
第二章
4
1 1 1 l1 ' l1 f ' 1 1 1 l2 ' l2 f'
1 1 1 3l1 l1 f ' 1 1 1 4l 2 l 2 f'
f '1 f '2 f '1 f '2 f ' d f '1 f 2 f '2 240mm
450 f '2 1200 300 450 f '2
第二章 10
f '1 f '2 f '1 f '2 f ' 100 d f '1 f 2 100 50 100 d 100 50 d 100mm
工程光学(理想光学系统)
重点内容 理想光学系统的共线理论、基点基面的确定; 图解法、解析法求像方法及多光组组合的等效系统的计算。 教学要求 掌握理想光学系统的共线理论以及系统的基点、基面的计算
方法;
掌握图解法求像的方法; 掌握理想光学系统的物象关系、放大率和两个光组的组合; 理解正切计算法求多光组的等效系统的计算。
18
由两对相似三角形△BAF、△FHM和△H’N’F’、△F’A’B’ 可得:
y' y f x
y' y x' f'
由此得到:xx’=ff ’ 垂轴放大率 2、高斯公式: 物和像的位置相对于光学系统的主点来确定:以主点为原点,用l、l’来表 示物距和像距。得l、l’与x、x’的关系:
当 L
结论:
, U→0
无限远的轴上物点发出的光线 与光轴平行。
5
2、像方焦点、焦平面;像方主点、主平面;像方焦距
焦距公式
f
h tg U
6
3、无限远的轴外物点发出的光线
由于光学系统的口径大小总是有限的,所以无限远的轴外物点发出的、能
进入光学系统的光线总是相互平行的,且与光轴有一定的夹角ω 。
M N H
M’
N’ H’ F’ A’
利用物方焦平面性质求轴上物点的像 M A N H
M’
N’ H’ B’ F’ A’
F
利用像方焦平面性质求轴上物点的像
12
B` B
F
H
H`
F`
物点B在F与H之间
13
A’ A F
Q
Q’
B’ B
H
H’
F’
实物在1倍焦距以内,成放大虚像
14
工程光学基础 习题参考答案-第二章_02
注意: 注意: − l + l ' ≠ 7200mm ,因为对于一般理想光学系统两主面不重合。 4、已知一透镜把物体放大 − 3× 投影在屏幕上, 投影在屏幕上,当透镜向物体移近 18mm 时,物体 将被放大 − 4 × ,试求透镜的焦距, 试求透镜的焦距,并用图解法校核之。 并用图解法校核之。 解:
tan U 1 ' = h1 100 = = 1 = tan U 2 f1 ' 100 h2 90 = 1+ = 2.8 = tan U 3 f2 50 h3 62 = 2 .8 + = 1.56 f3 − 50
h2 = h1 − d1 tan U 1 ' = 100 − 10 = 90 tan U 2 ' = tan U 2 +
3、设一系统位于空气中, 设一系统位于空气中,垂轴放大 率 β = −10 × , 由物面到像面的距离 (共轭距) 共轭距)为 7200mm,物镜两焦点 间距离为 1140mm。求该物镜焦距, 求该物镜焦距, 并绘出基点位置图。 并绘出基点位置图。 解: 由公式 β = − x' f = − (2-4) , f' x
1 1 1 d (2-33) = + − f ' f1 ' f 2 ' f1 ' f 2 '
f1 ' f 2 ' nr1 r2 f ' = − f = − ∆ = ( n − 1)[n( r − r ) + ( n − 1)d ] 2 1 1 Φ = f ' − dr2 l ' = H n( r2 − r1 ) + ( n − 1)d − dr1 l = H n( r2 − r1 ) + ( n − 1)d
工程光学基础 习题参考答案-第二章_02
3、设一系统位于空气中, 设一系统位于空气中,垂轴放大 率 β = −10 × , 由物面到像面的距离 (共轭距) 共轭距)为 7200mm,物镜两焦点 间距离为 1140mm。求该物镜焦距, 求该物镜焦距, 并绘出基点位置图。 并绘出基点位置图。 解: 由公式 β = − x' f = − (2-4) , f' x
f 2 ' = −240mm
8、一短焦距物镜 一短焦距物镜, 焦距物镜,已知其焦距为 35mm,筒长 L=65mm,工作距离 l k ' = 50mm ,按 最简单结构的薄透镜系统考虑, 最简单结构的薄透镜系统考虑,求系统结构。 求系统结构。 解: (仿照 (仿照 P32 P32 例 2) 利用正切计算法,设 h1 = 100mm ,有公式:
1 1 1 d (2-33) = + − f ' f1 ' f 2 ' f1 ' f 2 '
f1 ' f 2 ' nr1 r2 f ' = − f = − ∆ = ( n − 1)[n( r − r ) + ( n − 1)d ] 2 1 1 Φ = f ' − dr2 l ' = H n( r2 − r1 ) + ( n − 1)d − dr1 l = H n( r2 − r1 ) + ( n − 1)d
xx' = ff ' = − f ' 2 ∴ x' = − f2 x
代入数据得:
x = −∞, x' = 0.5625mm x = −10m, x' = 0.703mm x = −6m, x' = 0.9375mm x = −4m, x' = 1.406mm x = −2m, x' = 2.813mm
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.一个薄透镜对某一物体成实像,放大率为 1 ,今以另一个薄透镜紧贴在第一个透镜上,
则见像向透镜方向移动,放大率为原先的 3/4 倍,求两块透镜的焦距为多少?
解:
6.有一正薄透镜对某一物成倒立的实像,像高为物高的一半,今将物面向物体移近 100mm, 则所得像与物同大小,求该正透镜组的焦距。
解:由已知得: 1
的地方。
解:
(1)x= -∝ ,xx′=ff′ 得到:x′=0
(2)x′=0.5625
(3)x′=0.703
(4)x′=0.937
(5)x′=1.4
(6)x′=2.81
3.设一系统位于空气中,垂轴放大率 10 ,由物面到像面的距离(共轭距离)为 7200m
m, 物镜两焦点间距离为 1140mm。求该物镜焦距,并绘出基点位置图。 解:
,2 f , f , f / 2,0, f / 2, f , ,求像平面的位置。 解:1. f ' 0
al
F
F'
H
H'
bl 2 f 2 f '
F
A
A'
B
F'
B'
cl f f '
A
A'
B
F
B'
ﻬ
d l f / 2 f ' / 2
A
A'
F
B
B'
F'
el 0
A A'
F
B B'
l
' 2
1080 mm
∴ f ' 216mm
方法二:
1
f x1
3
2
f x2
4
f 216mm
x2 x1 18
方法三:
x' x
n' n
1 2
(3)(4) 12
x' 12 18 216
x' f'
1
2
x1' x2' f'
x ' f'
3 4 1
f ' x' 216mm
的薄透镜系统考虑,求系统结构,并画出光路图。
,按最简单结构
解:
Hale Waihona Puke 8. 一短焦距物镜,已知其焦距为 35mm ,筒长L= 65mm ,工作距 l 'k 50mm ,按最简单结
构的薄透镜系统考虑,求系统结构。
解:
9.已知一透镜 r1 200mm, r2 300mm, d 50mm, n 1.5 ,求其焦距,光焦度,基点位置。
lF
f
' (1
n
n
1
d
2
)
144.02mm
l
' H
f
'
n
n
1
d 1
13.99mm
lH
f
'
n
n
1
d
2
5.25mm
⑵ l l1 lH 5000 5.25 5005.25mm
工程光学习题解答--第二章理想光学系统
———————————————————————————————— 作者: ———————————————————————————————— 日期:
ﻩ
第二章 理想光学系统
1.针对位于空气中的正透镜组 f ' 0 及负透镜组 f ' 0 ,试用作图法分别对以下物距
解:已知 r1 200mm, r2 300mm, d 50mm, n 1.5
求: f ' , ,基点位置。
1/
f
' (n
1)(1
2)
(n
1)2 n
d1 2
0.69m 1
f ' 1440mm
l
' F
f
'(1
n
n
1
d 1
)
1560mm
lF
f
'(1
n
n
1
d
2
)
1360
mm
l
' H
l1' l1
1 2
2
l
' 2
l2
1
-
l'
1
l
l1 l2 100
由高斯公式: 1 1 1 1
l1'
l1
l
' 2
l2
解得: f ' l2 100mm 2
100
-l 2
l' 2
mm
7.希望得到一个对无限远成像的长焦距物镜,焦距 f ' 1200 mm ,由物镜顶点到像面的距
离 L= 700mm,由系统最后一面到像平面的距离(工作距)为
其焦距及基点位置。
解:
12. 一束平行光垂直入射到平凸透镜上,会聚于透镜后 480mm处,如在此透镜凸面上 镀银,则平行光会聚于透镜前 80mm 处,求透镜折射率和凸面曲率半径。
解:
13.一块厚透镜, n 1.6, r1 120mm, r2 320mm, d 30mm, 试求该透镜焦距和基点位置。
A
A'
F'
B
B'
F
(e)l 0
A A'
B
F'
B'
F
( f )l f / 2
F'
A' A
B
F
B'
(g)l f
F'
(h)l 2 f
B' F'
A'
(i)l
F
A
F
B
2. 已知照相物镜的焦距 f’=75mm,被摄景物位于(以 F 点为坐标原点)
x ,10m,8m,6m,4m,2m, 处,试求照相底片应分别放在离物镜的像方焦面多远
如果物距 l1 5m 时,问像在何处?如果平行光入射时,使透镜绕一和光轴垂直的轴转 动,而要求像点位置不变,问该轴应装在何处? 解:
A
H
H'
A'
-l H
-l ' H
l
-l l l
⑴
f
'
(n
1)n(r2
nr1r2 r1 )
(n
1)d
149.27mm
l
' F
f
' (1
n
n
1
d 1
)
135.28mm
F'
f l f / 2 f ' / 2
A'
A
FB B'
(g)l f f '
A B
(h)l 2 f 2 f '
A B
F
ﻬ
(i)l
F
2. f ' 0 (a)l
F'
F'
F'
F'
B'
A'
F'
F
(b)l 2 f
A
A'
B
F'
B'
F
(c)l f
A
A'
F
B
B'
(d)l f / 2
f
'
(
n
n
1)d1
120mm
lH
f
'
(
n
n
1)d
2
80mm
10. 一薄透镜组焦距为 100mm ,和另一焦距为 50mm 的薄透镜组合,其组合焦距仍为 100mm ,问两薄透镜的相对位置,并求基点位置,以图解法校核之。
解:
11. 长 60mm ,折射率为 1.5 的玻璃棒,在其两端磨成曲率半径为10mm 的凸球面,试求
F
H H'
-f
-
x
∵ 系统位于l 空气中, f ' f
F' f'
l'
y' l' 10 yl
由已知条件: f ' ( f ) x 1140
l ' (l) x 7200
解得: f ' 600mm x 60mm
4.已知一个透镜把物体放大 3 投影到屏幕上,当透镜向物体移近18mm 时,物体将被放大 4 ,试求透镜的焦距,并用图解法校核之。 解:方法一:
1
l1' l1
3
①
l1' 3l1 3l2 18
2
l
' 2
l2
4
②
l2' 4l2
l1 l2 18
③
l1 l2 18
1/ l1' 1/ l1 1/ f '
1
/
l
' 2
1/ l2
1/
f
'
1/ l1' 1/ l1 1/ l2' 1/ l2
④
将①②③代入④中得 l2 270mm
