研究生数学建模-历年题目-竞赛B题-
2023年研究生数学建模竞赛-b题

2023年研究生数学建模竞赛-b题2023年研究生数学建模竞赛b题涉及一个有关航运和港口设施规划的问题。
为了解决这个问题,我们将使用数学建模的方法来分析并提出最佳的规划方案。
该问题中,我们面临的挑战是如何设计一个最优的航运系统,以减少货物运输的时间和成本,并提高港口的运营效率。
具体来说,我们需要考虑以下几个方面的因素:1.货物流动模式:我们需要研究和分析货物的流动模式,包括货物的来源和目的地,货物的种类和数量。
通过对货物的流动模式进行建模和分析,我们可以确定最佳的航线和货物运输方案。
2.航线规划:针对货物的流动模式,我们需要设计最佳的航线,以确保货物可以以最短的时间和最低的成本从起点运输到目的地。
在航线规划中,我们需要考虑航线的距离、交通状况等因素,以便确定最佳的航运路径。
3.船只调度:在货物运输过程中,船只的调度非常重要。
我们需要确定最佳的船只调度方案,以确保船只在正确的时间和位置上提供服务。
在船只调度中,我们需要考虑船只的容量、速度和行驶时间等因素,以便优化船只的运营效率和运输能力。
4.港口设施规划:另一个重要的方面是港口设施的规划和布局。
我们需要确定最佳的港口设施规划,以便满足货物运输的需求。
在港口设施规划中,我们需要考虑港口的容量、装卸能力和设施布局等因素,以便优化港口的运营效率和货物的处理能力。
为了解决这个问题,我们可以使用数学建模的方法来分析和优化上述因素。
我们可以建立数学模型来描述货物的流动模式、航线规划、船只调度和港口设施规划等问题。
然后,我们可以使用数学和优化方法来求解这些模型,并得出最佳的规划方案。
在建立数学模型时,我们可以使用图论、线性规划、整数规划等数学方法来描述货物的流动模式、航线规划、船只调度和港口设施规划等问题。
我们可以将货物视为节点,航线视为边,并使用图论的方法来描述货物的流动模式和航线规划。
我们可以使用线性规划和整数规划的方法来描述船只调度和港口设施规划等问题,并使用数学优化方法来求解这些模型。
研究生数模竞赛B题(2013年)

(1) Saleh 模型 Saleh 模型是根据对行波管功率放大器(traveling wave tube amplifier, TWTA)的输 入输出数据进行统计分析后得到的,TWTA 的 AM-AM 和 AM-PM 失真特性相对来说 都比较明显,并且模型参数较少,参数的提取也比较方便,是目前一种常用的无记忆 功放模型[6]。 假设功放的输入信号为:
-3-
二、 问题假设
1. 2. 3. 4. 5. 6. 不考虑时间、温度、环境等外界因素的影响; 不考虑功放因温度漂移、老化等引起功放特性的变化; 不考虑外部信号或电路自身对该功率放大器的干扰; 不考虑当输入信号、负载和元件自身发生变化时,造成系统的不稳定性的影响; 不考虑功放的特性随时间变化,假设在一定时间内功放的特性都是恒定的; 假设功率放大器的非线性特性是可逆的;
[7] 简单起见,令 A r t 用 r 表示输入信号幅度,则模型的特性函数为 :
Ar
r
Ar 1 Ar 2
r 2 1 r 2
(3)
(4)
式(3)和(4)中, r 为输入信号的包络幅度, A , A , , 为待定参数,本文 通过 Yang[8][9]最新提出的智能优化算法——布谷鸟搜索算法对参数进行寻优,得到待 定参数 1 , 1 , Q , Q 分别为 1 =3.1344, 1 =0.5920, Q =0.0100, Q =10.0000。 (2) 复系数幂级数模型 由于功放的输入输出都为射频实信号,而功放建模与预失真都在基带进行,基带 信号为复信号,需要完成射频实信号到基带复信号的转换。实系数幂级数不能表征功 放的 AM-PM 特性,因此需要复系数幂级数对功放进行建模[10]。射频中,功放的输入 输出特性用 K 阶幂级数可以表示为:
第九届“华为杯”全国研究生数学建模竞赛B题-简体

【2012第九届全国研究生数学建模竞赛B题】基于卫星无源探测的空间飞行器主动段轨道估计与误差分析有些国家会发射特殊目的的空间飞行器,如弹道式导弹、侦察卫星等。
对他国发射具有敌意的空间飞行器实施监控并作出快速反应,对于维护国家安全具有重要的战略意义。
发现发射和探测其轨道参数是实现监控和作出反应的第一步,没有观测,后续的判断与反应都无从谈起。
卫星居高临下,是当今探测空间飞行器发射与轨道参数的重要平台。
观测卫星按轨道特点,可分为高轨地球同步轨道卫星和中低轨近圆轨道卫星。
其中同步轨道距地球表面约3.6万千米,轨道平面与地球赤道平面重合,理论上用3颗间隔120度分布的同步轨道卫星可覆盖地球绝大部分表面。
中低轨近圆轨道距地球表面数百到几千千米不等,根据观测要求,其轨道平面与赤道平面交成一定角度,且常由若干颗卫星实现组网探测。
装置于卫星上的探测器包括有源和无源两类:有源探测器采用主动方式(如雷达,激光)搜寻目标,同时具备定向和测距两种能力;无源探测器则被动接收目标辐射。
采用无源探测器的观测卫星常采用红外光学探测器,只接收目标的红外辐射信息,可定向但不能测距。
对于火箭尾部喷焰的高度敏感性是红外技术的长处,但易受气候影响与云层干扰则是其缺点。
探测的目的是为了推断空间飞行器的轨道参数,推断是基于观测数据并通过数学模型与计算方法作出的。
当观测卫星飞行一段时间,探测器测得目标相对于运动卫星的观测数据,以观测卫星和空间飞行器的运动模型和观测模型为基础,对空间飞行器的轨道参数(包括轨道位置、速度初值和其他模型参数)进行数学推断,为飞行器类别、飞行意图的判断提供信息基础。
空间飞行器轨道一般可分为三段,依次为:靠火箭推进的主动段、在地球外层空间的惯性飞行段和再入大气层后的攻击段。
主动段通常由多级火箭相继推进,前一级火箭完成推进后脱落,由后一级火箭接力。
惯性飞行段在空气阻力极小的大气层外,靠末级火箭关机前获得的速度在椭圆轨道上作无动力惯性飞行。
第十五届“华为杯”中国研究生数学建模竞题—B题【2018年研究生数学建模竞赛试题】

2018年中国研究生数学建模竞赛B题光传送网建模与价值评估1.背景2009年诺贝尔物理学奖授予了英籍华人高锟(Charles K. Kao)博士,以表彰他对光纤通信发展所做出的贡献,诺贝尔奖委员会在给公众的公开信中写到:“当诺贝尔物理学奖宣布的时候,世界大部分地方几乎瞬间收到了这条信息…文字、语音和视频信号沿着光纤在世界各地来回传输,几乎瞬时地被微小而便捷的设备接收,人们已经把这种情况当做习惯。
光纤通信正是整个通信领域急速发展的前提。
”从诞生至今,50多年里基于数字光纤通信技术的光传送网构建起了全球通信的骨架。
从城市内的传输,直到跨越大洋的传输,光传送网为人类提供了大容量、高可靠性和低能耗的信息传输管道,人类对通信容量的追求也成为光传送技术发展的源源不断的动力。
光传送网的规划与建设是运营商、设备商以及政府必须考虑的课题。
光传送的基本规律是——在相同技术条件下传输的容量会随着传输距离增加而减小。
网络规划者需要在有限资源的条件下,综合考虑传输距离,传输容量、网络拓扑等各种因素,以最大化网络的价值。
本课题中,请你们站在上述角度,从底层物理出发为光传送链路建模,制定光传送网规划,探索光传送网有关规律。
本课题的内容包括:1)对光传送链路进行简单建模2)制定光传送网的规划,并探讨网络的价值13)改进调制格式2.问题-1:光传送链路建模现代数字传输系统可认为是对0101二进制序列进行编码传输的系统,1个二进制的0或1称为1个比特(bit)。
无论是语音、视频还是任何类型的消息,都可以数字化为一串串”0101…”的二进制比特序列,经编码并调制为某个“载体信号”后,再经过特定的“信道”(信息的通道)传输到目的地。
图1中给出了简化的模型。
在光纤通信中,光纤就是信道,光纤传输的光波就是信息的载体。
信道中无法避免的噪声可能导致最终接收的二进制序列中比特出错,即产生误码。
图1 简化后的数字传输模型二进制序列通常需要将K个比特作为一个“符号”进行传输,每个符号有2K个不同状态。
数学建模-历年考题cumcm2000b
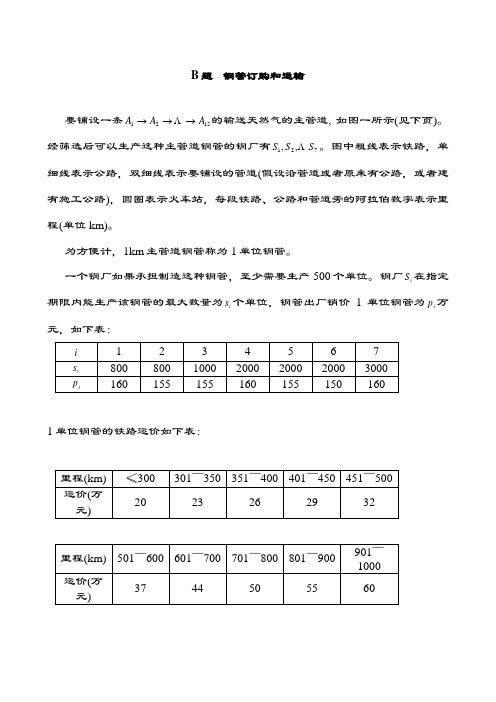
B 题 钢管订购和运输
要铺设一条1521A A A →→→ 的输送天然气的主管道, 如图一所示(见下页)。
经筛选后可以生产这种主管道钢管的钢厂有721,,S S S 。
图中粗线表示铁路,单细线表示公路,双细线表示要铺设的管道(假设沿管道或者原来有公路,或者建有施工公路),圆圈表示火车站,每段铁路、公路和管道旁的阿拉伯数字表示里程(单位km)。
为方便计,1km 主管道钢管称为1单位钢管。
一个钢厂如果承担制造这种钢管,至少需要生产500个单位。
钢厂i S 在指定期限内能生产该钢管的最大数量为i s 个单位,钢管出厂销价1单位钢管为i p 万元,如下表:
1单位钢管的铁路运价如下表:
1000km 以上每增加1至100km 运价增加5
公路运输费用为1单位钢管每公里0.1万元(不足整公里部分按整公里计算)。
钢管可由铁路、公路运往铺设地点(不只是运到点1521,,,A A A ,而是管道全线)。
(1)请制定一个主管道钢管的订购和运输计划,使总费用最小(给出总费用)。
(2)请就(1)的模型分析:哪个钢厂钢管的销价的变化对购运计划和总费用影响最大,哪个钢厂钢管的产量的上限的变化对购运计划和总费用的影响最大,并给出相应的数字结果。
(3)如果要铺设的管道不是一条线,而是一个树形图,铁路、公路和管道构成网络,请就这种更一般的情形给出一种解决办法,并对图二按(1)的要求给出模型和结果。
7
7。
江西省研究生数学建模竞赛B题

江西省研究生数学建模竞赛B题泄洪设施修建计划位于我国南方的某个偏远贫困乡,地处山区,一旦遇到暴雨,经常发生洪涝灾害。
以往下雨时,完全是依靠天然河流进行泄洪。
2010年入夏以来,由于史无前例的连日大雨侵袭,加上这些天然河流泄洪不畅,造成大面积水灾,不仅夏粮颗粒无收,而且严重危害到当地群众的生命财产安全。
为此,乡政府打算立即着手解决防汛水利设施建设问题。
从两方面考虑,一是在各村开挖一些排洪沟,以满足近两三年的短期防汛需要;二是从长远考虑,可以通过修建新泄洪河道的办法把洪水引出到主干河流。
经测算,修建新泄洪河道的费用为L.0(万元),其中Q表示泄洪河道的可泄洪量(万立方米/小P51.066Q时),L表示泄洪河道的长度(公里)。
请你们通过数学建模方法,解决以下问题:问题1:该乡的某个村区域内原有四条天然河流,由于泥沙沉积,其泄洪能力逐年减弱。
在表1中给出它们在近年来的可泄洪量(万立方米/小时)粗略统计数字。
水利专家经过勘察,在该村区域内规划了8条可供开挖排洪沟的路线。
由于它们的地质构造、长度不同,因而开挖的费用和预计的可泄洪量也不同,详见表2,而且预计每条排洪沟的可泄洪量还会以平均每年10%左右的速率减少。
同时开始修建一段20公里长的新泄洪河道。
修建工程从开工到完成需要三年时间,且每年投资修建的费用为万元的整数倍。
要求完成之后,通过新泄洪河道能够达到可泄洪量100万立方米/小时的泄洪能力。
乡政府从2010年开始,连续三年,每年最多可提供60万元用于该村开挖排洪沟和修建新泄洪河道,为了保证该村从2010至2014年这五年间每年分别能至少达到可泄洪量150、160、170、180、190万立方米/小时的泄洪能力,请作出一个从2010年起三年的开挖排洪沟和修建新泄洪河道计划,以使整个方案的总开支尽量节省(不考虑利息的因素在内)。
表1 现有四条天然河道在近几年的可泄洪量(万立方米/小时)表2 开挖各条排洪沟费用(万元)和预计当年可泄洪量(万立方米/小时)问题2:该乡共有10个村,分别标记为①—⑩,下图给出了它们大致的相对地理位置,海拔高度总体上呈自西向东逐渐降低的态势。
2023研究生数模竞赛b题

2023研究生数模竞赛b题摘要:1.问题背景及分析2.解题思路与方法3.具体计算过程与步骤4.结果分析与讨论5.总结与建议正文:一、问题背景及分析2023年研究生数模竞赛B题以某种实际问题为背景,要求我们解决一个关于数学建模的问题。
题目描述如下:(此处简要描述题目背景和需求)二、解题思路与方法1.问题分析:首先,我们需要对问题进行深入的分析,了解问题的本质和关键因素。
通过分析,我们可以确定问题的类型,进而选择合适的数学模型和方法。
2.数学模型建立:根据问题背景和分析结果,建立合适的数学模型。
这可能包括常微分方程、偏微分方程、概率论模型等。
3.求解方法选择:针对所建立的数学模型,选择适当的求解方法。
这可能包括数值方法、解析方法等。
4.模型验证与优化:对所得到的模型进行验证,检查其是否符合实际情况。
如果不符合,需要对模型进行优化和改进。
三、具体计算过程与步骤1.初步计算:根据所选模型和求解方法,进行初步的计算。
这可能包括参数估计、数值模拟等。
2.结果优化:根据初步计算的结果,进一步优化模型参数和求解方法,以提高计算精度和可靠性。
3.结果验证:将优化后的计算结果与实际情况进行对比,检查计算结果的正确性和有效性。
4.敏感性分析:对模型参数进行敏感性分析,探讨参数变化对计算结果的影响。
四、结果分析与讨论1.结果概述:对计算结果进行简要概述,阐述结果的主要特点和发现。
2.结果解释:深入分析计算结果,解释结果背后的原因和物理意义。
3.结果讨论:针对计算结果,展开一系列讨论,探讨问题的本质、解决方案的优缺点等。
五、总结与建议1.总结:对整个解题过程进行总结,强调解决问题的方法和技巧。
2.建议:针对问题解决方案的不足之处,提出改进和优化的建议。
3.拓展思考:对问题进行拓展思考,探讨未来研究方向和可能的改进空间。
通过以上步骤,我们可以完成2023年研究生数模竞赛B题的解答。
在实际操作过程中,我们需要不断调整和完善模型和方法,以获得更准确的计算结果。
2023高教社数学建模b题

2023高教社数学建模b题
2023年高教社数学建模竞赛B题:
B题碳排放交易政策下,企业如何调整生产计划
题目说明:
随着全球气候变化问题日益严重,碳排放权交易政策作为一种重要的减排手段,正在被越来越多的国家和地区采用。
在该政策下,企业需要为其排放的二氧化碳支付费用。
为了降低成本,企业需要制定合理的生产计划,以最小化碳排放并最大化利润。
任务要求:
1. 建立数学模型,以确定在碳排放交易政策下,企业如何调整生产计划以最小化碳排放并最大化利润。
2. 分析不同碳排放价格、生产成本和市场需求下,企业的最优生产策略。
3. 基于所建立的模型和数据,为企业提供一个具体的生产计划建议。
所提供的附件包括:附件1-3(具体内容略)。
附件1为企业生产某产品的历史数据,包括年产量、年碳排放量、生产成本等;附件2为碳排放权交易市场的历史数据,包括碳排放价格、交易量等;附件3为市场需求预测数据,包括未来5年的预测值。
题目给出的初始条件:假设附件1中企业年生产能力为100单位产品,附件2中碳排放价格未来5年的预测值分别为100元/吨、110元/吨、120元/吨、130元/吨和140元/吨。
附件3中未来5年市场需求预测值分别为90单位、95单位、100单位、105单位和110单位产品。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年全国研究生数学建模竞赛B题机动目标的跟踪与反跟踪目标跟踪是指根据传感器(如雷达等)所获得的对目标的测量信息,连续地对目标的运动状态进行估计,进而获取目标的运动态势及意图。
目标跟踪理论在军、民用领域都有重要的应用价值。
在军用领域,目标跟踪是情报搜集、战场监视、火力控制、态势估计和威胁评估的基础;在民用领域,目标跟踪被广泛应用于空中交通管制,目标导航以及机器人的道路规划等行业。
目标机动是指目标的速度大小和方向在短时间内发生变化,通常采用加速度作为衡量指标。
目标机动与目标跟踪是“矛”与“盾”的关系。
随着估计理论的日趋成熟及平台能力提升,目标作常规的匀速或者匀加速直线运动时的跟踪问题已经得到很好的解决。
但被跟踪目标为了提高自身的生存能力,通常在被雷达锁定情况下会作规避的机动动作或者释放干扰力图摆脱跟踪,前者主要通过自身运动状态的快速变化导致雷达跟踪器精度变差甚至丢失跟踪目标,后者则通过制造假目标掩护自身,因此引入了在目标进行机动时雷达如何准确跟踪的问题。
机动目标跟踪的难点在于以下几个方面:(1) 描述目标运动的模型[1,2]即目标的状态方程难于准确建立。
通常情况下跟踪的目标都是非合作目标,目标的速度大小和方向如何变化难于准确描述;(2) 传感器自身测量精度有限加之外界干扰,传感器获得的测量信息[3]如距离、角度等包含一定的随机误差,用于描述传感器获得测量信息能力的测量方程难于完全准确反映真实目标的运动特征;(3) 当存在多个机动目标时,除了要解决(1)、(2)两个问题外,还需要解决测量信息属于哪个目标的问题,即数据关联。
在一定的测量精度下,目标之间难于分辨,甚至当两个目标距离很近的时候,传感器往往只能获得一个目标的测量信息。
由于以上多个挑战因素以及目标机动在战术上主动的优势,机动目标跟踪已成为近年来跟踪理论研究的热点和难点。
不同类型目标的机动能力不同。
通常情况下战斗机的飞行速度在100~400m/s,机动半径在1km以上,机动大小一般在10个g以内,而导弹目标机动,加速度最大可达到几十个g,因此在对机动目标跟踪时,必须根据不同的目标类型选择相应的跟踪模型。
目标跟踪处理流程[4,5]通常可分为航迹起始、点迹航迹关联(数据关联)[6-8]、航迹滤波[9-18]等步骤。
如果某个时刻某雷达站(可以是运动的)接收到空间某点反射回来的电磁波,它将记录下有关的数据,并进行计算,得到包括目标相对于雷达站的距离、方位角和俯仰角等信息。
航迹即雷达站在接收到某一检测目标陆续反射回来的电磁波后记录、计算检测目标所处的一系列空中位置而形成的离散点列.航迹起始即通过一定的逻辑快速确定单个或者多个离散点序列是某一目标在某段时间内首先被检测到的位置.点迹航迹关联也称同一性识别,即依据一定的准则确定雷达站多个回波数据(点迹)中哪几部分数据是来自同一个检测目标(航迹). 航迹滤波是指利用关联上的点迹测量信息采用线性或者非线性估计方法(如卡尔曼滤波、拟合等)提取所需目标状态信息,通常包括预测和更新两个步骤。
预测步骤主要采用目标的状态方程获得对应时刻(被该目标关联上的点迹时间)目标状态和协方差预测信息;更新步骤则利用关联点迹的测量信息修正目标的预测状态和预测协方差。
现有3组机动目标的测量数据,数据分别包含在Data1.txt,Data2.txt,Data3.txt文件中,其中Data1.txt为多个雷达站在不完全相同时刻获得的单个机动目标的测量数据,Data2.txt为某个雷达站获得的两个机动目标的测量数据,Data3.txt为某个雷达站获得的空间目标的测量数据。
数据文件中观测数据的数据结构如下:目标距离(m)目标方位(°)目标俯仰(°)测量时间(s)传感器标号其中Data1.txt和Data2.txt数据的坐标系表示如下:原点O为传感器中心,传感器中心点与当地纬度切线方向指向东为x轴,传感器中心点与当地经度切线方向指向北为y轴,地心与传感器中心连线指向天向的为z轴,目标方位指北向顺时针夹角(从y轴正向向x轴正向的夹角,范围为0~360°),目标俯仰指传感器中心点与目标连线和地平面的夹角(即与xOy平面的夹角,通常范围-90°到90°)。
**中的雷达坐标和测量误差如下:雷达标号经度(°) 纬度(°) 高度(m) 测距误方位角俯仰角差(m) 误差( °) 误差(°)1 ** ** 0 50 ** **2 ** ** 0 40 ** **3 ** ** 0 60 ** ****雷达坐标为[0,0,0]。
对应两个目标的测量误差如下:目标测距误差(m) 方位角误差( °) 俯仰角误差(°) 1100** **2100** ****的雷达坐标和测量误差为:经度(°) 纬度(°) 高度(m)测距误差(m) 方位角误差( °)俯仰角误差(°)118 ** 0 100 ** **其余格式与Data1.txt和Data2.txt相同。
请完成以下问题:1. 根据附件中的Data1.txt数据,分析目标机动发生的时间范围,并统计目标加速度的大小和方向。
建立对该目标的跟踪模型,并利用多个雷达的测量数据估计出目标的航迹。
鼓励在线跟踪。
2. 附件中的Data2.txt数据对应两个目标的实际检飞考核的飞行包线(检飞:军队根据国家军标规则设定特定的飞行路线用于考核雷达的各项性能指标,因此包线是有实战意义的)。
请完成各目标的数据关联,形成相应的航迹,并阐明你们所采用或制定的准则(鼓励创新)。
如果用序贯实时的方法实现更具有意义。
若出现雷达一段时间只有一个回波点迹的状况,怎样使得航迹不丢失?请给出处理结果。
3. 根据附件中Data3.txt的数据,分析空间目标的机动变化规律(目标加速度随时间变化)。
若采用第1问的跟踪模型进行处理,结果会有哪些变化?4. 请对第3问的目标轨迹进行实时预测,估计该目标的着落点的坐标,给出详细结果,并分析算法复杂度。
5. Data2.txt数据中的两个目标已被雷达锁定跟踪。
在目标能够及时了解是否被跟踪,并已知雷达的测量精度为雷达波束宽度为3°,即在以雷达为锥顶,雷达与目标连线为轴,半顶角为1.5°的圆锥内的目标均能被探测到;雷达前后两次扫描时间间隔最小为0.5s。
为应对你们的跟踪模型,目标应该采用怎样的有利于逃逸的策略与方案?反之为了保持对目标的跟踪,跟踪策略又应该如何相应地变换?参考文献:1 X. R. Li and V. P. Jilkov, “Survey of Maneuvering Target Tracking, Part I: Dynamic Models,” IEEE Transactions on Aerospace and Electronic Systems, 39(4): 1333–1364, October 2003.2 X. R. Li and V. P. Jilkov, “Survey of Maneuvering Target Tracking. Part II: M otion Models of Ballistic Targets,” IEEE Transactions on Aerospace and Electronic Systems, 46(1):96–119, January 2010.3 X. R. Li and V. P. Jilkov, “A Survey of Maneuvering Target Tracking—Part III: Measurement Models,” In: Proceedings of SPIE - Signal and Data Processing of Small Targets 2001, 31 July–2 August 2001, San Diego, CA, USA, pp. 423–446.4Yaakov Bar-Shalom, X.Rong Li, Thiagalingam Kirubarajan.Estimation with Applications to Tracking and Navigation: Theory Algorithms and Software.5何友,修建娟,张晶炜等.雷达数据处理及应用[M]. 第2版. 北京:电子工业出版社, 20096 Bar-Shalom Y, Daum F E, Huang J. The Probabilistic Data Association Filter: Estimation in the Presence of Measurement Origin Uncertainty[J]. IEEE Control Systems Magazine, 2009, 29(6): 82~1007 Sinha A, Ding Z, Kirubarajan T, et al. Track Quality Based Multitarget Tracking Approach for Global Nearest-Neighbor Association[J]. IEEE Transactions on Aerospace and Electronic Systems,2012, 48(2):1179~11918 Fortmann T, Bar-Shalom Y, Scheffe M. Sonar Tracking of Multiple Targets Using Joint Probabilistic Data Association[J]. IEEE Journal of Oceanic Engineering, 1983,8(3):173~184.9 X. R. Li and V. P. Jilkov, “A Survey of Maneuvering Target Tracking—Part IV: Decision-Based Methods,” In: Proc. SPIE - Signal and Data Processing of Small Targets 2002, April 1–5, 2002, Orlando, FL, USA, pp. 511–53410 X. R. Li and V. P. Jilkov, “Survey of Maneuvering Target Tracking, Part V: Multiple-Model Methods,” IEEE Transactions on Aerospace and Electronic Systems, 41(4): 1255–1321, October 2005.11 X. R. Li and V. P. Jilkov, “A Survey of Maneuvering Target Tracking: Approximate Techniques for Nonlinear Filtering,” In: Proc. SPIE- Signal and Data Processing of Small Targets 2004, April 13–15, 2004, Orlando, FL, USA, pp. 537–550.12 X. R. Li and V. P. Jilkov, “A Survey of Maneuvering Target Tracking—Part VIa: Density-Based Exact Nonlinear Filtering,” Proc. 2010 SPIE Conf. Signal and Data Processing of Small Targets, Orlando, FL, USA, 6–8 April 201013 X. R. Li and V. P. Jilko v, “A Survey of Maneuvering Target Tracking—Part VIb: Approximate Nonlinear Density Filtering in Mixed Time,” Proc. 2010 SPIE Conf. Signal and Data Processing of Small Targets, Orlando, FL, USA, 6–8 April 201014 Julier S J, Uhlmann J K. A New Extension of The Kalman Filter to Nonlinear Systems[J].SPIE, 1997, (3068):182~19315 Julier S J, Uhlmann J K. A New Method for the Nonlinear Transformation of Means and Covariance in Filters and Estimations[J]. IEEE Transactions.on Automatic Control, 2000,45(3):477~48216 Singer R A. Estimating Optimal Tracking Filter Performance for Manned Maneuvering Targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 1970,AES-6(4):473~483.17 周宏仁,敬忠良,王培德.机动目标跟踪[M].北京:国防工业出版社,199418 胡小平. 导弹飞行力学基础[M]. 北京:国防工业出版社,2006。
