高三数学复习考试中档题7
江苏省高三数学复习中档题满分练习(含答案)

江苏省高三数学复习中档题满分练习(含答案)所以OA=OC1.又因为F为AC的中点,所以OF∥CC1且OF=CC1.因为E为BB1的中点,所以BE∥CC1且BE=CC1,所以BE∥OF且BE=OF,所以四边形BEOF是平行四边形,所以BF∥OE.又BF平面A1EC,OE平面A1EC,所以BF∥平面A1EC. (2)由(1)知BF∥OE,因为AB=CB,F为AC的中点,所以BFAC,所以OEAC.又因为AA1底面ABC,而BF底面ABC,所以AA1BF.由BF∥OE得OEAA1,而AA1,AC平面ACC1A1,且AA1AC=A,所以OE平面ACC1A1.因为OE平面A1EC,所以平面A1EC平面ACC1A1.3.(1)解由题意可知A1(-,0),A2(,0),椭圆C1的离心率e=.设椭圆C2的方程为+=1(a0),则b=.因为==,所以a=2.所以椭圆C2的方程为+=1.(2)证明设P(x0,y0),y00,则+=1,从而y=12-2x.将x=x0代入+=1得+=1,从而y2=3-=,即y=.因为P,H在x轴的同侧,所以取y=,即H(x0,).所以kA1PkA2H====-1,从而A1PA2H.又因为PHA1A2,所以H为△PA1A2的垂心.4.解 (1)S1=asin acos =a2sin 2,设正方形边长为x,则BQ=,RC=xtan ,+xtan +x=a,x==,S2==.(2)当a固定,变化时,令sin 2=t,则=(0利用单调性求得t=1时,=.2019届江苏省高三数学复习中档题满分练习的内容就是这些,希望对考生提高成绩有帮助。
适合高三刷的数学中档试卷

考试时间:120分钟满分:150分一、选择题(每题5分,共50分)1. 已知函数$f(x)=\sqrt{x^2+1}$,则函数的值域为()。
A. $[1,+\infty)$B. $[1,\sqrt{2}]$C. $[0,+\infty)$D. $[1,2]$2. 若$y=2\sin(2x-\frac{\pi}{4})+1$,则函数的周期为()。
A. $\pi$B. $\frac{\pi}{2}$C. $\frac{\pi}{4}$D. $2\pi$3. 在三角形ABC中,若$\angle A=\frac{\pi}{3}$,$\angle B=\frac{\pi}{4}$,则$\angle C$的度数为()。
A. $45^\circ$B. $60^\circ$C. $75^\circ$D. $90^\circ$4. 若等差数列$\{a_n\}$的前$n$项和为$S_n=4n^2+5n$,则$a_1$的值为()。
A. $-1$B. $0$C. $1$D. $2$5. 已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$($a>0$,$b>0$)的渐近线方程为$y=\pm\frac{b}{a}x$,则双曲线的离心率为()。
A. $\frac{a}{b}$B. $\frac{b}{a}$C. $\sqrt{1+\frac{b^2}{a^2}}$D. $\sqrt{1+\frac{a^2}{b^2}}$6. 函数$f(x)=x^3-3x^2+4x+6$的图像在区间$(-1,0)$上的变化趋势为()。
A. 单调递增B. 单调递减C. 先增后减D. 先减后增7. 在等比数列$\{a_n\}$中,若$a_1=2$,$a_4=32$,则该数列的公比为()。
A. $2$B. $4$C. $8$D. $16$8. 若不等式$|x-1|<3$的解集为()。
A. $(-2,4)$B. $(-4,2)$C. $(-2,2)$D. $(-4,1)$9. 已知函数$f(x)=x^2+2x+1$,则函数的对称轴方程为()。
山西省朔州市重点中学2024届高三高考数学试题系列模拟卷(7)

山西省朔州市重点中学2024届高三高考数学试题系列模拟卷(7)注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设x ∈R ,则“327x <”是“||3x <”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件2.棱长为2的正方体1111ABCD A B C D -内有一个内切球O ,过正方体中两条异面直线AB ,11A D 的中点,P Q 作直线,则该直线被球面截在球内的线段的长为( )A .2B 1CD .1 3.若函数32()39f x x ax x =++-在3x =-时取得极值,则a =( )A .2B .3C .4D .54.设双曲线22221y x a b-=(0a >,0b >)的一条渐近线与抛物线213y x =+有且只有一个公共点,且椭圆22221x y a b +=的焦距为2,则双曲线的标准方程为( )A .22143x y -= B .22143y x -= C .22123x y -= D .22132y x -= 5.函数()[]()cos 2,2f x x x ππ=∈-的图象与函数()sin g x x =的图象的交点横坐标的和为( ) A .53π B .2π C .76π D .π6.半正多面体(semiregular solid ) 亦称“阿基米德多面体”,是由边数不全相同的正多边形为面的多面体,体现了数学的对称美.二十四等边体就是一种半正多面体,是由正方体切截而成的,它由八个正三角形和六个正方形为面的半正多面体.如图所示,图中网格是边长为1的正方形,粗线部分是某二十四等边体的三视图,则该几何体的体积为( )A .83B .4C .163D .2037.已知等差数列{}n a 中,468a a +=则34567a a a a a ++++=( )A .10B .16C .20D .248.已知非零向量,a b 满足a b λ=,若,a b 夹角的余弦值为1930,且()()23a b a b -⊥+,则实数λ的值为( ) A .49- B .23 C .32或49- D .32 9.若某几何体的三视图如图所示,则该几何体的表面积为( )A .240B .264C .274D .28210.已知i 是虚数单位,则(2)i i +=( )A .12i +B .12i -+C .12i --D .12i -11.定义在R 上的偶函数f (x )满足f (x +2)=f (x ),当x ∈[﹣3,﹣2]时,f (x )=﹣x ﹣2,则( ) A .66f sin f cos ππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭> B .f (sin 3)<f (cos 3) C .4433f sin f cos ππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭< D .f (2020)>f (2019)12.在ABC ∆中,D 为BC 中点,且12AE ED =,若BE AB AC λμ=+,则λμ+=( ) A .1 B .23- C .13- D .34- 二、填空题:本题共4小题,每小题5分,共20分。
高三数学中档题冲刺训练
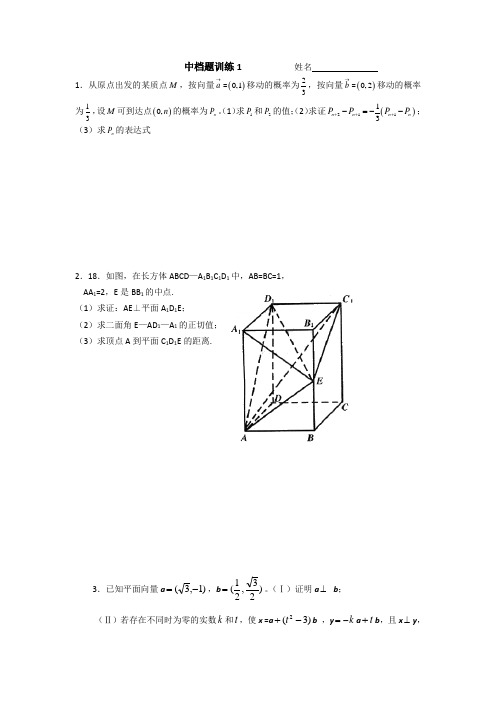
中档题训练1 姓名1.从原点出发的某质点M ,按向量a →=()0,1移动的概率为23,按向量b →=()0,2移动的概率为13,设M 可到达点()0,n 的概率为n P 。
(1)求1P 和2P 的值;(2)求证()21113n n n n P P P P +++-=--;(3)求n P 的表达式2.18.如图,在长方体ABCD —A 1B 1C 1D 1中,AB=BC=1, AA 1=2,E 是BB 1的中点. (1)求证:AE ⊥平面A 1D 1E ; (2)求二面角E —AD 1—A 1的正切值; (3)求顶点A 到平面C 1D 1E 的距离.3.已知平面向量a )1,3(-=,b )23,21(=。
(Ⅰ)证明a ⊥ b ; (Ⅱ)若存在不同时为零的实数k 和t ,使x =a )3(2-+t b ,y k -=a t +b ,且x ⊥y ,试求函数关系式)(t f k =;(Ⅲ)据(Ⅱ)的结论,讨论关于t 的方程0)(=-k t f 的解的情况。
4.已知函数11log )(--=x mxx f a是奇函数)1,0(≠>a a 。
(1) 求m 的值;(2)判断)(x f 在区间),1(+∞上的单调性并加以证明; (3)当)2,(,1-∈>a r x a 时,)(x f 的值域是),1(+∞,求r a 与的值. (1)m=-1…………3分 (2)由(1),).1,0(11log )(≠>-+=a a x x x f a任取11)(,11)(,11)(,),,1(2221112121-+=-+=-+=<+∞∈⋅x x x t x x x t x x x t x x x x 则令设,)1)(1()(21111)()(2112221121---=-+--+=-∴x x x x x x x x x t x t . ,,1,12121x x x x <>> ,0,01,011221>->->-∴x x x x1111),()(221121-+>-+>∴x x x x x t x t 即.……………………………………6分),1()(,11log 11log ,12211+∞-+>-+>∴在时当x f x x x x a a a上是减函数;……7分 当0<a <1时,),1()(+∞在x f 上是增函数.……………………8分(2)当a >1时,要使)(x f 的值域是),1(+∞,则111log >-+x x a ,011)1(,11>-++->-+∴x a x a a x x 即 而a >1,∴上式化为0111<--+-x a a x ①………………………………10分 又),121(log 11log )(-+=-+=x x x x f a a∴当x >1时,0)(>x f . 当0)(,1<-<x f x 时.因而,欲使)(x f 的值域是),1(+∞,必须1>x ,所以对不等式①,当且仅当111-+<<a a x 时成立.………………12分32,1,1,1121+==⎪⎪⎩⎪⎪⎨⎧>-+=-=∴a r a a a a r 得解之.…………………………14分中档题冲刺2 姓名1.设a 、b是两个不共线的非零向量(t ∈R )①若a与b 起点相同,t 为何值时,a,t b,31(a +b)三向量的终点在一直线上? ②若|a |=|b |且a 与b 夹角为60°,那么t 为何值时|a -t b |的值最小?解:①设a -t b =m[a -31(a +b )](m ∈R) 化简得 )132(-m a =)3(t m-b ∵a 与b 不共线 ∴⎪⎪⎪⎩⎪⎪⎪⎨⎧=-⎪⎪⎩⎪⎪⎨⎧==⇒=-0321230132t mt m m ∴t=21时,a、t b 、31(a +b )终点在一直线上②|a -t b |2=(a -t b )2=|a |2+t 2|b |-2t|a | |b |cos 60°=(1+t 2-t )|a |2, ∴t=21时,|a-t b |有最小值||23a2.已知曲线轴与y d cx bx ax y L +++=23:相交于点A ,以其上一动点P (x 0,y 0)为切点的直线l 与y 轴相交于Q 点.(Ⅰ)求直线l 的方程,并用x 0表示Q 点的坐标;(Ⅱ)求.sin sin lim0AQPAPQx ∠∠+∞→Ⅰ)解:c bx ax k c bx ax y d A ++=++='020223,23),,0(0002000200))(23(0),)(23(y x c bx ax y x x x c bx ax y y Q +-++==-++=-∴得令 )))(23(,0(00020y x c bx ax Q +-++∴(Ⅱ)由正弦定理得:2|||2|)(|2|lim sin sin lim )(|2|)(|23|sin sin 20203020203020203020203020200020300==++++=∠∠∴+++--=-+-+---==∠∠+∞→+∞→a a cx bx ax x bx ax AQP APQ cx bx ax x bx ax d y x d y cx bx ax AP AQ AQP APQ x x3.如图,直三棱柱111ABC A B C -中,底面是以ABC ∠为直角的等腰三角形,12,3,AC a BB a D ==是11A C 的中点,E 是1B C 的中点。
高三数学中档题训练(7-9)

高三数学中档题训练(7)班 级 姓 名1.34sin (cos )55i θθ-+-()是纯虚数,则=θ2tan2、等比数列}{n a 的前n 项和为S n ,已知S 1,2S 2,3S 3成等差数列,则}{n a 的公比为3、记数列{}n a 是首项1a a =,公差为2的等差数列;数列{}n b 满足2(1)n n b n a =+, 若对任意*n N ∈都有5n b b ≥成立,则实数a 的取值范围为4、已知不等式2210ax x +->的解集是A ,若⊆(3,4)A ,则实数a 的取值范围是5、已知不等式222xy ax y ≤+,若对任意[1,2]x ∈及[2,3]y ∈该不等式恒成立,则实 数a 的取值范围是6、已知)3,3(A ,O 是原点,点),(y x P 的坐标满足⎪⎩⎪⎨⎧≤-≤+-≥030230y x y x x ,求(1)OP OA ⋅的最大值 (2OP OA ⋅的取值范围.7、已知函数321()33f x x x x a =-+++.若()f x 在区间[]3,4-上的最小值为73,求a 的值.8、已知向量)20,0))(cos(,1(),2),(sin(πϕωϕωϕω<<>+=+=→→x b x a ,函数)(),)(()(x f y b a b a x f =-+=→→→→的图象的相邻两对称轴之间的距离为2,且过点.)27,1(M .(1)求)(x f 的表达式;(2)求)2011()3()2()1()0(f f f f f +⋅⋅⋅++++高三数学中档题训练(8)班 级 姓 名1、x t x y cos sin +=在0=x 处的切线方程为1+=x y ,则=t .2、已知无论k 取任何实数,直线0)142()32()41(=-+--+k y k x k 必经过一定点,则该定点坐标为 .3、面积为S 的ABC ∆的三边c b a ,,成等差数列,4,60==∠︒b B ,设ABC ∆外接圆的面积为'S ,则=S S :'4已知:圆M :0222=-+y y x ,直线l 的倾斜角为︒120,与圆M 交于P 、Q 两点,若0=⋅→→OQ OP (O 为原点),则l 在x 轴上的截距为 .5已知)1(-x f 为奇函数, )1(+x f 为偶函数, 1)2011(=f ,=)4(f .6设函数]3,4[,sin 2)(ππω-∈=x x x f ,其中ω是非零常数.(1)若)(x f 是增函数,则ϖ的取值范围是 ;(2)若)(x f 的最大值为2,则ϖ的最大值等于7已知二次函数)(x f 的二次项系数为a ,且不等式()2f x x >的解集为(1,3)-. (1)若函数()()g x xf x =在区间(,)3a-∞内单调递减,求a 的取值范围;(2)当1a =-时,证明方程3()21f x x =-仅有一个实数根.8已知ABC ∆中,5||,10||==AD AC ,0,115=∙=AB CD DB AD(1)求||AC AB -(2)设θ=∠BAC ,且已知54)cos(=+x θ,02<<-x π,求x sin9如图所示,某市政府决定在以政府大楼O 为中心,正北方向和正东方向的马路为边界 的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要 求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的 半径O M R = ,45MOP ∠= ,O B 与O M 之间的夹角为θ.(1)将图书馆底面矩形A B C D 的面积S 表示成θ的函数.(2)若45R m =,求当θ为何值时,矩形A B C D 的面积S 有最大值? 其最大值是多少?(精确到0.01m 2)ABCDMOPQ F高三数学中档题训练(9)班 级 姓 名1.不等式2(1)2x x --<的解集是2、函数()tan 42y x ππ=-的部分图像如图所示,则=∙+AB OB OA )(3、已知两个点(2,1)A -和(1,3)B -分布在直线320x y a -++=的 两侧,则a 的取值范围为4.已知⎪⎭⎫ ⎝⎛∈=ππαα,2,53sin ,则cos sin 44ππαα⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭的值为5、对于数列{n a },定义数列{n n a a -+1}为数列{n a }的“差数列”,若21=a ,{n a }的“差数列”的通项公式为n 2,则数列{n a }的前n6、函数)32sin(lg π+=x y 的单调递减区间为7、设A B C ∆的内角,,A B C 所对的边长分别为,,a b c ,且(2)cos cos b A C -=.(1)求角A 的大小;(2)若角6B π=,B C 边上的中线A M ABC ∆的面积.8、已知圆C 的圆心坐标为(2,-1),且与x 轴相切(1)求圆C 的方程; (2)求过点P(3,2)且与圆C 相切的直线方程; (3)若直线过点P(3,2)且与圆C 相切于点Q ,求线段PQ 的长。
高三数学中档练习题推荐

高三数学中档练习题推荐高三是学生们最为紧张和重要的一年,而数学作为一门重要的学科,占据着整个高考的很大比重。
为了帮助高三学生们更好地备考数学,我精心挑选了一些中档练习题,希望能给同学们提供有针对性的练习,提高数学解题能力。
1. 函数(1)已知函数f(x) = x^2 - 2x + 1,求f(3)的值。
(2)已知函数g(x) = 2^x,求g(0)的值。
2. 三角函数(1)已知直角三角形中的一条锐角的正弦值为1/2,求该角的大小。
(2)已知sin(a) = 3/5,cos(b) = 4/5,且a和b为锐角,求sin(a+b)的值。
3. 数列与数列求和(1)已知等差数列的首项为3,公差为4,求该数列的第5项。
(2)已知等比数列的首项为2,公比为3,求该数列的前6项的和。
4. 三角函数与解析几何(1)已知平面直角坐标系中有一条直线L,其斜率为-2,经过点(3, 4),求直线L的方程。
(2)已知平面直角坐标系中有一个圆心在原点,半径为3的圆,求该圆上的一点P(x, y),使得点P与直线y = 2x之间的距离最短。
5. 概率与统计(1)甲、乙、丙三个人依次从一副扑克牌中抽取一张纸牌,不放回,求出甲乙丙三个人抽到的纸牌分别为黑桃、红心、梅花的概率。
(2)某班级60名同学中,有20人擅长数学,30人擅长英语,并且既擅长数学又擅长英语的有10人。
从该班级中任意选出一名学生,求他既不擅长数学也不擅长英语的概率。
这些练习题涵盖了高三数学中的各个知识点,通过解答这些题目,可以加深对数学知识的理解和掌握,提高解题能力和应试水平。
希望同学们在备考中能够认真对待每一道题目,多思考、多总结,相信付出努力一定会有收获。
祝愿大家高考顺利!。
高三数学复习中档题7

中档题7一、填空题1.设集合{}2120A x x x =+-=,集合{}10B x kx =+=,如果A B A ⋃=,则由实数k 组成的集合中所有元素的积等于 . 2.假设复数()3,12a ia R i i-∈+为虚数单位是纯虚数,则实数a 的值为 . 3.已知向量()2,1,10,52=+==a b a b a ,则=b .4.假设命题“,x R ∃∈使2(1)10x a x +-+<”是假命题,则实数a 的取值范围为 .5.在数列{}n a 中,假设对任意的n 均有12n n n a a a ++++为定值()*n N ∈,且79982,3,4a a a ===,则此数列{}n a 的前100项的和100S = .6.已知函数()()[]432,0,1f x a x b a x =-+-∈,假设()2f x ≤恒成立,则a b +的最大值为 .7.过点()3,4C 且与x 轴,y 轴都相切的两个圆的半径分别为12,r r ,则12r r = . 8.如图,已知三棱锥A BCD -的底面是等边三角形,三条侧棱长都等于1,且30BAC ∠=,,M N 分别在棱AC AD 和上,则BM MN NB ++的最小值为 .二、解答题9.在ABC ∆中,已知,,a b c 分别是角,,A B C 的对边,不等式2cos 4sin 60x C x C ++≥对一切实数x 恒成立.〔1〕求角C 的最大值〔2〕假设角C 取得最大值,且2a b =,求角B 的大小.10.如图,在四棱锥P ABCD -中,底面ABCD 是正方形,侧面PAD ⊥底面ABCD ,PA PD =,且PD 与底面ABCD 所成的角为45.〔1〕求证:PA ⊥平面PCD〔2〕已知E 为棱AB 的中点,问在棱PD 上是否存在一点Q ,使//EQ 平面PBC ?假设存在,证明你的结论;假设不存在,试,说明理由.11.某医药公司经销某种品牌药品,每件药品的成本为6元,预计当每件药品的售价为x 元()911x ≤≤时,一年的销售量为485x -万件,并且全年该药品需支付2x 万元的宣传及管理费.〔1〕求该医药公司一年的利润L 〔万元〕与每件药品的售价x 的函数关系式;〔2〕当每件药品的售价为多少元时,该公司一年的利润L 最大,并求出L 的最大值.12.已知曲线221:14y C x +=与曲线22:1C y x =-,设点()()000,0P x y y >是曲线1C 上任意一点,直线0014y yx x +=与曲线2C 交于,A B 两点. 〔1〕判断直线0014y yx x +=与曲线1C 的位置关系;〔2〕以,A B 两点为切点分别作曲线2C 的切线,设两切线的交点为M ,求证:点M 到直线1:220l x y --=与2:220l x y ++=距离的乘积为定值.13.设函数)(x f 的定义域为M ,具有性质P :对任意M x ∈,都有)1(2)2()(+≤++x f x f x f .〔1〕假设M 为实数集R ,是否存在函数),1,0()(R x a a a x f x∈≠>= 具有性质P ,并说明理由;〔2〕假设M 为自然数集N ,并满足对任意M x ∈,都有N x f ∈)(. 记)()1()(x f x f x d -+=.求证:对任意M x ∈,都有)()1(x d x d ≤+.14.设非常数数列{a n }满足βαβα++=++n n n a a a 12,*∈N n ,其中常数βα,均为非零实数,且 0≠+βα.〔1〕证明:数列{}n a 为等差数列的充要条件是02=+βα;〔2〕已知25,141121====a a ,,βα,求证:数列{}11-+-n n a a()2,≥∈*n N n 与数列()*∈⎭⎬⎫⎩⎨⎧+N n n 21中没有相同数值的项.中档题7答案1、02、63、54、13a -≤≤5、2996、1747、25 89、〔1〕由条件知,当cos 0C =cos 0C ≠时,2cos 016sin 24cos 0C C C >⎧⎨∆=-≤⎩,即2cos 02cos 3cos 20C C C >⎧⎨+-≥⎩,1cos 2C ∴≥. C ABC ∆为的内角, 03C π∴<≤,∴角C 的最大值为3π. (2)有〔1〕知3C π=, 23A B π∴+=,由2a b =,得sin 2sin A B =.2sin 2sin 3B B π⎛⎫∴-= ⎪⎝⎭,即13sin 2sin 2sin 22B B B B B +==,即2tan 0,,36B B B ππ⎛⎫=∈∴= ⎪⎝⎭. 10、证明〔1〕过点P PH AD ⊥作交于H .侧面PAD ABCD ⊥底面,PH ABCD ∴⊥平面.PD ∴与平面ABCD 所成的角为45PDH ∠=.,45.PA PD PAD =∴∠=则90APD ∠=..,PA PD CD AD ∴⊥⊥平面PAD ABCD ⊥底面,.,CD PAD PA PAD ∴⊥⊂平面平面.CD PA ∴⊥,PD CD D ⋂=PA PDC ∴⊥平面. Q 为PD 的中点时,//EQ 平面PBC .证明如下:取PC 的中点F ,连,FQ FB .则1//,.//,2FQ CD FQ CD BE CD =12BE CD =,∴四边形BEQF 为平行四边形.//.BF EQ BF ∴⊂平面,PBC EQ ⊄平面PBC ,//EQ ∴平面PBC .11、〔1〕该公司一年的利润L 〔万元〕与售价x 的函数关系式为:()48625L x x x =-•--, []9,11x ∈.〔2〕()48625L x x x =-•--,令[]()4815,4,6,210t x t t L t t --=∈∴=--=483823838t t ⎛⎫-+≤-=- ⎪⎝⎭当且仅当482t t =,即5x =+L 取得最大值38-.则当每件售价为5+元时,该公司一年的利润L最大,最大值为38-.12、〔1〕直线直线0014y y x x +=与曲线1C 相切00221444y yx x y x ⎧+=⎪⎨⎪+=⎩,22004840x x x y ⇒-+-= ()()222220000816416440x y x y ⇒∆=--=+-=.〔2〕设()()1122,,,A x y B x y002441y y x x y x =-⎧⎨=-⎩,()2000012120044440,1x y x x x y x x x x y y ⎛⎫⇒+-+=⇒+=-=-+ ⎪⎝⎭ 22:12C y x y x '=-⇒=,切线()()2111:12AM y x x x x --=-,即:()21121y x x x =-+①同理切线()222:21BM y x x x =-+②联立①②得012002242x x x x y y y +⎧==-⎪⎪⎨⎪=--⎪⎩,即00024,2x M y y ⎛⎫--- ⎪⎝⎭, 设点M 到直线12,l l 距离分别为12,d d,1d ==2d ==20201222001161644555y x d d y y --===.13、证明:〔1〕因f (x )=a x (a >0且a ≠1),所以a x ≠a x +2,即f (x )≠f (x +2).由题设以及算术平均与几何平均不等式,得f (x )+f (x +2)=a x +a x +2>2a x a x +2=2 a x +1=2 f (x +1), 这与f (x )+f (x +2)≤2f (x +1)矛盾.故不存在函数f (x )=a x (a >0且a ≠1)满足性质P . 〔2〕(ⅰ)由题设对任意x ∈N ,f (x )+f (x +2)≤2f (x +1),所以f (x +2)-f (x +1)≤f (x +1)-f (x ).于是对任意x ∈N ,d (x +1)≤d (x ).14、〔1〕解:已知数列}{n a ,12n nn a a a αβαβ+++=+.①充分性:假设βα2-=,则有12122n nn n n a a a a a βββ+++-+==--,得n n n n a a a a -=-+++112,所以}{n a 为等差数列.②必要性:假设}{n a 为非常数等差数列,可令b kn a n +=(k ≠0). 代入12n n n a a a αβαβ+++=+,得[(1)]()(2)k n b kn b k n b αβαβ++++++=+.化简得2k k ααβ=+,即02=+βα.因此,数列{a n }为等差数列的充要条件是α+2β=0. 〔2〕由已知得2111[]5n n n n a a a a +++--=-.又因为21302a a -=≠,可知数列}{1n n a a -+(n ∈N *)为等比数列,所以11121131()()()552n n n n a a a a --+---=-=⋅ (n ∈N *).从而有n ≥2时, 1131()52n n n a a -+--=⋅,2131()52n n n a a ----=⋅.于是由上述两式,得 2111(556|)|n n n a a -+-⋅-=〔2n ≥〕.由指数函数的单调性可知,对于任意n ≥2,| a n +1-a n -1|=65·2)51(-n ≤65·22)51(-=65. 所以,数列11{||}(*,2)n n a a n n +--∈≥N 中项均小于等于65.而对于任意的n ≥1时,n +12≥1+12>65,所以数列{n +12}(n ∈N*)中项均大于65.因此,数列11{||}(*,2)n n a a n n +--∈≥N 与数列{n +12}(n ∈N*)中没有相同数值的项.。
高三数学中档题+详细答案(全)

高三数学中档题+详细答案〔全〕班级 姓名1.如图所示,在直三棱柱中,平面为的中点.〔1〕求证:平面;〔2〕求证:平面; 〔3〕在上是否存在一点,使得∠=45°,若存在,试确定的位置,并判断平面与平面是否垂直?若不存在,请说明理由.2. 设、分别是椭圆的左、右焦点,.1F 2F 1422=+y x )1,0(-B 〔Ⅰ〕若是该椭圆上的一个动点,求的最大值和最小值;〔Ⅱ〕若C 为椭圆上异于B 一点,且,求的值;〔Ⅲ〕设P 是该椭圆上的一个动点,求的周长的最大值.3. 已知定义在上的奇函数 〔〕,当 时,取极小值〔1〕求的值;〔2〕当时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论.〔3〕求证:对,都有4.设数列的前项和为,为常数,已知对,当时,总有.⑴ 求证:数列{}是等差数列;{}n a n n S d *∈∀N m n ,m n >d m n m S S S m n mn )(-+=--na⑵ 若正整数n, m, k 成等差数列,比较与的大小,并说明理由!k n S S +mS 2高三数学中档题训练27班级 姓名1. 在平面直角坐标系中,已知圆心在直线上,半径为的圆C 经过坐标原点O ,椭圆与圆C 的一个交点到椭圆两焦点的距离之和为10.xoy 4y x =+()222109x y a a +=>〔1〕求圆C 的方程;〔2〕若F 为椭圆的右焦点,点P 在圆C 上,且满足,求点P 的坐标.18.某厂为适应市场需求,提高效益,特投入98万元引进先进设备,并马上投入生产,第一年需要的各种费用是12万元,从第二年开始,所需费用会比上一年增加4万元,而每年因引入该设备可获得的年利润为50万元.请你根据以上数据,解决下列问题:〔1〕引进该设备多少年后,开始盈利?〔2〕引进该设备若干年后,有两种处理方案:第一种:年平均盈利达到最大值时,以26万元的价格卖出;第二种:盈利总额达到最大值时,以8万元的价格卖出,哪种方案较为合算?请说明理由′3.设二次函数在区间上的最大值、最小值分别是M、m,集合.〔1〕若,且,求M和m的值;〔2〕若,且,记,求的最小值.4.设数列满足,若是等差数列,是等比数列.〔1〕分别求出数列的通项公式;〔2〕求数列中最小项及最小项的值;〔3〕是否存在,使,若存在,求满足条件的所有值;若不存在,请说明理由.高三数学中档题训练28班级姓名1、已知分别是正三棱柱的侧面和侧面的对角线的交点,是棱的中点. 求证:〔1〕平面;〔2〕平面平面.2.在平面区域内有一个圆,向该区域内随机投点,当点落在圆内的概率最大时的圆记为⊙M.〔1〕试求出⊙M的方程;〔2〕过点P〔0,3〕作⊙M的两条切线,切点分别记为A,B;又过P作⊙N:x2+y2-4x+y+4=0的两条切线,切点分别记为C,D.试确定的值,使AB⊥CD.3.已知函数.〔1〕当a=1时,证明函数只有一个零点;〔2〕若函数在区间〔1,+∞〕上是减函数,求实数a 的取值范围.4. 已知函数,是方程的两个根,是的导数.设,.〔1〕求的值;〔2〕已知对任意的正整数有,记.求数列的前项和.高三数学中档题训练29班级姓名1.已知函数,.〔1〕求的最大值和最小值;〔2〕若不等式在上恒成立,求实数的取值范围2、已知椭圆:的两个焦点为,,点在椭圆上,且,,.〔1〕求椭圆的方程;〔2〕若直线过圆的圆心,交椭圆于,两点,且,关于点对称,求直线的方程.3.已知集合是满足下列性质的函数的全体:在定义域内存在,使得成立.〔1〕函数是否属于集合?说明理由;〔2〕若函数属于集合,试求实数和的取值范围;〔3〕设函数属于集合,求实数的取值范围.4.设常数,函数.0a ≥2()ln 2ln 1f x x x a x =-+-((0,))x ∈+∞ 〔1〕令,求的最小值,并比较的最小值与零的大小;〔2〕求证:在上是增函数; 〔3〕求证:当时,恒有.高三数学中档题训练30班级 姓名1.若函数的图象与直线y=m 相切,并且切点的横坐标依次成公差为的等差数列.〔Ⅰ〕求m 的值;〔Ⅱ〕若点图象的对称中心,且,求点A 的坐标.2.已知中心在原点,焦点在坐标轴上的椭圆过M 〔1,〕, N 〔 -,〕两点.〔Ⅰ〕求椭圆的方程;〔Ⅱ〕在椭圆上是否存在点P 〔x,y 〕,使P 到定点A 〔a,0〕〔其中0<a <3〕的距离的最小值为1?若存在,求出a 的值及P 点的坐标;若不存在,请给予证明.3.设A 〔x1 , y1〕,B 〔x2 ,y2〕是函数f 〔x 〕=+log2图象上任意两点,且=〔+〕,点M 的横坐标为.⑴求M 点的纵坐标;⑵若Sn==f 〔〕+f 〔〕+…+f 〔〕,n ∈N*,且n≥2,求Sn; ⑶已知an=n ∈N*,Tn 为数列{an}的前n 项和,若Tn<λ〔Sn+1+1〕 对一切n>1且n ∈N*都成立,求λ的取值范围.4.已知函数f 〔x 〕= +lnx 的图像在点P 〔m,f 〔m 〕〕处的切线方程为y=x ,设. ()2ln ng x mx xx =--〔1〕求证:当恒成立;〔2〕试讨论关于的方程: 根的个数.高三数学中档题训练261.证明:〔1〕连接与相交于,则为的中点.连结,又为的中点,MD C B //1∴,又平面,平面⊄C B 1BD A 1MD ⊂BD A 1//1C B ∴平面 . …………………………………………4′BD A 1〔2〕,∴平行四边形为菱形,, 又面⊥1AC BD A 1B A AC 11⊥∴,面 …………………………7′⊥∴B A 111C AB 111C B B A ⊥∴.又在直棱柱中,, 111C B A ABC -111C B BB ⊥⊥∴11C B 平面. ……………………………………9′A ABB 1〔3〕当点为的中点时,∠=45°,且平面平面. 设AB=a ,CE=x,∴,,111A B AC =1C E a x =-∴,1A E ==BE∴在中,由余弦定理得1A BE 22211112cos 45BE A B A E A B A E =+-⋅⋅︒即222222322a x a x a ax +=++--⋅2a x =-∴x=a ,即E 是的中点. ………………………………………13′12C C 1 D 、分别为、的中点,.E AC C C 11//AC DE ∴1AC 平面,平面.BD A 1⊥∴DE BD A 1又平面,∴平面平面. …………………………15′⊂DE BDE ⊥BD A 1BDE 2.解:〔Ⅰ〕易知所以,设,则())12,F F (),P x y())2212,,,3PF PF x y x y x y⋅=---=+-()2221133844x x x =+--=-因为,故当,即点为椭圆短轴端点时,有最小值[]2,2x ∈-0x =P 12PF PF ⋅2-当,即点为椭圆长轴端点时,有最大值 2x =±P 12PF PF ⋅1〔Ⅱ〕设C 〔〕, 由得,又 所以有解得. 220014x y +=2670λλ+-=舍去)01(7>=-=λλ〔Ⅲ〕 因为|P|+|PB|=4-|PF2|+|PB|≤4+|BF2|,∴的周长≤4+|BF2|+|B|≤8.1PBF ∆1F所以当P 点位于直线BF2与椭圆的交点处时,周长最大,最大值为8.3.解〔1〕∵函数图象关于原点对称,∴对任意实数,∴,即恒成立 ∴ …………4分 32322424ax bx cx d ax bx cx d ---+=-+--220bx d -=0,0b d ==∴,,3)(',)(23c ax x f cx ax x f +=+= ∵时,取极小值,∴,1x =()f x 23-2303a c a c +=+=-且解得 ………8分1,31-==c a〔2〕当时,图象上不存在这样的两点使结论成立. …………10分假设图象上存在两点,使得过此两点处的切线互相垂直,),(),,(2211y x B y x A则由知两点处的切线斜率分别为,1)('2-=x x f ,1211-=x k ,1222-=x k 且…………〔*〕 …………13分1x 、,2[1,1]x ∈-2222121210,10,(1)(1)0x x x x ∴-≤-≤∴-⋅-≥此与〔*〕相矛盾,故假设不成立. ………………16分4〔本小题满分18分〕 ⑴证明:∵当时,总有m n >d m n m S S S m n m n )(-+=--∴ 当时,即 2分2≥n d n S S S n n )1(11-+=--,)1(1d n a a n -+=且也成立 ………3分1=n∴ 当时,2≥n dd n a d n a a a n n =----+=--)2()1(111∴数列{}是等差数列 …………5分na⑵解: ∵正整数n, m, k 成等差数列,∴,2m k n =+ ∴)2)1((22)1(2)1(2111d m m ma d k k ka d n n na S S S m k n -+--++-+=-+ ))2(2(2)2(2222222k n k n d m k n d +-+=-+=……9分2)(4k n d-=∴ ① 当时,0>d k n S S +mS 2>② 当时, 0<d k n S S +mS 2<③ 当时, ……10分 高三数学中档题训练270=d k n S S +mS 2= 1. 解:〔1〕由已知可设圆心坐标为, …………………………∴得,∴圆心坐标为, …………………………()2248t t ++=2t =-()2,2-4'所以圆的方程为 ……………………………()()22228x x ++-=6'〔2〕由题意,椭圆中,即29b =,∴,∴ …………………………216c =()4,0F 8'设,则,(),P m n ()()224016m n -+-=()()22228m n ++-= ……………………………11'解之得:4050125m m n n ⎧=⎪=⎧⎪⎨⎨=⎩⎪=⎪⎩或即 …………………………………………()4120,0,55P P ⎛⎫⎪⎝⎭或14' 2. 解:〔1〕设引进设备几年后开始盈利,利润为y 万元则y=50n-[12n+×4]-98=-2n2+40n-98n(n -1)2由y>0可得10n <10+ ∵n ∈N*,∴3 ≤n ≤17,即第3年开始盈利 …………………… 5′〔2〕方案一:年平均盈利当且仅当即n=7时取“=”982n =n共盈利12×7+26=110万元 …………………………………………9′ 方案二:盈利总额y=-2n2+40n-98=-2〔n-10〕2+102 当n=10时,ymax=102共盈利102+8=110万元………………………………………13′方案一与方案二盈利客相同,但方案二时间长,∴方案一合算…………153. 〔1〕由 ……………………1′ 又{}2A 1212(1)0.ax b x c =+-+=,,故,是方程的两实根1-b 1+2=a ,c 2=a ⎧⎪⎪∴⎨⎪⎪⎩ ……………………………………………3′1,2a b ==-解得 ………………………………………4′ []22()22(1)1,2,2f x x x x x ∴=-+=-+∈-min 1()(1)1,1x f x f m ====当时,即 ………………………5′ max 2()(2)10,10.x f x f M =-=-==当时,即 ……………………6′〔2〕,4ca ⎧⎪⎧⎪∴⎨⎨⎩⎪=⎪⎩1-b 2+2=b=1-4a a 即c=4a ………………………8′[]2()(14)4,2,2f x ax a x a x ∴=+-+∈-4112,22a a a -==-其对称轴方程为x131,2,222a a ⎡⎫≥-∈⎪⎢⎣⎭又故 ……………………………10′(2)162,M f a ∴=-=- ………………………11′ 4181,24a a m f a a --⎛⎫==⎪⎝⎭ ………………………12′1()164g a M m a a ∴=+=-…………………………13′[)min 63()1,1().4g a a g a +∞∴==又在区间上为单调递增的,当时, ……15′4.解:〔1〕由成等差数列知其公差为1, 故 ……………………()12113n n a a n n +-=-+-⋅=-3'21322,1,b b b b -=--=-由等比数列知,其公比为,{}1n n b b +-12故 …………11122n n n b b -+⎛⎫-=-⋅ ⎪⎝⎭6' 11223211()()()()n n n n n n n a a a a a a a a a a -----=-+-+-+⋅⋅⋅+-+=()()()12(1)212n n n ---⋅-+⋅+6== ………232282n n n -+-+27182n n -+8' 11223211()()()()n n n n n n n b b b b b b b b b b -----=-+-+-+⋅⋅⋅+-+=+6=2+ …………………………………………………2121()2112n -⎛⎫-- ⎪⎝⎭-42n -10' 〔2〕由〔1〕题知,= ,所以当或时,取最小项,其值为3…〔3〕假设存在,使-2-=-则- 即 …………0<27142n n -+42n -12<2527132714n n n n n --+<<-+15' ∵是相邻整数22713714n n n n -+-+与∴,这与矛盾,所以满足条件的不存在 (52)nZ -∉52n Z -∈k 17'高三数学中档题训练282、证明:〔1〕连结,因为分别是侧面和侧面的对角线的交点,所以分别是的中点…………………………………………4分所以,且在平面中,而不在平面中,故平面…………………7分//EF BC BC ABC EF ABC //EF ABC〔2〕因为三棱柱为正三棱柱,所以平面,,故由得……9分又因为是棱的中点,且为正三角形,,故由得, (11)分D BC ABC ∆∴BC AD ⊥//EF BC EF AD ⊥ 而,平面,所以平面,又平面,故平面平面.……………………………………14分1A AAD A =1,A A AD ⊂1A AD EF ⊥1A AD EF ⊂AEF AEF ⊥1A AD2. 〔1〕设⊙M 的方程为〔x-a 〕2+〔y-b 〕2=r2〔r >0〕,则点〔a ,b 〕在所给区域的内部.2分于是有,,.r r r ==⎪= ………………………………………………8分〔未能去掉绝对值,每个方程给1分〕解得 a=3,b=4,r=,所求方程为〔x-3〕2+〔y-4〕2=5. …………………10分〔2〕当且仅当PM ⊥PN 时,AB ⊥CD . ………………………………14分因,故,解得=6. …………………………18分13PM k =λ3232PN k --==-λ当=6时,P 点在圆N 外,故=6即为所求的满足条件的解.〔本验证不写不扣分〕3.解:〔1〕当a=1时,,其定义域是,2121()21x x f x x x x --'∴=-+=-令,即,解得或.()0f x '=2210x x x ---=12x =-1x = ,舍去.x >12x ∴=-当时,;当时,.01x <<()0f x '>1x >()0f x '<∴函数在区间〔0,1〕上单调递增,在区间〔1,+∞〕上单调递减∴当x=1时,函数取得最大值,其值为.()f x 2(1)ln1110f =-+= 当时,,即.1x ≠()(1)f x f <()0f x < ∴函数只有一个零点. ()f x 〔2〕法一:因为其定义域为,所以222121(21)(1)()2a x ax ax ax f x a x a x x x -++-+-'=-+==①当a=0时,在区间上为增函数,不合题意1()0,()f x f x x'=>∴(0,)+∞ ②当a>0时,等价于,即.()0(0)f x x '<>(21)(1)0(0)ax ax x +->>1x a >此时的单调递减区间为.()f x 1(,)a +∞依题意,得解之得.11,0.a a ⎧≤⎪⎨⎪>⎩1a ≥③当a<0时,等价于,即·()0(0)f x x '<>(21)(1)(0)ax ax x +->>12x a >-此时的单调递减区间为,得()f x 1(,)2a -+∞11,0.a a ⎧-≤⎪∴⎨⎪<⎩12a ≤-综上,实数a 的取值范围是1(,][1,)2-∞-+∞法二:22()ln ,(0,)f x x a x ax x =-+∈+∞2221()a x ax f x x -++'∴=由在区间上是减函数,可得()f x (1,)+∞在区间上恒成立.22210a x ax -++≤(1,)+∞① 当时,不合题意0a =10≤② 当时,可得即0a ≠11,4(1)0a f ⎧<⎪⎨⎪≤⎩210,4210a a a a ⎧><⎪⎨⎪-++≤⎩或10,4112a a a a ⎧><⎪⎪∴⎨⎪≥≤-⎪⎩或或 1(,][1,)2a ∴∈-∞-+∞4. 〔1〕 由 得α∴=β=〔2〕(221122111n n n n n n n nn a a a a a a a a βαβα++++++++-==-⎛⎫ ⎪⎛⎫-== ⎪-⎝⎭又 ∴12n nb b +=1111ln4ln2a b a βα-===- ∴数列是一个首项为 ,公比为2的等比数列;{}n b 4ln∴)()1212421ln 122n n n S -+==--高三数学中档题训练291.解:〔1〕.又,,即,ππ,42x ⎡⎤∈⎢⎥⎣⎦∵ππ2π2633x -∴≤≤π212sin 233x ⎛⎫+- ⎪⎝⎭≤≤max min ()3,()2f x f x ==∴.〔2〕,,max ()2m f x >-∴且,min ()2m f x <+,即的取值范围是.2.〔1〕…………7分 〔2〕…………7分 3.〔本小题满分16分〕解:〔1〕,若,则存在非零实数,使得 ,……〔2分〕即,……〔3分〕因为此方程无实数解,所以函数.……〔4分〕 〔2〕,由,存在实数,使得 ,……〔6分〕 解得,……〔7分〕所以,实数和的取得范围是,.……〔8分〕 〔3〕由题意,,.由,存在实数,使得 ,……〔10分〕所以,,)1(21)1(20220+=++x a x a 化简得,……〔12分〕当时,,符合题意.……〔13分〕当且时,由△得,化简得0>a 2≠a 0≥0))(2(84224≥---a a a a a ,解得.……〔15分〕综上,实数的取值范围是.……〔16分〕4.解〔Ⅰ〕∵,∴112()1[ln (ln )]a f x x x x x x '=-⨯+⨯+2ln 21x ax x =-+,∴,∴,令,得,列表如下:()()2ln 2g x xf x x x a '==-+(0,)x ∈+∞22()1x g x x x-'=-=()0g x '=2x =∴在处取得极小值,(g x 即的最小值为. ()g x (2)22ln 22g a =-+(2)2(1ln 2)2g a=-+,∵,∴,又,∴. ln 21<1ln 20->0a ≥(2)0g >〔Ⅱ〕证明由〔Ⅰ〕知,的最小值是正数,∴对一切,恒有从而当时,恒有,故在上是增函数. 〔Ⅲ〕证明由〔Ⅱ〕知:在上是增函数,∴当时,, 又,1x >()(1)f x f >2(1)1ln 12ln110f a =-+-=∴,即,∴()0f x >21ln 2ln 0x x a x --+>2ln 2ln 1x x a x >-+ 故当时,恒有.高三数学中档题训练301x >2ln 2ln 1x x a x >-+ 1.解析:解:〔1〕 3分由于y=m 与的图象相切, 则; 5分)(x f y =221221-=+=m m 或〔2〕因为切点的横坐标依次成公差为等差数列,所以 2.解:〔Ⅰ〕设椭圆方程为mx+ny=1〔m >0,n,>0且m≠n 〕 ……………2分∵椭圆过M,N 两点,∴m+ …………………4分,1932=n 1229=+n m ∴m= ………………………………………………6分41,91=n ∴椭圆方程为 …………………………………………7分14922=+y x〔Ⅱ〕设存在点P 〔x,y 〕满足题设条件,∴|AP|=〔x-a 〕+y ,又,∴y=4〔1 -〕,∴|AP|=〔x-a 〕+ 4〔1 -〕=〔x-a 〕+4-a 〔|x|≤3〕,…………………10分若|AP|的最小值为4-a ,依题意,时,即350,359≤≤<a a 5424-a=1 ,∴a=;………………………………………12分542215±⎥⎦⎤ ⎝⎛∉35,0 若即时,当x=3时,,359〉a 335<a<|AP|的最小值为〔3-a 〕,〔3-a 〕=1,∴a=2,此时点P 的坐标是〔3,0〕 .…………………………………………15分 故当a=2时,存在这样的点P 满足条件,P 点的坐标是〔3,0〕.…………16分3.解:〔1〕 ∵x1+x2=1,∴yM===; 4分〔2〕 ∵对任意xÎ〔0,1〕都有f 〔x 〕+f 〔1-x 〕=1∴f 〔〕+f 〔1-〕=1,即f 〔〕+f 〔〕=1 而Sn==f 〔〕+f 〔〕+…+f 〔〕, 又Sn==f 〔〕+f 〔〕+…+f 〔〕两式相加得2Sn=n-1,∴Sn=. 10分21-n〔3〕 n≥2时,an==4〔〕,Tn=<,λ>,而≤=,等号成立当且仅当n=2,∴λ>. 16分4.〔本小题满分16分〕〔1〕由k=得m=1∴f 〔m 〕=1=n+0,n=1∴. ———2′()12ln 2ln n g x mx x x xx x =--=--∴,()()222221122110x x x g x x x x x --+'=+-==≥∴在是单调增函数,()g x [)1,+∞∴对于恒成立.———6′()g x ()1112ln10g ≥=--=[)1,x ∈+∞〔2〕方程,∴.∵ ,∴ 方程为.0x >22ln 2xx ex tx =-+令,22ln (),()2xL x H x x ex t x ==-+,当上为增函数;21ln ()2xL x x -'=()()(0,),0,(0,]x e L x L x e ''∈≥∴时在上为减函数,()()[,),0,[0,)x e L x L x e ''∈+∞≤∴时在当时, ———11′ex =max 2()().L x L e e == ()()2222H x x ex t x e t e =-+=-+-,∴、在同一坐标系的大致图象如图所示,()x 函数L ()H x∴①当时,方程无解.2222,t e e e e ->>+即t ②当时,方程有一个根.2222,t e e e e -==+即t ③当时,方程有两个根.—16′15、2222,t e e e e -<<+即t。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中档题7一、填空题1.设集合{}2120A x x x =+-=,集合{}10B x kx =+=,如果A B A ⋃=,则由实数k 组成的集合中所有元素的积等于 . 2.若复数()3,12a ia R i i-∈+为虚数单位是纯虚数,则实数a 的值为 . 3.已知向量()2,1,10,52=+==a b a b a g ,则=b .4.若命题“,x R ∃∈使2(1)10x a x +-+<”是假命题,则实数a 的取值范围为 . 5.在数列{}n a 中,若对任意的n 均有12n n n a a a ++++为定值()*n N ∈,且79982,3,4a a a ===,则此数列{}n a 的前100项的和100S = .6.已知函数()()[]432,0,1f x a x b a x =-+-∈,若()2f x ≤恒成立,则a b +的最大值为 .7.过点()3,4C 且与x 轴,y 轴都相切的两个圆的半径分别为12,r r ,则12r r = . 8.如图,已知三棱锥A BCD -的底面是等边三角形,三条侧棱长都等于1,且30BAC ∠=o,,M N 分别在棱AC AD 和上,则BM MN NB ++的最小值为 .二、解答题9.在ABC ∆中,已知,,a b c 分别是角,,A B C 的对边,不等式2cos 4sin 60x C x C ++≥对一切实数x 恒成立.(1)求角C 的最大值(2)若角C 取得最大值,且2a b =,求角B 的大小.10.如图,在四棱锥P ABCD -中,底面ABCD 是正方形,侧面PAD ⊥底面ABCD ,PA PD =,且PD 与底面ABCD 所成的角为45o .(1)求证:PA ⊥平面PCD(2)已知E 为棱AB 的中点,问在棱PD 上是否存在一点Q ,使//EQ 平面PBC ?若存在,证明你的结论;若不存在,试,说明理由.11.某医药公司经销某种品牌药品,每件药品的成本为6元,预计当每件药品的售价为x 元()911x ≤≤时,一年的销售量为485x -万件,并且全年该药品需支付2x 万元的宣传及管理费.(1)求该医药公司一年的利润L (万元)与每件药品的售价x 的函数关系式;(2)当每件药品的售价为多少元时,该公司一年的利润L 最大,并求出L 的最大值.12.已知曲线221:14y C x +=与曲线22:1C y x =-,设点()()000,0P x y y >是曲线1C 上任意一点,直线0014y yx x +=与曲线2C 交于,A B 两点. (1)判断直线0014y yx x +=与曲线1C 的位置关系;(2)以,A B 两点为切点分别作曲线2C 的切线,设两切线的交点为M ,求证:点M 到直线1:220l x y --=与2:220l x y ++=距离的乘积为定值.13.设函数)(x f 的定义域为M ,具有性质P :对任意M x ∈,都有)1(2)2()(+≤++x f x f x f .(1)若M 为实数集R ,是否存在函数),1,0()(R x a a a x f x∈≠>= 具有性质P ,并说明理由;(2)若M 为自然数集N ,并满足对任意M x ∈,都有N x f ∈)(. 记)()1()(x f x f x d -+=.求证:对任意M x ∈,都有)()1(x d x d ≤+.14.设非常数数列{a n }满足βαβα++=++n n n a a a 12,*∈N n ,其中常数βα,均为非零实数,且 0≠+βα.(1)证明:数列{}n a 为等差数列的充要条件是02=+βα;(2)已知25,141121====a a ,,βα,求证:数列{}11-+-n n a a()2,≥∈*n N n 与数列()*∈⎭⎬⎫⎩⎨⎧+N n n 21中没有相同数值的项.中档题7答案1、02、63、54、13a -≤≤5、2996、1747、25 8、2 9、(1)由条件知,当cos 0C =时,不合题意.当cos 0C ≠时,2cos 016sin 24cos 0C C C >⎧⎨∆=-≤⎩,即2cos 02cos 3cos 20C C C >⎧⎨+-≥⎩,1cos 2C ∴≥. C ABC ∆Q 为的内角, 03C π∴<≤,∴角C 的最大值为3π. (2)有(1)知3C π=, 23A B π∴+=,由2a b =,得sin 2sin A B =.2sin 2sin 3B B π⎛⎫∴-= ⎪⎝⎭,即3133cos sin 2sin ,cos 2sin 2222B B B B B +==,即32tan .0,,336B B B ππ⎛⎫=∈∴= ⎪⎝⎭Q . 10、证明(1)过点P PH AD ⊥作交于H .Q 侧面PAD ABCD ⊥底面,PH ABCD ∴⊥平面.PD ∴与平面ABCD 所成的角为45PDH ∠=o .,45.PA PD PAD =∴∠=o Q 则90APD ∠=o..,PA PD CD AD ∴⊥⊥Q 平面PAD ABCD ⊥底面,.,CD PAD PA PAD ∴⊥⊂Q 平面平面.CD PA ∴⊥,PD CD D ⋂=Q PA PDC ∴⊥平面.(2)存在.当Q 为PD 的中点时,//EQ 平面PBC . 证明如下:取PC 的中点F ,连,FQ FB .则1//,.//,2FQ CD FQ CD BE CD =Q 12BE CD =,∴四边形BEQF 为平行四边形.//.BF EQ BF ∴⊂Q 平面,PBC EQ ⊄平面PBC ,//EQ ∴平面PBC .11、(1)该公司一年的利润L (万元)与售价x 的函数关系式为:()48625L x x x =-•--, []9,11x ∈.(2)()48625L x x x =-•--Q ,令[]()4815,4,6,210t x t t L t t --=∈∴=--=484838238223886t t t t ⎛⎫-+≤-•=- ⎪⎝⎭.当且仅当482t t =,即526x =+时,L 取得最大值3886-.则当每件售价为526+元时,该公司一年的利润L 最大,最大值为3886-(万元).12、(1)直线直线0014y y x x +=与曲线1C 相切00221444y yx x y x ⎧+=⎪⎨⎪+=⎩,22004840x x x y ⇒-+-= ()()222220000816416440x y x y ⇒∆=--=+-=.(2)设()()1122,,,A x y B x y002441y y x x y x =-⎧⎨=-⎩,()2000012120044440,1x y x x x y x x x x y y ⎛⎫⇒+-+=⇒+=-=-+ ⎪⎝⎭22:12C y x y x '=-⇒=,切线()()2111:12AM y x x x x --=-,即:()21121y x x x =-+①同理切线()222:21BM y x x x =-+②联立①②得012002242x x x x y y y +⎧==-⎪⎪⎨⎪=--⎪⎩,即00024,2x M y y ⎛⎫--- ⎪⎝⎭, 设点M 到直线12,l l 距离分别为12,d d ,000001241222455x x y y y d ⎛⎫⎛⎫+-+--- ⎪ ⎪⎝⎭⎝⎭==, 000002241222455x x y y y d ⎛⎫⎛⎫-----+ ⎪ ⎪⎝⎭⎝⎭==,20201222001161644555y x d d y y --===.13、证明:(1)因f (x )=a x (a >0且a ≠1),所以a x ≠a x +2,即f (x )≠f (x +2).由题设以及算术平均与几何平均不等式,得f (x )+f (x +2)=a x +a x +2>2a x a x +2=2 a x +1=2 f (x +1), 这与f (x )+f (x +2)≤2f (x +1)矛盾.故不存在函数f (x )=a x (a >0且a ≠1)满足性质P . (2)(ⅰ)由题设对任意x ∈N ,f (x )+f (x +2)≤2f (x +1),所以f (x +2)-f (x +1)≤f (x +1)-f (x ).于是对任意x ∈N ,d (x +1)≤d (x ).14、(1)解:已知数列}{n a ,12n nn a a a αβαβ+++=+.①充分性:若βα2-=,则有12122n nn n n a a a a a βββ+++-+==--,得n n n n a a a a -=-+++112,所以}{n a 为等差数列.②必要性:若}{n a 为非常数等差数列,可令b kn a n +=(k ≠0). 代入12n n n a a a αβαβ+++=+,得[(1)]()(2)k n b kn b k n b αβαβ++++++=+.化简得2k k ααβ=+,即02=+βα.因此,数列{a n }为等差数列的充要条件是α+2β=0. (2)由已知得2111[]5n n n n a a a a +++--=-.又因为21302a a -=≠,可知数列}{1n n a a -+(n ∈N *)为等比数列,所以11121131()()()552n n n n a a a a --+---=-=⋅ (n ∈N *).从而有n ≥2时, 1131()52n n n a a -+--=⋅,2131()52n n n a a ----=⋅.于是由上述两式,得 2111(556|)|n n n a a -+-⋅-=(2n ≥).由指数函数的单调性可知,对于任意n ≥2,| a n +1-a n -1|=65·2)51(-n ≤65·22)51(-=65. 所以,数列11{||}(*,2)n n a a n n +--∈≥N 中项均小于等于65.而对于任意的n ≥1时,n +12≥1+12>65,所以数列{n +12}(n ∈N*)中项均大于65.因此,数列11{||}(*,2)n n a a n n +--∈≥N 与数列{n +12}(n ∈N*)中没有相同数值的项.。
