三角形三条中线、高、角平分线相交于一点的证明
等腰三角形的三线合一”定理应用

等腰三角形的三线合一”定理应用全文共四篇示例,供读者参考第一篇示例:等腰三角形是一种特殊的三角形,其中两条边长度相等。
在等腰三角形中,存在一个重要的定理,即“等腰三角形的三线合一”定理。
这个定理指出,在一个等腰三角形中,等腰线、中位线和高线三条线段会共点于一个点,这个点被称为三角形的垂心。
等腰三角形的三线合一定理在几何学中有着重要的应用。
通过这个定理,我们可以推导出很多三角形的性质,并且可以帮助我们解决一些几何问题。
下面我们将通过几个具体的例子来展示等腰三角形的三线合一定理的应用。
我们来看一个简单的例子。
设等腰三角形ABC中,AB=AC,BD是边AC的中位线,E是边BC的中点,连接DE。
我们要证明线段BD 与CE相交于垂心H。
根据等腰三角形的性质,我们知道角B和角C是等的,所以三角形ABC是等腰的。
根据等腰三角形的三线合一定理,我们知道线段BD、CE和AH相交于一个点H,即三角形ABC的垂心。
接下来,我们可以利用这个性质来解决几何问题。
我们可以通过这个定理来证明等腰三角形的顶角相等,或者计算等腰三角形的面积等等。
第二篇示例:等腰三角形是指具有两条边相等的三角形,其特点是具有对称性和稳定性,是几何学中常见的形状之一。
在等腰三角形中,有一定的定理和性质可以应用,在解决几何问题时起到重要作用。
本文将重点介绍等腰三角形的三线合一定理及其应用。
一、三线合一定理的概念在等腰三角形中,连接等腰三角形顶点与底边中点的直线被称为等腰三角形的三线合一。
三线合一定理指的是在等腰三角形中,三条线段的端点在同一直线上。
这是等腰三角形的一个重要性质,可以通过几何推理和证明加以验证。
假设在等腰三角形ABC中,AB=AC。
连接顶点A与底边BC的中点D,并将直线AD延长至E点。
因为AD是BC的中线,根据中线定理可知AD=DC。
又因为ABC 为等腰三角形,所以AB=AC,由此可得BD=DC。
考虑△ADE和△ACD,根据两边相等、夹角相等、以及对应边角对应相等的条件可以得出△ADE≌△ACD。
三角形三条中线高角平分线相交于一点的证明

三角形三条中线高角平分线相交于一点的证明要证明三角形的三条中线、高、角平分线相交于一点,可以通过构造证明和使用性质的方法进行推导。
首先构造证明:设三角形ABC的顶点为A,底边BC上的中点为D,AB上的中点为E,AC上的中点为F。
我们需要证明三条中线AD、BE、CF相交于一点。
1.连接BF和AE。
由于BF是BC的中线,所以BF平行于AC。
同理,AE平行于BC。
根据平行线性质,可以得出三角形ABF和AEC是全等的。
2.在三角形ABF和AEC中,角BFA等于角EAC(平行线交线与交线的外角性质),角ABF等于角CAE(角相等性质)。
3.根据全等三角形的性质可得,三角形ABF和AEC的角BFA等于角EAC,角ABF等于角CAE。
因此,角BFA等于角ABF,即角BFA是等腰三角形ABF的顶角。
4.同理,根据平行线性质和全等三角形的性质,可以得到三角形ACE 和ABD是全等的,并且角CAE等于角BAD。
因此,角CAE是等腰三角形ACE的顶角。
5.由于等腰三角形的顶角所对的两条边相等,所以可以得出角ABF等于角CAE。
6.角ABF等于角CAE,角BFA等于角ABF,所以角BFA等于角ABF等于角CAE。
7.因此,三角形ABF和AEC的三个角相等。
根据全等三角形的性质,可以得到三角形ABF和AEC是全等的。
8.因此,BF等于EC(全等三角形的对应边相等性质)。
所以,AD等于2BF,AD等于2EC。
9.同理,可以得到BE等于2AF,CF等于2BD。
10.因为AD等于2BF,BE等于2AF,所以AD和BE互相平行(长度相等且共线)。
同理,可以得到BE和CF互相平行,AD和CF互相平行。
11.由于三角形ABC是一个封闭的图形,所以AD、BE、CF相互平行,并且共线。
12.根据平行线的性质,可以得到AD与BE和CF的交点是同一个点,即三角形的三条中线相交于一点。
接下来使用性质来推导:我们可以利用三角形的性质来推导三条中线、高、角平分线相交于一点。
三角形三边中垂线、高线、角平分线、中线必交一点

证明:三角形三边中垂线必交与一点在三角形ABC中作AB和AC的中垂线,交于O点则由中垂线性质可知AO=BO,AO=CO故BO=CO过O作BC的垂线,垂足为D,则由BO=CO与OD=OD可证得Rt三角形ODB全等于Rt 三角形ODC故BD=CD,即OD为BC的中垂线则AB和AC、BC的中垂线都交于O证明:三角形三个内角角平分线必交与一点设三角形ABC,首先两条角平分线(假设是角A和角B的)肯定交于一点,设为D,分别过点D作三边垂线,AB BC AC上的垂足为E F G由角平分线定理,DE=DF,DE=DG所以DF=DG,由逆定理,CD也为角平分线证明:三角形三边高线必交于一点1如图:作AB的高CD和AC的高BE,显然,两高线比交与一点,设为G点,连接AG 延长交BC与F,现在要证明AF⊥BC。
由于∠ADC+∠AEB=180,所以ADGE四点共圆,所以∠DAG=∠DEG同理有DEBC四点共圆,所以有∠BCD=∠DEG所以∠BCG=∠DAG,又∠DGA=∠FGC,所以∠CFG=∠ADG=90度所以AF⊥BC2利用塞瓦定理证明三角形三条高线必交于一点:设三边AB、BC、AC的垂足分别为D、E、F,根据塞瓦定理逆定理,因为(AD:DB)*(BE:EC)*(CF:FA)=[(CD*ctgA)/[(CD*ctgB)]*[(AE*ctgB)/(AE*ctgC)]*[(BF*ctgC)/[(AE*ctgB)]=1,所以三条高CD、AE、BF交于一点。
1.塞瓦定理的逆定理设三边AB、BC、AC的垂足分别为D、E、F,根据塞瓦定理逆定理,因为(AD:DB)*(BE:EC)*(CF:FA)=[(CD*ctgA)/[(CD*ctgB)]*[(AE*ctgB)/(AE*ctgC)]*[(BF*ctgC)/[(AE*ctgB)]=1,所以三条高CD、AE、BF 交于一点。
3.解析法,把三条直线设出来,然后算出三条高线的解析式,证明它们交在一个点证明:三角形三边中线必交于一点三角形ABC的中线BE和CD交点O,连接并延长AO交BC于F,证明:F是BC中点。
三角形的中线、高线、角平分线
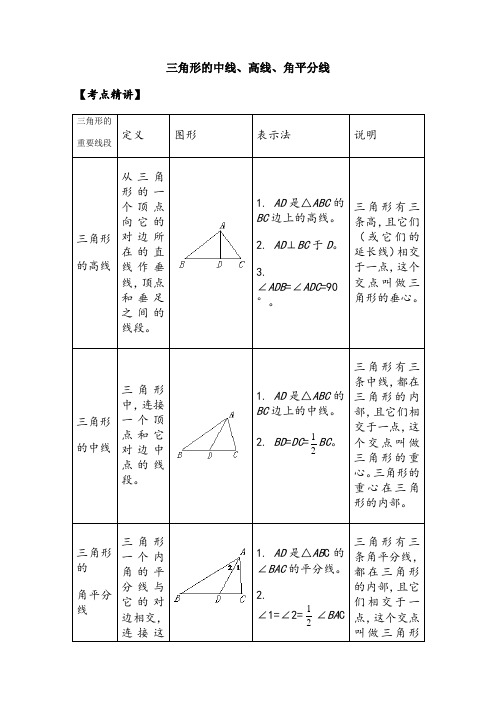
三角形的中线、高线、角平分线【考点精讲】三角形的重要线段定义图形表示法说明三角形的高线从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段。
1. AD是△ABC的BC边上的高线。
2. AD⊥BC于D。
3.∠ADB=∠ADC=90°。
三角形有三条高,且它们(或它们的延长线)相交于一点,这个交点叫做三角形的垂心。
三角形的中线三角形中,连接一个顶点和它对边中点的线段。
1. AD是△ABC的BC边上的中线。
2. BD=DC=12BC。
三角形有三条中线,都在三角形的内部,且它们相交于一点,这个交点叫做三角形的重心。
三角形的重心在三角形的内部。
三角形的角平分线三角形一个内角的平分线与它的对边相交,连接这1. AD是△AB C的∠BAC的平分线。
2.∠1=∠2=12∠BA C三角形有三条角平分线,都在三角形的内部,且它们相交于一点,这个交点叫做三角形个角的顶点与交点之间的线段。
的内心。
三角形的内心在三角形的内部。
【典例精析】例题1 如图,是甲、乙、丙、丁四位同学画的钝角△ABC 的高BE ,其中画对的是_______。
甲 乙 丙 丁思路导航:根据三角形的高是过一个顶点向对边引垂线,顶点与垂足之间的线段是该三角形的高,对各图形作出判断。
答案:丁点评:这是学生在画图时的一个易错点,通过本题理解画高时的两个注意点:一是过哪个点;二是垂直于哪条边。
这道题是过B 点,垂直于AC 边。
例题 2 等腰三角形一腰上的中线把这个三角形的周长分成12cm 和21cm 两部分,则这个等腰三角形的底边长是______。
思路导航:根据等腰三角形的性质和已知条件求出腰长和底边长,然后根据三边关系进行讨论,即可得出结论。
答案:设等腰三角形的腰长是x cm ,底边是y cm 。
根据题意,得:⎪⎪⎩⎪⎪⎨⎧=+=+212122x y x x 或⎪⎪⎩⎪⎪⎨⎧=+=+122212x y x x , 解得:⎩⎨⎧==178y x 或⎩⎨⎧==514y x根据三角形的三边关系,知:8,8,17不能组成三角形,应舍去。
等腰三角形的三线合一定理

等腰三角形的三线合一定理等腰三角形的三线合一定理是几何学中一个重要的定理,它描述了等腰三角形内部的三条特殊线段的关系。
在本文中,我将详细介绍这一定理的原理和应用。
让我们回顾一下等腰三角形的定义。
等腰三角形是一个具有两条边相等的三角形。
在等腰三角形ABC中,假设AB = AC,我们可以发现一些特殊的性质。
根据等腰三角形的三线合一定理,等腰三角形的顶点连线、底边中点连线和底边上的高线三条线段会相交于同一个点。
这个点被称为等腰三角形的顶点角平分线与底边的中点连线上的交点,也是底边上的高线与底边的中点连线上的交点。
这一点在几何学中被称为等腰三角形的顶心。
为了更好地理解这个定理,让我们来具体分析一下。
设等腰三角形ABC的底边为BC,顶点为A。
连接点A和BC的垂直线段为AD,垂足为D。
连接点A和BC的中点为M。
根据等腰三角形的性质,我们可以知道AD是BC的高线,而AM是BC的中线。
根据三线合一定理,我们可以得出以下结论:点D、M和顶点角平分线AN三者共线。
也就是说,这三条线段会相交于同一个点。
这个点被称为等腰三角形ABC的顶心。
等腰三角形的三线合一定理可以用于解决很多几何问题。
例如,我们可以利用这个定理来证明等腰三角形的顶点角平分线与底边的中线垂直。
根据三线合一定理,我们可以知道顶点角平分线AN与底边的中点连线AM相交于D点。
因为AM是BC的中线,所以AD = DM。
根据等腰三角形的性质,AD是BC的高线,所以AD ⊥ BC。
又因为AD = DM,所以DM ⊥ BC。
因此,顶点角平分线AN与底边的中线AM垂直。
另一个常见的应用是利用三线合一定理证明等腰三角形的顶点角平分线与高线相等。
根据等腰三角形的性质,AD是BC的高线,AN 是顶点角的平分线。
根据三线合一定理,AN与AM相交于D点,所以AD = DM。
因此,顶点角平分线与高线相等。
除了上述两个应用外,三线合一定理还可以用于证明等腰三角形的内切圆存在,并求取其半径。
证明三角形的高交于一点 塞瓦定理

证明三角形的高交于一点塞瓦定理全文共四篇示例,供读者参考第一篇示例:塞瓦定理,又被称为三角形的高定理,是三角形几何中一个非常基础而重要的定理。
它描述了三角形的三条高线所交于同一点。
在三角形几何中,高线是从一个角顶上垂直向对边所引出的线段,通常用字母h表示。
三角形的三条高线所交的点被称为垂心。
塞瓦定理的内容如下:对于任意一个三角形ABC,其三条高线AD、BE、CF相交于一点H,即H为三角形ABC的垂心。
在三角形ABC中,设AD是边BC的高线,垂足为D,BE是边AC 的高线,垂足为E,CF是边AB的高线,垂足为F。
根据三角形几何的性质,我们可以证明这三条高线交于同一点H,即垂心。
我们来证明垂心H的存在性。
假设三角形ABC是一个锐角三角形,即三个内角都是锐角。
我们知道,在锐角三角形中,三角形的三条高线不仅相交于同一点,还与三角形的顶点连线构成的垂直平分线相交于同一点,即垂心。
垂心H的存在性是显而易见的。
接下来,我们来证明垂心H的唯一性。
假设三角形ABC有两个垂心H1和H2,分别是两条高线的交点。
我们可以通过反证法来证明H1和H2实际上是同一个点。
假设H1和H2不相同,那么它们连线构成的直线H1H2肯定存在一个中垂线M,且M垂直于H1H2。
但是根据三角形几何的性质,两条高线的交点应该在三角形的顶点处,即H1和H2应该共线,那么连线H1H2上不可能存在中垂线M,从而得出矛盾。
垂心H的唯一性也得到了证明。
我们证明了塞瓦定理的内容:三角形的三条高线所交于同一点,即垂心。
在三角形几何中,塞瓦定理是一个非常基础而重要的定理,对于理解三角形的几何性质具有重要意义。
通过研究和理解塞瓦定理,我们可以更深入地认识三角形的特性,进而应用到具体的三角形问题中,提高解题的能力和水平。
在实际的数学学习中,塞瓦定理也经常被应用到三角形的面积计算中。
通过垂心的概念,我们可以建立垂心到三角形三个顶点的距离关系,从而推导出三角形的面积公式。
三角形三条高线交于一点的六种证明方法

三角形三条高线交于一点的六种证明方法一、欧拉线证明法:欧拉线证明方法是最常见的证明三角形三条高线交于一点的方法之一。
欧拉线又称欧拉三线,由数学家欧拉提出,并以他的名字命名。
该方法通过对三角形的边、高线和重心进行关联,最终证明三条高线交于一点。
欧拉线证明法的步骤如下:在给定的三角形ABC中,连接三条边的中点,分别记为D、E、F。
连接B和C的垂直平分线,交于点O。
则利用垂心定理可得,AO垂直于BC。
同理,连接A和C的垂直平分线与AB的中垂线交于点O',连接A和B的垂直平分线与AC的中垂线交于点O",可得BO'垂直于AC,CO"垂直于AB。
因此,三条高线通过点O、O'、O",即证明了三条高线交于一点。
二、重心证明法:重心证明法是另一种常用的证明方法。
重心是指三角形三条中线交于一点的点,也是三角形内切圆的圆心。
通过证明三角形的三条高线交于重心,可间接证明三条高线交于一点。
重心证明法的步骤如下:在给定的三角形ABC中,连接三个顶点与相对边的中点,分别记为D、E、F。
以点D为圆心,AC的中点D为半径画圆,与AB和BC相交于点G;以点E为圆心,AB的中点E为半径画圆,与AC和BC相交于点H;以点F为圆心,BC的中点F为半径画圆,与AB和AC相交于点I。
根据圆的性质可知,AG、BH和CI与三条高线垂直且交于一点,即证明了三条高线交于一点。
三、垂心证明法:垂心证明法是通过垂心的定义和性质来证明三角形三条高线交于一点的方法。
垂心是指三角形三条高线交于一点的点,也是三角形外接圆的圆心。
垂心证明法的步骤如下:在给定的三角形ABC中,连接任意两个顶点的垂线。
设垂足分别为D、E、F。
连接BD、CE和AF,得到三条高线。
根据垂心定义可知,BD、CE和AF都经过垂心点H。
因此,三条高线交于一点H,即证明了三条高线交于一点。
四、费马点证明法:费马点证明法是通过费马点的定义和性质来证明三角形三条高线交于一点的方法。
证明三角形的三条角平分线相交于一点

证明三角形的三条角平分线相交于一点一、概述三角形是初中数学中的重要概念,而其三条角平分线的相交性质更是三角形的重要性质之一。
那么,我们如何来证明三角形的三条角平分线相交于一点呢?本文将分步骤进行详细的证明。
二、定义和性质在开始证明之前,我们先来了解一下三角形的三条角平分线的概念和性质:1. 三角形的三条角平分线分别是指从三个顶点出发,分别平分三角形的内角的线段。
2. 三角形的三条角平分线相交于一点,这个点叫作三角形的内心。
三、证明证明的主要思路是利用角平分线的性质和几何定理,分别证明三条角平分线相交于一个点,并得出结论。
1. 先证明角平分线相交于一点:证明思路:对于三角形ABC,我们任取一个角A的角平分线AD,再任取一个角B的角平分线BE,我们需要证明这两条角平分线相交于一点。
而根据角平分线的性质,角平分线将角分成两个相等的角,即∠BAD ≌∠CAD,∠BCE ≌ ∠ABE。
我们可以利用两个相等的角组成的角相等的性质,得到∠DAB ≌ ∠EBA。
再根据角的性质,我们知道如果两个角分别相等于一个角,则这两个角也相等,即∠DAB ≌ ∠EBA ≌ 90°,所以根据角的性质我们知道∠DAB=∠EBA=90°。
因此∠DAB和∠EBA互为补角。
2. 再证明三条角平分线相交于一点:证明思路:在了解了角平分线相交于一点的性质后,我们再进行三条角平分线相交于一点的证明。
对于三角形ABC,我们有三个角A的角平分线AD、B的角平分线BE和C的角平分线CF,我们需要证明这三条角平分线相交于一点。
根据我们在前面证明过的结论,我们知道∠DAB ≌ ∠EBA,∠BAD ≌ ∠CAE,这意味着∠DAB和∠EBA互为补角、∠BAD 和∠CAE也互为补角。
而根据数学中的一个常识,如果两个角互为补角,那它们的角平分线将相交于一点。
因此我们可以得出结论:三角形的三条角平分线相交于一点,这个点叫作三角形的内心。
四、结论通过上述证明过程,我们成功地证明了三角形的三条角平分线相交于一点的几何性质,并得出结论:三角形的三条角平分线相交于一点,这个点称为三角形的内心。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
过点O 做ΔABC 三边的垂线OM 、OR 、ON
∵BN 、CM 是ΔABC 的角平分线
∴OM=OR=ON
∴点O 在∠BAC 的角平分线上
∴三角形的三条角平分线相交于一点
证明三条高线重合
求证:P 、Q 、O 三点重合
证明:如图,∵BE ⊥AC ,CF ⊥AB
∴∠AEB = ∠AFC = 90°
又∵∠BAE = ∠CAF
∴△ABE ∽ △ACF
∴AF
AE AC AB = 即AB ·AF = AC ·AE
又∵AD ⊥BC
∴△AEQ ∽ △ADC ,△AFP ∽ △ADB
∴AC AQ AD AE =,AB
AP AD AF = 即AC ·AE = AD ·AQ ,AB ·AF = AD ·AP
∵AB ·AF = AC ·AE ,AC ·AE = AD ·AQ ,AB ·AF = AD ·AP
∴AD ·AQ = AD ·AP
∴AQ = AP
∵点Q 、P 都在线段AD 上
∴点Q 、P 重合
∴AD 与BE 、AD 与CF 交于同一点
∵两条不平行的直线只有一个交点
∴BE 与CF 也交于此点
∴点Q 、P 、O 重合。
已知:△ABC的两条中线AD、CF相交于点O,连接并延长BO,交AC于点E。
求证:AE=CE .
证明:如图,延长OE到点G,使OG=OB。
∵OG=OB
∴点O是BG的中点
又∵点D是BC的中点
∴OD是△BGC的一条中位线
∴AD‖CG(三角形的中位线平行于第三边,且等于第三边的一半)
∵点O是BG的中点,点F是AB的中点
∴OF是△BGA的一条中位线
∴CF‖AG ∵AD‖CG,CF‖AG
∴四边形AOCG是平行四边形
∴AC、OG互相平分
∴AE=CE 命题得证。
