预备知识1线性模型
线性模型(1)——方差分析模型

在方差分析中,我们初步介绍了线性模型的思想,实际上,线性模型只是方差分析的模型化,其统计检验仍然是依照方差分解原理进行F检验。
线性模型作为一种非常重要的数学模型,通常可以分为方差分析模型、协方差分析模型、线性回归模型、方差分量模型等,根据表现形式又可以分为一般线性模型、广义线性模型、一般线性混合模型、广义线性混合模型。
下面我们就根据分析目的来介绍线性模型一、方差分析模型:使用线性模型进行方差分析的时候涉及一些基本概念:===============================================(1)因素与水平因素也称为因子,在实际分析中,因素就是会对结果产生影响的变量,通常因素都是分类变量,如果用自变量和因变量来解释,那么因素就是自变量,结果就是因变量。
一个因素下面往往具有不同的指标,称为水平,表现在分类变量上就是不同类别或取值范围,例如性别因素有男、女两个水平,有时取值范围是人为划分的。
(2)单元因素各水平之间的组合,表现在列联表中就是某个单元格,有些实验设计如拉丁方设计,单元格为空或无。
(3)元素指用于测量因变量值的最小单位,其实也就是具体的测量值。
根据具体的实验设计,列联表的一个单元格内可以有一个或多个元素,也可能没有元素。
(4)均衡如果一个实验设计中任一因素的各水平在所有单元格中出现的次数相同,且每个单元格内的元素数也相同,那么该实验就是均衡的。
不均衡的实验设计在分析时较为复杂,需要对方差分析模型作特别的设置才行。
(5)协变量有时,我们在分析某些因素的影响时,需要排除某个因素对因变量的影响,这个被排除的因素被称为协变量,(6)交互作用如果一个因素的效应大小在另一个因素的不同水平下表现的明显不同,则说明这两个因素之间存在交互作用。
交互作用是多因素分析时必须要做的,这样分析的结果才会全面。
(7)固定因素和随机因素是因素的两个种类,固定因素是指该因素的所有水平,在本次分析中全部出现,从分析结果就可以获知全部水平的情况。
对数线性模型(高教知识)

全面分析
13
比数比的不变性,不随1)总样本量2)行边缘分布3) 列边缘分布的变化而变化。所以,只要关心比数比的估 值,那么适用于简单随机样本的最大似然估计就可以被 直接应用到分层样本中了。
全面分析
14
3、与逻辑变换有关的: 对数线性模型的出现
令R表示行,C表示列,fij表示第i行第j列的观测频次。 那么期望频次Fij被设定为一个乘积的函数
且,对于一个多阶多项效应的复杂模型,采用整体检验 方式就意味着逐项效应的剔除测试,这样分析过程效率 太低。
全面分析
33
对数线性模型的统计检验
2、分层效应检验
当研究中涉及的因素较多时,不仅主效应项会增加,交 互效应项增加得更快。例如,四个因素的模型,主效应 4个,二阶交互效应6项,三阶交互效应4项,四阶交互 效应1项。如此,逐项检验筛选重要目标就太繁琐了。
全面分析
25
2、统计量
似然卡方比,根据相关计算,看原假设是否成立。 贝叶斯信息标准,不同模型而言越小的BIC越好。
全面分析
26
3、对数线性模型的统计 检验
四种主要检验: 1、对于假设模型的整体检验; 2、分层效应的检验; 3、单项效应的检验; 4、单个参数估计的检验。
全面分析
27Biblioteka 对数线性模型的统计检验Fij=ƮƮRiƮCjƮRCij
Ʈ代表概率里面的总概率值1,ƮR 和ƮC分别代表R和C的边 缘效应,ƮRC代表R与C的二维交互效应,而交互效应实 质上测量的就是R与C之间的比数比,当ƮRCij=1的时候就 是我们熟悉的独立模型。
相乘形式的不好计算,我们将其取对数
全面分析
15
上两式的数学变换使各种效应项相乘的关系被转换成相 加的关系,使各项效应独立化了。
线性模型总结

数学模型可以看做是人们对复杂的现实问题进行简化描述的数学表达式,由于统计学来源于数学,因此在统计分析中,也普遍使用模型来分析问题。
数学中模型的分类非常多,但统计学中最常用的模型是线性模型和非线性模型。
在此,首先明确几个概念1.线性关系线性关系是指自变量和因变量之间成比例的关系,即增量之间有固定的比例,比如X增加了m,那么Y就增加km,这里隐含着两个要点:(1)自变量与因变量是一次函数关系(2)函数图像呈一条过原点的直线,注意是要过原点2.非线性关系与线性关系相对应,非线性关系是指自变量和因变量之间没有固定的比例关系,二者之间不是一次函数关系,函数图像为曲线3.直线关系我们在做散点图考察变量关系时,发现呈直线趋势的话,就称其为具有线性关系,实际上这是不严谨的,因为线性关系特指函数图像为过原点的直线,当图像不过原点时,虽然也为直线,则不能称为线性关系,而应该称为直线关系。
只不过在统计分析中,大部分模型都有常数项,也就是截距,使得函数图不过原点,因此我们才会将二者等同起来。
4.线性模型线性模型中的“线性”有两重含义,一个是自变量的线性,即自变量与因变量是一次函数关系,另一个是参数的线性,即因变量与各模型参数是一次函数关系。
其中第二点最为重要,当自变量不满足条件时,我们可以通过变量变换使其满足条件,而参数不满足线性条件时,往往不能通过变量变换解决(也有例外),因此我们将参数为线性的模型称为线性模型5.非线性模型由上可知,因变量与各模型参数是非线性关系的模型为非线性模型。
根据以上概念,我们可以做出如下划分在统计分析中,一般线性模型是应用最广泛同时也是最重要的是一类模型,它通常包括线性回归模型、方差分析模型、协方差分析模型、方差分量模型等,而广义线性模型本质上还是属于非线性模型,但是同时有一些其他非线性模型所不具备的性质,最大的区别是一般非线性模型没有明确的随机误差分布,而广义线性模型的随机误差分布是明确的,如二项分布、Poisson分布、负二项分布等,而当其为正态分布时,广义线性模型和一般线性模型是等价的。
【线性回归】线性回归模型中几个参数的解释

【线性回归】线性回归模型中⼏个参数的解释【线性回归】线性回归模型中⼏个参数的解释R ⽅1. 决定系数/拟合优度类似于⼀元线性回归,构造决定系数。
称为y 关于⾃变量的样本复相关系数。
其中,,有SST=SSR+SSE总离差平⽅和记为SST ,回归平⽅和记为SSR ,残差平⽅和为SSE 。
由公式可见,SSR 是由回归⽅程确定的,即是可以⽤⾃变量x 进⾏解释的波动,⽽SSE 为x 之外的未加控制的因素引起的波动。
这样,总离差平⽅和SST 中能够由⽅程解释的部分为SSR ,不能解释的部分为SSE 。
1. 意义意味着回归⽅程中能被解释的误差占总误差的⽐例。
⼀般来说越⼤,拟合效果越好,⼀般认为超过0.8的模型拟合优度⽐较⾼。
需要注意的是当样本量⼩时,很⼤(例如0.9)也不能肯定⾃变量与因变量之间关系就是线性的。
随着⾃变量的增多,必定会越来越接近于1,但这会导致模型的稳定性变差,即模型⽤来预测训练集之外的数据时,预测波动将会⾮常⼤,这个时候就会对作调整,调整R ⽅可以消除⾃变量增加造成的假象。
F 检验0、预备知识(1)假设检验为了判断与检测X 是否具备对Y 的预测能⼒,⼀般可以通过相关系数、图形等⽅法进⾏衡量,但这只是直观的判断⽅法。
通过对回归参数做假设检验可以为我们提供更严格的数量化分析⽅法。
(2)全模型与简化模型我们称之为全模型(full Model,FM )通过对某些回归系数进⾏假设,使其取指定的值,把这些指定的值带⼊全模型中,得到的模型称为简化模型(reduced model,RM )。
常⽤的简化⽅法将在之后介绍。
1、F 检验检验是线性模型的假设检验中最常⽤的⼀种检验,通过值的⼤⼩可以判断提出的假设是否合理,即是否接受简化模型。
1. 为检验我们的假设是否合理,即评估简化模型相对全模型拟合效果是否⼀样好,需要先建⽴对两个模型拟合效果的评价⽅法。
这⾥我们通过计算模型的残差平⽅和()来衡量模型拟合数据时损失的信息量,也表⽰模型的拟合效果。
数模建模 全部内容讲解 线性非线性

模型假设:
1、椅子四条腿一样长,椅脚与地面接触 、椅子四条腿一样长, 处可视为一个点, 四脚的连线呈正方形。 处可视为一个点 , 四脚的连线呈正方形 。 2、地面高度是连续变化的,沿任何方向 、地面高度是连续变化的, 都不会出现间断( 都不会出现间断 ( 没有象台阶那样的情 即地面可视为数学上的连续曲面。 况 ) , 即地面可视为数学上的连续曲面 。 3、对于椅脚的间距和椅腿的长度而言, 、 对于椅脚的间距和椅腿的长度而言, 地面是相对平坦的, 地面是相对平坦的 , 使椅子在任何位置 至少有三只脚同时着地。 至少有三只脚同时着地。
引 言
本章主要讨论建立数学模型的意义、 本章主要讨论建立数学模型的意义、 方法和步骤, 方法和步骤,给读者以建立数学模型 初步的了解。 初步的了解。
一、从现实对象到数学模型
原型和模型 原型( 原型 ( Prototype) 指人们在现实世界里关 ) 研究或者从事生产、管理的实际对象。 心、研究或者从事生产、管理的实际对象。 模型( 模型(Model)指为了某个特定目的将原型 ) 的某一部分信息简缩、 的某一部分信息简缩、提练而构造的原型替 代物。 代物。 注意:为了某种目的构造模型, 注意:为了某种目的构造模型,模型不是原 型原封不动的复制品, 型原封不动的复制品,原型有各个方面和各 种层次的特征, 种层次的特征,而模型只要求反映与某种目 的有关的那些方面和层次。 的有关的那些方面和层次。
数学国际会议, 年起, 数学国际会议,1983年起,会议录由 年起 Harwood出版 出版 竞赛
国外数学建模情况
2、科研 、
会议 1977数学和计算机建模国际会议 数学和计算机建模国际会议 期刊
《Mathematical and computer Modeling》年刊 》 《Applied Mathematical Modeling》 》 SIAM Review、SIAM News 、 《J. of Mathematical Modeling for Teacher》 》
线性回归模型第一章
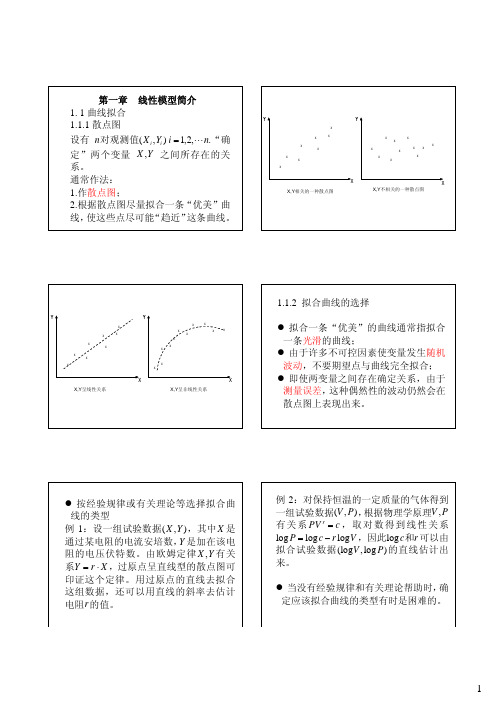
1.3.3 最小二乘法(least squared method) 考虑如下线性模型: Y = Xβ + e, ⎧ ⎨ 2 ⎩ Ee = 0, Cov (e) = σ I n . 参数的真 估计未知系数β 的基本出发点是: 值应该使模型误差 e = Y − Xβ 达到最小。令 2 2 Q ( β ) = e = Y − Xβ 来度量模型误差的大 小,则 β 的估计应最小化Q ( β ) ,即 2 ˆ β = Arg min Y − Xβ 。
一部分由 X 1 , L X p 的影响所致,这一部分可 以表为 X 1 , L X p 的函数形式 f ( X 1 , L X p ) ; 另 一部分则由其他众多未加考虑的因素,包 括随机因素的影响所致,这部分视为一种 随机误差,记为 e 。
2
在实际问题中,理论回归函数一般总是 未知的,统计回归分析的任务在于根据 X 1 ,L X p 和 Y 的观测值去估计回归函数及讨 论与此有关的一些统计推断问题。所用的方 法在很大程度上取决于对模型中回归函数 f 及随机误差 e 所作的假定。若对回归函数 f 的数学形式并无特殊假定,称为非参数回 归(non-parametric regression); 若假定 f 的形 式已知,只是其中若干参数未知,这种情况 称为参数回归(parametric regression)。
第一章 线性模型简介 1. 1 曲线拟合 1.1.1 散点图 设有 n 对观测值( X i , Yi ) i = 1,2,L n.“确 定”两个变量 X , Y 之间所存在的关 系。 通常作法: 1.作散点图; 2.根据散点图尽量拟合一条“优美”曲 线, 使这些点尽可能 “趋近” 这条曲线。
Y
X X X X X X X
一般说来 在参数回归中, f 关于未 若 知 参 数 是 线 性 的 , 称 为 线 性 回 归 (linear regression);若关于参数是非线性的,称为 非线性回归(nonlinear regression)。 对于随机误差 e ,已经假定其均值 Ee = 0,其方差Var (e) = σ 2 是模型的一重要 参数。由于 2 E (Y − f ( X 1 ,L X p ) ) = Ee 2 = σ 2 , 因此σ 2 越小,用回归函数 f ( X 1 ,L X p ) 逼近
线性回归与多项式回归以及梯度下降

二.什么是线性回归?
在N维空间中找一个形式像直线方程一样的函数来拟合数据。
举例:可以通过右侧的直线方程来预测房价。
三.什么是损失函数?
我们需要有一个评判的标准,来评判哪条直线才是最好的。 我们把所有实际房价和预测出来的房价的差距(距离)算出来然后做个加 和,我们就能量化出现在我们预测的房价和实际房价之间的误差。
Tensor(张量) 的使用方法:
(1) Tensor的创建和使用
import torch #定义一个Tensor矩阵 a = torch.Tensor([[1, 2], [3, 4],[5, 6], [7, 8]]) print(a) print('{}'.format(a)) #改变元素值 Print(a[1, 1]) a[1, 1] = 3 Print(a[1, 1]) #转换为Numpy f = a.numpy() print(f) #转换为Tensor g = torch.from_numpy(f) print(g)
(2)改变torch.后面函数名称,生成不同类型的数据
import torch #定义一个Tensor矩阵 a = torch.Tensor([[1, 2], [3, 4],[5, 6], [7, 8]]) print('{}'.format(a)) b = torch.zeros((4, 2)) print(b) c = torch.IntTensor([[1, 2], [3, 4],[5, 6], [7, 8]]) print(c) d = torch.LongTensor([[1, 2], [3, 4],[5, 6], [7, 8]]) print(d) e = torch.DoubleTensor([[1, 2], [3, 4],[5, 6], [7, 8]]) print(e)
线性分类模型(一):线性判别模型分析

线性分类模型(一):线性判别模型分析前言前几篇文章介绍了线性回归算法,线性分类模型分为判别式模型和生成式模型,本文首先简单复习了与算法相关的数学基础知识,然后分析各线性判别式分类算法,如最小平方法,Fisher线性判别法和感知器法,最后总结全文。
目录1、相关的数学知识回顾2、判别式模型和生成性模型3、最小平方法4、Fisher线性判别函数5、感知器算法6、总结相关数学知识回顾1、直线方程和平面方程拓展到分类思想:直线l为分类决策方程,坐标点落在直线l上方时,则分类为C1;坐标点落在直线l下方时,则分类为C2(如下图)。
平面方程类似,在这里不展开。
2、点到直线和点到平面的距离点到直线的距离:点到平面的距离拓展到分类思想:平面方程为决策方程,正确分类的情况下,当点P到决策方程的距离越大,则分类模型越好;错误分类的情况下,点P到决策方程的距离作为损失函数,损失函数最小化过程即是模型参数最优化过程。
3、向量内积的数学意义几何意义:向量A与向量B的内积等于向量A在向量B的投影与向量B的乘积,当向量B是单位向量时,则等于向量A在单位向量方向的投影,单位向量类似于基函数或者可以理解成坐标轴,即向量A在向量B的投影可理解成向量A在向量B方向的坐标,如下图,B'是B 在OA坐标轴方向的投影。
拓展到分类思想:C1与C2属于不同的类,给定一条决策性直线l,当C1与C2在直线L2的投影间距越大,则分类效果越好。
增加不同类间的距离可以作为模型参数优化的方向。
如下图,C1和C2的在直线L2的投影距离|C1'C2'|大于|C1'C2'|,因此决策方程直线L2优于直线L1.4、梯度下降法函数f(x0,x1,...,xn)在梯度方向是函数值变化(增加或减少)最快的方向(本文只给出结论,后续文章会有详细的说明)。
拓展到分类思想:损失函数最小化过程即是模型参数最优化过程,损失函数最小化可通过梯度下降法来实现,当迭代到一定程度,损失函数收敛,则迭代结束,参数w即是要求的最优参数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ESSA E
2 i i.. ...
i j k
bm i2 a 12
i
ESSB am
2 j
b
12
j
ESSe E
ijk
ij.
2
ab
m 1
2
i j k
ESST E
2
i j ij ijk ...
i j k
bm i2 am 2j m
i2j abm 12
如果
这里 为已知协方差矩阵
估计量
方差
预备知识2:固定效应模型
可加效应模型
yijk i j ijk
i
1,, a, ijk i.i.d
j 1,, N 0, 2
b,
k
1,,
m
i 0,
j 0
i
j
方差分析( analysis of variance, ANOVA)
假设
H01 : 1 2 a 0 H02 : 1 2 b 0 偏差平方和的分解
预备知识1:线性模型
二元回归模型
矩阵形式
最小二乘估计(ordinary least squares,OLS)
估计量
估计量方差
其中
总平方和
回归平方和 残差平方和
为f预测值
i
判定系数(coefficient of determination)R
squared
调整R squared
广义最小二乘(generalized leastsquares,GLS)
2
EMSAB
E
a
SSAB
1b 1
m
2
2
am2 m2
EMSe
E
SSe
abm
1
2
F1
MSA MSAB
F2
MSB MSAB
F3
MSAB MSe
预备知识3:三大检验
似然比检验LR Wald检验 拉格朗日乘子检验LM
三大检验的引入
(1)模型是非线性的 (2)约束是非线性的 (3)扰动项分布是非正态的,
极大似然估计(ML)
(一)极大似然原理
假设对于给定样本 Y, X, 其联合概率分布存
在 f Y, X;
。将该联合概率密度函数视为未知参数
的函数,则 f Y, X; 称为似然函数(Likelihood Function), 即观
在这些情况下,F检验不再适用,通常需要 采用LR、Wald、LM其中之一来检验约束条 件是否成立。
三大检验方法共同点
这三个检验方法都是渐进等价的,他们所 用统计量的小样本分布是未知的,但大样 本下都渐进服从自由度为约束个数的卡方 分布。
三大检验方法是三种基于极大似然法的大 样本检验方法。
根据模型的特点采用不同的检验方法。 模型视为给定参数的数据生成过程的集合。
i j
b i2 a 12
i
同理ESSB a 2j b 12
j
ESST E
2 i j ij ..
i j
b i2 a 2j ab 12
i
j
ESSe a 1b 12
EMSA
E SSA a 1
b
i2
i
a 1
2
EMSB
E SSB b 1
a
2 j
j
b 1
检验统计量
j
ij
yi.. i j b j b
i i. i..
y... .. ...
i..
ESSA E
2
i i. .. i.. ...
i j k
bma
12
ma
1
2
a
12
同理 ESSB amb 12 mb 1 2 b 12
H01 : 2 0 H02 : 2 0 H03 : 2 0
偏差平方和的分解
SST
2
yijk y...
i jk
2
2
2
yi.. y...
y.j. y...
yijk yij.
i jk
i jk
i jk
2
yij. yi.. y.j. y...
i jk
SSA SSB SSe SSAB
2
EMSe
E
a
SSe
1b
1
2
F1
MSA MSe
F2
MSB MSe
交互效应模型
yij k i j ij ij k
i 1,, a, j 1,, b, k 1,, m
ij k i.i.d N 0, 2
i 0,
j 0
i
j
ij 0, j 1,, b
i
ij 0, i 1,a
j
方差分析
假设
H01 : 1 2 a 0 H02 : 1 2 b 0
H03 : ij 0 对一切i 1,, a j 1,, b
偏差平方和的分解
SST
yijk y...
i jk
2
2
yi.. y...
y.j. y...
i jk
i jk
2
2
yijk yij.
yij. yi.. y.j. y...
i jk
i jk
SSA SSB SSe SSAB
检验统计量
yi.. i i.. y. j. j . j. y... ...
yij. i j ij ij.
随机效应模型
yijk i j ij ijk i 1,, a, j 1,, b, k 1,, m
ijk i.i.d N 0, 2
i
i.i.d
N
0,
2
j i.i.d N 0, 2
ij
i.i.d
N
0,
2
诸ijk、诸i、诸j、诸ij 相互独立
方差分析
假设
i
j
ij
ESSAB m i2j a 1b 12
ij
EMSA
E SSA a 1
bm i2
i
a 1
2
EMSB
E
SSB b 1
am 2j
j
b 1
2
EMSAB
E
a
SSAB
1b
1
m i2j
j
a 1b 1
2
EMSe
E
SSe
abm
1
2
FA
MSA MSe
FB
MSB MSe
FAB
MSAB MSe
ESSe E
ijk
ij.
2
ab
m 1 2
i j k
ESST E
i
j
ij
..
ijk
...
2
i j k
bma
12
amb
12
mab
1
2
abm
12
ESSAB
a
1b
12
ma
1b
1
2
EMSA
E SSA Biblioteka a 12m2
bm2
EMSB
E
SSB b 1
SST
2
yij y..
ij
2
2
2
yi. y..
y.j y..
yij yi. y.j y..
ij
ij
ij
SSA SSB SSe 检验统计量
yi. i i. y.j j .j y.. ..
ESSA E
2 i i. ..
