正四面体中的常见公式及应用(例题)
专题02 正四面体模型(解析版)

专题02 正四面体模型(解析版)一、解题技巧归纳总结1.正四面体如图,设正四面体ABCD的的棱长为a,将其放入正方体中,则正方体的棱长为22a,显然正四面体和正方体有相同的外接球.正方体外接球半径为236224R a a=⋅=,即正四面体外接球半径为64R a=.二、典型例题例1.棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图,则图中三角形(正四面体的截面)的面积是().A.22B.32C.2D.3【解析】如图球的截面图就是正四面体中的∆ABD,已知正四面体棱长为2,所以=3AD=1AC,所以=2CD2故选:C.例2.正四面体的棱长为1,则其外接球的表面积为 . 【解析】解析:依题意,正四面体的外接球半径64R =,其表面积为23=42S R ππ=,故答案为32π. 三、配套练习1.棱长为1的正四面体的外接球的半径为( ) A .64B .34C .1D .33【解析】已知正四面体A BCD -的棱长为1,过B 作BE CD ⊥,交CD 于E ,A 作AF ⊥平面BCD ,交BE 于F ,连结AE ,设球心为O ,则O 在AF 上,连结BO ,22131()22BE AE ==-=,2333BF BE ==,1336EF BE ==, 22336()()263AF =-=, 设球半径为R ,则BO AO R ==, 22236()()33R R ∴=+-, 解得64R =. 故选:A .2.棱长为a的正四面体的外接球和内切球的体积比是()A.9:1B.4:1C.27:1D.8:1【解析】把棱长为a的正四面体镶嵌在棱长为x的正方体内,∴外接球和内切球的球心重合,为正方体的中心O,∴外接球的球半径为:23322x x=,22113(2)634x x h=⨯⨯⨯,33xh=,内切球的半径为:3333 2236x x x xh-=-=,∴外接球和内切球的半径之比为:33:3:1 26x x=,∴正四面体的外球和内切球的体积比是27:1,故选:C.3.如图所示,在正四面体A BCD-中,E是棱AD的中点,P是棱AC上一动点,BP PE+的最小值为7,则该正四面体的外接球的体积是()A6πB.6πC 36D.32π【解析】将侧面ABC∆和ACD∆展成平面图形,如图所示:设正四面体的棱长为a则BP PE+的最小值为22172cos120742aBE a a a=+-︒==,2a∴=.在正四面体A BCD -的边长为2, 外接球的半径6642R a ==外接球的体积3463V R ππ==.故选:A .4.表面积为83( ) A .43πB .12πC .8πD .6π【解析】表面积为8322将正四面体补成一个正方体,则正方体的棱长为2,正方体的对角线长为3 正四面体的外接球的直径为正方体的对角线长,∴外接球的表面积的值为24(3)12ππ=.故选:B .5.一个正四面体的棱长为2,则这个正四面体的外接球的表面积为( ) A .6πB .8πC 6πD .11π【解析】26, 正四面体的外接球的直径为正方体的对角线长,∴外接球的表面积的值为264()62ππ=. 故选:A .6.在棱长为2的正四面体的外接球中,相互垂直的两个平面分别截球面得两个圆.若两圆的圆心距为2,则两圆的公共弦长是( )A .34B .34C .1D .12【解析】正四面体扩展为正方体,它们的外接球是同一个球,正方体的对角线长就是球的直径,正方体的棱长为:1;对角线长为:3, 所以球的半径为:32R =, 设相互垂直两圆的圆心分别为1O 、2O ,球心为O ,公共弦为AB ,其中点为E , 则12OO EO 为矩形,于是对角线12O O OE =, 而222232()22OE OA AE AE =-=-=, 12AE ∴=,则1AB =; 故选:C .7.如图所示,正四面体ABCD 中,E 是棱AD 的中点,P 是棱AC 上一动点,BP PE +的最小值为14,则该正四面体的外接球表面积是( )A .12πB .32πC .8πD .24π【解析】将三角形ABC 与三角形ACD 展成平面,BP PE +的最小值,即为BE 两点之间连线的距离,则14BE =设2AB a =,则120BAD ∠=︒,由余弦定理221414222a a a a+--=,解得2a =, 则正四面体棱长为22,因为正四面体的外接球半径是棱长的64倍, 所以,设外接球半径为R ,则62234R ==, 则表面积244312S R πππ===. 故选:A .8.已知正四面体的棱长为4,则此四面体的外接球的表面积是( ) A .24πB .18πC .12πD .6π【解析】将正四面体补成一个正方体,则正方体的棱长为26 6,∴外接球的表面积的值为24(6)24ππ=.故选:A .9.一个棱长为6的正四面体内部有一个任意旋转的正方体,当正方体的棱长取得最大值时,正方体的外接球的表面积是( ) A .4πB .6πC .12πD .24π【解析】正方体可以在正四面体纸盒内任意转动,∴正方体在正四面体的内切球中,∴正方体棱长最大时,正方体的对角线是内切球的直径,点O 为内切球的圆心,连接PO 并延长交底面ABC 与点D , 点D 是底面三角形ABC 的中心,PD ∴⊥底面ABC ,OD ∴为内切球的半径,连接BO ,则BO OP =,在Rt BDP ∆中,236233BD ==2226PD PB BD -在Rt BDO ∆中,2222222()OD BD OB BD OP BD OP OD =+=+=+-,代入数据得62OD =,令正方体棱长为a ,则236a =,解得2a =, ∴正方体棱长的最大值为2,此时正方体的外接球半径:36222r =⨯=. ∴当正方体的棱长取得最大值时,正方体的外接球的表面积是:22644()62S r πππ==⨯=. 故选:B .10.如图,在棱长为1的正四面体ABCD 中,G 为BCD ∆的重心,M 是线段AG 的中点,则三棱锥M BCD -的外接球的表面积为( )A .πB .32πC 6D 6 【解析】连接BG ,四面体ABCD 中,由G 为BCD ∆的重心, 可得AG ⊥面BCD ,M 是线段AG 的中点,3BG ,226AG AB BG =-M 为线段AG 的中点,6MG ∴=设三棱锥M BCD -外接球的半径为R ,则23(R =226)(R +, 6R ∴=, ∴三棱锥M BCD -外接球的表面积为2342R ππ=. 故选:B .11.正四面体(四个面均为正三角形的四面体)的外接球和内切球上各有一个动点P 、Q ,若线段PQ 长463,则这个四面体的棱长为 4 . 【解析】设这个四面体的棱长为a , 则它的外接球与内切球的球心重合,且半径64R a =外,612r a =内, 依题意得66464123a a +=, 4a ∴=.故答案为:4.12.已知正四面体ABCD 的棱长为1,M 为棱CD 的中点,则二面角M AB D --的余弦值为 63;平面MAB 截此正四面体的外接球所得截面的面积为 .【解析】如图,M 为棱CD 的中点,AM CD ∴⊥,BM CD ⊥,又AMBM M =,CD ∴⊥平面AMB ,则AMB ∠为二面角A CD B --的平面角,由对称性,可知二面角C AB D --的平面角等于AMB ∠. 由正四面体ABCD 的棱长为1,可得3AM BM ==则2231()()1622cos()23AMB -∠==平面AMB 平分二面角C AB D --,∴二面角M AB D --的余弦值16cos()2AMB =∠;设BCD ∆的外心为G ,连接AG ,求得233BG BM ==,22361()3AG =-= 设正四面体ABCD 的外接球的半径为R ,则22263()(R R -+=,解得6R =平面MAB 过正四面体ABCD 的外接球的球心,∴平面MAB 截此正四面体的外接球所得截面的面积为263(8ππ⨯=.故答案为:63;38π. 13.已知某正四面体的内切球体积是1,则该正四面体的外接球的体积是 27 . 【解析】正四面体的外接球和内切球的半径之比为3:1,∴正四面体的外接球和内切球的体积比是27:1,正四面体的内切球体积是1,∴该正四面体的外接球的体积是27.故答案为:27.14.一个正四面体的展开图是边长为22的正三角形,则该四面体的外接球的表面积为 3π . 【解析】如图,一个正四面体的展开图是边长为2∴2,设底面三角形的中心为G ,则22162332AG AD ==-=, 正四面体的高2323PG =-. 再设正四面体外接球的球心为O ,连接OA , 则22263(()R R =+,解得3R =. ∴该四面体的外接球的表面积为234(3ππ⨯=. 故答案为:3π.15.如图所示,正四面体ABCD 中,E 是棱AD 的中点,P 是棱AC 上一动点,BP PE +的最小值为14,则该正四面体的外接球的体积是 3π .【解析】将侧面ABC ∆和ACD ∆展成平面图形,如图所示: 设正四面体的棱长为a ,则BP PE +的最小值为2272cos12014422a a BE a a a =+-︒==, 22a ∴=.在棱锥A BCD -中,设底面三角形BCD 的中心为M ,外接球的球心为O ,F 为BC 的中点,则362DF a ==, 22633DM DF ∴==,22433AM AD DM =-=. 设外接球的半径OA OD r ==,则433OM r =-, 在Rt OMD ∆中,由勾股定理可得:2224326()()33r r =-+, 解得:3r =.∴外接球的体积为34433r ππ=.故答案为:43π.。
正四面体表面积与棱长的关系

正四面体表面积与棱长的关系
正四面体是几何中的一种特殊的多面体,由四个三角形平行排列组成。
它的平面构成形状可以想象成一个立方体,它的棱长与表面积有着特殊的关系,是几何学中最重要的基础知识。
首先,我们来观察正四面体的形状。
它的形状可以用以下公式来描述:a×a×a,其中a为正四面体棱长。
从这个公式中可以看出,正四面体棱长和它的体积有关系。
其次,我们来要研究正四面体表面积和棱长的关系。
正四面体的表面积计算的公式如下:S=6a,其中S为正四面体的表面积,而a为棱长。
从公式中可以看出棱长和表面积有着线性关系,也就是说,当正四面体的棱长增加一倍时,它的表面积也将增加六倍。
最后,要特别提醒一点就是,正四面体表面积和棱长的关系受到了一般几何公式的限制,因此在使用时要特别注意。
总而言之,正四面体的表面积和棱长有着特殊的关系,是几何学中重要的基础知识。
要想掌握正四面体的表面积和棱长的关系,就必须先要掌握关于几何的基本公式,然后深入学习一些关于正四面体表面积与棱长的特殊公式。
正四面体表面积与棱长的关系关系决定了几何中正四面体在多种领域的运用,但在使用时也要特别注意以免出现问题,只有掌握这一关系才能实现理论与实际的有效结合。
- 1 -。
正四面体二面角8种求法(学生版)
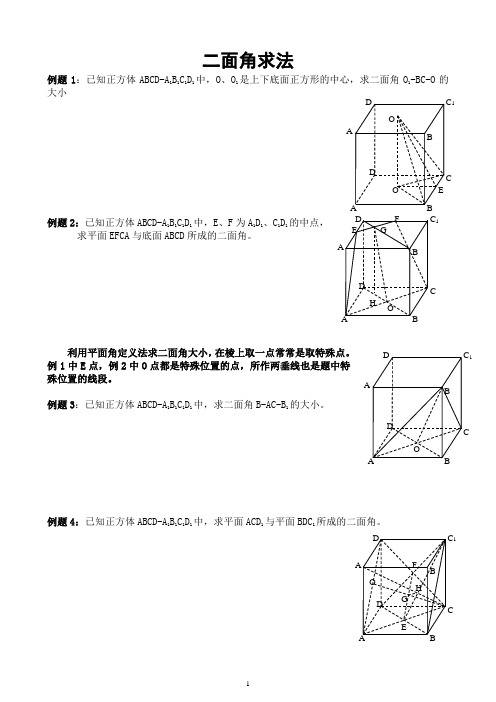
二面角求法例题1:已知正方体ABCD-A1B1C1D1中,O、O1是上下底面正方形的中心,求二面角O1-BC-O的大小例题2:已知正方体ABCD-A1B1C1D1中,E、F为A1D1、C1D1的中点,求平面EFCA与底面ABCD所成的二面角。
利用平面角定义法求二面角大小,在棱上取一点常常是取特殊点。
例1中E点,例2中O点都是特殊位置的点,所作两垂线也是题中特殊位置的线段。
例题3:已知正方体ABCD-A1B1C1D1中,求二面角B-AC-B1的大小。
例题4:已知正方体ABCD-A1B1C1D1中,求平面ACD1与平面BDC1例题5:已知正方体ABCD-A1B1C1D1中,求二面角B-A1C-D的大小。
例题6:已知正方体ABCD-A1B1C1D1中,E、F分别是BB1、DD1的中点,求平面BC1D与平面EC1F所成的二面角。
利用线面垂直法要根据条件寻作棱的特殊位置上的垂面,并找准面面交线所成的平面角。
例题7:已知正方体ABCD-A1B1C1D1中,求平面BDC1与平面ACC1A1所成的二面角。
例题8:已知正方体ABCD-A1B1C1D1中,O1、O是上下底面正方形的中心,V是OO1的中点,求平面AVB与平面CVD所成的二面角。
例题9:已知正方体ABCD-A1B1C1D1中,H是BC棱上一点且BH:BC=1:3,求二面角H-AA1-C1的大小。
例题10:已知正方体ABCD-A1B1C1D1中,O1、O是上下底面正方形的中心,E是AB棱上一点,且AE:EB=1:2,求二面角A1-O1O-E的大小。
此公式法求二面角大小要注意公式中EF、d、m、n、θEF、d、m、n四个量才可以求得θ。
例题11:已知正方体ABCD-A1B1C1D1中,G、E、F是所在棱的中点,求平面EFG与平面ABCD所成的二面角。
例题12:已知正方体ABCD-A1B1C1D1中,O1是上底面正方形的中心,E、F是AB、CD的中点,求平面AO1D与平面EO1F例题13:已知正方体ABCD-A1B1C1D1中,E是BC的中点,F在AA1上,且A1F:FA=1:2,求平面B1EF与底面A1B1C1D1所成的二面角。
正四面体常用结论

正四面体常用结论
正四面体是一种具有四个等边三角形的三维几何体,其常用结论包括以下几个方面。
1. 正四面体的性质
正四面体的四个面都是等边三角形,四个顶点相互连通,其中每个顶点都是三个面的公共点,每条边都是两个面的公共边。
正四面体的底面中心、顶点以及每个面的重心三点共线,且共线比为1:3。
正四面体的每个内角都是70.53度,每个外角为109.47度。
2. 正四面体的体积公式
正四面体的体积公式为V=√2/12a³,其中a为正四面体的棱长。
这个公式可以通过正四面体的高度和底面积来推导得到,也可以通过计算四个棱锥的体积并相加得到。
3. 正四面体的表面积公式
正四面体的表面积公式为S=√3a²,其中a为正四面体的棱长。
这个公式可以通过将正四面体分解成四个等腰三角形和一个正三角形来推导得到。
4. 正四面体的对称性
正四面体具有旋转对称性和镜像对称性。
它有6个旋转对称轴,分
别为通过两个相邻顶点的轴,以及通过中心垂直于某个面的轴。
它也有6个镜像对称面,分别为通过两个相邻顶点和中心的面,以及通过棱中点和面中心的面。
5. 正四面体的嵌入
正四面体可以嵌入到三维空间中的不同形状中。
其中最著名的是嵌入到八面体中,也就是四面体与另外一个四面体共享一个顶点,中心分别连接形成六个正方形。
正四面体作为一种基本几何体,具有独特的性质和应用。
掌握正四面体的常用结论,可以帮助我们更好地理解三维几何空间中的形状和应用。
3.4基本几何体之正四面体

基本几何体之正四面体设正四面体的棱长为a ,如下图1、侧面中线AM a =2、高线AH =3、外接球半径R =4、内切球半径12r a =5、对棱距离(BC 与AD 两异面直线的距离)2EF a =其中E 、F 为相应中点,EF 既垂直于BC 又垂直于AD6、AC 垂直BD 、AB 垂直CD 、AD 垂直BC (实际所有正三棱锥都有这个结论,正四面体是特殊的正三棱锥)注1:外接球与内切球半径的求法首先在正四面体中,外接球与内切球的球心是合一的,而且必须在高线AH 上,设球心为O ,外接球半径为R ,内切球半径为r ,而且H 必是一个切点。
如下图所示则有222r R AH R r BH ⎧+==⎪⎨⎪+=⎩又H 还是BCD的重心,有2233BH BM ===因此解222r R a R r ⎧+=⎪⎪⎨⎫⎪+=⎪⎪⎪⎝⎭⎩,即可求得R 与r注2:对棱间距的求法将正四面体放在正方体中讨论(以后会经常这样子做)。
只要在正方体中取不相邻的四个顶点就构成了正四面体。
如下:显然EF等于正方体的棱长,即2a例1 (05年北京)在正四面体P —ABC 中,D 、E 、F 分别是AB 、BC 、CA 的中点,下面四个结论中不成立的是(C )解析:如下图,做出PO为该四面体的高线,O必在AE上。
A:BC//DF可以得到BC//面PDF,对B:PO DFDF PAEAE DF⊥⎫⇒⊥⎬⊥⎭面,也对C:PO显然不在面PDF中,因此面PDF垂直面ABC不可能D:PO在面PAE内,因此面PAE与面ABC垂直要解此题,必须对正四面体的性质十分熟练。
如O必落在AE上,且O必不在DF上。
因为必有O为ABC的重心。
2=3AO AE,而EF为中位线,所以O必不在EF上。
正四面体的常用结论公式

正四面体的常用结论公式正四面体是我们生活中常见的一种几何图形,它的结构和性质一直以来都是数学家们研究的重点。
在这篇文章中,我将从理论和实践两个方面来探讨正四面体的常用结论公式。
我们来看一下正四面体的定义和性质。
正四面体是一个由四个边长相等的三角形组成的立体图形,它的每个面都是一个等边三角形。
正四面体的特点是它的六个顶点都在同一个球面上,这个球心被称为正四面体的外接球心。
由于正四面体的对称性,我们只需要知道其中一个面的面积和高,就可以计算出其他面的面积和高。
接下来,我将介绍一些常用的结论公式。
一、正四面体的体积公式1.1 底面积公式正四面体的底面积可以用以下公式表示:S = (a2 * b2) / (4 * GCD(a, b))其中,a和b分别是正四面体的两个相邻边的边长,GCD(a, b)表示a和b的最大公约数。
1.2 体积公式正四面体的体积可以用以下公式表示:V = S * h / 3其中,h是正四面体的高,可以通过勾股定理计算得出。
二、正四面体的表面积公式2.1 三个侧面的面积之和公式正四面体的三个侧面的面积分别为A1、A2和A3,它们可以表示为:A1 = a * b * sin60° = ab * √3 / 2A2 = a * c * sin60° = ac * √3 / 2A3 = b * c * sin60° = bc * √3 / 2所以,三个侧面的面积之和为:A_total = A1 + A2 + A3 = (ab + ac + bc) * √3 / 22.2 六个面的总面积公式正四面体的六个面的总面积为:A_total = 3 * (A1 + A2 + A3) = 3 * (ab + ac + bc) * √3 / 2三、正四面体的外接球半径公式3.1 外接球心到任意顶点的距离公式设正四面体的外接球心为O,任意一个顶点为P,那么OP就是外接球心到顶点P的距离。
正四面体性质及其应用

正四面体性质及其应用 Document number:NOCG-YUNOO-BUYTT-UU986-1986UT正四面体的性质及其应用正四面体是四个面都是等边三角形的凸多面体,它是一个很规则的几何体,因此具有一些特有的性质,设正四面体的棱长为a ,则 (1) 全面积S 全= 3 a 2; (2) 高h = 63a ;(3) 体积V = 212 a 3;(4) 对棱中点的连线是对棱的公垂线,其长为d = 22a(5) 相邻两面所成的二面角α=arccos 13; (6) 棱与其相交的面所成的角 β=arctan 2 ;(7) 正四面体的内切球和外接球的球心重合,内切球半径 r = 612a ,外接球半径R= 64a ,r ︰R =1︰3; (8) 正四面体内任一点到四个面的距离之和为定值(等于正四面体的高)。
将正四面体置于正方体中,结合正方体的性质以上诸性质容易得到证明。
考查正四面体的性质多出选择或填空题,熟记以上八条性质对快速求解相关问题有很大帮助,例如:例1:已知半径为1的球面上有A 、B 、C 三个点,且它们之间的球面距离都为π3,则球心O 到平面ABC 的距离为( ) A 3 2 B 6 3 C 12 D 21 7解析:如右图所示,OA=OB=OC =1 又3π===⌒⌒⌒CA BC AB ,球的半径r =1∴∠AOB=∠BOC=∠COA =π3,则AB=BC=CA =1所以O -ABC 为棱长为1的正四面体,则由正四面体的性质得球心O 到平面ABC的距离即其高为 63,答案B 。
例2:(05年湖南省十所示范校联考)已知棱长为a 的正四面体ABCD 有内切球O ,经过该棱锥A -BCD 的中截面为M ,则O 到平面M 的距离为( ) A a 4 B 6 6a C 6 12a D 2 8a解析:直接运用正四面体的性质,内切球的半径r = 612a ,中截面到底面的距离为高的一半 6 6a ,则O 到平面M 的距离为 6 6a - 6 12a = 612a ,因此选C 。
正四面体二面角8种求法(教师版)

正四⾯体⼆⾯⾓8种求法(教师版)⼆⾯⾓求法例题1:已知正⽅体ABCD-A 1B 1C 1D 1中,O 、O 1是上下底⾯正⽅形的中⼼,求⼆⾯⾓O 1-BC-O 的⼤⼩。
解:取BC 中点E ,连接OE 、O 1E ,易证⊿BOC 、⊿BO 1C 是等腰三⾓形。
∴OE ⊥BC ,O 1E ⊥BC ,∴∠OEO 1是⼆⾯⾓O 1-BC-O 的平⾯⾓,连OO 1,OO 1⊥平⾯ABCD ,∴OO 1⊥OE 在RT ⊿OEO 1中,OO 1=1,DE=21∴tan ∠OEO 1=22111==OE OO∴所求⼆⾯⾓θ=arctan2。
例题2:已知正⽅体ABCD-A 1B 1C 1D 1中,E 、F 为A 1D 1、C 1D 1的中点,求平⾯EFCA 与底⾯ABCD 所成的⼆⾯⾓。
解:连B 1D 1交EF 于G ,连BD 交AC 于O ,作GH ⊥BD ,H 是垂⾜,连GO ,易证GO ⊥AC ,⼜BD ⊥AC∴∠GOH 是所求⼆⾯⾓的平⾯⾓, GH=1,OH=42∴tan ∠GOH=22421==OH GH ∴所求⼆⾯⾓θ=arctan 22。
利⽤平⾯⾓定义法求⼆⾯⾓⼤⼩,在棱上取⼀点常常是取特殊点。
例1中E 点,例2中O 点都是特殊位置的点,所作两垂线也是题中特殊位置的线段。
例题3:已知正⽅体ABCD-A 1B 1C 1D 1中,求⼆⾯⾓B-AC-B 1的⼤⼩。
解:连接BD 交于AC 为O 点,连OB 1,∵BB 1⊥平⾯ABCD ,BO ⊥AC ∴B 1O ⊥AC ,∠BOB 1是⼆⾯⾓B-AC-B 1的平⾯⾓,tan ∠BOB 1=22211==BO BB ∴所求⼆⾯⾓θ=arctan 2. 例题4:已知正⽅体ABCD-A 1B 1C 1D 1中,求平⾯ACD 1与平⾯BDC 1所成的⼆⾯⾓。
解:设AC 与BD 交于E ,CD 1与C 1D 交于F ,连EF 是所求⼆⾯⾓B-EF-C 的棱,连A 1C ,易证A 1C ⊥平⾯BDC 1,垂⾜为H ,取AD 1中点O ,连OC 交EF 于G∵EF ∥AD 1,OC ⊥AD 1 ∴OC ⊥EF 即CG ⊥EF 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正四面体中的常用公式
公式:设正四面体的边长为a ,则其高a h 36=,体积3122a V =,表面积23a S =表,外接球半径a R 4
6=外,内切求半径a R 12
6=
内。
应用: 1、一个空间四边形ABCD 的四条边及对角线AC 的长均为2,二面角D —AC —B 的余弦值为
31,则下列论断正确的是( ) 【答案】A
A. 四边形ABCD 的四个顶点在同一球面上且此球的表面积为π3
B. 四边形ABCD 的四个顶点在同一球面上且此球的表面积为π4
C. 四边形ABCD 的四个顶点在同一球面上且此球的表面积为π33
D. 不存在这样的球使得四边形ABCD 的四个顶点在此球面上
一个棱长为12的正四面体纸盒内放一个正方体,若正方体可以在纸盒内任意转动,则正方体棱长的最大值是( )
【答案】B A.2 B.22 C.3 D.32
3、在等腰梯形ABCD 中,AB =2CD =2,∠DAB =60o ,E 为AB 的中点,将△ADE 与△BEC 分别沿ED 、EC 向上折起,使A 、B 重合于点P ,则三棱锥P-DCE 的外接球的体积为 。
【答案】π8
6 椎体外接球问题解题技巧:
侧棱垂直锥补柱;
侧棱相等找射影;
对棱相等长方体;
最值问题d 加R 。
