空间关系
人文地理学的空间概念

人文地理学的空间概念
人文地理学的空间概念是该学科研究的重要内容之一,它强调了地理现象与空间的关系。
以下是一些人文地理学中常用的空间概念:
1. 地域:地域是指一定范围内具有一定界限、特定特征和联系的地理区域,如国家、地区、城市等。
2. 地方:地方是一个相对而言的概念,表示地理空间上与其他地区有明显差异的一个区域,它具有独特的自然环境、社会文化和经济特征。
3. 地景:地景是在人类活动过程中形成的具有某种特色的地理环境,包括自然景观和人文景观。
地景反映了特定地区的人文和自然条件。
4. 空间关系:空间关系是指地理现象在地理空间中的相互联系和相互作用。
它可以包括地理位置、距离和接近程度、区域之间的连接等方面。
5. 区域性:区域性是指在一定范围内具有相似性和差异性的地理现象。
人文地理学关注不同区域的特点和区域发展的规律。
6. 地域差异:地域差异是指地理空间上不同区域之间在环境、文化、经济等方面的差异。
人文地理学试图解释这些差异的形成原因。
7. 位置:位置是指一个区域在地理空间中的具体坐标或相对关系。
位置可以影响一个地区的人文特征、经济发展和区域关系等。
8. 空间分析:空间分析是通过空间数据和空间模型对地理现象进行研究和解释的方法。
它包括地理信息系统(GIS)和空间
统计等技术和方法。
这些空间概念在人文地理学研究中被广泛应用,帮助理解人类活动与地理环境之间的相互关系,揭示地方和区域发展的规律。
ARCGIS矢量数据空间关系

空间关系: 1, esriSpatialRelTouches(邻接) 应用范围: 除点与点之间的关系外,其它的要素之间都可以具有该关系。 描述: 如果二个要素有相同的边界,且它们内部不相交的话,称这二个要素之间 的关系是邻接的关系,图 1-1、2-1、3-1、3-2,注意图 3-3 中点与线是 包涵的关系。 当查询要素和被查询要素具有该关系时,即 spatialRel 的值是 esriSpatialRelTouches,则会返回查询要素。 2, esriSpatialRelCrosses (交叉) 应用范围: 线与面,线与线等。不能用于面与面(面与面相交部分是面,不能二个要 素中的最高维数低一),面与点,点与线(二个要素的维数差 2)。 描述: 如果二个要素的相交部分不为空,并且相交部分形状的维数比两个要素中 最高维数低 1(即线面交叉是线,线线交叉是点)则称这二个要素具有交 叉关系,图 2-4、4-1,图 2-1 中中二条线的关系属于邻接关系,而不属 于交叉关系,因为它们的内部相交部分为空。 当查询要素和被查询要素具有该关系时,即 spatialRel 的值是 esriSpatialReCrosses,则会返回查询要素。 3, esriSpatialRelOverlaps(重叠关系) 应用范围: 线与线,面与面之间,其它的不具有该关系。 描述: 二个同维的要素之间的相交部分的图形具有与这二个要素相同的维数的, 且不与任何一个要素完全相同,则称这二个要素重叠。图 1-2、2-2 均是 重叠关系,但是 2-3 中的二条线不是重叠关系,因为相交的部分与黄色的 线完全相同。 当查询要素和被查询要素具有该关系时,即 spatialRel 的值是
空间线面关系的判定

目录
• 空间线面关系的基本概念 • 空间线与平面位置关系的判定 • 空间面与面位置关系的判定 • 空间线面关系的应用 • 空间线面关系判定的注意事项
01
空间线面关系的基本概念
空间直线与平面的定义
空间直线
在三维空间中,直线是无限长的线段, 它有两个方向,并且可以无限延伸。 直线可以用两点来确定,也可以用方 向向量来表示。
加合理、稳定的船舶。
数学建模中的应用
几何建模
在几何建模中,空间线面关系的判定是 基础,它可以帮助数学家更好地理解几 何形状的特点,从而建立更加准确、可 靠的几何模型。
VS
计算几何
在计算几何中,空间线面关系的判定是重 要的研究内容之一,它可以帮助数学家更 好地理解几何形状的计算方法,从而为计 算机图形学、计算机辅助设计等领域提供 更加高效、精确的算法和工具。
平面与平面垂直判定定理一
如果一个平面内的两条不平行的直线分别垂直于另一个平面 ,则这两个平面垂直。
平面与平面垂直判定定理二
如果一个平面与另一个平面的垂线平行,则这两个平面垂直 。
平面与平面相交判定定理
平面与平面相交判定定理一
如果两个平面有一个公共点,则它们相交。
平面与平面相交判定定理二
如果一个平面内的直线与另一个平面相交,则这两个平面相交。
空间平面
在三维空间中,平面是一个无厚度的 二维区域。它由三个非共线的点确定, 并且可以无限延伸。平面可以用一个 点、一个方向向量和一个距离来确定。
空间线面关系的分类
直线与平面平行
当直线与平面平行时,直线不与平面相交,且直线与 平面内任意直线都平行。
直线与平面相交
当直线与平面相交时,直线与平面有一个唯一的交点, 或者直线完全在平面内。
空间中的平行关系

1.空间两条互相平行的直线指的是( ) A.在空间没有公共点的两条直线 B.分别在两个平面内的两条直线 C.分别在两个不同的平面内且没有公共点的两条直线 D.在同一平面内且没有公共点的两条直线
答案:D
2.
(
设 AA1 是正方体的一条棱, 这个正方体中与 AA1 平行的棱共有 ) A.1 条 B.2 条 C .3 条 D.4 条
如图:空间四边形ABCD中, AC、BD是它的对角线
空间四边形的常见画法经常用一个平面衬托,如下图
中的两种空间四边形ABCD和ABOC.
空间两条直线的位置关系有三种:
位置关系 相交直线 共面情况 在同一平面内 公共点个数 有且只有一个
平行直线
异面直线
在同一平面内
不在任何一平面内
没 有
没 有
类型一 基本性质 4 的应用 【例 1】
变式训练 1 已知棱长为 a 的正方体 ABCD-A′B′C′D′ 中,M、N 分别为 CD、AD 的中点. 求证:四边形 MNA′C′是梯形.
证明:如图,连结 AC,
1 ∵M、N 分别为 CD、AD 的中点,∴MN=2AC. 1 由正方体的性质可知 AC=A′C′,∴MN=2A′C′.∴四边形 MNA′C′是梯形.
证明:如图所示,在正方体 AC1 中,取 A1B1 的中点 M,连结 BM、MF1,
1 则 BF=A1M=2AB. 又 BF∥A1M,
∴四边形 A1FBM 为平行四边形. ∴A1F∥BM. 而 F1,M 分别为 C1D1,A1B1 的中点,则 F1M 綊 C1B1. 而 C1B1 綊 BC,∴F1M∥BC,且 F1M=BC.
答案:C
3.空间中有两个角 α,β,它们的两边互相平行,且 α=60° , 则 β 为( ) A.60° B.120° C.30° D.60° 或 120°
高二数学 空间平行关系
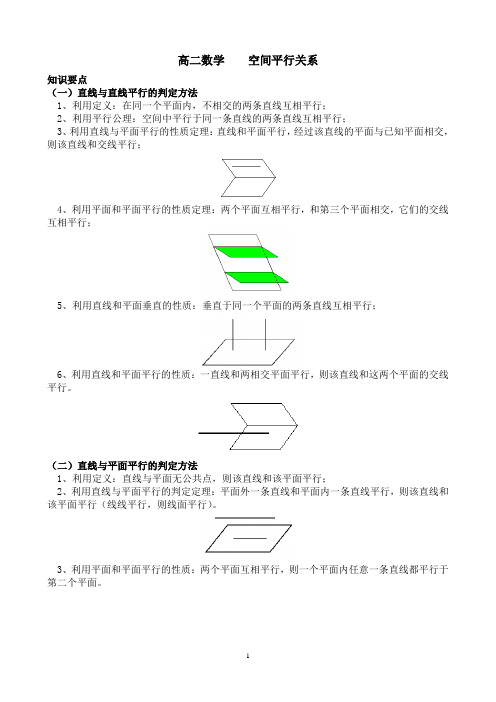
高二数学空间平行关系知识要点(一)直线与直线平行的判定方法1、利用定义:在同一个平面内,不相交的两条直线互相平行;2、利用平行公理:空间中平行于同一条直线的两条直线互相平行;3、利用直线与平面平行的性质定理:直线和平面平行,经过该直线的平面与已知平面相交,则该直线和交线平行;4、利用平面和平面平行的性质定理:两个平面互相平行,和第三个平面相交,它们的交线互相平行;5、利用直线和平面垂直的性质:垂直于同一个平面的两条直线互相平行;6、利用直线和平面平行的性质:一直线和两相交平面平行,则该直线和这两个平面的交线平行。
(二)直线与平面平行的判定方法1、利用定义:直线与平面无公共点,则该直线和该平面平行;2、利用直线与平面平行的判定定理:平面外一条直线和平面内一条直线平行,则该直线和该平面平行(线线平行,则线面平行)。
3、利用平面和平面平行的性质:两个平面互相平行,则一个平面内任意一条直线都平行于第二个平面。
(三)平面和平面平行的判定方法1、利用定义:两个平面没有公共点,则这两个平面平行;2、利用平面与平面平行的判定定理:一个平面内有两条相交直线分别与另一个平面内两条相交直线平行,则这两个平面平行;3、利用平面与平面平行的判定:一个平面内有两条相交直线分别平行于另一个平面,则这两个平面平行;4、利用平面与平面平行的传递性:平行于同一个平面的两个平面互相平行.5、利用直线与平面垂直的性质:垂直于同一条直线的两个平面互相平行;(四)直线与平面平行的性质1、性质定理:直线和平面平行,经过该直线的平面与已知平面相交,则该直线和交线平行;2、直线和平面平行的性质:一直线和两相交平面平行,则该直线和这两个平面的交线平行。
(五)平面与平面平行的性质1、平面与平面平行的性质定理:如果两个平行平面同时与第三个平面相交,那么它们的交线平行。
2、平面与平面平行的性质:两个平面互相平行,则一个平面内任意一条直线均平行于第二个平面。
文档:空间中三种平行关系的转化

空间中三种平行关系的转化平行关系是空间中线面位置关系的重要类型,空间中的直线和直线平行,直线和平面平行,平面和平面平行三者之间有着互为因果、相互转化的关系:线线平行线面平行面面平行.因此,我们在判定空间的平行关系时,不可孤立地对待,要将三者联系起来.本文举例说明.一、线与面平行关系转化一般来说,线线或面面平行关系都可以转化为线面平行关系来分析解决,其关系如下表所示:线线平行−−−←−−→−性质判定线面平行−−−←−−→−性质判定面面平行. 例1 如图1,平面四边形ABCD 的四个顶点A B C D ,,,均在平行四边形A B C D ''''所确定的平面外,且AA BB CC DD '''',,,互相平行.求证:四边形ABCD 是平行四边形. 证明:四边形A B C D ''''是平行四边形,A DBC ''''∴∥.AA BB ''∥,且,是平面AA D D ''内的两条相交直线,,是平面BB C C ''内的两条相交直线,平面AA D D ''∥平面BB C C ''. 又AD BC ,分别是平面ABCD 与平面AA D D '',平面BB C C ''的交线,故AD BC ∥.四边形ABCD 是平行四边形.点评:该题灵活应用判定定理与性质之间的转化关系,先将线线平行转化为面面平行,再由面面平行转化为线线平行,从而使问题轻松获解.二、创设辅助线与面如果已知条件中找不出现成的平行或垂直关系,此时要根据ABDC C 1D 1A 1B 1 MN图1题意灵活作出有理有据的辅助线或辅助面,适当添加辅助线或辅助面是面是促进转化的重要环节.例2 正方体ABCD —ABCD 中,M 、N 分别是对角线AB 、BC 上两点,且MA M B 1=NBNC 1,求证:MN ∥平面ABCD .分析:在图中,根据已知条件找不出现成的线线平行关系,怎么办?往往通过两条途径去探索证明思路:①用“面面平行线面平行”;②添加辅助线,创设使用线面平行判定定理的条件,具体方法如下:⑴由“面面平行线面平行”去证.在面AB 内,作M K ∥AB ,交BB 于K 点,连接K N ,由平行线截割定理知MA M B 1=KB K B 1,而MA M B 1=NB N C 1已知),∴KB K B 1 =NBNC 1 ,则K N ∥BC , ∴平面M K N ∥平面ABCD , 即平面M K N 平面ABCD =, 而MN 平面M K N , ∴MN ∥平面ABCD .⑵添加辅助线,由“线线平行线面平行”去证.连接BM 并延长交AB 于P 点,连接P C ,则可证△BM P ∽△AMB ,∴MA M B 1=MB PM ,而MA M B 1=NBN C 1(已知),∴MB PM =NBN C 1,由平行截割定理得:MN ∥P C , 而P C 平面ABCD ,∴MN ∥平面ABCD .点评:辅助线、辅助面所具有的性质,一定要以某一性质定理为依据,决不能凭主观臆断.类题练习:1.正方体中,E、F分别为CD 、的中点,M、N分别为、上的点,并且M=A BDCC 1D 1A 1B 1MKN ABDC C 1D 1 A 1 B 1N MABC DO EN HMA 1B 1C 1D 1 图1AN ,求证:(1)EF ∥平面11BDD B ,(2)MN∥平面11CDD C . 证明:(1)如图1,设BD 的中点为O,连结OE ,则OE ∥21BC ∥F. ∴O∥EF .又O平面11BDD B ,EF 平面11BDD B , ∴ EF ∥平面11BDD B . (2)作MH ∥,连结NH . ∵111111D A HA C A M A =,且AN=M,=, ∴1111D A H A AD AN=. 故NH∥∥. ∴ 平面MNH ∥平面11CDD C . ∴MN∥平面11CDD C .2. 如图:已知正方体ABCD —ABCD 中,面对角线A B ,BC 上分别有两点E 、F ,且B E = CF .求证:⑴EF ∥平面ABCD ;⑵平面AC D ∥平面ABC .⑴证明:过E 、F 分别作AB 、BC 的垂线,EM 、FN 分别交AB 、BC 于M 、N ,连接MN ,∵BB ⊥平面ABCD ,∴BB ⊥AB ,BB ⊥BC ,∴EM ∥BB ,FN ∥BB ,∴EM ∥FN . ∵A B = BC ,BE = CF ,∴AE = BF ,又∠BAB =∠CBC = 45°,∴Rt △AME ≌Rt △BNF ,∴EM = FN .∴四边形MNFE 是平行四边形,∴EF ∥MN . 又MN 平面ABCD ,∴EF ∥平面ABCD .⑵证明:如图 ∵正方体ABCD —ACD 中,AD ∥BC ,CD ∥B A , 又ADCD = D ,BCB A = B , ∴平面ACD ∥平面ABC .C 1D 1ABDCA 1B 1。
空间关系——空间方位拓扑相似及相关关系

资
源
与
环武
境汉
科大
学 学
学
院
第七章 空间关系(二)
§7-1 空间方位
1、定义
实体在地理空间中的某种顺序,如左右、东南西北等。 是描述两个物体之间位置关系的另一种度量,常以角度来表示。
2、两个点的方位关系
在平面上,方位的计算以正北方向为起算方向,并沿顺时针方 向进行的。
在球面上,过AB 两点之间的大圆平面与过A点的子午圈平面间 的夹角
空 间 分 析
资
源
与
环武
境汉
科大
学 学
学
院
§7-1 空间方位
3.方位的定性描述
在地理分析中,往往并不需要对方位进行定量的描述,对方位的定 性描述有时会更简单而且更容易理解。一般用前、后、左、右、南、北、 东、西等方位术语来进行语义的描述,是一种模糊的概念,定性的描述。
在描述空间物体之间的方位时,应注意以下两点: 1) 方位除非特别需要(如航空、航海等),应当概略描述而非精确定
空 间 分 析
资
源
与
环武
境汉
科大
学 学
学
院
§7-2空间拓扑关系
2)计算点与多边形顶点连线的方向角之和。
如果点与多边形顶点连线形成的方向角之和为360度,则点必位于多 边形内,否则位于多边形外。
空 间 分 析
资
源
与
环武
境汉
科大
学 学
学
院
§7-2空间拓扑关系
3.线线关系计算
线线关系的判断主要是相交与否的判断。 1)解方程组方法 线线相交关系的判断通过解二元一次方程组即可完成,可以先简单判断
空间里的平行关系(精选7篇)

空间里的平行关系(精选7篇)空间里的平行关系篇1教学建议一、知识结构在平行线知识的基础上,教科书以学生对长方体的直观认识为基础,通过观察长方体的某些棱与面、面与面的不相交,进而把它们想象成空间里的直线与平面、平面与平面的不相交,来建立空间里平行的概念.培养学生的空间观念.二、重点、难点分析能认识空间里直线与直线、直线与平面、平面与平面的平行关系既是本节教学重点也是难点.本节知识是线线平行的相关知识的延续,对培养学生的空间观念,进一步研究空间中的点、线、面、体的关系具有重要的意义.1.我们知道在同一平面内的两条直线的位置关系有两种:相交或平行,由于垂直和平行这两种关系与人类的生产、生活密切相关,所以这两种空间位置关系历来受到人们的关注,前面我们学过在平面内直线与直线垂直的情况,以及在空间里直线与平面,平面与平面的垂直关系.2.例如:在图中长方体的棱AA'与面ABCD垂直,面A'ABB'与面ABCD互相垂直并且当时我们还从观察中得出下面两个结论:(1)一条棱垂直于一个面内两条相交的棱,这条棱与这个面就互相垂直.(2)一个面经过另一个面的一条垂直的棱,这两个面就互相垂直.正如上述,在空间里有垂直情况一样,在空间里也有平行的情况,首先看棱AB与面A'B'C'D'的位置关系,把棱AB向两方延长,面A'B'C'D'向各个方向延伸,它们总也不会相交,像这样的棱和面就是互相平行的,同样,棱AB与面DD'C'C是互相平行的,棱AA'与面BB'C'C、与面DD'C'C 也是互相平行的.再看面ABCD与A'B'C'D',这两个面无论怎样延展,它们总也不会相交,像这样的两个面是互相平行的,面AA'B'B与DD'C'C也是互相平行的.3.直线与平面、平面与平面平行的判定(1)不在平面内的一条直线,只要与平面内的某一条直线平行,那么,这条直线与这个平面平行。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§2.1 地理实体及其描述
四、空间关系
空间关系是指各空间实体之间的空间关系,包括拓扑空间关系,顺序空间关系和度量空间关系。
由于拓扑空间关系对GIS查询和分析具有重要意义,在GIS中,空间关系一般指拓扑空间关系。
1、定义
拓扑关系是一种对空间结构关系进行明确定义的数学方法。
是指图形在保持连续状态下变形,但图形关系不变的性质。
可以假设图形绘在一张高质量的橡皮平面上,将橡皮任意拉伸和压缩,但不能扭转或折叠,这时原来图形的有些属性保留,有些属性发生改变,前者称为拓扑属性,后者称为非拓扑属性或几何属性(表2-1-1)。
这种变换称为拓扑变换或橡皮变换。
2、拓扑关系的种类
点(结点)、线(链、弧段、边)、面(多边形)三种要素是拓扑元素。
它们之间最基本的拓扑关系是关联和邻接。
1)关联:不同拓扑元素之间的关系。
如结点与链,链与多边形等。
2)邻接:相同拓扑元素之间的关系。
如结点与结点,链与链,面与面等。
邻接关系是借助于不同类型的拓扑元素描述的,如面通过链而邻接。
在GIS的分析和应用功能中,还可能用到其它拓扑关系,如:
3)包含关系:面与其它拓扑元素之间的关系。
如果点、线、面在该面内,则称为被该面包含。
如某省包含的湖泊、河流等。
4)几何关系:拓扑元素之间的距离关系。
如拓扑元素之间距离不超过某一半径的关系。
5)层次关系:相同拓扑元素之间的等级关系。
如国家由省(自治区、直辖市)组成,省(自治区、直辖市)由县组成等。
2、拓扑关系的表示
在目前的GIS中,主要表示基本的拓扑关系,而且表示方法不尽相同。
在矢量数据中拓扑关系可以由图2-1-6中的四个表格来表示。
3、拓扑关系的意义
空间数据的拓扑关系,对于GIS数据处理和空间分析具有重要的意义,因为:
1)拓扑关系能清楚地反映实体之间的逻辑结构关系,它比几何关系具有更大的稳定性,不随地图投影而变化。
2)有助于空间要素的查询,利用拓扑关系可以解决许多实际问题。
如某县的邻接县,--面面相邻问题。
又如供水管网系统中某段水管破裂找关闭它的阀门,就需要查询该线(管道)与哪些点(阀门)关联。
3)根据拓扑关系可重建地理实体(图2-1-7)。
例如根据弧段构建多边形,实现面域的选取;根据弧段与结点的关联关系重建道路网络,进行最佳路径选择等
完。
