27961高等数学
高等数学第六教材解析

高等数学第六教材解析高等数学是大学数学学科中的一门重要课程,对于培养学生的数学思维和解决实际问题的能力具有重要意义。
本文将对高等数学第六教材进行解析,从内容构成、重点知识点和学习方法三个方面进行阐述,以帮助学生更好地学习和掌握这门学科。
一、内容构成高等数学第六教材主要包括微分方程、无穷级数和曲线积分三个部分。
微分方程是高等数学的重要分支之一,研究的是含有未知函数及其导数的方程。
无穷级数是数列或函数项级数的和的概念和性质的推广,涉及到收敛性判定、性质及其应用等内容。
曲线积分是高等数学中的一种数学工具,用于计算曲线上的物理量或进行数学分析。
二、重点知识点1. 微分方程微分方程的解的存在唯一性及其应用是学习微分方程的重点,其中包括常微分方程和偏微分方程。
学生需要熟练掌握解微分方程的方法,如可分离变量法、线性方程法、齐次方程法等,并能够应用到实际问题中去。
2. 无穷级数无穷级数的收敛性以及常见级数的性质是学习无穷级数的重点,如几何级数、调和级数等。
学生需要熟悉级数的收敛判定方法,如比较判别法、比值判别法、根值判别法等,并能够应用到级数求和、函数展开等计算中去。
3. 曲线积分曲线积分的计算方法和应用是学习曲线积分的重点,包括第一类曲线积分和第二类曲线积分。
学生需要了解曲线积分的定义和性质,熟练掌握计算曲线积分的方法,如参数法、格林公式、斯托克斯公式等,并能够应用到物理问题和数学分析中去。
三、学习方法1. 理论与实践结合高等数学是一门理论与实践相结合的学科,学生需要边学习理论知识,边进行实际问题的训练。
通过做题、解题以及应用实例分析,加深对知识的理解,并提高解决实际问题的能力。
2. 多角度思考问题高等数学中的许多概念和定理都有多个角度的解释和应用,学生可以尝试从不同的角度和方法去理解和思考问题。
这样可以拓宽思维的广度,并提高问题解决的灵活性和创新性。
3. 学会合理利用资源在学习高等数学的过程中,学生可以利用教材、参考书、网络资源等多种资源来加深对知识的理解。
2023年7月江苏自考开考专业及科目

2023年7月江苏自考开考专业及科目2023年7月江苏自考开考专业及科目一览表自考本科是指通过自学考试获得本科学历。
相比传统全日制大学本科,自考本科的特点是学制比较敏捷、学习时间可以本身决议、费用相对较低等。
下面介绍2023年江苏自考本科相关信息:2023年7月江苏自考开考专业及科目2023年7每月江苏自考考试科目布置表专业名称考试科目适时间布置7月1日(星期六)7月2日(星期日)上午9:0011:30下午14:3017:00上午9:0011:30下午14:3017:00X1630302会计08119管理会计X1690202人力资源管理27015创业教育00166企业劳动工资管理00071社会保障概论X1630701市场营销27015创业教育X1690206行政管理27015创业教育X1670102学前教育00389学前教育科学讨论00384学前心理学00386幼儿文学00383学前教育学29761幼儿园课程与教育活动设计X1670121心理健康教育28660人格心理学28793学习心理与辅导X1560102机械制造与自动化02191机械制造技术X1620302中药学03044中药药剂学03040中药鉴定学02976医古文(一)02930中医学基础(一)03050药理学(三)03047分析化学(二)X1630601工商企业管理27015创业教育27870管理学基础27873经济法概论27871统计基础27877市场营销27884人力资源管理27882生产管理X1560301机电一体化技术27015创业教育27877市场营销27964机械制造基础27972农业机械27961高等数学27979电气掌控技术27984自动检测技术X1510118农业经济管理27015创业教育27870管理学基础27873经济法概论27871统计基础27877市场营销27876财务会计27879农业政策与法规X2120237审计学06073财政审计27049社会审计27050内部审计06072企业财务审计X2023301金融学27090上市公司案例分析27089公司财务04009国际金融市场27016日语27309税收学27017法语27018俄语27087金融企业会计27088国际投资学X2120231工商管理07524公司理财30447数据、模型与决策30445宏观经济分析27016日语27017法语27018俄语X2023401国际经济与贸易27040电子商务27309税收学27184国际经济合作27188ERP(企业信息系统)27185WTO与国际经贸惯例X2120233会计学30448会计信息系统27309税收学11240证券投资理论与实务27016日语27017法语27018俄语X2120232市场营销27040电子商务10492销售管理学08770消费者行为学(一)X2120901旅游管理30464旅游电子商务27129国际旅游与客源国概况27128旅游美学27016日语30463酒店管理概论27017法语27018俄语27131旅游文化学27871统计基础X2120801电子商务27016日语27017法语27018俄语X2120236人力资源管理05962聘请管理03871市场调查与市场分析10052职业生涯规划与管理06093人力资源开发与管理27016日语27017法语27018俄语X2120601物流管理07006供应链与企业物流管理07724物流系统工程07729仓储技术和库存理论X2120233工程管理06087工程项目管理30585房屋构造06962工程造价确定与掌控06086工程监理06289工程招标与合同管理X2030101法学27016日语27017法语27018俄语X2330101监所管理27016日语27018俄语X2120402行政管理27016日语27017法语27018俄语X2040106学前教育28041现代科学技术概论28042中外文学精读28054数学基础27016日语28052儿童进展28053幼儿园老师道德与法律修养29768教育伦理学27017法语27018俄语28050学前教育讨论方法28051当代世界学前教育X2340102心理健康教育00266社会心理学(一)29658犯罪心理学29657公共关系心理学27016日语27017法语27018俄语X2040107小学教育28041现代科学技术概论28042中外文学精读28063教育统计学27016日语28066小学制造教育29768教育伦理学27017法语27018俄语28064文艺概论28068小学语文专题讨论28069小学数学专题讨论X2050107秘书学27190现代企业制度27189申论30462文书档案管理27016日语27017法语27018俄语27191秘书文化学X2050101汉语言文学00814中国古代文论选读00821现代汉语语法讨论2895620世纪欧美文学史27016日语27039周树人讨论27017法语27018俄语X2050201英语30460英语应用文写作30461英语文化概论00839第二外语(俄语)00840第二外语(日语)00841第二外语(法语)X2050262商务英语00952国际市场营销学(二)08959BEC商务英语(二)00839第二外语(俄语)00840第二外语(日语)00841第二外语(法语)03412第二外语(韩语)X2050303广告学27623广告设计实务00641中外广告史27412市场调研与统计27016日语27413广告策划与创意27418广告媒介实务27017法语27018俄语X2050301新闻学27020广播电视概论27016日语27017法语27018俄语X2130508数字媒体艺术07887平面设计11733动画视听语言X2080202机械设计制造及其自动化02204经济管理30587机械掌控工程基础30454机械CAD/CAM 技术02209机械制造装备设计02277微型计算机原理及应用X2080201机械工程30453机电一体化技术及应用30586机械优化设计27054工程数学X2080901计算机科学与技术27016日语27017法语27018俄语X2080703通信工程08166操作系统及其安全27054工程数学X2080903网络工程02358单片机原理及应用X2080905物联网工程12580无线通信技术02358单片机原理及应用07025数据通信与网络06016传感器原理及应用12586物联网应用技术与设计10052职业生涯规划与管理X2081001土木工程30449工程建设监理X2082502环境工程28528环境规划与管理28540环境质量评价28727水污染掌控工程27457环境法学X2081301化学工程与工艺27060化学反应工程02485化工热力学06116化工分别过程27063工厂设计概论X2082701食品科学与工程03281食品微生物学(二)03286食品营养学03283食品安全与质量掌控03284食品原材料学04175食品添加剂03285食品工厂设计(二)X2080208汽车服务工程08315掌控工程基础30459汽车维护和修理技术与设备08586汽车应用英语(一)09087汽车电器与电路分析X2120232信息管理与信息系统06627网页制作与网站建设06385网络信息检索与利用02115信息管理基础02124信息分析方法X2090502园林00293城市生态学04045园林植物病虫害防治(二)01437园林工程预算11216园林工程学(二)11235造园史X2090401动物医学30457兽医病理学02678农业推广学02798畜牧微生物学02787兽医药理学02799兽医临床医学30458兽医传染病学X2120301农林经济管理06187农业概论02678农业推广学06173特种经济动物饲养管理学02680农产品加工27016日语27017法语27018俄语X2100801中药学03034药事管理学03040中药鉴定学03050药理学(三)03049数理统计05081中药文献学07793医药市场营销学X2100701药学01763药事管理学(二)01757药物分析(三)02911无机化学(三)03049数理统计05524药用植物与生药学06831药理学(四)07793医药市场营销学2江苏自学制多少年江苏自考无学制限制,没有固定的毕业日期。
吉林大学出版社高职高专《高等数学》第01章

39
注: 函数
与其反函数
的图形关于直线
对称 .
y Q(b, a)
yx y f (x)
例如 ,
指数函数 y ex , x (, )
对数函数
o
x
互为反函数 ,
它们都单调递增, 其图形关于直线
若A B,A B =A,A B =B。
9
2)区间---9种类型的区间
设实数 a b,开区间 (a,b)={x | a x b},记作 (a,b). 数轴上表示点 a 与点b 之间的线段,但不包括端点 a 及端 点b. 闭区间[a,b] ={x | a x b},记作[a,b] . 在数轴上表示点 a 与点b 之间的线段,包括两个端点.. 集合{x | a x b}记作 (a,b],称为左开右闭区间. 集合{x | a x b}记作[a,b) ,称为左闭右开区间. 以上区间都称为有限区间,数 b a 称为这些区间的长度.
46
两个以上函数也可构成复合函数. 例如,
y u, u0
u 1v2
v x , x (, ) 2
邻域: 设a与是两个实数 , 且 0.
称数集{x a x a }为点a的邻域 ,
记作U(a,),称点a为该邻域的中心 ,为该邻域的半径
a
a
a
x
点a的去心的邻域, 记作U 0 (a, ).
U 0 (a, ) {x 0 x a }
12
一、函数的定义
33
【例4】 f(x)=sinx和f(x)=cosx
大一高讲义数课件第二章2-6-1

(2)炮弹在时t刻 0的速度大.小
解 (1) 在t0时刻的运动方向即 轨迹在t0时刻的切线方向, 可由切线的斜率来反映.
dy(v0tsin12gt2) dx (v0tcos)
v0 sin gt v0 cos
dy dxtt0
v0si ng0t. v0cos
y
vy v
v0
vx
o
x
xv0tcos ,
dt
dy dx
t 2
sin
1
2 cos
1.
2
当 t时 ,xa ( 1 ),ya .
2
2
所求切线方程为
yaxa(1) 即yxa(2)
2
2
例7 不计空气的阻, 以 力初速度 v0, 发射角发射炮弹 ,
其运动方程为xy
v0t cos, v0tsin
1 gt2, 2
求(1)炮弹在时t刻 0的运动方;向
x
x
一般地 f(x ) u (x ) v (x ) ( u (x ) 0 )
lf ( n x ) v ( x ) l u ( x n )
又 dln f(x)1df(x) dx f(x)dx
f(x)f(x)dln f(x) dx
f(x ) u (x )v (x )[v (x )lu n (x ) v (x )u (x )] u (x )
设xx(t)及y y(t)都是可导,函 而数 变量 x与y之间存在
某种关,从 系而它们的变 dx化 与d率 y之间也存在一,定 dt dt
这样两个相互依化赖率的称变为相关.变化率
相关变化率问题: 已知其中一个变化率时如何求出另一个变化率?
三、由参数方程所确定的函数的导数
若 参 数 x y 方 ((tt))程 确 定 y与 x间 的 函,称 数此 关为 系由
高等数学第六版(同济大学)上册课后习题答案解析

高等数学第六版上册课后习题答案及解析第一章习题1-11. 设A =(-∞, -5)⋃(5, +∞), B =[-10, 3), 写出A ⋃B , A ⋂B , A \B 及A \(A \B )的表达式.解 A ⋃B =(-∞, 3)⋃(5, +∞),A ⋂B =[-10, -5),A \B =(-∞, -10)⋃(5, +∞), A \(A \B )=[-10, -5).2. 设A 、B 是任意两个集合, 证明对偶律: (A ⋂B )C =A C ⋃B C . 证明 因为x ∈(A ⋂B )C ⇔x ∉A ⋂B ⇔ x ∉A 或x ∉B ⇔ x ∈A C 或x ∈B C ⇔ x ∈A C ⋃B C , 所以 (A ⋂B )C =A C ⋃B C .3. 设映射f : X →Y , A ⊂X , B ⊂X . 证明 (1)f (A ⋃B )=f (A )⋃f (B );(2)f (A ⋂B )⊂f (A )⋂f (B ). 证明 因为y ∈f (A ⋃B )⇔∃x ∈A ⋃B , 使f (x )=y⇔(因为x ∈A 或x ∈B ) y ∈f (A )或y ∈f (B ) ⇔ y ∈f (A )⋃f (B ), 所以 f (A ⋃B )=f (A )⋃f (B ). (2)因为y ∈f (A ⋂B )⇒∃x ∈A ⋂B , 使f (x )=y ⇔(因为x ∈A 且x ∈B ) y ∈f (A )且y ∈f (B )⇒ y ∈ f (A )⋂f (B ),所以 f (A ⋂B )⊂f (A )⋂f (B ).4. 设映射f : X →Y , 若存在一个映射g : Y →X , 使X I f g = , Y I g f = , 其中I X 、I Y 分别是X 、Y 上的恒等映射, 即对于每一个x ∈X , 有I X x =x ; 对于每一个y ∈Y , 有I Y y =y . 证明: f 是双射, 且g 是f 的逆映射: g =f -1.证明 因为对于任意的y ∈Y , 有x =g (y )∈X , 且f (x )=f [g (y )]=I y y =y , 即Y 中任意元素都是X 中某元素的像, 所以f 为X 到Y 的满射. 又因为对于任意的x 1≠x 2, 必有f (x 1)≠f (x 2), 否则若f (x 1)=f (x 2)⇒g [ f (x 1)]=g [f (x 2)] ⇒ x 1=x 2. 因此f 既是单射, 又是满射, 即f 是双射.对于映射g : Y →X , 因为对每个y ∈Y , 有g (y )=x ∈X , 且满足f (x )=f [g (y )]=I y y =y , 按逆映射的定义, g 是f 的逆映射. 5. 设映射f : X →Y , A ⊂X . 证明: (1)f -1(f (A ))⊃A ;(2)当f 是单射时, 有f -1(f (A ))=A .证明 (1)因为x ∈A ⇒ f (x )=y ∈f (A ) ⇒ f -1(y )=x ∈f -1(f (A )), 所以 f -1(f (A ))⊃A .(2)由(1)知f -1(f (A ))⊃A .另一方面, 对于任意的x ∈f -1(f (A ))⇒存在y ∈f (A ), 使f -1(y )=x ⇒f (x )=y . 因为y ∈f (A )且f 是单射, 所以x ∈A . 这就证明了f -1(f (A ))⊂A . 因此f -1(f (A ))=A . 6. 求下列函数的自然定义域: (1)23+=x y ;解 由3x +2≥0得32->x . 函数的定义域为) ,32[∞+-.(2)211xy -=;解 由1-x 2≠0得x ≠±1. 函数的定义域为(-∞, -1)⋃(-1, 1)⋃(1, +∞). (3)211x x y --=;解 由x ≠0且1-x 2≥0得函数的定义域D =[-1, 0)⋃(0, 1]. (4)241x y -=; 解 由4-x 2>0得 |x |<2. 函数的定义域为(-2, 2). (5)x y sin =;解 由x ≥0得函数的定义D =[0, +∞). (6) y =tan(x +1);解 由21π≠+x (k =0, ±1, ±2, ⋅ ⋅ ⋅)得函数的定义域为 12-+≠ππk x (k =0, ±1, ±2,⋅ ⋅ ⋅).(7) y =arcsin(x -3);解 由|x -3|≤1得函数的定义域D =[2, 4]. (8)xx y 1arctan 3+-=;解 由3-x ≥0且x ≠0得函数的定义域D =(-∞, 0)⋃(0, 3). (9) y =ln(x +1);解 由x +1>0得函数的定义域D =(-1, +∞). (10)xe y 1=.解 由x ≠0得函数的定义域D =(-∞, 0)⋃(0, +∞).7. 下列各题中, 函数f (x )和g (x )是否相同?为什么? (1)f (x )=lg x 2, g (x )=2lg x ; (2) f (x )=x , g (x )=2x ; (3)334)(x x x f -=,31)(-=x x x g .(4)f (x )=1, g (x )=sec 2x -tan 2x . 解 (1)不同. 因为定义域不同.(2)不同. 因为对应法则不同, x <0时, g (x )=-x . (3)相同. 因为定义域、对应法则均相相同. (4)不同. 因为定义域不同.8. 设⎪⎩⎪⎨⎧≥<=3||03|| |sin |)(ππϕx x x x , 求)6(πϕ, )4(πϕ, )4(πϕ-, ϕ(-2), 并作出函数y =ϕ(x )的图形.解 21|6sin |)6(==ππϕ, 22|4sin |)4(==ππϕ, 22|)4sin(|)4(=-=-ππϕ, 0)2(=-ϕ.9. 试证下列函数在指定区间内的单调性:(1)xx y -=1, (-∞, 1);(2)y =x +ln x , (0, +∞).证明 (1)对于任意的x 1, x 2∈(-∞, 1), 有1-x 1>0, 1-x 2>0. 因为当x 1<x 2时,0)1)(1(112121221121<---=---=-x x x x x x x x y y , 所以函数x x y -=1在区间(-∞, 1)内是单调增加的.(2)对于任意的x 1, x 2∈(0, +∞), 当x 1<x 2时, 有 0ln)()ln ()ln (2121221121<+-=+-+=-x x x x x x x x y y , 所以函数y =x +ln x 在区间(0, +∞)内是单调增加的.10. 设 f (x )为定义在(-l , l )内的奇函数, 若f (x )在(0, l )内单调增加, 证明f (x )在(-l , 0)内也单调增加.证明 对于∀x 1, x 2∈(-l , 0)且x 1<x 2, 有-x 1, -x 2∈(0, l )且-x 1>-x 2. 因为f (x )在(0, l )内单调增加且为奇函数, 所以f (-x 2)<f (-x 1), -f (x 2)<-f (x 1), f (x 2)>f (x 1),这就证明了对于∀x 1, x 2∈(-l , 0), 有f (x 1)< f (x 2), 所以f (x )在(-l , 0)内也单调增加.11. 设下面所考虑的函数都是定义在对称区间(-l , l )上的, 证明: (1)两个偶函数的和是偶函数, 两个奇函数的和是奇函数;(2)两个偶函数的乘积是偶函数, 两个奇函数的乘积是偶函数, 偶函数与奇函数的乘积是奇函数.证明 (1)设F (x )=f (x )+g (x ). 如果f (x )和g (x )都是偶函数, 则 F (-x )=f (-x )+g (-x )=f (x )+g (x )=F (x ), 所以F (x )为偶函数, 即两个偶函数的和是偶函数. 如果f (x )和g (x )都是奇函数, 则F (-x )=f (-x )+g (-x )=-f (x )-g (x )=-F (x ), 所以F (x )为奇函数, 即两个奇函数的和是奇函数.(2)设F (x )=f (x )⋅g (x ). 如果f (x )和g (x )都是偶函数, 则 F (-x )=f (-x )⋅g (-x )=f (x )⋅g (x )=F (x ),所以F (x )为偶函数, 即两个偶函数的积是偶函数. 如果f (x )和g (x )都是奇函数, 则F (-x )=f (-x )⋅g (-x )=[-f (x )][-g (x )]=f (x )⋅g (x )=F (x ), 所以F (x )为偶函数, 即两个奇函数的积是偶函数. 如果f (x )是偶函数, 而g (x )是奇函数, 则F (-x )=f (-x )⋅g (-x )=f (x )[-g (x )]=-f (x )⋅g (x )=-F (x ), 所以F (x )为奇函数, 即偶函数与奇函数的积是奇函数.12. 下列函数中哪些是偶函数, 哪些是奇函数, 哪些既非奇函数又非偶函数?(1)y =x 2(1-x 2); (2)y =3x 2-x 3;(3)2211x x y +-=; (4)y =x (x -1)(x +1); (5)y =sin x -cos x +1;(6)2x x a a y -+=. 解 (1)因为f (-x )=(-x )2[1-(-x )2]=x 2(1-x 2)=f (x ), 所以f (x )是偶函数. (2)由f (-x )=3(-x )2-(-x )3=3x 2+x 3可见f (x )既非奇函数又非偶函数.(3)因为())(111)(1)(2222x f x x x x x f =+-=-+--=-, 所以f (x )是偶函数. (4)因为f (-x )=(-x )(-x -1)(-x +1)=-x (x +1)(x -1)=-f (x ), 所以f (x )是奇函数.(5)由f (-x )=sin(-x )-cos(-x )+1=-sin x -cos x +1可见f (x )既非奇函数又非偶函数.(6)因为)(22)()()(x f a a a a x f x x x x =+=+=-----, 所以f (x )是偶函数.13. 下列各函数中哪些是周期函数?对于周期函数, 指出其周期: (1)y =cos(x -2);解 是周期函数, 周期为l =2π. (2)y =cos 4x ;解 是周期函数, 周期为2π=l .(3)y =1+sin πx ;解 是周期函数, 周期为l =2. (4)y =x cos x ; 解 不是周期函数. (5)y =sin 2x .解 是周期函数, 周期为l =π.14. 求下列函数的反函数:(1)31+=x y 错误!未指定书签。
机电一体化课程表
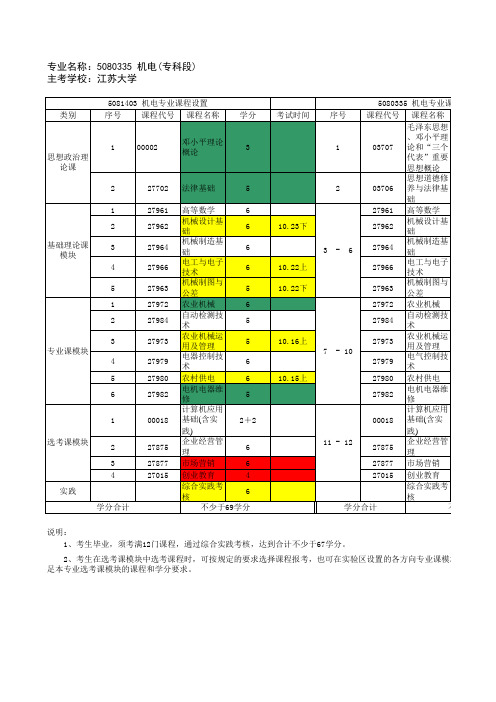
5 机电专业课程设置 学分
备注
4
必考 课程
8
2
6
6
任选4门课
6
程,不少于 23
23学分 6
5 6 5
5
任选4门课
程,不少于 22
6
22学分
6
5
2+2
任选2门课
6
程,不少于 10
10学分
6
4
6
6
不少于67学分
69
方向专业课模块中选择报考,但须满
00018
27875 27877 27015
高等数学
6
机械设计基 础
6
机械制造基 础
6
电工与电子 技术
6
机械制图与 公差
5
农业机械
6
自动检测技 术
5
农业机械运 用及管理
5
电器控制技 术
6
农村供电6电机电器维 Nhomakorabea修 计算机应用 基础(含实 践)
5 2+2
企业经营管 理
6
市场营销
6
创业教育
4
综合实践考 核
27877 市场营销
27015 创业教育
学分合计
综合实践考 核
不少于67学分
说明: 1、考生毕业,须考满12门课程,通过综合实践考核,达到合计不少于67学分。
2、考生在选考课模块中选考课程时,可按规定的要求选择课程报考,也可在实验区设置的各方向专业课模块中选择报考 足本专业选考课模块的课程和学分要求。
机械设计基 础 机械制造基 础 电工与电子 技术 机械制图与 公差
27972 农业机械
7 - 10
27984 27973 27979
同济六版七版高等数学课件
例1 脉冲发生器产生一个单三角脉冲,其波形如图
所示,写出电压U与时间
的函数关系式.
解
单三角脉冲信号的电压
例2 解
故
三、函数的特性
1.函数的有界性:
y M
y=f(x)
o
x
有界 X
-M
y M
o
X
x 无界
-M
2.函数的单调性:
y
o
x
y
o
x
3.函数的奇偶性:
y
-x o x
x
偶函数
y
-x
o
xx
意义 关于无穷大的讨论,都可归结为关于无穷小 的讨论.
四、小结
无穷小与无穷大是相对于过程而言的. 1、主要内容: 两个定义;四个定理;三个推论. 2、几点注意:
(1) 无穷小( 大)是变量,不能与很小(大)的数混 淆,零是唯一的无穷小的数; (2)无穷多个无穷小的代数和(乘积)未必是无穷小. (3) 无界变量未必是无穷大.
1.幂函数
2.指数函数
3.对数函数
4.三角函数 正弦函数
余弦函数
正切函数
余切函数
正割函数
余割函数
5.反三角函数
幂函数,指数函数,对数函数,三角函数和反 三角函数统称为基本初等函数.
二、复合函数 初等函数
1.复合函数
定义:
注意:1.不是任何两个函数都可以复合成一个复 合函数的;
一、基本概念
1.集合: 具有某种特定性质的事物的总体. 组成这个集合的事物称为该集合的元素.
有限集 无限集
数集分类: N----自然数集 Q----有理数集
数集间的关系:
Z----整数集 R----实数集
江苏自考27961高等数学大纲共10页文档
高纲1230江苏省高等教育自学考试大纲27961 高等数学江苏大学编江苏省高等教育自学考试委员会办公室一、课程性质及其设置目的与要求(一)课程性质和特点《高等数学》课程是我省高等教育自学考试理工类各专业的一门重要的公共基础课程,其任务是培养应考者系统地理解高等数学的基本概念和基本理论,掌握高等数学的基本方法。
是培养学生运算能力、抽象概括问题的能力、逻辑推理能力、综合运用所学知识分析和解决问题能力的课程,是学生学习后继课程和进一步获得近代科学技术知识的必备基础(二)本课程的考试目标本课程的考试目标是考查应考者的高等数学的基本概念、基本理论、基本方法和常用的运算技能,并以此检测应考者分析问题和解决问题的能力。
二、课程内容与考核目标第一章函数与极限(一)函数1.考试内容函数的定义,函数的表示法,分段函数,反函数,复合函数,隐函数,函数的性质(有界性、奇偶性、周期性、单调性),基本初等函数,初等函数。
2.考试要求(1)理解函数的概念,掌握函数的表示法,会求函数的定义域。
(2)理解函数的有界性、奇偶性、周期性和单调性。
(3)理解分段函数、反函数、复合函数、隐函数的概念。
(4)掌握基本初等函数的性质和图像。
理解初等函数的概念。
(5)会根据实际问题建立函数表达式。
(二)极限1.考试内容数列极限的定义和性质,函数极限的定义和性质,函数的左极限与右极限,无穷小和无穷大的概念及其关系,无穷小的性质和无穷小的比较,极限的四则运算法则,两个重要极限:2.考试要求(1)理解数列极限和函数极限的概念(2)会求数列的极限。
会求函数的极限(含左极限、右极限)。
了解函数在一点处极限存在的充分必要条件。
(3)掌握极限的性质和四则运算法则。
(4)理解无穷小和无穷大的概念。
掌握无穷小的性质、无穷小与无穷大的关系。
了解高阶、同阶、等价无穷小的概念。
会用等价无穷小求极限。
(5)掌握利用两个重要极限求极限的方法。
(三)连续1.考试内容函数连续的概念,连续函数的四则运算法则,复合函数的连续性,反函数的连续性,初等函数的连续性,闭区间上连续函数的性质(有界性定理,最大值、最小值定理和介值定理)。
2023年江苏省高等教育自学考试4月考试日程表
江苏省高等教育自学考试4月考试日程表
阐明: 1.部分专业考试计划中设置了不考外语旳换考课程, 为防止外语课程和其换考课程反复报考, 请应考者详细查看各专业考试计划后选择报考。
2.部分专业考试计划中安排了“实践”、“含实践”课程、专业综合技能考核或毕业论文(设计), 请考生于每次报名期间到网上报名系统查询考核时间和措施, 并按照规定报考。
3.“00018计算机应用基础”课程, 全省不统一组织考试。
考生凡获得全国计算机等级考试一级及以上证书者, 或获得全国计算机应用技术证书考试(NIT)《计算机操作基础》模块和其他任一模块(共两个模块)证书者, 可免考“00018计算机应用基础”课程(包括理论和实践两个部分)。
高等数学c教材目录
高等数学c教材目录1. 高等数学C教材目录本教材旨在为大学高等数学C课程提供全面、系统的教学内容。
通过深入浅出的讲解和丰富的例题,帮助学生建立起扎实的高等数学基础,提高数学分析和推理的能力。
以下是本教材的目录:第一章:数列与极限1.1 数列的概念与性质1.1.1 数列的定义1.1.2 数列的收敛性1.1.3 数列极限的性质1.2 函数极限与极限运算1.2.1 函数极限的定义1.2.2 函数极限的运算法则1.2.3 极限存在准则1.3 极限存在性的证明方法1.3.1 夹逼定理1.3.2 单调有界原理1.3.3 无穷小量的性质与运算第二章:一元函数微分学2.1 导数的概念与性质2.1.1 导数的定义2.1.2 导数的性质与运算法则 2.1.3 高阶导数2.2 导数的几何意义与应用2.2.1 切线与法线方程2.2.2 凹凸与拐点2.2.3 最值与最优化问题2.3 微分与高阶导数2.3.1 微分的概念与性质2.3.2 高阶导数的计算方法2.3.3 泰勒级数与近似计算第三章:一元函数积分学3.1 定积分的概念与性质3.1.1 定积分的定义3.1.2 定积分的性质与运算法则3.1.3 牛顿—莱布尼兹公式 3.2 不定积分与基本积分公式 3.2.1 不定积分的定义与性质 3.2.2 基本积分公式及其应用 3.2.3 分部积分与换元积分法 3.3 定积分的应用3.3.1 曲线长度与曲面面积 3.3.2 弧长与弓高问题3.3.3 物理应用案例分析第四章:常微分方程4.1 常微分方程的基本概念4.1.1 常微分方程的定义4.1.2 解的存在唯一性定理 4.1.3 初值问题与通解4.2 一阶常微分方程4.2.1 可分离变量方程4.2.2 一阶线性微分方程4.2.3 齐次方程与非齐次方程4.3 解的方法与特解形式4.3.1 可降阶的二阶微分方程4.3.2 常系数二阶线性微分方程 4.3.3 模拟解法与特解形式第五章:多元函数微分学5.1 多元函数的导数与偏导数5.1.1 多元函数的导数定义5.1.2 偏导数的概念与性质5.1.3 方向导数与梯度5.2 高阶偏导数与复合函数求导5.2.1 高阶偏导数的计算5.2.2 链式法则与隐函数求导5.2.3 多元函数极值的判定5.3 多元函数微分学的几何应用5.3.1 驻点与极值问题5.3.2 条件极值与拉格朗日乘数法5.3.3 二重积分的几何应用第六章:多元函数积分学6.1 二重积分的概念与性质6.1.1 二重积分的定义6.1.2 二重积分的计算与性质6.1.3 二重积分的应用6.2 三重积分与曲线、曲面积分6.2.1 三重积分的定义与计算6.2.2 三重积分的性质与应用6.2.3 曲线积分与曲面积分的概念 6.3 向量场与曲线、曲面积分6.3.1 向量场的定义与性质6.3.2 曲线积分的计算与应用6.3.3 曲面积分的计算与应用第七章:无穷级数7.1 收敛级数的概念与性质7.1.1 数项级数的定义7.1.2 正项级数的收敛性7.1.3 收敛级数的性质与判别法7.2 幂级数与泰勒级数7.2.1 幂级数的定义与性质7.2.2 幂级数的收敛域7.2.3 泰勒级数与函数展开7.3 函数项级数7.3.1 函数项级数的收敛性7.3.2 傅里叶级数与函数逼近通过本教材的学习,相信学生们能够系统地掌握高等数学C的核心概念和重要知识点,提高数学思维和解决实际问题的能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省高等教育自学考试大纲高纲123027961高等数学江苏大学编一、课程性质及其设置目的与要求(一)课程性质和特点《高等数学》课程是我省高等教育自学考试理工类各专业的一门重要的公共基础课程,其任务是培养应考者系统地理解高等数学的基本概念和基本理论,掌握高等数学的基本方法。
是培养学生运算能力、抽象概括问题的能力、逻辑推理能力、综合运用所学知识分析和解决问题能力的课程,是学生学习后继课程和进一步获得近代科学技术知识的必备基础(二)本课程的考试目标本课程的考试目标是考查应考者的高等数学的基本概念、基本理论、基本方法和常用的运算技能,并以此检测应考者分析问题和解决问题的能力。
二、课程内容与考核目标第一章函数与极限(一)函数1.考试内容函数的定义,函数的表示法,分段函数,反函数,复合函数,隐函数,函数的性质(有界性、奇偶性、周期性、单调性),基本初等函数,初等函数。
2.考试要求(1)理解函数的概念,掌握函数的表示法,会求函数的定义域。
(2)理解函数的有界性、奇偶性、周期性和单调性。
(3)理解分段函数、反函数、复合函数、隐函数的概念。
(4)掌握基本初等函数的性质和图像。
理解初等函数的概念。
(5)会根据实际问题建立函数表达式。
(二)极限1.考试内容数列极限的定义和性质,函数极限的定义和性质,函数的左极限与右极限,无穷小和无穷大的概念及其关系,无穷小的性质和无穷小的比较,极限的四则运算法则,两个重要极限:e 11lim 1sin lim 0=⎪⎭⎫ ⎝⎛+=→∞→xx x x xx 2.考试要求(1)理解数列极限和函数极限的概念 (2)会求数列的极限。
会求函数的极限(含左极限、右极限)。
了解函数在一点处极限存在的充分必要条件。
(3)掌握极限的性质和四则运算法则。
(4)理解无穷小和无穷大的概念。
掌握无穷小的性质、无穷小与无穷大的关系。
了解高阶、同阶、等价无穷小的概念。
会用等价无穷小求极限。
(5)掌握利用两个重要极限求极限的方法。
(三)连续1.考试内容函数连续的概念,连续函数的四则运算法则,复合函数的连续性,反函数的连续性,初等函数的连续性,闭区间上连续函数的性质(有界性定理,最大值、最小值定理和介值定理)。
2.考试要求(1)理解函数连续性的概念。
(2)掌握连续函数的四则运算法则。
(3)理解复合函数、反函数和初等函数的连续性。
(4)掌握闭区间上连续函数的性质,并会应用这些性质。
第二章 导数与微分1.考试内容导数和微分的定义,导数的几何意义,函数的可导性、可微性与连续性的关系,导数和微分的四则运算法则,导数和微分的基本公式,复合函数、反函数、隐函数求导法,高阶导数。
2.考试要求(1)理解导数的概念及其几何意义。
(2)理解函数可导性、可微性、连续性之间的关系。
(3)会求平面曲线的切线方程和法线方程。
(4)熟练掌握导数的基本公式、四则运算法则及复合函数的求导方法。
(5)会求反函数、隐函数的导数。
(6)了解高阶导数的概念。
会求简单函数的高阶导数。
(7)了解微分的概念。
了解微分的四则运算法则,会求函数的微分。
第三章导数的应用1.考试内容微分中值定理(罗尔定理、拉格朗日中值定理、柯西中值定理),洛必达法则,函数单调性的判别,函数的极值,函数的最大、最小值。
2.考试要求(1)理解并会应用罗尔定理、拉格朗日中值定理。
了解柯西中值定理。
(2)熟练掌握用洛必达法则求未定式极限的方法。
(3)掌握利用导数判断函数单调性的方法。
(4)理解函数极值的概念。
掌握求函数的极值与最大、最小值的方法,并会求解简单的应用问题。
第四章积分学(一)定积分1.考试内容定积分的概念和基本性质,定积分的几何意义,变上限积分定义的函数及其导数,牛顿-莱布尼茨公式。
2.考试要求(1)理解定积分的概念。
了解定积分的几何意义。
掌握定积分的基本性质。
(2)理解变上限积分作为其上限的函数的含义,会求这类函数的导数。
(3)掌握牛顿-莱布尼茨公式。
(二)不定积分1.考试内容原函数和不定积分的概念,不定积分的基本性质。
2.考试要求(1)理解原函数和不定积分的概念。
掌握不定积分的基本性质。
(2)熟练掌握不定积分的基本公式。
(三)定积分的运算1.考试内容不定积分的基本公式,不定积分换元积分法和分部积分法。
定积分的换元法和分部积分法。
2.考试要求(1)熟练掌握不定积分的第一类换元法,掌握不定积分的第二类换元法(仅限于三角代换与简单的根式代换)。
(2)熟练掌握不定积分的分部积分法。
(3)熟练掌握定积分的换元法和分部积分法。
(四)积分式的建立与积分应用1.考试内容元素法,定积分的应用(平面图形的面积、平行截面面积已知立体体积)。
2.考试要求(1)会用元素法建立简单积分式。
(2)会应用定积分计算平面图形的面积和平行截面面积已知立体的体积。
第五章二元函数微积分简介(一)二元函数的微分学1.考试内容二元函数的概念,二元函数的极限和连续性,一阶偏导数与全微分。
复合函数与隐函数的求导法。
二阶偏导数,二元函数的极值。
2.考试要求(1)了解二元函数的概念。
了解二元函数的极限和连续性的概念。
(2)理解偏导数的概念。
了解全微分的概念。
(3)会求二元函数的一阶、二阶偏导数,会求二元函数的全微分。
(4)掌握复合函数一阶偏导数的求法。
(5)会求由方程f(x,y,z)=0所确定的隐函数z=z(x,y)的一阶偏导数。
(6)了解二元函数极值存在的必要条件、充分条件。
会求二元函数的极值。
(二)二元函数的积分学1.考试内容二重积分的概念与性质二重积分的计算法2.考试要求(1)了解二重积分的概念与性质。
(2)掌握在直角坐标系下二重积分的计算方法,会交换积分次序。
三、有关说明和实施要求(一)关于“课程内容与考核目标”中有关提法的说明本大纲对内容的要求由低到高。
对概念和理论分为“了解、理解”两个层次,对方法和运算分为“会、掌握、熟练掌握”三个层次。
它们的含义是:1.理解:要求应考者能够记忆规定的有关知识点的主要内容,并能够清晰明白规定的有关知识点的内涵与外延,熟悉其内容要点和它们之间的区别与联系,并能根据考核的不同要求,做出正确的解释、说明和阐述。
2.了解:要求应考者能够记忆规定的有关知识点的主要内容,能够知道内容要点之间的区别与联系。
3.领会:是指应考者能够用相关知识点的知识求解简单的问题。
4.掌握:要求应考者正确理解和记忆相关知识点内容的原理、方法步骤,并能用来求解一般性问题。
5.熟练掌握:要求应考者必须准确理解课程中的核心内容和重要知识点的方法技巧等,并能熟练用来求解较为综合的问题。
(二)自学教材本课程使用教材为:《高等数学》(基础篇),主编邱曙熙厦门大学出版社2008年7月第1版(三)自学方法的指导本课程作为一门的公共基础课程,综合性强、内容多、难度大,应考者在自学过程中应该注意以下几点:1.学习前,应仔细阅读课程大纲的第一部分,了解课程的性质、地位和任务,熟悉课程的基本要求以及本课程与有关课程的联系,使以后的学习紧紧围绕课程的基本要求。
2.在阅读某一章教材内容前,应先认真阅读大纲中该章的考核知识点、自学要求和考核要求,注意对各知识点的能力层次要求,以便在阅读教材时做到心中有数。
3.阅读教材时,应根据大纲要求,要逐段细读,逐句推敲,集中精力,吃透每个知识点。
对基本概念必须深刻理解,基本原理必须牢固掌握。
4.学完教材的每一章节内容后,应认真完成教材中的习题和自测题,这一过程可有效地帮助自学者理解、消化和巩固所学的知识,增加分析问题、解决问题的能力。
(四)对社会助学的要求1.应熟知考试大纲对课程所提出的总的要求和各章的知识点。
2.应掌握各知识点要求达到的层次,并深刻理解各知识点的考核要求。
3.对应考者进行辅导时,应以指定的教材为基础,以考试大纲为依据,不要随意增删内容,一面与考试大纲脱节。
4.辅导时应对应考者进行学习方法的指导,提倡应考者“认真阅读教材,刻苦钻研教材,主动提出问题,依靠自己学懂”的学习方法。
5.辅导时要注意基础、突出重点,要帮助应考者对课程内容建立一个整体的概念,对应考者提出的问题,应以启发引导为主。
6.注意对应考者能力的培养,特别是自学能力的培养,要引导应考者逐步学会独立学习,在自学过程中善于提出问题、分析问题、做出判断和解决问题。
7.要使应考者了解试题难易与能力层次高低两者不完全是一回事,在各个能力层次中都存在着不同难度的试题。
(五)关于命题和考试的若干规定1.本大纲各章所提到的考核要求中,各条细目都是考试的内容,试题覆盖到章,适当突出重点章节,加大重点内容的覆盖密度。
2.试卷对不同能力层次要求的试题所占的比例大致是:“会”20%,“掌握”40%,“熟练掌握”为40%。
3.试题难易程度要合理,可分为四档:易、较易、较难、难,这四档在各份试卷中所占的比例约为2∶3∶3∶2。
4.本课程考试试卷可能采用的题型有:单项选择题、填空题、简答题及综合题等类型(见附录题型示例)。
5.考试方式为闭卷笔试,考试时间为120分钟。
评分采用百分制,60分为及格。
附录题型举例一、选择题如:设函数)(xf在(−∞,+∞)内有定义,且0)(>xf,函数()()2)(axfaxfxF-+=(其中a为常数),则在(−∞,+∞)内)(xF为答:[]A.奇函数 B.偶函数C.非奇非偶函数 D.奇偶性与a有关的函数二、填空题如:.1limxxxx→∞-⎛⎫=⎪⎝⎭__________。
三、简答题如:中心法则如:设平面曲线的方程为33222=+-yxyx,求曲线上点(2,1)处的切线方程。
再如:求极限2sinlimsinxx xx x→-。
四、综合题如:求22(1)d dDx y x y--⎰⎰,其中D是由22,0,1y x y x y==+=在第一象限内所围成的区域。
