2.运筹学_整数规划案例
简单的运筹学实际应用案例

简单的运筹学实际应用案例运筹学(Operations Research)是一门研究如何有效利用有限资源进行决策的学科,它通过数学、统计学和经济学等方法,帮助管理者做出最佳决策。
下面将介绍几个简单的运筹学实际应用案例。
1.生产线优化假设一公司拥有多条生产线,每条生产线对应不同的产品。
公司希望通过优化生产线的调度,以达到最大的产出和利润。
运筹学可以通过数学模型和算法,对生产线进行优化调度。
例如,可以使用线性规划模型来确定每条生产线的产量和调度,以最大化总利润;也可以使用整数规划模型来考虑生产线的限制和约束条件。
2.物流网络设计一家物流公司需要设计其物流网络,以最小化成本并满足客户对快速物流的需求。
运筹学可以通过数学模型和算法,帮助物流公司优化物流网络的设计。
例如,可以使用网络流模型来确定货物在物流网络中的最佳路线和节点,以最小化总运输成本;也可以使用线性规划模型来决定在不同节点上的仓库和货物库存量,以满足客户的需求。
3.航班调度问题一家航空公司需要制定最佳航班调度计划,以最大化航班利润并排除延误风险。
运筹学可以通过数学模型和算法,帮助航空公司优化航班调度。
例如,可以使用线性规划模型来决定不同航班的起降时间和机型,以最大化航班利润;也可以使用排队论模型来评估航班的延误风险,并制定相应的调度策略。
4.人员调度问题一家超市需要制定最佳的员工调度计划,以最大化服务质量和节约人力成本。
运筹学可以通过数学模型和算法,帮助超市优化员工调度。
例如,可以使用整数规划模型来决定不同时间段需要多少员工,并考虑员工的技能匹配和工作时间的合理安排;也可以使用模拟仿真方法来评估不同调度策略的效果,并做出相应的决策。
以上是几个简单的运筹学实际应用案例,运筹学在实际生产和管理中有着广泛的应用。
通过数学模型和算法的应用,可以帮助企业优化资源配置、提高效率和决策质量,从而实现最佳的经济效益。
整数规划解法与实际案例分析

整数规划解法与实际案例分析整数规划是运筹学中的一个重要分支,它在实际问题中有着广泛的应用。
整数规划问题是指决策变量被限制为整数的线性规划问题,通常用于需要做出离散决策的情况。
在本文中,我们将介绍整数规划的基本概念和解法,并结合一个实际案例进行分析,以帮助读者更好地理解整数规划的应用。
### 整数规划的基本概念整数规划是一种特殊的线性规划问题,其决策变量被限制为整数。
一般来说,整数规划可以分为纯整数规划和混合整数规划两种情况。
纯整数规划要求所有的决策变量都是整数,而混合整数规划则允许部分决策变量为整数,部分为连续变量。
整数规划可以用数学模型来描述,通常形式如下:$$\begin{aligned}\text{Maximize} \quad & c^Tx \\\text{Subject to} \quad & Ax \leq b \\& x \in \mathbb{Z}^n\end{aligned}$$其中,$c$、$x$、$b$ 分别为目标函数系数向量、决策变量向量和约束条件右端常数向量,$A$ 为约束条件系数矩阵,$x \in\mathbb{Z}^n$ 表示 $x$ 是一个整数向量。
### 整数规划的解法整数规划问题的求解相对复杂,因为整数约束使得问题的解空间不再是连续的,而是离散的。
针对整数规划问题,通常有以下几种解法:1. **穷举法**:穷举法是最直接的方法,即枚举所有可能的整数解,然后逐一计算目标函数值,找出最优解。
然而,穷举法在问题规模较大时会变得非常低效。
2. **分支定界法**:分支定界法是一种常用的整数规划求解方法。
它通过不断将整数规划问题分解为子问题,并对子问题进行求解,直到找到最优解为止。
3. **割平面法**:割平面法是一种基于线性规划的整数规划求解方法。
它通过不断添加线性不等式约束(割平面)来逼近整数解,直到找到最优解为止。
4. **分支定价法**:分支定价法是一种高级的整数规划求解方法,通常用于解决混合整数规划问题。
运筹学中整数规划问题的近似算法

运筹学中整数规划问题的近似算法运筹学是一门研究如何在有限资源下做最优决策的学科,其中整数规划是其中一种重要的决策方法。
整数规划问题是指在线性规划问题的基础上,对决策变量的取值加以限定,限定为整数值。
整数规划问题在实际应用中非常常见,例如优化生产计划、物流配送、资源分配等。
然而,整数规划问题的解空间通常是离散的,由于整数规划问题的NP难解性质,寻找准确解的效率很低,因此近似算法成为解决整数规划问题的重要手段。
一、近似算法的概念近似算法是指在可接受的误差范围内,通过有效的计算方法得到问题的近似最优解。
在整数规划问题中,近似算法主要通过松弛约束条件、局部搜索等方法寻找问题的近似解。
二、近似算法的分类近似算法可以根据问题的特性和解决方法的不同进行分类,下面介绍几种常见的近似算法。
1. 线性松弛算法(Linear Relaxation)线性松弛算法是整数规划问题中常用的近似算法之一。
该算法的基本思想是将整数规划问题的整数约束放宽为实数约束,得到一个线性规划问题。
然后通过求解线性规划问题的松弛解,并将松弛解的整数部分作为整数规划问题的一个近似解。
2. 近似局部搜索算法(Approximate Local Search)近似局部搜索算法通过在整数规划问题的解空间中进行局部搜索,通过一系列的改进和优化策略来逐步提高解的质量。
该算法在每一步都根据某种准则选择当前最优解,并通过局部搜索来寻找局部最优解。
然后,通过重复进行局部搜索和改进操作,逐渐向全局最优解靠近。
3. 启发式算法(Heuristic Algorithm)启发式算法是一种基于经验和直觉的算法,通过在可行解空间中搜索一组近似解,并根据某种评价准则选择最优解。
在解决整数规划问题时,启发式算法通过寻找有效的近似解,来替代寻找准确解,从而节省计算资源和时间。
三、近似算法的应用案例近似算法在实际问题中有广泛的应用,下面以物流配送问题为例,介绍近似算法的应用。
假设某物流公司需要将一批货物从仓库分配到多个客户,其中仓库和客户的位置已知,货物的需求和供应量也已知。
运筹学基础-整数规划(2)
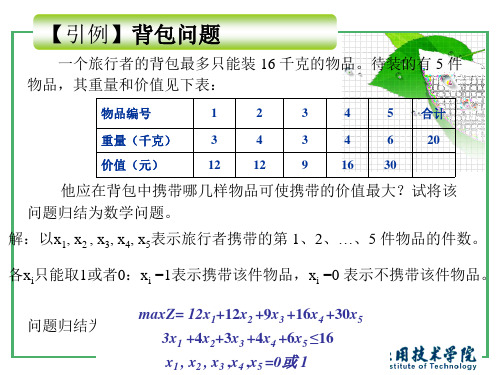
【例 2 】求解 0-1 规划最优解
minZ= 4x1+3x2 +2x3 2x1 -5x2+3x3 ≤4 (1) 4x1 + x2+3x3 ≥3 (2) x2+x3 ≥1 (3) x1 , x2 , x3 =0或 1
解: 先将问题化为如下的标准问题
minZ= 4x1+3x2 +2x3 2x1 - 5x2+3x3 ≤4 (1) - 4x1 - x2 - 3x3 ≤-3 (2) (3) - x2 - x3 ≤ - 1 x1 , x2 , x3 =0或 1
0 13 aij-列min 6 (0) 0 (0) 5 0 0 1 (0) 7 0 6 9 3 2 0 (0) 0 2 15 10 4 9 14 7 8 13 14 16 11 4 15 13 9
(a)从行开始,对只有一个的零元素,打上(),用直线划去所在列 (b)再从列开始,对只有一个的零元素,打上(),用直线划去所在行
∑ ∑
指派问题的解法--匈牙利法 指派问题的解法--匈牙利法 --
从时间表(效率表)出发构建效率矩阵 效率矩阵。 效率矩阵
时间表
任务 人员 甲 乙 丙 丁 E 2 10 9 7 J 15 4 14 8 G 13 14 16 11 R 4 15 13 9
2 15 10 4 9 14 7 8
13 14 16 11
分配表
任务 人员 甲 乙 丙 丁
合计
E x11 x21 x31 x41 1
i
J x12 x22 x32 x42 1
G x13 x23 x33 x43 1
ij x ij
R x14 x24 x34 x44 1
合计
1 1 1 1
运筹学 第八章(二)

所需时间 工人 工作 小时) (小时) A 15 19 26 19 B 18 23 17 21 C 21 22 16 23 D 24 18 19 17
甲 乙 丙 丁
8
引入0—1变量 x ij,并令 解: 引入 变量 当指派第 i 个人去完成第 j 项工作时 ; 1 , x ij = 0 , 当不指派第 i 个人去完成第 j 项工作时 . 使总消耗时间最少,则目标函数为: 使总消耗时间最少,则目标函数为: min z = 15 x11 + 18 x12 + 21x13 + 24 x14 + 19 x21 + 23 x22 + 22 x23 + 18 x24 + 26 x31 + 17 x32 + 16 x33 + 19 x34 + 19 x41 + 21x42 + 23 x43 + 17 x44 . 每人只能干一项工作的约束条件可以写为: 每人只能干一项工作的约束条件可以写为: x11 + x12 + x13 + x14 = 1, (甲只干一项工作) 甲只干一项工作)
项任务的成本(如所需时间, 并设 c ij 第 i 个人去完成 j 项任务的成本(如所需时间,费用 等),则一般指派问题的数学模型为: ),则一般指派问题的数学模型为: 则一般指派问题的数学模型为
运筹学基础及应用_(第四章_整数规划与分配问题)

(d) 8
(e)1号、
4号、6号、9号开采时不能超过两个,试表示上
述约束条件。
Next
基础教研室
(a)当x8=1 当x8=0 ∴ x8 x6
x6=1,x6≠0 x6=1,x6=0
(b)当x5 =1 当x5 =0 ∴ x5 + x3 1
x3=0, x3 ≠1 x3=0, x3 =1
基础教研室
【例1】求下述整数规划的最优解
Max z= 3x1 + 2x2 st . 2x1 + 3x2 14 x1 + 0.5x2 4.5 x10,x20,且为整数
基础教研室
x2 x1+0.5x2=4.5
4
(3.25, 2.5) 2 2x1+3x2=14
2
4
6
x1
3x1+2x2=6
二、整数规划的求解方法
1 -选择电网供应 设 y1 0 -不选择电网供应
10 d j x j f (1 y1 ) M j 1 10 0.3d j x j p (1 y2 ) M j 1 y1 y2 1 y1 , y2 0或1
基础教研室
【例3】投资决策问题 某公司准备1000万元资金在10个地点中选择若干个建立 工厂(工厂名称用地点名来命名),有关数据如下:
由于各个工厂之间有配套和协作关系,因此必须满足条件: 1、 建工厂1就必须同时建工厂2; 2、 若建工厂2就不允许建工厂3; 3、 工厂4和工厂5至少建一个; 4、 工厂6,7,8恰好建2个; 5、 工厂8,9,10最多建2个; 6、 建工厂4或者建工厂6,就不能建工厂8,反过来也一样; 7、 条件2,3,5最多满足2个。 问选择哪几个地点建厂最有利? Next
第六章 运筹学 整数规划案例
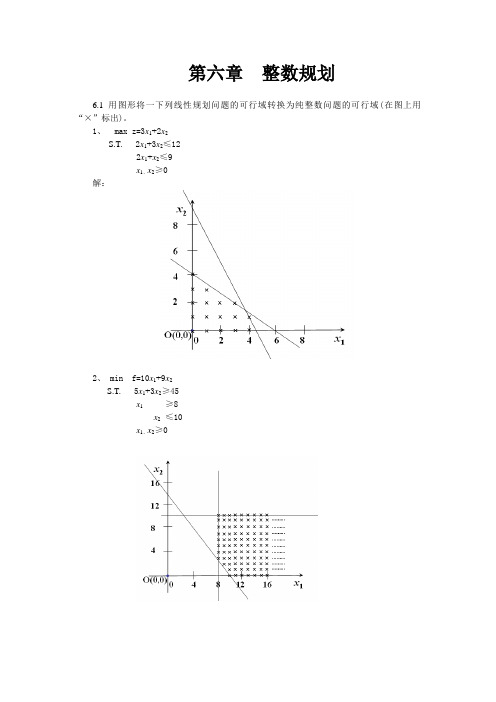
第六章整数规划6.1 用图形将一下列线性规划问题的可行域转换为纯整数问题的可行域(在图上用“×”标出)。
1、 max z=3x1+2x2S.T. 2x1+3x2≤122x1+x2≤9x1、x2≥0解:2、 min f=10x1+9x2S.T. 5x1+3x2≥45x1≥8x2≤10x1、x2≥06.2 求解下列整数规划问题1、 min f=4x1+3x2+2x3S.T. 2x1-5x2+3x3≤44x1+x2+3x3≥3x2+x3≥1x1、x2、x3=0或1解:最优解(0,0,1),最优值:22、 min f=2x1+5x2+3x3+4x3S.T. -4x1+x2+x3+x4≥2-2x1+4x2+2x2+4x2≥4x1+x2-x2+x2≥3x1、x2、x3、x3=0或1解:此模型没有可行解。
3、max Z=2x1+3x2+5x3+6x4S.T. 5x1+3x2+3x3+x4≤302x1+5x2-x2+3x2≤20-x1+3x2+5x2+3x2≤403x1-x2+3x2+5x2≤25x1、x2、x3、x3=正整数解:最优解(0,3,4,3),最优值:474、min z =8x1 +4 x2+3 x3+5 x4+2 x5+3 x6+4 x7+3 x8+4 x9+9 x10+7 x11+5 x12 +10 x13+4 x14+2 x15+175 x16+300 x17+375 x18 +500 x19约束条件x1 + x2+x3≤30x4+ x5+x6-10 x16≤0x7+ x8+x9-20 x17≤0x10+ x11+x12-30 x18≤0x13+ x14+x15-40 x19≤0x1 + x4+ x7+x10+ x13=30x2 + x5+ x8+x11+ x14=20x3 + x6+ x9+x12+ x15=20x i为非负数(i=1,2…..8)x i为非负整数(i=9,10…..15)x i为为0-1变量(i=16,17…..19)解:最优解(30,0,0,0,0,0,0,0,0,0,0,0,0,20,20,0,0,0,1),最优值:8606.3 一餐饮企业准备在全市范围内扩展业务,将从已拟定的14个点中确定8个点建立分店,由于地理位置、环境条件不同,建每个分店所用的费用将有所不同,现拟定的14个店的费用情况如下表:公司办公会决定选择原则如下:(1)B5、B3和B7只能选择一个。
运筹学01整数规划

第四节 0-1整数规划
• 问题的提出:
0-1整数规划是线性规划及整数规划的一种特殊形式。 模型结构和形式是线性规划,只是决策变量取0或1。 例1:投资场所的选定——相互排斥的计划 某公司拟在城市的东、西、南三区建立分公司,拟议中有七 个位置Ai(i=1, 2,…,7), 规定在东区A1,A2,A3个点中至多选二个; 在 西区A4,A5两点中至少选一个; 在南区A6,A7中至少选一个, 如选用Ai 点,设备投资估计为bi元, 每年可获利润估计为ci元, 但投资总额不能 超过B元, 问应选择哪几个点可年利润最大?
解:求解过程见下表
(x1,x2,x3) (0,0,0)
(0,0,1) (0,1,0) (0,1,1) (1,0,0) (1,0,1) (1,1,0) (1,1,1)
Z值 0 5 -2 3 3 8 1 6
约束条件
过滤条件 Z0 Z5
Z8
所以,最优解为(x1,x2,x3)T=(1,0,1)T, 最优值为8.
令
xi
1
0
当Ai点被选用 当Ai点未被选用
i=1, …,7
7
max Z c i x i
i1
7
bixi
B
i1
x1 x 2 x 3 2
s .t
x
4
x5
1
x
0 or 1
例2: 相互排斥的约束条件
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
背包问题应用(作业) 要把7种规格的包装箱装到两辆铁路平板车上去,包装 箱的宽和高相同,但厚度和重量不同,见下表:
每辆车有10.2m长的地方可以用来装箱(类似面包片), 载重为40吨。C5, C6 , C7 ,三类包箱所占总空间 (厚度)不超过302.7cm,试建立数学模型,尽量将这 些包装箱装到平板车上去,使浪费的空间最小。
地区1 地区2 地区3 地区4 地区5 地区6 0 10 16 28 27 20 10 0 24 32 17 10 16 24 0 12 27 21 28 32 12 0 15 25 27 17 27 15 0 14 20 10 21 25 14 0
解:Xj=1表地区设消防站, Xj=0表地区不设消 防站。Z=消防站总数,则模型如下: MinZ=X1+X2+X3+X4+X5+X6 s.t: X1+X2≥1 X1+X2+X6≥1 X3+X4≥1 X3+X4+X5≥1 X4+X5+X6≥1 X2+X5+X6≥1 Xj=0,1;j=1,2,3,4,5,6。
20
15
18
14
8
4
10
解:
令xi=1表示登山队员携带物品i,xi=0表示 不带物品i。则问题可写为: Max z =20x1+15x2+18x3 +14x4+8x5+4x6+10x7 s.t. 5x1+ 5x2 + 2x3 +6x4+12x5+2x6+4x7≤25 xi=1或0,i=1,2,…,7
min z cij xij ai yi
i 1 j 1 i 1 n ij n m
上述问题的数学模型为
x
j 1 m
Di yi,i 1,2, ,m b j,j 1,2, , n
x
i 1
ij
xij 0,yi 0或1
4.集合覆盖和布点问题
集合覆盖问题也是典型的整数规划问题,在集合 覆盖问题中,一个给定集合(集合一)的每一个元素 必须被另一个集合(集合二)的元素所覆盖。在满足 覆盖集合一所有元素的前提下,集合覆盖问题的目标 是求需要的集合二的元素最少,该问题之所以又称为 布点问题,是因为它常被用于一些公共设施,如:学 校、医院、商业区、消防队等设施的布点问题,解决 如何既满足公共要求,又使布的点最少,以节约投资 费用。
该公司只有600万元资金可用于投资,由于技术上 的原因,投资受到以下约束:①在项目1、2和3中必须 有一项被选中;②项目3和4只能选一项;③项目5被选 中的前提是项目1必须被选中。问如何在上述条件下选 择一个最好的投资方案,使投资收益最大。
解:
令0-1变量为决策变量,即xi=1表示选中项目i, 否则xi=0表示项目i未被选中。则模型可以表示为:
0-1变量的作用
1. xj= 1…方案j被选中
0…方案j未被选中
2. 从n个方案中必须选中一个: 3. 从n个方案中最多选中m个:
x
x
j 1
n
j 1 n
j
1
m
j
4. 方案i只有在方案j选中时,才可能被选中:
xi x j
5. 方案i与方案j是否选中是同时的:
xi x j
与0-1变量相关的几个实际问题
某市有8个区,救护车从一个区开往另一个区所需时间:
该市只有两辆救护车,且希望救护车,所在的位置能使 尽可能多的人口位于救护车在两分钟内可达到的范围内 ,请帮助该市构造一个整数规划模型来解决这个问题。
5. 指派问题
在生活中经常遇到这样的问题,某单位需要 完成n项任务,恰好有n个人可以承担这些任务, 由于每个人的专长不同,个人完成不同任务的效 率(时间、费用等)也不同。 于是产生了指派哪个人去完成哪项任务,使总 效率最高,称为指派问题(Assignment Problem)。
例2 :一登山队员做登山准备,他需要携带的物品有: 食品、氧气、冰镐、绳索、帐篷、照相机和通讯设备 每种物品的重要系数和重量如下表所示,假定登山队 员可携带的最大重量为25千克。问他如何抉择?
序号 物品 重量 (千克)
1
2
3
冰镐
4
绳索
5
帐篷
6
照相 器材
7
通讯 设备
食品 氧气
5
5
2
6
12
2
4
重要系数
3. 工厂选址运输问题
例3.一公司考虑在四个城市:北京、上海、广州和武汉设立库房。 这些库房负责向三个地区:华北、华中和华南地区发运货物,每 个库房每月可处理货物1000件。在北京设库房每月的成本为4.5万 元。上海为5万元,广州为7万元,武汉为4万元。每个地区的月平 均需求量为:华北每月600件,华中每月700件,华南每月800件。 发运货物的费用(元/件)见下表:
max c j x j
j 1 n
则可得到如下整数规划问题: a j x j b
j 1
x j 0或1,j 1, ,n 2,
例1:华美公司有5个项目被列入投资计划,各项目的投 资额和期望的投资收益见下表:
项目 1 2 3 4 5 投资额(万元) 210 300 100 130 260 投资收益(万元) 150 210 60 80 180
作业
区号 1 2 3 4 5 6 7 8 1 0 2 4 6 8 9 8 10 2 2 0 5 4 8 6 12 9 3 4 5 0 2 2 3 5 7 4 6 4 2 0 3 2 5 4 5 8 8 2 3 0 2 2 4 6 9 6 3 2 2 0 3 2 7 8 12 5 5 2 3 0 2 8 10 9 7 4 4 2 2 0 人口(万人) 40 30 35 20 15 50 45 60
华北 北京 上海 广州 武汉 200 300 600 300 华中 400 250 400 150 华南 500 450 250 350
公司希望在满足地区需要的前提下使平均月成本最小,且还 要满足以下条件:①如果在上海设立库房,则必须也在武汉设库 房;②最多设立三个库房;③武汉和广州不能同时设立库房。 请建立一个满足上述要求的整数规划模型。
整数规划建模
应用最广泛的整数规划问题是各种类型的决策问 题,决策者希望模型能回答诸如:是否要执行某些项 目(或某些活动),在什么时候或什么地点执行等决 策问题,回答这类“是—否”或“有—无”问题可借助整 数规划中的0-1整数变量。 0-1整数变量只有两个选择,0由于它在数学上的 特性可以很好的代表“无”或“否”,而1则可以很好地 表“有”或“是”。0-1变量由于它的特殊性也被称为二 制变量、决策变量或3;210x2 +60x3 +80x4 +180x5 s.t. 210x1 +300x2 +100x3 +130x4 +260x5 x1 +x2 +x3 x3 +x4 x1 -x5 x1, x2, x 3, x 4, x 5=0 ≤600 =1 =1 ≥0 或1
2. 背包问题
5.指派问题(作业) A 仰泳
37.7 43.3
B
32.9 33.1
C
33.8 42.2
D
37.0 34.9
E
35.4 41.8
蛙泳 蝶泳
自由泳
33.3
29.2
28.5
26.4
38.9
29.6
30.4
28.5
33.6
31.1
已知上面5名运动员各种姿势游泳成绩(50m), 试问如何从中选拔一个200m混合泳的接力队,使预期 比赛成绩最好。(列出整数规划模型)
y3+y4 ≤ 1
工厂选址运输问题
设有n个需求点,有m个可供选择的厂址, 每个厂址只能建一个工厂,在i处建厂,生产 能力为Di,单位时间的固定成本为ai,需求点 j的需求量为bj,从厂址i到需求点j的单位运费 为Cij,问应如何选择厂址才能获得经济上的总 花费最小的方案。
设在单位时间内,从厂址i运往需 求点j的产品数量为xij, 1…在i地建厂 引入0-1变量yi= 0…否则 设在单位时间内的总花费为z,则 m
设每个月从仓库i运往地区j的产品的货物数量为xij,引入0- 1变量yi= 1表示在Ai设立仓库,否则不设。 设每个月的总花费为z,则上述问题的数学模型为 Min z=200x11+400x12+500x13+300x21+250x22+450x23 +600x31+400x32+250x33+300x41+150x42+350x43+45000y1+5000 0y2+70000y3+40000y4 s.t. x11+x12+x13≤1000y1 x21+x22+x23≤1000y2 x31+x32+x33≤1000y3 x41+x42+x43≤1000y4 x11+x21+x31+x41≥600 x12+x22+x32+x42≥700 x13+x23+x33+x43≥800 y2-y4≤0 y1+y2+y3+y4≤3
1. 投资问题 现有总额为b的资金可用于投资,共有n个项目可 供投资者选择,已知项目j所需投资额为aj,投资后可 得利润cj(j = 1,2,…,n),不妨设b,aj,cj 均是 整数,试问为使所得利润最大,应选取那些项目进行 投资? 1…对项目j投资 先引入0-1变量xj,令 xj= 0…否则 n
背包问题由来以久,它是从旅行者如何选择放在 背包中的用品引出的。 旅行者可背负的重量有限,但旅行者需要携带的 物品很多,如:食品、水、衣物、帐篷、急救用品等 等,旅行者不可能将所有想携带的物品都统统背上, 他只能选择那些最重要的物品随身携带,又不超过他 可能负担的最大重量,为解决这个问题,旅行者可给 每种物品指定一个重要性系数,他的目标是在小于一 定重量的前提下,使所携带的物品的重要性系数之和 最大。
