高中数学A版2.3.2离散型随机变量的方差优秀课件
合集下载
高中数学2-3-2 离散型随机变量的方差 名师公开课市级获奖课件(人教A版选修2-3)
0.2 0.3 0.2 0.1
∴ D(2X － 1) ＝ ( － 1 － 2.6)2×0.2 ＋ (1 － 2.6)2×0.2 ＋ (3 － 2.6)2×0.3＋(5－2.6)2×0.2＋(7－2.6)2×0.1＝6.24. 方法 2：利用方差的性质 D(aX＋b)＝a2D(X)． ∵D(X)＝1.56. ∴D(2X－1)＝4D(X)＝4×1.56＝6.24.
2 ( x － E ( X )) 则 i 描述了 x (i＝1,2，…，n)相对于均值 E(X)的
i
偏离程度，而 D(X)＝
i＝1
xi－EX2pi
n
为这些偏离程度的加权
平均，刻画了随机变量 X 与其均值 E(X)的 平均偏离程度． 我 们称 D(X)为随机变量 X 的方差，其算术平方根 DX为随机变 量 X 的 标准差．
[答案]
[ 解析 ]
B．2 和 2.4 D．6 和 5.6
B
∵ X ～ B(10,0.6) ，∴ E(X) ＝ 10×0.6 ＝ 6 ， D(X) ＝
10×0.6×(1－0.6)＝2.4， ∴E(η)＝8－E(X)＝2，D(η)＝(－1)2D(X)＝2.4.
建模应用引路
方差的实际应用
A、B 是治疗同一种疾病的两种药，用若干试验组 进行对比实验． 每个试验组由 4 只小白鼠组成， 其中 2 只服用 A， 另 2 只服用 B，然后观察疗效．若在一个试验组中，服用 A 有效 的小白鼠的只数比服用 B 有效的多， 就称该试验组为甲类组． 设 2 1 每只小白鼠服用 A 有效的概率为 ，服用 B 有效的概率为 . 3 2 (1)求一个试验组为甲类组的概率； (2)观察 3 个试验组，用 ξ 表示这 3 个试验组中甲类组的个 数，求 ξ 的分布列和数学期望．
《离散型随机变量的方差》人教版高中数学选修2-3PPT课件(第2.3.2课时)
课堂练习
1.填空 （1）已知x~B(100,0.5),则
Ex=_5_0_,Dx=__2_5_,sx=_5__. E(2x-1)=__9_9_, D(2x-1)=_1_0_0_, s(2x-1)=__1_0__.
课堂练习
2.选择
x
1
2
P
0.3
0.7
（1）已知随机变量x的分布列如上表,则E x与D x的值为( )
EX1 = 1200 0.4 + 1 4பைடு நூலகம்0 0.3 + 1600 0.2 + 1800 0.1 = 1400
DX1 = (1200 -1400) 2 0. 4 + (1400 -1400 ) 2 0.3 + (1600 -1400 )2 0.2
+ (1800 -1400) 2 0. 1 = 40 000
P（ξ=0）= 9 3 12 4
②当ξ=1时，即第一次取出次品，第二次取得正品，试验停止，则
P（ξ=1）= 3 9 9 12 11 44
课堂练习
继续答题
③当ξ=2时，即第一、二次取出次品，第三次取得正品，试验停止，则
P（ξ=2）=
329 = 9 12 11 10 220
④当ξ=3时，即第一、二、三次取出次品，第四次取得正品，试验停止，则
变量 X 的方差(variance). 其算术平方根 DX 为随机变量X的标准差(standard deviation). 记为 σX
随机变量的方差和标准差都反映了随机变量取值偏离于均值的平均程度.方差或标准差越小，则随 机变量偏离于均值的平均程度越小.
新知探究
说明：随机变量集中的位置是随机变量的均值；方差或标准差这种度量指标是一种加权平均的度 量指标. 思考 随机变量的方差与样本的方差有何联系与区别? 随机变量的方差是常数，而样本的方差是随着样本的不同而变化的，因此样本的方差是随机变量. 对于简单随机样本，随着样本容量的增加，样本方差越来越接近总体方差，因此常用样本方差来 估计总体方差.
2016-2017学年高中数学人教A版选修2-3课件：2.3.2离散型随机变量的方差
7.错用公式DaX＋b＝a2DX
[典例] X P 已知随机变量 X 的分布列如下表： －2 0.1 －1 0.2 0 0.4 1 0.1 2 0.2
且 Y＝3X＋1，求 E(Y)，D(Y)．
[解] 因 为 E(X) ＝ － 2×0.1 ＋ ( － 1)×0.2 ＋ 0×0.4 ＋
1×0.1＋2×0.2＝0.1， 所以 E(Y)＝E(3X＋1)＝3E(X)＋1＝1.3.
刻画了随机变量 X 与其均值 E(X)的平均偏离程度． 称 D(X)为随机
算术平方根 DX 为随机变量 X 的标准差． 变量 X 的方差，其__________________
2．意义 随机变量的方差和标准差都反映了随机变量取值偏离平均值 的平均程度．方差或标准差 越小 ，则随机变量偏离于均值的平均 程度 越小 ． 3．性质
若 E(X)＝0，D(X)＝1，则 a＝______，b＝______.
解析：由题意得 a＋b＋c＋ 1 ＝1， 12 1 －1×a＋0×b＋1×c＋2× ＝0， 12 1 2 2 2 2 －1－0 ×a＋0－0 ×b＋1－0 ×c＋2－0 ×12＝1， 5 1 解得 a＝12，b＝c＝4. 5 答案：12 1 4
2
答案：A
2．已知 ξ～B(n，p)，E(ξ)＝8，D(ξ)＝1.6，则 n 与 p 的值分别 为 A．100 和 0.08 C．10 和 0.2 B．20 和 0.4 D．10 和 0.8 ( )
解析：由于
np＝8， ξ～B(n，p)，所以 np1－p＝1.6，
解得 n＝10，p＝0.8. 答案：D
[类题通法] 解此类问题，首先要确定正确的离散型随机变量，然 后确定它是否服从特殊分布，若它服从两点分布，则其方 差为 p(1－p)； 若其服从二项分布， 则其方差为 np(1－p)(其 中 p 为成功概率)．
高二数学人教A版选修2-3：离散型随机变量的方差课件
n
(xi E( X ))2 pi 为随机变量X的方差.
i 1
( X ) D( X ) 为随机变量X的标准差.
方差与标准差
关系 标准差是方差的算术平方根；方差是标准差的平方；
作用 反应离散型随机变量偏离于均值的平均程度的量；
结论 值越小，则随机变量偏离于均值的平均程度越小， 即越集中于均值.
例1.随机抛掷一枚质地均匀的骰子,求向上一面的点数的方差和标准差. 解：抛掷骰子所得点数X：1，2，3，4，5，6，其散布列为：
0.4
0.2
0.2
0.3 0.2
0.2
0.1
8
91
10 X1
0
8
19
0.4 10 X2
E( X1)
E( X
)
2
分析：
D( X1) D( X 2)
甲、乙射击的平均水平没有差别， 在多次射击中平均得分差别不会很大.
甲通常发挥比较稳定，多数得分在9环， 而乙得分比较分散，近似平均散布在8－10.
练习：有甲乙两个单位都愿意聘请你，而你能获得如下信息：
X2 1000 1400 1800 2200
P1 0.4 0.3 0.2 0.1
P2 0.4 0.3 0.2 0.1
通过散布列，可以分别求出两个公司工资的期望与方差：
E(X1) 1200 0.4+1400 0.3+1600 0.2+1800 0.1=1400.
E(X2) 10000.4+1400 0.3+1800 0.2+2200 0.1=1400.
练习： 1.已知 h 3x 1 ，且 D(x ) 13 ，则 D(h) __1_1_7_ .
8 解：∵h 3x 1，
(xi E( X ))2 pi 为随机变量X的方差.
i 1
( X ) D( X ) 为随机变量X的标准差.
方差与标准差
关系 标准差是方差的算术平方根；方差是标准差的平方；
作用 反应离散型随机变量偏离于均值的平均程度的量；
结论 值越小，则随机变量偏离于均值的平均程度越小， 即越集中于均值.
例1.随机抛掷一枚质地均匀的骰子,求向上一面的点数的方差和标准差. 解：抛掷骰子所得点数X：1，2，3，4，5，6，其散布列为：
0.4
0.2
0.2
0.3 0.2
0.2
0.1
8
91
10 X1
0
8
19
0.4 10 X2
E( X1)
E( X
)
2
分析：
D( X1) D( X 2)
甲、乙射击的平均水平没有差别， 在多次射击中平均得分差别不会很大.
甲通常发挥比较稳定，多数得分在9环， 而乙得分比较分散，近似平均散布在8－10.
练习：有甲乙两个单位都愿意聘请你，而你能获得如下信息：
X2 1000 1400 1800 2200
P1 0.4 0.3 0.2 0.1
P2 0.4 0.3 0.2 0.1
通过散布列，可以分别求出两个公司工资的期望与方差：
E(X1) 1200 0.4+1400 0.3+1600 0.2+1800 0.1=1400.
E(X2) 10000.4+1400 0.3+1800 0.2+2200 0.1=1400.
练习： 1.已知 h 3x 1 ，且 D(x ) 13 ，则 D(h) __1_1_7_ .
8 解：∵h 3x 1，
2014-2015学年高中数学(人教版选修2-3)配套课件第二章 2.3.2 离散型随机变量的方差
栏 目 链 接
1 1 1 解析：因为 ＋ ＋p＝1，所以 p＝ . 2 3 6 1 1 1 2 又 E(ξ)＝0× ＋1× ＋x× ＝ .所以 x＝2. 2 3 6 3
2 2 1 2 2 1 2 2 1 15 故 (1)D(ξ)＝ 0－3 × ＋ 1－3 × ＋ 2－3 × ＝ 2 3 6 27
解得 p＝0.2，n＝10，故选 C. 答案：( B ) A．E(X)＝3.5，D(X)＝3.52 35 B．E(X)＝3.5，D(X)＝ 12 C．E(X)＝3.5，D(X)＝3.5 35 D．E(X)＝3.5，D(X)＝ 16
栏 目 链 接
栏 目 链 接
题型一 方差与标准差的计算 例1 已知离散型随机变量X的概率分布列为：
X P
1 1 7
2 1 7
3 1 7
4 1 7
5 1 7
6 1 7
7 1 7
栏 目 链 接
求其方差与标准差．
1 1 1 解析：∵E(X)＝1× ＋2× ＋„＋7× ＝4； 7 7 7 1 1 1 2 2 2 ∴D(X)＝(1－4) × ＋(2－4) × ＋„＋(7－4) × ＝4. 7 7 7 ∴ DX＝2.
第二章
随机变量及其分布
2．3 离散型随机变量的均值与方差
2.3.2 离散型随机变量的方差
栏 目 链 接
1．通过实例理解取有限值的离散型随机变量方
差的概念． 2．能计算简单离散型随机变量的方差，并能解 决一些实际问题．
栏 目 链 接
栏 目 链 接
基 础 梳 理 1．一般地，若离散型随机变量X的概率分布列为：
栏 目 链 接
例如：设ξ～B(n，p)，且E(ξ)＝2.4，D(ξ) ＝1.44，求n，p. 答案：n＝6，p＝0.4
1 1 1 解析：因为 ＋ ＋p＝1，所以 p＝ . 2 3 6 1 1 1 2 又 E(ξ)＝0× ＋1× ＋x× ＝ .所以 x＝2. 2 3 6 3
2 2 1 2 2 1 2 2 1 15 故 (1)D(ξ)＝ 0－3 × ＋ 1－3 × ＋ 2－3 × ＝ 2 3 6 27
解得 p＝0.2，n＝10，故选 C. 答案：( B ) A．E(X)＝3.5，D(X)＝3.52 35 B．E(X)＝3.5，D(X)＝ 12 C．E(X)＝3.5，D(X)＝3.5 35 D．E(X)＝3.5，D(X)＝ 16
栏 目 链 接
栏 目 链 接
题型一 方差与标准差的计算 例1 已知离散型随机变量X的概率分布列为：
X P
1 1 7
2 1 7
3 1 7
4 1 7
5 1 7
6 1 7
7 1 7
栏 目 链 接
求其方差与标准差．
1 1 1 解析：∵E(X)＝1× ＋2× ＋„＋7× ＝4； 7 7 7 1 1 1 2 2 2 ∴D(X)＝(1－4) × ＋(2－4) × ＋„＋(7－4) × ＝4. 7 7 7 ∴ DX＝2.
第二章
随机变量及其分布
2．3 离散型随机变量的均值与方差
2.3.2 离散型随机变量的方差
栏 目 链 接
1．通过实例理解取有限值的离散型随机变量方
差的概念． 2．能计算简单离散型随机变量的方差，并能解 决一些实际问题．
栏 目 链 接
栏 目 链 接
基 础 梳 理 1．一般地，若离散型随机变量X的概率分布列为：
栏 目 链 接
例如：设ξ～B(n，p)，且E(ξ)＝2.4，D(ξ) ＝1.44，求n，p. 答案：n＝6，p＝0.4
新人教A版选修2-32.3离散型随机变量的均值与方差 课件三
24元 / kg
36元 / kg
? 元 / kg
它是三种糖果价格的一 种加权平均.这里 1 1 1 的权数分别是 , 和 . 2 3 6
权是秤锤,权数是起权衡轻重作用 的数
值.加权平均是指在计算若 干个数量的平 均数时, 考虑到每个数量在总量 中所具有 的重要性不同 , 分别给予不同的权数 .
思考 随机变量的均值与样本 的平均值有何联系 与区别? 可以看到 ,随机变量的均值是常数 ,而样本的平均值 是随机变量 .对于简单随机样本 ,随着样本容量增加 , 样本平均值越来越接近 于总体均值 . 思考 在实际问题中 ,如何估计随机变ቤተ መጻሕፍቲ ባይዱ的总 体均 值呢?
例1 在篮球比赛中 , 罚球命中 1次得1分,不 中得0分.如果某运动员罚球命中 率为 0.7, 那么他罚球 1次的得分X的均值是多少 ?
解 因为PX 1 0.7,PX 0 0.3,
1 0.7 0 0.3 0.7 .
所以 EX 1 PX 1 0 PX 0
根据两点分布的均值公 式,如果罚球命中率 为0.8,那么罚球 1 次的得分均值是多少 ?
一般地, 如果随机变量X服从两点分布, 那么EX 1 p 0 1 p p. 于是有
若X服从两点分布 ,则EX p.
k k 1 如果X ~ Bn, p , 则由kC nC n 1, 可得 n n n k 1 k 1 n 1 k 1 q k k n k npC n 1p EX kCnp q k 1
np C p q
k k n 1 k 0
2.3.1 离散型随机变量的均值
18元 / kg
思考 某商场要将单价分别为 18元 / kg,24元 / kg,36元 / kg的三 种糖果按 3 : 2 : 1的比例混合销 售,如何对混合糖果定价才 合理 ?
离散型随机变量的方差 课件
因为D(XA)<D(XB),所以A种钢筋质量较好.
反思在解决此类实际问题时,应先比较均值,均值较大的质量好.
若均值相等,再比较方差,方差较小的数据较稳定,质量较好.
题型三 离散型随机变量方差的综合应用
【例3】 A,B两个投资项目的利润率分别为随机变量X1和X2,根据
市场分析,X1和X2的分布列分别为
100
4
2
2
2 [x
100
4
=
100 1
+3(100-x) ]
2
2
2 (4x -600x+3×100 ).
100
600
当 x=2×4=75 时,f(x)=3 为最小值.
反思解均值与方差的综合问题时需要注意:
(1)离散型随机变量的分布列、均值和方差三个是紧密联系的,一
般在试题中综合在一起考查,其解题的关键是求出分布列;
(2)在求分布列时,要注意利用等可能事件、互斥事件、相互独立
事件的概率公式计算概率,并注意结合分布列的性质,简化概率计
算;
(3)在计算均值与方差时要注意运用均值和方差的性质以避免一
些复杂的计算.若随机变量X服从两点分布、超几何分布或二项分
布可直接利用对应公式求解.
题型四
易错辨析
易错点:对方差性质掌握不准确致错
错因分析忽略了随机变量分布列的性质出现错误,这里只是机械
地套用公式,且对D(ax+b)=a2D(x)应用错误.
正解:∵0.2+0.2+a+0.2+0.1=1,
∴a=0.3.
∴E(X)=0×0.2+1×0.2+2×0.3+3×0.2+4×0.1=1.8.
反思在解决此类实际问题时,应先比较均值,均值较大的质量好.
若均值相等,再比较方差,方差较小的数据较稳定,质量较好.
题型三 离散型随机变量方差的综合应用
【例3】 A,B两个投资项目的利润率分别为随机变量X1和X2,根据
市场分析,X1和X2的分布列分别为
100
4
2
2
2 [x
100
4
=
100 1
+3(100-x) ]
2
2
2 (4x -600x+3×100 ).
100
600
当 x=2×4=75 时,f(x)=3 为最小值.
反思解均值与方差的综合问题时需要注意:
(1)离散型随机变量的分布列、均值和方差三个是紧密联系的,一
般在试题中综合在一起考查,其解题的关键是求出分布列;
(2)在求分布列时,要注意利用等可能事件、互斥事件、相互独立
事件的概率公式计算概率,并注意结合分布列的性质,简化概率计
算;
(3)在计算均值与方差时要注意运用均值和方差的性质以避免一
些复杂的计算.若随机变量X服从两点分布、超几何分布或二项分
布可直接利用对应公式求解.
题型四
易错辨析
易错点:对方差性质掌握不准确致错
错因分析忽略了随机变量分布列的性质出现错误,这里只是机械
地套用公式,且对D(ax+b)=a2D(x)应用错误.
正解:∵0.2+0.2+a+0.2+0.1=1,
∴a=0.3.
∴E(X)=0×0.2+1×0.2+2×0.3+3×0.2+4×0.1=1.8.
离散型随机变量的均值与方差(课件)-(课件)-2022届新高考高三数学人教A版选修2-3
ξ＝4k
＝
a 2k
(k＝
1,2,3,4)，则Pξ>12＝
1 5
，随机变量ξ的数学期望E(ξ)＝
13 30 .
解析：因为随机变量ξ的分布列为Pξ＝4k＝2ak(k＝1,2,3,4)，所以a2＋2a2＋2a3＋2a4
＝1，解得a＝1165，所以随机变量ξ的分布列为
ξ
1 4
1 2
3 4
1
P
8 15
4 15
3．(2021·河北衡水调研)一个袋中放有大小、形状均相同的小球，其中红球1 个、黑球2个．现随机等可能取出小球，当有放回地依次取出两个小球时，记取出 的红球数为ξ1；当无放回地依次取出两个小球时，记取出的红球数为ξ2，则( B )
A．E(ξ1)<E(ξ2)，D(ξ1)<D(ξ2) B．E(ξ1)＝E(ξ2)，D(ξ1)>D(ξ2) C．E(ξ1)＝E(ξ2)，D(ξ1)<D(ξ2) D．E(ξ1)>E(ξ2)，D(ξ1)>D(ξ2)
1．已知X的分布列为
X
－1
0
1
P
1 2
1
1
3
6
设Y＝2X＋3，则E(Y)的值为( A )
7 A.3
B．4
C．－1
D．1
解析：∵E(X)＝－12＋16＝－13，∴E(Y)＝E(2X＋3)＝2E(X)＋3＝－23＋3＝73.
2．(2021·浙江丽水模拟)已知某口袋中有 3 个白球和 a 个黑球(a∈N*)，现从中2．方差ຫໍສະໝຸດ 设离散型随机变量X的分布列为：
X
x1
x2
…
xi
…
xn
P
p1
p2
方差
甲单位不同职位月工资X1/元
获得相应职位的概率P 1
1200 0.4
1400 0.3
1600 0.2
1800 0.1
乙单位不同职位月工资X2/元
获得相应职位的概率P 2
1000 0.4
根据工资待遇的差异情况，你愿意选择哪家单位？
1400 0.3
1800 0.2
2200 0.1
解：根据月工资的分布列，可算得
4.标准差= D(X ) (同样刻画稳定性)
探究：要从两名同学中挑出一名，代表班级参加射击比赛，根据以往的成绩记录，两名同学击中
目标靶的环数 X 和 Y 的分布列分别为
X
5
6
7
8
9
10
P
0.03 0.09 0.20 0.31 0.27 0.10
如果其他班级参赛选手的射击成绩都在9环左右，
Y
5
6
7
8
D(Y ) (5 8)2 0.01 (6 8)2 0.05 (7 8)2 0.20 (8 8)2 041 (9 8)2 0.33 0.82
因此，第一名同学的射击成绩稳定性较差，第二名同学的射击成绩稳定性较好。
建议挑第二名同学参加比赛
【问题探究】
类似的：离散型随机变量 X 的方差为 D( X ) 若随机变量 Y 满足Y aX b ，则 D(Y ) ?
[基础自测]
1．判断(正确的打“√”，错误的打“×”)
(1)离散型随机变量 ξ 的期望 E(ξ)反映了 ξ 取值的概率的平均值； ( )
(2)离散型随机变量 ξ 的方差 D(ξ)反映了 ξ 取值的平均水平； ( )
(3)离散型随机变量 ξ 的方差 D(ξ)反映了 ξ 取值的波动水平． ( )
2.3.2 人教A版数学选修2-3 第2章 随机变量及其分布
2.3.2 离散型随机变量的方差、标准差填一填1.(1)定义：设离散型随机变量X 的分布列为X x 1 x 2 … x i … x n Pp 1p 2…p i…p n则(x i －E (X ))2描述了x i (i ＝1,2，…，n )相对于均值E (X )的偏离程度，而D (X )＝∑i ＝1n(x i －E (X ))2p i 为这些偏离程度的加权平均，刻画了随机变量X 与其均值E (X )的平均偏离程度．称D (X )为随机变量X 的方差，其算术平方根D (X )为随机变量X 的标准差．(2)意义：随机变量的方差和标准差都反映了随机变量取值偏离于均值的平均程度．方差或标准差越小，则随机变量偏离于均值的平均程度越小．2．随机变量的方差与样本方差的关系随机变量的方差是总体的方差，它是一个常数，样本的方差则是随机变量，是随样本的变化而变化的．对于简单随机样本，随着样本容量的增加，样本的方差越来越接近于总体的方差．3．服从两点分布与二项分布的随机变量的方差 (1)若X 服从两点分布，则D (X )＝p (1－p )； (2)若X ～B (n ，p )，则D (X )＝np (1－p )．4．离散型随机变量方差的线性运算性质设a，b为常数，则D(aX＋b)＝a2D(X).判一判判断(1．离散型随机变量ξ的期望E(ξ)反映了ξ取值的概率的平均值．(×)2．离散型随机变量ξ的方差D(ξ)反映了ξ取值的平均水平．(×)3．离散型随机变量ξ的方差D(ξ)反映了ξ取值的波动水平．(√)4．离散型随机变量的方差越大，随机变量越稳定．(×)5．若a是常数，则D(a)＝0.(√)6．若随机变量X服从两点分布，且成功的概率p＝0.5，则D(X)为0.5.(×)7．牧场的10头牛，因误食疯牛病毒污染的饲料被感染，已知该病的发病率为0.02，设发病牛的头数为X，则D(X)等于0.196.(√)8．若X为随机变量则D(X－D(X))＝D(X)．(√)想一想1.提示：随机变量X的方差和标准差都反映了随机变量X取值的稳定与波动，集中与离散的程度，D(X)(或D(X))越小，稳定性越好，波动越小，显然D(X)≥0(D(X)≥0)．2．离散型随机变量的方差与标准差的单位相同吗？提示：不同，方差的单位是随机变量单位的平方；标准差与随机变量本身有相同的单位．3．随机变量的方差与样本的方差有何联系与区别？提示：样本的方差是随着样本的不同而变化的，因此它是一个变量，而随机变量的方差是通过大量试验得出的，刻画了随机变量X 与其均值E (X )的平均偏离程度，因此它是一个常数(量)．对于简单随机样本，随着样本容量的增加，样本方差越来越接近于总体的方差．4．决策问题中如何运用均值与方差？提示：离散型随机变量的均值反映了离散型随机变量取值的平均水平，而方差反映了离散型随机变量取值的稳定与波动、集中与离散的程度．因此在实际决策问题中，需先计算均值，看谁的平均水平高，然后再计算方差，分析谁的水平发挥相对稳定．当然不同的情形要求不同，应视情况而定。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
今天，我们将对随机变量取值的稳定与 波动、集中与离散的程度进行研究.
2.3.2离散型随机变 量的方差
教学目标
知识与技能
（1）了解离散型随机变量的方差、标准差的 意义；
（2）会根据离散型随机变量的分布列求出方 差或标准差.
过程与方法
了解方差公式“D(aξ+b)=a2Dξ”，以及 “若ξ~Β(n，p)，则Dξ=np(1-p)”，并会应用 上述公式计算有关随机变量的方差 .
P
P
0.5
0.5
0.4
0.4
0.3
0.3
0.2
0.2
0.1
0.1
O 5 6 7 8 9 10 X1
(1)
O 5 6 7 8 9 X2
(2)
1.方差
知识要点
设离散型随机变量X的分布列为
X x1 x2 … xi … xn P p1 p2 … pi … pn
则(xi-E(X))2描述了xi(i=1，2，…，n)相对于 均值E(X)的偏离程度.
n
DX = (xi - EX)2 pi
i =1
为这些偏离程度的加权平均，刻画了随机变量 X 与其均值 EX 的平均偏离程度.我们称 DX为随机 变量 X 的方差(variance). 其算术平方根 DX 为随 机变量X的标准差(standard deviation). 记为 σX
随机变量的方差和标准差都反映了随机变量取 值偏离于均值的平均程度.方差或标准差越小，则 随机变量偏离于均值的平均程度越小.
1200 0.4
1400 1600 1800 0.3 0.2 0.1
乙单位不同职位月工资X2/元 1000 1400 1800 2200
获得相应职位的概率P2
0.4 0.3 0.2 0.1
根据工资待遇的差异情况，你愿意选择哪家单位？
解：根据月工资的分布列，利用计算器可算得
EX1 = 1200 0.4 + 1 400 0.3 + 1600 0.2 + 1800 0.1 = 1400
知识要点
2.几点重要性质
（1）若X服从两点分布，则D(X)=p(1-p); （2）若X~B(n，p)，则D(X)=np(1-p); （3）D(aX+b)=a2D(X).
例题1
A、B两台机床同时加工零件，每生产一批数 量较大的产品时，出次品的概率如下表所示：
次品数ξ1 0 1 2
3
概率P 0.7 0.2 0.06 0.04
情感、态度与价值观
承前启后，感悟数学与生活的和谐之美 ,体 现数学的文化功能与人文价值.
教学重难点
重点
离散型随机变量的方差、标准差.
难点
比较两个随机变量的期望与方差
的大小，从而解决实际问题 .
思考
要从两名同学中挑选出一名，代表班级参加射 击比赛. 根据以往的成绩记录，
第一名同学击中目标靶的环数X1的分布列为
现在，可以用两名同学射击成绩的方差来 刻画他们各自的特点，为选派选手提供依据.由 前面的计算结果及方差的定义，得
10
DX1 = (i - 8)2 P(X1 = i)= 1.50 ,
i=5
9
DX2 = (i - 8)2 P(X2 = i) = 0.82
i=5
因此第一名同学的射击成绩稳定性较差， 第二名同学的射击成绩稳定性较好，稳定于8 环左右.
次品数ξ1 0 1
2
3
概率P 0.8 0.06 0.04 0.10问哪一台机床加工质量较好？
解：
Eξ1=0×0.7+1×0.2+2×0.06+3×0.04=0.44, Eξ2=0×0.8+1×0.06+2×0.04+3×0.10=0.44. 它们的期望相同，再比较它们的方差
Dξ1=(0-0.44)2×0.7+(1-0.44)2×0.2+(2-0.44)2 ×0.06+(3-0.44)2×0.04=0.6064,
导入新课
复习回顾
n
1 .离散型随机变量 X 的均值 EX = xipi
i =1
均值反映了离散型随机变量取值的平均水平. 2 . 两种特殊分布的均值
（1）若随机变量X服从两点分布，则EX=p. （2）若X~B(n，p) ，则EX=np.
数学期望是离散型随机变量的一个特征数， 它反映了离散型随机变量取值的平均水平，表示 了随机变量在随机实验中取值的平均值，所以又 常称为随机变量的平均数、均值.
E(X1)=8，E(X2)=8， 发现两个均值相等，因此只根据均值不 能区分这两名同学的射击水平.
思考
除平均中靶环数外，还有其他刻画两名 同学各自射击特点的指标吗？
怎样定量刻画随
机变量的稳定性? 图(1)(2)分别表示X1和X2的分布列图. 比较两 个图形，可以发现，第二名同学的射击成绩更集 中于8环，即第二名同学的射击成绩更稳定.
说明：随机变量集中的位置是随机变量的均 值；方差或标准差这种度量指标是一种加权平均 的度量指标.
思考
随机变量的方差与样本的方差有何联系与区别?
随机变量的方差是常数，而样本的方差是随 着样本的不同而变化的，因此样本的方差是随机 变量.
对于简单随机样本，随着样本容量的增加， 样本方差越来越接近总体方差，因此常用样本方 差来估计总体方差.
Dξ2=(0-0.44)2×0.8+(1-0.44)2×0.06+(2-0.44)2 ×0.04+(3-0.44)2×0.10=0.9264.
∴Dξ1< Dξ2 故A机床加工较稳定、质量较好.
例题2
有甲乙两个单位都愿意聘用你，而你能获得如下 信息：
甲单位不同职位月工资X1/元 获得相应职位的概率P1
DX1 = (1200 -1400) 2 0. 4 + (1400 -1400 ) 2 0.3 + (1600 -1400 )2 0.2
+ (1800 -1400) 2 0. 1 = 40 000
EX2 = 1 000 0.4 + 1 400 0.3 + 1 800 0.2 + 2200 0.1 = 1400 DX2 = (1000 -1400)2 0. 4 + (1 400 -1400)2 0.3 + (1800 -1400)2 0.2
X1 5 6 7 8 9 10 P 0.03 0.09 0.20 0.31 0.27 0.10
第二名同学击中目标靶的环数X2的分布列为
X2 5 6 7 8 9 P 0.01 0.05 0.20 0.41 0.33
根据已学知识，可以从平均中靶环数来比较两 名同学射击水平的高低，即通过比较X1和X2的均值 来比较两名同学射击水平的高低. 通过计算
2.3.2离散型随机变 量的方差
教学目标
知识与技能
（1）了解离散型随机变量的方差、标准差的 意义；
（2）会根据离散型随机变量的分布列求出方 差或标准差.
过程与方法
了解方差公式“D(aξ+b)=a2Dξ”，以及 “若ξ~Β(n，p)，则Dξ=np(1-p)”，并会应用 上述公式计算有关随机变量的方差 .
P
P
0.5
0.5
0.4
0.4
0.3
0.3
0.2
0.2
0.1
0.1
O 5 6 7 8 9 10 X1
(1)
O 5 6 7 8 9 X2
(2)
1.方差
知识要点
设离散型随机变量X的分布列为
X x1 x2 … xi … xn P p1 p2 … pi … pn
则(xi-E(X))2描述了xi(i=1，2，…，n)相对于 均值E(X)的偏离程度.
n
DX = (xi - EX)2 pi
i =1
为这些偏离程度的加权平均，刻画了随机变量 X 与其均值 EX 的平均偏离程度.我们称 DX为随机 变量 X 的方差(variance). 其算术平方根 DX 为随 机变量X的标准差(standard deviation). 记为 σX
随机变量的方差和标准差都反映了随机变量取 值偏离于均值的平均程度.方差或标准差越小，则 随机变量偏离于均值的平均程度越小.
1200 0.4
1400 1600 1800 0.3 0.2 0.1
乙单位不同职位月工资X2/元 1000 1400 1800 2200
获得相应职位的概率P2
0.4 0.3 0.2 0.1
根据工资待遇的差异情况，你愿意选择哪家单位？
解：根据月工资的分布列，利用计算器可算得
EX1 = 1200 0.4 + 1 400 0.3 + 1600 0.2 + 1800 0.1 = 1400
知识要点
2.几点重要性质
（1）若X服从两点分布，则D(X)=p(1-p); （2）若X~B(n，p)，则D(X)=np(1-p); （3）D(aX+b)=a2D(X).
例题1
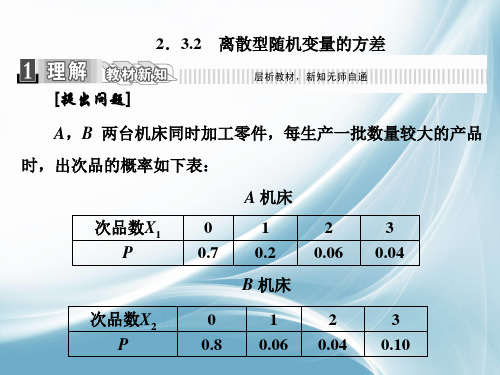
A、B两台机床同时加工零件，每生产一批数 量较大的产品时，出次品的概率如下表所示：
次品数ξ1 0 1 2
3
概率P 0.7 0.2 0.06 0.04
情感、态度与价值观
承前启后，感悟数学与生活的和谐之美 ,体 现数学的文化功能与人文价值.
教学重难点
重点
离散型随机变量的方差、标准差.
难点
比较两个随机变量的期望与方差
的大小，从而解决实际问题 .
思考
要从两名同学中挑选出一名，代表班级参加射 击比赛. 根据以往的成绩记录，
第一名同学击中目标靶的环数X1的分布列为
现在，可以用两名同学射击成绩的方差来 刻画他们各自的特点，为选派选手提供依据.由 前面的计算结果及方差的定义，得
10
DX1 = (i - 8)2 P(X1 = i)= 1.50 ,
i=5
9
DX2 = (i - 8)2 P(X2 = i) = 0.82
i=5
因此第一名同学的射击成绩稳定性较差， 第二名同学的射击成绩稳定性较好，稳定于8 环左右.
次品数ξ1 0 1
2
3
概率P 0.8 0.06 0.04 0.10问哪一台机床加工质量较好？
解：
Eξ1=0×0.7+1×0.2+2×0.06+3×0.04=0.44, Eξ2=0×0.8+1×0.06+2×0.04+3×0.10=0.44. 它们的期望相同，再比较它们的方差
Dξ1=(0-0.44)2×0.7+(1-0.44)2×0.2+(2-0.44)2 ×0.06+(3-0.44)2×0.04=0.6064,
导入新课
复习回顾
n
1 .离散型随机变量 X 的均值 EX = xipi
i =1
均值反映了离散型随机变量取值的平均水平. 2 . 两种特殊分布的均值
（1）若随机变量X服从两点分布，则EX=p. （2）若X~B(n，p) ，则EX=np.
数学期望是离散型随机变量的一个特征数， 它反映了离散型随机变量取值的平均水平，表示 了随机变量在随机实验中取值的平均值，所以又 常称为随机变量的平均数、均值.
E(X1)=8，E(X2)=8， 发现两个均值相等，因此只根据均值不 能区分这两名同学的射击水平.
思考
除平均中靶环数外，还有其他刻画两名 同学各自射击特点的指标吗？
怎样定量刻画随
机变量的稳定性? 图(1)(2)分别表示X1和X2的分布列图. 比较两 个图形，可以发现，第二名同学的射击成绩更集 中于8环，即第二名同学的射击成绩更稳定.
说明：随机变量集中的位置是随机变量的均 值；方差或标准差这种度量指标是一种加权平均 的度量指标.
思考
随机变量的方差与样本的方差有何联系与区别?
随机变量的方差是常数，而样本的方差是随 着样本的不同而变化的，因此样本的方差是随机 变量.
对于简单随机样本，随着样本容量的增加， 样本方差越来越接近总体方差，因此常用样本方 差来估计总体方差.
Dξ2=(0-0.44)2×0.8+(1-0.44)2×0.06+(2-0.44)2 ×0.04+(3-0.44)2×0.10=0.9264.
∴Dξ1< Dξ2 故A机床加工较稳定、质量较好.
例题2
有甲乙两个单位都愿意聘用你，而你能获得如下 信息：
甲单位不同职位月工资X1/元 获得相应职位的概率P1
DX1 = (1200 -1400) 2 0. 4 + (1400 -1400 ) 2 0.3 + (1600 -1400 )2 0.2
+ (1800 -1400) 2 0. 1 = 40 000
EX2 = 1 000 0.4 + 1 400 0.3 + 1 800 0.2 + 2200 0.1 = 1400 DX2 = (1000 -1400)2 0. 4 + (1 400 -1400)2 0.3 + (1800 -1400)2 0.2
X1 5 6 7 8 9 10 P 0.03 0.09 0.20 0.31 0.27 0.10
第二名同学击中目标靶的环数X2的分布列为
X2 5 6 7 8 9 P 0.01 0.05 0.20 0.41 0.33
根据已学知识，可以从平均中靶环数来比较两 名同学射击水平的高低，即通过比较X1和X2的均值 来比较两名同学射击水平的高低. 通过计算