年金的终值和现值
年金终值和年金现值的计算

一、年金终值:年金终值是指在一段时间内,定期支付一定金额的现金流,经过一定的利率增长后所积累的总金额。
年金终值计算的目的是评估未来一段时间内现金流的价值。
年金终值的计算可以通过如下的公式进行:FV=P*((1+r)^n-1)/r其中,FV表示年金终值,P表示每期支付的金额,r表示每期支付的利率,n表示支付的期数。
例如,每年支付1000元,利率为5%,持续支付10年,则年金终值的计算为:年金终值的计算方法可以应用于各种不同的现金流情况,如每月、每季度、每半年等的现金支付。
二、年金现值:年金现值是指将未来一段时间内的现金流按照一定的利率折算到现在的价值,将未来的现金流所得到的总金额。
年金现值的计算的目的是评估未来现金流的现值,以便做出更加准确的投资决策。
年金现值的计算可以通过如下的公式进行:PV=P*(1-(1+r)^(-n))/r其中,PV表示年金现值,P表示每期支付的金额,r表示每期支付的利率,n表示支付的期数。
例如,每年支付1000元,利率为5%,持续支付10年,则年金现值的计算为:所以,每年支付1000元,利率为5%,持续支付10年,年金现值为7721.73元。
年金现值的计算方法也可以适用于各种不同的现金流情况。
三、年金终值和年金现值的应用:在投资决策中,投资者可以利用年金终值和年金现值来比较不同投资方案的收益。
通过计算不同方案的年金终值和年金现值,可以判断哪种投资方案更加有利可图,从而做出更加明智的决策。
在退休规划中,个人可以利用年金终值和年金现值来评估自己的退休金需求和储蓄目标。
通过计算所需的年金终值和现值,可以规划合理的退休储蓄计划,确保在退休时有足够的资金支持。
总之,年金终值和年金现值是评估一定时间内或一系列现金流价值的重要工具。
通过运用年金终值和年金现值的计算方法,可以帮助人们做出更加准确的投资决策和退休规划。
年金终值和现值得计算

1.4 资本回收额
[例题]:某企业想投资100万元购买设备, 预计可使用3年,社会平均利润率8%。 则该设备每年至少带来多少收益是可行 的?
A= P/ (P/A, 8%, 3)=100/2.577=38.88万元
1.4 资本回收额
[例题]:某公司借入2000万元,约定8内, 按i=12%均匀偿还,则每年还本付息多 少?
年金的终值及现值的计算
年金
定义:年金是指一定时期内每期相等金 额的收付款项。
按付款时间分类: 普通年金(或称后付年金) 先付年金(或称即付年金、预付年金) 延期年金(或称递延年金) 永续年金
1. 普通年金(0rdinary Annuity)
普通年金,即后付年金,是指在一定时期 内,每期期末有等额收付款项的年金。
定义:普通年金现值是指一定时期内每期期末等 额的系列收付款项的现值之和. 令P——年金现 值
公式:P=A﹡ [(1+i)n-1]/i(1+i) n=A ﹡ [1-(1+i)-n ]/i [1−(1+i)-n]/ i被称做年金现值系数或年金贴现系数 记作(P/A, i, n)
普通年金现值,通常借助于“年金现值系数表”计算。 P=A ﹡(P/A,i, n)
1.1 普通年金终值
定义:普通年金终值是一定时期内每期 期末等额收付款项的复利终值之和。
令:A——年金数额 i ——利息率 n ——计息期数 F——年金终值
1.1 普通年金终值
计算公式: F=A﹡ [(1+i)n −1]/i 其中[(1+i)n −1]/i被称作年金终值系数, 记作(F/A, i, n) 普通年金终值,通常借助于“年金终值系 数表”计算。 F=A ﹡(F/A, i, n)
年金现值与终值的比较

年金现值与终值的比较年金现值与终值是财务管理中两个重要的概念,用于评估不同时期的现金流量的价值。
年金现值是指在未来一段时间内产生的现金流量,在当下的价值,而年金终值则是指在未来一段时间内产生的现金流量的未来价值。
在财务决策中,对于年金现值和终值的比较是至关重要的。
本文将就年金现值与终值的比较进行探讨。
首先,我们来看看年金现值的计算方法。
年金现值是指未来一系列现金流量在当下的价值。
计算年金现值的方法可以用现值公式来表示,即PV = PMT × [(1 - (1 + r)^-n) / r],其中PV代表年金现值,PMT代表每期现金流量,r代表折现率,n代表期数。
通过这个公式,我们可以计算出不同时期的现金流量在当下的价值,帮助我们做出更明智的决策。
然后,我们来看看年金终值的计算方法。
年金终值是指未来一系列现金流量在未来的价值。
计算年金终值的方法可以用终值公式来表示,即FV = PV × (1 + r)^n,其中FV代表年金终值,PV代表现值,r代表折现率,n代表期数。
通过这个公式,我们可以计算出未来一系列现金流量的未来价值,帮助我们更好地规划未来的财务安排。
接着,我们来比较年金现值和终值在财务决策中的作用。
年金现值可以帮助我们评估不同时期的现金流量在当下的价值,有助于我们做出投资决策、贷款决策等。
而年金终值则可以帮助我们评估未来一系列现金流量的未来价值,有助于我们规划未来的财务安排和退休计划等。
因此,在财务管理中,年金现值和终值都扮演着重要的角色,需要根据具体情况灵活运用。
最后,需要注意的是,在比较年金现值和终值时,我们应该根据具体情况综合考虑两者的影响因素。
在实际应用中,我们可能需要同时考虑年金现值和终值,综合分析现金流量在不同时间点的价值,以便做出更全面的财务决策。
综上所述,年金现值与终值的比较在财务管理中具有重要意义。
通过对年金现值和终值的计算和比较,我们可以更好地评估现金流量的价值,帮助我们做出明智的财务决策。
普通年金终值现值及年金的计算有图解分解

➢ 在实务中
几乎所有的消费贷款和房屋按揭贷款都要求等 额偿还,并且通常是按月进行的。 你是选择一次性付款,还是分期等额付款呢?
➢ 这时,你需要掌握年金的计算与分析。
第1页/共23页
年金
➢年金是(Annuity)指等额、定期的系列收 支。
等期等额付款赊购 等期等额偿还贷款 等期等额发放养老金 等期等额支付工程款 每年相同的销售收入等,都属于年金收付形式。
➢ 如果已知
(F/P,10%,1)=1.10 (F/P,10%,2)=1.21 你能求出(F/A,10%,3)的值吗?
第6页/共23页
普通年金终值计算公式的推导
每年的支付金额为A;利率为I ; 期数 为n; ■ 则每按年复的等利式计两边算同乘的(普1+i通):年金终值F为 :
■ 上述两式相减, 整理后,得到:
即根据年金现值计算的年金,即已知现值求年 金。
第20页/共23页
年资本回收额公式的推导
➢ 根据普通年金现值计算公式:
可知:
普通年金现值系数的倒数,称资本回收系数 记作(A/P,i,n)
第21页/共23页
资本回收系数与年金现值系数互为倒数
投投资资回回报报率率为为10%%时时,,每每年年至至少少要要收收回回40.21万万元元,,才才能能确确保保3年年后后收收回回初初始始投投资资额额100万万元元。。
➢ 按年金的收付时点,可以将年金划分为
普通年金、预付年第金2页/、共23页递延年金、永续年金
普通年金
➢普通年金(Ordinary Annuity)又称后付 年金
是指各期期末收付的年金。
普通年0 图24-1。 5
金的1 收付2形式见3
现值和终值的计算公式

终值和现值的计算公式是什么?
公式如下:
1、年金终值计算公式为:F=A*(F/A,i,n)=A*(1+i)n-1/i
其中(F/A,i,n)称作“年金终值系数”。
2、年金现值计算公式为:P=A*(P/A,i,n)=A*[1-(1+i)-n]/i
其中(P/A,i,n)称作“年金现值系数”。
扩展资料:
如果年金的期数n很多,用上述方法计算现值显然相当繁琐。
由于每年支付额相等,折算现值的系数又是有规律的,所以,可找出简便的计算方法。
先付年金现值:是其最后一期期末时的本利和,相当于各期期初等额收付款项的复利现值之和。
n期先付年金与n期普通年金的收付款次数相同,但由于付款时间不同,n期先付年金现值比n期普通年金的现值多计算一期利息。
因此在n期普通年金现值的基础上乘以(1+i)而将分母加1就得出n期先付年金的现值了。
年金终值和年金现值的计算

六、年金终值和年金现值的计算(一)年金的含义年金是指一定时期内每次等额收付的系列款项。
通常记作A 。
具有两个特点:一是金额相等;二是时间间隔相等。
也可以理解为年金是指等额、定期的系列收支。
在现实工作中年金应用很广泛。
例如,分期付款赊购、分期偿还贷款、发放养老金、分期支付工程款、每年相同的销售收入等,都属于年金收付形式。
老师手写板:①②年、月、半年、2年1年 2年 3年1年 1年 1年(二)年金的种类年金按其每次收付款项发生的时点不同,可以分为四种:普通年金(后付年金):从第一期开始每期期末收款、付款的年金。
预付年金(先付年金、即付年金):从第一期开始每期期初收款、付款的年金。
与普通年金的区别仅在于付款时间的不同。
递延年金:从第二期或第二期以后开始每期期末收付的年金。
永续年金:无限期的普通年金。
注意:各种类型年金之间的关系(1)普通年金和即付年金区别:普通年金的款项收付发生在每期期末,即付年金的款项收付发生在每期期初。
联系:第一期均出现款项收付。
【例题1·单选题】2007年1月1日,甲公司租用一层写字楼作为办公场所,租赁期限3年,每年12月31日支付租金10万元,共支付3年。
该租金有年金的特点,属于( )。
(2010年考试真题)A .普通年金B .即付年金C .递延年金D .永续年金【答案】A【解析】每年年末发生等额年金的是普通年金。
(2)递延年金和永续年金二者都是在普通年金的基础上发展演变起来的,它们都是普通年金的特殊形式。
它们与普通年金的共同点有:它们都是每期期末发生的。
区别在于递延年金前面有一个递延期,也就是前面几期没有现金流,永续年金没有终点。
在年金的四种类型中,最基本的是普通年金,其他类型的年金都可以看成是普通年金的转化形式。
【提示】1.这里的年金收付间隔的时间不一定是1年,可以是半年、一个季度或者一个月等。
A A A A A A A A A A 300万 200万 100万2.这里年金收付的起止时间可以是从任何时点开始,如一年的间隔期,不一定是从1月1日至12月31日,可以是从当年7月1日至次年6月30日。
普通年金的终值与现值
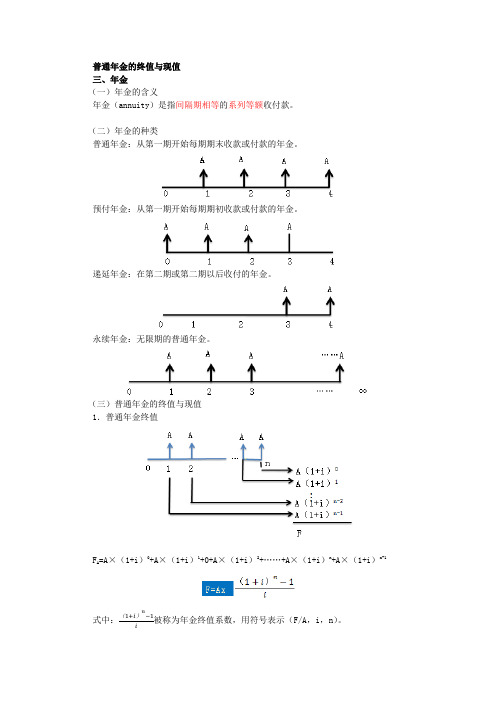
【例题.计算题】某投资項目于2018年年初动工,假设当年投产,从投产之日起每年年末可得收益40000元。按年利率6%计算,计算预期10年收益的现值。
【解析】
P=40000×(P/A,6%,10)=40000×7.3601=294404(元)。
【例题•计算题】
(1)某人存入银行10万元,若存款利率4%,第5年年末取出多少本利和?
【解析】
F=1000×(F/A,2%,9)=1000×9.7546=9754.6(元)
2.普通年金现值
PA=A×(1+i)-1+A×(1+i)-2+……..+A×(1+i)-n
经计算可得:
式中: 被称为年金现值系数,
记作(P/A,i,n)。
年金现值系数表(P/A,i,n)
期限利率
4%
5%
6%
7%
8%
1.普通年金终值
FA=A×(1+i)0+A×(1+i)1+0+A×(1+i)2+……+A×(1+i)n+A×(1+i)n-1
式中: 被称为年金终值系数,用符号表示(F/A,i,n)。
年金终值系数表(F/A,i,n)
利率期数
1%
2%
3%
4%
5%
5
5.1010
5.2040
5.3091
5.4163
5.5256
6
5.2421
5.0757
4.9173
4.7665
4.6229
7
6.0021
5.7864
5.5824
5.3893
终值和现值

终值和现值1.年金终值和年金现值(1)年金现值(普通年金现值)普通年金现值是指将在一定时期内按相同时间间隔在每期期末收付的相等金额折算到第一期期初的现值之和。
根据复利现值的方法计算年金现值的公式为:P A=A(1+i)-1+A(1+i)-2+A(1+i)-3+···+A(1+i)-n=A式中称为“年金现值系数”记做(P/A,i,n)【例题】某投资项目于2017年年初完工,假定当年投产,从投产之日起每年末可获得收益100000元。
按年利率5%计算,预期5年收益的现值是多少元?(P/A,5%,5)=4.3295【答案】P A=A×(P/A,i,n)=100000×(P/A,5%,5)=100000×4.3295=432950(元)。
【例题·单选题】2017年1月1日,某企业的投资项目正式投入运营,从运营之日起,该企业每年年末可从该项目中获得收益200000元,预计收益期为4年。
假设年利率6%,已知(P/A,6%,4)=3.4651。
不考虑其他因素,2017年1月1日该项目预期4年总收益的现值为()元。
(2018年)A.693020B.200000C.2772080D.800000【答案】A【解析】P A=200000×(P/A,6%,4)=200000×3.4651=693020(元)。
【例题·单选题】下列各项中,属于普通年金形式的是()。
(2018年)A.企业在某中学设立奖励基金,用于每年发放等额奖学金B.企业租房2年,每个月初向出租方支付等额房租C.企业生产线使用年限为5年,从年初投产之日起每年年末获得等额现金收益D.企业设立一项公益基金,连续10年于每年年初投入等额奖金【答案】C【解析】普通年金是年金的最基本形式,它是指从第一期起,在一定时期内每期期末等额收付的系列款项,又称为后付年金,即选项C正确。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1000 0.7511000 0.683 2000 0.621
=3791(元)
我们可以将例题2的图示和计算列式一般化,将 期限为n,利率为i的 年金A的现值用下面的图表和 计算公式表示,就可以得出计算年金现值的一般性 解:
现值
A (1 i)1
A
: : (1 i)2 A (1 i)n1
A
+(1 i)n
风险可能给人带来意外收益,也可能带来意外损失。 但人们对意外损失的关切比对意外收益的关切更强烈。 因此人们研究风险主要是为了减少损失,主要是从不利 的方面来考察风险,经常把风险看成是不利事件发生的 可能性。
从财务角度来看,风险:主要是指出现财务损失的 可能性或预期收益的不确定性。
2、风险的种类(A)
A(1 i)n-A(1 i)0=A(1 i)n- A =A((1 i)n 1)
即:FVAn• i= A ((1 i)n 1)
所以,FVAn=
A• (1 i) n 1 =
i
A • FVIFA(i,n) 2.3
其中:A—年金,i—利率,n—期限
我们称年金终值计算公式(2.3式)中的 (1 i)n 1为年金终值系数,也可
=12210 我们可以将以上例题的图示和计算列式一般化,
将期限为n,利率为i的 年金A的终值用下面的图表 和计算公式表示,就可以得出计算年金终值的一般 性解:
012
AA
…
n-1 n
终值
…
AA
A(1 i)0
A(1 i)1
::
A(1 i)n2
+ A(1 i)n1
FVAn
普通年金终值计算图示
上述计算可以列式如下: FVAn =
【例题2 】假设某人出租房屋,每年末
收取1000元,租期5年,问在利率为10%时,
这些现金相当于现在的多少金额?
现值
1
2
3
4
5 年末
1000 1000 1000 1000 1000
1000
(1 10%)1 1000
(1 10%)2 1000
(1 10%)3 1000
(1 10%)4 1000
财务风险,是指因借款而导致的风险,是筹资决 策带来的风险。
二、风险与收益的关系
人是厌恶风险的,所以,如果要冒风险就必须获 得额外的报酬。这个道理可以用很多实例来解释。 例如股票、国库券以及银行存款等。正因此,我们 可以得出这样的结论:高收益投资必定存在高风险, 而高风险投资必须以高收益来补偿。风险与收益之 间的的这种关系在财务上有专门的证明,典型的模 型是资本资产定价模型(CAPM)。 风险报酬率=风险系数×(市场平均报酬率-无风 险资产报酬率) 某资产的必要报酬率=无风险资产报酬率+该资产 的风险系数× (市场平均报酬率-无风险资产报酬 率)
公司特有风险(非系统风险),是指发生于个别 公司的特有事件造成的风险,如罢工、新产品开发 失败、诉讼失败、没有争取到重要合同等。
这类事件是随机发生的,可以通过多 角化投资来分散,因此又称为可分散风险。
(2)从公司本身来看,风险分为经营 风险(或商业风险)和财务风险(或筹资风险)。
经营风险,是指由于生产经营的不确定性所带来 的风险,主要来自于市场销售、生产成本和生产技 术等,这使得企业的报酬(息前利润)变得不确定。
A(1 i)0+ A(1 i)1 + + + … A(1 i)n2 A(1 i)n1 (1)
将(1)式两边乘以(1+i),得(2)式: FVAn (1+i)=
A(1 i)1+ A(1 i)+2 + + + … A(1 i)n2 A(1 i)n1 A(1 i)n
(2)
(2)式减(1)得:
FVAn (1+i) -FVA = n
i
以编成表,以便于计算,教材P336。
用公式2.3计算例题1的结果为: FVA5 = A • FVIFA(10%,5)=2000×6.105 = 12210(元)
结论:年金终值等于年金与年金终值系数的乘积
2)普通年金的现值(PVAn )
普通年金的现值:是指在一定期间内(n),在一定 利率下(i),每期期末等额系列收付金额(A)的现值之和。 这里也先以例题来进行说明。
的终值。
1
2
3
4
5 年初
终值
3000 3000 3000
列式计算为:
3000
3000
300(0 110%)1 300(0 110%)2 300(0 110%)3 300(0 110%)4
+ 300(0 110%)5
FVAD5 =20146.83
第二节 风险与收益
一、风险及其度量
1、什么是风险? 一般来说,风险是指在一定情况下和一定时期内事 件发生结果的不确定性。这种不确定性是不可控制的。
• 沉没成本:是指项目决策中,在项目分析之前发 生的成本费用.
知识回顾 Knowledge Review
祝您成功!
PVAn
012
…
AA
…
普通年金现值计算图示
n-1 n
AA
上述计算可以列式如下:
PVAn =
+ + + + A
A
(1 i)1 (1 i)2
…
A
A
(1 i)n1 (1 i)n
(3)
将(3)式两边乘以(1+i),得(4)式:
+ + + + + PVAn (1+i)=
A
A
(1 i)0 (1 i)1
所以9000元年金的终值为: FVA 3=9000×FVIFA(3%, 3)
=9000×3.091 =27819(元)
练习2:你买了一份10年期的医疗保单,交费方 式有两种:一是每年年末交400元,一种是一次性缴 足交2300元,两种交费方式在交费期间和到期的待 遇一样,假设利率为10%,你认为哪种方式更合算?
0
1
2
3
4
5 年末
期限为5年,利率为10%,金额为2000元的年金的终值计算图
例题1用列式来计算就是:
FVA5=
200(0 110%)+0 200(0 110%)+1 200(0 110%)+2 200(0 110%)+3 200(0 110%)4
2000 20001.1 20001.21 20001.331 20001.464
从查表可知: PVIFA(10%,10)=6.145
所以400元年金的现值为: PAV10 =400×6.1446=2458(元)>2300元
结论:从计算上来看一次性交足更合算。
2、预付年金的终值和现值
预付年金:是指收付款项发生在每期期初的年金。
1
2
3
4
5 年初
3000 3000 3000 3000 3000
解题思路: 事实上这是一道已知年金求其现值的问题,只 不过要进行一个小小的比较,然后再得出结论。
我们先求出400元年金的现值,然后再与2300相 比较,如果大于一次性交足数,则一次性交足更合 算,否则按期交更合算。
已知:普通年金的现值等于普通年金乘以普通 年金现值系数,即PVA =An×PVIFA(i, n), 这里的 A=400,i=10%, n=10。
…AABiblioteka A(1 i)n3 (1 i)n2 (1 i)n1
(4)
(4)式减(3)得:
PVA n(1+i) -PVA = n
- = - = A
A
(1 i)0 (1 i)n
A
A
(1 i)n
A
•
[1
1 (1 i)n
]
即:PVAn• i=
= A •
[1
1 (1 i)n ]
A • [1 (1 i)n ]
年金的终值和现值
【例题1 】求每年收入为2000元, 期限为5年,利息率为10%的这一系列金额 的终值。
终值
2000 2000
2000
2000
200(0 110%)4 200(0 110%)3 200(0 110%)2 200(0 110%)1 200(0 110%)0
+
2000 FVA5=12210
结论:年金现值等于年金与年金现值系数的乘积
三、年金的终值和现值计算
1、普通年金的终值和现值
练习1:如果你从现在开始每年年末替你存一 笔教育金9000元,准备3年后给你深造之用,假设 年利率为3%(不考虑利息税)。请问三年后这笔 钱有多少?
解题思路:
先要弄清楚这是一个什么问题,显然这是一个 已知普通年金求其终值的问题。我们前面已经知道 普通年金终值等于普通年金乘以年金终值系数,即: FVA =A×n FVIFA(i, n)。这里n=3, i=3%, A=9000,查 表可知FVIFA(3%, 3)=3.091
由于财务上的风险往往指投资风险, 所以,
(1)从投资主体的角度看,风险分 为市场风险和公司特有风险(或者系统风 险和非系统风险。
市场风险(或系统风险),是指影响整个市场的 因素所引起的风险,如战争、经济衰退、通货膨胀、 税收改革、世界金融危机、能源危机等。
这类风险涉及所有的投资对象,不能通过多角 化投资来分散,因此又称为不可分散风险。
(1 10%)5
PVA5 =3791 期限为5年,利率为10%,金额为1000元的年金的终值计算
例题2用列式来计算就是:
PVA5 =
+ + + + 1000
1000
(110%)1 (110%)2
1000 (1 10%)3
1000
1000
(110%)4 (110%)5
1000 0.909 1000 0.826
所以,PVAn=
A • 1 (1 i)n =A • PVIFA(i,n)
