《结构动力学》课程作业解析
结构动力学思考题解答by李云屹

结构动力学思考题made by 李云屹思考题一1、结构动力学与静力学的主要区别是什么结构的运动方程有什么不同主要区别为:(1)动力学考虑惯性力的影响,静力学不考虑惯性力的影响;(2)动力学中位移等量与时间有关,静力学中位移等量不随时间变化;(3)动力学的求解方法通常与荷载类型有关,静力学一般无关。
运动方程的不同:动力学的运动方程包括位移项、速度项和加速度项;静力学的平衡方程只包括位移项。
2、什么是动力自由度什么是静力自由度区分动力自由度和静力自由度的意义是什么动力自由度:确定结构体系质量位置的独立参数;静力自由度:确定结构体系在空间中的几何位置的独立参数。
意义:通过适当的假设,当静力自由度数大于动力自由度数时,使用动力自由度可以减少未知量,简化计算,提高计算效率。
3、采用集中质量法、广义坐标法和有限元法都可以使无限自由度体系简化为有限自由度体系,它们所采用的手法有什么不同4、在结构振动的过程中引起阻尼的原因有哪些(1)材料的内摩擦或材料变形引起的热耗散;(2)构件连接处或结构构件与非结构构件之间的摩擦;(3)结构外部介质的阻尼。
5、在建立结构运动方程时,如考虑重力的影响,动位移的运动方程有无改变如果满足条件:(1)线性问题;(2)重力的影响预先被平衡;则动位移的运动方程不会改变,否则会改变。
思考题二1、刚度系数k ij和质量系数m ij的直接物理意义是什么如何直接用m ij的物理概念建立梁单元的质量矩阵[M]k ij:由第j自由度的单位位移所引起的第i自由度的力;m ij:由第j自由度的单位加速度所引起的第i自由度的力。
依次令第j(j=1,2,3,4)自由度产生单位加速度,而其他的广义坐标处保持静止,使用平衡方程解出第i自由度上的力,从而得到m ij,集成得到质量矩阵[M]。
2、如何用刚度矩阵和质量矩阵,以矩阵的形式表示多自由度体系的势能和动能{}[]{}1=2TT u M u && {}[]{}1=2TV u K u3、建立多自由度体系运动方程的直接动力平衡法和拉格朗日方程法的优缺点是什么 (1)直接动力平衡法:优点:概念直观,易于通过各个结构单元矩阵建立整体矩阵,便于计算机编程。
《结构动力学》课程作业解析

研究生课程考核试卷(适用于课程论文、提交报告)科目:结构动力学大作业教师:姓名:学号:专业:岩土工程类别:专硕上课时间:2015年9 月至2015 年11 月考生成绩:卷面成绩平时成绩课程综合成绩阅卷评语:阅卷教师(签名)重庆大学研究生院制土木工程学院2015级硕士研究生考试试题1 题目及要求1、按规范要求设计一个3跨3层钢筋混凝土平面框架结构(部分要求如附件名单所示;未作规定部分自定)。
根据所设计的结构参数,求该结构的一致质量矩阵、一致刚度矩阵;2、至少采用两种方法求该框架结构的频率和振型;3、输入地震波(地震波要求如附件名单所示),采用时程分析法,利用有限元软件或自编程序求出该框架结构各层的线性位移时程反应。
2 框架设计2.1 初选截面尺寸取所设计框架为3层3跨,跨度均为4.5m ,层高均为3.9m 。
由于基础顶面离室内地面为1m ,故框架平面图中底层层高取 4.9m 。
梁、柱混凝土均采用C30,214.3/c f N mm =,423.010/E N mm =⨯,容重为325/kN m 。
估计梁、柱截面尺寸如下: (1)梁:梁高b h 一般取跨度的11218,取梁高b h =500mm ; 取梁宽300b b mm =;所以梁的截面尺寸为:300500mm mm ⨯ (2)柱:框架柱的截面尺寸根据柱的轴压比限值,按下列公式计算: ①柱组合的轴压力设计值...E N F g n β=其中:β:考虑地震作用组合后柱轴压力增大系数; F :按简支状态计算柱的负荷面积;E g :折算在单位建筑面积上的重力荷载代表值,可近似取为21214/KN m ;n :验算截面以上的楼层层数。
②c N cNA u f ≥其中:N u :框架柱轴压比限值;8度(0.2g ),查抗震规范轴压比限值0.75N u =;c f :混凝土轴心抗压强度设计值,混凝土采用30C ,214.3/c f N mm =。
经计算取柱截面尺寸为:300300mm mm ⨯ 该榀框架立面图如图2.1所示。
结构动力学课后习题答案

结构动力学课后习题答案结构动力学是研究结构在动态载荷作用下的响应和行为的学科。
它涉及到结构的振动、冲击响应、疲劳分析等方面。
课后习题是帮助学生巩固课堂知识、深化理解的重要手段。
以下内容是结构动力学课后习题的一些可能答案,供参考:习题1:单自由度系统自由振动分析解答:对于一个单自由度系统,其自由振动的频率可以通过以下公式计算:\[ f = \frac{1}{2\pi}\sqrt{\frac{k}{m}} \]其中,\( k \) 是系统的刚度,\( m \) 是系统的总质量。
系统自由振动的振幅随着时间的衰减可以通过阻尼比 \( \zeta \) 来描述,其衰减系数 \( \delta \) 可以通过以下公式计算:\[ \delta = \sqrt{1-\zeta^2} \]习题2:单自由度系统受迫振动分析解答:当单自由度系统受到周期性外力作用时,其受迫振动的振幅可以通过以下公式计算:\[ A = \frac{F_0}{\sqrt{(k-m\omega^2)^2+(m\zeta\omega)^2}} \] 其中,\( F_0 \) 是外力的幅值,\( \omega \) 是外力的角频率。
习题3:多自由度系统模态分析解答:对于多自由度系统,可以通过求解特征值问题来得到系统的模态。
特征值问题通常表示为:\[ [K]{\phi} = \lambda[M]{\phi} \]其中,\( [K] \) 是系统的刚度矩阵,\( [M] \) 是系统的质量矩阵,\( \lambda \) 是特征值,\( {\phi} \) 是对应的特征向量,即模态形状。
习题4:结构的冲击响应分析解答:对于结构的冲击响应分析,通常需要考虑冲击载荷的持续时间和冲击能量。
结构的冲击响应可以通过冲击响应谱(IRF)来分析,它描述了结构在不同频率下的响应。
冲击响应分析的结果可以用来评估结构的耐冲击性能。
习题5:疲劳分析解答:结构的疲劳分析需要考虑结构在重复载荷作用下的寿命。
结构动力学思考题解答by李云屹

结构动力学思考题made by 李云屹思考题一1、结构动力学与静力学的主要区别是什么结构的运动方程有什么不同主要区别为:(1)动力学考虑惯性力的影响,静力学不考虑惯性力的影响;(2)动力学中位移等量与时间有关,静力学中位移等量不随时间变化;(3)动力学的求解方法通常与荷载类型有关,静力学一般无关。
运动方程的不同:动力学的运动方程包括位移项、速度项和加速度项;静力学的平衡方程只包括位移项。
2、什么是动力自由度什么是静力自由度区分动力自由度和静力自由度的意义是什么动力自由度:确定结构体系质量位置的独立参数;静力自由度:确定结构体系在空间中的几何位置的独立参数。
意义:通过适当的假设,当静力自由度数大于动力自由度数时,使用动力自由度可以减少未知量,简化计算,提高计算效率。
3、采用集中质量法、广义坐标法和有限元法都可以使无限自由度体系简化为有限自由度体系,它们所采用的手法有什么不同4、在结构振动的过程中引起阻尼的原因有哪些(1)材料的内摩擦或材料变形引起的热耗散;(2)构件连接处或结构构件与非结构构件之间的摩擦;(3)结构外部介质的阻尼。
5、在建立结构运动方程时,如考虑重力的影响,动位移的运动方程有无改变 如果满足条件: (1)线性问题;(2)重力的影响预先被平衡;则动位移的运动方程不会改变,否则会改变。
思考题二1、刚度系数k ij 和质量系数m ij 的直接物理意义是什么如何直接用m ij 的物理概念建立梁单元的质量矩阵[M]k ij :由第j 自由度的单位位移所引起的第i 自由度的力; m ij :由第j 自由度的单位加速度所引起的第i 自由度的力。
依次令第j (j=1,2,3,4)自由度产生单位加速度,而其他的广义坐标处保持静止,使用平衡方程解出第i 自由度上的力,从而得到m ij ,集成得到质量矩阵[M]。
2、如何用刚度矩阵和质量矩阵,以矩阵的形式表示多自由度体系的势能和动能{}[]{}1=2TT u M u {}[]{}1=2TV u K u3、建立多自由度体系运动方程的直接动力平衡法和拉格朗日方程法的优缺点是什么 (1)直接动力平衡法:优点:概念直观,易于通过各个结构单元矩阵建立整体矩阵,便于计算机编程。
结构动力学-习题解答
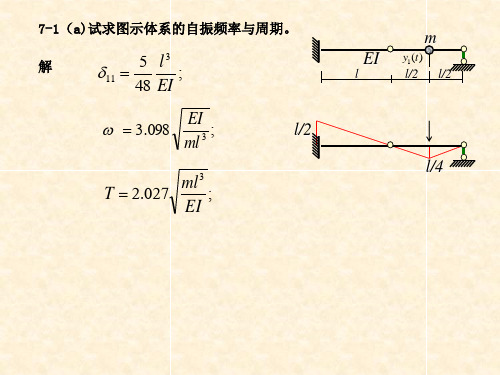
7-1(a)试求图示体系的自振频率与周期。
解
11
5 48
l3 EI
;
3.098
EI ml 3
;
l/2
T 2.027
ml 3 ;
7-6 某结构在自振10个周期后,振幅降为原来初始位移的10% (初位移为零),试求其阻尼比。
解: 1 ln10 0.0366 2 10
8-1试求图示梁的自振频率和振型。 m
y1(t)
解
EI 2m
a
a
y2
(t
)
a
12
21
1 4
a3 EI
a
I 2 m 0
11m1 1/ 2
m212
0
m1 21
22m2 1/ 2
1 1.153
a/2
2 0.181
令
1
11m1
2
1 1/ 2
0
1/ 4 1/3 2 4 / 3 5 / 24 0
x11 / x21 3.277; x12 / x22 0.61
;
9l / 64 (a)
5l / 32
11.817
EI ml 3 ;
l/2
T 0.531
ml3 ;
(b)
EI
7-1(c)试求图示体系的自振频率与周期。
m 刚性杆
解 由右面竖杆的平衡可求出铰处约束力。
EI
由水平杆的平衡:
[美]R.克里夫《结构动力学》补充详解及习题解
![[美]R.克里夫《结构动力学》补充详解及习题解](https://img.taocdn.com/s3/m/198055225627a5e9856a561252d380eb629423b8.png)
前言结构动力学是比较难学的一门课程,但是你一旦学会并且融会贯通,你就会为成为结构院士、大师和总工垫定坚实的基础。
结构动力学学习的难点主要有以下两个方面。
1 概念难理解,主要表现在两个方面,一是表达清楚难,如果你对概念理解的很透彻,那么你写的书对概念的表述也会言简意赅,切中要害(克里夫的书就是这个特点),有的书会对一个概念用了很多文字进行解释,但是还是没有说清楚,也有的书受水平限制,本身表述就不清楚。
二是理解难,有点只可意会不可言传的味道,老师讲的头头是道,自己听得云山雾绕。
2 公式推导过程难,一是力学知识点密集,推导过程需要力学概念清析,并且需要每一步的力学公式熟悉;二是需要一定的数学基础,而且有的是在本科阶段并没有学习的数学知识。
克里夫《结构动力学》被称为经典的结构动力学教材,但是也很难看懂。
之所以被称为经典,主要就是对力学的概念表达的语言准确,概念清楚。
为什么难懂呢?是因为公式的推导过程比较简单,省略过多。
本来公式的推导过程既需要力学概念清楚也需要数学公式熟悉,但是一般人不是力学概念不清楚,就是数学公式不熟悉,更有两者都不熟悉者。
所以在学习过程中感觉很难,本学习详解是在该书概念清楚的基础上,对力学公式推导过程进行详细推导,并且有的加以解释,帮助你在学习过程中加深理解和记忆。
达到融会贯通,为你成为结构院士、大师和总工垫定坚实的基础。
以下黑体字是注释,其它为原书文字。
[美] R∙克里夫《结构动力学》辅导学习详解第1章结构动力学概述… …第Ⅰ篇单自由度体系第2章基本动力体系的组成… …§2-5 无阻尼自由振动分析如上一节所述,有阻尼的弹簧-质量体系的运动方程可表示为mv̈(t)+cv̇(t)+kν(t)=p(t)(2-19)其中ν(t)是相对于静力平衡位置的动力反应;p(t)是作用于体系的等效荷载,它可以是直接作用的或是支撑运动的结构。
为了获得方程(2-19)的解,首先考虑方程右边等于零的齐次方程,即mv̈(t)+cv̇(t)+kν(t)=0(2-20)mv(t)+kν(t)=0(2-20a)此处公式应该为mv(t)+kν(t)=0,因为该节是无阻尼自由振,而且(2-20)的解,式(2-21)也是公式mv(t)+kν(t)=0的解在作用力等于零时产生的运动称为自由振动,现在要研究的即为体系的自由振动反应。
结构动力学 (邹经湘 王本利 王世忠 著) 哈尔滨工业大学出版社 课后答案

∑ F ,得到系统的运动微分方程;
(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
kh
2、 动量距定理法 适用范围:绕定轴转动的单自由度系统的振动。 解题步骤: (1) 对系统进行受力分析和动量距分析;
̇̇ = (2) 利用动量距定理 J θ
(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。 3、 拉格朗日方程法: 适用范围:所有的单自由度系统的振动。
w .c
所以:系统的固有频率为
om
kg P
ω0 =
kg P
x
T平动 = T转动 =
1 ̇2; Mx 2
图 1-35
而势能
课 后
答
̇⎞ ̇⎞ 1 ⎛x 1 ⎛ MR ⎞ ⎛ x I⎜ ⎟ = ⎜ ⎟⎜ ⎟ ; 2 ⎝R⎠ 2 ⎝ 2 ⎠⎝ R ⎠
2
2
2
T=
1 1 3 ̇ 2 + Mx ̇ 2 = Mx ̇2 ; Mx 2 4 4 1 Kx 2 ; 2
系统的势能为:
U=
da
r 2 1 1 1 1⎛ K A ϕ A 2 + K Bϕ B 2 = K Aϕ A 2 + K Bϕ B 2 = ⎜ K A + K B A 2 2 2 2 2⎜ rB ⎝
w .c
B
D
(
)
⎞ 2 ⎟ϕ A ; ⎟ ⎠
图 1-36
系统的机械能为
kh
T +U =
r 2 1 1⎛ ̇A2 + ⎜KA + KB A (m A + m B )rA 2ϕ 4 2⎜ rB 2 ⎝
w
图 1-34 0
B
w
结构动力学大作业分析

结构动力学大作业姓名:学号:习题1用缩法减进行瞬态构造动力学剖析以确立对有限上涨时间得恒定力的动力学响应。
是一根钢梁支撑着集中质量并蒙受一个动向荷载。
实质构造钢梁长L,支撑着一个集中质量M。
这根梁蒙受着一个上涨时间为t,最大值为F1的动向荷载F(t)。
梁的质量能够忽视,需确立产生最大位移响应时间t max及响应y max 。
同时要确立梁中的最大曲折应力bend。
:资料特征:E x 2E5 MPa ,质量M=,质量阻尼ALPHAD=8;几何尺寸:L=450mm mm4h=18mm;荷载为:F1=20N t =提示:减少法需定义主自由度。
荷载需三个荷载步〔0至加质量,再至,最后至1s〕ANSYS命令以下:FINISH/CLE$/CONFIG,NRES,2000/prep7L=450$H=18ET,1,BEAM3ET,2,MASS21,,,4R,1,1,800.6,18R,2,30!MASS21的实常数次序N,1,0,0,0N,2,450/2,0,0N,3,450,0,0E,1,2$E,2,3!创办单元TYPE,2$REAL,2E,2M,2,UYFINISH/SOLU!进入求解层ANTYPE,TRANSTRNOPT,REDUC!定义时间积分步长ALPHAD,8 !质量阻尼为8D,1,UY$D,3,UX,,,,,UY!节点1Y方向,拘束节点3X、Y方向拘束F,2,FY,0LSWRITE,1 !生成荷载步文件1FDELE,ALL,ALLF,2,FY,20LSWRITE,2 !生成荷载步文件 2TIME,1LSWRITE,3 !生成荷载步文件 3LSSOLVE,1,3,1!求解荷载文件1,2,3FINISH/SOLU!扩展办理SOLVEFINISH/POST26NUMVAR,0FILE,fdy,rdsp!注意,成立的工程名称为fdy,否那么高出最大变量数200,结果无效NSOL,2,2,U,Y,NSOL PLVAR,2 !时间位移曲线PRVAR,2 !得出在该时间点上跨中位移最大/POST1 !查察某个时辰的计算结果SET,FIRSTPLDISP,1 !系统在秒时总变形图ETABLE,Imoment,SMISC,6 !单元I点弯矩ETABLE,Jmoment,SMISC,12 !单元J点弯矩ETABLE,Ishear,SMISC,2 !单元I点剪力ETABLE,Jshear,SMISC,8 !单元J点剪力PLLS,IMOMENT,JMOMENT,1,0 !画出弯矩图PLLS,ISHEAR,JSHEAR,,1,0 !画出剪力争结果以下;跟着时间位移的大小:可知系统在秒时总变形最大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
研究生课程考核试卷(适用于课程论文、提交报告)科目:结构动力学大作业教师:姓名:学号:专业:岩土工程类别:专硕上课时间:2015年9 月至2015 年11 月考生成绩:卷面成绩平时成绩课程综合成绩阅卷评语:阅卷教师(签名)重庆大学研究生院制土木工程学院2015级硕士研究生考试试题1 题目及要求1、按规范要求设计一个3跨3层钢筋混凝土平面框架结构(部分要求如附件名单所示;未作规定部分自定)。
根据所设计的结构参数,求该结构的一致质量矩阵、一致刚度矩阵;2、至少采用两种方法求该框架结构的频率和振型;3、输入地震波(地震波要求如附件名单所示),采用时程分析法,利用有限元软件或自编程序求出该框架结构各层的线性位移时程反应。
2 框架设计2.1 初选截面尺寸取所设计框架为3层3跨,跨度均为4.5m ,层高均为3.9m 。
由于基础顶面离室内地面为1m ,故框架平面图中底层层高取 4.9m 。
梁、柱混凝土均采用C30,214.3/c f N mm =,423.010/E N mm =⨯,容重为325/kN m 。
估计梁、柱截面尺寸如下: (1)梁:梁高b h 一般取跨度的11218,取梁高b h =500mm ; 取梁宽300b b mm =;所以梁的截面尺寸为:300500mm mm ⨯ (2)柱:框架柱的截面尺寸根据柱的轴压比限值,按下列公式计算: ①柱组合的轴压力设计值...E N F g n β=其中:β:考虑地震作用组合后柱轴压力增大系数; F :按简支状态计算柱的负荷面积;E g :折算在单位建筑面积上的重力荷载代表值,可近似取为21214/KN m ;n :验算截面以上的楼层层数。
②c N cNA u f ≥其中:N u :框架柱轴压比限值;8度(0.2g ),查抗震规范轴压比限值0.75N u =;c f :混凝土轴心抗压强度设计值,混凝土采用30C ,214.3/c f N mm =。
经计算取柱截面尺寸为:300300mm mm ⨯ 该榀框架立面图如图2.1所示。
图2.1 框架立面图2.2 框架几何刚度特征(1)梁:截面惯性矩:3394300500 3.125101212b bh I mm ⨯===⨯; 刚度:491323.010 3.125109.37510b EI N mm =⨯⨯⨯=⨯⋅ 293750KN m =⋅ 梁的单位长度质量(按照计算重力荷载代表值的方法计算): 一二层(考虑楼板恒载及楼面活载作用):分布质量:b (0.30.52500 4.50.12500 4.5200)2400/m kg m =⨯⨯+⨯⨯+⨯= 顶层(仅考虑楼板恒载不考虑屋面活载作用):分布质量:b (0.30.52500 4.50.122500)1725/m kg m =⨯⨯+⨯⨯=; (2)柱:截面惯性矩:3384300300 6.75101212c bh I mm ⨯===⨯; 刚度:481323.010 6.7510 2.02510c E I N mm =⨯⨯⨯=⨯⋅ 220250KN m =⋅ 分布质量:c 0.30.32500/225/m bh kg m kg m γ==⨯⨯=根据以上计算结果,将其列入表中,如下表2.1所示:表2.1 梁柱力学参数截面尺寸(2mm )力学参数300500⨯300300⨯截面惯性矩I (4mm ) 93.12510⨯ 86.7510⨯ 刚度EI (2kN m ⋅)49.37510⨯ 42.02510⨯单位长度质量m (/kg m ) 一、二层2400 225顶层17252.3 动力自由度框架单元编号及动力自由度编号见图2.2所示:图2.2框架单元编号及自由度编号框架结构可以理想化为在节点处相互连接的单元(梁和柱)的集合。
设梁、柱的轴向变形均忽略不计,只考虑节点的转角和横向位移,则该框架有3个平动自由度和12个转角自由度,共15个自由度。
3一致质量矩阵、一致刚度矩阵3.1 一致质量矩阵在节点位移作用下框架梁和柱上所引起的变形形状采用Hermite 多项式。
因此均布质量梁的一致质量矩阵为:2222156542213541561322221343420132234L L L L mL L LL L L L LL -⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥---⎣⎦式(3.1)下面开始计算质量影响系数,依次对每一个自由度施加单位加速度,利用式(3.1)的系数确定质量影响系数:1图3.1.1()()1121415161718191101111225 3.915643156431725 4.524591.2420420225 3.9544544451.3420420225 3.92222 3.9179.3420420225 3.91313 3.9105.9420420c b c c c m h m m L m h m m h m m m m h m h m m m m h ⨯=⨯⨯+=⨯⨯+⨯⨯=⨯=⨯⨯=⨯⨯=⨯====⨯=⨯⨯=⨯====⨯-=⨯-⨯=-2图3.1.2221232425262728292102112122225 3.915683156832400 4.535007.4420420225 3.9544544451.3420420225 3.91313 3.9105.942042022220420420c b c c c c m h m m L m h m m m h m m m m h m h m hm m m m h h m ⨯=⨯⨯+=⨯⨯+⨯⨯=⨯==⨯⨯=⨯⨯=⨯====⨯=⨯⨯=====⨯-+⨯==,,,()132142152225 3.91313 3.9105.9420420c m h m m m h ⨯===⨯-=⨯-⨯=-,,,()()3图3.1.3123323225 3.9225 4.91564156431564156442042042042032400 4.535341.7225 3.9544544451.3420420c c b c m h m h m m L m h m ⨯⨯=⨯⨯+⨯⨯+=⨯⨯+⨯⨯+⨯⨯=⨯=⨯⨯=⨯⨯=839310,311,3225 3.91313 3.9105.9420420c m h m m m m h ⨯====⨯=⨯⨯= ()1212,313,314,315,312225 3.9222222 3.9420420420225 4.922 4.9103.7420c c m h m h m m m m h h ⨯====⨯-+⨯=⨯-⨯⨯+⨯⨯=()4图3.1.422224422542284142225 3.91725 4.5444 3.94 4.51624.24204204204201725 4.5(3)(3) 4.51122.8420420225 3.9(3)(3) 3.995.3420420225 3.92222 3.9179.3420420c b b c c m h m L m h L m L m L m h m h m h m h m ⨯⨯=⨯+⨯=⨯⨯+⨯⨯=⨯=⨯-=⨯-⨯=-⨯=⨯-=⨯-⨯=-⨯=⨯=⨯⨯=4225 3.91313 3.9105.9420420c m h h ⨯=⨯=⨯⨯=由于框架为对称结构,对自由度4V 施加单位加速度引起的质量影响系数与对自由度7V 施加单位加速度引起的质量影响系数相同,可得结果如下:22227722672211,717225 3.91725 4.5444 3.94 4.51624.24204204204201725 4.5(3)(3) 4.51122.8420420225 3.9(3)(3) 3.995.3420420225 3.92222 3.9179.3420420c b b c c m h m L m h L m L m L m h m h m h m h ⨯⨯=⨯+⨯=⨯⨯+⨯⨯=⨯=⨯-=⨯-⨯=-⨯=⨯-=⨯-⨯=-⨯=⨯=⨯⨯=27225 3.91313 3.9105.9420420c m h m h ⨯=⨯=⨯⨯=5图3.1.52222552245652295225 3.91725 4.54244 3.924 4.53121.24204204204201725 4.5(3)(3) 4.51122.8420420225 3.9(3)(3) 3.993.5420420c b b c m h m L m h L m L m m L m h m h ⨯⨯=⨯+⨯⨯=⨯⨯+⨯⨯⨯=⨯==⨯-=⨯-⨯=-⨯=⨯-=⨯-⨯=-1525225 3.92222 3.9179.3420420225 3.91313 3.9105.9420420c c m h m h m h m h ⨯=⨯=⨯⨯=⨯=⨯=⨯⨯=由于框架为对称结构,对自由度5V 施加单位加速度引起的质量影响系数与对自由度6V 施加单位加速度引起的质量影响系数相同,可得结果如下:2222662256762210,6225 3.91725 4.54244 3.924 4.53121.24204204204201725 4.5(3)(3) 4.51122.8420420225 3.9(3)(3) 3.993.5420420c b b c m h m L m h L m L m m L m h m h ⨯⨯=⨯+⨯⨯=⨯⨯+⨯⨯⨯=⨯==⨯-=⨯-⨯=-⨯=⨯-=⨯-⨯=- 1626225 3.92222 3.9179.3420420225 3.91313 3.9105.9420420c c m h m h m h m h ⨯=⨯=⨯⨯=⨯=⨯=⨯⨯=8图3.1.6()()2222882298224812,818225 3.92400 4.54244 3.924 4.52337.14204204204202490 4.5(3)(3) 4.51562.1420420225 4.5(3)(3) 4.595.3420420225 3.91313420420c b b c c m h m L m h L m L m L m h m m h m h m h ⨯⨯=⨯⨯+⨯=⨯⨯⨯+⨯⨯=⨯=⨯-=⨯-⨯=-⨯==⨯-=⨯-⨯=-⨯=⨯-=⨯-2838 3.9105.922220420420225 3.91313 3.9105.9420420c c c m h m h m h h m h m h ⨯=-=⨯-+⨯=⨯=⨯=⨯⨯=()由于框架为对称结构,对自由度8V 施加单位加速度引起的质量影响系数与对自由度11V 施加单位加速度引起的质量影响系数相同,可得结果如下:()222211,112210,11227,1115,111,11225 3.92400 4.54244 3.924 4.52337.14204204204202490 4.5(3)(3) 4.51562.1420420225 4.5(3)(3) 4.595.342042022513420c b b c c m h m L m h L m L m L m h m m h m h m h ⨯⨯=⨯⨯+⨯=⨯⨯⨯+⨯⨯=⨯=⨯-=⨯-⨯=-⨯==⨯-=⨯-⨯=-=⨯-=()2,113,11 3.913 3.9105.942022220420420225 3.91313 3.9105.9420420c c c m h m h m h h m h m h ⨯⨯-⨯=-=⨯-+⨯=⨯=⨯=⨯⨯=()(7)对自由度9V 施加单位加速度,并约束其他自由度,如图3.1.7所示。
