双因素方差分析数据
双因素方差分析

(6.35)
MSE = SSE rn(m − 1)
则检验因素 A 与 B 影响是否显著的统计量分别是:
(6.36)
FA
=
MSA MSE
~
F (r
− 1, rnm
−
rn)
(6.37)
FB
=
MSB MSE
~
F (n
− 1, rnm
−
rn)
检验交互影响是否显著的统计量度是:
(6.38)
FAB
=
MSAB MSE
X rn1 X rn2 M X rnm
表中的 X ijl 表示的是在因素水平组合( Ai ,B j )下第l次试验的结果。在此组 合下试验结果的平均值为:
X
ij.
=
1 m
m
∑ X ijl
l =1
进一步记:
(6.23)
X
i..
=
1 nm
nm
∑ ∑ X ijl
j=1l =1
(6.24)
X . j.
=
1 rm
~
F[(r
− 1)(n
− 1), rnm
−
rn]
(6.39)
【例 6-3】为了分析光照因素 A 与噪音因素 B 对工人生产有无影响,光照效
应与噪音效应有交互作用,在此两因素不同的水平组合下做试验,结果如表 6-8
(表中数据为产量):
表 6-8
因素 B
B1
B2
B3
因
15 15 17 19 19 16 16 18 21
各个方差对应的均方差是:
对因素A而言:
MSA = SSA r −1
(6.18)
对因素B而言:
双因素试验的方差分析

i 1
j 1
要判断因素A,B及交互作用AB对试验结果是否 有显著影响,即为检验如下假设是否成立:
H01 :1 2 a 0
H02 : 1 2 b 0
H03 : ij 0 i 1, 2, , a; j 1, 2, ,b
➢ 总离差平方和的分解定理 仿单因素方差分析的方法,考察总离差平方和
a
Ti.2
b,
i1
p T 2 ab ,
DB
b
T.
2 j
a,
j1
ab
R
X
2 ij
i1 j1
例1 设甲、乙、丙、丁四个工人操作机器Ⅰ、Ⅱ、Ⅲ各一天, 其产品产量如下表,问工人和机器对产品产量是否有显著 影响?
机器 B 工人 A
ⅠⅡ
Ⅲ
甲
50 63 52
乙
47 54 42
丙
47 57 41
F值
F 值临介值
因素A 因素B
SS A SSB
df A
MS A
SS A df A
FA
MS A MSE
df B
MSB
Байду номын сангаас
SSB df B
FB
MSB MSE
F (a 1 ,
ab n 1) F (b 1 ,
ab n 1)
A B
误差 总和
SS AB
SSE SST
df AB df E dfT
MS AB SS AB
F0.01 3,6 9.78 F0.05 3,6 4.76 F0.01 2,6 10.92
FB F0.01 2,6
结论:工人对产品的产量有显著影响, 机器对产品的产量有极显著影响。
无交互影响的双因素方差分析

1、无交互影响的双因素方差分析如果某一试验结果受到A和B两个因素的影响,这两个因素分别可取K和M个水平,则双因素分析实际上就是要比较因素A的K个水平的均值之间是否存在显著差异,因素B 的M个水平的均值之间是否存在显著差异。
假定试验的结果如下表所示(在假定两个因素无交互影响的情形下,通常采用不重复试验)。
表9-8 无交互影响的双因素分析试验观察值无交互影响的双因素方差分析结果如下表:表9-9 无交互影响的双因素分析表在显著性水平α下,如果F > 临界值Fα,则拒绝原假设,认为差异显著。
小案例9-1:有4个品牌的彩电在5个地区销售,为分析彩电的品牌(品牌因素)和销售地区(地区因素)对销售量的影响,对每个品牌在各地区的销售量取得表9-10的数据。
试分析品牌和销售地区对彩电的销售量是否有显著影响?(α=0.05)表9-10 不同品牌的彩电在5个地区的销售量数据提出假设:对品牌因素提出的假设为:H0:m1=m2=m3=m4 (品牌对销售量无显著影响)H1:mi (i =1,2, …, 4) 不全相等(有显著影响)对地区因素提出的假设为:H0:m1=m2=m3=m4=m5 (地区对销售量无显著影响)H1:mj (j =1,2,…,5) 不全相等(有显著影响)表9-11 方差分析表结论:F品牌=18.10777>Fα=3.4903,拒绝原假设H0,说明彩电的品牌对销售量有显著影响。
F地区=2.100846<Fα=3.2592,不拒绝原假设H0,无证据表明销售地区对彩电的销售量有显著影响。
资料来源:贾俊平、何晓群、金勇进,《统计学》[M].北京: 中国人民大学出版社,2004.10第2版。
双因素试验的方差分析(精)
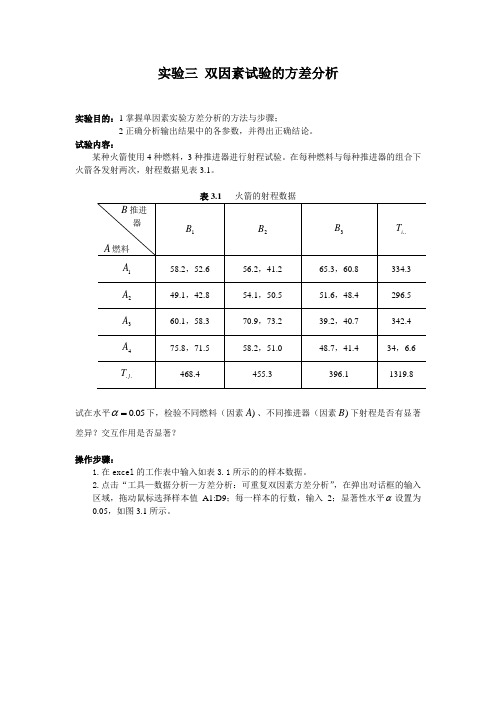
实验三 双因素试验的方差分析实验目的:1掌握单因素实验方差分析的方法与步骤;2正确分析输出结果中的各参数,并得出正确结论。
试验内容:某种火箭使用4种燃料,3种推进器进行射程试验。
在每种燃料与每种推进器的组合下火箭各发射两次,射程数据见表3.1。
表3.1 火箭的射程数据试在水平05.0=α下,检验不同燃料(因素)A 、不同推进器(因素)B 下射程是否有显著差异?交互作用是否显著?操作步骤:1.在excel 的工作表中输入如表3.1所示的的样本数据。
2.点击“工具—数据分析—方差分析:可重复双因素方差分析”,在弹出对话框的输入区域,拖动鼠标选择样本值A1:D9;每一样本的行数,输入2;显著性水平α设置为0.05,如图3.1所示。
图3.1 应用excel“数据分析”功能求双因素等重复方差分析的有关参数3.点击确定,输出参数的窗口如图3.2所示。
图3.2 应用excel“数据分析”功能求双因素等重复方差分析的有关参数结果分析:图3.2 中仅列示了输出结果中的方差分析表。
“样本”即燃料因子,“列”即推进器因子,“交互”为燃料和推进器因子的交互作用,SS 为平方和;df 是自由度;P-value 为P 值,即所达到的临界显著水平;F crit 是Fα(t-1,N-t)的值。
由方差分析表可知,因子A (燃料)的作用是一般显著的(P-value的值为0.025969<0.05);因子B(推进器)的作用是高度显著的(P-value的值为0.003506<0.01);而交互作用是极其显著的(P-value的值为6.15E-05<<0.01),这说明燃料的作用于与推进器之间有着密切的关系,也即每种推进器都有各自最合自得最佳燃料。
双因素方差分析

y ij ij ij 2 , ij ~ N ( 0, )
假定 ij 相互独立
i 1,2,, r , j 1,2,, s
沿用有重复试验的有关记号,模型可以改写为
yij i j ij ij ~ N (0, 2 ) i 0, j 0, j i
FA B
S A B ( r 1)( s 1) S E rs( t 1)
~ F (( r 1)( s 1), rs( t 1))
表1 双因素方差分析表
来源
因子A 因子B 交互作用 误差 总和
平方和
自由度
均方
SA SA r 1 SB SB s 1
S A B S A B ( r 1)(s 1)
1 t yij yijk t k 1 1 r t y j yijk rt i 1 k 1
引入总的偏差平方和(总变差):
ST yijk y
i 1 j 1 k 1 r s t
2
可以证明
其中
ST S E S A S B S AB
S E yijk yij
§4.2
双因素方差分析
有重复试验的方差分析
无重复试验的方差分析
一、有重复试验的双因素方差分析
设有两个因素A,B作用于试验指标。
因素A有r个水平 A1 , A2 , Ar , 因素B有s个水平B1 , B2 ,, Bs , 现对因素A,B的每对组合 ( Ai , B j ) 都作 t (t 2)次试 验(称为等重复试验)。
表2 方差分析表
来源
因子A 因子B 误差 总和
平方和
双因素重复测量方差分析spss

双因素重复测量方差分析spss
一、双因素重复测量方差分析(two-way repeated measures ANOVA)
双因素重复测量方差分析(Two-Way repeated measures ANOVA)可以用来检测一个
变量的变化在两个或多个独立变量的作用下是否发生变化。
在双因素重复测量方差分析中,变量1是因素1,因素1有若干水平,变量2是因素2,因素2也有若干水平。
双因素重
复测量方差分析可以检验两个因素是否共同影响变量1的变化,或者检测某个因素是否单
独地影响变量1的变化。
1、打开spss统计软件,点击文件、数据,从窗口中打开需要分析数据文件;
2、点击“分析”菜单,然后从子菜单中点击“多维分析”,再单击“双因素重复测
量方差分析”;
3、在弹出的窗口中,在“变量”框中选择需要分析的变量;
4、在“因素”框中,选择双因素,比如实验组和对照组;
5、点击“定义”按钮,设定因素的水平,比如实验组的水平为A,对照组的水平为B;
6、在“多重比较”框中,勾选“重复测量”框,并且可以设定多重比较的参数;
7、选择“显著性水平”框,设定检验的显著性,通常设定为0.05;
8、单击“OK”按钮,查看分析结果,该分析结果将显示两个因素及其交互作用对变
量1的影响情况。
论文—双因素试验的方差分析

X ijk ~ N (ij , 2 ) ( ij 和 2 未 知 ), 记 X ijk i = ijk , 即 有
ijk X ij ijk ~ N (0, 2 ), 故 X ijk ijk 可视为随机误差. 从而得到如下数学模型
X ijk ij ijk, ijk ~ N(0, 2), 各 ijk 相互独立, i 1, , r; j 1, , s; k 1, , t;
1 st
1 rt
X
j 1 k 1
r t
s
t
ijk
,i=1,2, ,r,
X
j =
X
i 1 k 1
类似地,引入记号: , i , j , i , j , 易见
i 1
r
i 0 ,
j 1
s
j
0.
为水平 B j 的效应. 这样可以将
仍称 为总平均,称 i 为水平 A i 的效应,称 成
ij
j
ij
表示
= + i + j +
ij
( i 1, , r; j 1, , s ) ,
(3)
与无重复试验的情况类似,此类问题的检验方法也是建立在偏差平方和的分解上的。 2. 偏差平方和及其分解 引入记号: X =
1 rst
X
i 1 j 1 k 1
r
s
t
ijk
,
X
ij =
1 X ijk ,i=1,2, ,r,j=1,2, ,s, t k 1
t
X
i =
试 验 结 因 素 果 A 因 素 B
交互作用双因子方差分析

H 03 的 拒 绝 域 为
W 03
S A SE
B 2
2
k3
(6.35)
为 了 确 定 界 限 值 k1 、k 2 、k3 , 按 照 显 著 性 检 验 的 一 般
步骤,我们需要知道当相应的原假设成立时各检验统
计量的分布,
可以证明,
在 H 01 成 立 时
S A 2 r 1 ~ F r 1, rs t 1 S E 2 rs t 1
后的剩余部分,称为水平组合
Ai,Bj 的交互效应。
于 是 X ij ~ N u ij , 2 可 以 等 价 的 表 示 为 :
X ij u ij ij u i j ij ij
ij ~ N 0, 2
,
i 1,2, , r ; j 1,2, , s
这 表 明 , 在 因 素 A, B 的 不 同 水 平 组 合 下 , 试 验 结 果 的 相 对 差 异 u ij u ( 视 为 总 效 应 ) 是 由 如 下 四 部 分 组 成 :
i 1 j 1 k 1
S
2 A
r
s
t
x i•• x 2
A
称为因素 的主效应偏差平方和。
i 1 j 1 k 1
S
2 B
r
s
t
x • j• x 2
B
称为因素 的主效应偏差平方和。
i 1 j 1 k 1
S 2 A B
rst
A B
x ij • x i • • x • j • x 2 称 为
的交互效应
i1 j1 k 1
偏差平方和。
则得到总变差平方和的分解式:
ST 2
SE2
SA2
SB2
