(完整版)全等三角形经典例题
全等三角形证明经典45题及答案
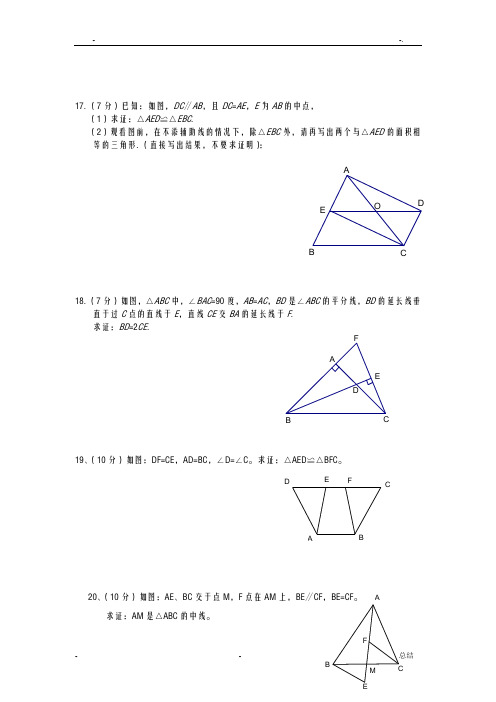
17.(7分)已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点, (1)求证:△AED ≌△EBC .(2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):18.(7分)如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F . 求证:BD =2CE .19、(10分)如图:DF=CE ,AD=BC ,∠D=∠C 。
求证:△AED ≌△BFC 。
20、(10分)如图:AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE=CF 。
求证:AM 是△ABC 的中线。
O ED C B A FE D C B AFAFE DCBA21、(10分)如图:在△ABC中,BA=BC,D是AC的中点。
求证:BD⊥AC。
22、(10分)AB=AC,DB=DC,F是AD的延长线上的一点。
求证:BF=CF23、(12分)如图:AB=CD,AE=DF,CE=FB。
求证:AF=DE。
DCBAF DCBAF BA24.公园里有一条“Z ”字形道路ABCD ,如图所示,其中AB ∥CD ,在AB ,CD ,BC 三段路旁各有一只小石凳E ,F ,M ,且BE =CF ,M 在BC 的中点,试说明三只石凳E ,F ,M 恰好在一条直线上.25.已知:点A 、F 、E 、C 在同一条直线上, AF =CE ,BE ∥DF ,BE =DF .求证:△ABE ≌△CDF .26.已知:如图所示,AB =AD ,BC =DC ,E 、F 分别是DC 、BC 的中点,求证: AE =AF 。
27.如图,在四边形ABCD 中,E 是AC 上的一点,∠1=∠2,∠3=∠4,求证: ∠5=∠6.D A FE 654321E DCADCBAE28.已知AB ∥DE ,BC ∥EF ,D ,C 在AF 上,且AD =CF ,求证:△ABC ≌△DEF .29.已知:如图,AB =AC ,BD ⊥AC ,CE ⊥AB ,垂足分别为D 、E ,BD 、CE 相交于点F ,求证:BE =CD .30如图,△ABC 中,AD 是∠BAC 的平分线,DE ⊥AB 于E ,DF ⊥AC 于F .求证:(1)AD ⊥EF ;(2)当有一点G 从点D 向A 运动时,GE ⊥AB 于E ,GF ⊥AC 于F ,此时上面结论是否成立?31.已知:如图, AC ⊥BC 于C , DE ⊥AC 于E , AD ⊥AB 于A , BC =AE .若AB = 5 ,求AD 的长?AC B DEF AEBF32.如图:AB=AC ,ME ⊥AB ,MF ⊥AC ,垂足分别为E 、F ,ME=MF 。
全等三角形经典例题(含答案)

全等三角形经典例题(含答案)全等三角形是指两个三角形的所有对应边和对应角都相等。
判断两个三角形是否全等的条件有三种:SSS(边-边-边)、SAS(边-角-边)、ASA(角-边-角)。
下面介绍几个经典的全等三角形例题:例题一:已知△ABC和△DEF,已知AB=DE,AC=DF,∠C=∠F,是否可以断定△ABC≌△DEF?如果可以,请说明理由;如果不可以,请给出反例。
解析:根据题目可知,已知△ABC和△DEF的所有对应边和对应角都相等,即满足ASA条件。
因此,可以断定△ABC≌△DEF。
因为已知条件满足△ABC和△DEF的全等条件。
例题二:已知△ABC和△DEF,已知AB=DE,BC=EF,AC=DF,是否可以断定△ABC≌△DEF?如果可以,请说明理由;如果不可以,请给出反例。
解析:根据题目可知,已知△ABC和△DEF的所有对应边都相等,即满足SSS条件。
因此,可以断定△ABC≌△DEF。
因为已知条件满足△ABC和△DEF的全等条件。
例题三:已知△AB C和△DEF,已知∠A=∠D,∠C=∠F,BC=EF,是否可以断定△ABC≌△DEF?如果可以,请说明理由;如果不可以,请给出反例。
解析:根据题目可知,已知△ABC和△DEF的对应角相等,BC=EF,但没有给出第三边的长度。
无法判断是否满足SSS或SAS条件,因此无法断定△ABC≌△DEF。
例题四:已知△ABC和△DEF,已知AB=DE,BC=EF,∠B=∠E,是否可以断定△ABC≌△DEF?如果可以,请说明理由;如果不可以,请给出反例。
解析:根据题目可知,已知△ABC和△DEF的对应边和对应角相等,即满足SAS条件。
因此,可以断定△ABC≌△DEF。
因为已知条件满足△ABC和△DEF的全等条件。
例题五:已知两个全等的三角形ABC和DEF,若∠A=60°,AC=6,DF=9,求BC和EF的长度。
解析:由于△ABC≌△DEF,根据全等三角形的性质可知BC=EF。
全等三角形经典50题(含答案)

1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠24. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=ACAD BC BACDF21E5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠ C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD8. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB AD BC A9.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF和EF。
∵BC=ED,CF=DF,∠BCF=∠EDF。
∴三角形BCF全等于三角形EDF(边角边)。
∴BF=EF,∠CBF=∠DEF。
连接BE。
在三角形BEF中,BF=EF。
∴ ∠EBF=∠BEF 。
又∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
10. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CG∠CGD =∠EFD又EF ∥AB∴∠EFD =∠1∠1=∠2∴∠CGD =∠2∴△AGC 为等腰三角形,AC =CG又 EF =CG∴EF =AC11. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CB ACDF21 E证明:延长AB 取点E ,使AE =AC ,连接DE∵AD 平分∠BAC∴∠EAD =∠CAD∵AE =AC ,AD =AD∴△AED ≌△ACD (SAS )∴∠E =∠C∵AC =AB+BD∴AE =AB+BD∵AE =AB+BE∴BD =BE∴∠BDE =∠E∵∠ABC =∠E+∠BDE∴∠ABC =2∠E∴∠ABC =2∠C12. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA∵AC 平分∠BAD∴∠DAC =∠FAC又∵AC =AC∴△ADC ≌△AFC (SAS )CD B A∴AD =AF∴AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形经典题型50题(含答案)
全等三角形证明经典50题(含答案)1.已知:AB=4 , AC=2 , D 是BC 中点,AD 是整数,求 AD延长AD 至U E,使DE=AD, 则三角形ADC 全等于三角形EBD即 BE=AC=2 在三角形 ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=512.已知:D 是 AB 中点,/ ACB=90 °,求证: CD - AB2为BC=ED,CF=DF, / BCF= / EDF 。
所以 三角形BCF 全等于三角形 EDF (边角边)。
所以BF=EF, / CBF= / DEF 。
连接 BE 。
在三角形 BEF 中,BF=EF 。
所以 / EBF= / BEF 。
/ ABE= / AEB 。
所以 AB=AE 。
在三角形 ABF 和 / ABF= / ABE+ / EBF= / AEB+ / BEF= / AEF 。
所以/ C= / D , F 是 CD 中点,求证:/ 1 = / 2证明:连接BF 和EF 。
因又因为 / ABC= / AED 。
所以 三角形 AEF 中, AB=AE,BF=EF, 三角形ABF 和三角形AEF 全等。
所以 / BAF= / EAF ( / 仁/ 2)。
A3因为 EB = EF ,CE = CE , 所以△ CEBCEF 所以/ B = / CFE 因为/ B +/ D = 180° / CFE + / CFA = 180° 所以/ D = / CFA 因为 AC 平分/ BAD 所以/ DAC = / FAC 又因为 AC = AC 所以△ ADC 也厶AFC ( SAS ) 所以AD = AF 所以AE = AF + FE = AD + BE12.如图,四边形 ABCD 中,AB // DC ,BE 、CE 分别平分/ ABC 、/ BCD ,且点 E 在AD 上。
全等三角形经典题型50题带答案

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB从D 做辅助线3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
A C DEF 21 ADBCDAB4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形经典例题(含答案)

新思路全等三角形的经典例题 判定方法条件 注意 ⑴边边边公理(SSS )三边对应相等 三边对应相等 ⑵边角边公理(SAS)两边和它们的夹角对应相等 (“两边夹一角”) 必须是两边夹一角,不能是两边对一角 ⑶角边角公理(ASA)两角和它们的夹边对应相等 (“两角夹一边”) 不能理解为两角及任意一边⑷角角边公理(AAS) 两角和其中一角的对边对应相等例1:已知:如图,过∆ABC 的顶点A ,作AF ⊥AB 且AF=AB ,作AH ⊥AC ,使AH=AC ,连结BH 、CF ,且BH 与CF 交于D 点。
求证:(1)BH=CF (2)BH ⊥CF分析:从图中可观察分析,若证BH=CF ,显然,若能证出∆ABH ≌∆AFC ,问题就能解决。
从已知看,已经知道AF=AB ,AC=AH 。
这两个三角形已经具备两条边对应相等了。
还要证明第三条边相等,显然不可能用“边边边”公理了。
只能寻求两对应边的夹角了。
从已知看,∠BAF 和∠HAC 都是直角。
而图中的∠BAC 显然是公共角,根据等式性质,问题可以顺利解决。
证明:(1)∵AF ⊥AB ,AH ⊥AC∴∠BAF=∠HAC=90︒∴∠BAF +∠BAC=∠HAC +∠BAC∴即∠F AC=∠BAH在∆ABH 和∆AFC 中()()()AB AF BAH FAC AH AC =∠=∠=⎧⎨⎪⎪⎩⎪⎪已知已证已知 ∴∆ABH ≌∆AFC (边角边)∴BH=FC (全等三角形对应边相等)(2)设AC 与BH 交于点P在∆APH 中∵∠HAP=90︒∴∠2+∠3=90︒(直角三角形中两个锐角互余)∵∠1=∠2(全等三角形对应角相等)∠3=∠4∴∠1+∠4=∠2+∠3=90︒在∆PDC 中∵∠1+∠4=90︒∴∠HDC=90︒ ∴BH ⊥CF例2:已知,如上图:BD 、CE 是∆ABC 的高,分别在高上取点P 与Q ,使BP=AC ,CQ=AB 。
求证:AQ=AP 分析:从要证的结论AQ=AP ,只有在∆ABP 和∆QCA 中找对应原素,不难发现,已经有BP=AC 、CQ=AB ,也就是这两个三角形中已经有两条对应边相等。
(完整版)全等三角形证明经典50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠24. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CDAB B A CDF2 1 EAC D E F 21 A D BC A6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
13.已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠C14. P 是∠BAC 平分线AD 上一点,AC>AB ,求证:PC-PB<AC-AB15. 已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BED C B A FE PD A CB16. 已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC18.如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .19.如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N .求证:∠OAB =∠OBA20.(5分)如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .21.如图,△ABC 中,AD 是∠CAB 的平分线,且AB =AC +CD ,求证:∠C =2∠B22.(6分)如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M .(1)求证:MB =MD ,ME =MF(2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.F AEDCB P E D CB A DC B A23.已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点, (1)求证:△AED ≌△EBC . (2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):24.(7分)如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .证明:25、如图:DF=CE ,AD=BC ,∠D=∠C 。
全等三角形经典题型50题(含答案解析)
全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF和三ADBC角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DG E ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE ∴∠C=∠E DC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形经典例题(全等三角形的概念和性质)类型一、全等形和全等三角形的概念1、全等三角形又叫做合同三角形,平面内的合同三角形分为真正合同三角形与镜面合同三角形,假设△ABC 和△A 1B 1C 1是全等(合同)三角形,点A 与点A 1对应,点B 与点B 1对应,点C 与点C 1对应,当沿周界A→B→C→A,及A 1→B 1→C 1→A 1环绕时,若运动方向相同,则称它们是真正合同三角形(如图1),若运动方向相反,则称它们是镜面合同三角形(如图2),两个真正合同三角形都可以在平面内通过平移或旋转使它们重合,两个镜面合同三角形要重合,则必须将其中一个翻转180°,下列各组合同三角形中,是镜面合同三角形的是( )(答案)B ;提示:抓住关键语句,两个镜面合同三角形要重合,则必须将其中一个翻转180°,B 答案中的两个三角形经过翻转180°就可以重合,故选B ;其它三个选项都需要通过平移或旋转使它们重合.类型二、全等三角形的对应边,对应角 类型三、全等三角形性质3、如图,将长方形ABCD 沿AE 折叠,使D 点落在BC 边上的F 点处,如果60BAF ∠=︒,那么DAE∠等于( ).A.60° B.45° C.30° D.15°(答案)D ;(解析)因为△AFE 是由△ADE 折叠形成的,所以△AFE ≌△ADE ,所以∠FAE =∠DAE ,又因为60BAF ∠=︒,所以∠FAE =∠DAE =90602︒-︒=15°.(点评)折叠所形成的三角形与原三角形是全等的关系,抓住全等三角形对应角相等来解题.举一反三:(变式)如图,在长方形ABCD 中,将△BCD 沿其对角线BD 翻折得到△BED ,若∠1=35°,则∠2=________.(答案)35°;提示:将△BCD 沿其对角线BD 翻折得到△BED ,所以∠2=∠CBD ,又因为AD ∥BC ,所以∠1=∠CBD ,所以∠2=35°.4、 如图,△ABE 和△ADC 是△ABC 分别沿着AB ,AC 翻折180°形成的,若∠1∶∠2∶∠3=28∶5∶3,∠α的度数是_________.(答案)∠α=80°(解析)∵∠1∶∠2∶∠3=28∶5∶3,设∠1=28x ,∠2=5x ,∠3=3x ,∴28x +5x +3x =36x =180°,x =5° 即∠1=140°,∠2=25°,∠3=15°∵△ABE 和△ADC 是△ABC 分别沿着AB ,AC 翻折180°形成的, ∴△ABE ≌△ADC ≌△ABC ∴∠2=∠ABE ,∠3=∠ACD∴∠α=∠EBC +∠BCD =2∠2+2∠3=50°+30°=80°(点评)此题涉及到了三角形内角和,外角和定理,并且要运用全等三角形对应角相等的性质来解决问题.见“比例”设未知数x 是比较常用的解题思路. 举一反三:(变式)如图,在△ABC 中,∠A :∠ABC:∠BCA =3:5:10,又△MNC≌△ABC,则∠BCM:∠BCN 等于( )A .1:2 B .1:3 C .2:3 D .1:4(答案)D ;提示:设∠A=3x ,∠ABC =5x ,∠BCA=10x ,则3x +5x +10x =18x =180°,x =10°.又因为△MNC≌△ABC,所以∠N =∠B =50°,CN =CB ,所以∠N =∠CBN =50°,∠ACB =∠MCN =100°,∠BCN =180°-50°-50°=80°,所以∠BCM:∠BCN=20°:80°=1:4.(全等三角形判定一(SSS ,SAS ))类型一、全等三角形的判定1——“边边边”1、如图,在△ABC 和△ADE 中,AB =AC ,AD =AE ,BD =CE ,求证:∠BAD =∠CAE.(答案与解析)证明:在△ABD 和△ACE 中,AB AC AD AE BD CE =⎧⎪=⎨⎪=⎩∴△ABD ≌△ACE (SSS )∴∠BAD =∠CAE (全等三角形对应角相等).(点评)把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等,综合应用全等三角形的判定和性质. 要证∠BAD =∠CAE ,先找出这两个角所在的三角形分别是△BDA 和△CAE ,然后证这两个三角形全等.举一反三:(变式)已知:如图,AD =BC ,AC =BD.试证明:∠CAD =∠DBC.(答案)证明:连接DC , 在△ACD 与△BDC 中()AD BC AC BDCD DC ⎧=⎪=⎨⎪=⎩公共边∴△ACD≌△BDC(SSS )∴∠CAD =∠DBC (全等三角形对应角相等)类型二、全等三角形的判定2——“边角边”2、3、举一反三:(变式)已知,如图,在四边形ABCD 中,AC 平分∠BAD ,CE ⊥AB 于E ,并且AE =12(AB +AD ),求证:∠B +∠D =180°.(答案)证明:在线段AE 上,截取EF =EB ,连接FC ,∵CE ⊥AB ,∴∠CEB =∠CEF =90°在△CBE 和△CFE 中,CEB CEF EC =EC EB EF =⎧⎪∠=∠⎨⎪⎩∴△CBE 和△CFE (SAS )∴∠B =∠CFE∵AE =12(AB +AD ),∴2AE = AB +AD ∴AD =2AE -AB∵AE =AF +EF ,∴AD =2(AF +EF )-AB =2AF +2EF -AB =AF +AF +EF +EB -AB =AF +AB -AB ,即AD =AF在△AFC 和△ADC 中(AF AD FAC DAC AC AC =⎧⎪∠=∠⎨⎪=⎩角平分线定义)∴△AFC ≌△ADC (SAS )∴∠AFC =∠D∵∠AFC +∠CFE =180°,∠B =∠CFE.∴∠AFC +∠B =180°,∠B +∠D =180°. 类型三、全等三角形判定的实际应用4、如图,公园里有一条“Z 字形道路ABCD ,其中AB ∥CD ,在AB ,BC ,CD 三段路旁各有一个小石凳E ,M ,F ,且BE =CF ,M 在BC 的中点.试判断三个石凳E ,M ,F 是否恰好在一条直线上?Why ?(答案与解析)三个小石凳在一条直线上证明:∵AB 平行CD (已知)∴∠B =∠C (两直线平行,内错角相等)∵M 在BC 的中点(已知)∴BM =CM (中点定义)在△BME 和△CMF 中BE CF B D BM M C =⎧⎪∠=∠⎨⎪=⎩∴△BME ≌△CMF (SAS )∴∠EMB =∠FMC (全等三角形的对应角相等)∴∠EMF =∠EMB +∠BMF =∠FMC +∠BMF =∠BMC =180°(等式的性质)∴E ,M ,F 在同一直线上(点评)对于实际应用问题,首先要能将它化成数学模型,再根据数学知识去解决. 由已知易证△BME ≌△CMF ,可得∠EMB =∠FMC ,再由∠EMF =∠EMB +∠BMF =∠FMC +∠BMF =∠BMC =180°得到E ,M ,F 在同一直线上.(全等三角形判定二(ASA ,AAS ))类型一、全等三角形的判定3——“角边角”1、如图,G 是线段AB 上一点,AC 和DG 相交于点E.请先作出∠ABC 的平分线BF ,交AC 于点F ;然后证明:当AD∥BC,AD =BC ,∠ABC=2∠ADG 时,DE =BF.(答案与解析)证明:∵AD∥BC,∴∠DAC=∠C∵BF 平分∠ABC ∴∠ABC=2∠CBF ∵∠ABC =2∠ADG ∴∠CBF=∠ADG在△DAE 与△BCF 中⎪⎩⎪⎨⎧∠=∠=∠=∠C DAC BC AD CBF ADG∴△DAE≌△BCF(ASA )∴DE=BF(点评)利用全等三角形证明线段(角)相等的一般方法和步骤如下: (1)找到以待证角(线段)为内角(边)的两个三角形; (2)证明这两个三角形全等;(3)由全等三角形的性质得出所要证的角(线段)相等.(变式)已知:如图,在△MPN 中,H 是高MQ 和NR 的交点,且MQ =NQ .求证:HN =PM.(答案)证明:∵MQ 和NR 是△MPN 的高, ∴∠MQN =∠MRN =90°, 又∵∠1+∠3=∠2+∠4=90°,∠3=∠4 ∴∠1=∠2在△MPQ 和△NHQ 中,12MQ NQ MQP NQH ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△MPQ ≌△NHQ (ASA ) ∴PM =HN类型二、全等三角形的判定4——“角角边”2、已知:如图,90ACB ∠=︒,AC BC =,CD 是经过点C 的一条直线,过点A 、B 分别作AE CD ⊥、BF CD ⊥,垂足为E 、F ,求证:CE BF =. (答案与解析)证明:∵ CD AE ⊥,CD BF ⊥ ∴︒=∠=∠90BFC AEC∴︒=∠+∠90B BCF∵,90︒=∠ACB ∴︒=∠+∠90ACF BCF ∴B ACF ∠=∠在BCF ∆和CAE ∆中⎪⎩⎪⎨⎧=∠=∠∠=∠BC AC B ACE BFC AEC ∴BCF ∆≌CAE ∆(AAS )∴BF CE =(点评)要证BF CE =,只需证含有这两个线段的BCF ∆≌CAE ∆.同角的余角相等是找角等的好方法. 3、平面内有一等腰直角三角板(∠ACB =90°)和一直线MN .过点C 作CE ⊥MN 于点E ,过点B 作BF ⊥MN 于点F .当点E 与点A 重合时(如图1),易证:AF +BF =2CE .当三角板绕点A 顺时针旋转至图2的位置时,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段AF 、BF 、CE 之间又有怎样的数量关系,请直接写出你的猜想,不需证明.(答案与解析)解:图2,AF +BF =2CE 仍成立, 证明:过B 作BH ⊥CE 于点H ,∵∠CBH +∠BCH =∠ACE +∠BCH =90°∴∠CBH =∠ACE在△ACE 与△CBH 中, 90ACH CBH AEC CHB AC BC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴△ACE ≌△CBH .(AAS )∴CH =AE ,BF =HE ,CE =EF , ∴AF +BF =AE +EF +BF =CH +EF +HE =CE +EF =2EC .(点评)过B 作BH ⊥CE 与点H ,易证△ACH ≌△CBH ,根据全等三角形的对应边相等,即可证得AF +BF =2CE .正确作出垂线,构造全等三角形是解决本题的关键. 举一反三:(变式)错误!未找到引用源。
