四川大学数学分析-2001答案
(详细解析)2001年普通高等学校招生全国统一考试数学试题及答案(理)

2001年普通高等学校招生全国统一考试数 学(理工农医类)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分.第I 卷1至2页.第II 卷3至9页.共150分.考试时间120分钟.第I 卷(选择题 60分)注意事项:1. 答第I 卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写 在答题卡上.2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需 改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上.3.考试结束,监考人将本试卷和答题卡一并收回.一、选择题:本大题共12小题;第每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若0cos sin >θθ,则θ在A .第一、二象限B .第一、三象限C .第一、四象限D .第二、四象限 【答案】B【解析】0cos sin >θθ,则sin θ与cos θ同号,B 正确.2.过点(1,1)(1,1)A B --,且圆心在直线02=-+y x 上的圆的方程是 A .()()41322=++-y x B .()()41322=-++y xC .()()41122=-+-y x D .()()41122=+++y x【答案】C【解析】显然过A B ,两点的直线与已知直线平行,过A B ,两点分别作,x y 轴的垂线,与已知直线相交于点(1,1)M ,则(1,1)M 为圆心,半径为2,C 正确.3.设{}n a 是递增等差数列,前三项的和为12,前三项的积为48,则它的首项是 A .1 B .2 C .4 D .6 【答案】B【解析】由已知得12312313212,48,2a a a a a a a a a ++==+=,解得12a =.4.若定义在区间(10)-,内的函数()2log (1)a f x x =+满足0)(>x f ,则a 的取值范围是 A .1(0,)2 B .1(0,]2C .1(,)2+∞ D .(0,)+∞【答案】A【解析】当(10)x ∈-,,则1(0,1)x +∈,由0)(>x f ,则021a <<,则1(0,)2a ∈.5.极坐标方程)4sin(2πθρ+=的图形是【答案】C【解析】化为直角坐标方程为2222((122x y -+-=,只有C 正确.6.函数)0(1cos ≤≤-+=x x y π的反函数是A .)20)(1arccos(≤≤--=x x yB .)20)(1arccos(≤≤--=x x y πC .)20)(1arccos(≤≤-=x x yD .)20)(1arccos(≤≤-+=x x y π 【答案】A【解析】∵0x π-≤≤,∴02y ≤≤,又0x π≤-≤,∴1cos cos()y x x -==-, ∴cos(1)x arc y -=-,即cos(1)x arc y =--,反函数为)20)(1arccos(≤≤--=x x y .7.若椭圆经过原点,且焦点为)0,3(),0,1(21F F ,则其离心率为 A .43 B .32 C .21 D .41 【答案】C【解析】易知椭圆的中心为(2,0),且2,1a c ==,则12c e a ==.8.若0,sin cos ,sin cos 4a b παβααββ<<<+=+=,则A .b a <B .b a >C .1<abD .2>ab 【答案】A【解析】由题设sin(),sin()44a b ππαβ=+=+,又4442ππππαβ<+<+<,所以b a <.9.在正三棱柱111C B A ABC -中,若12BB AB =,则1AB 与B C 1所成的角的大小为A .60︒B .90︒C .105︒D .75︒【答案】B则【解析】如图,取11A B 的中点D ,连接1,BD C D ,若12AB BB =,1111,,AB BD AB C D BD C D D ⊥⊥=,∴1AB ⊥平面1C DB ,而1C B ⊂面1C DB ,∴11AB C B ⊥,故答案为90︒.10.设()()f x g x ,都是单调函数,有如下四个命题:①若)(x f 单调递增,)(x g 单调递增,则)()(x g x f -单调递增; ②若)(x f 单调递增,)(x g 单调递减,则)()(x g x f -单调递增; ③若)(x f 单调递减,)(x g 单调递增,则)()(x g x f -单调递减; ④若)(x f 单调递减,)(x g 单调递减,则)()(x g x f -单调递减; 其中,正确的命题是A .①③B .①④C .②③D .②④ 【答案】C【解析】若)(x g 单调递减,则()g x -单调递增,所以)()(x g x f -单调递增,②正确;同理③正确.11.一间民房的屋顶有如图三种不同的盖法:①单向倾斜;②双向倾斜;③四向倾斜.记三种盖法屋顶面积分别为123P P P ,,.若屋顶斜面与水平面所成的角都是α,则A .123P P P >>B .123P P P =>C .123P P P >=D .123P P P ==【答案】D【解析】本题考查平面图形在另一平面内的射影理解与有关计算,其斜面与房屋的底面所成的角都是α,又有cos S S α=底斜,故有123P P P ==.【编者注】此公式《新课标》不作要求.12.如图,小圆圈表示网络的结点,结点之间的连线表示它们有网线相连.连线标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A 向结点B 传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为A .26B .24C .20D . 19 【答案】D【解析】从A 到B 有四条线路,从上到下记为1234,,,l l l l ,且123412,12l l l l +≤+≤,在单位时间内可以通过的最大信息量分别为3,4,6,6,D 正确.第II 卷(非选择题 90分)注意事项:1. 第II 卷共7页,用钢笔或圆珠笔直接答在试题卷中. 2. 答卷前将密封线内的项目填写清楚.二.填空题:本大题共4小题;每小题4分,共16分,把答案填在题中横线上.13.若一个圆锥的轴截面是等边三角形,其面积为3,则这个圆锥的侧面积是 . 【答案】2π【解析】由已知可得圆锥的的底面半径和母线长分别为1和2,侧面积为2rl ππ=.14.双曲线116922=-y x 的两个焦点为12F F ,,点P 在双曲线上.若12PF PF ⊥,则点P 到x 轴的距离为 .【答案】516 【解析】方法一:设(,)P x y ,12(5,0)(5,0)F F -,,由12PF PF ⊥得00155y y x x --⋅=-+-,即 2225x y +=,与双曲线方程联立得225625y =,则165y =. 方法二:设12,PF m PF n ==,由抛物线定义和题设222126,100m n m n FF -=+==,可得32mn =,利用面积相等关系12121122P PF PF F F y ⋅=⋅得165y =.15.设{}n a 是公比为q 的等比数列,n S 是它的前n 项和.若{}n S 是等差数列,则=q . 【答案】1【解析】若{}n S 是等差数列,则1322S S S +=,11231223()2()a a a a a a a a +++=+⇒=,所以1q =.16.圆周上有2n 个等分点(1>n ),以其中三个点为顶点的直角三角形的个数为 . 【答案】2(1)n n -【解析】由题意知,只有三角形的一条边过圆心,才能组成直角三角形,∵圆周上有2n 个等分点,∴共有n 条直径,每条直径可以和除去本身的两个定点外的点组成直角三角形, ∴可做22n -个直角三角形,根据分步计数原理知共有(22)2(1)n n n n -=-.三、解答题:本大题共6小题;共74分,解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)如图,在底面是直角梯形的四棱锥ABCD S -中,∠90=ABC °,SA ⊥面ABCD ,11,2SA AB BC AD ====. (Ⅰ)求四棱锥ABCD S -的体积;(Ⅱ)求面SCD 与面SBA 所成的二面角的正切值.【解】本小题考查线面关系和棱锥体积计算,以及空间想象能力和逻辑推理能力.满分12分.(I )直角梯形ABCD 的面积是()110.531224M BC AD AB +=+⋅=⨯=底面, ……2分 ∴四棱推ABCD S -的体积是113113344V SA M =⨯⨯=⨯⨯=底面.……4分(II )延长,BA CD 相交于点E ,连结SE ,则SE 是所求二面角的棱. ……6分∵//,2AD BC BC AD =,∴EA AB SA ==,∴SE SB ⊥. ∵SA ⊥面ABCD ,得面AEB ⊥面EBC ,EB 是交线, 又BC EB ⊥,∴BC ⊥面SEB ,故SB 是CS 在面SEB 上的射影,∴CS SE ⊥,所以BSC ∠是所求二面角的平面角. ……10分222,1,SB SA AB BC BC SB ∴=+==⊥.2tan 2BC BSC SB ∴∠==. 即所求二面角的正切值为22. ……12分18.(本小题满分12分)已知复数31)1(i i z -=. (Ⅰ)求1arg z 及1z ;(Ⅱ)当复数z 满足1=z ,求1z z -的最大值.【解】本小题考查复数的基本性质和基本运算,以及分析问题和解决问题的能力.满分12分.(Ⅰ)31(1)22z i i i =-=-, ……3分将1z 化为三角形式,得⎪⎭⎫⎝⎛+=47sin 47cos 221ππi z ,∴47arg 1π=z ,221=z . ……6分 (Ⅱ)设cos sin z i αα=+,则1(cos 2)(sin 2)z z i αα-=-++,()()22212sin 2cos ++-=-ααz z942sin()4πα=+-, ……9分当sin()14πα+=时,21z z -取得最大值249+.从而得到1z z -的最大值为122+. ……12分19.(本小题满分12分)设抛物线)0(22>=p px y 的焦点为F ,经过点F 的直线交抛物线于A B ,两点. 点C 在抛物线的准线上,且//BC x 轴. 证明直线AC 经过原点O .【解】本小题考查抛物线的概念和性质,直线的方程和性质,运算能力和逻辑推理能力.满分12分. 证明一:因为抛物线)0(22>=p px y 的焦点为(,0)2pF ,所以经过 点F 的直线AB 的方程可设为2p my x +=, 代人抛物线方程得2220y pmy p --=,若记1122(,),(,)A x y B x y ,则12,y y 是该方程的两个根,所以212y y p =-.因为BC ∥x 轴,且点C 在准线2p x =-上,所以点C 的坐标为2(,)2py -, 故直线CO 的斜率为111222x y y p p y k ==-=即k 也是直线OA 的斜率,所以直线AC 经过原点O . 证明二:如图,记x 轴与抛物线准线l 的交点为E ,过A 作AD l ⊥,D 是垂足.则////AD FE BC .……2分 连结AC ,与EF 相交手点N ,则||||||||||,||||||||||EN CN BF NF AF AD AC AB BC AB === ……6分根据抛物线的几何性质,||||,||||AF AD BF BC == ……8分||||||||||||||||AD BF AF BC EN NF AB AB ⋅⋅∴===,即点N 是EF 的中点,与抛物线的顶点O 重合,所以直线AC 经过原点O .…12分20.(本小题满分12分)已知n m i ,,是正整数,且n m i <≤<1.(Ⅰ)证明:in i i m i P m P n <; (Ⅱ)证明:mn n m )1()1(+>+.【解】本小题考查排列、组合、二项式定理、不等式的基本知识和逻辑推理能力.满分12分.(Ⅰ)证明:对于1i m <≤有(1)im p m m i =⋅⋅-+,⋅-⋅=m m m m m p i i m 1…mi m 1+-⋅, 同理 11...i n i p n n n i n n n n--+=⋅⋅⋅…, ……4分由于m n <,对整数1,2,,1k i =-,有mkm n k n ->-, 所以 i im i i n mp n p >,即im i i n i p n p m >. ……6分(Ⅱ)证明:由二项式定理有()inni inCm m ∑==+01,()i mmi i mCn n ∑==+01, ……8分由(Ⅰ)知i n i p m >(1)i im n p i m n <≤<,而 !i p C i m im=,!i p C i n in =, ……10分所以,(1)i i i in m m C n C i m n ><≤<.因此,∑∑==>mi im i mi i niC n Cm 22. 又 10000==m n C n C m ,mn nC mC m n ==11,()n i m C m in i ≤<>0.∴∑∑==>mi im i ni i niC n Cm 0. 即(1)(1)nmm n +>+. ……12分21.(本小题满分12分)从社会效益和经济效益出发,某地投入资金进行生态环境建设,并以此发展旅游产业.根据规划,本年度投入800万元,以后每年投入将比上年减少51.本年度当地旅游业收入估计为400万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加41.(Ⅰ)设n 年内(本年度为第一年)总投入为n a 万元,旅游业总收入为n b 万元.写出n n b a ,的表达式;(Ⅱ)至少经过几年旅游业的总收入才能超过总投入?【解】本小题主要考查建立函数关系式、数列求和、不等式等基础知识;考查综合运用数学知识解决实际问题的能力.满分12分.(I )第1年投入为800万元.第2年投入为1800(1)5⨯-万元,……,第n 年投入为11800(1)5n -⨯-万元.所以,n 年的总收入为111111800800(1)800(1)800(1)555n n k n k a --==+⨯-+⋅⋅⋅+⨯-=⨯-∑44000[1()]5n =⨯-. ……3分第1年旅游业收入为 400万元,第 2年旅游业收入为 1400(1)4⨯+万元,……,第n 年旅游业收人为11400(1)4n -⨯+万元.所以,n 年内的旅游业总收入为111111400400(1)400(1)400(1)444n n k n k b --==+⨯++⋅⋅⋅+⨯+=⨯+∑51600[()1]4n =⨯-. ……6分(Ⅱ))设至少经过年旅游业的总收入才能超过总投入,由此0n n b a ->,即541600[()1]4000[1()]045n n ⨯--⨯-> 化简得455()2()7054n n ⨯+⨯->, ……9分设4()5n x =,代入上式得25720x x -+>,解此不等式,得2,15x x <>(舍去).即 42()55n <,由此得 5n ≥.答:至少经过5年旅游业的总收入才能超过总投入. ……12分22.(本小题满分14分)设)(x f 是定义在R 上的偶函数,其图象关于直线1=x 对称,对任意]21,0[,21∈x x ,都有1212()()()f x x f x f x +=⋅,且0)1(>=a f .(Ⅰ)求)21(f 及)41(f ; (Ⅱ)证明)(x f 是周期函数; (Ⅲ)记)212(nn f a n +=,求)(ln lim n n a ∞→.【解】本小题主要考查函数的概念、图象,函数的奇偶性和周期性以及数列极限等基础知识;考查运算能力和逻辑思维能力,满分14分.(Ⅰ)因为对121,[0,]2x x ∈,都有1212()()()f x x f x f x +=+,所以()()()0,[0,1]22x xf x f f x =⋅≥∈.∵211111(1)()()()[()]22222f f f f f =+=⋅=,2111111()()()()[()]244444f f f f f =+=⋅=. ……3分0)1(>=a f ,∴112411(),()24f a f a ==. ……6分(Ⅱ)证明:依题设()y f x =关于直线1x =对称,故()(11)f x f x =+-,即()(2),f x f x x R =-∈, ……8分 又由()f x 是偶函数知()(),f x f x x R -=∈,∴()(2),f x f x x R -=-∈, 将上式中x -以x 代换,得()(2),f x f x x R =+∈.这表明()f x 是R 上的周期函数,且2是它的一个周期. ……10分 (Ⅲ)由(Ⅰ)知()0,[0,1]f x x ≥∈.∵111111()()((1))()((1))222222f f n f n f f n n n n n n =⋅=+-⋅=⋅-⋅ 111()()()222f f f n n n ==⋅⋅⋅1[()]2n f n=,121()2f a =,资料内容仅供您学习参考,如有不当之处,请联系改正或者删除 ----完整版学习资料分享---- ∴121()2n f a n=. ∵()f x 的一个周期是2, ∴11(2)()22f n f n n+=,因此12n n a a =, ……12分 ∴1lim(ln )lim(ln )02n n n a a n→∞→∞==. ……14分。
2001考研数学一试题及答案解析.doc

2001考研数学一试题及答案解析2001 年全国硕士研究生入学统一考试数学一试题一、填空题(本题共 5 小题,每小题 3 分,满分 15 分.把答案填在题中横线上.)(1)设 y= e x (C1 sin x + C2 cos x) ( C1 , C2 为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为_____________. (2)设 r= x 2 + y 2 + z 2 ,则 div(gradr)(1, ?2 , 2 )=_____________.(3)交换二次积分的积分次序: (4)设矩阵 A 满足 A (5) 设随机变量2∫0 ?1dy ∫1? y 2f ( x, y )dx =_____________.+ A ? 4 E = 0 ,其中 E 为单位矩阵,则 ( A ? E ) ?1 =_____________.X 的方差是 2 ,则根据切比雪夫不等式有估计yP{ X ? E ( X ) ≥ 2} ≤_____________. 二、选择题(本题共 5 小题每小题 3 分,满分 15 分.) 本题共小题,每小题满分 (1)设函数则yf ( x) 在定义域内可导, y = f ( x) 的图形如右图所示,Ox= f ′( x) 的图形为(2)设 (A)f ( x, y ) 在点 (0, 0) 附近有定义,且 f x′ (0,0) = 3, f y′ (0,0) = 1 ,则d z |(0,0) = 3dx + dy .(B) 曲面 z= f ( x, y ) 在 (0, 0, f (0, 0)) 处的法向量为{3,1,1}.(C) 曲线 ?? z = f ( x, y ) 在 (0, 0, f (0, 0)) 处的切向量为{1,0,3}. ? y=0 ? z = f ( x, y ) 在 (0, 0, f (0, 0)) 处的切向量为{3,0,1}. ? y=0(D) 曲线 ?(3)设 (A)f (0) = 0 ,则 f (x) 在 x =0 处可导的充要条件为1 f (1 ? cosh) 存在. h →0 h2 1 (C) lim 2 f ( h ? sinh) 存在. h →0 h lim1 f (1 ? eh ) 存在. h →0 h 1 (D) lim [ f (2h) ? f (h)] 存在. h →0 h(B)lim?1 ?1 (4)设 A = ? ?1 ? ?11 1 1? ?4 ? ?0 1 1 1? ,B = ? ?0 1 1 1? ? ? 1 1 1? ?00 0 0? 0 0 0? ?,则 A与 B 0 0 0? ? 0 0 0?(B) 合同但不相似. (D) 不合同且不相似.(A) 合同且相似. (C) 不合同但相似.(5)将一枚硬币重复掷 n 次,以 X 和 Y 分别表示正面向上和反面向上的次数, 则 X 和 Y 的相关系数等于 (A)-1. (B) 0. (C)1 . 2(D) 1.三、(本题满分 6 分) 求arctan e x ∫ e 2 x dx .四、(本题满分 6 分) 设函数 z= f ( x, y ) 在点 (1,1) 处可微,且 f (1,1) = 1 ,.?f ?f |(1,1) = 2 , |(1,1) = 3 , ? ( x) = f ( x, ?x ?y f ( x, x)) .求d 3 ? ( x) dxx =1五、(本题满分 8 分)∞ ? 1+ x arctan x, x ≠ 0, (?1) n 设 f (x ) = ? x 将 f (x ) 展开成 x 的幂级数,并求级数∑的和. 2 x = 0, 1, n =1 1 ? 4 n ?2六、(本题满分 7 分) 计算 I 面= ∫ ( y 2 ? z 2 )dx + (2 z 2 ? x 2 )dy + (3x 2 ? y 2 )dz ,其中 L 是平面 x + y + z = 2 与柱Lx + y = 1 的交线,从 Z 轴正向看去, L 为逆时针方向.七、(本题满分 7 分) 设f ( x) 在 (?1,1) 内具有二阶连续导数且 f ′′( x) ≠ 0 ,试证:(1)对于 (?1,1) 内的任一 x ≠ 0 ,存在惟一的θ ( x ) ∈ (0,1) ,使 f (x ) = f (0) + xf ′(θ ( x ) x ) 成立; (2) lim θ ( x ) =x →01 . 2八、(本题满分 8 分) 设有一高度为 h(t ) ( t 为时间)的雪堆在融化过程,其侧面满足方程 z= h(t ) ?2( x 2 + y 2 ) (设 h(t )长度单位为厘米,时间单位为小时),已知体积减少的速率与侧面积成正比(比例系数为 0.9),问高度为 130(厘米)的雪堆全部融化需多少小时? 九、(本题满分6 分) 设α 1 , α 2 , ? , α s 为线性方程组 Ax = 0 的一个基础解系, β1= t1α1 + t2α 2 , β 2 = t1α 2 + t2α 3 ,? ,β s = t1α s + t2α1 ,其中 t1 ,t 2 为实常数.试问 t1 ,t 2 满足什么条件时, β 1 , β 2 ,?, β s 也为 Ax = 0 的一个基础解系. 十、(本题满分 8 分) 已知 3 阶矩阵 A 与三维向量 x ,使得向量组x, Ax, A (1)记 P =( x, Ax, A (2)计算行列式22x 线性无关,且满足 A3 x = 3 Ax ? 2 A 2 x .x ),求 3 阶矩阵 B ,使 A = PBP ?1 ; A+ E .十一、(本题满分 7 分)设某班车起点站上客人数X 服从参数为λ ( λ > 0 )的泊松分布,每位乘客在中途下车的概率为p ( 0 < p < 1 ),且中途下车与否相互独立.以 Y 表示在中途下车的人数,求:(1)在发车时有 n 个乘客的条件下,中途有 m 人下车的概率; (2)二维随机变量( X , Y ) 的概率分布.十二、(本题满分 7 分) 设总体X 服从正态分布 N ( ? , σ 2 ) ( σ > 0 ), 从该总体中抽取简单随机样本n 1 2n ∑ X i ,求统计量 Y = ∑ ( X i + X n+i ? 2 X ) 2 的 2n i =1 i =1X 1 , X 2 , ? , X 2n ( n ≥ 2 ),其样本均值为 X =数学期望 E (Y ) .2001 年考研数学一试题答案与解析一、填空题 (1)【分析】由通解的形式可知特征方程的两个根是 r1 , r2= 1 ± i ,从而得知特征方程为(r ? r1 )(r ? r2 ) = r 2 ? (r1 + r2 )r + r1r2 = r 2 ? 2r + 2 = 0 .由此,所求微分方程为y '' ? 2 y ' + 2 y = 0 .(2)【分析】先求 grad gradr. gradr= grad ?? ?r ?r ?r ? ? x y z ? , , ? = ? , , ?. ? ?x ?y ?z ? ? r r r ?? x ? y ? z ( )+ ( )+ ( ) ?x r ?y r ?z r 1 x2 1 y2 1 z2 3 x2 + y 2 + z 2 2 ? 3 )+( ? 3 )+( ? 3) = ? = . r r r r r r r r3 r再求divgrad gradr= grad=(于是divgrad (1, ?2,2) = gradr| grad2 2 |(1,?2,2) = . r 3y ≤0时(3)【分析】这个二次积分不是二重积分的累次积分,因为 ?1 ≤1 ? y ≤2 .由此看出二次积分∫ dy ∫?121? yf ( x, y )dx 是二重积分的一个累次积分,它与原式只差一个符号.先把此累次积分表为∫0 ?1dy ∫21? yf ( x, y )dx = ∫∫ f ( x, y )dxdy .D由累次积分的内外层积分限可确定积分区域 D :?1 ≤ y ≤ 0,1 ? y ≤ x ≤ 2 .见图.现可交换积分次序原式= ?0 ?1 2 2 0 2 1? x∫dy ∫1? yf ( x, y )dx = ? ∫ dx ∫11? xf ( x, y )dy = ∫ dx ∫1f ( x, y )dy .(4)【分析】矩阵 A 的元素没有给出,因此用伴随矩阵、用初等行变换求逆的路均堵塞.应当考虑用定义法. 因为故按定义知( A ? E )( A + 2 E ) ? 2 E = A2 + A ? 4 E = 0 , ( A ? E )( A + 2 E ) = 2 E ,即 ( A ? E ) ?1 = 1 ( A + 2E) . 2 ( A ? E) ? A + 2E = E. 2(5)【分析】根据切比雪夫不等式P{ X ? E ( X ) ≥ε } ≤于是D( x)ε 2,P{ X ? E ( X ) ≥ 2} ≤D( x) 1 = . 22 2二、选择题 (1)【分析】当 x < 0 时, f ( x ) 单调增 ? f ( x) ≥ 0 ,(A),(C)不对;'当 x > 0 时, f ( x ) :增——减——增 ? f ( x ) :正——负——正,(B)不对,(D)对.'应选(D). (2)【分析】我们逐一分析.关于(A),涉及可微与可偏导的关系.由微.因此(A)不一定成立. 关于(B)只能假设 Bf ( x, y ) 在(0,0)存在两个偏导数 ? f ( x, y ) 在(0,0)处可f ( x, y ) 在(0,0)存在偏导数?f (0, 0) ?f (0, 0) , ,不保证曲面 z = f ( x, y ) 在 ?x ?y? ? ?f (0, 0) ?f (0, 0) (0, 0, f (0, 0)) 存在切平面.若存在时,法向量 n= ± ? ,, 1? = ± {3,1,-1}与{3,1,1}不 ? 与 ?y ? ?x ?共线,因而(B)不成立.? x = t, ? 关于(C),该曲线的参数方程为 ? y = 0, ? z = f (t , 0), ?{t ', 0,因此,(C)成立.它在点 (0, 0, f (0, 0)) 处的切向量为d f (t , 0)} |t = 0 = {1, 0, f x' (0, 0)} = {1, 0,3} . dt(3)【分析】当f ( x) f ( x) f ( x) ? ? lim = lim ?. x →0 x →0+ x →0 ? x x x 1 f (1 ? cos h) 1 ? cos h 1 f (t ) 关于(A): lim 2 f (1 ? cos h) = lim ? t = 1 ? cos h lim , 2 h →0 h h → 0 1 ? cos h h 2 t →0 + t 1 由此可知 lim 2 f (1 ? cos h) ? ? f +' (0) ? . h →0 h f (0) = 0 时, f ' (0) = lim 若f ( x) 在 x = 0 可导 ? (A)成立,反之若(A)成立 ? f +' (0)'? ? f ' (0)? .如 f ( x) =| x | 满足(A),但 f (0) 不 ? . 关于(D):若 f ( x ) 在 x = 0 可导, ?1 f (2h) f (h) lim [ f (2h) ? f (h)] = lim[2 ? ] = 2 f ' (0) ? f '(0) . h →0 h h →0 2h h? (D)成立.反之(D)成立 ? lim( f (2h) ? f (h)) = 0 ? f ( x) 在 x = 0 连续, ? f ( x) 在 x = 0 可h →0导.如 f ( x ) = ? 再看(C):? 2 x + 1, x ≠ 0 x=0 ? 0,满足(D),但 f ( x ) 在 x = 0 处不连续,因而 f (0) 也不 ? .'lim1 h ? sin h f (h ? sin h) h ? sin h f (t ) f (h ? sin h) = lim ? = lim ? (当它们都 ? 时).2 2 h →0 h h →0 h →0 h h ? sin h h2 t注意,易求得 limh ? sin h f (t ) = 0 .因而,若 f ' (0) ? ? (C)成立.反之若(C)成立 ? lim (即 2 h →0 t →0 h t f (t ) ' f ' (0) ? ).因为只要有界,任有(C)成立,如 f ( x ) =| x | 满足(C),但 f (0) 不 ? . t因此,只能选(B).(4)【分析】由| λ E ? A |= λ 4 ? 4λ 3 = 0 ,知矩阵 A 的特征值是 4,0,0,0.又因 A 是实对称矩阵, A必能相似对角化,所以 A 与对角矩阵 B 相似. 作为实对称矩阵,当 A ?B 时,知 A 与 B 有相同的特征值,从而二次型 xT Ax 与 xT Bx 有相同的正负惯性指数,因此 A 与 B 合同. 所以本题应当选(A). 注意,实对称矩阵合同时,它们不一定相似,但相似时一定合同.例如?1 0 ? ?1 0 ? A=? ? 与 B = ?0 3 ? , ?0 2? ? ?它们的特征值不同,故 A 与 B 不相似,但它们的正惯性指数均为 2,负惯性指数均为 0.所以 A 与 B 合同.(5)【分析】解本题的关键是明确 X 和 Y 的关系: X+ Y = n ,即 Y = n ? X ,在此基础上利用性质:相关系数ρ XY 的绝对值等于 1 的充要条件是随机变量 X 与 Y 之间存在线性关系,即 Y = aX + b (其中 a, b 是常数),且当 a > 0 时, ρ XY = 1 ;当 a < 0 时, ρ XY = ?1 ,由此便知ρ XY = ?1 ,应选(A). 事实上, Cov ( X , Y ) = Cov ( X , n ? X ) = ? DX , DY = D ( n ? X ) = DX ,由此由相关系数的定义式有ρ XY =Cov( X , Y ) = DX DY? DX = ?1 . DX DY三、【解】1 1 ?2 x de x x ?2 x x ] 原式= ? ∫ arctan e d (e ) = ? [e arctan e ? ∫2 x 2 2 e (1 + e 2 x )1 ?2 x de x de x x = ? (e arctan e ? ∫ 2 x + ∫ ) 2 e 1 + e2 x=?1 ?2 x (e arctan e x + e ? x + arctan e x ) + C . 2四、【解】求先求 ? (1) =f (1, f (1,1)) = f (1,1) = 1 .d 3 ? ( x) |x =1 = 3? 2 (1)? ' (1) = 3? ' (1) ,归结为求 ? '(1) .由复合函数求导法 dx d ? ' ( x) = f1' ( x, f ( x, x)) + f 2' ( x, f ( x, x)) f ( x, x) , dx? ' (1) = f1' (1,1) + f 2' (1,1)[ f1' (1,1) + f 2' (1,1)] .注意f1' (1,1) =?f (1,1) ?f (1,1) = 2 , f 2' (1,1) = =3. ?x ?y,因此? ' (1) = 2 + 3(2 + 3) = 17d 3 ? ( x) |x =1 = 3 ×17 = 51 . dx2五、【分析与求解】关键是将 arctan x 展成幂级数,然后约去因子 x ,再乘上 1 + x 并化简即可. '直接将 arctan x 展开办不到,但 (arctan x ) 易展开,即(arctan x)' =x∞ 1 = ∑ (?1) n x 2 n , | x |< 1 , 1 + x 2 n =0①积分得arctan x = ∫ (arctan t )' dt = ∑ (?1) n ∫ t 2 n dt = ∑x 0 n =0 0∞(?1) n 2 n +1 x , x ∈ [?1,1] . ② n = 0 2n + 1∞因为右端积分在 x = ±1 时均收敛,又 arctan x 在 x = ±1 连续,所以展开式在收敛区间端点x = ±1 成立. 1 + x2 现将②式两边同乘以得 x∞ 1 + x2 (?1) n 2 n ∞ (?1)n 2 n ∞ (?1) n x 2 n + 2 arctan x = (1 + x 2 )∑ x =∑ x +∑ x 2n + 1 n = 0 2n + 1 n = 0 2n + 1 n =0(?1) n 2 n ∞ (?1)n ?1 2 n x +∑ x =∑ n = 0 2n + 1 n = 0 2n ? 1∞=1 +∑ (?1) ( 2n + 1 ? 2n ? 1) xn n =1∞112n= 1+ ∑(?1) n 2 2 n x 2 n =1 1 ? 4n∞,x ∈ [?1,1] , x ≠ 0上式右端当 x = 0 时取值为 1,于是f ( x) = 1 + ∑∞(?1) n 2 2 n x , x ∈ [?1,1] . 2 n =1 1 ? 4n∞上式中令 x = 1 ?(?1) n 1 1 ππ 1 ∑ 1 ? 4n2 = 2 [ f (1) ? 1] = 2 (2 × 4 ? 1) = 4 ? 2 . n =1y+ z = 2上L所六、【解】用斯托克斯公式来计算.记 S 为平面 x +为围部分.由 L 的定向,按右手法则 S 取上侧, S 的单位法向量n = (cos α , cos β , cos γ ) =于是由斯托克斯公式得1 (1,1,1) . 3cos γ ? ?z 3x 2 ? y 2 dScos α I = ∫∫Scos β ? ?y 2 z 2 ? x2? ?x y2 ? z2=∫∫ [(?2 y ? 4 z )S1 1 1 + ( ?2 z ? 6 x ) + (?2 x ? 2 y ) ]dS3 3 3=?2 2 ∫∫ (4 x + 2 y + 3z )dS (利用x + y + z = 2) ?3 ∫∫ (6 + x ? y)dS .3 S S于是'2 '2 1+ Zx + Z y = 1+1+1 = 3 .按第一类曲面积分化为二重积分得I =?2 ∫∫ (6 + x ? y ) 3dxdy = ?2∫∫ (6 + x ? y)dxdy ,3 D D | x | + | y |≤ 1 (图).由 D 关于 x, y 轴的对称性及被积函数的奇其中 D 围 S 在 xy 平面上的投影区域偶性得∫∫ ( x ? y)dxdy = 0D?I = ?12∫∫ dxdy = ?12( 2) 2 = ?24 .D七、【证明】 (1)由拉格朗日中值定理, ? x ∈ (1, ?1) ,x ≠ 0 , ? θ∈ (0,1) ,使f ( x) = f (0) + xf ' (θ x)(θ与x 有关);又由 f '' ( x) 连续而 f '' ( x) ≠ 0 , f'' ( x) 在 (1, ?1) 不变号, f ' ( x) 在 (1, ?1) 严格单调, θ唯一. (2)对f ' (θ x) 使用 f '' (0) 的定义.由题(1)中的式子先解出 f ' (θ x) ,则有f ' (θ x) =再改写成f ( x) ? f (0) . x f ( x) ? f (0) ? xf ' (0) . xf ' (θ x)? f ' (0) =f ' (θ x) ? f ' (0) f ( x) ? f (0) ? xf ' (0) , ?θ = x2 θx解出θ ,令 x → 0 取极限得1 '' f (0) 1 f ( x) ? f (0) ? xf (0) f (θ x) ? f (0)2 lim θ= lim / lim = '' = . 2 x →0 x →0 x→0 2 x f (0) θx' ' '八、【解】先求(1)设 t 时刻雪堆的体积为 V (t ) ,侧面积为S (t ) . t 时刻雪堆形状如图所示S (t ) 与 V (t ) .侧面方程是z = h(t ) ?2( x 2 + y 2 ) h 2 (t ) (( x, y ) ∈ Dxy : x 2 + y 2 ≤ ). 2 h(t ) ??z 4 x ?z 4y =? , =? . ?x h(t ) ?y h(t )?S (t ) = ∫∫Dxy?z 2 ?z 2 h 2 (t ) + 16( x 2 + y 2 ) 1 + ( ) + ( ) dxdy = ∫∫ dxdy . ?x ?y h(t ) Dxy作极坐标变换: x = r cos θ , y = r sin θ ,则Dxy : 0 ≤θ≤ 2π , 0 ≤ r ≤1 h(t ) . 2S (t ) =?1 h (t ) 1 2π dθ∫2 h 2 (t ) + 16r 2 rdr ∫0 0 h(t )3 h (t ) 2π 12 13π 2 ? [h (t ) + 16r 2 ] 2 |0 2 = h (t ). h(t ) 48 12 1=用先二后一的积分顺序求三重积分V (t ) = ∫h(t )dz∫∫ dxdy ,D( x)其中 D ( z ):2( x 2 + y 2 ) 1 ≤ h(t ) ? z (t ) ,即 x 2 + y 2 ≤ [h 2 (t ) ? h(t ) z ] . h(t ) 2V (t ) = ∫h (t )?π2[h 2 (t ) ? h(t ) z ]dz =π1 π [h3 (t ) ? h(t )3 ] = h3 (t ) .2 2 4 dV = ?0.9 S dt(2)按题意列出微分方程与初始条件.dV ,它与侧面积成正比(比例系数 0.9),即 dt π 2 dh 13π 2 将 V (t ) 与 S(t ) 的表达式代入得 3h (t ) = ?0.9 h (t ) ,即 4 dt 12 dh 13 =? . dt 10 体积减少的速度是 ?①②h(0) = 130 .(3)解①得 h(t ) = ? 令 h(t ) = 0 ,得 t13 t +C . 10由②得C = 130 ,即 h(t ) = ?13 t + 130 . 10= 100 .因此,高度为 130 厘米的雪堆全部融化所需时间为 100 小时.九、【解】由于β i (i= 1, 2? s ) 是α1 , α 2 ,?α s 线性组合,又α1 , α 2 ,?α s 是 Ax = 0 的解,所以根据齐次线性方程组解的性质知β i (i = 1, 2? s ) 均为 Ax = 0 的解. 从α1 , α 2 ,?α s 是 Ax = 0 的基础解系,知 s = n ? r ( A) . 下面来分析β1 , β 2 ,? β s 线性无关的条件.设 k1β1 + k 2 β 2 + ?? k s β s = 0 ,即(t1k1 + t2 ks )α1 + (t2 k1 + t1k2 )α 2 + (t2 k2 + t1k3 )α 3 + ? + (t2 ks ?1 + t1k s )α s = 0 .由于α1 , α 2 ,?α s 线性无关,因此有?t1k1 + t2 k s = 0, ?t k + t k = 0, ?2 1 1 2 ? ?t2 k2 + t1k3 = 0, ? ? ? ?t2 ks ?1 + t1k s = 0. ?因为系数行列式(*)t1 0 0? 0 t2 t2 t1 0 ? 0 0s 0 t2 t1 ? 0 0 = t1s + (?1) s +1 t2 ,? ? ? ?? 0 0 0? t2 t1所以当 t1s s + (?1) s +1 t2 ≠ 0 时,方程组(*)只有零解 k1 = k2 = ? = ks = 0 . 从而β1 , β 2 ,? β s 线性无关.十、【解】(1)由于 AP= PB ,即A( x, Ax, A2 x) = ( Ax, A2 x, A3 x) = ( Ax, A2 x,3 Ax ? 2 A2 x)?0 0 0 ? = ( x, Ax, A x) ?1 0 3 ? , ? ? ?0 1 ? 2 ? ? ?2?0 0 0 ? ? ? . 所以 B = 1 0 3 ? ? ? ?0 1 ? 2 ? ?(2)由(1)知 A ?B ,那么 A + E ? B + E ,从而1 0 0 | A + E |=| B + E |= 1 1 3 = ?4 . 0 1 ?1m = m | X = n} = Cn p m (1 ? p )n ? m , 0 ≤ m ≤ n, n = 0,1, 2,? . 十一、【解】 (1) P{Y (2) P{ X= n, Y = m} = P{ X = n}P{Y = m | X = n}=λnn!m e ? λ ? Cn p m (1 ? p )n ? m , 0 ≤ m ≤ n, n = 0,1, 2,?.十二、【解】易见随机变量 ( X 1 +X n +1 ) , ( X 2 + X n + 2 ) , ? , ( X n + X 2 n ) 相互独立都服从正态分布N (2 ? , 2σ 2 ) .因此可以将它们看作是取自总体 N (2 ? , 2σ 2 ) 的一个容量为 n 的简单随机样本.其样本均值为1 n 1 2n ( X i + X n +i ) = ∑ X i =2 X , ∑ n i =1 n i =1 1 n 1 ∑ ( Xi + X n +i ? 2 X ) 2 = n ? 1 Y . n ? 1 i =11 Y ) = 2σ2 ,即 E (Y ) = 2(n ? 1)σ 2 . n ?1样本方差为因样本方差是总体方差的无偏估计,故 E (。
2011年四川大学硕士研究生考试-数学分析

四川大学2011年硕士研究生考试——数学分析一、计算: 1、lim n →∞⎛ ⎝2、211limnn k n k→∞=+∑3、若01lim 1lim arccossin axx x x x→∞→⎛⎫+= ⎪⎝⎭,求a4、()1220lim 3sin 1xxx e x x →++-二、计算下列积分: 1、 求()cos ln x dx ⎰; 2、 411dx x +∞+⎰;3、 求L I y ds =⎰,其中L 是球面2222x y z ++=和平面x y =的交线;4、 求()2I x y y dS ∑=++⎰⎰,其中2222:x y z R ∑++=;5、 已知函数()f x 在 上连续可导,求()()()22211Ly f xy x I dx y f xy dy yy+=+-⎰,其中L 是上半球面()0y >内以()2,3为起点()3,2为终点的有向“分段光滑”曲线。
6、计算2I ∑=⎰⎰∑为下半球面:z =的上侧。
三、函数(),z f x y =有二阶连续偏导数且0y f ≠,证明:对任意实数c ,(),f x y c =是一条直线的充要条件是:()()2220y xx x y xy x yy f f f f f f f -+=四、讨论函数1sin x x和1sinx在()0,+∞上的一致连续性,说明理由。
五、偶函数()f x 的二阶导数()f x ''在0x =的某领域内连续,且()01f =,()02f ''=证明:级数111n f n ∞=⎛⎫⎛⎫-⎪ ⎪⎝⎭⎝⎭∑绝对收敛。
六、函数()[]():0,10,1f x →在[]0,1上可导,且()1f x ''≠,证明:方程()f x x =在()0,1内有唯一的实根。
七、设()f x 在[]0,1上可积,在1x =处连续,证明:()()10lim 1nn n x fx dx f →∞=⎰八、设函数(),f x y 在区域22:1D x y +≤上有二阶连续偏导数且()222222x yf f exy-+∂∂+=∂∂,证明:2D f f I x y dxdy xy e π⎛⎫∂∂=+= ⎪∂∂⎝⎭⎰⎰。
2001年考研数学一试题及完全解析(Word版)
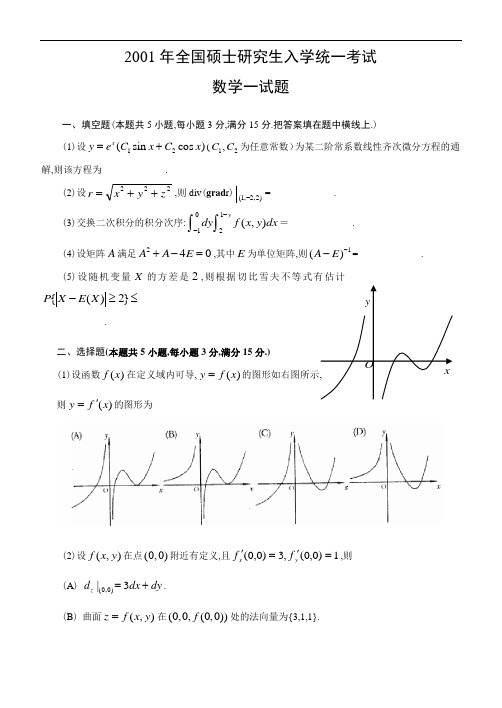
yOx2001年全国硕士研究生入学统一考试数学一试题一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上.)(1)设12(sin cos )xy e C x C x =+(12,C C 为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为_____________.(2)设222z y x r++=,则div (grad r ))2,2,1(-=_____________.(3)交换二次积分的积分次序:⎰⎰--0112),(y dx y x f dy =_____________.(4)设矩阵A 满足240A A E +-=,其中E 为单位矩阵,则1()A E --=_____________.(5)设随机变量X 的方差是2,则根据切比雪夫不等式有估计≤≥-}2)({X E X P_____________.二、选择题(本题共5小题,每小题3分,满分15分.) (1)设函数)(x f 在定义域内可导,)(x f y =的图形如右图所示,则)(x f y'=的图形为(2)设),(y x f 在点(0,0)附近有定义,且1)0,0(,3)0,0(='='y x f f ,则(A ) (0,0)|3z d dx dy =+. (B ) 曲面),(y x f z=在(0,0,(0,0))f 处的法向量为{3,1,1}.(C ) 曲线⎩⎨⎧==0),(y y x f z 在(0,0,(0,0))f 处的切向量为{1,0,3}.(D ) 曲线⎩⎨⎧==0),(y y x f z 在(0,0,(0,0))f 处的切向量为{3,0,1}.(3)设0)0(=f ,则)(x f 在x =0处可导的充要条件为(A ) 201lim (1cosh)h f h →-存在.(B )01lim(1)h h f e h →-存在. (C ) 201lim (sinh)h f h h→-存在.(D ) 01lim [(2)()]h f h f h h→-存在.(4)设1111400011110000,,1111000011110000A B ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦则A 与B (A ) 合同且相似. (B ) 合同但不相似. (C ) 不合同但相似.(D ) 不合同且不相似.(5)将一枚硬币重复掷n 次,以X 和Y 分别表示正面向上和反面向上的次数, 则X 和Y 的相关系数等于(A )-1.(B ) 0.(C )12. (D ) 1.三、(本题满分6分)求dx e e xx⎰2arctan .四、(本题满分6分) 设函数),(y x f z=在点(1,1)处可微,且(1,1)1f =,(1,1)|2fx∂=∂,(1,1)|3f y ∂=∂,()(,x f x ϕ=(,))f x x .求13)(=x x dxd ϕ.五、(本题满分8分)设)(x f =210,arctan ,0,1,x x x x x +⎧≠⎨=⎩将)(x f 展开成x 的幂级数,并求级数∑∞=--1241)1(n nn 的和.六、(本题满分7分) 计算dz y x dy x z dx z y I L)3()2()(222222-+-+-=⎰,其中L 是平面2=++z y x 与柱面1=+y x 的交线,从Z 轴正向看去,L 为逆时针方向.七、(本题满分7分) 设)(x f 在(1,1)-内具有二阶连续导数且0)(≠''x f ,试证:(1)对于(1,1)-内的任一0x ≠,存在惟一的)1,0()(∈x θ,使)(x f =)0(f +))((x x f x θ'成立;(2)01lim ()2x x θ→=.八、(本题满分8分)设有一高度为()h t (t 为时间)的雪堆在融化过程,其侧面满足方程)()(2)(22t h y x t h z +-=(设长度单位为厘米,时间单位为小时),已知体积减少的速率与侧面积成正比(比例系数为0.9),问高度为130(厘米)的雪堆全部融化需多少小时?九、(本题满分6分)设s ααα,,,21 为线性方程组0Ax =的一个基础解系,11122t t βαα=+,21223,t t βαα=+,121s s t t βαα=+,其中21,t t 为实常数.试问21,t t 满足什么条件时,s βββ,,,21 也为0Ax =的一个基础解系.十、(本题满分8分) 已知3阶矩阵A 与三维向量x ,使得向量组2,,x Ax A x 线性无关,且满足x A Ax x A 2323-=.(1)记P =(x A Ax x 2,,),求3阶矩阵B ,使1-=PBP A ;(2)计算行列式E A +.十一、(本题满分7分)设某班车起点站上客人数X 服从参数为λ(0λ>)的泊松分布,每位乘客在中途下车的概率为p (01p <<),且中途下车与否相互独立.以Y 表示在中途下车的人数,求:(1)在发车时有n 个乘客的条件下,中途有m 人下车的概率; (2)二维随机变量(,)X Y 的概率分布.十二、(本题满分7分) 设总体X 服从正态分布2(,)N μσ(0σ>),从该总体中抽取简单随机样本12,X X ,,2n X (2n ≥),其样本均值为∑==ni i X n X 2121,求统计量∑=+-+=ni i n i X X X Y 12)2(的数学期望()E Y .2001年考研数学一试题答案与解析一、填空题(1)【分析】 由通解的形式可知特征方程的两个根是12,1r r i =±,从而得知特征方程为22121212()()()220r r r r r r r r r r r r --=-++=-+=.由此,所求微分方程为'''220y y y -+=.(2)【分析】 先求grad r .grad r=,,,,r r r x y z x y z r r r ∂∂∂⎧⎫⎧⎫=⎨⎬⎨⎬∂∂∂⎩⎭⎩⎭. 再求 div grad r=()()()x y zx r y r z r∂∂∂++∂∂∂=222222333311132()()()x y z x y z r r r r r r r r r++-+-+-=-=.于是div grad r|(1,2,2)-=(1,2,2)22|3r -=.(3)【分析】 这个二次积分不是二重积分的累次积分,因为10y -≤≤时12y -≤.由此看出二次积分0211(,)ydy f x y dx --⎰⎰是二重积分的一个累次积分,它与原式只差一个符号.先把此累次积分表为0211(,)(,)yDdy f x y dx f x y dxdy --=⎰⎰⎰⎰.由累次积分的内外层积分限可确定积分区域D :10,12y y x -≤≤-≤≤.见图.现可交换积分次序原式=02202111111(,)(,)(,)xyxdy f x y dx dx f x y dy dx f x y dy -----=-=⎰⎰⎰⎰⎰⎰.(4)【分析】 矩阵A 的元素没有给出,因此用伴随矩阵、用初等行变换求逆的路均堵塞.应当考虑用定义法.因为2()(2)240A E A E E A A E -+-=+-=,故()(2)2A E A E E -+=,即 2()2A EA E E +-⋅=. 按定义知11()(2)2A E A E --=+.(5)【分析】 根据切比雪夫不等式2(){()}D x P X E X εε-≥≤,于是2()1{()2}22D x P XE X -≥≤=.二、选择题(1)【分析】 当0x <时,()f x 单调增'()0f x ⇒≥,(A ),(C )不对;当0x >时,()f x :增——减——增'()f x ⇒:正——负——正,(B )不对,(D )对.应选(D ).(2)【分析】 我们逐一分析.关于(A ),涉及可微与可偏导的关系.由(,)f x y 在(0,0)存在两个偏导数⇒(,)f x y 在(0,0)处可微.因此(A )不一定成立.关于(B )只能假设(,)f x y 在(0,0)存在偏导数(0,0)(0,0),f f x y∂∂∂∂,不保证曲面(,)z f x y =在 (0,0,(0,0))f 存在切平面.若存在时,法向量n=(0,0)(0,0)1f f x y ⎫∂∂⎧±-=±⎨⎬∂∂⎩⎭,,{3,1,-1}与{3,1,1}不共线,因而(B )不成立.关于(C ),该曲线的参数方程为,0,(,0),x t y z f t =⎧⎪=⎨⎪=⎩它在点(0,0,(0,0))f 处的切向量为'0{',0,(,0)}|{1,0,(0,0)}{1,0,3}t x dt f t f dt===. 因此,(C )成立.(3)【分析】 当(0)0f =时,'0()(0)limx f x f x →=∃00()()lim lim x x f x f x x x→+→-⇔=∃.关于(A ):220001(1cos )1cos 1()lim (1cos )lim 1cos lim1cos 2h h t f h h f t f h t h h h h t→→→+---=⋅=--, 由此可知 201lim (1cos )h f h h→-∃ ⇔ '(0)f + ∃.若()f x 在0x =可导⇒(A )成立,反之若(A )成立⇒'(0)f + ∃⇒'(0)f ∃.如()||f x x =满足(A ),但'(0)f 不∃. 关于(D ):若()f x 在0x =可导,⇒''001(2)()lim [(2)()]lim[2]2(0)(0)2h h f h f h f h f h f f h h h→→-=-=-. ⇒(D )成立.反之(D )成立0lim((2)())0h f h f h →⇒-=⇒()f x 在0x =连续,⇒()f x 在0x =可导.如21,0()0,0x x f x x +≠⎧=⎨=⎩ 满足(D ),但()f x 在0x =处不连续,因而'(0)f 也不∃.再看(C ):2220001sin (sin )sin ()lim(sin )lim lim sin h h h h h f h h h h f t f h h h h h h h t→→→----=⋅=⋅-(当它们都∃时).注意,易求得20sin lim0h h h h →-=.因而,若'(0)f ∃⇒(C )成立.反之若(C )成立⇒0()lim t f t t→(即 '(0)f ∃).因为只要()f t t有界,任有(C )成立,如()||f x x =满足(C ),但'(0)f 不∃.因此,只能选(B ).(4)【分析】 由 43||40E A λλλ-=-=,知矩阵A 的特征值是4,0,0,0.又因A 是实对称矩阵,A 必能相似对角化,所以A 与对角矩阵B 相似.作为实对称矩阵,当AB 时,知A 与B 有相同的特征值,从而二次型T x Ax 与T x Bx 有相同的正负惯性指数,因此A 与B 合同.所以本题应当选(A ).注意,实对称矩阵合同时,它们不一定相似,但相似时一定合同.例如1002A ⎡⎤=⎢⎥⎣⎦与1003B ⎡⎤=⎢⎥⎣⎦, 它们的特征值不同,故A 与B 不相似,但它们的正惯性指数均为2,负惯性指数均为0.所以A 与B 合同.(5)【分析】 解本题的关键是明确X 和Y 的关系:XY n +=,即Y n X =-,在此基础上利用性质:相关系数XY ρ的绝对值等于1的充要条件是随机变量X 与Y 之间存在线性关系,即YaX b =+(其中,a b 是常数),且当0a >时,1XY ρ=;当0a <时,1XY ρ=-,由此便知1XY ρ=-,应选(A ).事实上,(,)(,)Cov X Y Cov X n X DX =-=-,()DY D n X DX =-=,由此由相关系数的定义式有1XY ρ===-.三、【解】原式=222211arctan ()[arctan ]22(1)x x x x xxx de e d e e e e e ---=--+⎰⎰=2221(arctan )21x x x xx xde de e e e e ---++⎰⎰=21(arctan arctan )2xx x x e e e e C ---+++.四、【解】 先求(1)(1,(1,1))(1,1)1f f f ϕ===.求 32''1()|3(1)(1)3(1)x d x dxϕϕϕϕ===,归结为求'(1)ϕ.由复合函数求导法 '''12()(,(,))(,(,))(,)dx f x f x x f x f x x f x x dxϕ=+,'''''1212(1)(1,1)(1,1)[(1,1)(1,1)]f f f f ϕ=++.注意'1(1,1)(1,1)2f f x∂==∂,'2(1,1)(1,1)3f f y ∂==∂. 因此'(1)23(23)17ϕ=++=,31()|31751x d x dxϕ==⨯=.五、【分析与求解】 关键是将arctan x 展成幂级数,然后约去因子x ,再乘上21x +并化简即可.直接将arctan x 展开办不到,但'(arctan )x 易展开,即'221(arctan )(1),||11n n n x x x x ∞===-<+∑, ①积分得 '2210000(1)arctan (arctan )(1)21n xx nnn n n x t dt t dt x n ∞∞+==-==-=+∑∑⎰⎰,[1,1]x ∈-. ② 因为右端积分在1x =±时均收敛,又arctan x 在1x =±连续,所以展开式在收敛区间端点1x =±成立.现将②式两边同乘以21x x+得2222220001(1)(1)(1)arctan (1)212121n n n n n n n n n x x x x x x x n n n +∞∞∞===+---=+=++++∑∑∑=12200(1)(1)2121n n n nn n x x n n -∞∞==--++-∑∑=21111(1)()2121n n n x n n ∞=+--+-∑221(1)2114n nn x n ∞=-=+-∑ ,[1,1]x ∈-,0x ≠上式右端当0x =时取值为1,于是221(1)2()1,[1,1]14n nn f x x x n∞=-=+∈--∑. 上式中令1x =21(1)111[(1)1](21)1422442n n f n ππ∞=-⇒=-=⨯-=--∑.六、【解】用斯托克斯公式来计算.记S 为平面2x y z ++=上L 所为围部分.由L 的定向,按右手法则S 取上侧,S 的单位法向量(cos ,cos ,cos )3n αβγ==. 于是由斯托克斯公式得222222cos cos cos 23SI dS x y z y z z x x y αβγ∂∂∂=∂∂∂---⎰⎰=[(24(26(22]333Sy z z x x y dS --+--+--⎰⎰=(423)(2)(6)33S Sx y z dS x y z x y dS ++++=-+-利用. 于是'2'211113x y Z Z ++=++=按第一类曲面积分化为二重积分得(6)32(6)3D DI x y dxdy x y dxdy =+-=-+-⎰⎰, 其中D 围S 在xy 平面上的投影区域||||1x y +≤(图).由D 关于,x y 轴的对称性及被积函数的奇偶性得()0Dx y dxdy -=⎰⎰⇒21212(2)24DI dxdy =-=-=-⎰⎰.七、【证明】 (1)由拉格朗日中值定理,(1,1)x ∀∈-,0,(0,1)x θ≠∃∈,使'()(0)()f x f xf x θ=+(θ与x 有关);又由''()f x 连续而''()0f x ≠,''()f x 在(1,1)-不变号,'()f x 在(1,1)-严格单调,θ唯一. (2)对'()f x θ使用''(0)f 的定义.由题(1)中的式子先解出'()f x θ,则有'()(0)()f x f f x xθ-=.再改写成'''()(0)(0)()(0)f x f xf f x f x θ---=.'''2()(0)()(0)(0)f x f f x f xf x xθθθ---⋅=, 解出θ,令0x →取极限得'''''2''0001(0)()(0)(0)()(0)12lim lim /lim (0)2x x x f f x f xf f x f x x f θθθ→→→---===.八、【解】 (1)设t 时刻雪堆的体积为()V t ,侧面积为()S t .t 时刻雪堆形状如图所示先求()S t 与()V t .侧面方程是222222()()()((,):)()2xy x y h t z h t x y D x y h t +=-∈+≤. ⇒44,()()z x z yx h t y h t ∂∂=-=-∂∂. ⇒()xyxyD D S t dxdy ==⎰⎰.作极坐标变换:cos ,sin x r y r θθ==,则:02,0()xy D r t θπ≤≤≤≤.⇒2(003()22221()()2113[()16]().()4812t t S t d h t h t r h t h t πθππ==⋅+=⎰用先二后一的积分顺序求三重积分()()()h t D x V t dzdxdy =⎰⎰⎰,其中222()():()()()x y D z h t z t h t +≤-,即2221[()()]2x y h t h t z +≤-. ⇒()233301()[()()][()()]()2224h t V t h t h t z dz h t h t h t πππ=-=-=⎰. (2)按题意列出微分方程与初始条件.体积减少的速度是dV dt -,它与侧面积成正比(比例系数0.9),即 0.9dVS dt=- 将()V t 与()S t 的表达式代入得 22133()0.9()412dh h t h t dt ππ=-,即1310dh dt =-.①(0)130h =.②(3)解①得13()10h t t C =-+. 由②得130C =,即13()13010h t t =-+. 令()0h t =,得100t =.因此,高度为130厘米的雪堆全部融化所需时间为100小时.九、【解】由于(1,2)i i s β=是12,,s ααα线性组合,又12,,s ααα是0Ax =的解,所以根据齐次线性方程组解的性质知(1,2)i i s β=均为0Ax =的解.从12,,s ααα是0Ax =的基础解系,知()s n r A =-.下面来分析12,,s βββ线性无关的条件.设11220s s k k k βββ++=,即11212112222133211()()()()0s s s s t k t k t k t k t k t k t k t k αααα-++++++++=.由于 12,,s ααα线性无关,因此有112211222132110,0,0,0.s s s t k t k t k t k t k t k t k t k -+=⎧⎪+=⎪⎪+=⎨⎪⎪+=⎪⎩(*)因为系数行列式12211211221000000000(1)000s s st t t t t t t t t t +=+-, 所以当112(1)0ss st t ++-≠时,方程组(*)只有零解120s k k k ====.从而12,,s βββ线性无关.十、【解】 (1)由于AP PB = ,即22322(,,)(,,)(,,32)A x Ax A x Ax A x A x Ax A x Ax A x ==-2000(,,)103012x Ax A x ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦,所以000103012B ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦.(2)由(1)知AB ,那么A E B E ++,从而100||||1134011A EB E +=+==--.十一、【解】 (1){|}(1),0,0,1,2,mmn mn P Y m X n C p p m n n -===-≤≤=.(2){,}P Xn Y m ==={}{|}P X n P Y m X n ====(1),0,0,1,2,.!nm mn m n e C p p m n n n λλ--⋅-≤≤=十二、【解】 易见随机变量11()n X X ++,22()n X X ++,2,()n n X X +相互独立都服从正态分布2(2,2)N μσ.因此可以将它们看作是取自总体2(2,2)N μσ的一个容量为n 的简单随机样本.其样本均值为21111()2n ni n i i i i X X X X n n +==+==∑∑, 样本方差为2111(2)11n i n ii X X X Y n n +=+-=--∑. 因样本方差是总体方差的无偏估计,故21()21E Y n σ=-,即2()2(1)E Y n σ=-.。
2001年考研数学一试题答案与解析

2001年考研数学一试题答案与解析一、(1)【分析】 由通解的形式可知特征方程的两个根是12,1r r i =±,从而得知特征方程为22121212()()()220r r r r r r r r rr r r --=-++=-+=.由此,所求微分方程为'''220y y y -+=.(2)【分析】 grad r=,,,,r r r x y z x y z r r r ∂∂∂⎧⎫⎧⎫=⎨⎬⎨⎬∂∂∂⎩⎭⎩⎭.再求 divgrad r=()()()x y z x r y r z r ∂∂∂++∂∂∂ =222222333311132()()()x y z x y z r r r r r r r r r++-+-+-=-=.于是 divgra d r|(1,2,2)-=(1,2,2)22|3r -=. (3)【分析】 这个二次积分不是二重积分的累次积分,因为10y -≤≤时12y -≤.由此看出二次积分是二重积0211(,)ydy f x y dx --⎰⎰分的一个累次积分,它与原式只差一个符号.先把此累次积分表为0211(,)(,)yDdy f x y dx f x y dxdy --=⎰⎰⎰⎰.由累次积分的内外层积分限可确定积分区域D :10,12y y x -≤≤-≤≤.见图.现可交换积分次序原式=02202111111(,)(,)(,)xyxdy f x y dx dx f x y dy dx f x y dy -----=-=⎰⎰⎰⎰⎰⎰.(4)【分析】 矩阵的元素没A 有给出,因此用伴随矩阵、用初等行变换求逆的路均堵塞.应当考虑用定义法.因为 2()(2)240A E A E E A A E -+-=+-=,故()(2)2A E A E E -+=,即2()2A E A E E +-⋅=.按定义知11()(2)2A E A E --=+. (5)【分析】 根据切比雪夫不等式2(){()}D x P X E X εε-≥≤, 于是2()1{()2}22D x P XE X -≥≤=. 二、(1)【分析】 当0x <时,()f x 单调增'()0f x ⇒≥,(A ),(C )不对;当0x>时,()f x :增——减——增'()f x ⇒:正——负——正,(B )不对,(D )对.应选(D ).(2)关于(A ),涉及可微与可偏导的关系.由(,)f x y 在(0,0)存在两个偏导数⇒(,)f x y 在(0,0)处可微.因此(A )不一定成立.关于(B )只能假设(,)f x y 在(0,0)存在偏导数(0,0)(0,0),f f x y∂∂∂∂,不保证曲面在(,)z f x y =(0,0,(0,0))f 存在切平面.若存在时,法向量n=(0,0)(0,0)1f f x y ⎫∂∂⎧±-=±⎨⎬∂∂⎩⎭,,{3,1,-1}与{3,1,1}不共线,因而(B )不成立.关于(C ),该曲线的参数方程为,0,(,0),x t y z f t =⎧⎪=⎨⎪=⎩它在点处的切(0,0,(0,0))f 向量为'0{',0,(,0)}|{1,0,(0,0)}{1,0,3}t x dt f t f dt===.因此,(C )成立. (3)【分析】 当(0)0f =时,'0()(0)lim x f x f x →=∃00()()lim lim x x f x f x x x→+→-⇔=∃.关于(A ):220001(1cos )1cos 1()lim (1cos )lim 1cos lim1cos 2h h t f h h f t f h t h h h h t→→→+---=⋅=--, 由此可知201lim (1cos )h f h h →-∃ ⇔ '(0)f + ∃.若()f x 在0x =可导⇒(A )成立,反之若(A )成立⇒'(0)f + ∃⇒'(0)f ∃.如()||f x x =满足(A ),但'(0)f 不∃.关于(D ):若()f x 在0x =可导,⇒''001(2)()lim [(2)()]lim[2]2(0)(0)2h h f h f h f h f h f f h h h→→-=-=-. ⇒(D )成立.反之(D )成立0l i m ((2)())0h f h f h →⇒-=⇒()f x 在0x =连续,⇒()f x 在0x =可导.如21,0()0,0x x f x x +≠⎧=⎨=⎩ 满足(D ),但在处不连续()f x 0x =,因而'(0)f 也不∃.再看(C ):2220001sin (sin )sin ()lim(sin )lim lim sin h h h h h f h h h h f t f h h h h h h h t→→→----=⋅=⋅-(当它们都∃时). 注意,易求得20sin lim 0h h h h →-=.因而,若'(0)f ∃⇒(C )成立.反之若(C )成立⇒0()lim t f t t →(即 '(0)f ∃).因为只要有界()f t t ,任有(C )成立,如()||f x x =满足(C ),但'(0)f 不∃.因此,只能选(B ).(4)【分析】 由43||40E A λλλ-=-=,知矩阵的特征A 值是4,0,0,0.又因是实对称A 矩阵,A 必能相似对角化,所以与对角矩A 阵B 相似.作为实对称矩阵,当A B 时,知与有相同的A B 特征值,从而二次型与T x Ax T x Bx 有相同的正负惯性指数,因此A 与B 合同.所以本题应当选(A ).注意,实对称矩阵合同时,它们不一定相似,但相似时一定合同.例如1002A ⎡⎤=⎢⎥⎣⎦与1003B ⎡⎤=⎢⎥⎣⎦,它们的特征值不同,故A 与B 不相似,但它们的正惯性指数均为2,负惯性指数均为0.所以A 与B 合同.(5)【分析】 解本题的关键是明确和的关XY系:X Y n +=,即Y n X =-,在此基础上利用性质:相关系数的绝XY ρ对值等于1的充要条件是随机变量与之间XY存在线性关系,即Y aX b =+(其中,a b 是常数),且当0a >时,1XY ρ=;当0a <时,1XY ρ=-,由此便知1XY ρ=-,应选(A ).事实上,(,)(,)Cov X Y Cov X n X DX =-=-,()DY D n X DX =-=,由此由相关系数的定义式有(,)1XY Cov X Y DXDX DY DX DYρ-===-.三、【解】原式=222211arctan ()[arctan ]22(1)x x x x xx xde e d e e e e e ---=--+⎰⎰=2221(arctan )21x x x x x xde de e e e e---++⎰⎰=21(arctan arctan )2x x x xe e e e C ---+++. 四、【解】先求(1)(1,(1,1))(1,1)1f f f ϕ===.求32''1()|3(1)(1)3(1)x d x dxϕϕϕϕ===,归结为求'(1)ϕ.由复合函数求导法'''12()(,(,))(,(,))(,)dx f x f x x f x f x x f x x dxϕ=+,'''''1212(1)(1,1)(1,1)[(1,1)(1,1)]f f f f ϕ=++.注意 '1(1,1)(1,1)2f f x∂==∂,'2(1,1)(1,1)3f f y∂==∂.因此'(1)23(23)17ϕ=++=,31()|31751x d x dxϕ==⨯=. 五、【分析与求解】关键是将展成arctan x 幂级数,然后约去因子x ,再乘上并化简21x +即可. 直接将展开办arctan x不到,但'(arctan )x 易展开,即'221(arctan )(1),||11n n n x x x x ∞===-<+∑, ①积分得 '2210000(1)arctan (arctan )(1)21n xx nnn n n x t dt t dt x n ∞∞+==-==-=+∑∑⎰⎰,[1,1]x ∈-. ② 因为右端积分在1x =±时均收敛,又arctan x 在1x =±连续,所以展开式在收敛区间端点1x =±成立.现将②式两边同乘以21x x+得2222220001(1)(1)(1)arctan (1)212121n n n n n n n n n x x x x x x x n n n +∞∞∞===+---=+=++++∑∑∑=12200(1)(1)2121n n n n n n x x n n -∞∞==--++-∑∑ =21111(1)()2121nnn x n n ∞=+--+-∑221(1)2114n nn x n∞=-=+-∑,[1,1]x ∈-,0x ≠上式右端当时0x=取值为1,于是221(1)2()1,[1,1]14n nn f x x x n ∞=-=+∈--∑.上式中令1x =21(1)111[(1)1](21422442n n f nππ∞=-⇒=-=⨯-=--∑.六、【解】用斯托克斯公式来计算.记为平面上所S2x y z ++=L为围部分.由L的定向,按右手法则取S 上侧,S 的单位法向量1(cos ,cos ,cos )(1,1,1)3n αβγ== .于是由斯托克斯公式得222222cos cos cos 23SI dSx y z y z z x x y αβγ∂∂∂=∂∂∂---⎰⎰=111[(24)(26)(22)]333Sy z z x x y dS --+--+--⎰⎰ =22(423)(2)(6)33S Sx y z dS x y z x y dS -++++=-+-⎰⎰⎰⎰利用.于是'2'211113x y Z Z ++=++=.按第一类曲面积分化为二重积分得2(6)32(6)3D DI x y dxdy x y dxdy =-+-=-+-⎰⎰⎰⎰,其中围在平面D S xy 上的投影区域||||1x y +≤(图).由关于轴的对D ,x y 称性及被积函数的奇偶性得()0Dx y dxdy -=⎰⎰⇒ 21212(2)24DI dxdy =-=-=-⎰⎰.七、【证明】 (1)由拉格朗日中值定理,(1,1)x ∀∈-,0,(0,1)x θ≠∃∈,使'()(0)()f x f xf x θ=+(θ与x 有关);又由''()f x 连续而''()0f x ≠,''()f x 在(1,1)-不变号,'()f x 在(1,1)-严格单调,θ唯一. (2)对使用的定义'()f x θ''(0)f .由题(1)中的式子先解出'()f x θ,则有'()(0)()f x ff x xθ-=.再改写成'''()(0)(0)()(0)f x f xf f x f x θ---=.'''2()(0)()(0)(0)f x f f x f xf x x θθθ---⋅=, 解出θ,令x →取极限得'''''2''0001(0)()(0)(0)()(0)12lim lim /lim (0)2x x x f f x f xf f x f x x f θθθ→→→---===. 八、【解】(1)设时刻雪堆的t 体积为()V t ,侧面积为()S t .t 时刻雪堆形状如图所示,先求()S t 与()V t .侧面方程是222222()()()((,):)()2xy x y h t z h t x y D x y h t +=-∈+≤.⇒44,()()z x z yx h t y h t ∂∂=-=-∂∂. ⇒ 22222()16()()1()()()xyxyD D z z h t x y S t dxdy dxdy x y h t ∂∂++=++=∂∂⎰⎰⎰⎰.作极坐标变换:cos ,sin x r y r θθ==,则1:02,0()2xy D r h t θπ≤≤≤≤. ⇒12()2220013()222221()()16()2113[()16]|().()4812h t h t S t d h t r rdr h t h t r h t h t πθππ=+=⋅+=⎰⎰用先二后一的积分顺序求三重积分()0()()h t D x V t dz dxdy=⎰⎰⎰,其中222()():()()()x y D z h t z t h t +≤-,即2221[()()]2x y h t h t z +≤-.⇒()233301()[()()][()()]()2224h t V t h t h t z dz h t h t h t πππ=-=-=⎰. (2)按题意列出微分方程与初始条件. (3)体积减少的速度是dVdt-,它与侧面积成正比(比例系数0.9),即将与的表达0.9dV S dt =-()V t ()S t 式代入得22133()0.9()412dh h t h t dt ππ=-,即1310dh dt =-. ①(0)130h =.②(3)解①得13()10h t t C =-+. 由②得130C =,即13()13010h t t =-+. 令()0h t =,得100t =.因此,高度为130厘米的雪堆全部融化所需时间为100小时. 九、【解】由于是线性组(1,2)i i s β= 12,,s ααα 合,又12,,s ααα 是0Ax =的解,所以根据齐次线性方程组解的性质知均为(1,2)i i s β= 0Ax =的解.从是的基础解12,,s ααα 0Ax =系,知()s n r A =-.下面来分析线12,,s βββ 性无关的条件.设11220s s k k k βββ++= ,即11212112222133211()()()()0s s s s t k t k t k t k t k t k t k t k αααα-++++++++= .由于线性无关12,,s ααα ,因此有112211222132110,0,0,0.s s s t k t k t k t k t k t k t k t k -+=⎧⎪+=⎪⎪+=⎨⎪⎪+=⎪⎩(*) 因为系数行列式1221121122100000000(1)000s s st t t t t t t t t t +=+-,所以当112(1)0s s st t ++-≠时,方程组(*)只有零解120s k k k ==== .从而线性无关12,,s βββ .十、【解】(1)由于AP PB =,即22322(,,)(,,)(,,32)A x Ax A x Ax A x A x Ax A x Ax A x ==-2000(,,)103012x Ax A x ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦, 所以000103012B ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦.(2)由(1)知A B ,那么A E B E ++ ,从而100||||1134011A EB E +=+==--.十一、【解】 (1){|}(1),0,0,1,2,m mn m n P Y m X n C p p m n n -===-≤≤= .(2){,}P X n Y m ==={}{|}P X n P Y m X n ====(1),0,0,1,2,.!nm mn m n e C p p m n n n λλ--⋅-≤≤=十二、【解】 易见随机变量11()n X X ++,22()n X X ++,2,()n n X X + 相互独立都服从正态分布2(2,2)N μσ.因此可以将它们看作是取自总体的一个容2(2,2)N μσ量为的简单随n 机样本.其样本均值为21111()2n ni n i i i i X X X X n n +==+==∑∑,样本方差为2111(2)11n i n ii X X X Y n n +=+-=--∑. 因样本方差是总体方差的无偏估计,故21()21E Y n σ=-,即.2()2(1)E Y n σ=-。
数学二解析2001

2001年数学(二)真题解析一、填空题(1)【答案】72T【解】方法一i . 丿3 —工—%/ ] + g lim X-*l x 2 x 一 21. %/3 — x — V 1 ~F lim —----——--------x->i (jc + 2) (jc 一1)lim --------------- ]------ ----Li (x + 2)(丿3 — 工 + 丿1 + 工)2(1 ―工)x 一 1方法二lim = lim -4-7工~* 1 x + 工一2工一1 + 111x 2 x 一 2 a /3 — x 2 丿]+ 匚(2)【答案】夕=*工+1.【解】e 2x+y — cos xy = e — 1两边对x 求导得严•+ sin xy •夕+熄) = 0,将X =0,y = 1代入得字I = — 2 ,ckr 丨 z=o则法线方程为夕一1 = *(久一0),即夕=*広+ 1-(3)【答案】 v-O【解】方法一sin 2 x cos 2 x dx — 2 sin 2 x cos 2 x dr4 J 。
,三=2 I 2 sin 2 j; • (1 一 sin 2 jc )dz = 2(12 — I 4 )2” (z 3 + sin 2 jc )cosx dx =方法二(x 3 + sin 2 )cos 2jc dj?=2 sin 2 x cos 2 jc dj? J 0丄72 sin 2 d(2工)=*sin 2x djro2 J 0 o(4)【答案】j/arcsin x = x【解】方法一丄由 j/arcsin x H — …一 =19得(jyarcsin x Y = 19解得 j/arcsin x = x + C 9J \ — 2因为曲线经过点(j,0),所以C=-y,故所求曲线为jarcsin x =x ----.方法二jy'arcsin x ~\-------------= 1 化为 y' ~\—,… ------------y =-----\-----,71-x 2 Jl —/arcsin z arcsln 工f d~r _ f 1 丄解得夕=([——?——e +C )e =(工 +c )・ ———\J arcsin x / arcsin x 因为曲线经过点(y,o ),所以C=-y,1x 2故所求曲线为—丄arcsin x因为r (A ) y^r (A ),所以方程组无解;(5)【答案】—2.a11【解】由题意得1a 1=(a + 2) (a 一 1 )2=0,解得 a = — 2 ,或 a = 1,11a /I 111 \I 1111 \当a =1时,才=b11100—3 ,\i11—2丿'o0 '当 a = — 2 时,A =_2111 \1-2111-2—2)因为r (A )=r (A )=2 V 3,所以a = —2时方程组有无数个解.二、选择题(6)【答案】(E ).【解】y[y (z )] = ]'9丨心)丨€1,丨心)丨>1,而 I /(J7 ) | ^ 1 (一°°<工 <+ °°),故 /[/(J : )] = 1 ,从而 f)]} =1,应选(E ).(7)【答案】(E ).1 2【解】(1 — cos x )ln ( 1 + z 2)〜—x 4 , x sin 工”〜x n+i , e" — 1 ~ j ?2 , 由题意得2 < n+l<4,解得n =2,应选(E ).(8)【答案】(C ).【解】<‘ = C ; • 2(工一3)2+© • 2(工一1) • 2(工一 3) +C ; • 2(工一I )?,令夕"=4 (3工 $ — 12_z + 11) = 0,得工 16+V336 — 4^3工2当工<C X 1时当久1 •< X X 2时j/'<0,当鼻 > 工2时j/‘>0,故曲线有两个拐 点,应选(C ).(9) 【答案】(A ).【解】 由拉格朗日中值定理得/(工)一/(1)= /'(£)(工一1),其中e 介于1与工之间,当工 6 (1-^,1)时 HVWV 1,再由 f'(x )单调递减得 > /(I ) =1,于是 y z ($)(— 1)<工一1,即 y (x )•— 1<久一1,或 f (兀)<工;当工e (1,1十厂 时1 vw <工,再由单调递减得1 =y'(i )>/"(£),于是 — 1) <工一1,即/•(#) — 1 V# — 1,或/(工)<工,应选(A ).(10) 【答案】(D ).【解】 从题设图形可见,在夕轴的左侧,曲线夕=/■&)是严格单调增加的,因此当工<0时,一定有于'(工)〉0,对应夕=于'(工)的图形必在工轴的上方,由此可排除(A ),(C ); 又的图形在y 轴右侧有三个零点,因此由罗尔中值定理可知,其导函数y=f\x )的图形在y 轴右侧一定有两个零点,进一步可排除(E ).应选(D ).三、解答题(11)【解】djr(2jc 12 + 1)丿兴 + ]1(]___\ 2 3_(1 + j//2 ) 2 ' 4工丿 (4jc + 1) 2Z )= 肿一 I = ~~2'sec 21(2tan 2i + 1 )sec tdtr cos tJ 2sinS + cosL弓豐將=arctan(sin/)+C=arctan .- + C.Jx 2 + 1(12) 【解】f(x ) =Sin "B ,nr = lim [(1 + $1叮一 sm ”)t-~x 'sin x / L 、 sin x /fCx)的间断点为工=kit (k e z),由lim/(j?) = e 得工=0为/(j :)的可去间断点;•z —*0由f (n — Q) — + °°,/(7r + 0) = 0得工=7T 为第二类间断点,同理工=kn(k 6 Z 且怡H0)为第二类间断点.(13) 【解】“=士,『=—— ,2 V j c 4工』工4«zdp _ dp / dj? ds ds / dr131••4( 4 工 +1)2--------------- ---------=6 J~x , 丿4无+ ]2 J~x6d 2 p d ( 6 \/~t ) /dj?2 \[x 6& $ ds/dx g + 1+ 12则^兽-伴)(4h +l)72一;… 一 — 36 无=9.J 4 无 + ](14)【解】gCt)dt x 2e 两边求导,得g[_f (j? )]/,(jc ) = (jc 2 +2工)『9 即) = (e + 2)e° 9积分得 /(^) = (h +1)『+ C9由 /(O) = 0 得 C = — 1,故/'(z ) = («z + 1)『一1.(15)【解】 由 g"Q ) = 2e J 一厂(2 )得 g 〃(H ) + g(z ) = 2e J ,解得 g (工)=C] cos x + C 2 sin x + e r ・ 由 g (0)=2 得 Ci = 1 ;由 g'(0) = 2 — /(0) = 2 得 C 2 = 19从而 g (jc ) = cos x + sin jr + e * 9 于是 fCx)= sin jc — cos 无 + e° ,rg(H )1 + zg (工)/(j ?)_1+乂 (1 + )2dj : +/(j : )d土)J 0g&) 1, fCx )i+7d " +TT7lo _Jg (#)1 +Ax_/(7T )_e n + 1= i + tt = 7t + r(16)r 解】(i )丨 op |=好 +$2,切线方程为Y —y =j/(X —乂),令X = 0,则切线在y 轴上的截距为Y = y — xy',由题意得y — xy' = Jx 2 + j^2,整理得字=2 — /1 + (―),dr jc \ \戈丿令u =—,则"+ z 学 =u — \/1 + z/2,变量分离得 d ----=——工 山 丿1 + / 工______ ______ 「积分得 ln(“ + \/m 2 + 1 ) = In C — In x ,即"+ a /m 2 + 1 = 一,x 再由 -“ + vV +1 =咅得“=*岸-咅),或$=*9 -青),因为曲线经过点(*,0),所以C=y,故所求曲线为夕=土一工2.(H)曲线汁* —在第一象限与两坐标轴所围成的面积为设切点为P1X 22) 9切线为y —=一 2a (jc 一 a ) 9令夕=0得z =二 + #;令工=0得,=++/oa z 4切线与L 及两个坐标轴围成的位于第一象限的面积为4a112 5Sa • 4a令s'++斜4a 2T + fl24a 24)=°得「古所求的切线方程为丿—(土―召),整理得(17)[解】 设/时刻雪堆的半径为r(Z ),r(0) =r 0,v 2 3 Q 9 2 dV 2 "V = —nr , o = Z7tr 9 -7— = Z7ir • —3 dt dtdV" d 厂由题意得不=TS,整理得不=T,解得")=f+c°,由厂(0)=厂 ° 得 C =r Q= —kt +r 09再由 r (3) = #•得怡=¥•,故 r ⑺=----t + r 0 ,Z令r (?) =0得t =6,故雪堆全部融化需要6小时.(18) ( I )【解】/(^)的带拉格朗日余项的一阶麦克劳林公式为/(J?) = /(0) + /''(0)工 + I ;£)乂2= /,(0)jf + [『力2,其中£介于0与工之间.(II )【证明】/(j : ) =/,(0)j' +食,)工2两边在[—a ,a ]上积分得[/(jc)dj- = _1_[ /7,($)2d:r ,J —au J —a因为f'\x )在[—a ,a ]上连续,所以f'\x )在[—a ,a ]上取到最小值m 和最大值M,由W */"(£)広2 C yMjr 2 得扌a 3 C yj 厂(£)工'dr < y-a 3 ,m ra m 3 f a即百^3 W /(工)clr W —a 3 9或 Tzz — /(j : )djc M ,3 J —a 3 a J —a由介值定理,存在少E [—a,a],使得/'"(可)=弓[/'(工)山,a J —a故 a "/■"(”)=3〕/ ( jc ) d j ?.(19)【解】 由 AXA +BXB =AXB + BXA + E 得(A -B)XCA -B) =E,解得 X = [(A -B)2]"1 ,/I — 1 — 1而A - B = 0 1 一 1'o 0 1/!-1一1\J 1(AB)2=01-11 0'001丿'0I 1_ 2-110°\I 1由01-2010 -* 0'0100J'0-1-1I 1-2一1\1-1=01-201/'o 01 100125\10012|得0100/]25\X =-012 •、00J(20)【解】0] ,p 2,“3,04为AX =0的基础解系的充分必要条件是01 ,庆,/h ,力线性无关,1t0100t '而(01 902 9 03,04)=(。
2001-数二真题、标准答案及解析

(A)1.
(B)2.
(C)3.
(D)4. 【】
【答】 应选(B).
【详解] 由题设,知
( ) (1− cos x) ln 1+ x2
lim
x→0
x sin xn
= lim x→0
1 x2 ⋅ x2 2
x ⋅ xn
=
1 lim
2 x→0
1 xn−3
=
1 lim x3−n 2 x→0
= 0.
n应满足 n ≤ 2;
求 f (x).
【详解】 等式两边对 x 求导得
g ⎡⎣ f ( x)⎤⎦ f ' ( x) = 2xex + x2ex
而
g ⎡⎣ f ( x)⎤⎦ = x,
故
xf ' ( x) = 2xex + x2ex .
当 x ≠ 0 时,有
f ' ( x) = 2ex + xex
积分得
f ( x) = ( x +1) ex + C
抛物线上介于点
A(1,1) 与
M
之间的弧长,计算 3ρ
d2ρ ds2
−
⎛ ⎜⎝
dρ ds
⎞2 ⎟⎠
的值.(在直角坐标系下曲
y ''
率公式为 K =
)
3
( ) 1+ y'2 2
【详解】 y' = 1 , y'' = − 1 ,
2x
4 x3
抛物线在点 M ( x, y)( x ≥ 1) 处三维曲率半径
3
【】
于是
f ⎡⎣ f ( x)⎤⎦ = 1,
{ } 从而 f f ⎡⎣( x)⎤⎦ = 1.
数学分析课本-习题及答案01

第一章 实数集与函数习题§1实数1、 设a 为有理数,x 为无理数。
证明:(1)a+ x 是无理数;(2)当a ≠0时,ax 是无理数。
2、 试在数轴上表示出下列不等式的解:(1)x (2x -1)>0;(2)|x-1|<|x-3|;(3)1-x -12-x ≥23-x 。
3、 设a 、b ∈R 。
证明:若对任何正数ε有|a-b|<ε,则a = b 。
4、 设x ≠0,证明|x+x1|≥2,并说明其中等号何时成立。
5、 证明:对任何x ∈R 有(1)|x-1|+|x-2|≥1;(2)|x-1|+|x-2|+|x-3|≥2。
6、 设a 、b 、c ∈+R (+R 表示全体正实数的集合)。
证明 |22b a +-22c a +|≤|b-c|。
你能说明此不等式的几何意义吗7、 设x>0,b>0,a ≠b 。
证明x b x a ++介于1与ba 之间。
8、 设p 为正整数。
证明:若p 不是完全平方数,则p 是无理数。
9、 设a 、b 为给定实数。
试用不等式符号(不用绝对值符号)表示下列不等式的解:(1)|x-a|<|x-b|;(2)|x-a|< x-b ;(3)|2x -a|<b 。
§2数集、确界原理1、 用区间表示下列不等式的解:(1)|1-x|-x ≥0;(2)| x+x1|≤6; (3)(x-a )(x-b )(x-c )>0(a ,b ,c 为常数,且a<b<c );(4)sinx ≥22。
2、 设S 为非空数集。
试对下列概念给出定义:(1)S 无上界;(2)S 无界。
3、 试证明由(3)式所确定的数集S 有上界而无下界。
4、 求下列数集的上、下确界,并依定义加以验证:(1)S={x|2x <2};(2)S={x|x=n !,n ∈+N };(3)S={x|x 为(0,1)内的无理数};(4)S={x|x=1-n21,n ∈+N }。
