江苏省梅村高级中学2013-2014学年高一下学期期中考试数学试题
江苏省梅村高级中学2023-2024学年高一下学期3月月考数学试题
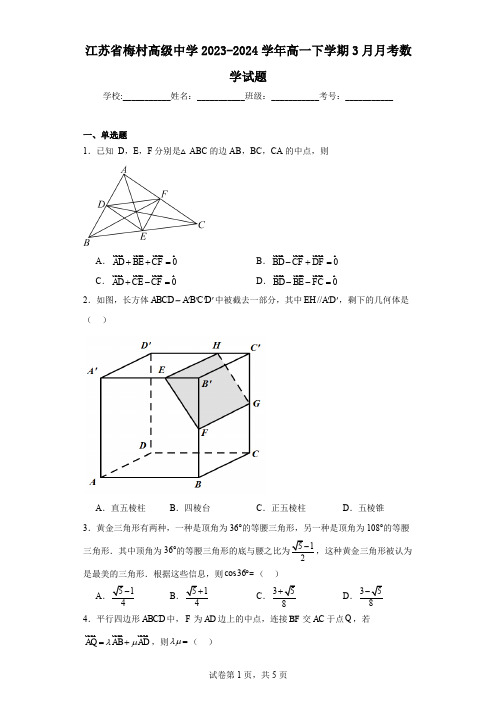
江苏省梅村高级中学2023-2024学年高一下学期3月月考数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知 D ,E ,F 分别是△ABC 的边AB ,BC ,CA 的中点,则A .0AD BE CF ++=u u u r u u u r u u u r rB .0-+=u u u r u u u r u u u r r BD CF DFC .0+-=u u u r u u u r u u u r r AD CE CF D .0--=u u u r u u u r u u u r r BD BE FC2.如图,长方体ABCD A B C D -''''中被截去一部分,其中//EH A D '',剩下的几何体是( )A .直五棱柱B .四棱台C .正五棱柱D .五棱锥3.黄金三角形有两种,一种是顶角为36°的等腰三角形,另一种是顶角为108°的等腰三角形.其中顶角为36°,这种黄金三角形被认为是最美的三角形.根据这些信息,则cos36︒=( )A B C D 4.平行四边形ABCD 中,F 为AD 边上的中点,连接BF 交AC 于点Q ,若AQ AB AD λμ=+u u u r u u u r u u u r,则λμ=( )A .1B .56C .13D .195.在ABC V 中,角,,A B C 所对的边分别为,,a b c ,且π8,6c B ==.若ABC V 有两解,则b 的值可以是( )A .4B .5C .8D .106.一质点受到平面上的三个力123,,F F F (单位:牛顿)的作用而处于平衡状态.已知12,F F 成060角,且12,F F 的大小分别为2和4,则3F 的大小为 A .6B .2C.D.7.已知a r ,b r 是两个互相垂直的单位向量,则向量2a b -r r 在向量b r 上的投影向量为( )A .b rB .2b -rC .12b -rD .b -r8.在ABC V 中,角,,A B C 所对的边分别为,,a b c ,2sin sin 3sin a A b B c C -=,若S 表示ABC V 的面积,则2Sb 的最大值为( ) ABCD二、多选题9.已知△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,下列命题中正确的有( ) A .若cos cos cos a b cA B C==,则△ABC 一定是等边三角形 B .若22tan tan a B b A =,则△ABC 一定是等腰三角形 C .A B >是sin sin A B >成立的充要条件D .若2220a b c +->,则△ABC 一定是锐角三角形 10.下列关于向量的命题正确的是( )A .非零向量,,,a b c r r r 满足a b b c r r r r//,//,则a c r r ∥B .向量a b r r ,共线的充要条件是存在实数λ,使得b a λ=r r成立C .与向量()3,4a =-r 同向的单位向量为34,55⎛⎫- ⎪⎝⎭D .若()()3,12,AB AC m BAC ==∠u u u r u u u r,,为锐角,则实数m 的范围是()6,-+∞ 11.点O ,H 分别是ABC V 的外心、垂心,则下列选项正确的是( )A .若||||BA BC BD BA BC λ⎛⎫=+ ⎪⎝⎭u u u r u u u ru u u r u u u r u u u r 且(1)BD BA BC μμ=+-u u ur u u u r u u u r ,则AD DC =u u u r u u u rB .若2BO BA BC =+u u u r u u u r u u u r ,且2AB =,则4AC AB ⋅=u u u r u u u rC .若π3B ∠=,OB mOA nOC =+u u ur u u u r u u u r ,则m n +的取值范围为[)2,1-D .若2340HA HB HC ++=u u u r u u u r u u u r r ,则cos BHC ∠=三、填空题12.如图所示,水平放置的ABC V 斜二测直观图是图中的A B C '''V ,已知46A C B C ''=''=,,则ABC V 的面积为.13.折扇又名“撒扇”、“纸扇”,是一种用竹木或象牙做扇骨,韧纸或绫绢做扇面的能折叠的扇子,如图1.其展开几何图是如图2的扇形AOB ,其中120AOB ∠=︒,2OC =,5OA =,点E 在»CD上,则EA EB ⋅u u u r u u u r的最小值是.14.如图所示,四边形ABCD 中,7AC AD CD ===,120ABC ︒∠=,sin BAC ∠=,则ABC ∆的面积为,BD =.四、解答题15.已知()()4,3,23261a b a b a b ==-⋅+=r r r r r r .(1)求a r 与b r的夹角;(2)求a b +r r ;(3)若()()2a kb ka b ++r r r r//,求实数k 的值.16.已知ABC V 的内角A ,B ,C 的对边分别为a ,b ,c ,∠A 的平分线交BC 于点D ,且()1cos cos cos 02A cB bC a ++=.(1)求A :(2)若7a =,ABC V 的周长为15,求AD 的长.17.在①(sin sin )()(sin sin )a A C b c B C -=-+,②2cos()3b C ac π-=+, ③向量(1cos )m B C =+r与(,)n c b =-r ,且m n ⊥r r ,三个条件中选一个填在下面试题的横线上,并加以解析. 在ABC V 中,,,a b c 分别是内角,,A B C 所对的边,且___________. (1)求角B 的大小;(2)若ABC V 是钝角三角形,且b a c +的取值范围.18.某校高中“数学建模”实践小组欲测量某景区位于:“观光湖”内两处景点A ,C 之间的距离,如图,B 处为码头入口,D 处为码头,BD 为通往码头的栈道,且100m BD =,在B 处测得π6π4ABD CBD ∠=∠=,,在D 处测得2π3π34BDC ADC ∠=∠=,.(A ,B ,C ,D 均处于同一测量的水平面内)(1)求A ,C 两处景点之间的距离;(2)栈道BD 所在直线与A ,C 两处景点的连线是否垂直?请说明理由.19.如图,在ABC V 中,已知41060AB AC BAC ==∠=︒,,,BC 边上的中点为M ,AC 边上的中点为N ,AM ,BN 相交于点P .(1)求BC;的余弦值;(2)求MPNV分成的上下两部分图形的(3)过点P作直线交边AB,BC于点E,F,求该直线将ABC面积之比的取值范围.。
江苏省无锡市梅村高级中学2020-2021学年高一下学期第一次月考数学试题

江苏省无锡市梅村高级中学2020-2021学年高一下学期第一次月考数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题 1.已知312iz i-=-,则z 的虚部是( ) A .iB .i -C .1D .1-2.在ABC 中,E 为AB 边的中点,D 为AC 边上的点,BD ,CE 交于点F .若3177AF AB AC =+,则 AC AD 的值为( ) A .2 B .3 C .4 D .53.在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,若3B π=,6b =,sin 2sin 0A C -=,则a =A .3B .C .D .124.加强体育锻炼是青少年生活学习中非常重要的组成部分.某学生做引体向上运动,处于如图所示的平衡状态时,若两只胳膊的夹角为60︒,每只胳膊的拉力大小均为400N ,则该学生的体重(单位:kg )约为( )(参考数据:取重力加速度大小为210/ 1.732g m s ≈=) A .63B .69C .75D .815.如图所示,平面四边形ABCD 中,90BCD ∠=︒,135ABC ∠=︒,AB 6=,AC =CD =ABCD 的面积为( )A .39B .36C .42D .486.已知锐角ABC 三边长分别为x 1x +,则实数x 的取值范围为( ) A .()1,2B .()2,3C .2,25⎛⎫ ⎪⎝⎭D .()2,57.点M 是边长为2的正六边形ABCDEF 内或《晓观数学》公众号边界上一动点,则AB AM ⋅的最大值与最小值之差为( )A .2B .4C .6D .88.设点P 为ABC ∆内一点,且220PA PB PC ++=,则:ABP ABC S S ∆∆=( )A .15B .25C .14D .13二、多选题9.已知复数122i z =-(i 为虚数单位)在复平面内对应的点为1P ,复数2z 满足2i 1z -=,则下列结论正确的是( ) A .1P 点的坐标为()2,2- B .122i z =+(1z 为1z 的共轭复数)C .21z z -D .21z z -的最小值为10.在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,则下列各组条件中使得ABC 有唯一解的是( )A .3a =,c =2cos 3C = B .3a =,4c =,1cos 3C = C .1a =,4b =,2sin 3B =D .1b =,1sin 3B =,3C π=11.若ABC 内接于以O 为圆心,1为半径的圆,且3450++=OA OB OC ,则下列结论不正确的是( ) A .2BOC π∠=B .2AOB π∠=C .45OB CA ⋅=-D .15OC AB ⋅=-12.在△ABC 中,A ,B ,C 的对边分别为a ,b ,c ,且c =6.记S 为△ABC 的面积,下列命题正确的是( )A .若3C π=,则S 有最大值B .若6A a π==,S 有最小值C .若a =2b ,则cos C 有最小值0 D .若a +b =10,则sin C 有最大值2425三、填空题13.已知复数24z i =+,其中i 是虚数单位,2(1)=1z z ω-+,则=ω_________.14.若1,2,a b a ==与b 的夹角为60°,若()()35a b ma b +⊥-,则实数m 的值为_______.15.在ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,若sin sin 02c A C π⎛⎫+= ⎪⎝⎭,6c ==,且点M 满足13AM AB =,则CM 的长为___________.16.赵爽是我国古代数学家大约在公元222年,他为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形由4个全等的直角三角形再加上中间的一个小正方形组成)类比“赵爽弦图”,可构造如图所示的图形,它是由3个全等的三角形与中间一个小等边三角形拼成的一个较大的等边三角形,设AD AB AC λμ=+,若2DF AF =,则可以推出λμ+=_________.四、解答题17.已知向量(3,2)a =-,(2,1)=b ,(3,1)c =-,,m t ∈R . (1)求||a tb +的最小值及相应的t 的值; (2)若a mb -与c 共线,求实数m .18.已知复数z 满足34i 13i z ++=+. (1)求z ;(2)求()()21i 43i 2z++的值.19.在ABC 中, a b c 、、分别为内角、、A B C 的对边,且2sin (2)sin (2)sin a A b c B c b C =+++(Ⅰ)求A 的大小;(Ⅱ)若sin sin 1B C +=,试判断ABC 的形状.20.如图,在矩形ABCD 中,36BC AB ==,E 为AB 的中点,F 是BC 边上靠近点B 的三等分点,AF 与DE 于点G .设AB a =,AD b =.(1)求EGF ∠的余弦值; (2)用a 和b 表示AG .21.在ABC 中,2BAC π∠=,点D 在边BC 上,满足=AB .(1)若6BAD π∠=,求C ∠;(2)若2,4CD BD AD ==,求ABC 的面积.22.在气象台A 正西方向300km 处有一台风中心,它正向东北方向移动,移动速度的大小为40km/h ,距台风中心250km 以内的地区都将受到影响,若台风中心的这种移动趋势不变,气象台所在地是否会受到台风的影响?如果会,大约多长时间后受到影响?持续时间有多长(精确到1min1.4142.646)参考答案1.D 【分析】根据复数除法运算化简z ,由共轭复数定义得到z ,由虚部定义得到结果. 【详解】()()()()31235511212125i i i i z i i i i -+-+====+--+,1z i ∴=-, z ∴的虚部为1-.故选:D. 2.C 【分析】设AC AD λ=,可得3177AF AB AD λ=+,由B ,F ,D 三点在同一条直线上,可求得λ的值,即可得解. 【详解】 设AC AD λ=, 因为3177AF AB AC =+, 所以3177AF AB AD λ=+, 因为B ,F ,D 三点在同一条直线上, 所以31177λ+=,所以4λ=,所以4ACAD=. 故选:C 3.C 【分析】先根据正弦定理得2a c =,再根据余弦定理列方程解得结果. 【详解】因为sin 2sin 0A C -=,所以由正弦定理得2a c =,因此2222222cos 362cos 48,423a ab ac ac B a a a a π=+-∴=+-⨯∴== C.【点睛】解三角形问题,多为边和角的求值问题,这就需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系,从而达到解决问题的目的. 4.B 【分析】根据平行四边形法则得到该学生的体重||||G F '=,利用余弦定理即可求出||F '得解. 【详解】如图,设该学生的体重为G ,则G F '=.由余弦定理得22222||4004002400400cos()3400,||3F F π''=+-⨯⨯⨯=⨯∴=所以||69G =≈kg . 故选:B 【点睛】本题主要考查向量的平行四边形法则和余弦定理解三角形,意在考查学生对这些知识的理解掌握水平. 5.A 【分析】题意题意,四边形ABCD 的面积ABC 和ACD △面积之和,ABC 中,由正弦定理,sin sin AC AB =ABC BCA ∠∠,求得sin cos ACD ∠∠, cos sin BCA ACD ∠=∠,再由90BCD ∠=︒,可得sin cos ACD ∠∠,结合面积公式即可得解. 【详解】在ABC 中,由正弦定理,sin sin AC AB=ABC BCA∠∠,解得sin cos ACD ∠∠,cos sin BCA ACD ∠==∠, 由余弦定理,2222cos AC AB BC AB BC ABC =+-⋅⋅∠,即2540BC +-=,解得BC = 则ABCD 的面积11sin sin 3922ABC ACD S S S AB BC ABC AC CD ACD =+=⋅⋅∠+⋅⋅∠=△△, 故选:A . 6.A 【分析】利用余弦定理建立不等式,解不等式求出实数x 的取值范围. 【详解】显然边长x <x +1,1x +的对角均为锐角即可,由余弦定理得:()()222215021510x x x x x x ⎧++->⎪+⎪⎨⎪+-+>,解得:12x <<. 故选:A 【点睛】已知三边,判断是锐角三角形还是钝角三角形的方法:①如果一个三角形的最长边平方=其他两边的平方和,这个三角形是直角三角形; ②如果一个三角形的最长边平方>其他两边的平方和,这个三角形是钝角三角形; ③如果一个三角形的最长边平方<其他两边的平方和,这个三角形是锐角三角形; ④特别地:如果一个三角形的三条边相等,这个三角形是等边三角形,也是锐角三角形。
2014-2015学年高一下学期期中考试数学试卷-Word版含答案

2014-2015学年高一下学期期中考试数学试卷-Word版含答案2014——2015学年下学期高一年级期中考数学学科试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 不等式0121≤+-x x 的解集为( )A.⎝ ⎛⎭⎪⎫-∞,-12∪[1,+∞) B.⎣⎢⎡⎦⎥⎤-12,1C.⎝ ⎛⎦⎥⎤-∞,-12∪[1,+∞) D. ⎝ ⎛⎦⎥⎤-12,12. 若0<<b a ,则下列不等式不能成立的是 ( ) A.ba11> B .b a 22> C .b a > D .b a )21()21(> 3. 不等式16)21(1281≤<x 的整数解的个数为 ( )A .10B .11C .12D .134. 等差数列{}n a 中,如果39741=++a a a ,27963=++a a a ,则数列{}n a 前9项的和为( )A .297B .144C .99D .665. 已知直线1l :01)4()3(=+-+-y k x k 与2l :032)3(2=+--y x k 平行,则k 的值是( )A .1或3B .1或5C .3或5D .1或26. 在△ABC 中,80=a ,70=b ,45=A ,则此三角形解的情况是 ( ) A 、一解 B 、两解 C 、一解或两解 D 、无解7. 如果0<⋅C A ,且0<⋅C B ,那么直线0=++C By Ax 不通过( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限8.已知点()5,x 关于点),1(y 的对称点为()3,2--,则点()y x p ,到原点的距离为( )A .4B .13C .15D .179. 计算机是将信息转换成二进制进行处理的,二进制即“逢二进一”,如(1 101)2表示二进制数,将它转换成十进制数是1×23+1×22+0×21+1×20=13,那么将二进制数(11…114个01)2转换成十进制数是( )A .216-1B .216-2C .216-3D .216-4 10. 数列{}n a 满足21=a ,1111+-=++n n n a a a ,其前n 项积为n T ,则=2014T ( ) A.61B .61- C .6 D .6- 11. 已知0,0>>y x ,且112=+yx,若m m y x 222+>+恒成立,则实数m 的取值范围是( )A .(-∞,-2]∪[4,+∞)B .(-2,4)C .(-∞,-4]∪[2,+∞)D .(-4,2) 12. 设数列{}n a 的前n 项和为n S ,令nS S S T nn +++=21,称n T 为数列n a a a ,,,21 的“理想数”,已知数列50021,,,a a a 的“理想数”为2004,那么数列12,50021,,,a a a 的“理想数”为( ) A .2012 B .2013 C .2014 D .2015第Ⅱ卷(非选择题 共90分)19.(12分) 已知直线l 过点)2,3(P ,且与x 轴、y 轴的正半轴分别交于A ,B 两点,如图所示,求OAB ∆的面积的最小值及此时直线l 的方程.20. (12分) 某观测站C 在城A 的南偏西20˚的方向上,由A 城出发有一条公路,走向是南偏东40˚,在C 处测得距C 为31千米的公路上B 处有一人正沿公路向A 城走去,走了20千米后,到达D 处,此时C 、D 间距离为21千米,问还需走多少千米到达A 城?21. (12分) 在各项均为正数的等差数列{}n a 中,对任意的*N n ∈都有12121+=+++n n n a a a a a . (1)求数列{}n a 的通项公式n a ;(2)设数列{}n b 满足11=b ,na n nb b 21=-+,求证:对任意的*N n ∈都有212++<n n n b b b .22. (12分)设函数())0(132>+=x xx f ,数列{}n a 满足11=a ,)1(1-=n n a f a ,*N n ∈,且2≥n .(1)求数列{}n a 的通项公式; (2)对*N n ∈,设13221111++++=n n n a a a a a a S ,若ntS n 43≥恒成立,求实数t 的取值范围.答案一、选择题:(每题5分,共60分)13、 3 14、349π15、 2 16、 ①②⑤三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17. 解:(1)由题意,得⎩⎪⎨⎪⎧a 3a 6=55,a 3+a 6=a 2+a 7=16.∵公差d>0,∴⎩⎪⎨⎪⎧a 3=5,a 6=11,∴d =2,a n =2n -1.(2)∵b n =a n +b n -1(n≥2,n ∈N *), ∴b n -b n -1=2n -1(n≥2,n ∈N *).∵b n =(b n -b n -1)+(b n -1-b n -2)+…+(b 2-b 1)+b 1(n≥2,n ∈N *),且b 1=a 1=1,∴b n =2n -1+2n -3+…+3+1=n 2(n≥2,n ∈N *). ∴b n =n 2(n ∈N *).题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 D BBCCACDCDDA18. 解析 27(1)4sin cos 2180,:22B C A A B C +-=++=︒由及得 22272[1cos()]2cos 1,4(1cos )4cos 5214cos 4cos 10,cos ,20180,60B C A A A A A A A A -+-+=+-=-+=∴=︒<<︒∴=︒即 22222222(2):cos 211cos ()3.2223123,3: 2 :.221b c a A bcb c a A b c a bc bc b c b b a b c bc bc c c +-=+-=∴=∴+-=+===⎧⎧⎧=+==⎨⎨⎨===⎩⎩⎩由余弦定理得代入上式得由得或 19. 解:由题意设直线方程为x a +y b =1(a >0,b >0),∴3a +2b =1.由基本不等式知3a +2b ≥26ab,即ab≥24(当且仅当3a =2b,即a =6,b =4时等号成立).又S =12a ·b ≥12×24=12,此时直线方程为x 6+y4=1,即2x +3y -12=0.∴△ABO 面积的最小值为12,此时直线方程为2x +3y -12=0. 20. 解 据题意得图02,其中BC=31千米,BD=20千米,CD=21千米,∠CAB=60˚.设∠ACD = α ,∠CDB = β . 在△CDB 中,由余弦定理得:71202123120212cos 222222-=⨯⨯-+=⋅⋅-+=BD CD BC BD CD β,734cos 1sin 2=-=ββ.()CDA CAD ∠-∠-︒=180sin sin α ()β+︒-︒-︒=18060180sin()143523712173460sin cos 60cos sin 60sin =⨯+⨯=︒-︒=︒-=βββ在△ACD 中得1514352321143560sin 21sin sin =⨯=⋅︒=⋅=αA CD AD . 所以还得走15千米到达A 城. 21. 解:(1)设等差数列{a n }的公差为d.令n =1,得a 1=12a 1a 2.由a 1>0,得a 2=2.令n =2,得a 1+a 2=12a 2a 3,即a 1+2=a 1+2d ,得d =1.从而a 1=a 2-d =1.故a n =1+(n -1)·1=n. (2)证明:因为a n =n ,所以b n +1-b n =2n ,所以b n =(b n -b n -1)+(b n -1-b n -2)+…+(b 2-b 1)+b 1 =2n -1+2n -2+…+2+1 =2n -1.又b n b n +2-b 2n +1=(2n -1)(2n +2-1)-(2n +1-1)2=-2n <0, 所以b n b n +2<b 2n +1.22. 解:(1)由a n =f ⎝⎛⎭⎪⎫1a n -1,可得a n -a n -1=23,n ∈N *,n≥2.所以{a n }是等差数列.又因为a 1=1,所以a n =1+(n -1)×23=2n +13,n ∈N *.(2)因为a n =2n +13,所以a n +1=2n +33,所以1a n a n +1=92n +12n +3=92⎝⎛⎭⎪⎫12n +1-12n +3.所以S n =92⎝ ⎛⎭⎪⎫13-12n +3=3n 2n +3,n ∈N *. S n ≥3t 4n ,即3n 2n +3≥3t 4n ,得t≤4n 22n +3(n ∈N *)恒成立.令g(n)=4n 22n +3(n ∈N *),则g(n)=4n 22n +3=4n 2-9+92n +3=2n +3+92n +3-6(n ∈N *).令p =2n +3,则p≥5,p ∈N *.g(n)=p +9p -6(n ∈N *),易知p =5时,g(n)min =45.所以t≤45,即实数t 的取值范围是⎝⎛⎦⎥⎤-∞,45.。
江苏省无锡市梅村高级中学2018年高一数学理下学期期末试题含解析

江苏省无锡市梅村高级中学2018年高一数学理下学期期末试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知集合A与B都是集合U的子集,那么如图中阴影部分表示的集合为()A.A∩B B.A∪B C.?U(A∪B)D.?U(A∩B)参考答案:C【考点】Venn图表达集合的关系及运算.【分析】阴影部分所表示的为不在集合B中也不在集合A中的元素构成的部分【解答】解:阴影部分所表示的为不在集合B中也不在集合A中的元素构成的部分,故阴影部分所表示的集合可表示为?U(A∪B),故选:C2. 已知集合A={1,2,3},B={(x,y)|x∈A,y∈A,x+y∈A},则B中所含元素的个数为()A.2 B.3 C.4 D.6参考答案:B【考点】12:元素与集合关系的判断.【分析】本题的关键是根据A={1,2,3},B={(x,y)|x∈A,y∈A,x+y∈A},写出集合B,并且找到集合B的元素个数【解答】解:∵A={1,2,3},B={(x,y)|x∈A,y∈A,x+y∈A},∴B={(1,1),(1,2),(2,1)}则B中所含元素的个数为:3故选:B3. 将函数y=sinx图象上所有的点向左平移个单位长度,再将图象上所有的点的横坐标伸长到原来的2倍(纵坐标不变),则所得图象的函数解析式为()A.B.C.D.参考答案:A【考点】HJ:函数y=Asin(ωx+φ)的图象变换.【分析】第一次变换得到函数y=sin(x+)的图象,再进行第二次变换得到函数y=sin(x+)的图象,由此得出论.【解答】解:将函数y=sinx图象上所有的点向左平移个单位长度,得到函数y=sin(x+)的图象,再将图象上所有的点的横坐标伸长到原来的2倍(纵坐标不变),可得函数y=sin(x+)的图象,故所求函数的解析式为,故选A.4. 过点M(﹣2,m)、N(m,4)的直线的斜率等于1,则m的值为()A.1 B.4 C.1或3 D.1或4参考答案:A【考点】直线的斜率.【分析】根据斜率k=,直接求出m 的值.【解答】解:过点M(﹣2,m)、N(m,4)的直线的斜率等于1,所以k===1解得m=1故选A5. cos390°的值为()A.B.C.D.参考答案:A6. 向量,且,则()A. B. C. D.参考答案:C【分析】先根据求出的值,再利用诱导公式化简即得解.【详解】因为,所以,所以.所以.故选:C【点睛】本题主要考查向量平行的坐标表示和诱导公式,意在考查学生对这些知识的理解掌握水平和分析推理能力.7. 设m,n是两条不同的直线,α,β是两个不同的平面,下列命题正确的是()A.m⊥α,n⊥β,且α⊥β,则m⊥n B.m∥α,n∥β,且α∥β,则m∥nC.m⊥α,n?β,m⊥n,则α⊥βD.m?α,n?α,m∥β,n∥β,则α∥β参考答案:A【考点】空间中直线与平面之间的位置关系.【分析】利用线面垂直、面面垂直的性质定理和判定定理对选项分别分析选择.【解答】解:对于A,m⊥α,n⊥β,且α⊥β,利用面面垂直的性质定理得到作垂直于交线的直线n'与β垂直,又n⊥β,得到n∥n',又m⊥α,得到m⊥n',所以m⊥n;故A正确;对于B,m∥α,n∥β,且α∥β,则m与n位置关系不确定,可能相交、平行或者异面;故B错误;对于C,m⊥α,n?β,m⊥n,则α与β可能平行;故C错误;对于D,m?α,n?α,m∥β,n∥β,则α与β可能相交;故D错误;故选:A.8. 若函数都是奇函数,且在上有最大值6,则在上()A.有最小值-2 B.有最大值-5C.有最小值-1 D.有最大值-3参考答案:A略9. 如图给出的是计算的值的一个程序框图,则图中判断框内(1)处和执行框中的(2)处应填的语句是()A. B.C. D.参考答案:C10. 某校为了解1000名高一新生的身体生长状况,用系统抽样法(按等距的规则)抽取40名同学进行检查,将学生从1~1000进行编号,现已知第18组抽取的号码为443,则第一组用简单随机抽样抽取的号码为()A.16 B.17 C.18 D.19参考答案:C二、填空题:本大题共7小题,每小题4分,共28分11. 下图是一个四棱锥的三视图,那么该四棱锥的体积是________;参考答案:略12. 若=,=,则在上的投影为________________。
【首发】江苏省盐城市2013-2014学年高一下学期期终考试数学(三星)Word版含答案

三星高中使用2013/2014学年度第二学期高一年级期终考试数 学 试 题注意事项:1.本试卷考试时间为120分钟,试卷满分160分,考试形式闭卷. 2.本试卷中所有试题必须作答在答题卡上规定的位置,否则不给分.3.答题前,务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上. 参考公式:柱体体积公式:V Sh =一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上. 1.直线30x y -+=在y 轴上的截距为 ▲ . 2.若角α的终边经过点(3,2)P ,则tan α的值为 ▲ .3.已知圆柱的底面半径为1,母线长与底面的直径相等,则该圆柱的体积为 ▲ . 4.已知点)2,1(A ,)5,3(B ,向量()=,6a x ,若a //AB ,则实数x 的值为 ▲ . 5.过点(2,1)A ,且与直线230x y -+=平行的直线方程为 ▲ .6.已知向量与的夹角为120,且||2a =,1||=b ,则=+|2|b a ▲ . 7.若等比数列{}n a 的前n 项和为n S ,且141,8a a ==,则5S = ▲ . 8.若54)6sin(=+πx ,则=-)3cos(πx ▲ .9.直线+10x +=被圆032:22=--+x y x C 截得的弦长为 ▲ .10.设,m n 是两条不同的直线,βα,是两个不重合的平面,给定下列四个命题: ①若n m ⊥,α⊂n ,则α⊥m ; ②若m α⊥,m β⊂,则βα⊥; ③若α⊥m ,α⊥n ,则n m //; ④若α⊂m ,β⊂n ,βα//,则n m //. 其中真命题的序号为 ▲ .11.在ABC ∆中,角C B A ,,所对的边分别为c b a ,,,若4=a ,2=b ,31cos =A ,则B sin 的值为▲ .12.在平面直角坐标系xOy 中,若圆C 的圆心在第一象限,圆C 与x 轴相交于(1,0)A 、(3,0)B 两点,且与直线01=+-y x 相切,则圆C 的标准方程为 ▲ .13.若数列{}n a 是一个单调递减数列,且2=n a n n λ+,则实数λ的取值范围是 ▲ .14.已知点()5,0A -,()1,3B --,若圆()2220x y r r +=>上恰有两点M ,N ,使得MAB ∆和NAB ∆ 的面积均为5,则r 的取值范围是 ▲ .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分)如图,在三棱锥P ABC -中,90ABC ∠=,PA ⊥平面ABC ,E ,F 分别为PB ,PC 的中点. (1)求证://EF 平面ABC ; (2)求证:平面AEF ⊥平面PAB .16.(本小题满分14分)已知函数()22sin cos f x x x x =+,x R ∈. (1)求函数()f x 的最小正周期; (2)求函数()f x 在区间⎥⎦⎤⎢⎣⎡4,0π上的值域. 17.(本小题满分14分)在四边形ABCD 中,已知9=AB ,6=BC ,PD CP 2=. (1)若四边形ABCD 是矩形,求BP AP ⋅的值;(2)若四边形ABCD 是平行四边形,且6=⋅BP AP ,求AB 与AD 夹角的余弦值.A18.(本小题满分16分)为绘制海底地貌图,测量海底两点C ,D 间的距离,海底探测仪沿水平方向在A ,B 两点进行测量,A ,B ,C ,D 在同一个铅垂平面内. 海底探测仪测得30,BAC ∠=45,DAC ∠=45,ABD ∠=75,DBC ∠=A ,B 两点的距离为3海里.(1)求ABD ∆的面积; (2)求C ,D 之间的距离.19.(本小题满分16分)设n S 是数列{}n a 的前n 项和,且22n n a S An Bn C +=++.(1)当0A B ==,1C =时,求n a ;(2)若数列{}n a 为等差数列,且1A =,2C =-. ①求n a ;②设=2n n n b a ,求数列{}n b 的前n 项和n T .DCBA20.(本小题满分16分)已知圆O 的方程为1322=+y x ,直线:l 00+13x x y y =,设点00(,)A x y .(1)若点A 为()34,,试判断直线l 与圆C 的位置关系; (2)若点A 在圆O 上,且02x =,00y >,过点A 作直线,AM AN 分别交圆O 于,M N 两点,且直线AM 和AN 的斜率互为相反数.①若直线AM 过点O ,求直线MN 的斜率;②试问:不论直线AM 的斜率怎样变化,直线MN 的斜率是否为定值?若是,求出该定值;若不是,说明理由.三星高中使用高一数学试题参考答案一、填空题:每小题5分,共计70分. 1.3 2.23 3.2π 4.4 5.230x y --= 6.2 7. 31 8.549. 10.②③ 11.32 12.2)1()2(22=-+-y x 13.1(,)3-∞- 14.()15,二、解答题:本大题共6小题,共计90分.15.证明:(1)在PBC ∆中,F E , 分别为PC PB ,的中点BC EF //∴………………3分 又⊂BC 平面ABC ,⊄EF 平面ABC //EF ∴平面ABC …………………………………7分(2)由条件,⊥PA 平面ABC ,⊂BC 平面ABCBC PA ⊥∴︒=∠90ABC ,即BC AB ⊥,………………………………………………10分 由//EF BC ,∴EF AB ⊥,EF PA ⊥又A AB PA =⋂,AB PA ,都在平面PAB 内 EF ∴⊥平面PAB又⊂EF 平面AEF ∴平面AEF ⊥平面PAB ………………………………………………14分16.解: (1)由条件可得sin 22sin(2)3y x x x π+=+,……………………………4分所以该函数的最小正周期22T ππ==………………………………………………………6分 (2)⎥⎦⎤⎢⎣⎡∈4,0πx ,⎥⎦⎤⎢⎣⎡∈+∴65,332πππx ,……………………………………………………8分 当12π=x 时,函数y 取得最大值为2,当4π=x 时,函数y 取得最小值为1∴函数y 的值域为[]2,1…………………………………………………………………………14分17.解:(1)因为四边形ABCD 是矩形,所以0=⋅由PD CP 2=得:DC DP 31=,3232-==.………………………………3分 ∴ BP AP ⋅)()(CP BC DP AD +⋅+=)32()31(-⋅+=229231-⋅-=18819236=⨯-=.………………………………7分(2)由题意,DP AD AP +=AB AD DC AD 3131+=+=3232-=+=+=∴ )32()31(-⋅+=⋅221239AD AB AD AB =-⋅-136183AB AD =-⋅-1183AB AD =-⋅………………………………………………10分 又6=⋅BP AP ,∴ 11863AB AD -⋅=, ∴ 36AB AD ⋅=.又θθθcos 54cos 69=⨯⨯==⋅AD AB ∴ 54cos 36θ=,即2cos 3θ=.(利用坐标法求解,同样给分)………………………14分 18.解:(1)如图所示,在ABD ∆中︒=︒+︒=∠+∠=∠754530DAC BAC BAD ︒=∠∴60ADB由正弦定理可得,ABDADADB AB ∠=∠sin sin ,260sin 45sin 3=︒︒=AD …………………4分 则ABD ∆的面积11sin 22S AB AD BAD =⋅∠==(平方海里)…………8分 (2)︒=︒+︒=∠+∠=∠1207545DBC ABD ABC ,︒=∠=∠30BCA BAC3==∴AB BC 3=∴AC …………………………………………………………………12分在ACD ∆中,由余弦定理得,5cos 2222=∠⋅-+=DAC AD AC AD AC CD即5=CD (海里)答:ABD ∆的面积为433+平方海里,C ,D 间的距离为5海里.……………………16分 19.解:(1)由题意得,21n n a S +=,∴1121(2)n n a S n --+=≥,两式相减,得123n n a a -=,……………………………………………………………………3分 又当1n =时,有131a =,即113a =,∴数列{}n a 为等比数列,∴112=33n n a -⎛⎫⎪⎝⎭.………………………………………………5分(2)①Q 数列{}n a 为等差数列,由通项公式与求和公式,得2211113222(1)()()222222n n d d d da S a n d n a n n a n a d +=+-++-=+++-,Q 1,2A C ==-, ∴12d=,12a d -=-,∴2d =,11a =,∴21n a n =-.………10分②由题()=2=212n n n n b a n -,()121232212n n T n =⋅+⋅++-⋅ (ⅰ) 2n T = ()()23+11232232212n n n n ⋅+⋅++-⋅+-⋅ (ⅱ)……………………13分(ⅰ)式-(ⅱ)式得:()()()31121+121222222212=2+21212n nn n n T n n -+⋅--=+⋅++⋅--⋅---()()3112221212n n n -+=+⋅---⋅,∴()1232+6n n T n +=-⋅.…………………………………………………………………………16分20.解:(1)当点A 的坐标为()34,时,直线l 的方程为34130x y +-=, 圆心到直线l的距离135d r , ∴ 直线l 与圆O 分 (2)①由点A 在圆O 上,且02x =,00y >,得03y =,即)3,2(A .由题意,AM 是圆的直径,所以点M 的坐标为)3,2(--,且23=AM k . 又直线AM 和AN 的斜率互为相反数,所以23-=AN k …………………………………7分 直线AN 的方程为623+-=x y ,由⎪⎩⎪⎨⎧=++-=.13,62322y x x y 得:13)236(22=-+x x , 解得:2=x 或1346=x ,所以)139,1346(N∴ 直线MN 的斜率为3213721348213463139==++=MNk .…………………………………………10分 ②记直线AM 的斜率为k ,则直线AM 的方程为:32y kx k =+-. 将32y kx k =+-代入圆O 的方程得:22(12)33kx x k +-+=, 化简得:22232(1)2(32)(130)k x k k x k ++-+-=-,∵ 2是方程的一个根, ∴ 2232)2(131M k x k -=+-, ∴226221M x k k k --+=,由题意知:k k AN-=,同理可得,226221N x k k k +-+=,…………………………………13分 ∴ 32(32)4M N M N M N MN M N M N M Ny y kx k kx k x x k k x x x x x x -+---+++-===---,∴ 2222222222228421222362621116262111MN k k k k k k k k k k k k k k k k k k --+-+++---+-=⋅=⋅=--+-+++, ∴ 不论直线AM 的斜率怎样变化,直线MN 的斜率总为定值23.…………………… 16分。
2024-2025学年江苏省无锡市梅村高级中学空港分校高一(上)月考数学试卷(10月份)(含答案)

2024-2025学年江苏省无锡市梅村高级中学空港分校高一(上)月考数学试卷(10月份)一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合A ={x|x =3k +2,k ∈Z},则下列判断正确的是( )A. 3∈AB. 4∈AC. −3∈AD. −4∈A2.命题“∃x ≥1,使x 2>1.”的否定形式是( )A. “∃x <1,使x 2>1.”B. “∃x <1,使x 2≤1.”C. “∀x ≥1,使x 2>1.”D. “∀x ≥1,使x 2≤1.”3.下列图象中,以M ={x|0≤x ≤1}为定义域,N ={x|0≤x ≤1}为值域的函数是( )A. B.C. D.4.图中U 是全集,A ,B 是U 的两个子集,则阴影部分所表示的集合为( )A. ∁U (A ∪B)B. ∁A (A ∩B)C. (∁U A)∪(∁U B)D. (∁U A)∩B5.已知f( x −1)=x−2 x ,则f(x)的解析式为( )A. f(x)=x 2−1B. f(x)=x 2+1(x ≥−1)C. f(x)=x 2−1(x ≥−1)D. f(x)=x 2+16.已知函数y =f(x)的定义域为[−1,4],则y =f(2x +1)x−1的定义域为( )A. [−5,5]B. (1,32]C. (1,5]D. [−5,32]7.函数y =3x kx 2+2kx +1的定义域为R ,则实数k 的取值范围为( )A. (−∞,0)∪(1,+∞)B. (−∞,0]∪[1,+∞)C. (0,1)D. [0,1)8.已知关于x的不等式组{x2−2x−8>02x2+(2k+7)x+7k<0仅有一个整数解,则k的取值范围为( )A. (−5,3)∪(4,5)B. [−5,3)∪(4,5]C. (−5,3]∪[4,5)D. [−5,3]∪[4,5]二、多选题:本题共3小题,共18分。
江苏省南京市梅村中学高一数学文下学期期末试卷含解析

江苏省南京市梅村中学高一数学文下学期期末试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 函数的图象()A.关于轴对称 B.关于轴对称C.关于原点对称 D.关于直线对称参考答案:B2. 若,,,则()A. B. C. D.参考答案:A3. 已知函数,则f(2)=()A.9 B.3 C.0 D.﹣2参考答案:D【考点】函数的值.【专题】计算题.【分析】可根据解析式,先计算f(2)=f(1)=f(0),按照由内到外的顺序计算即可.【解答】解:∵,∴f(2)=f(2﹣1)=f(1)=f(1﹣1)=f(0)=﹣2.故选D.【点评】本题考察差函数的求值,关键在于理解函数解析式的意义,属于基础题.4. (5分)已知函数,则f[f()]=()A. 4 B.C.﹣4 D.﹣参考答案:B考点:分段函数的解析式求法及其图象的作法;函数的值.分析:将函数由内到外依次代入,即可求解解答:根据分段函数可得:,则,故选B点评:求嵌套函数的函数值,要遵循由内到外去括号的原则,将对应的值依次代入,即可求解.5. 三个数的大小关系为()A BC D参考答案:D略6. 如果角的终边经过点,则()参考答案:A7. 设f(x)=a sin(x+)+b cos(x+)+4,其中a、b、、均为非零实数,若f(1988)=3,则f(2013)的值为( )A.1B.5C.3D.不确定参考答案:B8. 当时,不等式恒成立,则实数的取值范围为()A. B. C.D.参考答案:B9. 若变量x,y满足约束条件,则的最大值为()A.1 B.5 C.3 D.4参考答案:C10. 已知函数,则f[f(2)]=()A.3 B.2 C.1 D.0参考答案:C【考点】函数的值.【分析】由题意得f(2)=﹣2+1=﹣1,利用函数性质能求出f(f(2))=f(﹣1),由此能求出结果.【解答】解:f(2)=﹣2+1=﹣1,f(f(2))=f(﹣1)=﹣1+1=0.故选:C.二、填空题:本大题共7小题,每小题4分,共28分11. (4分)在空间直角坐标系中,已知点A(1,0,﹣2),B(1,﹣3,1)),点 M在y轴上,且|MA|=|MB|,则M 的坐标是.参考答案:(0,﹣1,0)考点:空间两点间的距离公式.专题:空间位置关系与距离.分析:设出点M(0,y,0),由|MA|=|MB|,建立关于参数y的方程,求y值即可.解答:设设M(0,y,0),由|MA|=|MB|,可得,即y2+5=(y+3)2+2,解得:y=﹣1.M的坐标是(0,﹣1,0).故答案为:(0,﹣1,0).点评:本题考点是点、线、面间的距离计算,空间两点距离公式的应用,考查计算能力.12. 函数的定义域是;参考答案:13. 如图是计算的值的程序框图.(I)图中空白的判断框应填 **** .执行框应填 ******* ;(II)写出与程序框图相对应的程序.参考答案:解:(I)判断框:i<=2010;…………… 3分或执行框:S=S+i+1/i …………… 6分(II)程序:14. 设函数则实数a的取值范围是.参考答案:15. 已知函数f(x)=ln(+x),若实数a,b满足f(a+2)+f(b)=0,则a+b等于.参考答案:-2【考点】对数函数的图象与性质.【分析】推导出f(x)为奇函数,且单调递增,从侧由实数a,b满足f(a+2)+f(b)=0,得f(a+2)=﹣f(b)=f(﹣b),由此能求出结果.【解答】解:∵函数f(x)=ln(+x),∴函数f(x)的定义域为R,关于原点对称,又f(﹣x)=ln(﹣x)=ln(+x)﹣1=﹣ln(x)=﹣f(x),∴f(x)为奇函数,观察知函数f(x)单调递增,∵实数a,b满足f(a+2)+f(b)=0,∴f(a+2)=﹣f(b)=f(﹣b),∴a+2=﹣b,∴a+b=﹣2.故答案为:﹣2.16. 已知等腰三角形底角正弦值为,则顶角的余弦值是_________参考答案:【分析】利用诱导公式及二倍角公式求解即可。
江苏省梅村高级中学高三上学期第一次阶段检测——数学数学

江苏省梅村高级中学2015届高三上学期第一次阶段检测数 学 试 题一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在相应位置上.1.满足条件的集合M 的个数是________________.2.已知复数为虚数单位,若为纯虚数,则=________________.3.已知α,β表示两个不同的平面,m 为平面α内的一条直线, 则“α⊥β”是“m ⊥β”的________________条件.(填“充分不必要”、 “必要不充分”、“充要”或“既不充分也不必要”)4.不等式032)2(2≥---x x x 的解集是________________.5.在如图所示的算法流程图中,若输入m =4,n =3,则输出的a =________________.6.在一个样本的频率分布直方图中,共有5个小矩形,若中间一个小矩形的面积等于其他4个小矩形的面积和的,且中间一组的频数为25,则样本容量为________________.7.设实数x ,y ,b 满足⎩⎪⎨⎪⎧2x -y ≥0,y ≥x ,y ≥-x +b,若z =2x +y 的最小值为3,则实数b 的值为________________. 8.已知数字发生器每次等可能地输出数字1或2中的一个数字,则连续输出的4个数字之和能被3整除的概率是_________________.9.设a ∈R ,函数f (x )=e x +a e x 是偶函数,若曲线y =f (x )的一条切线的斜率是32,则切点的横坐标为________________.10.在△ABC 中,已知∠BAC =90°,AB =6,若D 点在斜边BC 上,CD =2DB ,则AB →·AD →的值为________________.11..设a ,b 均为正实数,则的最小值是________________.12.设△ABC 的三边长分别为a 、b 、c ,△ABC 的面积为S ,内切圆半径为r ,则r =2S a +b +c;类比这个结论可知:四面体S -ABC 的四个面的面积分别为S 1、S 2、S 3、S 4,内切球的半径为R ,四面体P -ABC 的体积为V ,则R =________________.13.已知数列是各项均不为的等差数列,为其前项和,且.若不等式对任意的恒成立,则实数的最大值为________________.14.已知函数2211,2()31ln(),22x x x f x x x +⎧<-⎪⎪=⎨⎪+⎪⎩≥-,.若存在使得,则实数的取值范围是________________. 二、解答题:本大题共六小题,共计90分.请在指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(本小题满分(1)若,求;(216. (本小题满分14分) 设函数x x x x f cos sin 32cos 6)(2-=(1)求的最小正周期和值域;(2)在锐角中,角A 、B 、C 的对边分别为a,b,c,若且,,求a 和.17.(本小题满分14分) 在正三棱柱ABC -A 1B 1C 1中,AB =AA 1,D 、E 分别是棱A 1B 1、AA 1的中点,点F 在棱AB 上,且.(1)求证:EF ∥平面BDC 1;(2)求证:平面.18 .(本小题满分16分)某小区想利用一矩形空地建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中,,且中,,经测量得到.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点作一直线交于,从而得到五边形的市民健身广场,设.(1)将五边形的面积表示为的函数;(2)当为何值时,市民健身广场的面积最大?并求出最大面积.19.(本小题满分16分)设数列{a n }的前n 项和为,且其中.(1)证明:数列是等比数列;(2)设数列的公比,数列满足,)2,)((1≥∈=*-n N n b f b n n 求数列的通项公式;(3) 记,,求数列的前项和.20.(本小题满分16分)设函数,,其中为实数.(1)若在上是单调减函数,且在上有最小值,求的取值范围;(2)若在上是单调增函数,试求的零点个数,并证明你的结论.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省梅村高级中学2013-2014学年高一下学期期中考试数学试题一.填空题(本大题共14小题,每小题5分,共计70分) 1.不等式401x x->-的解集是 . 2.在等差数列51,47,43,……中,第一个负数项是第 项.3.若直线210ax y ++=与直线(1)10x a y +--=互相平行,那么a 的值等于 .4.已知两点()3,1A 、()4,1--B 分别在直线013=++y ax 的异侧,则a 的取值范围 是 .5.在△ABC中,若π,4B b ∠==,则C ∠= . 6.已知{}n a 为等差数列,20,86015==a a ,则=75a . 7.已知数列121,,,9a a 是等差数列,数列1231,,,,9b b b 是等比数列,则212b a a +的值为 .8.已知正数a 、b 满足210a b +=,则ba 21+的最小值为 . 9.在正项等比数列{}n a 中,公比,1≠q ,2log ),log (log 219321721521a a Q a a P +=+= 则P 与Q 的大小关系是 .10.在ABC ∆中,三个内角,,A B C 所对的边分别是,,,a b c 已知2,,3c C ABC π==∆的则a b += .11.已知2,,z x y x y =+满足2y xx y x m ≥⎧⎪+≤⎨⎪≥⎩,且z 的最大值是最小值的4倍,则m 的值是 .12.已知数列{}n a 是以3为公差的等差数列,n S 是其前n 项和,若10S 是数列{}n S 中 的唯一最小项,则数列{}n a 的首项1a 的取值范围是 .13.若0a >,0b >,2a b +=.则下列不等式:①1ab ≤;+≤; ③222a b +≥; ④111>+ba .其中成立的是 (写出所有正确命题的序号). 14.定义函数[]()f x x x ⎡⎤=⎣⎦,其中[]x 表示不超过x 的最大整数, 如:[]1.5=1,[]1.3-=-2.当[)()0,x n n N *∈∈时,设函数()f x 的值域为A ,记集合A 中的元素个数构成一个数列{}n a ,则数列{}n a 的通项公式为_________.二.解答题(本大题共6小题,计90分) 15.(本小题14分)在△ABC 中,已知234AB BC CA ===,,,AD 是BAC ∠的平分线,AM 是BC 边上的中线.(1)求BD 的长;(2)求AM 的长.(写出推理过程)16.(本小题14分)已知在等比数列{}n a 中,143,81a a ==,若数列{}n b 满足:3log n n b a =,数列{}n c 满足:11n n n c b b +=,且数列{}n c 的前n 项和为n S .(1)求数列{}n a 的通项公式;(2)求数列{}n b 的通项公式;(3)求n S .17.(本小题14分)已知在△ABC 中, a 、b 、c 分别为角A 、B 、C 的对边,且272cos )]cos(1[2=-+-A C B (1)若C B A cos sin 2sin =,试判断△ABC 的形状; (2)若a=3,b+c=3,求b 和c 的值.18.(本小题16分)某市欲在2014年4月中旬举办一次花卉展,现有一占地1800平方米的矩形地块,中间三个矩形设计为花圃(如图),种植有不同品种的观赏花卉,周围则均是宽为1米的赏花小径,设花圃占地面积为s 平方米,设矩形一边的长为x (如图所示) (1)试将s 表示为x 的函数;(2)问应该如何设计矩形地块的边长,使花圃占地面积s 取得最大值.19.(本小题16分)若关于x 的实系数方程20x ax b ++=有两个根,一个根在区间(0,1)内,另一根在区间 (1,3)内,记点(,)a b 对应的区域为S .(1)设2z a b =-,求z 的取值范围;(2)过点(5,1)-的一束光线,射到x 轴被反射后经过区域S ,求反射光线所在直线经过区域S 内的整点(即横纵坐标为整数的点)时直线的方程. 20.(本小题16分)已知()x x f m log =(m 为常数,0>m ,且1≠m ),设()()()n a f a f a f ,,,21 ()+∈N n 是首项为4,公差为2的等差数列.()1求证:数列{}n a 是等比数列;()2若()n n n a f a b ⋅=,且数列{}n b 的前n 项和为n S ,当2=m 时,求n S ;()3若n n na a c lg =,问是否存在m ,使得{}n c 中的每一项恒小于它后面的项?若存在,求出m 的范围;若不存在,说明理由.江苏省梅村高级中学2013—2014学年度第二学期高一数学期中试卷答案二.解答题15. 解:(1)1BD =;(参见教材第10页例5) …7分(2)AM =.(参见教材第16页例6) …14分 16. 解:(1) ∵ 在等比数列{}n a 中,143,81a a ==, ∴ 3q =∴ 113n n n a a q -== ……………………………………………5分 (2) ∵ 3log n n b a = ∴ 3log 3n n b n ==…………………………9分 (3) 由(2)可得 111(1)1n c n n n n ==-++ ∴ 1111111(1)()()()223341n S n n =-+-+-+⋅⋅⋅+-+1111nn n =-=++ . ……………………………………14分18.解:(1) 由题知(2)2(3)(38)s a x a x a x =-+-=-,又180033,a x +=则6001,a x=- 所以6004800(1)(38)18083s x x x x=--=--;………………………8分 (2)480016001808318083()180********s x x x x=--=-+≤-=.(当且仅当40x = 时取等号),此时另一边长为45米.答:当40x =米,另一边长为45米时花圃占地面积s 取最大值1568平方米.… 16分 19.解:(1)方程20x ax b ++=的两根在区间(0,1)和(1,3)上的几何意义是:函数2()y f x x ==ax b ++与x 轴的两个交点的横坐标分别在区间(0,1)和(1,3)内,由此可得不等式组(0)0(1)0(3)0f f f >⎧⎪<⎨⎪>⎩,即010390b a b a b >⎧⎪++<⎨⎪++>⎩,………………………………………3分 则在坐标平面aOb 内,点(,)a b 对应的区域S 如图阴影部分所示,易得图中,,A B C 三点的坐标分别为(4,3),(3,0),(1,0)---, ………5分 令2z a b =-,则直线2b a z =-经过点A 时 z 取得最小值,经过点C 时z 取得最大值,即min max 11,2z z =-=-,又,,A B C 三点的值没有取到,所以112z -<<-; ………10分(2)过点(5,1)-的光线经x 轴反射后的光线必过点(5,1)--,……………11分 由图可知可能满足条件的整点为(3,1),(3,2),(2,2),(2,1)----,再结合不等式知点(3,1)-符合条件, ………………………………………13分所以此时直线方程为:1(1)1(5)3(5)y x --+=⋅+---,……………………………………14分即4y x =+ ………………………………………16分20. (1)由题意()42(1)22n f a n n =+-=+,即22,22log +=∴+=n n n m m a n a 2222)1(21m m m a a n n nn ==∴++++∴m>O 且m ≠1,∴m 2为非零常数,∴数列{}n a 是以4m 为首项,2m 为公比的等比数列………………………4分 (2)由题意222222)22(log )(+++⋅+===n n m n n n n m n m m a f a b当2=m 时,212)1(2)22(++⋅+=⋅+=n n n n n b25432)1(242322+⋅+++⋅+⋅+⋅=∴n n n S ① ①式乘以2,得326542)1(22423222++⋅++⋅++⋅+⋅+⋅=n n n n n S ②②—①并整理,得3265432)1(222222++⋅++-----⋅-=n n n n S ,3333254332)1(21]21[222)1(]2222[2+++⋅++----=⋅++++++--=n n n n n nn n n n n ⋅=⋅++-+-=++333322)1()21(22 ………………………………………10分(3)由题意m m n a a c n n n n lg )22(lg 22+⋅+==, 要使c n-1<c n 对一切n ≥2成立,即m m n m n lg )1(lg 2⋅⋅+<对一切n ≥2成立, ①当m>l 时,n<(n+l)m 2对n ≥2恒成立 ………12分②当O<m<1时,n>(n+1)m 2221m m n ->∴对一切n ≥2成立,只需2122<⋅-m m 解得3636<<-m ,考虑到O<m<l ,360<<∴m。
