梯形中常见的辅助线

合集下载

全等梯形问题中常见的8种辅助线的作法(有答案解析)

全等梯形问题中常见的8种辅助线的作法(有答案解析)梯形是一种四边形，其中两条边是平行而另外两条边不平行。

在解决全等梯形问题时，我们可以使用一些辅助线的方法来简化问题并找到解答。

以下是常见的8种辅助线的作法，每种方法都附有答案解析。

1. 垂直辅助线法：垂直辅助线法是最基本的辅助线作法之一，它通过引入垂直辅助线来将梯形划分为上下两个小三角形或小梯形，并利用全等三角形的性质来解题。

2. 高度辅助线法：高度辅助线法通过引入高度辅助线来找到梯形的高，并利用相似三角形的性质来解题。

3. 中位线辅助线法：中位线辅助线法通过引入中位线辅助线来将梯形划分为两个全等的平行四边形，并利用平行四边形的性质来解题。

4. 对角线辅助线法：对角线辅助线法通过引入对角线辅助线来将梯形划分为两个全等的三角形，并利用全等三角形的性质来解题。

5. 平行边辅助线法：平行边辅助线法通过引入平行边辅助线来将梯形划分为两个全等的梯形，并利用梯形的性质来解题。

6. 外接圆辅助线法：外接圆辅助线法通过引入外接圆辅助线来找到梯形的外接圆，并利用外接圆的性质来解题。

7. 中心对称辅助线法：中心对称辅助线法通过引入中心对称辅助线来将梯形划分为两个全等的三角形，并利用全等三角形的性质来解题。

8. 连接线辅助线法：连接线辅助线法通过引入连接线辅助线来划分梯形并利用形成的图形的性质来解题。

这些辅助线的作法可以帮助我们在解决全等梯形问题时更简单而有条理地进行推导和解答。

通过灵活运用这些方法，我们可以提高解决问题的效率和准确性。

请注意：本文档中的答案解析仅供参考，具体解答的正确性应根据实际情况进行确认。

初中数学常用辅助线添加技巧

初中数学常用辅助线添加技巧人们从来就是用自己的聪明才智创造条件解决问题的，当问题的条件不够时，添加辅助线构成新图形，形成新关系，使分散的条件集中，建立已知与未知的桥梁，把问题转化为自己能解决的问题，这是解决问题常用的策略。

一.添辅助线有二种情况：1 按定义添辅助线：如证明二直线垂直可延长使它们相交后证交角为90°;证线段倍半关系可倍线段取中点或半线段加倍;证角的倍半关系也可类似添辅助线。

2 按基本图形添辅助线：每个几何定理都有与它相对应的几何图形，我们把它叫做基本图形，添辅助线往往是具有基本图形的性质而基本图形不完整时补完整基本图形，因此“添线”应该叫做“补图”!这样可防止乱添线，添辅助线也有规律可循。

举例如下：(1)平行线是个基本图形：当几何中出现平行线时添辅助线的关键是添与二条平行线都相交的等第三条直线(2)等腰三角形是个简单的基本图形：当几何问题中出现一点发出的二条相等线段时往往要补完整等腰三角形。

出现角平分线与平行线组合时可延长平行线与角的二边相交得等腰三角形。

(3)等腰三角形中的重要线段是个重要的基本图形：出现等腰三角形底边上的中点添底边上的中线;出现角平分线与垂线组合时可延长垂线与角的二边相交得等腰三角形中的重要线段的基本图形。

(4)直角三角形斜边上中线基本图形出现直角三角形斜边上的中点往往添斜边上的中线。

出现线段倍半关系且倍线段是直角三角形的斜边则要添直角三角形斜边上的中线得直角三角形斜边上中线基本图形。

(5)三角形中位线基本图形几何问题中出现多个中点时往往添加三角形中位线基本图形进行证明当有中点没有中位线时则添中位线，当有中位线三角形不完整时则需补完整三角形; 当出现线段倍半关系且与倍线段有公共端点的线段带一个中点则可过这中点添倍线段的平行线得三角形中位线基本图形;当出现线段倍半关系且与半线段的端点是某线段的中点，则可过带中点线段的端点添半线段的平行线得三角形中位线基本图形。

梯形的中位线和常用辅助线[下学期]

同学们好
梯形的常用辅助线的研究梯形的中位线的研究
需要更完整的资源请到新世纪教育网 -
开动脑筋
在梯形中常用的作辅助线方法
平移腰
作高
补为三角形
平移对角线其他方法
灵活应用
需要更完整的资源请到新世纪教育网 -
∴ OB=AB= 4，OC=CD=11
需要更完整的资源请到新世纪教育网 -
∴ BC=OC-OB=7
例2：已知，梯形ABCD中，AD∥BC，E是腰AB的中点，
DE ⊥CE, 求证： AD+BC=CD。 A 证明：（一）延长DE交CB延长线于F D ∵在梯形ABCD中AD//B ,∠A= ∠ ABF

OF是梯形ABCD 的中位线 OF
∥
AD=CE
AD+BC=BC+CE=BE

OF

1 （AD+BC）且OF ∥AD∥ BC 新世纪教 2 需要更完整的资源请到育网 -
AO=OE F是AB中点
1 2
BE
梯形的中位线平行于两底，并且等于两底和的一半·
A
2
D
2 3
B
3
3 2
45 °
60°
C
3
E E`
3
需要更完整的资源请到新世纪教育网 -
三 .反馈练习
（一）、填空：
1. 梯形的上底是3cm，中位线长是5cm，则它的下底是 7 cm. 2. 直角梯形的上底是3cm，高是4cm，一个底角为45度，则与底不垂 60 cm. 直的腰长为 3. 等腰梯形上底是4cm，下底是16cm，腰与底夹角为45度，则等腰梯形的面积为 4√2 cm 2 （二）、选择题： 1. 梯形中位线的长是高的2倍，面积是18cm ，则梯形的中位线的长是（ B ）. （A）6√2 cm （B）6 cm （C）3√2 cm （D） 3 cm 2. 如图，直角梯形ABCD的中位线EF的长为a，垂直于底的腰长 AB 为b，图中阴影部分的面积为（ A ）. A D

第8课时：梯形的性质与判定培优

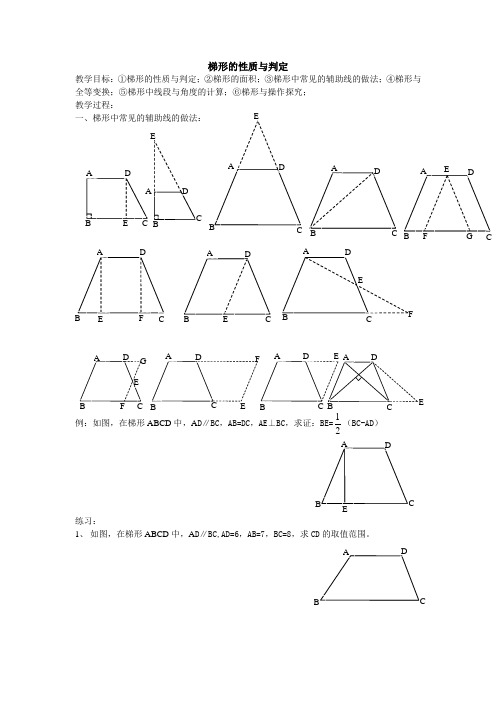
梯形的性质与判定教学目标：①梯形的性质与判定；②梯形的面积；③梯形中常见的辅助线的做法；④梯形与全等变换；⑤梯形中线段与角度的计算；⑥梯形与操作探究；教学过程：一、梯形中常见的辅助线的做法：例：如图，在梯形ABCD 中，A D ∥BC ，AB=DC ，AE ⊥BC ，求证：BE=21（BC-AD ）练习：1、如图，在梯形ABCD 中，A D ∥BC,AD=6，AB=7，BC=8，求CD 的取值范围。

A B C DE AB C D EAB CDE AB C DEABCD EF F A B D C E A B D C A B DCEF GFG FA BD CE A BDC EA BDC E ABDCEA B C D EA B C D2、如图，在直角梯形ABCD 中，∠B=∠C=90°，M 为BC 上的一点，MA=MD,且∠AMB=75°, ∠DMC=45°，求证：AB=BC3、如图，在梯形ABCD 中，AB ∥CD ，M 、N 分别是CD 、AB 的中点，∠A+∠B=90°求证：MN=21(AB-CD)4、如图，梯形ABCD 中，AM 、BM 分别平分∠DAB 、∠CBA ，交点M 在CD 上，求证：M 为CD 中点。

（注意变式习题）二、梯形与面积：例：如图，在梯形ABCD 中，A D ∥BC,E 是CD 的中点，EF ⊥AB 于F 点，AB=6，EF=5，求梯形ABCD 的面积。

解析：梯形的面积问题有以下几种解决途径：①直接法：S 梯形=21h(a+b)；②S 梯形=中位线高；③若梯形对角线垂直，S 梯形=21对角线乘积； ④过腰中点，转化为同面积的三角形；⑤过腰中点，转化为同面积的平行四边形；此题可以转化为等面积的三角形，平行四边形，直角梯形练习：1、如图，梯形ABCD 中，AD ∥BC ，AD=DC=3，AB=4，BC=8，求梯形ABCD 的面积。

梯形的常用辅助线

梯形的常用辅助线一、平移1、平移一腰：从梯形的一个顶点作一腰的平行线，把梯形转化为一个三角形和一个平行四边形。

［例1］，梯形ABCD的上底AB=3，下底CD=8，腰AD=4，求另一腰BC的取值范围。

2、平移两腰：利用梯形中的某个特殊点，过此点作两腰的平行线，把两腰转化到同一个三角形中。

［例2］，在梯形ABCD中，AD//BC，∠B＋∠C=90°，AD=1，BC=3，E、F分别是AD、BC的中点，连接EF，求EF的长。

3、平移对角线：过梯形的一个顶点作对角线的平行线，将已知条件转化到一个三角形中。

［例3］如图3，在等腰梯形ABCD中，AD//BC，AD=3，BC=7，BD=25，求证：AC⊥BD。

变式训练1.已知等腰梯形ABCD的两条对角线AC ，BD互相垂直,上底AD=11，下底BC=19，求梯形ABCD的面积2.在梯形ABCD中，AD//BC，AC=15cm，BD=20cm，高DH=12cm，求梯形ABCD的面积。

二、延长即延长两腰相交于一点，可使梯形转化为三角形。

［例3］在梯形ABCD中，AD//BC，∠B=50°，∠C=80°，AD=2，BC=5，求CD的长。

三、作梯形的高作一条高，从底边的一个端点作另一条底边的垂线，把梯形转化为直角三角形或矩形。

［例4］在直角梯形ABCD中，AB//DC，∠ABC=90°，AB=2DC，对角线AC⊥BD，垂足为F，过点F作EF//AB，交AD于点E，求证：四边形ABFE 是等腰梯形。

C第9题图跟踪练习1等腰梯形的上底、下底、高之比为1∶3∶1，则下底角的度数是（） A 30° B 45° C 60° D 75°2.在梯形ABCD 中，AD ∥BC ,∠B =90°，∠C =45°，CD =10 cm ，BC =2AD ，则梯形的面积为_______.3.梯形的上底长为5 cm ，将一腰平移到上底的另一端点位置后与另一腰和下底所构成的三角形的周长为20 cm ，那么梯形的周长为_______.4直角梯形的斜腰长为12cm ，这条腰和一底所成的角为30°，则另一腰是________5如图4-84，ABCD 是一梯形，DC AB //，AB ＝5，23=BC ，︒=∠45BCD ，︒=∠60CDA ，DC 的长度是（）A ．338+B ．8C ．219 D ．38+6 如图，梯形ABCD 中，AD ∥BC ，AB=CD ，AC ⊥BD 于点O ，∠BAC=60°，若，则此梯形的面积为（）A ．2 B．1C．27.梯形ABCD中，AD ∥BC ，AB=CD=AD=1，∠B=60°，直线MN 为梯形ABCD 的对称轴，P 为MN上一点，那么PC+PD 的最小值为8 如图2，等腰等形ABCD 中，AD ∥BC ，AD=5， ∠B=60°，BC=8，且AB ∥DE ，（1）求ΔDEC 的周长和面积（2）求梯形的面积9已知：如图，在梯形ABCD 中，AD ∥BC ，AD=2，BD=6，AC=BC=8。

梯形常见辅助线作法(教案)

梯形常见辅助线作法(教案)第一章：梯形的基本概念1.1 梯形的定义介绍梯形的定义：一个四边形，其中两边平行，两边不平行。

强调梯形的两个底和两个腰的概念。

1.2 梯形的性质介绍梯形的性质：对角相等，同底边上的角互补。

解释梯形的高的概念，并说明高的作法。

第二章：梯形的画法2.1 画一个梯形介绍画梯形的步骤：先画两个平行的底，再画两个腰。

强调画梯形时要注意的要点，如保持直角和角度的准确性。

2.2 用尺规作图画梯形介绍用尺规作图画梯形的步骤：先画一个圆，再画两个与圆相切的直线，连接两个切点与圆的端点。

强调用尺规作图时要注意的要点，如保持半径和角度的准确性。

第三章：梯形的对称性3.1 梯形的轴对称性介绍梯形的轴对称性：梯形关于底边的中垂线对称。

解释对称轴的概念，并说明如何找到梯形的对称轴。

3.2 梯形的中心对称性介绍梯形的中心对称性：梯形绕其中心点对称。

解释中心点的概念，并说明如何找到梯形的中心点。

第四章：梯形的面积计算4.1 梯形的面积公式介绍梯形的面积公式：梯形的面积等于上底加下底的和乘以高除以2。

强调面积公式的应用，并解释如何将梯形的形状分解为更简单的形状。

4.2 梯形的面积计算实例通过实例讲解如何计算梯形的面积：先画出梯形的辅助线，应用面积公式。

强调在计算面积时要准确地测量和计算底边和高的长度。

第五章：梯形的应用5.1 梯形在实际问题中的应用介绍梯形在实际问题中的应用：例如，计算梯形形状的农田的面积。

解释如何将实际问题转化为梯形的面积计算问题。

5.2 梯形的实际测量和作图介绍如何进行梯形的实际测量和作图：使用尺子和直尺测量底边和高的长度，并用画图工具画出梯形的形状。

强调在实际测量和作图时要准确地测量和绘制图形。

第六章：梯形的平行线性质6.1 梯形平行线的性质介绍梯形平行线的性质：如果一个梯形有两对平行边，这两对平行边之间的对应角相等。

强调平行线性质在解决梯形问题中的应用。

6.2 利用平行线性质解题通过实例讲解如何利用梯形平行线性质解决问题：如已知梯形的一对平行线和一对对应角，如何求另一对对应角。

梯形中常用的辅助线

图５
例４在课外活动课上，师让同学们老做～个对角线互相垂直的等腰梯形形状的风
ＡＥＢＦＢＣ。Ｈ？Ｄ。Ｇ｝Ｄ．故Ｅ ∥ ＧＦ ∥ Ｅ即四边形ＥＧＦＨ，ＧＨ，ＦＨ
是平行四边形．
１＇
（）ｏｃ６
（）０Ｄ６√
Ｄ
解：如图４所示，点Ｄ作过
构造全等三角形
Ｄ／Ａ交ＢＥ／ＣＣ的延长线于点Ｅ，则
四边形ＡＥ为ＣＤ
ＣＥ
例６在梯形ＡＣ中，Ｄ／Ｂ，Ｅ＝ＢＤＡ／ＣＡ
ＢＤＥ，Ｆ＝Ｃ求证：Ｆ．
故Ｊ形＝ＡＣ）ｅｓ＾去（Ｂ＋ＤＡ梯黝
＝ ×２５× １２＝１ｏ．５
ＦＧ是三角形的中位线，则
４平移对角线— — 构造平行四边形和以．
两条对角线为边的三角形
Ｆ
Ｃ
ＥＩＣ。Ｉ／ＦＡＦＧ／
因为ＡＢ∥ ＣＡＤ，Ｐ∥ Ｂ，以，Ｃ所四边形
ＡＣＰＢ是平行四边形．因而有
ＡＰＤ＝Ｃ＝３。ＡＰ＝ＢＣ，０，ＡＢ＝ＰＣ．
可得Ｆ＝０，ＦＢ＝Ｆ，Ｄ＝Ｆ．５￣Ａ
则ＢＦ＝Ａ４ＣＢ＝，Ｆ＝ＣＤ＝１．０
１
Ｅ／Ｂ，Ｆ＝１Ａ）Ｆ／ＣＥ（Ｄ＋．
证明：图如６联结Ａ并，Ｆ
ＡＤ
平行四边形，从

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

梯形中的常见辅助线
一、平移
1、平移一腰:
例1.如图所示，在直角梯形ABCD中，/ A = 90° AB // DC, AD = 15, AB = 16, BC = 17.求CD的长.
例2如图，梯形ABCD的上底AB=3，下底CD=8，腰AD=4，求另一腰BC的取值范围。

2、平移两腰：
例3 如图，在梯形ABCD 中，AD//BC，/ B + Z C=90° , AD=1 , BC=3 , E、F 分别是AD、BC 的中点,连接EF，求EF的长。

3、平移对角线:
例4、已知：梯形ABCD 中，AD//BC , AD=1 , BC=4 , BD=3 , AC=4，求梯形ABCD 的面积.
例5 如图，在等腰梯形ABCD 中，AD//BC , AD=3 , BC=7 , BD= 5 - 2，求证：AC 丄BD。

例6如图，在梯形ABCD 中，AD//BC , AC=15cm , BD=20cm，高DH=12cm，求梯形ABCD 的面积。

二、延长
即延长两腰相交于一点，可使梯形转化为三角形。

例7如图，在梯形ABCD 中，AD//BC，/ B=50 °，/ C=80 ° , AD=2 , BC=5，求CD 的长。

例8.如图所示，四边形ABCD中，AD不平行于BC, AC = BD , AD = BC.判断四边形ABCD的形状,
并证明你的结论
三、作对角线
即通过作对角线，使梯形转化为三角形。

例9如图6,在直角梯形ABCD中，AD//BC ,AB 丄AD , BC=CD , BE 丄CD 于点E，求证:
四、作梯形的高
1、作一条高
例10如图，在直角梯形ABCD中，AB//DC，/ ABC=90 ° , AB=2DC，对角线AC丄BD，垂足为F,
过点F作EF//AB，交AD于点E,求证：四边形ABFE是等腰梯形。

2、作两条高
例11、在等腰梯形ABCD 中，AD//BC , AB=CD，/ ABC=60 ° , AD=3cm , BC=5cm ,
AD=DE 。

£
1
n c
B
求：⑴腰AB 的长；(2)梯形ABCD 的面积.
例12如图，在梯形 ABCD 中，AD 为上底，AB>CD ，求证：BD>AC 。

五、作中位线
1、已知梯形一腰中点，作梯形的中位线。

例13如图，在梯形 ABCD 中，AB//DC ，O 是BC 的中点，/ AOD=90 °，求证：AB + CD=AD 。

2、已知梯形两条对角线的中点，连接梯形一顶点与一条对角线中点，并延长与底边相交，使问题转化为三角形中位线。

例14如图，在梯形 ABCD 中，AD//BC , E 、F 分别是 BD 、AC 的中点，求证：(1) EF//AD ;
( 2)
1
EF — (BC AD)。

2
I ___ B
3、在梯形中出现一腰上的中点时，过这点构造出两个全等的三角形达到解题的目的。

例15、在梯形ABCD 中，AD // BC, / BAD=90 0, E 是DC 上的中点，连接AE 和BE ,求/ AEB=2 / CBE。

L A
例16、已知：如图，在梯形ABCD中，AD//BC , AB丄BC, E是CD中点，试问：线段AE和BE之间有
怎样的大小关系？
例17、已知：梯形ABCD中，AD//BC , E为DC中点, EF 丄AB 于F 点，AB=3cm ,EF=5cm，求梯形ABCD的面积.
课后作业（答题时间：40分钟）
1.若等腰梯形的锐角是60° 它的两底分别为11cm, 35cm,则它的腰长为_______________________ cm.
2.如图所示，已知等腰梯形ABCD中，AD // BC,Z B = 60° AD = 2, BC= 8,则此等腰梯形的周长为
()
A. 19
B. 20
C. 21
D. 22
△n
**3.如图所示，AB // CD , AE 丄DC , AE = 12, BD = 20, AC = 15,则梯形ABCD 的面积为( )
A.130
B.140
C.150
D. 160
*4.如图所示，在等腰梯形 ABCD 中，已知AD // BC ,对角线AC 与BD 互相垂直，且 AD = 30, BC = 70,
求BD 的长.
5.
如图所示，已知等腰梯形的锐角等于 60°，它的两底分别为 15cm 和
49cm ，求它的腰长
6. 如图所示，已知等腰梯形 ABCD 中，AD // BC , AC 丄BD , AD + BC = 10, DE 丄BC 于E ,求DE 的长.
7. 如图所示，梯形 ABCD 中，AB // CD ，/ D = 2/ B , AD + DC = 8,求 AB 的长.
**8.如图所示，梯形 ABCD 中，AD // BC ,( 1)若E 是AB 的中点，且 AD + BC = CD ，贝U DE 与CE 有
何位置关系？ ( 2) E 是/ ADC 与/ BCD 的角平分线的交点，则 DE 与CE 有何位置关系？
A
D
C
A D
D
C
D
A D
（此文档部分内容来源于网络，如有侵权请告知删除，文档可自行编辑修改内容，供参考，感
谢您的配合和支持）。