决策树学习介绍
机器学习-决策树-ppt

例如:我们要对“这是好瓜吗”这样的问题进行决策时,通常 会进行一系列的判断:我们先看“它是什么颜色”,如果是“青 绿色”再看“它的根蒂是什么形态”,如果是“蜷缩”,我们在判 断“它敲起来是什么声音”,最后,我们得出最终的决策:这是 个好瓜,这个过程如下:
决策树的基本组成部分:决策结点、分支和叶子。
主要内容
决策树基本概念 基本流程 划分选择 剪枝处理
决策树
决策树基本概念
决策树是数据挖掘分类算法的一个重要方法。在各种分类算 法中,决策树是最直观的一种。在机器学习中也是一种常用方法。
我们希望从给定的训练集中学得一个模型用来对新示例进行 分类,这一分类过程称为“决策”过程。决策树是基于树结构进 行决策的。
一般而言,信息增益越大,则意味着使用属性a来进行划分所 获得的“纯度”(即分支节点所包含的样本尽可能属于同一类 别)
以下表的西瓜数据为例
以属性“色泽”为例,它有三个可能取值{青绿,乌 黑,浅白},记为:D1==青绿,D2=乌黑,D3=浅白算 D1包含{1,4,6,10,13,17}6个样例,其中正比例 P1=3/6,反比例P2=3/6;D2包含{2,3,7,8,9,15}6个 样例,其中正比例P1=4/6,反比例P2=2/6;D3包含 {5,11,12,14,16}5个样例,其中正比例P1=1/5,反比 例P2=4/5。
决策树算法
目前已有多种决策树算法:CLS、ID3、CHAID、C4.5、 CART、 SLIQ、SPRINT等。 著名的ID3(Iterative Dichotomiser3)算法是 J.R.Quinlan在1986 年提出的,该算法引入了信息论中的理论,是基于信息 熵的决策树分类算法。
决策树ID3算法
剪枝分为“预剪枝”和“后剪枝”。预剪枝是在 决策树生成过程中,对每个节点在划分之前先 进行估计,若当前节点的划分不能带来决策树 的泛化性能的提升,则停止划分并将当前节点 标记为叶节点。
第3章_决策树学习

表3-2 目标概念PlayTennis的训练样例
Day Outlook Temperature Humidity
D1
Sunny
Hot
High
D2
Sunny
Hot
High
D3 Overcast
Hot
High
D4
Rainy
Mild
High
D5
Rainy
Cool
Normal
D6
Rainy
Cool
Normal
• S的正反样例数量不等, 熵介于0,1之间
• 抛一枚均匀硬币的信息熵是多少? 解:出现正面与反面的概率均为0. 5,信息熵 是
q
E x p xi log p xi i1
(0.5log 0.5 0.5log 0.5)
1
• 用信息增益度量期望的熵降低
– 属性的信息增益,由于使用这个属性分割样例 而导致的期望熵降低
• 返回root
最佳分类属性
• 信息增益(Information Gain)
– 用来衡量给定的属性区分训练样例的能力 – ID3算法在增长树的每一步使用信息增益从候选属性中
选择属性
• 用熵度量样例的均一性
– 给定包含关于某个目标概念的正反样例的样例集S,那 么S相对这个布尔型分类的熵为
E n tr o p y (S ) p lo g 2 p plo g 2 p
ID3算法的核心问题是选取在树的每个节点要测试的属性。
表3-1 用于学习布尔函数的ID3算法
• ID3(Examples, Target_attribute, Attributes)
• 创建树的root节点
• 如果Examples都为正,返回label=+的单节点树root
李航-统计学习方法-笔记-5:决策树
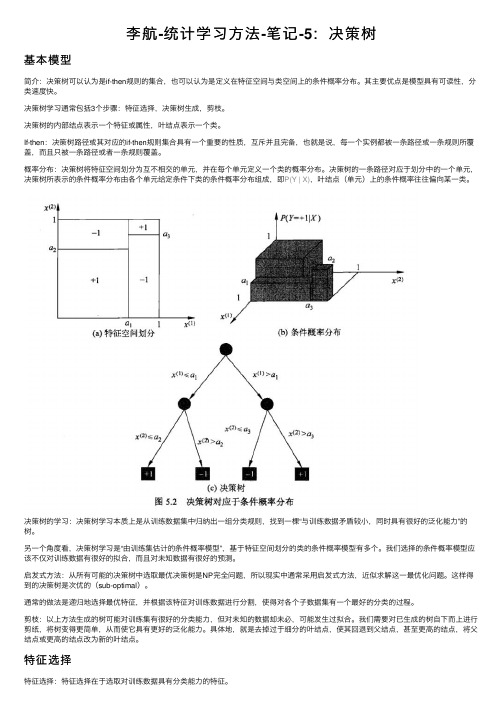
李航-统计学习⽅法-笔记-5:决策树基本模型简介:决策树可以认为是if-then规则的集合,也可以认为是定义在特征空间与类空间上的条件概率分布。
其主要优点是模型具有可读性,分类速度快。
决策树学习通常包括3个步骤:特征选择,决策树⽣成,剪枝。
决策树的内部结点表⽰⼀个特征或属性,叶结点表⽰⼀个类。
If-then:决策树路径或其对应的if-then规则集合具有⼀个重要的性质,互斥并且完备,也就是说,每⼀个实例都被⼀条路径或⼀条规则所覆盖,⽽且只被⼀条路径或者⼀条规则覆盖。
概率分布:决策树将特征空间划分为互不相交的单元,并在每个单元定义⼀个类的概率分布。
决策树的⼀条路径对应于划分中的⼀个单元,决策树所表⽰的条件概率分布由各个单元给定条件下类的条件概率分布组成,即P(Y | X),叶结点(单元)上的条件概率往往偏向某⼀类。
决策树的学习:决策树学习本质上是从训练数据集中归纳出⼀组分类规则,找到⼀棵“与训练数据⽭盾较⼩,同时具有很好的泛化能⼒”的树。
另⼀个⾓度看,决策树学习是“由训练集估计的条件概率模型”,基于特征空间划分的类的条件概率模型有多个。
我们选择的条件概率模型应该不仅对训练数据有很好的拟合,⽽且对未知数据有很好的预测。
启发式⽅法:从所有可能的决策树中选取最优决策树是NP完全问题,所以现实中通常采⽤启发式⽅法,近似求解这⼀最优化问题。
这样得到的决策树是次优的(sub-optimal)。
通常的做法是递归地选择最优特征,并根据该特征对训练数据进⾏分割,使得对各个⼦数据集有⼀个最好的分类的过程。
剪枝:以上⽅法⽣成的树可能对训练集有很好的分类能⼒,但对未知的数据却未必,可能发⽣过拟合。
我们需要对已⽣成的树⾃下⽽上进⾏剪纸,将树变得更简单,从⽽使它具有更好的泛化能⼒。
具体地,就是去掉过于细分的叶结点,使其回退到⽗结点,甚⾄更⾼的结点,将⽗结点或更⾼的结点改为新的叶结点。
特征选择特征选择:特征选择在于选取对训练数据具有分类能⼒的特征。
《决策树与随机森林》课件

交叉验证
使用交叉验证来评估模型的泛化能力,以避 免过拟合。
随机森林的参数调整
1 2
决策树数量
调整决策树的数量,以找到最优的模型性能。
特征子集大小
调整在每一步分裂中选择的特征子集大小,以找 到最优的模型性能。
3
决策树深度
调整决策树的深度限制,以防止过拟合或欠拟合 。
05
决策树与随机森林的应用场景
分类问题
THANKS
感谢观看
随机森林的优缺点
可解释性强
每棵决策树都可以单独解释,有助于理解模型的工作原理。
鲁棒
对异常值和噪声具有较强的鲁棒性。
随机森林的优缺点
对参数敏感
随机森林中的参数如树的数量、特征选择比例等对模型性能影响较大。
可能产生过拟合
当数据集较小或特征过多时,随机森林可能产生过拟合。
04
随机森林算法
随机森林的生成
决策树的基本原理
特征选择
选择最能划分数据集的特征进行分裂,以减少决 策树的深度和复杂度。
剪枝
通过去除部分分支来降低过拟合的风险,提高模 型的泛化能力。
决策规则
将每个叶子节点映射到一个类别或值,根据该节 点所属类别或值进行预测。
决策树的优缺点
优点
易于理解和解释,分类效果好,对异常值和缺失值容忍度高 。
在构建每棵决策树时,随 机选择一部分特征进行划 分,增加模型的泛化能力 。
多样性
通过生成多棵决策树,增 加模型的多样性,降低过 拟合的风险。
集成学习
将多棵决策树的预测结果 进行汇总,利用投票等方 式决定最终输出,提高分 类任务的准确率。
随机森林的优缺点
高效
能够处理大规模数据集,计算效率高 。
决策树

预修剪技术
预修剪的最直接的方法是事先指定决策树生长的最 大深度, 使决策树不能得到充分生长。 目前, 许多数据挖掘软件中都采用了这种解决方案, 设置了接受相应参数值的接口。但这种方法要求 用户对数据项的取值分布有较为清晰的把握, 并且 需对各种参数值进行反复尝试, 否则便无法给出一 个较为合理的最大树深度值。如果树深度过浅, 则 会过于限制决策树的生长, 使决策树的代表性过于 一般, 同样也无法实现对新数据的准确分类或预测。
决策树的修剪
决策树学习的常见问题(3)
处理缺少属性值的训练样例 处理不同代价的属性
决策树的优点
可以生成可以理解的规则; 计算量相对来说不是很大; 可以处理连续和离散字段; 决策树可以清晰的显示哪些字段比较重要
C4.5 对ID3 的另一大改进就是解决了训练数据中连续属性的处 理问题。而ID3算法能处理的对象属性只能是具有离散值的 数据。 C4.5中对连续属性的处理采用了一种二值离散的方法,具体 来说就是对某个连续属性A,找到一个最佳阈值T,根据A 的取值与阈值的比较结果,建立两个分支A<=T (左枝)和 A>=T (右枝),T为分割点。从而用一个二值离散属性A (只 有两种取值A<=T、A>=T)替代A,将问题又归为离散属性的 处理。这一方法既可以解决连续属性问题,又可以找到最 佳分割点,同时就解决了人工试验寻找最佳阈值的问题。
简介
决策树算法是建立在信息论的基础之上的 是应用最广的归纳推理算法之一 一种逼近离散值目标函数的方法 对噪声数据有很好的健壮性且能学习析取(命题 逻辑公式)表达式
信息系统
决策树把客观世界或对象世界抽象为一个 信息系统(Information System),也称属性--------值系统。 一个信息系统S是一个四元组: S=(U, A, V, f)
决策树的数学原理

决策树的数学原理决策树是一种常用的机器学习算法,它通过将数据集划分为不同的分支,逐步生成一棵树状结构,从而实现对数据的分类和预测。
本文将介绍决策树的数学原理,包括信息增益、基尼指数和决策树的生成过程。
一、信息增益在构建决策树时,我们需要选择最佳的属性来进行分割。
信息增益是一种衡量属性对决策结果贡献程度的指标,信息增益越大,表示属性的划分结果对结果的影响越大。
信息增益的计算基于信息熵的概念。
信息熵衡量了数据集的混乱程度,熵越大表示数据集越不纯净。
在决策树的构建中,熵的计算公式为:$$ H(D) = -\sum_{i=1}^{n}p_i\log_2p_i $$其中,$D$表示数据集,$n$表示数据集中类别的数量,$p_i$表示第$i$个类别的概率。
对于某一属性$A$,我们将数据集$D$基于属性$A$的取值划分为多个子集$D_v$,每个子集对应一个取值$v$。
属性$A$对数据集$D$的信息增益定义如下:$$ Gain(A) = H(D) - \sum_{v=1}^{V}\frac{|D_v|}{|D|}H(D_v) $$其中,$V$表示属性$A$的取值数量,$|D_v|$表示子集$D_v$的样本数量。
通过比较不同属性的信息增益,我们可以选择最佳的属性作为决策树的分割标准。
二、基尼指数另一种常用的属性选择指标是基尼指数。
基尼指数衡量了数据集的不纯度,越小表示数据集越纯净。
对于某一属性$A$,基尼指数的计算公式为:$$ Gini(A) = \sum_{v=1}^{V}\frac{|D_v|}{|D|}Gini(D_v) $$其中,$V$表示属性$A$的取值数量,$|D_v|$表示子集$D_v$的样本数量。
选择最佳属性时,我们需要计算每个属性的基尼指数,并选择基尼指数最小的属性作为划分标准。
三、决策树的生成过程决策树的生成通常通过递归的方式进行。
生成过程可以分为以下几个步骤:1. 若数据集$D$中的样本全属于同一类别$C$,则以$C$为叶节点,返回决策树;2. 若属性集$A$为空集,即无法再选择属性进行划分,将数据集$D$中样本数量最多的类别作为叶节点,返回决策树;3. 对于属性集$A$中的每一个属性$A_i$,计算其信息增益或基尼指数;4. 选择信息增益或基尼指数最大的属性$A_j$作为划分标准,生成一个根节点;5. 根据属性$A_j$的取值将数据集$D$划分为若干子集$D_v$;6. 对于每个子集$D_v$,递归地生成决策树,将子树连接到根节点上;7. 返回决策树。
决策树(完整)

无缺失值样本中在属性 上取值 的样本所占比例
ቤተ መጻሕፍቲ ባይዱ
谢谢大家!
举例:求解划分根结点的最优划分属性
根结点的信息熵:
用“色泽”将根结点划分后获得3个分支结点的信息熵分别为:
属性“色泽”的信息增益为:
若把“编号”也作为一个候选划分属性,则属性“编号”的信息增益为:
根结点的信息熵仍为:
用“编号”将根结点划分后获得17个分支结点的信息熵均为:
则“编号”的信息增益为:
三种度量结点“纯度”的指标:信息增益增益率基尼指数
1. 信息增益
香农提出了“信息熵”的概念,解决了对信息的量化度量问题。香农用“信息熵”的概念来描述信源的不确定性。
信息熵
信息增益
一般而言,信息增益越大,则意味着使用属性a来进行划分所获得的“纯度提升”越大。决策树算法第8行选择属性
著名的ID3决策树算法
远大于其他候选属性信息增益准则对可取值数目较多的属性有所偏好
2. 增益率
增益率准则对可取值数目较少的属性有所偏好著名的C4.5决策树算法综合了信息增益准则和信息率准则的特点:先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的。
3. 基尼指数
基尼值
基尼指数
著名的CART决策树算法
过拟合:学习器学习能力过于强大,把训练样本自身的一些特点当作了所有潜在样本都会具有的一般性质,导致泛化性能下降。欠拟合:学习器学习能力低下,对训练样本的一般性质尚未学好。
过拟合无法彻底避免,只能做到“缓解”。
不足:基于“贪心”本质禁止某些分支展开,带来了欠拟合的风险
预剪枝使得决策树的很多分支都没有“展开”优点:降低过拟合的风险减少了训练时间开销和测试时间开销
决策树学习AI技术中的决策树模型与应用

决策树学习AI技术中的决策树模型与应用决策树是一种常用的机器学习算法,被广泛应用于人工智能技术中。
它通过构建一棵树状结构来对数据进行分类或预测,具有可解释性强、灵活性高等优点。
本文将介绍决策树模型的基本原理、训练过程以及常见的应用场景。
决策树模型的基本原理决策树模型是一种基于树状结构的预测模型,它将训练数据的特征进行分割,并根据分割结果构建一棵树。
在该树的每个内部节点,它都根据某个特征对数据进行分割;而在每个叶子节点,它都代表一个类别或预测的结果。
通过根据特征分割数据样本,不断细分出更纯的数据集,决策树能够对未知样本进行分类或预测。
决策树训练过程决策树的训练过程分为特征选择、树的构建和剪枝三个步骤。
特征选择是指在每个节点上选择一个最优的特征作为分割依据。
常见的特征选择算法有信息增益、信息增益比、基尼指数等。
它们通过计算每个特征的纯度或不纯度,选择使得分割后各个子集纯度最高或不纯度最低的特征。
树的构建是指根据特征选择的结果,递归地构建决策树的过程。
从根节点开始,选择一个特征进行分割,将样本划分到对应的子节点中。
然后对每个子节点递归地执行相同的分割过程,直到满足停止条件,如节点中的样本属于同一类别、达到最大深度等。
剪枝是为了避免过拟合而对决策树进行修剪。
过拟合指的是模型在训练集上表现良好但在测试集上表现差的情况。
常见的剪枝方法有预剪枝和后剪枝。
预剪枝是在树的构建过程中,在每次分割时进行判断,若分割后的性能没有显著提升,则停止分割。
后剪枝则是先构建完整的决策树,再通过将一些节点合并或删除来提高泛化能力。
决策树的应用场景决策树在许多领域都有广泛的应用,下面介绍几个常见的应用场景。
1. 医学诊断决策树可以根据病人的症状和检查结果对疾病进行诊断。
通过构建一个合适的决策树模型,医生可以根据病人的个人信息和检查数据判断疾病的种类和严重程度,为治疗提供指导。
2. 金融风险评估决策树可以用于预测个人或企业的信用风险。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
寒冷
适中 寒冷 适中 适中 适中 炎热 适中
正常
高 正常 正常 正常 高 正常 高
强
弱 弱 弱 强 强 弱 强
去
不去 去 去 去 去 去 不去
决策树学习原理简介—(ID3)
S: (9+, 5-) 湿度 S: (9+, 5-) 风
高
(3+, 4-)
正常 (6+, 1-)
弱 (6+, 2-)
强 (3+, 3-)
node = root 循环 { 1. 为当下一个节点选择一个最好的属性 x 2. 将属性x分配给节点node 3. 对于x的所有可能数值,创建一个降序排列的节点node 4. 将所有训练样本在叶子节点排序分类 5. 如果分类结果达到了错误率要求,跳出循环,否则, 在叶子节点开始新循环-〉递归 }
基本的决策树学习算法—(ID3)
Gain( S , x) Entropy( S )
vValues ( x )
Sv Entropy( Sv ) S
x v的子集
信息增益(Information Gain)
问题:哪一个属性(特征)更好?分析极端的情况 E=1.0 S: (8+, 8-) 温度 高 E=1.0 (4+, 4-) 正常 (4+, 4-) 好 E=0.0 (8+, 0-) E=1.0 S: (8+, 8-)
在某一个操作之前的系统熵与操作之后的系统熵的差值 也即是不确定性的减小量
信息增益(Information Gain)
选择特征的标准:选择具有最大信息增益(Information Gain) 的特征 假设有两个类, + 和 假设集合S中含有p个类别为+的样本,n个类别为-的样本 将S中已知样本进行分类所需要的期望信息定义为:
问题:哪一个属性(特征)更好?
内容
决策树的基本原理和算法 熵、信息增益和特征选择 决策树学习中的过拟合问题
交叉验证与树的修剪
熵
熵:物理学概念 ������ ������ 宏观上:热力学定律—体系的熵变等于可逆过程吸收或耗散的热量 微观上:熵是大量微观粒子的位置和速度的分布概率的函数,是描 除以它的绝对温度(克劳修斯,1865) 述系统中大量微观粒子的无序性的宏观参数(波尔兹曼,1872) ������ 结论:熵是描述事物无序性的参数,熵越大则无序性越强 ,在信息
7
8 9 10 11 12 13 14
阴天
晴天 晴天 下雨 晴天 阴天 阴天 下雨
寒冷
适中 寒冷 适中 适中 适中 炎热 适中
正常
高 正常 正常 正常 高 正常 高
强
弱 弱 弱 强 强 弱 强
去
不去 去 去 去 去 去 不去
内容
决策树的基本原理和算法 熵、信息增益和特征选择 决策树学习中的过拟合问题
p 表示训练集合中反例样本的比例 p 表示训练集合中正例样本的比例
I (S ) p log 2 ( p ) p log 2 ( p ) 表示训练集合的熵
信息增益(Information Gain)
信息的增加意味着不确定性的减少,也就是熵的减小; 信息增益在诸多系统中定义为:
心情
坏 (0+,8-)
Gain(S, 温度) =1.0-(8/16)*1.0-(8/16)*1.0 =0.0
Gain(S, 心情) =1.0-(8/16)*0.0-(8/16)*0.0
I ( p, n) p p n n log 2 log 2 pn pn pn pn
信息增益(Information Gain)
假设特征x将把集合S划分成 K份 {S1, S2 , …, SK} 如果 Si 中包含 pi 个类别为 “+”的样本, ni 个类别为 “-”, 的样本。那么划分后的熵就是:
第1.2节 决策树学习 (Decision Tree)
内容
决策树的基本原理和算法 熵、信息增益和特征选择 决策树学习中的过拟合问题
交叉验证与树的修剪
如何根据下表数据学习一个是否去打球的模型?
编号 1 2 3 4 5 6 天气 晴天 晴天 阴天 下雨 下雨 下雨 炎热 炎热 炎热 适中 寒冷 寒冷 温度 高 高 高 高 正常 正常 湿度 弱 强 弱 弱 弱 强 风 是否去打球 不去 不去 去 去 去 不去
表-1:是否去打球的数据统计—训练数据
编号 1 2 3 4 5 6 天气 晴天 晴天 阴天 下雨 下雨 下雨 炎热 炎热 炎热 适中 寒冷 寒冷 温度 高 高 高 高 正常 正常 湿度 弱 强 弱 弱 弱 强 风 是否去打球 不去 不去 去 去 去 不去
7
8 9 10 11 12 13 14
阴天
晴天 晴天 下雨 晴天 阴天 阴天 下雨
领域定义为“熵越大,不确定性越大”(香浓,1948年)
熵
随机变量的熵 I ( X )
I ( X ) P( X i) log 2 P( X i)
i 1 n
熵 比较多的用于信源编码,数据压缩,假设 是最有效的编码方式是使用 位编码
X i
于是对于随即变量的最有效编码位之和:
熵
S
表示训练集合中的样本
ID3的思想
自顶向下构造决策树 从“哪一个特征将在树的根节点被测试”开始 使用统计测试来确定每一个实例特征单独分类训练样例的能力
ID3的过程
分类能力最好的特征被选作树的根节点 根节点的每个可能值产生一个分支 训练样例排列到适当的分支 重复上面的过程
基本的决策树学习算法—(ID3)
E ( x)
i 1
K
pi ni I ( pi , ni ) pn
在x上进行决策分枝所获得的信息增益为:
Gain( x) I ( p, n) E( x)
信息增益(Information Gain)
Gain(S , x)
表示给定特征
x 后不确定性的减少,即信息增益
表示了特征与数据集合的互信息
交叉验证与树的修剪
决策树学习——决定是否去打球
看看天气 晴天 看看湿度 高 不去打球 正常 去打球 去打球 大 不去打球 小 去打球 下雨
阴天
看看风速
节点:每一个节点测试一维特征, xi 分支:特征的可选数值(此处为离散值) 叶子节点:最终预测
Y or P(Y | Y Leaf )
基本的决策树学习算法—(ID3)
