编译原理第三章作业
蒋立源编译原理 第三版 第三章 习题与答案(修改后)

第3章习题3-1 试构造一右线性文法,使得它与如下得文法等价S→AB A→UT U→aU|a D→bT|b B→cB|c 并根据所得得右线性文法,构造出相应得状态转换图。
3-2 对于如题图3-2所示得状态转换图(1) 写出相应得右线性文法;(2) 指出它接受得最短输入串;(3) 任意列出它接受得另外4个输入串;(4) 任意列出它拒绝接受得4个输入串。
3-3 对于如下得状态转换矩阵:(1) 分别画出相应得状态转换图;(2) 写出相应得3型文法;(3) 用自然语言描述它们所识别得输入串得特征。
3-4 将如下得NFA确定化与最小化:3-5 将如题图3-5所示得具有ε动作得NFA确定化。
题图3-5 具有ε动作得NFA3-6 设有文法G[S]:S→aA A→aA|bB B→bB|cC|c C→cC|c 试用正规式描述它所产生得语言。
3-7 分别构造与如下正规式相应得NFA。
(1) ((0* |1)(1* 0))*(2) b|a(aa*b)*b3-8 构造与正规式(a|b)*(aa|bb)(a|b)*相应得DFA。
第3章习题答案3-1 解:根据文法知其产生得语言就是:L[G]={a m b n c i| m,n,i≧1}可以构造与原文法等价得右线性文法:S→aA A→aA|bB B→bB|cC|c C→cC|c 其状态转换图如下:3-2 解:(1) 其对应得右线性文法就是G[A]:A →0D B→0A|1C C→0A|1F|1D→0B|1C E→0B|1C F→1A|0E|0(2) 最短输入串为011(3) 任意接受得四个输入串为:0110,0011,000011,00110(4) 任意拒绝接受得输入串为:0111,1011,1100,10013-3 解:(1) 相应得状态转换图为:(2) 相应得3型文法为:(ⅰ) S→aA|bS A→aA|bB|b B→aB|bB|a|b(ⅱ) S→aA|bB|a A→bA|aC|a|b B→aB|bC|b C→aC|bC|a|b(ⅲ) S→aA|bB|b A→aB|bA|a B→aB|bB|a|b(ⅳ) S→bS|aA A→aC|bB|a B→aB|bC|b C→aC|bC|a|b(3) 用自然语言描述得输入串得特征为:(ⅰ) 以任意个(包括0个)b开头,中间有任意个(大于1)a,跟一个b,还可以有一个由a,b组成得任意字符串。
编译原理作业集-第三章-修订版

第三章词法分析本章要点1.词法分析器设计,2.正规表达式与有限自动机,3.词法分析器自动生成。
本章目标:1.理解对词法分析器的任务,掌握词法分析器的设计;2.掌握正规表达式与有限自动机;3.掌握词法分析器的自动产生。
本章重点:1.词法分析器的作用和接口,用高级语言编写词法分析器等内容,它们与词法分析器的实现有关。
应重点掌握词法分析器的任务与设计,状态转换图等内容。
2.掌握下面涉及的一些概念,它们之间转换的技巧、方法或算法。
(1)非形式描述的语言↔正规式(2)正规式→ NFA(非确定的有限自动机)(3)NFA → DFA(确定的有限自动机)(4)DFA →最简DFA本章难点(1)非形式描述的语言↔正规式(2)正规式→ NFA(非确定的有限自动机)(3)NFA → DFA(确定的有限自动机)(4)DFA →最简DFA作业题一、单项选择题(按照组卷方案,至少15道)1. 程序语言下面的单词符号中,一般不需要超前搜索a. 关键字b. 标识符c. 常数d. 算符和界符2. 在状态转换图的实现中,一般对应一个循环语句a. 不含回路的分叉结点b. 含回路的状态结点c. 终态结点d. 都不是3. 用了表示字母,d表示数字, ={l,d},则定义标识符的正则表达式可以是:。
(a)ld*(b)ll*(c)l(l | d)*(d)ll* | d*4. 正规表达式(ε|a|b)2表示的集合是(a){ε,ab,ba,aa,bb} (b){ab,ba,aa,bb}(c){a,b,ab,aa,ba,bb} (d){ε,a,b,aa,bb,ab,ba}5. 有限状态自动机可用五元组(V T,Q,δ,q0,Q f)来描述,设有一有限状态自动机M的定义如下:V T={0,1},Q={q0,q1,q2},Q f={q2},δ的定义为:δ(q0,0)=q1δ(q1,0)=q2δ(q2,1)=q2δ(q2,0)=q2M所对应的状态转换图为。
蒋立源编译原理第三版第三章习题与答案(修改后)
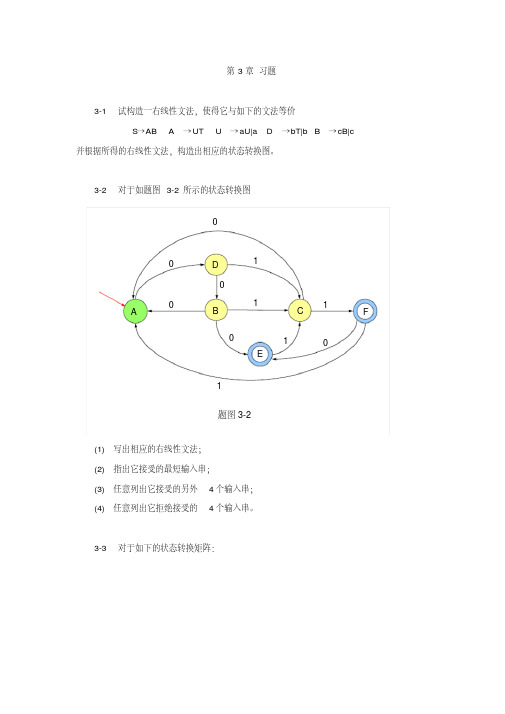
{2} a ={4} a ={1}, {2} b ={4} b ={4}
所以 2 和 4 不可区分, 故子集 {S,B} 已不能再分裂。此时 π 2=π 1 ,子集分裂的过程宣告
结束。
( ⅳ) 现选择状态 2 作为 {2,4} 的代表, 将状态 4 从状态转换图中删去, 并将原来引
至 4 的矢线都引至 2,这样,我们就得到了最小化后的 所示。
但
{1}
b=
故 1 和 2 可区分,于是便得到下一分划
π1: {1}, {2}, {3}
此时子集已全部分裂,故最小化的过程宣告结束, M′即为状态数最小的 DFA。
(3) 将 NFA M确定化后得 DFA M′,其状态转换矩阵如答案图 3-4-(3) 之 (a) 所示, 给各状态重新命名,即令:
[S]=1, [A]=2, [S,B]=3 且由于 3 的组成中含有 M的终态 B,故 3 为 DFAM′的终态。于是,所构造之 DFAM′的 状态转换矩阵和状态转换图如答案图 3-4-(3) 之(b) 及(c) 所示。
答案图 3-3
a, b C
(2) 相应的 3 型文法为:
( ⅰ ) S →aA|bS
A→aA|bB| b
B→ aB|bB|a|b
( ⅱ) S →aA|bB| a
A→bA|aC| a|b
B→aB|bC| b
C→ aC|bC|a|b
( ⅲ) S →aA|bB| b A→aB|bA| a
B→aB| bB|a|b
示。
a
b
ab
[S]
[Z]
[R,U]
1
[Z]
2
[R,U] [S,X]
[Z]
342
[S,X] [Z] [R,U,Y]
编译原理教程-课后习题答案第三章语法分析

由 A′→ABl 得 FIRST(′l′) FOLLOW(B) , 即 FOLLOW(B)={l};
由 A→aA′ 得 FOLLOW(A) FOLLOW(A′) , 即 FOLLOW(A′)={#,d};
第三章 语法分析
由 B→dB′ 得 FOLLOW(B) FOLLOW(B′) , 即 FOLLOW(B′)={l}。
c. 最左推导和最右推导必定相同
d. 可能存在两个不同的最左推导,但它们对应的语法树 相同
第三章 语法分析
(3) 采用自上而下分析,必须 。
a. 消除左递归
b. 消除右递归
c. 消除回溯
d. 提取公共左因子
(4) 设a、b、c是文法的终结符,且满足优先关系 ab和bc,则 。
a. 必有ac
b. 必有ca
第三章 语法分析
(2) 为了构造字母表Σ ={a,b}上同时只有奇数个a 和奇数个b的所有串集合的正规式,我们画出如图3-3 所示的DFA,即由开始符S出发,经过奇数个a到达状态 A,或经过奇数个b到达状态B;而由状态A出发,经过 奇数个b到达状态C(终态);同样,由状态B出发经过奇 数个a到达终态C。
第三章 语法分析
第三章 语法分析
3.1 完成下列选择题:
(1) 文法G:S→xSx|y所识别的语言是 。
a. xyx
b. (xyx)*
c. xnyxn(n≥0)
d. x*yx*
(2) 如果文法G是无二义的,则它的任何句子α 。
a. 最左推导和最右推导对应的语法树必定相同
b. 最左推导和最右推导对应的语法树可能不同
“A→α · ”动作的一定是 。
a. LALR文法 b. LR(0)文法
c. LR(1)文法 d. SLR(1)文法
编译原理教程课后习题答案——第三章

第三章语法分析3.1 完成下列选择题:(1) 文法G:S→xSx|y所识别的语言是。
a. xyxb. (xyx)*c. xnyxn(n≥0)d. x*yx*(2) 如果文法G是无二义的,则它的任何句子α。
a. 最左推导和最右推导对应的语法树必定相同b. 最左推导和最右推导对应的语法树可能不同c. 最左推导和最右推导必定相同d. 可能存在两个不同的最左推导,但它们对应的语法树相同(3) 采用自上而下分析,必须。
a. 消除左递 a. 必有ac归b. 消除右递归c. 消除回溯d. 提取公共左因子(4) 设a、b、c是文法的终结符,且满足优先关系ab和bc,则。
b. 必有cac. 必有bad. a~c都不一定成立(5) 在规范归约中,用来刻画可归约串。
a. 直接短语b. 句柄c. 最左素短语d. 素短语(6) 若a为终结符,则A→α·aβ为项目。
a. 归约b. 移进c. 接受d. 待约(7) 若项目集Ik含有A→α·,则在状态k时,仅当面临的输入符号a∈FOLLOW(A)时,才采取“A→α·”动作的一定是。
a. LALR文法b. LR(0)文法c. LR(1)文法d. SLR(1)文法(8) 同心集合并有可能产生新的冲突。
a. 归约b. “移进”/“移进”c.“移进”/“归约”d. “归约”/“归约”【解答】(1) c (2) a (3) c (4) d (5) b (6) b (7) d (8) d3.2 令文法G[N]为G[N]: N→D|NDD→0|1|2|3|4|5|6|7|8|9(1) G[N]的语言L(G[N])是什么?(2) 给出句子0127、34和568的最左推导和最右推导。
【解答】(1) G[N]的语言L(G[N])是非负整数。
(2) 最左推导:NNDNDDNDDDDDDD0DDD01DD012D0127NNDDD3D34NNDNDDDDD5DD56D568最右推导:NNDN7ND7N27ND27N127D1270127NNDN4D434NNDN8ND8N68D685683.3 已知文法G[S]为S→aSb|Sb|b,试证明文法G[S]为二义文法。
编译原理 第3章习题解答
第三章习题参考解答3.1 构造自动机A,使得①②③当从左至右读入二进制数时,它能识别出读入的奇数;④它识别字母表{a, b}上的符号串,但符号串不能含两个相邻的a,也不含两个相邻的b;⑤它能接受字母表{0, 1}上的符号串,这些符号串由任意的1、0和随后的任意的11、00对组成。
⑥它能识别形式如±dd*⋅ d*E ±dd的实数,其中,d∈{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}。
3.2 构造下列正规表达式的DFSA:① xy*∣yx*y∣xyx;② 00∣(01)*∣11;③ 01((10∣01)*(11∣00))*01;④ a(ab*∣ba*)*b。
3.3 消除图3.24所示自动机的空移。
bεq1q2q3aba,bqaq6q4q5abεεε图3.24 含空移的自动机3.4 将图3.25所示NDFSA确定化和最小化。
xyqq1q2q4q3xyxyx,yx图3.25 待确定化的NDFSA3.5 设e、e1、e2是字母表∑上的正规表达式,试证明① e∣e=e;② {{e}}={e};③ {e}=ε∣e{e};④ {e1 e2} e1= e1{e2 e1};⑤ {e1∣e2}={{e1}{e2}}={{e1}∣{e2}}。
3.6 构造下面文法G[Z]的自动机,指明该自动机是不是确定的,并写出它相应的语言: G[Z]:Z→A0A→A0∣Z1∣03.7 设NDFSA M=({x, y},{a, b},f, x, {y}), 其中,f(x, a)={x, y}, f(x, b)={y}, f(y, a)=∅, f(y, b)={x, y}。
试对此NDFSA确定化。
3.8 设文法G[〈单词〉]:〈单词〉→〈标识符〉∣〈无符号整数〉〈标识符〉→〈字母〉∣〈标识符〉〈字母〉∣〈标识符〉〈数字〉〈无符号整数〉→〈数字〉∣〈无符号整数〉〈数字〉〈字母〉→a∣b〈数字〉→1∣2试写出相应的有限自动机和状态图。
编译原理第三章练习题答案
编译原理第三章练习题答案一、选择题1. 在编译原理中,词法分析器的作用是什么?A. 将源代码转换为汇编代码B. 将源代码转换为中间代码C. 识别源代码中的词法单元D. 检查源代码的语法正确性答案:C2. 词法单元中,标识符和关键字的区别是什么?A. 标识符可以重定义,关键字不可以B. 标识符和关键字都是常量C. 标识符是用户自定义的,关键字是语言预定义的D. 标识符和关键字都是变量名答案:C3. 下列哪个不是词法分析器生成的属性?A. 行号B. 列号C. 词法单元的类型D. 词法单元的值答案:A4. 词法分析器通常使用哪种数据结构来存储词法单元?A. 栈B. 队列C. 链表D. 数组答案:C5. 词法分析器的实现方法有哪些?A. 手工编写正则表达式B. 使用词法分析器生成器C. 编写扫描程序D. 所有上述方法答案:D二、简答题1. 简述词法分析器的基本工作流程。
答案:词法分析器的基本工作流程包括:读取源代码字符,根据正则表达式匹配词法单元,生成词法单元的类型和值,并将它们作为输出。
2. 什么是正规文法?它在词法分析中有什么作用?答案:正规文法是一种形式文法,它使用正则表达式来定义语言的词法结构。
在词法分析中,正规文法用于描述程序设计语言的词法规则,帮助词法分析器识别和生成词法单元。
三、应用题1. 给定一个简单的词法分析器,它需要识别以下词法单元:标识符、关键字(如if、while)、整数、运算符(如+、-、*、/)、分隔符(如逗号、分号)。
请描述该词法分析器的实现步骤。
答案:实现步骤如下:- 定义词法单元的类别和对应的正则表达式。
- 读取源代码字符,逐个字符进行匹配。
- 使用状态机或有限自动机来识别词法单元。
- 根据匹配结果生成相应的词法单元类型和值。
- 输出识别的词法单元。
2. 设计一个简单的词法分析器,它可以识别以下C语言关键字:int, float, if, else, while, return。
蒋立源编译原理第三版第三章习题与答案(修改后)
3-1 试构造一右线性文法,使得它与如下的文法等价 S→AB A → UT U → aU|a D →bT|b B → cB|c
并根据所得的右线性文法,构造出相应的状态转换图。
3-2 对于如题图 3-2 所示的状态转换图 0
0 0 A
D
1
0 1
B
C1
F
0
1
0
E
1 题图 3-2
(1) 写出相应的右线性文法; (2) 指出它接受的最短输入串; (3) 任意列出它接受的另外 4 个输入串; (4) 任意列出它拒绝接受的 4 个输入串。
但
{1}
b=
故 1 和 2 可区分,于是便得到下一分划
π1: {1}, {2}, {3}
此时子集已全部分裂,故最小化的过程宣告结束, M′即为状态数最小的 DFA。
(3) 将 NFA M确定化后得 DFA M′,其状态转换矩阵如答案图 3-4-(3) 之 (a) 所示, 给各状态重新命名,即令:
[S]=1, [A]=2, [S,B]=3 且由于 3 的组成中含有 M的终态 B,故 3 为 DFAM′的终态。于是,所构造之 DFAM′的 状态转换矩阵和状态转换图如答案图 3-4-(3) 之(b) 及(c) 所示。
π0:{1,2}, {3}
( ⅱ) 为得到下一分划,考察子集 {1,2} 。因为
{2} b ={3}
但
{1}
b=
故 1 和 2 可区分,于是便得到下一分划
π1: {1}, {2}, {3}
此时子集已全部分裂,故最小化的过程宣告结束, M′即为状态数最小的 DFA。
(4) 将 NFA M确定化后得 DFA M′,其状态转换矩阵如答案图 3-4-(4) 之 (a) 所示, 给各状态重新命名,即令:
蒋立源编译原理第三版第三章习题与答案
第 3 章习题3-1 试构造一右线性文法,使得它与如下的文法等价4AB A f UT U faU|a D fbT|b B fcB|c并根据所得的右线性文法,构造出相应的状态转换图。
3-2 对于如题图3-2 所示的状态转换图(1) 写出相应的右线性文法;(2) 指出它接受的最短输入串;(3) 任意列出它接受的另外 4 个输入串;(4) 任意列出它拒绝接受的 4 个输入串。
3-3 对于如下的状态转换矩阵:(1) 分别画出相应的状态转换图;(2) 写出相应的 3 型文法;(3) 用自然语言描述它们所识别的输入串的特征。
3-4 将如下的NFA确定化和最小化:3-5 将如题图3-5所示的具有£动作的NFA确定化。
题图3-5 具有£动作的NFA试用正规式描述它所产生的语言。
3-7 分别构造与如下正规式相应的 NFA(1) ((0 |1)(1 0)) ⑵ b|a(aa *b)*b3-8 构造与正规式(a|b) *(aa|bb)(a|b)*相应的 第3章习题答案3-1 解:根据文法知其产生的语言是L[G]={am 3n c i| m,n,i 仝 1}可以构造与原文法等价的右线性文法其状态转换图如下:3-2 解:4 aA L aA|bB 4 bB|cC|c C^ cC|cDFAA ^ aA|bB4 bB|cC|cC^ cC|cc4 0A|1C0110,0011,000011,00110Df0B|1CEf0B|1CFf 1A|0E|0(2) 最短输入串为 O11(3) 任意接受的四个输入串为:(1) 其对应的右线性文法是 G[A]:0A|1F|1 (4) 任意拒绝接受的输入串为: 0111,1011,1100,10013-3 解:(1) 相应的状态转换图为:(2) 相应的 3 型文法为: (i ) S f aA|bS AfaA|bB| b Bf aB|bB|a|b(ii) S f aA|bB| AfbA|aC| a|b BfaB|bC| b Cf aC|bC|a|b(iii) S f aA|bB| AfaB|bA| a BfaB|bB|a|b (iv) S f bS|aAAfaC|bB| aBfaB|bC| bCf aC|bC|a|b(3) 用自然语言描述的输入串的特征为:(i )以任意个(包括0个)b 开头,中间有任意个(大于1) a ,跟一个b ,还可以有一个由 a,b 组成的任意字符串。
编译原理第3章 习题解答
第3章习题解答1.构造正规式1(0|1)*101相应的DFA.[答案]先构造NFA确定化0 1X AA A ABAB AC ABAC A ABYABY AC AB重新命名,令AB为B、AC为C、ABY为D0 1X AA A BB C BC A DD C B转化成DFA:============================================================== 2.将下图确定化:[答案]0 1S VQ QUVQ VZ QUQU V QUZVZ Z ZV ZQUZ VZ QUZZ Z Z重新命名,令VQ为A、QU为B、VZ为C、V为D、QUZ为E、Z为F。
0 1S A BA C BB D EC F FD FE C EF F F转化为DFA:================================================================ 3.把下图最小化:[答案](1)初始分划得Π0:终态组{0},非终态组{1,2,3,4,5}对非终态组进行审查:{1,2,3,4,5}a {0,1,3,5}而{0,1,3,5}既不属于{0},也不属于{1,2,3,4,5} ∵{4} a {0},所以得新分划 (2)Π1:{0},{4},{1,2,3,5} 对{1,2,3,5}进行审查: ∵{1,5} b {4}{2,3} b {1,2,3,5},故得新分划 (3)Π2:{0},{4},{1, 5},{2,3} {1, 5} a {1, 5}{2,3} a {1,3},故状态2和状态3不等价,得新分划 (3)Π3:{0},{2},{3},{4},{1, 5} 这是最后分划了 (4)最小DFA :======================================= 4.构造一个DFA ,它接收Σ={0,1}上所有满足如下条件的字符串:每个1都有0直接跟在右边。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正则式
规则1 A→xB B→y 规则2 A→xA|y
规则3 A→x A→y
A=xy A=x*y
A=x|y
用代入法解正规式方程组
最后只剩下一个开始符号定义的正则式,其中不含 非终结符
1. 将每条产生式改写为正规式
由S → 0A | 1B 由A → 1S | 1
由B → 0S | 0
得 S=0A | 1B
S = (01|10)*(01|10)
作业中的问题 正规文法到正规式可以直接转换,不用将正规 文法转换成DFA,再将DFA转换成正规式 错误1:将(01|10)*(01|10)写成= (01|10)*
错误2:将(01|10)*(01|10)写成(01|10)+,在正规式 中可以出现的算符只有‘.’,‘*’, ‘(’, ‘)’, ‘|’,没有‘+’
{ T0,T1,T2,T3} { T4 } { T5 }
{ T0,T1,T2} {T3} { T4 } { T5 }
{ T0} {T1,T2} {T3} { T4 } { T5 }
在等价状态子集{T1,T2}中选状态T2做代表,消去其 他状态T1,把从消去状态T1射出和射入的弧都引到代 表状态T2上 0 T0 1 T1 0 1 T2 T3 1
Y
(0|1)* 2 0|1 ε 5 0 ε 5 2 2 1 3 4 1 0 1
X
3
4 0
Y
1 Y
1
3
0
4
1 Y
X
0 1
A0 A1
ε
A2
ε
A3
1
A4
0
A5
1
A6
1
(2)将NFA转换成DFA 采用子集法,即DFA的每个状态对应NFA的一 个状态集合 构造DFA的状态集C,假定C={T0,T1,…Ti},
第三章 词法分析 第1题 构造正规式相应的DFA:1(0|1)*101 由正规表达式构造有穷自动机,共分三步: 1) 由正规表达式构造转换系统(NFA)
2) 由转换系统(NFA)构造确定的有穷自动 机DFA 3) DFA的最小化
(1)构造与1(0|1)*101等价的 NFA
1(0|1)*101
X
1 1 1 X 1 1 1 ε ε
T0 T1 T2 T3 T4 T5
Ti0 {} {A2,A3 }=T2 {A2,A3 }=T2 {A2,A5,A3}=T4 {A2,A3 }=T2 {A2,A5,A3}=T4 0
Ti1 {A1,A2,A3}=T1 {A2,A4,A3}=T3 {A2,A4,A3}=T3 {A2,A4,A3}=T3 {A2,A4,A6,A3}=T5 {A2,A4,A3}=T3
DFA的状态转换图 T0 1 T1 0 T2 0 1
1 T3 0 T4 1
0 1 T5
1
(3)化简DFA:分割法,把DFA的状态集分成一些 不相交的子集,使得不同的两子集的状态是可区别的, 同一子集的状态是等价的。 0 T0 1 1 T2 T3
0
0 T4 1
1
T1
0
0
1
T5
1
首先,将状态分成两个子集:一个由终态组成,一个 由非终态组成: { T0,T1,T2,T3,T4 } { T5 }
0
0 T4 1 1 T5
0
1
得到化简后的DFA: 0 0 1 1 0 0
T0
1
T2Βιβλιοθήκη T3T41
1
T5
作业中的问题:
1. 只给出了NFA,没有转换成DFA,或者没有进行 DFA的化简
2. 按课本上的方法构造的NFA,这种方法引进的状态 个数和标记为ε的边较多,给转换成DFA带来了麻烦, 容易出错 与1(0|1)*101等价的NFA为: ε
错误3:转换到这一步S = 01S|01|10S|10的时候,
=(01S|01) | (10S|10) 由S=01S|01,得 S=(01)*(01)
由S=10S|10,得S=(10)*(10)
最终得正规式(01)*(01) | (01)*(01),是错误的 规则2:A→xA|y 得A=x*y 规则3:A→x|y (A→x A→y)得A=x|y 规则2和3都是描述“或”产生式如何转换,规则2 中A递归定义,规则3不是,产生式递归定义的时 候,产生式中的或关系,不能对应到正规式的或关 系上 如规则2不能按规则3来转换,得A=x*x和 A=y,最 终得正规式x*x|y。
(用规则3:A→x A→y得 A=x|y)
得A=1S | 1 (用规则3)
得B=0S | 0 (用规则3)
2. 用代入法解正规式方程组,将A、B代入S解方程组 S = 0(1S|1) | 1(0S|0) =01S|01|10S|10=(01|10)S|(01|10) 用规则2:A→xA|y 得 A=x*y
ε 1 ε 2 4 ε
0
1
X
1
0
ε
3 ε
5
ε
6
ε
7
1
8
0
9
1
Y
3. 区分NFA和DFA:
NFA有标记为ε的边而DFA没有
DFA中一个状态对应一个输入符,转向一个状态, 而NFA中一个状态对应一个输入符,转向一个状态 集合。
0 1 5 1 1 0 1 Y 4
不是DFA
X
3
第2题 给出下述文法所对应的正则式: S → 0A | 1B A → 1S | 1 将正规文法转换称正规式 将每条产生式改写为正规式 产生式到正则式的转换规则: 文法产生式 B → 0S | 0
其中T0= ε- closure(A0), 对于任何a∈Σ
Tia= ε-closure(Move(Ti,a))
0 1
A0 A1
ε
A2
ε
A3
1
A4
0
A5
1
A6
1 Ti {A0} {A1,A2,A3} {A2,A3 } {A2,A3,A4} Ti0 Ti1 {A1,A2,A3}=T1 {A2,A4,A3}=T3 {A2,A4,A3}=T3 {A2,A4,A3}=T3
T0 { }
T1 {A2,A3 }=T2 T2 {A2,A3 }=T2 T3 {A2,A5,A3}=T4 T4 {A2,A3 }=T2
{A2,A3,A5}
{A2,A4,A6,A3}=T5
{A2,A4,A3}=T3
{A2,A3,A4,A6} T5 {A2,A5,A3}=T4
Ti {A0} {A1,A2,A3} {A2,A3 } {A2,A3,A4} {A2,A3,A5} {A2,A3,A4,A6}
从描述的语言上看: S→ 01S|01|10S|10,以及它的正确转换 (01|10)*(01|10),描述的都是01和10,任意次 序,任意多个组成的串,如10010110…, 而错误的转换(01)*(01) | (01)*(01),描述的是 01组成的任意长的串,如010101…或者10组 成的任意长的串101010…,与原文法描述的 语言不等
