数控机床插补运算
数控技术(插补)

xi +1 = xi + 1 yi +1 = yi Fi +1 = xe y i −( xi + 1) ye = ( xe yi − xi ye ) − ye
于是有 Fi+1 = Fi -Ye
E(xe,ye) Pi(Xi,Yi) Pi+1(Xi+1,Yi+1)
0
x
第三章轮廓加工的数学基础
为了逼近曲线的相对位置沿 2).若Fi<0为了逼近曲线的相对位置沿+y向走 为了逼近曲线的相对位置 一步即 y
y E(xe,ye)
0
x
设动点pi ( xi , yi )的Fi 值为
为便于计算机编程计算, 为便于计算机编程计算,
Fi = xe yi − xi ye
y
的计算予以简化。 将F的计算予以简化。 的计算予以简化 为了逼近曲线的相对位置沿 向走一步 向走一步, 1).若Fi>0为了逼近曲线的相对位置沿+x向走一步,即 为了逼近曲线的相对位置
第三章轮廓加工的数学基础
3.1.1直线插补原理 3.1.1直线插补原理 1.偏差函数 1.偏差函数
如图所示, 如图所示,设规定轨迹为 直线段OE,起点在原点,终 起点在原点, 点E的坐标A(XeYe) , Pi(xi, yi)为加工点 。
Y
E ( Xe,Ye)
Pi(xi,yi) 0 x
则下式成立。 (1).若P正好处在 OE 上,则下式成立。
3
F<0 ∆Y F=F+5 5
F计算 计算 -3 终点判别(n-1→n) → 终点判别 7 ≠0 6 ≠0 5 ≠0 4 ≠0 3 ≠0
0
Pi(xi,yi)
数控机床装置的插补原理

▪ ④终点判别:
▪ 可采用二种方法,一是每走一步判断最大坐标的终点坐标 值(绝对值)与该坐标累计步数坐标值之差是否为零,若 等于零,插补结束。二是把每个程序段中的总步数求出来, 即N=Xe+Ye,每走一步,进行N-1,直到N=0时为止。因 而直线插补方法可归纳为:
▪ 当F0时,沿+X方向走一步,然后计算新的偏差和终点判 别计算
▪ c:只设置一个计数器J,存入两坐标方向的进 给总步数之和,无论X还是Y进了一步,J就减1, 直至J=0,表示达到终点。
▪ d:设置一个长度计数器J,存入某个选定计数 方向的计数长度,加工时,该方向每进一步,J 就减去1,直至J=0,表示达到终点。
▪ 加工直线时,计数方向的选取原则是:取终点坐 标值较大(即进给距离较大)的坐标方向作为计 数方向。
▪ 其中(Xi,Yi)为第一象限内任一点坐标, Y
▪ 根据动点所在区域不同,有下列三种情况:
▪
F>0
动点在圆弧外
▪
F=0
动点在圆弧上
▪
F<0
动点在圆弧内
X
▪ 设圆弧上任点坐标为(X,Y),则下式成
立:
( x 2 y 2 ) ( xo2 yo2 ) 0
选择判别函数F为
F ( xi2 yi2 ) ( xo2 yo2 )
其中(Xi,Yi)为第一象限内任一点坐标,
根据动点所在区域不同,有下列三种情况:
F>0
动点在圆弧外
F=0
动点在圆弧上
F<0
动点在圆弧内
我们把F〉0和F=0合并在一起考虑,按下述原则,就可以实现第一象限逆时针方
▪ F(x,y)>0,点在曲线上方;
▪ F(x,y)=0,点在曲线上;
数控机床的工作原理

终点判别 N=12
N=12-1=11 N=12-2=10 N=12-3=9 N=12-4=8 N=12-5=7 N=12-6=6 N=12-7=5 N=12-8=4 N=12-9=3 N=12-10=2 N=12-11=1 N=12-12=0
圆弧插补的象限处理
四个象限圆弧插补进给方向和偏差计算
其他象限的圆弧插补以|Xi|和|Yi|代替Xi和Yi。
-X
F2,2=F2,1+|Xe|=2 F3,2=F2,2-|Ye|=-1
n=3+1=4<N n=4+1=5<N
6
F3,2=-
+Y
1<0
F3,3=F3,2+|Xe|=3
n=5+1=6<N
2. 逐点比较法圆弧插补
如右图所示逆圆弧AE,C、D、B点分别在圆弧的外、
内部和圆弧上。
C点在圆弧的外部,则有
y
(X
+ΔX -ΔX -ΔX
Fi1 Fi 2Yi 1 Yi1 Yi 1
+ΔY -ΔY +ΔY
NR3(逆)
+ΔX
-ΔY
圆弧插补举例
用逐点比较法加工第二象限顺圆弧AB,起点为A (-5,0),终点为B(-3,4)
序
偏差判别
进
号
给
偏差计算
终点判别
0
F5,0=0
N=6
1
F5,0=0
+X
2
F4,0=-9<0
N=6-1=5 N=6-2=4 N=6-3=3 N=6-4=2 N=6-5=1 N=6-6=0
A(-4,3)
插补轨迹
y
y B(-3,4)
数控机床逐点比较法圆弧插补
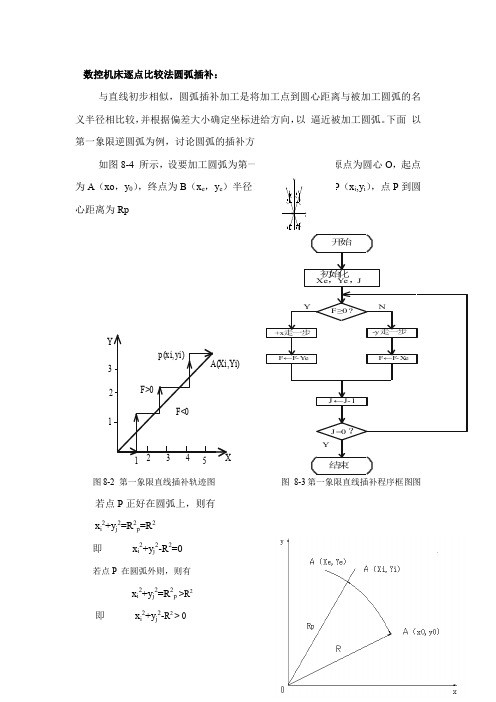
第一象限逆圆弧为例,讨论圆弧的插补方法。
如图8-4 所示,设要加工圆弧为第一象限逆圆弧AB ,原点为圆心O ,起点为A (xo ,y 0),终点为B (x e ,y e )半径R ,瞬时加工点为P (x i ,y i ),点P 到圆心距离为Rp<0+△y>0-△x <0+△x <0+△y>0-△x<0-△y <0-△y>0+△x yx图8-2 第一象限直线插补轨迹图 图 8-3第一象限直线插补程序框图图12345X123YF>0p(xi,yi)A(Xi,Yi)F<0开始初始化Xe ,Y e ,JF≥0?+x 走一步F←F -Y e F←F -X e-y 走一步YNJ ←J-1J =0?Y结束若点P 在圆弧内则,则有x i2+y j2=R2p<R2即x i2+y j2-R2 < 0显然,若令F i,j= x i2+y j2-R2(8-4)图8-4 逆圆弧插补则有:(1)F i,j= F i,j=0, 则点P在圆弧上(2)F i,j >0则点P在圆弧外则(3)F i,j<0则点P在圆弧不则常将8-4称为圆弧插补偏差判别式。
当F i,j≥时,为逼近圆弧,应向-x方向进给一步;当F i,j<0时,应向+y 方向走一步。
这样就可以获得逼近圆弧的折线图。
与直线插补偏差计算相似,圆弧插补的偏差的计算也采用递推的方法以简化计算。
若加工点P(x i,y i)在圆弧外或者圆弧上,则有:F i,j=x i2+y j2-R2≥0 为逼近该圆沿-x方向进给一步,移动到新加工点P(x i=1,y i),此时新加工点的坐标值为x i+1=x i-1,y i=y i新加工点的偏差为:F i+1,j=(x i-1)2+y i2-R2=x i2-2x i+1+ y i2-R2= x i2+ y i2-R2+1即F i+1,j= F i,j-2x i+1 (8-5)若加工P(x i,y i)在圆弧内,则有F i,j=x i2+y j2-R2<0若逼近该圆需沿+y方向进给一步,移到新加工点P(x i,y i),此时新加工点的坐标值图8-5 第一象限圆弧插补程序框图为新加工点的偏为:F i,j+1=x i2+(y i+1)2-R2=x i2+ y i2+1 -R2= x i2+ y i2-R2+1+2y iF i,j+1= F i,j-2y i+1 (8-6)从(8-5)和式(8-6)两式可知,递推偏差计算仅为加法(或者减法)运算,大大降低了计算的复杂程度。
数控机床直线插补公式

数控机床直线插补公式数控机床直线插补是数控机床加工过程中最基本的插补方式之一。
它通过控制机床的各轴运动,使切削工具按照一定的轨迹进行直线运动,实现对工件的加工。
直线插补是数控机床实现高速、高精度加工的关键技术之一。
首先,直线插补的数学模型是线性插补方程。
设机床坐标系为Oxyz,工件坐标系为OXYz,设直线的起点为P1(x1, y1, z1),终点为P2(x2, y2, z2)。
则直线插补方程可以表示为:x=x1+(x2-x1)*t;y=y1+(y2-y1)*t;z=z1+(z2-z1)*t,其中t为时间参数,取值范围为[0,1]。
通过控制t的变化,可以实现直线插补运动。
其次,直线插补的速度规划是实现高速加工的关键。
直线插补过程中,速度的规划要考虑到工件形状、机床的动态特性和加工精度要求等因素。
一般来说,直线插补速度规划可以分为两个阶段:加速段和匀速段。
加速段的目的是使机床迅速加速到设定的速度,而匀速段则是保持恒定的速度进行加工。
速度规划的目标是使机床在考虑动态特性和加工精度要求的前提下,尽可能地提高加工效率。
同时,直线插补的误差补偿是保证加工精度的关键。
由于机床本身的误差和外部环境的影响,直线插补过程中会产生一定的误差。
为了保证加工精度,需要对误差进行补偿。
误差补偿一般分为两类:静态误差补偿和动态误差补偿。
静态误差补偿是在刀具轨迹上对误差进行修正,常用的方法有坐标误差补偿、用户自定义的曲线修正等;而动态误差补偿是通过改变刀具轨迹,使得误差在加工过程中得以消除,常用的方法有加速度预测和最优轨迹规划等。
最后,直线插补的应用范围非常广泛。
它适用于各种形状的工件加工,如直线、圆弧、椭圆等。
在汽车制造、航空航天、电子设备等行业中,直线插补广泛应用于零件的加工。
直线插补可以实现高速加工和高精度加工,大大提高了生产效率和产品质量。
总结起来,数控机床直线插补是实现高速、高精度加工的重要技术。
它通过控制机床轴的运动,使切削工具按照一定的轨迹进行直线运动,从而实现对工件的加工。
数控系统插补的方法和原理

数控系统插补的方法和原理数控机床上进行加工的各种工件,大部分由直线和圆弧构成。
因此,大多数数控装置都具有直线和圆弧的插补功能。
对于非圆弧曲线轮廓轨迹,可以用微小的直线段或圆弧段来拟合。
插补的任务就是要根据进给速度的要求,在轮廓起点和终点之间计算出若干中间掌握点的坐标值。
由于每个中间点计算的时间直接影响数控装置的掌握速度,而插补中间点的计算精度又影响整个数控系统的精度,所以插补算法对整个数控系统的性能至关重要,也就是说数控装置掌握软件的核心是插补。
插补的方法和原理许多,依据数控系统输出到伺服驱动装置的信号的不同,插补方法可归纳为脉冲增量插补和数据采样插补两种类型。
一、脉冲增量插补这类插补算法是以脉冲形式输出,每次插补运算一次,最多给每一轴一个进给脉冲。
把每次插补运算产生的指令脉冲输出到伺服系统,以驱动工作台运动。
一个脉冲产生的进给轴移动量叫脉冲当量,用δ表示。
脉冲当量是脉冲安排计算的基本单位,依据加工的精度选择,一般机床取δ=0.01mm,较为精密的机床取δ=1μm或0.1μm 。
插补误差不得大于一个脉冲当量。
这种方法掌握精度和进给速度低,主要运用于以步进电动机为驱动装置的开环掌握系统中。
二、数据采样插补数据采样插补又称时间标量插补或数字增量插补。
这类插补算法的特点是数控装置产生的不是单个脉冲,而是数字量。
插补运算分两步完成。
第一步为粗插补,它是在给定起点和终点的曲线之间插入若干个点,即用若干条微小直线段来拟合给定曲线,每一微小直线段的长度△L 都相等,且与给定进给速度有关。
粗插补时每一微小直线段的长度△L 与进给速度F和插补T周期有关,即△L=FT。
图1 数据采样插补其次步为精插补,它是在粗插补算出的每一微小直线上再作“数据点的密化”工作。
这一步相当于对直线的脉冲增量插补。
数据采样插补方法适用于闭环、半闭环的直流或沟通伺服电动机为驱动装置的位置采样掌握系统中。
数控机床其它插补方法介绍

时间分割插补法是典型的数据插补方法。
3、扩展DDA数据采样插补法
扩展DDA算法是在数字积分原理的基础上发展起来的。
课堂总结
1、数字积分插补法及直线插补算法;
2、数据采样插补法的相关知识。
15
5分
3、例题
设有一直线OA,起点为原点O,终点A坐标为(8,10),累加器和寄存器的位数为4位,其最大容量为24=16。试用数字积分法进行插补计算并画出走步轨迹图。
4、习题
(1)设有一直线OA,起点为原点O,终点A坐标为(7,11),累加器和寄存器的位数为4位,其最大容量为24=16。试用数字积分法进行插补计算并画出走步轨迹图。
设加工第一象限逆圆AB,已知起点A(8,0),终点B(0,8)。试进行插补计算并画出走步轨迹图。
讲授新课
一、数字积分插补法
主要采用图解法、讨论法、引导法和演示法。
1、概述
数字积分法又称数字微分分析法(DDA),是在数字积分器的基础上建立起来的一种插补法。
数字积分法具有运算速度快、脉冲分配均匀、易实现多坐标联动等优点。
学生练习习题,巩固所学的知识
6分
10分Biblioteka 8分20分教与学互动设计
教师活动内容
学生活动内容
时间
6、例题
设加工第一象限逆圆弧,其圆心在圆点,起点A坐标为(6,0),终点B(0,6),累加器为三位,试用数字积分法插补计算,并画出走步轨迹图。
二、数据采样插补法
主要采用讲解法、引导法和归纳法。
1、概述
数据采样插补用小段直线来逼近给定轨迹,插补输出的是下一个插补周期内各轴要运动的距离,不需要每走一个脉冲当量插补一次,可达到很高的进给速度。
教案
数控机床的插补原

多项式插补的优缺点
优点
多项式插补能够生成光滑的曲线,适用于复杂形状的加工;可以通过增加控制点来提高插补精度;可以处理多种 类型的插补需求。
缺点
计算量大,需要较高的计算能力;对于某些特殊形状的加工,可能需要特殊的多项式函数形式;需要精确的已知 数据点,否则可能导致插补误差较大。
05
样条插补
样条插补的定义
样条曲线法
样条曲线法是一种更加高级的插补方法,它使用多项式样 条曲线来描述加工路径,能够实现更加复杂的形状加工, 并提高加工精度和表面质量。
插补算法的精度和效率
精度
插补算法的精度是衡量其性能的重要指标之一。高精度的插 补算法能够生成更加精确的路径,从而提高加工精度和表面 质量。
效率
插补算法的效率也是需要考虑的因素之一。高效的插补算法 能够缩短加工时间,从而提高生产效率。在实际应用中,需 要根据具体需求选择精度和效率之间的平衡点。
确定已知数据点
首先需要确定起始点和终止点的坐标位置,以及可能的其他控制点。
构造多项式函数
根据已知数据点,选择合适的多项式函数形式,如线性函数、二次函 数或更高次的多项式。
求解插值方程
通过求解插值方程,得到多项式函数的系数,使得该函数在已知数据 点处的值与实际值相等。
生成加工路径
将多项式函数与机床的坐标系统关联起来,生成加工路径,控制机床 的运动轨迹。
04
多项式插补
多项式插补的定义
多项式插补是一种数学方法,用于在 两个已知数据点之间生成一条光滑曲 线。它通过构造一个多项式函数来逼 近给定的数据点,使得该函数在数据 点处的值与实际值尽可能接近。
VS
在数控机床中,多项式插补被用于生 成零件加工的路径,使得加工过程更 加精确和光滑。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10
3.泰勒展开的NURBS曲线插补及实现
数控机床的插补运算
PPT模板下载:/moban/ 节日PPT模板:/jieri/ PPT背景图片:/beijing/ 优秀PPT下载:/xiazai/ Word教程: /word/ 资料下载:/ziliao/ 范文下载:/fanwen/ 教案下载:/jiaoan/
式中:
(i=0,1,…,n)为权因子,分别与控制顶点 (i=1,2,…,n)相联系;
是由节点矢量U=[
]。按德布尔-考克斯递推公式决定的k次规范
B样条基函数。递推公式为:
2.插补的预处理 插补就是求出每个周期下一个插补点的坐标,用递推算法最为合理,为避免每步 插补的重复递推,以免影响插补的实时性,经典的DeBoor递推算法的显示表示方 法最为合适。在不影响精度的情况下,为避免繁琐的计算,采用三次NURBS曲线。 义 NURBS插补 曲面插补 高速高精度采样插补技术 数控技术的发展趋势
数控技术发展历程 从1952年诞生世界上第一台数控铣床开始到现在,数控技术的发 展大致经历了两个阶段和六个时代。
1、NC阶段: 随着电子器件的发展,NC阶段的数控系统经历了三个时代: 第一代数控:1952一1959年采用电子管构成数控系统。第二代数控:从1959 年开始采用晶体管构成数控系统。第三代数控:从1965年开始采用小、中规 模的集成电路。以上所述的三代数控系统,机床的各项功能控制,都是由硬 件逻辑完成的,因此称它们为“硬线”数控(亦即NC)。NC一经设计之后,就 无法进行更改,而且电路复杂,难于编程,限制了其进一步的发展和应用。
插补在数控技术中的重大作用
插补控制功能是数控制造系统的一个重要组成部分,是数控技术中的 核心技术。它的性能直接代表制造系统的先进程度,它的好坏直接影 响着数控加工技术的优劣,是目前数控技术急需提高和完善的环节之 一。
插补的含义 插补,就是根据零件轮廓的几何形状、几何尺寸以及轮廓加工的精度 要求和工艺要求,在零件轮廓的起点和终点之间插入一系列中间点 (折线端点)的过程,即所谓“数据点的密化过程”,其对应的算法 称为插补算法。
与直线插补对比NURBS插补的优点
由于插补周期非常小,每个周期内刀具走过的距离也非常小,可近似认 为其与该圆弧段的弧长相等,则瞬时速度 V(t)近似为机床进给速度。
4.算法的实现 根据数据采样插补法,实时插补的任务是根据给定的进给速度产生插 补直线,用以逼近实际曲线,求得各坐标轴的进给增量。计算公式为:
其中 为进给步长,由于CNC系统的插补周期已知,为T实时插补 当前的速度为 ,则当前插补周期的无约束进给步长为:
NURBS曲线插补算法将定义NURBS曲线的三个参数(控制顶点、权 因子、节点矢量)和进给速度等作为NC程序指令,在CNC系统内部生 成NURBS曲线,驱动机床动作,加工出NURBS曲线的形状,即为NURBS 曲线插补。在参数空间中,曲线轨迹参数u的插补计算可由二阶泰 勒级数表示:
其中:
插补周期
根据微分几何知识,曲线上第i个插补点的瞬时速度为
机床运动
高速高精度采 样插补技术
大幅度提高采样插补频率 有实效地提高系统分辨率
NURBS插补
NURBS 曲线由以下三个参数定义: l )控制顶点确定曲线的位置,通常不在曲线上。 2 )权因子w ,确定控制点的权值,它相当于控制点的“引力”,其值 越大曲线就越接近控制点。 3 )节点矢量NURBS 曲线随着参数的变化而变化,与控制顶点相对应的 参数化点,称为节点,节点的集合称为节点矢量。
2、CNC阶段 1970年,在美国芝加哥机床的博览会上,展出了由小型计算机为核心的计算 机数控系统(CNC),标志着数控系统进入了以计算机为主体的第四代。 1974年,出现了以微处理器为基础的CNC,象征着数控系统进入第五代。 1977年,美国麦道飞机公司推出了多处理器的分布式CNC系统,使CNC进入第 六代。其特征是大规模集成电路,大容量高可靠的磁泡存储器的应用,可编 程接口和为FMS用的遥控接口,控制功能更为完备,基本上完成了标准型单机 系统的开发。
行业PPT模板:/hangye/ PPT素材下载:/sucai/ PPT图表下载:/tubiao/ PPT教程: /powerpoint/ Excel教程:/excel/ PPT课件下载:/kejian/ 试卷下载:/shiti/
若将定义NURBS 曲线的三个参数(控制点、权值、节点矢量)作为NC 程序指 令的一部分,让CNC 在内部计算并生成NURBS 曲线,并按照该NURBS 曲线 醚动机床动作,加工出NURBS 曲线的形状,这就是NURBS 插补。
NURBS曲线理论
1.NURBS曲线插补的数学模型 一条k次NURBS曲线可以表示为一分段有理多项式矢函数:
NURBS插补
定义NURBS 曲线的三个参数 (控制点、权值、节点矢量)作 为NC 程序指令的一部分,让
CNC 在内部计算并生成 NURBS 曲线,并按照该 NURBS 曲线醚动机床动作, 加工出NURBS 曲线的形状
插补 分类
曲面插补
将曲面加工的复杂刀具运动轨 迹产生功能集成到CNC中,由 CNC直接根据待加工曲面的几 何信息和工艺参数实时地完成 连续刀具轨迹插补,以此控制
