华科船舶静力学大作业
华南理工大学_814船舶静力学2004--2017年_考研真题

第
2 页
4.(13 分)某内河船的排水量=580t,重心高 zG=2.5m,浮心高 zC=1.56m,该船各横倾 角的形状稳性力臂如下表: 10 20 30 40 50 60 0 ls(m) 0.390 0.715 0.970 1.110 1.150 1.130 请列表计算和绘制出静稳性臂曲线和动稳性臂曲线, 根据所绘制的静稳性臂曲线和动 稳性臂曲线求出: (1)最大复原力臂、最大复原力矩、极限静倾角。 (2)该船正浮时(ϕ0=0o) ,在外力作用下所能承受的最大动倾力矩以及与之对应的 动倾角。 (3)当横摇角 ϕ0=-15o 时,在外力作用下所能承受的最大动倾力矩和与之对应的动倾 角。
814
华南理工大学 2017 年攻读硕士学位研究生入学考试试卷
(试卷上做答无效,请在答题纸上做答,试后本卷必须与答题纸一同交回) 科目名称:船舶静力学 适用专业:船舶与海洋工程;船舶与海洋工程(专硕) 共 3 页 一、填空题(每小题 1.5 分,共 15 分) 1.梯形法基本原理是:用若干直线段组成的 近似地代替曲线,即以若干梯形 面积之和来代替 曲线下所包围的面积。 2.船舶漂浮的平衡条件为 ; 。 3. 军用舰艇五种典型的排水量为: 、标准排水量、 、满载排水 量、 。 4.对于民用船舶来说,两种最基本的典型排水量为: 和 。 5.船舶由淡水驶入海水时, 不变, 发生了变化,还有可能发生 。 6.在等体积倾斜的情况下, 的交线必然通过原水线面的 。 7.静水力曲线是将船舶在正浮状态的 与 之间的函数 关系绘制在同一张图上。 8.利用 曲线可方便地求得船舶在纵倾状态下的 。 9.从动稳性角度考虑,在船舶倾斜过程中当稳性力矩等于外力矩时,船舶仍不能终止 倾斜是因为 大于 。 10.大倾角静稳性臂公式 l=lb-lg 中,lb 称为 ,lg 称为 。 二、名词解释(每小题 2.5 分,共 25 分) 1 三舱制船 2.极限动横倾角 3.棱形系数 4.损失浮力法 5.正浮 6.稳性消失角 7.设计水线长
船舶静力学习题答案

Exercise 1-3
某内河驳船的水下体积V=4400m3,吃水d=2.6m,方形系数Cb=0.815,水线面系 数Cw=0.882,求水线面面积Aw。
已知:Cb=0.815;Cw=0.882;V=4400t 解:Cvp=Cb/Cw=0.815/0.882=0.924
∵Cvp=V/(Aw.d) ∴Aw=V/(Cvp.d)=4400/(0.924*2.6)=1831.5 m2
Exercise 1-1
∵Am=πr2/2 Aw=2*0.2*4r*r=4r2 V=1/3(πr2)*2r=2/3 πr3
∴Cm=Am/(2r*r)= π/4=0.785 Cp=V/(1/2πr2*4r)= 1/3=0.333 Cwp=Aw /(4r*2r)= 1/2=0.500 Cb=V/(4r*2r*r)=π/12=0.261 Cvp=V/(4r2*r)=π/6=0.522
船舶静力学作业
船舶静力学习题答案
响砂山月牙泉
Exercise 1-1
1-1 两相等的正圆锥体在底部处相连接,每个锥体的高等于其底部直径.这个组 合体浮于水面,使其两个顶点在水表面上,试绘图并计算: (1)中横剖面系数Cm,(2)纵向棱形系数Cp, (3)水线面系数Cw,(4)方形系数Cb。
V=(A *h)/3 d
Exercise 1-4源自各站型值:Bx2
y2[1(0.5L)2]
序
0
1
2
3
4
5
6
7
8
9
10
x -30
-24
-18
-12
-6
0
6
12
18
24
30
y
0
1.512 2.688 3.528 4.032 4.2 4.032 3.528 2.688 1.512
华科大有限元分析题及大作业题答案——船海专业(DOC)

图1-9(a)NDIV为5的网格划分及约束受载图
图1-9(b)NDIV为5的位移分布图
图1-9(c)NDIV为5的应力分布图
(2)NDIV为10的常应变三节点单元(单元数80)
图1-10(a)NDIV为10的网格划分及约束受载图
图1-10(b)NDIV为10的位移分布图
姓名:
学号:
班级:
有限元分析及应用作业报告
一、问题描述
图示无限长刚性地基上的三角形大坝,受齐顶的水压力作用,试用三节点常应变单元和六节点三角形单元对坝体进行有限元分析,并对以下几种计算方案进行比较:
1)分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算;
2)分别采用不同数量的三节点常应变单元计算;
3)定义材料参数
4)生成几何模
a. 生成特征点
b.生成坝体截面
5)网格化分:划分网格时,拾取所有线段设定input NDIV 为10,选择网格划分方式为Tri+Mapped,最后得到200个单元。
6)模型施加约束:
约束采用的是对底面BC全约束。
大坝所受载荷形式为Pressure,作用在AB面上,分析时施加在LAB上,方向水平向右,载荷大小沿LAB由小到大均匀分布(见图1-2)。以B为坐标原点,BA方向为纵轴y,则沿着y方向的受力大小可表示为:
(Hale Waihona Puke )其中ρ为水的密度,取g为9.8m/s2,可知Pmax为98000N,Pmin为0。施加载荷时只需对LAB插入预先设置的载荷函数(1)即可。
网格划分及约束受载情况如图1-3(a)和1-4(a)所示。
7)分析计算
8)结果显示
四、计算结果及结果分析
船舶静力学习题答案共60页

11、用道德的示范来造就一个人,显然比用法律来约束他更有价值。—— 希腊
12、法律是无私的,对谁都一视同仁。在每件事上,她都不徇私情。—— 托马斯
13、公正的法律限制不了好的自由,因为好人不会去做法律不允许的事 情。——弗劳德
14、法律是为了保护无辜而制定的。——爱略特 15、像房子一样,法律和法律都是相互依存的。——伯克
谢谢!
51、 天 下 之 事 常成 等 于是呼 吸,生 命是活 动。——卢 梭
53、 伟 大 的 事 业,需 要决心 ,能力 ,组织 和责任 感。 ——易 卜 生 54、 唯 书 籍 不 朽。——乔 特
55、 为 中 华 之 崛起而 读书。 ——周 恩来
船舶静力学讲稿

绪论船舶静力学是研究船舶航海性能的科学,是船舶设计与制造专业的一门重要专业技术基础课程,本学科要求有《高等数学》、《材料力学》、《理论力学》、《流体力学》等学科作为基础,也是今后学习《船舶强度与结构规范设计》、《船舶设计原理》、《造船工艺学》等课程的基础,因此要求同学们重视这门课的学习。
本课程包括六章。
其中第六章船舶的下水计算因在造船工艺学有阐述故在船舶静力学中不加以阐述。
第二、三、四章是重点章节。
通过本课程的学习,学生应对船舶浮性、稳性、抗沉性有一个全面的了解,在船舶设计时保证船舶具有合理的浮态(船舶在静水中的平衡状态,参数有吃水d、横倾角θ以及纵倾角ψ)和足够的稳性和抗沉性,同时学生应掌握衡量船舶稳性、浮性、抗沉性各种指标及其计算方法,能在设计时提供各种必要的计算说明书和曲线等数据。
一、船舶原理的内容船舶原理是研究船舶航海性能的科学。
(1)浮性——船舶在一定的装载情况下浮于一定水面位臵的能力(保持平衡位臵能力)。
(2)稳性——船舶在外力作用下,船舶发生倾斜而不致倾覆,当外力的作用消失后,仍能回到原来的平衡位臵的能力。
(3)抗沉性——当船体破损,海水进入舱室,船舶仍能保持一定的浮性和稳性而不致沉没和倾覆的能力。
(4)船舶快速性(速航性)——船舶尽可能消耗低的功率而达到一定航速的能力,包括船舶阻力与推进两部分,前者研究船舶在航行过程所遭受的各种阻力。
后者是研究克服阻力的推进器及其与船体间的相互作用(推力减额和伴流分数)。
(5)适航性(或称耐波性)——船舶在风流情况下的运动性能,主要研究船舶的横摇(rolling)、纵摇(pithing)、升沉等习惯上称为摇荡(摇摆、振荡)(6)操纵性——包括航向稳定性和船舶机动性(航向稳定性和船舶机动性是相互制约的,对船体的要求也是相互制约的)是按照驾驶员的意图保持原定航向和改变航向的能力。
船舶原理=船舶静力学+船舶动力学船舶静力学是以流体静力学为基础,研究船舶在不同条件下的浮性、稳性、抗沉性等问题。
华南理工大学《814船舶静力学》考研专业课真题试卷

四、计算题(50 分) 1.(5 分)已知某游艇的排水体积 =30 m3,长宽比 L/B=5,宽度吃水比 B/d=2.8,方 形系数 CB=0.53。试求该游艇的主尺度 L,B 和 d。 2.(13 分)某海船船长 L=110 m,首吃水 dF=4.6 m,尾吃水 dA=5.1 m,每厘米吃水吨 数 TPC=97 t/cm,每厘米纵倾力矩 MTC=102 tm/cm,漂心纵坐标 xF=-3.8 m。今在船 上装载 100t 的货物,问装在何处可使船平浮?
第
1 页
3.(7 分)某海船水线间距为 0.5m,各水线对应的水线面积为: 0 1 2 3 水线 WL
4
42 151 194 242 242 水线面积 AW(m2) 求吃水为 2.0 m 时的排水体积,浮心垂向坐标 KB,垂向掕形系数 CVP 及每厘米吃水 吨数 TPC. 4. (12 分)已知某驳船的船长 L=50 m,吃水 d=3 m,排水体积=735 m3,重心垂向坐 标 KG=2.81m,浮心垂向坐标 KB 可按下式估算: KB
二、简答题(42 分) 1. 提高数值积分的方法有哪些? 2. 何谓邦戎曲线?它有什么用途? 3. 衡量船舶初稳性好坏的主要指标是什么?如何应用它判断船舶的稳定性?为什么 船通常是横向倾覆而不是纵向倾覆? 4. 船舶进水舱可分为哪几类?各有什么特点?μ=0.85 表示什么意思? 5. 船舶在纵向重力下水方式过程中,船尾上浮是船舶下水过程中必然发生的现象; 该现象出现在下水过程中的哪个阶段?可能出现哪些不利影响?可采取什么措施 消除不利的影响? 6. 静稳性曲线有哪些特征? 三、问答题(34 分) 1. 什么是船舶静水力曲线?它包括哪几种性质的曲线?静水力曲线有什么用途? 2. 船舶因重量移动产生了一个初始横倾角Φ0 ,现在船再受到一阵风作用,问阵风 自出水舷吹来危险?还是自入水舷吹来危险?请作图说明原因。
船舶静力学大题汇总
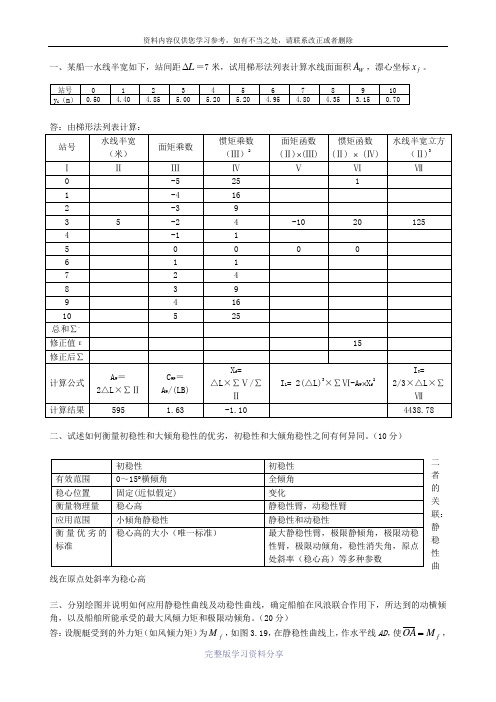
一、某船一水线半宽如下,站间距L ∆=7米,试用梯形法列表计算水线面面积W A ,漂心坐标f x 。
答:由梯形法列表计算:二、试述如何衡量初稳性和大倾角稳性的优劣,初稳性和大倾角稳性之间有何异同。
(10分) 二者的关联:静稳性曲线在原点处斜率为稳心高三、分别绘图并说明如何应用静稳性曲线及动稳性曲线,确定船舶在风浪联合作用下,所达到的动横倾角,以及船舶所能承受的最大风倾力矩和极限动倾角。
(20分) 答:设舰艇受到的外力矩(如风倾力矩)为f M ,如图3.19,在静稳性曲线上,作水平线AD ,使f M OA =,并移动垂线CD 使BCD OAB S S =,即可确定动横倾角d φ。
但是,由于要凑得两块面积相等,实际操作比较麻烦,故通常直接应用动稳性曲线来确定d φ。
φM R (l)o BA CφdoT R (ld )φM fDM fm a x φd57.3o M fM fm a xφd m a x φd m a x C 'A 'B 'D 'NC 1D 1图1 静、动稳性曲线的应用横倾力矩fM所作的功为 φφd M T f f ⎰=0由于fM为常数,所以fT 为一直线,其斜率为fM,故当1=φ弧度=53.3°时,ff M T =。
因此,在动稳性曲线上的横坐标=φ°处作一垂线,并量取f M得N 点,连接ON ,则直线ON 即为f T 随φ而变的规律。
fT 与TR 两曲线的交点C1表示横倾力矩fM所作的功与复原力矩MR 所作的功相等。
与C1点相对应的倾角即为d φ。
潜艇所能承受的最大风倾力矩max f M(或力臂m ax f l)在静稳性曲线图上,如图1所示,如增大倾斜力矩f M ,则垂线CD 将向右移,当D 点达到下降段上的D ‘位置时,'''''D C B B OA S S =,如倾斜力矩f M 再增大,复原力矩所作的功不能与倾斜力矩所作的功相等,所以,这时的倾斜力矩即为所求的最大倾斜力矩max f M (或力臂m ax f l ),D ‘点相对应的倾角称为极限动横倾角m ax d φ。
船舶静力学考研真题

船舶静力学考研真题船舶静力学是船舶与水的力学相互作用的研究,是船舶工程领域中的重要分支。
本文将通过一道船舶静力学考研真题,来探讨船舶静力学的相关知识。
一、题目描述某船舶的重心高度为G=12m,初始浮心高度为B=14m,船体折割点偏心量为e=1.6m。
当此船停泊在一水深为H=20m的水上时,请计算此时船舶是否会发生侧翻。
二、问题分析在本题中,我们需要计算船舶是否会发生侧翻,即判断船舶的倾覆稳定性。
船舶的倾覆稳定性受到重力和浮力的相互作用影响,需要通过计算浮力和重力的力矩来判断。
三、计算过程1. 确定水面与船体折割点间的距离:h = H - e = 20m - 1.6m = 18.4m。
2. 计算重力矩:Mg = G * Tg,其中Tg为船舶总重力。
3. 计算浮力矩:Mf = B * Tf,其中Tf为船舶的浮力。
4. 判断船舶是否会发生侧翻:- 若Mf > Mg,则船舶不会发生侧翻,稳定。
- 若Mf <= Mg,则船舶会发生侧翻,不稳定。
四、计算结果1. 计算重力矩:- 船舶总重力Tg = m * g,其中m为船舶的质量,g为重力加速度。
- 假设船舶的质量为100吨,则m = 100 * 1000 kg。
根据题目中给出的重心高度G=12m,计算得到:- Mg = G * Tg = 12m * 100 * 1000 kg * 9.8 m/s^2。
2. 计算浮力矩:- 船舶的浮力Tf = V * ρ * g,其中V为船舶的体积,ρ为水的密度。
由于题目未给出具体船舶形状和尺寸,故无法准确计算船舶的体积。
因此,我们假设船舶的体积为1000立方米。
同时,水的密度ρ = 1000 kg/m^3。
根据题目中给出的初始浮心高度B=14m,计算得到:- Mf = B * Tf = 14m * 1000 m^3 * 1000 kg/m^3 * 9.8 m/s^2。
3. 判断船舶是否会发生侧翻:- 若Mf > Mg,则船舶不会发生侧翻,稳定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
表4:表4给出了用不同船型不同方法在低速阻力 测试试验中得出的外形因子的汇总;从表中可以 看出,无论是直接法还是间接法,除了较小尺寸 的模型船都得到了较好的可以接受的结果,而用 间接法可以得出一致性更好的结果。特别地,间 接法更具有优势:得出的结果既不依赖于指数n也 不依赖于多项式方程的形式。因此选择以下约定 作为标准: » 直接法进行计算 » 取指数n=5 » 采用二次拟合
单击此处编辑母版标题样式 理论研究
然而,在模型试验中,还有一种方法能够在保持 傅汝德数相同的基础上改变雷诺数,即改变实船 与模型船之间的缩尺比。将缩尺比记为λ ,则雷 1 诺数与 λ^ .5成正比。
4、模型试验
1)本研究中,共选了12种不同的船型,如下表1 所示;模型试验从1992年到2006年共进行了15年, 如表2所示;
上式中,a是与波形阻力系数相关的常量;n代表波形 阻力的大小,是个常量。从物理的角度看指数n一般在4-6 之间变化,其值取决于船型。在本次研究中分别用n=4、5、 6来研究不同的指数取值对实验结果的影响。
单击此处编辑母版标题样式 理论研究
在间接法的计算中,用从低速船模试验中的数据 FnN/CFM和CTM/CFM对应,并为了应用方便,用如下 符号进行替换:
单击此处编辑母版标题样式 试验及分析
单击此处编辑母版标题样式 试验及分析
单击此处编辑母版标题样式 试验及分析
一般情况下,由于在速度十分接近设计速度 的时测量出的阻力值是离散的,所以在设计速度 下很难得出一致的有实际意义的形状因数。如表5 所示,然而,得到有实用价值的数据是完全有可 以的。 当得出在设计速度下的外形因数时,应当明白它 是另外的流体动力学问题。与低速范围的情形形 成对比,在设计速度下产生的船行波会影响到外 形阻力,也即是说外形阻力受到雷诺数和傅汝德 数的双重影响。然而没有方法去估计雷诺数、傅 汝德数和用目前的研究结果的得出的外形因子之 间的相互关系。
单击此处编辑母版标题样式 试验及分析
Table1
单击此处编辑母版标题样式 试验及分析
Table2
单击此处编辑母版标题样式 试验及分析
2)为了系统地分析试验结果,把选中的12种船型分为4 组:the fine higher-speed ship group, the gas carrier group, the full slow-speed ship group, and the special ship group;如下表所 示:
单击此处编辑母版标题样式 研究方向
所以研究ITTC提出的外形因子概念的有效性是非 常有必要的。因此作者进行了以下三个基本研究: (1)依据ITTC的定义求解船舶外形系数的方 法 (2)船舶外形因子与雷诺数之间的关系 (3)在给定航速时求解船舶外形系数的方法 所有基本的和必须的试验都是在HMRI(现 代重工海事研究所)的深水池中进行。试验水池 长220m,宽14m,深6m。一些特殊的测试在汉堡船 模试验水池(HSVA)和瑞典的SSPA进行。在本 文中,作者仅给出了在HMRL试验中得出的数据 与试验结果。
然后用最小二乘法对上式分别进行二次拟合 和三次拟合,即可将外形因子表示成常量形式。
单击此处编辑母版标题样式 理论研究
2、关于在设计航速下外形因子计算的建议
当雷诺数大于107时流体可以看成全部处于紊 流状态,此时的外形因子无限接近一个常量。因 此试验要尽可能在雷诺数大于107的速度下进行。 幸运的是作者发现当模型船的长度大于6m且当其 速度与实船的设计速度相对应时,这种情况就更 令人满意。 下面关于波形阻力系数的表达式是在当模型 速度与设计速度保持很小差别时外形因子几乎保 持为常量的假设的基础上引入的:
单击此处编辑母版标题样式 研究方向
汉堡船模试验水池(HSVA) HSVA home page: /valanto.htm SSPA简介:SSPA海事齐询公司设于CHARLMER理工大学校园 内。CHARLMER是瑞典著名的工学院,尤其是船舶工程。冷 战时期这里是绝密之地,至今仍保留着一套安全体系。然 而,更优秀的是发达的软件业即计算机辅助设计及电脑模 拟。 SSPA home page:http://www.sspa.se/home
5.实验结果及分析 5.实验结果及分析
1).低速阻力测试实验与外形因子的计算 如前面提到的,为了求取外形因子,对选定 的32条模型船反复地进行低速阻力测试试验。下 面图4、5、6展示了依据ITTC定义推出的外形因子 随傅汝德数变化的趋势:
图4:小尺寸模型船的阻力变化趋势与大尺寸的变化不同, 这种现象在试验中相当常见。因为在这一系列试验中雷诺 数约为10^5,此时船模周围的流体为层流或者过渡状态。
Fig. 3 Models of the 317,000-TDW very large crude carrier (VLCC)
Fig. 2 Models of the 155,000-m3 liquefied natural gas (LNG) carrier
单击此处编辑母版标题样式 试验及分析
单击此处编辑母版标题样式 试验及分析
单击此处编辑母版标题样式 试验及分析
单击此处编辑母版标题样式 试验及分析
单击此处编辑母版标题样式 试验及分析
Table 4 Sample form factors determined from low-speed resistance tests
单击此处编辑母版标题样式 试验及分析
单击此处编辑母版标题样式 理论研究
为此,作者尝试提出一种依据ITTC定义来计算船 舶外形因子的通用方法。 2).直接法 (1) 数据选取。 对于CTM/CFM的值来说需要极小的傅汝德数, 这就要求进行较低速的阻力测试。为了使用方便 进行如下代换: x=FN, y=CTM/CFM (6) 利用最小二乘法将数据拟合成下面的多项式 等式曲线:
在该理论中,利用ITTC'57曲线计算摩擦阻力系 数:
上式中,RN为雷诺数,V为船舶航行速度,L为船长, 为运动粘性系数 υ
单击此处编辑母版标题样式 ITTC'78简介 简介
单击此处编辑母版标题样式 ITTC'78简介 ITTC'78简介
尽管这个方法已经被ITTC所采取并作为标准 计算方法,然而依据该理论进行的实船阻力性能 预测的结果却随着模型试验水池的变化而变化, 这已是业内专家所熟知现象。这种现象的发生可 能是由两个原因造成:一是外形因子的确定,首 先在低速情况下测量阻力是十分困难的,所以根 据外形因子的定义准确地得出外形因数是十分困 难的;二是两个基本假设本身的准确性。 但事实上,作者也支持外形因子这个概念。 该作者认为无论在何种情况下,能够分别出与船 体外形有பைடு நூலகம்的阻力成分都是具有实际意义的。
单击此处编辑母版标题样式 试验及分析
3)为了求取外形因子,依据ITTC定义,对 32条模型船全部进行低速阻力测试试验; 对12条条模型船在速度接近设计航速时进 行阻力测试试验。下列图标分别给出了四 种模型船及相应的不同尺寸的模型:
单击此处编辑母版标题样式 试验及分析
Fig. 1 Models of the 8,600-TEU container carrier
单击此处编辑母版标题样式 理论研究
利用大型的模型船进行试验,在几个与设计 速度相差极小的速度下便可分别测出其对应的阻 力值,再将在两个相邻的速度上获得的阻力值带 入上述方程组便可解出外形因子和波形阻力因子。
单击此处编辑母版标题样式 理论研究
3、外形因子与雷诺数之间的联系
1)说明: 随着船舶速度的增大,产生的船行波对外形 阻力的影响便不断增强,也就是外形因子开始受傅汝德 数与雷诺数的双重影响。如果要研究船行波对外形阻力 的影响,还需要再一系列基本的研究。为了本研究的进 展,船行波对外形的影响已经被排除,即假设外形阻力 仅与雷诺数有关。 2)研究理论 为了研究外形因子与雷诺数之间的关系, 外形因子的测量应该在不同的雷诺数下进行。试验中如 果保持一定的实模比,应通过增大拖拽速度而使雷诺数 增加,但如此一来便不能够采用ITTC的定义来计算外形 因子了。
单击此处编辑母版标题样式 理论研究
1、利用ITTC定义计算外形因子的建议 利用ITTC定义计算外形因子的建议 ITTC
1).概要 模型船的总阻力系数表述如下: CTM=(1+k)CFM+CW (5) 如果能够同步地测量出模型船的总阻力和波形阻 力,那么利用式(5)便可求得较精确的外形因子。然 而,由于测量波形阻力不仅困难而且误差也很大,所以 这种方法并没有实际意义。此外,利用定义(2)直接 计算外形因子也是不可能的。而在实际应用中,通常通 过测量模型船低速运动的阻力来间接求取外形因子,可 问题是准确地测量模型船的低速阻力是很困难的。
单击此处编辑母版标题样式 试验及分析
2).在速度接近设计速度时的阻力测试和外形因 子的计算 回顾前面所述的计算方法:
在等式13中 取用不同的指数n 在等式13中,取用不同的指数n,既n=6,参数选 13 n=6, 取的依据是不同速度范围的波浪阻力理论。 取的依据是不同速度范围的波浪阻力理论。所有 为求取外形因子而进行的低速阻力试验和速度接 近设计速度的模型试验结果均被汇集在表5 近设计速度的模型试验结果均被汇集在表5中。
考虑到船体外形主尺度对船舶阻力的影响, 考虑到船体外形主尺度对船舶阻力的影响,1978 年国际拖曳水池会议(ITTC) 年国际拖曳水池会议(ITTC)通过了船舶阻力测 试方法,在两个基本假设的基础上引入了外形因 试方法, 子的概念。两个基本假设为: 子的概念。两个基本假设为: 1)模型船的外形因子与实船相同 2)外形因子与船舶航行速度无关 然而,依据ITTC'78定义的方法不仅很难确定外 ITTC'78定义 然而,依据ITTC'78定义的方法不仅很难确定外 形因子, 形因子,而且两个基本假设本身也有许多无法解 决的问题, 决的问题,为此作者进行了三次关于船体外形因 子的基本研究, 子的基本研究,为实船的阻力性能计算提出了一 个新的理论。 个新的理论。
