大学物理变化的电磁场总复习内容深入超赞
(完整word版)《大学物理》下册复习资料

《大学物理》(下) 复习资料一、电磁感应与电磁场1. 感应电动势——总规律:法拉第电磁感应定律 dtd m i Φ-=ε , 多匝线圈dt d i ψ-=ε, m N Φ=ψ。
i ε方向即感应电流的方向,在电源内由负极指向正极。
由此可以根据计算结果判断一段导体中哪一端的电势高(正极)。
①对闭合回路,i ε方向由楞次定律判断; ②对一段导体,可以构建一个假想的回路(使添加的导线部分不产生i ε)(1) 动生电动势(B 不随t 变化,回路或导体L运动) 一般式:() d B v b ai ⋅⨯=ε⎰; 直导线:()⋅⨯=εB v i动生电动势的方向:B v ⨯方向,即正电荷所受的洛仑兹力方向。
(注意)一般取B v⨯方向为 d 方向。
如果B v ⊥,但导线方向与B v⨯不在一直线上(如习题十一填空2.2题),则上式写成标量式计算时要考虑洛仑兹力与线元方向的夹角。
(2) 感生电动势(回路或导体L不动,已知t /B ∂∂的值):⎰⋅∂∂-=s i s d t Bε,B与回路平面垂直时S t B i ⋅∂∂=ε 磁场的时变在空间激发涡旋电场i E :⎰⎰⋅∂∂-=⋅L s i s d t B d E(B增大时t B ∂∂[解题要点] 对电磁感应中的电动势问题,尽量采用法拉第定律求解——先求出t 时刻穿过回路的磁通量⎰⋅=ΦSm S d B ,再用dtd m i Φ-=ε求电动势,最后指出电动势的方向。
(不用法拉弟定律:①直导线切割磁力线;②L不动且已知t /B ∂∂的值)[注] ①此方法尤其适用动生、感生兼有的情况;②求m Φ时沿B 相同的方向取dS ,积分时t 作为常量;③长直电流r π2I μ=B r /;④i ε的结果是函数式时,根据“i ε>0即m Φ减小,感应电流的磁场方向与回路中原磁场同向,而i ε与感应电流同向”来表述电动势的方向:i ε>0时,沿回路的顺(或逆)时针方向。
2. 自感电动势dtdI Li -=ε,阻碍电流的变化.单匝:LI m=Φ;多匝线圈LI N =Φ=ψ;自感系数I N I L m Φ=ψ= 互感电动势dt dI M212-=ε,dtdIM 121-=ε。
大学物理变化的电磁场总复习,内容深入超赞
本章难点:涡旋电场,位移电流,场概念的理解
11章
4
§1 电磁感应 一 法拉第电磁感应定律 二 动生电动势 三 感生电动势 涡旋电场
11章
5
§1 电磁感应 一、电磁感应定律 1.电磁感应现象
2.楞次定律(1833)
闭合回路中感应电流的方向,总是抵抗产生它的 原因。
外力为了维持导体的运动,须克服安培力做功。
如图,设长为l的导体匀速运动,外力的功率:
P=Fv=BIlv=I ,即电功率与外力的功率相等.
11章
15
例3.(11.9)与长度为a的导线OC共面放置一通有电
流I的长直导线,O端到无限长导线的距离为d,OC
以速度v沿如图所示方向运动,求CO两端电势差.
解. 取动生电动势的假定正
源的闭合线圈间有相对运动 初级载流线圈中电流即
11章产生的磁场发生变化.
8
对定律中物理量的说明: 任意指定回路的绕行方向,规定
(1)电动势方向与绕行方向一致时为正
(2)当磁场线方向与绕行方向成右螺时
磁通量为正
d 0
dt
与回路绕行方
向相反
L
d 0
dt
与回路绕行方 向相同
(这套方法严谨但繁琐,解题时不推荐用)
dB
dS
dt AEO
R2 (L / 2)2 dB
L
2
dt
11章
方向:AC
27
例7: 在半径为R的圆柱形空间存在轴向均匀磁场,一长
为2R的导体棒在垂直磁场的平面内以速度v 横扫过磁场。
磁场以 dB / dt变化0 ,求导体棒运动到图示位置时,
棒上感应电动势的大小和方向。
物理复习题电磁学重点梳理

物理复习题电磁学重点梳理在物理复习中,电磁学是一个非常重要的部分。
电磁学涉及电荷、电场、电势、电流、磁场等内容,是理解电磁现象和应用的基础。
为了帮助大家进行复习,本文将对电磁学的重点内容进行梳理和总结。
1. 电荷和电场1.1 电荷的性质电荷是物质的一种基本性质,分为正电荷和负电荷。
同性电荷相互排斥,异性电荷相互吸引。
电荷守恒定律指出,在封闭系统中,电荷的总量保持不变。
1.2 电场的描述电场是由电荷产生的一种力场。
电场的描述通过电场强度来实现,电场强度的定义是单位正电荷所受到的力。
电场强度与距离的平方成反比。
2. 电势和静电能2.1 电势能和势能差电势能是电荷由于位置而具有的能量,与电荷的位置和电场强度有关。
电势能差指的是两个位置上电荷的电势能之差。
2.2 电势差和电位电势差是电场中两点之间的电势能差,与路径无关,只与起点和终点有关。
电位是单位正电荷在某一点的电势值。
电势差等于两点之间的电场强度沿路径的线积分。
3. 电流和电路3.1 电流的定义电流指的是单位时间内电荷通过某一截面的数量,常用安培(A)作为单位。
3.2 电流的方向和电流密度电流的方向约定为正电荷流动的方向,但实际电流方向与正电荷的运动方向相反。
电流密度指的是单位截面上的电流值。
3.3 电路中的电阻和电压电阻是电路中对电流流动的阻碍,单位是欧姆(Ω)。
电压是单位电荷通过元件时所做的功。
4. 磁场和安培环路定理4.1 磁场的描述和磁感应强度磁感应强度描述了磁场的强弱,是单位磁力所受的力。
磁感应强度与距离的平方成反比。
4.2 安培环路定理安培环路定理描述了磁场中闭合回路上的磁感应强度与该回路内电流之间的关系。
根据安培环路定理,磁感应强度的环路积分等于该回路内电流的代数和乘以真空中的磁导率。
5. 法拉第电磁感应定律和自感现象5.1 法拉第电磁感应定律法拉第电磁感应定律描述了磁场变化时感生电动势的产生,电动势的大小与磁场的变化率和回路的面积有关。
大学物理易考知识点电磁场

大学物理易考知识点电磁场电磁场是大学物理中的重要知识点之一,也是考试中常考的内容。
学好电磁场的基本概念和原理,对于理解电磁现象和解决相关问题具有重要意义。
本文将从电荷和电场、电场力和电场能、电场的高斯定律、电位和电势能、静电场中的导体和电容、电容器及电容等方面,详细论述大学物理易考的电磁场知识点。
一、电荷和电场电荷是物质的一种性质,它具有正电荷和负电荷两种状态。
同性电荷相互排斥,异性电荷相互吸引,这是电荷的基本性质。
在物质周围存在电场。
电场是电荷在周围产生的一种特殊的物理场,用来描述电荷之间相互作用的力的传递方式。
电场的强度用E表示,单位是牛顿/库仑(N/C)。
二、电场力和电场能电场力是电荷在电场中产生的受力。
当一个电荷在电场中受力时,根据库仑定律,电场中的电场力与电荷的大小和电场强度有关。
电场能是电场对电荷做功的能量。
当电荷沿电场方向从一个位置移动到另一个位置时,其受力方向与位移方向相同,电场力对电荷做正功;当电荷沿相反方向移动时,电场力对电荷做负功。
电场能的大小与电荷的大小和电势差有关。
三、电场的高斯定律电场的高斯定律是描述电场分布与电荷分布之间关系的重要定律。
根据高斯定律,通过任意闭合曲面的电场通量与该曲面内电荷的代数和成正比。
根据高斯定律可以推导出电场的分布规律,例如对于均匀带电线的电场分布、均匀带电球壳的电场分布等。
高斯定律是解决电场问题的重要方法之一。
四、电位和电势能电位是描述电场势能分布的物理量。
在电场中,沿着某一路径从一个位置移到另一个位置,电势差即电位的变化。
电势能是电荷在电场中具有的能量。
它与电场强度和电荷的位置有关。
电势能的大小与电荷的大小、电场强度和电势差有关。
五、静电场中的导体和电容导体是一种能够自由移动电荷的物质。
在静电场中,导体内部的电荷分布趋向稳定,电场强度为零。
因此,导体内部的电荷分布是关键的。
电容是描述导体储存电荷能力的物理量。
电容器是一种用于存储电荷的装置。
大学物理电磁学总结(精华)ppt课件(2024)

34
创新实验设计思路分享
组合实验法
将多个相关实验进行组合设计,以提高实验 效率和准确性。
对比实验法
通过对比不同条件下的实验结果,探究物理 现象的本质和规律。
仿真模拟法
利用计算机仿真技术模拟实验过程,以降低 成本和提高安全性。
2024/1/28
改进测量方法
针对传统测量方法的不足之处进行改进和创 新,提高测量精度和效率。
2024/1/28
23
自感和互感现象分析
自感现象是指一个线圈中的电 流发生变化时,在线圈自身中 产生感应电动势的现象。
互感现象是指两个相邻的线圈 中,一个线圈中的电流发生变 化时,在另一个线圈中产生感 应电动势的现象。
2024/1/28
自感和互感现象的产生都与磁 场的变化有关,它们是电磁感
应现象的重要组成部分。
麦克斯韦方程组可以推导出电磁波的存在和传播,是无线通信的理论基础 。
18
电磁波产生条件与传播方式
01
02
03
电磁波产生的条件是变 化的电场或磁场,即振 荡电路中的电荷或电流
。
电磁波的传播方式是横 波,电场和磁场相互垂 直且与传播方向垂直。
电磁波在真空中的传播 速度等于光速,且在不 同介质中的传播速度不
7
02
静电场与恒定电流
2024/1/28
8
静电场中的导体和电介质
静电场中的导体特性
静电感应现象
静电平衡条件
2024/1/28
9
静电场中的导体和电介质
导体表面电荷分布
电介质极化现象
电偶极子概念
2024/1/28
10
静电场中的导体和电介质
电介质极化机制
大学物理电磁方面总复习

5、磁场能量 磁场能量:
1 1 1 2 Wm V w m dV V BHdV= LI 2 2 2
1 we BH 2
6. 位移电流的性质 位移电流正比于电场强度的时间变化率,在磁效 应上,它与传导电流等效。 传导电流与位移电流的不同: 1)传导电流和自由电荷的运动相当,位移电流在真 空中则与电场的变化相当,根本没有电荷在运动。 2)介质中的位移电流不产生焦耳热。 3)传导电流仅能在导体中存在,位移电流可在导体、 电介质以及真空中存在。
1、点电荷 F qE
2、电偶极子在电场 中的力矩(均匀场)
M pe E
pe qre
3、带电粒子在电场中的运动
dv qE ma m dt
5、导体性质 静电平衡条件:
(1)导体内部电场强度处处为零:E内 0
(2)导体为等势体,导体表面为等势面; (3)导体表面的电场处处 与它的表面垂直
B dl 0 I
L
H dl I
L
磁场的性质 磁场的高斯定理 (无源场闭合)
B dS 0
S
2、电荷、电流在磁场中的作用 (1)磁场对运动电荷
(1)粒子的速度
v 与 B 平行
F qv B
洛伦兹力
粒子作匀速直线运动。
E附 近 en
0
(4)净电荷只分布在导体外表面。
6、电容器电容 电容的定义式
平行板电容器
q C V A VB
q 0S C V A VB d
计算电容小结 i)让电容器两极上分别带电荷 q,计算电容两极间 的场强分布。
ii) 计算出两极板间的电势差VA VB 。
大学物理复习——变化的电磁场

⼤学物理复习——变化的电磁场变化的电磁场电磁感应定律电磁感应现象:当穿过闭合回路的磁通量发⽣变化时,不管这种变化是由于什么原因引起的,回路中都有电流产⽣,这种现象称为电磁感应现象,回路中产⽣的电流称为感应电流法拉第电磁感应定律电磁感应定律定量表达式:导体回路中产⽣的感应电动势的⼤⼩,与穿过导体回路的磁通量对时间的变化率成正⽐\varepsilon_i=-\frac{dN\Phi_m}{dt}其中N为匝数据此,穿过导线截⾯的感应电量为:q=-\int_{t_1}^{t_2}\frac{1}{R}\frac{d\Phi_m}{dt}dt=\frac{1}{R}(\Phi_1-\Phi_2)楞次定律楞次定律:闭合回路中感应电流的⽅向总是使其所激发的磁场来阻⽌或者补偿引起感应电流的磁通量变化动⽣电动势和感⽣电动势动⽣电动势:动⽣电动势使由于导体或者导体回路在恒定磁场中运动⽽产⽣的电动势动⽣电动势公式:\varepsilon_i=\int_b^a(\vec v \times \vec B)\cdot d\vec l感⽣电动势和感⽣电场感⽣电动势由于磁场发⽣变化⽽激发的电动势麦克斯韦假设:变化的磁场在其周围空间会激发⼀种涡旋状的电场,称为涡旋电场或感⽣电场\oint_L \vec E_涡\cdot\vec l=-\int_s\frac{\partial\vec B}{\partial\vec t}\cdot d\vec S⾃感与互感⾃感现象回路⾃⾝电流、回路的形状、或回路周围的磁介质发⽣变化时,穿过该回路⾃⾝的磁通量随之变化,从⽽在回路中产⽣感应电动势的现象\psi=LI其中L为⾃感系数\psi=N\phi_m,单位为亨利,则⾃感电动势为:\varepsilon_L=-\frac{d(LI)}{dt}=-L\frac{dI}{dt}-I\frac{dL}{dt}若只有电流⼤⼩发⽣了改变,则\varepsilon_L=-L\frac{dI}{dt}L总是阻碍电流的变化互感现象因两个载流线圈中电流变化⽽在对⽅线圈中激起感应电动势的现象称为互感应现象\Psi_{21}=M_{21}I_1,\Psi_{12}=M_{12}I_2其中M为互感系数,据实验M_{21}=M_{12}\varepsilon_{12}=-\frac{d\Psi_{12}}{dt}=-M\frac{dI_2}{dt},\varepsilon_{21}=-\frac{d\Psi_{21}}{dt}=-M\frac{dI_1}{dt}⾃感线圈的串联等效电感为:L=L_1+L_2+2ML=L_1+L_2-2M为了反应两个回路磁场耦合的松紧程度,引⼊了耦合系数的概念M=k\sqrt{L_1L_2}其中k即为耦合系数在⼀般情况下,由于漏磁等现象,k<1磁场能量⾃感能量在⼀仅有电阻与电感的电路中,电流的随时间变化有如下公式i=\frac{\varepsilon}{R}(1-e^{-\frac{R}{L}t})在完成充电之后,电感拥有能量W=\frac{1}{2}LI^2互感能量两个相邻的线圈分别与电源相连,在通电过程中,两线圈的磁能为:W=\frac{1}{2}L_1I_1^2+\frac{1}{2}L_2I_2^2+MI_1I_2磁场的能量由螺线管特例W=\frac{1}{2}BHV可以推出W=\int_vwdV=\int_v\frac{1}{2}BHdV麦克斯韦电磁场理论电容器上极板在充放电过程中,造成极板上电荷累积随时间变化,单位时间内极板上电荷的增加或减少等于通⼊或流⼊极板的电流I=\frac{dQ}{dt}=\int_s\frac{\partial\vec D}{\partial t}\cdot d\vec S此即是位移电流,其电流密度为\vec j_d=\frac{\partial\vec D}{\partial t}全电流定律全电流定律:通过某⼀截⾯的全电流是通过这⼀截⾯的传导电流、运流电流和位移电流的代数和麦克斯韦⽅程\begin{cases}\oint_s\vec D\cdot d\vec S=\sum q&说明静电场是有源场\\\oint_L\vec E\cdot d\vec l=0&说明静电场是保守场、⽆旋场\\\oint_s \vec B\cdot d\vec S=0&稳恒磁场是⽆源场 \\\oint_L\vec H\cdot d\vec l=\sum I&稳恒磁场是⾮保守场\end{cases}⾃由空间的麦克斯韦⽅程\begin{cases}\oint_s\vec D\cdot d\vec S=0\\\oint_L\vec E \cdot d\vec l=-\int_s\frac{\partial\vec B}{\partial t}\cdot d\vec S\\\oint_s\vec B\cdot d \vec S=0\\\oint_L\vec H\cdot d\vec l=\int_s\frac{\partial\vec D}{\partial t}d\vec S\end{cases}介质的物质⽅程\vec D=\varepsilon\vec E\vec B=\mu E\vec j=\sigma\vec E其中\sigma为电导率电磁波据麦克斯韦理论:\oint_L\vec E \cdot d\vec l=-\int_s\frac{\partial\vec B}{\partial t}\cdot d\vec S,\oint_L\vec H\cdot d\vec l=\int_s\frac{\partial\vec D}{\partialt}d\vec S这样,电场与磁场可以互相激发,以波的形式在空间中传播电磁波的性质1. 电磁波是横波,电场强度,磁场强度,电磁波速度相互垂直,构成正交右旋,2. 电磁波是偏振波3. 电场强度与磁场强度同相位4. 同⼀点的电场强度与磁场强度满⾜\sqrt\varepsilon E=\sqrt\mu H5. 传播速度为v=\frac{1}{\sqrt{\varepsilon\mu}}近似光速电磁波的能量能量密度据w_e=\frac{1}{2}\varepsilon E^2,w_m=\frac{1}{2}\mu H^2得到电磁场的能量密度为w=\varepsilon E^2=\mu E^2能流密度单位时间内穿过垂直于传播⽅向的单位⾯积的辐射能量(s)\vec S=\vec E \times \vec H电磁波的辐射电磁振荡⼀个不计电阻的LC电路可以实现电磁振荡,且有频率\omega=\frac{1}{\sqrt{LC}}缺点(1)振荡频率低(2)电磁场仅局限于电容器与⾃感线圈之间Processing math: 0%。
大物电磁知识点总结

大物电磁知识点总结一、电场1. 电场的概念:电场是一种物质周围的空间中存在的力场,它可以对带电粒子产生力的作用。
在空间的任意一点,电场强度的大小和方向决定了该点中带电粒子所受的电力的大小和方向。
电场的强度用电场强度矢量表示,单位是牛顿/库仑。
2. 电场的描述:电场可以由电场线来描述,电场线的密度表示了电场强度的大小,而电场线的方向表示了电场强度的方向。
在均匀电场中,电场线是平行的且等间隔分布的。
对于点电荷,其电场线以点电荷为中心呈放射状分布。
3. 电场叠加原理:当有多个电荷在同一点产生电场时,它们产生的电场可以叠加。
即在同一点的电场强度是矢量和,大小和方向由各电荷产生的电场强度方向和大小决定。
4. 电势能和电势:电场中的带电粒子会受到电场力的作用,从而具有电势能。
电场中单位正电荷所具有的电势能称为电势,用V表示,单位是伏特。
电场中的电势可以通过电势函数来描述,电场力可通过电势函数求导得到。
5. 电容器和电容:电容器是用来存储电荷和能量的元件,其电容量取决于电容器的几何形状和材料特性。
电容器两端的电位差称为电容器的电压。
电容器的电容量用法拉表示,单位是库仑。
6. 极板电容器:极板电容器是由两块平行金属板和介质组成的,当极板上施加电压时,金属板上会积聚电荷,从而形成电场。
极板电容器的电容量与极板的面积、介质的相对介电常数和极板之间的距离有关。
二、磁场1. 磁场的概念:磁场是指物质周围的空间中存在的力场,它可以对旋转的带电粒子或者带电体系产生力的作用。
对物质中的电流来说,它也可以产生磁场。
磁场的强度用磁场强度矢量表示,单位是特斯拉。
2. 磁感应强度和磁力:磁感应强度是描述磁场强度的物理量,用磁感应强度矢量表示,单位是特斯拉。
当带电粒子在磁场中运动时,会受到磁力的作用,磁力是与磁感应强度、电荷的速度和磁场之间的夹角有关的力。
3. 洛伦兹力和毕奥萨法尔定律:带电粒子在磁场中运动时,它会受到磁力的作用。
洛伦兹力是电场力和磁场力的合力,在磁场中受力的带电粒子将做圆周运动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
dt
3.计算互感系数: (1)给任一回路通电流;
(2)计算穿过另一回路的磁通量;
(3)代入定义式或定义方程
例3:长直导线与矩形线圈共面,线圈中通有电
流I(t),计算长直导线中的互感电动势。
问题:长直导线是 解:设长直导线通有电流 I1
回路吗?
矩形线圈内的磁通量
I 1 I(t)
ds l
m S
BdS
=0
Lddtmddt(L)I
LdI dt
I
dL dt
当线圈形状、匝数、介质等不变时,L是常量.
εL
LdI dt
L L
dI dt
自感电动势与电流的变化率成正比
3.自感系数计算 考虑方法同计算电容。
(1)令回路通电流;
B
(2)计算穿过回路的磁通量;
(3)代入定义式或定义方程。
I
例1.计算长直螺线管(N,l,R)的自感系数:
da d
0 I1ldx 2 x
0Ill 2
nda d
o x d a
M m 0l lnd a
I1
M
2 d
dI 0llndadI
dt 2 d dt
三、磁场的能量
L
考虑自感线圈中电流的建立过程:
L
L di dt
K1
在移动dq=idt的过程中,电源反抗
自感电动势做功 dALdqLidt Lidi
在i从0到I过程中,做功
•单位:伏V
正
第十一章 变化的电磁场
§1 电磁感应 §2自感与互感 §3 Maxwell’s 方程组
本章重点:感应电动势、自感、互感 的计算
本章难点:涡旋电场,位移电流,场概念的理解
§1 电磁感应 一 法拉第电磁感应定律 二 动生电动势 三 感生电动势 涡旋电场
§1 电磁感应 一、电磁感应定律 1.电磁感应现象
(1)动生电B动势的 公式:
(v B)dl
A
与法拉第定律一致.
I Iv l
C
B B'
前例1,由法拉第定律: εdΦBldxBlv
dt
dt
(2)功能关系:ref.P271-中
外力为了维持导体的运动,须克服安培力做功。
如图,设长为l的导体匀速运动,外力的功率:
P=Fv=BIlv=I ,即电功率与外力的功率相等.
解: 设长直螺线管中通有电流I,其内部磁场:
B 0 NI l
L 0R2N2 l
穿过匝线圈的磁通量(磁链数):
NNBS 0N l 2IR2
LN
I
例2.由定义方程 求自感系数:
一自感线圈中,电流强度在0.002s内均匀地由 10A增加到12A,此过程中线圈中的自感电动势 为400V,则线圈的自感系数为
d
变化率。
dt
磁铁(或载流线圈)与不含电 源的闭合线圈间有相对运动
线圈之间无相对运动,但 初级载流线圈中电流即 产生的磁场发生变化.
对定律中物理量的说明: 任意指定回路的绕行方向,规定
(1)电动势方向与绕行方向一致时为正
(2)当磁场线方向与绕行方向成右螺时
磁通量为正
d 0 dt
与回路绕行方
例计6算. 感长应为电L的动金势属。棒放在i磁场E 中涡 , ddB l/d t0
解:涡旋电场分布
rR:
r dB Ek 2 dt
做辅助线OA、 OC,
RE
B E
OA CO AAC CO
E
O
OACO0
ACOAC
A
E
L
C
dB
dS
R2(L/2)2 dB L
即:感生电场的电场线,在管内外都是与螺线管同
轴的同心圆.同一条场线上各点E相同,方向沿圆
的切线. 取回路L方向与场线相同,计算E大小
Ekdl Ek2r
r dB Ek 2 dt
L
(1)rR:
dm
dBr2
dt dt
(2)rR:
ER
Ek
2r
dBR2
dt
EL
B r
E
R2 dB
方向:AC
dt AEO
2
dt
例7: 在半径为R的圆柱形空间存在轴向均匀磁场,一长
为2R的导体棒在垂直磁场的平面内以速度v 横扫过磁场。 磁场以 dB/d变 t化0,求导体棒运动到图示位置时,
棒上感应电动势的大小和方向。
解.设动R生电动势为
ε1 (vB)dl
,1感生电动势为 ,则2
vBR方向: 右左
aB
I vl
b
i
d dt
B0co stdal ——感生
(3) BB0sin t,导线以速度v向右移动.
Bvtl B0sin tvtl
i
d dt
v0 lsB it n vt0c lB ots
4.对定律应用的进一步讨论:
(1)如果围绕磁场的线圈有N匝,则电动势:
d dN
N
dt
dt
称N为磁通链匝数(磁链).
A
I
Lidi
1
LI
2
0
2
即自感线圈贮存了能量(磁能):
Wm
1 2
LI2
以充满 介质的长直螺线管(磁场全 部集
中在管内)为例:
B
πR2N2
L
n2Sl
n2V
l
S lI
Wm
1 2
LI2
1
2
n2VI2
(2)当回路电阻为R时,电流 I 1 d
R dt
(3)通过回路的电量为:
q
t2 Idt 1
t2
d dt
1
2
t1
R t1 dt
R
电量与 成正比而与d /dt 无关。
例2:一通有电流 I 的无限长直导线所在平面内 , 有 一半径为 r 、电阻为 R 的导线小环 , 环中心距直导 线为a , 如图所示 , 且a>>r 。当直导线的电流被切 断后 , 沿着小环导线流过的电荷约为?
§2 自感与互感 一.自感应 1.自感现象
磁2.自感感应系强数度与电一流般成,由正毕比-萨,定律d:B40 Idlr3r
所以磁通量也与电流成正比: I
定义式: L N ——自感系数:
I
自感系数L的单位:亨利(H),常用mH,H等.
为了建立感应电动势与电流的关系 V4.0
定义方程: 自感电动势
解. L L
dI
dI 1210 dt 0.002
dt
L=0.4H
二、互感应 1.互感现象
2.互感系数
定义式:
I1
I1
M Φ12 Φ21
I2
I1
单位与自感相同:亨利(H),常用mH,H等.
定义方程:
由
i
d
dt
M 12 21
dI2
dI1
有
21
M
dI1 dt
12
M
dI2 dt
dt
解: q 1 2
1
R
BS
0I 2a
r 2
I
r
2 0 q 0I r2
a
2Ra
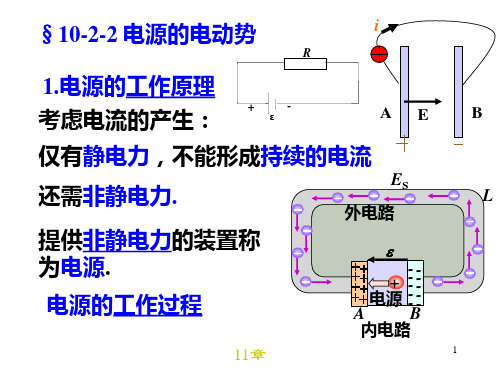
(4)非静电力,其力场强度为Ek
ES
根据电源的电动势
B AEk dl
Ek
Fk q0
结合法拉第定律有:
LE kdld d mtd d tSB dS
外电路
A
+ 电源
-----B-----
内电路
L
思考:应该存在一种非静电力,是什么? (后面两段将讨论两种非静电场力)
可见感生电场是不同于静电场的另一种电场.
由于 E涡dl 0,是非保守力场 不可引入电势。
L
但当场空间有导体时,感生电场(涡旋电场)力驱 动电荷在导体两端堆积,形成静电场(电源),可 以比较导体两端电势高低。
(6)感生电场假设源于法拉第电磁感应定律又高 于法拉第电磁感应定律。
揭示了电场与磁场间更为本质的关系。 无论有无导体,只要 dB 就0有涡旋电场。
2.楞次定律(1833) 闭合回路中感应电流的方向,总是抵抗产生它的 原因。
或:闭合回路中感应电流的方向,总是使它产生 的磁场去阻碍引起感应电流的磁通量的变化。
S
N
G
外力做功转化为感应 电流的能量
楞次定律是能量守恒在电磁感应中的体现.
3.法拉第电磁感应定律
回路中感应电动势的大小,正比
计算涡旋电场的场强Ek ,只要求会此一种
rR:
BB(t)
dB
0
rR: B0 dt
ER
B I' I'E
r dB Ek 2 dt
E
E
E
R2 dB Ek 2r dt
0Rr
例5.在半径为R 的圆柱形空间内,存在磁感应强度
为B 的均匀磁场 ,B 的方向垂直纸面向里. 磁感应
问题:前例1(2)中,导线不动, 电源中的非静电力?
电磁感应定律:
D
A
d d
LEkdldtdtSBdS
l
当仅 有磁场的变B 化时
LE感
生 dl
S
t
dS
C
B
你能看出什么?
Maxwell 假设: 变化的磁场可以激发电场.
dB
电dt荷激,发充了当一了种电电源场中(感的生非电静场电),力该。电场力驱动
εε1ε2
2 0 R R 2 R
B
ε 2 0E d l 0E 1 d l RE 2 d l
OR
做 O 辅助A 线COOA A 、 OACC , CO=0
F
Rv R
