用RLS算法实现自适应均衡器的MATLAB程序
自适应均衡器
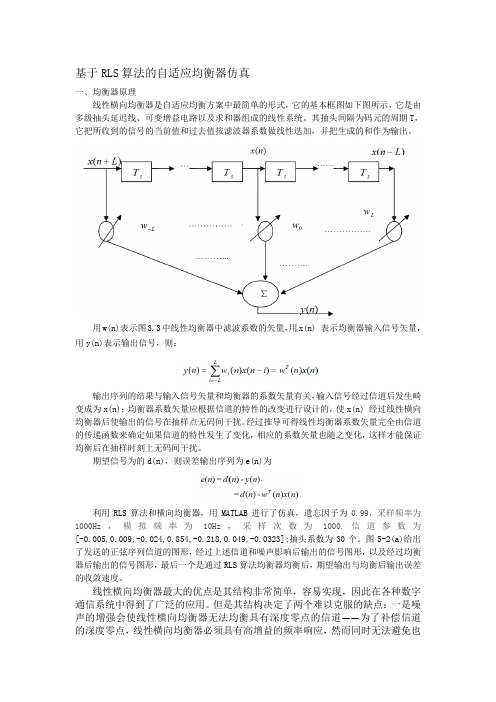
基于RLS算法的自适应均衡器仿真一、均衡器原理线性横向均衡器是自适应均衡方案中最简单的形式,它的基本框图如下图所示,它是由多级抽头延迟线、可变增益电路以及求和器组成的线性系统。
其抽头间隔为码元的周期T,它把所收到的信号的当前值和过去值按滤波器系数做线性迭加,并把生成的和作为输出。
用w(n)表示图3.3中线性均衡器中滤波系数的矢量,用x(n) 表示均衡器输入信号矢量,用y(n)表示输出信号,则:输出序列的结果与输入信号矢量和均衡器的系数矢量有关,输入信号经过信道后发生畸变成为x(n);均衡器系数矢量应根据信道的特性的改变进行设计的,使x(n) 经过线性横向均衡器后使输出的信号在抽样点无码间干扰。
经过推导可得线性均衡器系数矢量完全由信道的传递函数来确定如果信道的特性发生了变化,相应的系数矢量也随之变化,这样才能保证均衡后在抽样时刻上无码间干扰。
期望信号为的d(n),则误差输出序列为e(n)为利用RLS算法和横向均衡器,用MATLAB进行了仿真,遗忘因子为0.99,采样频率为1000Hz,模拟频率为10Hz,采样次数为1000.信道参数为[-0.005,0.009,-0.024,0.854,-0.218,0.049,-0.0323];抽头系数为30个。
图5-2(a)给出了发送的正弦序列信道的图形,经过上述信道和噪声影响后输出的信号图形,以及经过均衡器后输出的信号图形,最后一个是通过RLS算法均衡器均衡后,期望输出与均衡后输出误差的收敛速度。
线性横向均衡器最大的优点是其结构非常简单,容易实现,因此在各种数字通信系统中得到了广泛的应用。
但是其结构决定了两个难以克服的缺点:一是噪声的增强会使线性横向均衡器无法均衡具有深度零点的信道——为了补偿信道的深度零点,线性横向均衡器必须具有高增益的频率响应,然而同时无法避免也会放大噪声;二是线性均衡器与接收信号的幅度信息关系密切,而幅度会随着多径衰落信道中相邻码元的改变而改变,因此滤波器抽头系数的调整不是独立的。
Matlab中的自适应控制设计方法

Matlab中的自适应控制设计方法自适应控制是一种广泛应用于工程领域的控制策略,它通过实时地调整控制器参数,以适应系统动态特性的变化。
Matlab是一个功能强大的工具,提供了丰富的工具箱和函数,使得自适应控制的设计和实现变得更加便捷。
本文将介绍几种常见的自适应控制设计方法,并说明在Matlab中的实现。
1. 最小均方(LMS)算法最小均方算法是一种基于误差信号的单参数自适应调整方法。
通过最小化误差信号的均方值,实时更新参数以使系统逐渐趋于稳定。
Matlab中可使用函数"lms"来实现LMS算法的设计。
该函数可以根据输入信号和期望输出信号的数据进行参数的自适应调整。
2. 递归最小二乘(RLS)算法递归最小二乘算法是一种多参数自适应调整方法,它通过将参数更新与误差信号相关联,实现对参数的在线更新。
相较于LMS算法,RLS算法具有更好的收敛性能和稳定性。
Matlab中的函数"rls"可以实现递归最小二乘算法的设计,用户可以根据系统的要求自定义相关参数。
3. 自适应模型预测控制(MPC)算法自适应模型预测控制算法中,控制器利用系统的模型对未来的输出进行预测,并根据预测结果进行参数调整。
通过不断更新模型中的参数和系统输出的观测值,实现了对动态特性的自适应调整。
Matlab提供了函数"mpc"用于实现自适应模型预测控制的设计。
用户可以通过设定模型和目标函数等参数,实现对系统的自适应控制。
4. 遗传算法(GA)优化方法遗传算法是一种基于自然进化原理的优化方法,通过模拟自然选择、交叉和变异等过程,寻找最优的参数组合。
Matlab中的函数"ga"可以实现遗传算法的设计,用户可以根据系统的需求和约束,设定适应度函数以及参数的取值范围,实现对系统参数的自适应优化。
自适应控制在实际的工程中有着广泛的应用,例如航空、汽车、机器人等领域。
通过Matlab中提供的强大工具和函数,工程师可以轻松地实现自适应控制的设计和实现。
RLS算法自适应去噪 引言: 我们组研究的题目是《RLS均衡算法及应用

RLS算法自适应去噪一,引言:我们组研究的题目是《RLS均衡算法及应用》,主要是其在自适应噪声消除中的应用。
在目前的移动通信领域中,克服多径干扰,提高通信质量是一个非常重要的问题,特别是当信道特性不固定时,这个问题就尤为突出,而自适应滤波器的出现,则完美的解决了这个问题。
其核心便是自适应算法,RLS算法便是其中的一种。
我们组主要了解了下RLS算法的基本原理,以及用程序实现了用RLS算法自适应消除语音信号中的噪声。
我们知道语音识别技术很难从实验室走向真正应用很大程度上受制于应用环境下的噪声. 自适应信号处理的理论和技术经过40 多年的发展和完善,已逐渐成为人们常用的语音去噪技术。
本文正是想通过这一与我们生活相关的问题,对简单的语音噪声进行消除,更加深刻地了解RLS算法。
二,算法原理:RLS算法即递规最小二乘算法,对于如下图所示的自适应横向滤波器:RLS算法的基本思想是:给定n-1次迭代滤波器抽头权向量最小二乘估计,依据新到达的数据计算n次迭代权向量的最新估计。
递规最小二乘算法利用二乘方的平均最小化准则,即使得误差的平方和最小。
依这一准则我们可以得出方程组:11(1)()()1(1)()H P n U n k n U P n U n λλ---=+- (1)11()(1)()()(1)HP n P n K n U n P n λλ--=--- (2)*()(1)[()()(1)]Hw n w n k d n U n w n =-+--*(1)()()w n K n n ξ=-+ (3)*()()(1)H n d n U w n ξ=--()(1)()H d n W n U n =-- (4)(1),(2),(3),(4)式即组成了RLS 算法。
(4)式描叙了该算法的滤波过程,据次激励横向滤波器以计算先验估计误差()n ξ。
(3)式描述了该算法的自适应过程,据次可通过在其过去的基础上增加一个量来递推抽头权向量,该量等于先验估计误差()n ξ复共轭与时变增益向量k (n )的乘积。
自适应均衡器的设计与仿真

2014届毕业设计(论文)摘要在移动通信领域中,码间干扰始终是影响通信质量的主要因素之一。
为了提高通信质量,减少码间干扰,在接收端通常采用均衡技术抵消信道的影响。
由于信道响应是随着时间变化的,通常采用自适应均衡器。
自适应均衡器能够自动的调节系数从而跟踪信道,成为通信系统中一项关键的技术。
本篇论文在对无线通信信道进行研究的基础上,阐述了信道产生码间干扰的原因以及无码间干扰的条件,介绍了奈奎斯特第一准则和时域均衡的原理。
深入研究了均衡器的结构和自适应算法,在均衡器的结构中主要介绍了4种自适应均衡器结构即线性横向均衡器、线性格型均衡器、判决反馈均衡器和分数间隔均衡器,并对这几种结构进行了比较。
对于系数调整算法主要介绍了常用的几种算法,包括LMS算法、RLS算法以及盲均衡常用的恒模算法(CMA),并讨论了它们各自的优缺点。
最后选用线性横向均衡器结构与上述3种系数调整算法,利用MATLAB进行仿真,并对结果进行分析与比较。
关键字:自适应均衡器,LMS,RLS,CMA ,MATLABAbstractIn the field of mobile communications, the inter-symbol interferences (ISI) is always one of the primary factor which effects transmission. Adaptive equalization is mainly solution of dealing with ISI. Equalizers are often used to combat the influence of channels for improving communication’s quality and decreasing ISI in receivers. Sometimes, channel response varies due to time, the adaptive equalizer is always necessary. Equalizer coefficients can be automatically adjusted to track the channel as a key communication system technology.On the basis of studying on wireless communication channel, this paper discusses the reasons of resulting inter-symbol interference (ISI) and without conditions, introduces Nyquist first rule and the theory of adaptive equalizers. The equalizer structures and the adaptive algorithm are particularly studied in this paper. Mainly introducing and comparing four adaptive equalizer structures, such as linear horizontal equalizer, line personality type equalizer, decision feedback equalizer, fractionally spaced equalizers. Then we research the algorithms of the adaptive equalizer which are often used, including LMS, RLS, CMA, and discuss their respective advantages and disadvantages. Finally, we choose different adaptive equalizer structures and algorithms, and use the MATALB tool to simulate, at the end of this paper we analyze and compare the results.Keywords: adaptive equalizer, LMS, RLS, CAM, MATLAB目录摘要 (I)ABSTRACT (II)目录 (III)第一章绪论 (1)1.1引言 (1)1.2国内(外)研究现状 (1)1.3论文研究的内容及主要工作 (2)第二章信道、码间干扰及均衡技术 (3)2.1信道 (3)2.1.1 恒参信道 (4)2.1.2 变参信道 (4)2.2通信信道模型 (6)2.3码间干扰 (7)2.4自适应均衡的原理与特点 (10)2.5本章小结 (11)第三章均衡器结构 (12)3.1自适应均衡简介 (12)3.2均衡器的分类 (12)3.3线性横向均衡器结构(LTE) (13)3.4线性格型均衡器(LLE) (14)3.5判决反馈均衡器(DFE) (15)3.6分数间隔均衡器(FSE) (17)3.7本章总结 (20)第四章自适应均衡算法的理论基础 (22)4.1最小均衡误差算法(LMS) (22)4.2递归最小二乘算法(RLS) (25)4.3盲均衡算法 (27)4.4本章小结 (30)第五章均衡器的仿真与实现 (31)5.1采用线性横向均衡器与LMS算法 (31)5.2采用线性横向均衡器与RLS算法 (31)5.3利用恒模算法和线性横向均衡器 (32)总结 (35)参考文献 (36)致谢 (37)附录 (38)第一章绪论1.1引言通常信道特性是一个复杂的函数,它可能包括各种线性失真、非线性失真、交调失真、衰落等。
RLS算法的自适应滤波器MATLAB仿真作业

RLS 自适应滤波器仿真作业工程1班220150820 王子豪1. 步骤1)令h M(-1)=0,计算滤波器的输出d(n)=X M T=h M(n-1);2)计算误差值e M(n)=d(n)-d(n,n-1);3)计算Kalman增益向量K M(n);4)更新矩阵的逆R M-1(N)=P M(N);5)计算h M(n)=h M(n-1)+K M(n)e M(n);2. 仿真RLS 中取T (-1)=10,λ=1及λ= 0.98;信号源x(n)与之前LMS算法仿真不变,对自适应滤波器采用RLS算法。
通过对比不同遗忘因子λ的情况下RLS的误差收敛情况。
取λ=0.98和λ=1两种情况下的性能曲线如图1所示。
其系数收敛情况如图2所示。
图1 不同λ值下的RLS算法性能曲线(100次实验平均)图2 不同λ值下的RLS算法系数收敛情况(100次实验平均)3. 结果分析RLS算法在算法的稳态阶段、即算法的后期收敛阶段其性能和LMS算法相差不明显。
但在算法的前期收敛段,RLS算法的收敛速度要明显高于LMS算法。
但是RLS算法复杂度高,计算量比较大。
遗忘因子λ越小,系统的跟踪能力越强,同时对噪声越敏感;其值越大,系统跟踪能力减弱,但对噪声不敏感,收敛时估计误差也越小。
4. Matlab程序clear;clc;N=2048; %信号的取样点数M=2;%滤波器抽头的个数iter=500;%迭代次数%初始化X_A=zeros(M,1); %X数据向量y=zeros(1,N); %预测输出err=zeros(1,iter); %误差向量errp=zeros(1,iter); %平均误差wR=zeros(M,iter); %每一行代表一次迭代滤波器的M个抽头参数T=eye(M,M)*10; %RLS算法下T参数的初始化,T初始值为10X=zeros(1,M);lamuta=0.98 ; %遗忘因子for j=1:100ex=randn(1,N); %噪声信号e(n)x=filter(1,[1,-1.6,0.8],ex);%经过系统H(Z)之后输出xd=x; %参考信号for k=(M+1):iter-1X=x(k-1:-1:k-M)';K=(T*X)/(lamuta+X'*T*X); %k时刻增益值e1=x(k)-wR(:,k-1)'*X;wR(:,k)=wR(:,k-1)+K*e1; %k时刻权值y(k)=wR(:,k)'*X;err(k)=x(k)-y(k);T=(T-K*X'*T)/lamuta; %k时刻的维纳解enderrp=errp+err.^2;enderrp=errp/100;figure(1);subplot(2,1,i);plot(errp) ;title(['100次平均得到的性能曲线,λ=',num2str(lamuta_v(i))]) ;learn1=wR(1,1:iter-1);learn2=wR(2,1:iter-1);figure(2);subplot(1,2,1;plot(learn1);title('λ=0.98'时a1的学习曲线');subplot(1,2,2);plot(learn2);title('λ=0.98时a2的学习曲线');THANKS !!! 致力为企业和个人提供合同协议,策划案计划书,学习课件等等打造全网一站式需求欢迎您的下载,资料仅供参考。
rls算法及matlab实现

RLS(Recursive Least Squares)算法是一种自适应滤波算法,用于在线估计线性系统的参数。
与最小二乘法类似,RLS算法通过最小化误差平方和来计算参数估计值。
不同的是,RLS算法采用递归方式,可以逐步更新参数估计值,适应系统变化。
RLS算法的基本思想是利用前一时刻的参数估计值和当前时刻的观测数据,计算当前时刻的参数估计值。
具体实现过程如下:1.初始化参数:选定一个合适的初始参数向量,并设置初始协方差矩阵和遗忘因子。
2.计算增益向量:利用前一时刻的参数估计值、协方差矩阵和当前时刻的观测数据,计算增益向量。
3.更新参数估计值:利用增益向量和前一时刻的参数估计值,计算当前时刻的参数估计值。
4.更新协方差矩阵:利用前一时刻的协方差矩阵、增益向量和当前时刻的观测数据,更新协方差矩阵。
5.返回参数估计值:输出当前时刻的参数估计值。
下面是一个简单的MATLAB实现:matlab复制代码function[theta, P] = rls(theta, P, x, y, lambda)% theta: 参数向量% P: 协方差矩阵% x: 输入向量% y: 输出标量% lambda: 遗忘因子K = P * x / (lambda + x' * P * x); % 计算增益向量theta = theta + K * (y - x' * theta); % 更新参数估计值P = (P - K * x' * P) / lambda; % 更新协方差矩阵end上述代码中,输入参数包括前一时刻的参数向量theta、协方差矩阵P、当前时刻的输入向量x和输出标量y,以及遗忘因子lambda。
输出参数为当前时刻的参数估计值theta和协方差矩阵P。
在实际应用中,可以将该函数嵌入到主程序中,通过循环调用实现递归计算。
基于RLS算法的自适应均衡仿真.

加大,会使RLS权系数的收敛性能变差权系数的均方误差随n的增加而线 性减小,所以,RLS算法权系数按均方渐近收敛于最佳值。 RLS算法经过n=2M次迭代,即可使均方误差达到最小误差的1.5倍,而 LMS算法达此水平至少需20M次迭代。因此,RLS比LMS至少快一个数量 级。若n趋于无限大,在不考虑量化误差的条件下, RLS算法无失调。而LMS始终存在与步长有关的失调。RLS算法的均方误 差收敛特性与R的特征值散布无关。RLS收敛快的原因在于采用类似归一 化步长。 RLS算法的主要问题:每次迭代中的计算量与阶数M的平方成正比。虽然 比之最小二乘法(M的三次方成正比)好,但比LMS算法(M成正比)要差。
vn=sqrt(sigma)*randsrc(2*M+Lb+N,1);
S=zeros(2*M+Lb+1,N); %发射信号矩阵S
V=zeros(2*M+1,N); %加性白高斯噪声矩阵V
for k=1:N
S(:,k)=s(2*M+Lb+k:-1:k);
V(:,k)=vn(2*M+k:-1:k);
信道为 hb=[0.407 0.815 0.407]下的仿真结果
不同信道自适应均衡器RLS算法 matlab仿真图
信道为: hb=[0.04 -0.05 0.07 -0.21 -0.50
0.72 0.36 0.00 0.21 0.03 0.07]下的仿真结果
不同信道自适应均衡器RLS算法 matlab仿真图
end
基于RLS算法自适应均衡器
lambda = 0.990; %RLS遗忘因子
MATLAB环境下ISI信道仿真及自适应均衡器设计程序说明

MATLAB环境下ISI信道仿真及自适应均衡器设计程序说明MATLAB是一种广泛用于科学计算和工程领域的高级编程语言和环境。
在MATLAB环境下,可以进行ISI(Inter-Symbol Interference)信道仿真及自适应均衡器设计。
ISI是指传输过程中,当前符号对后续符号产生的干扰,会导致接收端的误码率增加。
自适应均衡器旨在消除ISI,提高信号的传输质量。
下面是一个示例程序,用于说明在MATLAB环境下进行ISI信道仿真及自适应均衡器设计的步骤和方法:1.生成发送信号:首先,定义发送信号的长度和发送符号序列。
可以使用随机数生成器或自定义发送符号序列。
例如,可以使用randi函数生成一个长度为N的随机二进制序列。
2.传输信号:将发送信号通过ISI信道传输。
可以使用MATLAB中的conv函数来模拟信号通过ISI信道,conv函数将发送信号与信道冲激响应进行卷积操作。
信道冲激响应可以根据具体的信道特性进行定义,例如,可以使用瑞利衰落信道或AWGN(Additive White Gaussian Noise)信道。
3.加入噪声:在传输信号的基础上添加噪声。
可以使用MATLAB中的awgn函数来添加高斯白噪声。
awgn函数通过指定信号的信噪比(SNR)来控制噪声的强度。
4.接收信号:接收被噪声污染的信号。
可以使用MATLAB中的corr函数来计算接收信号与发送信号之间的相关性,以便后续均衡器设计。
5.自适应均衡器设计:使用自适应均衡器算法来消除ISI。
在MATLAB环境中,有多种自适应均衡器算法可供选择,包括LMS(Least Mean Squares)、NLMS (Normalized Least Mean Squares)、RLS(Recursive Least Squares)等算法。
6.误码率评估:使用误码率作为性能指标来评估均衡器的性能。
可以通过比较接收信号与发送信号之间的误差来计算误码率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用RLS算法实现自适应均衡器的MATLAB程序
考虑一个线性自适应均衡器的原理方框图如《现代数字信号处理导论》p.275自适应均衡器应用示意图。
随机数据产生双极性的随机序列x[n],它随机地取+1和-1。
随机信号通过一个信道传输,信道性质可由一个三系数FIR滤波器刻画,滤波器系数分别是0.3,0.9,0.3。
在信道输出加入方差为σ平方高斯白噪声,设计一个有11个权系数的FIR结构的自适应均衡器,令均衡器的期望响应为x[n-7],选择几个合理的白噪声方差σ平方(不同信噪比),进行实验。
用RLS算法实现这个自适应均衡器,画出一次实验的误差平方的收敛曲线,给出最后设计滤波器系数。
一次实验的训练序列长度为500。
进行20次独立实验,画出误差平方的收敛曲线。
给出3个步长值的比较。
仿真结果:
用RLS算法设计的自适应均衡器系数
序
1 2 3 4 5 6 7 8 9 10 11 号
20
0.0051 -0.0118 0.0290 -0.0792 0.2077 -0.5458 1.4606 -0.5405 0.1926 -0.0663 0.0173 次
1
0.0069-0.01570.0265-0.07420.1966-0.5349 1.4514-0.53930.1987-0.07560.0251次
结果分析:
可以看到,RLS算法的收敛速度明显比LMS算法快,并且误差也比LMS算法
小,但是当用更小的忘却因子时,单次实验结果明显变坏,当忘却因子趋于0
时,LS算法也就是LMS算法。
附程序:
1. RLS法1次实验
% written in 2005.1.13
% written by li***
clear;
N=500;
db=25;
sh1=sqrt(10^(-db/10));
u=1;
m=0.0001*sh1^2;
error_s=0;
for loop=1:1
w=zeros(1,11)';
p=1/m*eye(11,11);
V=sh1*randn(1,N );
Z=randn(1,N)-0.5;
x=sign(Z);
for n=3:N;
M(n)=0.3*x(n)+0.9*x(n-1)+0.3*x(n-2);
end
z=M+V;
for n=8:N;
d(n)=x(n-7);
end
for n=11:N;
z1=[z(n) z(n-1) z(n-2) z(n-3) z(n-4) z(n-5) z(n-6) z(n-7) z(n-8) z(n-9) z(n-10)]';
k=u^(-1).*p*z1./(1+u^(-1).*z1'*p*z1);
e(n)=d(n)-w'*z1;
w=w+k.*conj(e(n));
p=u^(-1).*p-u^(-1).*k*z1'*p;
y(n)=w'*z1;
e1(n)=d(n)-w'*z1;
end
error_s=error_s+e.^2;
end
w
error_s=error_s./1;
n=1:N;
plot(n,error_s);
xlabel('n (忘却因子u=1;DB=25时)');
ylabel('误差');
title('RLS法1次实验误差平方的均值曲线');
2. RLS法20次实验
% written in 2005.1.13
% written by li***
clear;
N=500;
db=25;
sh1=sqrt(10^(-db/10));
u=1;
m=0.0001*sh1^2;
error_s=0;
for loop=1:20
w=zeros(1,11)';
p=1/m*eye(11,11);
V=sh1*randn(1,N );
Z=randn(1,N)-0.5;
x=sign(Z);
for n=3:N;
M(n)=0.3*x(n)+0.9*x(n-1)+0.3*x(n-2);
end
z=M+V;
for n=8:N;
d(n)=x(n-7);
end
for n=11:N;
z1=[z(n) z(n-1) z(n-2) z(n-3) z(n-4) z(n-5) z(n-6) z(n-7) z(n-8) z(n-9) z(n-10)]';
k=u^(-1).*p*z1./(1+u^(-1).*z1'*p*z1);
e(n)=d(n)-w'*z1;
w=w+k.*conj(e(n));
p=u^(-1).*p-u^(-1).*k*z1'*p;
y(n)=w'*z1;
e1(n)=d(n)-w'*z1;
end
error_s=error_s+e.^2;
end
w
error_s=error_s./20;
n=1:N;
plot(n,error_s);
xlabel('n (忘却因子u=1;DB=25时)');
ylabel('误差');
title('RLS法20次实验误差平方的均值曲线');。
