八年级数学《正方形的性质》练习题
2021-2022学年鲁教版八年级数学下册《6-3正方形的性质与判定》同步达标测试题(附答案)
2021-2022学年鲁教版八年级数学下册《6-3正方形的性质与判定》同步达标测试题（附答案）一．选择题（共8小题，满分40分）1．下列关于▱ABCD的叙述，正确的是（）A．若AC＝BD，则▱ABCD是矩形B．若AB＝AD，则▱ABCD是正方形C．若AB⊥BC，则▱ABCD是菱形D．若AC⊥BD，则▱ABCD是正方形2．如图，正方形ABCD的面积为4，菱形AECF的面积为2，则EF的长是（）A．1B．C．2D．23．如图，在正方形ABCD外侧，作等边三角形ADE，AC，BE相交于点F，则∠BFC为（）A．75°B．60°C．55°D．45°4．如图，在正方形ABCD中，对角线AC与BD相交于点O，E为BC上一点，CE＝6，F 为DE的中点．若OF的长为1，则△CEF的周长为（）A．14B．16C．18D．125．如图，四边形ABCD中，AB＝BC，∠ABC＝∠CDA＝90°，BE⊥AD于点E，且四边形ABCD的面积为8，则BE＝（）A．2B．3C．D．6．如图，在平面直角坐标系xOy中，正方形ABCD的顶点D在y轴上且A（﹣2，0），B （2，b），则正方形ABCD的面积是（）A．34B．25C．20D．167．如图，正方形ABCD的边长为2，E为AB边的中点，点F在BC边上，点B关于直线EF的对称点记为B'，连接B'D，B'E，B'F．当点F在BC边上移动使得四边形BEB'F成为正方形时，B'D的长为（）A．B．C．2D．38．如图，点P是正方形ABCD的对角线BD上一点，PE⊥BC，PF⊥CD，垂足分别为点E，F，连接AP，EF，给出下列四个结论：①AP＝EF；②∠PFE＝∠BAP；③PD＝EC；④△APD一定是等腰三角形．其中正确的结论有（）A．1个B．2个C．3个D．4个二．填空题（共7小题，满分35分）9．用4张全等的直角三角形纸片拼接成如图所示的图案，得到两个大小不同的正方形．若正方形ABCD的面积为10，AH＝3，则正方形EFGH的面积为．10．已知：如图，正方形ABCD和EFGH的边长都等于1，点E恰好是AC、BD的交点，则两个正方形的重叠部分（阴影部分）的面积是．11．如图，点A，B，E在同一条直线上，正方形ABCD，BEFG的边长分别为3，4，H为线段DF的中点，则BH＝．12．如图，点O是正方形ABCD的中心，过点O的直线与AD、BC交于点M、点N，DE ⊥MN，交AB于点E，若AM＝1，DM＝3，则DE的长为．13．如图，E，F，M，N分别是边长为4的正方形ABCD四条边上的点，且AE＝BF＝CM ＝DN．那么四边形EFMN的面积的最小值是．14．如图，在边长为2的正方形ABCD中，E，F分别是边DC，CB上的动点，且始终满足DE＝CF，AE，DF交于点P，则∠APD的度数为；连接CP，线段CP的最小值为．15．如图，在矩形ABCD中，AB＝6，BC＝8．（1）如果E、F分别是AD、BC的中点，G是对角线AC上的点，∠EGF＝90°，则AG 的长为；（2）如果E、F分别是AD、BC上的点，G，H是对角线AC上的点．下列判断正确的是．①在AC上存在无数组G，H，使得四边形EGFH是平行四边形；②在AC上存在无数组G，H，使得四边形EGFH是矩形；③在AC上存在无数组G，H，使得四边形EGFH是菱形；④当AG＝时，存在E、F、H，使得四边形EGFH是正方形．三．解答题（共5小题，满分45分）16．如图，P是正方形ABCD对角线AC上一点，点E在BC上，且PE＝PB．（1）求证：PE＝PD；（2）连接DE，试判断∠PED的度数，并证明你的结论．17．如图，在梯形ABCD中，AD∥BC（BC＞AD），∠D＝90°，BC＝CD＝12，∠ABE＝45°，若AE＝10．求CE的长度．18．在正方形ABCD中，F是线段BC上一动点（不与点B，C重合）连接AF，AC，分别过点F，C作AF、AC的垂线交于点Q．（1）依题意补全图1，并证明AF＝FQ；（2）过点Q作NQ∥BC，交AC于点N，连接FN．若正方形ABCD的边长为1，写出一个BF的值，使四边形FCQN为平行四边形，并证明．19．如图，已知正方形ABCD，P是对角线AC上任意一点，PM⊥AD，PN⊥AB，垂足分别为点M和N，PE⊥PB交AD于点E．（1）求证：四边形MANP是正方形；（2）求证：EM＝BN．20．如图，已知四边形ABCD为正方形，AB＝3，点E为对角线AC上一动点，连接DE，过点E作EF⊥DE，交BC于点F，以DE、EF为邻边作矩形DEFG，连接CG．（1）求证：矩形DEFG是正方形；（2）探究：CE+CG的值是否为定值？若是，请求出这个定值；若不是，请说明理由．参考答案一．选择题（共8小题，满分40分）1．解：∵▱ABCD中，AC＝BD，∴四边形ABCD是矩形，选项A符合题意；∵▱ABCD中，AB＝AD，∴四边形ABCD是菱形，不一定是正方形，选项B不符合题意；∵▱ABCD中，AB⊥BC，∴四边形ABCD是矩形，不一定是菱形，选项C不符合题意；∵▱ABCD中，AC⊥BD，∴四边形ABCD是菱形，选项D不符合题意；故选：A．2．解：连接AC，∵正方形ABCD的面积为4，∴AC2＝4，解得AC＝，∵菱形AECF的面积为2，∴AC•EF＝2，即×EF＝2，解得EF＝，故选：B．3．解：∵四边形ABCD是正方形，∴∠BAD＝90°，AB＝AD，∠BAF＝45°，∵△ADE是等边三角形，∴∠DAE＝60°，AD＝AE，∴∠BAE＝90°+60°＝150°，AB＝AE，∴∠ABE＝∠AEB＝（180°﹣150°）＝15°，∴∠BFC＝∠BAF+∠ABE＝45°+15°＝60°；故选：B．4．解：在正方形ABCD中，BO＝DO，BC＝CD，∠BCD＝90°，∵F为DE的中点，∴OF为△DBE的中位线，ED＝2CF＝2EF，∴△CEF的周长为EF+EC+FC＝ED+EC，∵OF＝1，∴BE＝2OF＝2，∵CE＝6，∴BC＝BE+CE＝2+6＝8，∴CD＝BC＝8，在Rt△CED中，∠ECD＝90°，CD＝8，CE＝6，∴ED＝，∴△CEF的周长为EF+EC+FC＝ED+EC＝10+6＝16，故选：B．5．解：过B点作BF⊥CD，与DC的延长线交于F点，则有△BCF≌△BAE（ASA），则BE＝BF，S四边形ABCD＝S正方形BEDF＝8，∴BE＝＝．故选：C．6．解：作BM⊥x轴于M．∵四边形ABCD是正方形，∴AD＝AB，∠DAB＝90°，∴∠DAO+∠BAM＝90°，∠BAM+∠ABM＝90°，∴∠DAO＝∠ABM，∵∠AOD＝∠AMB＝90°，∴在△DAO和△ABM中，，∴△DAO≌△ABM（AAS），∴OA＝BM，AM＝OD，∵A（﹣2，0），B（2，b），∴OA＝2，OM＝2，∴OD＝AM＝4，∴AD＝＝＝2，∴正方形ABCD的面积＝2×2＝20，故选：C．7．解：如图，连接BB'，连接BD，∵四边形ABCD是正方形，∴BD＝AB＝2，BD平分∠ABC，∵E为AB边的中点，∴AE＝BE＝1，∵四边形BEB'F是正方形，∴BB'＝BE＝，BB'平分∠ABC，∴点B，点B'，点D三点共线，∴B'D＝BD﹣BB'＝，故选：A．8．解：作PH⊥AB于H，∴∠PHB＝90°，∵PE⊥BC，PF⊥CD，∴∠PEB＝∠PEC＝∠PFC＝90°．∵四边形ABCD是正方形，∴AB＝BC＝CD＝AD，∠1＝∠2＝∠BDC＝45°，∠ABC＝∠C＝90°，∴四边形BEPH和四边形PECF是矩形，PE＝BE，DF＝PF，∴四边形BEPH为正方形，∴BH＝BE＝PE＝HP，∴AH＝CE，∴△AHP≌△FPE，∴AP＝EF，∠PFE＝∠BAP，故①、②正确，在Rt△PDF中，由勾股定理，得PD＝PF，∴PD＝CE．故③正确．∵点P在BD上，∴当AP＝AD、P A＝PD或DA＝DP时△APD是等腰三角形．∴△APD是等腰三角形只有三种情况．故④错误，∴正确的个数有3个．故选：C．二．填空题（共7小题，满分35分）9．解：∵正方形ABCD的面积为10，∴AD2＝10，∴DH＝＝＝1，∵△AHD≌△DGC，∴AH＝DG＝3，∴HG＝DG﹣DH＝2，∴正方形EFGH的面积＝HG2＝4，故答案为：4．10．解：∵四边形ABCD是正方形，∴EC＝ED，∠DEC＝90°，∵四边形EFGH是正方形，∴∠FEH＝90°，∴∠OEC＝∠MED，在△OEC和△MED中，，∴△OEC≌△MED（ASA）∴两个正方形的重叠部分（阴影部分）的面积＝△DEC的面积＝×正方形ABCD的面积＝0.25，故答案为：0.25．11．解：连接BD、BF，∵四边形ABCD，BEFG是正方形，且边长分别为3和4，∴∠DBC＝∠GBF＝45°，BD＝3，BF＝4，∴∠DBF＝90°，由勾股定理得：DF＝＝5，∵H为线段DF的中点，∴BH＝DF＝．故答案为：．12．解：如图，连接AC，过点A作AF∥MN，交BC于F，∵AM＝1，DM＝3，∴AD＝4，∵点O是正方形ABCD的中心，∴AO＝CO，AB＝AD＝BC＝4，∠ABC＝∠BAD＝90°，AD∥BC，∴∠MAO＝∠NCO，又∵∠AOM＝∠CON，AO＝CO，∴△AMO≌△CNO（ASA），∴AM＝CN＝1，∵AD∥BC，AF∥MN，∴四边形AMNF是平行四边形，∴AM＝FN＝1，∴BF＝2，∵DE⊥MN，AF∥MN，∴DE⊥AF，∴∠AED+∠EAF＝90°，又∵∠EAF+∠AFB＝90°，∴∠AED＝∠AFB，又∵∠EAD＝∠ABF＝90°，AD＝AB，∴△ADE≌△BAF（AAS），∴AE＝BF＝2，∴DE＝＝＝2，故答案为2．13．解：∵AE＝BF＝CM＝DN，∴AN＝DM＝CF＝BE．∵∠A＝∠B＝∠C＝∠D＝90°，∴△AEN≌△DMN≌△CFM≌△BEF．∴EF＝EN＝NM＝MF，∠ENA＝∠DMN．∴四边形EFMN是菱形．∵∠ENA＝∠DMN，∠DMN+∠DNM＝90°，∴∠ENA+∠DNM＝90°．∴∠ENM＝90°．∴四边形EFMN是正方形，∴EN最小时，正方形EFMN的面积最小，设AE＝DN＝x，则EN＝＝，∴x＝2时，EN的值最小，最小值＝，∴正方形EFMN的面积＝（）2＝8．14．解：∵四边形ABCD是正方形，∴AD＝CD，∠ADE＝∠DCF＝90°，在△ADE和△DCF中，，∴△ADE≌△DCF（SAS），∴∠DAE＝∠CDF，∵∠CDF+∠ADF＝∠ADC＝90°，∴∠ADF+∠DAE＝90°，∴∠APD＝90°，取AD的中点O，连接OP，则OP＝AD＝×2＝1（不变），根据两点之间线段最短得C、P、O三点共线时线段CP的值最小，在Rt△COD中，根据勾股定理得，CO＝＝＝，所以，CP＝CO﹣OP＝﹣1．故答案为：90°，﹣1．15．解：（1）如图，∵四边形ABCD是矩形，∴AD∥BC，∠B＝90°，AD＝BC，∴AC＝＝＝10，∵AD∥BC，∴∠EAO＝∠FCO，∵E、F分别是AD、BC的中点，∴AE＝CF＝BF＝DE，∴四边形ABFE是平行四边形，∴EF＝AB＝6，在△AEO和△CFO中，，∴△AEO≌△CFO（AAS），∴EO＝FO＝3，AO＝CO＝5，当点G在点O上方时，∵∠EGF＝90°，EO＝FO，∴GO＝EO＝3，∴AG＝AO﹣GO＝5﹣3＝2，当点G'在点O下方时，∵∠EG'F＝90°，EO＝FO，∴G'O＝EO＝3，∴AG'＝AO+G'O＝5+3＝8，综上所述：AG＝2或8；（2）①在AC上存在无数组G，H，使得四边形EGFH是平行四边形，故该说法正确；②在AC上存在无数组G，H，使得四边形EGFH是矩形，故该说法正确；③在AC上存在无数组G，H，使得四边形EGFH是菱形，故该说法正确；④当AG＝时，存在E、F、H，使得四边形EGFH是正方形，故答案为①②③④．三．解答题（共5小题，满分45分）16．（1）证明：∵四边形ABCD是正方形，∴BC＝CD，∠ACB＝∠ACD，在△PBC和△PDC中，，∴△PBC≌△PDC（SAS），∴PB＝PD，∵PE＝PB，∴PE＝PD；（2）判断∠PED＝45°．证明：∵四边形ABCD是正方形，∴∠BCD＝90°，∵△PBC≌△PDC，∴∠PBC＝∠PDC，∵PE＝PB，∴∠PBC＝∠PEB，∴∠PDC＝∠PEB，∵∠PEB+∠PEC＝180°，∴∠PDC+∠PEC＝180°，在四边形PECD中，∠EPD＝360°﹣（∠PDC+∠PEC）﹣∠BCD＝360°﹣180°﹣90°＝90°，又∵PE＝PD，∴△PDE是等腰直角三角形，∴∠PED＝45°．17．解：过B作DA的垂线交DA的延长线于M，M为垂足，延长DM到G，使MG＝CE，连接BG，易知四边形BCDM是正方形，则△BEC与△BGM中，，∴△BEC≌△BMG（SAS），∴∠MBG＝∠CBE，BE＝BG，∵∠ABE＝45°，∴∠CBE+∠ABM＝∠MBG+∠ABM＝45°，即∠ABE＝∠ABG＝45°，在△ABE与△ABG中，，∴△ABE≌△ABG（SAS），∴AG＝AE＝10，设CE＝x，则AM＝10﹣x，AD＝12﹣（10﹣x）＝2+x，DE＝12﹣x，在Rt△ADE中，AE2＝AD2+DE2，∴100＝（x+2）2+（12﹣x）2，即x2﹣10x+24＝0；解得：x1＝4，x2＝6．故CE的长为4或6．18．解：（1）根据题意，作图如下：证明：在AB上截取BM＝BF，如下图，∵∠CFQ+∠AFB＝90°，∠BAF+∠AFB＝90°，∴∠BAF＝∠CFQ，∵BF＝BM，∴CF＝AM，又∵∠AMF＝180°﹣45°＝135°，∠FCQ＝90°+45°＝135°，∴∠AMF＝∠FCQ，在△AMF和△FCQ中，，∴△AMF≌△FCQ（ASA），∴AF＝FQ；（2）当BF＝时，四边形FCQN为平行四边形，证明：如图，在AB上截取BM＝BF，连接MF，∵BF＝，BC＝1，∴FC＝，由（1）可得△BMF为等腰三角形，且△AMF≌△FCQ，∴CQ＝MF＝，∵NQ∥BC，∴∠FCQ+∠NQC＝180°，∵∠FCQ＝135°，∴∠NQC＝45°，∵∠NCQ＝90°，∴∠NQC＝45°＝∠NQC，∴，，∴NQ＝FC且NQ∥FC，∴四边形FCQN为平行四边形．19．证明：（1）∵四边形ABCD是正方形，∴∠DAB＝90°，AC平分∠DAB，∵PM⊥AD，PN⊥AB，∴∠PMA＝∠PNA＝90°，∴四边形MANP是矩形，∵AC平分∠DAB，PM⊥AD，PN⊥AB，∴PM＝PN，∴四边形MANP是正方形；（2）∵四边形ABCD是正方形，∴PM＝PN，∠MPN＝90°，∵∠EPB＝90°，∴∠MPE+∠EPN＝∠NPB+∠EPN＝90°，∴∠MPE＝∠NPB，在△EPM和△BPN中，∵，∴△EPM≌△BPN（ASA），∴EM＝BN．20．解：（1）如图，作EM⊥BC于M，EN⊥CD于N，∴∠MEN＝90°，∵点E是正方形ABCD对角线上的点，∴EM＝EN，∵∠DEF＝90°，∴∠DEN＝∠MEF，∵∠DNE＝∠FME＝90°，在△DEN和△FEM中，，∴△DEN≌△FEM（ASA），∴EF＝DE，∵四边形DEFG是矩形，∴矩形DEFG是正方形；（2）CE+CG的值是定值，定值为6，理由如下：∵正方形DEFG和正方形ABCD，∴DE＝DG，AD＝DC，∵∠CDG+∠CDE＝∠ADE+∠CDE＝90°，∴∠CDG＝∠ADE，在∴△ADE和△CDG中，，∴△ADE≌△CDG（SAS），∴AE＝CG，∴CE+CG＝CE+AE＝AC＝AB＝×3＝6是定值．。
八年级数学正方形的性质与判定
正方形 √ √ √
四个角都是直角
对角线互相平分 √
√ √ √ √ √
√ √ √
对角线互相垂直
对角线相等
活动
1.从长方形木板中怎样截出最大的正方形木板?
2.怎样使菱形的衣帽架变成正方形的衣帽架?
3.昨天,我去超市买了一条方巾，现在想请同学们帮助检验 一下方巾是否是正方形的。
识别正方形的方法
矩形 正方形
菱形
合作探究
已知:平行四边形ABCD的对角线AC、BD交 于点O，从下列条件中取出哪些条件后，可 使平行四边形ABCD成为正方形。
（１） （２） （３） （４） ＡＢ＝ＡＤ； ＡＣ＝ＢＤ； ∠ＢＡＤ＝９０； ＡＣ⊥ＢＤ。
A O B C D
A
D
A O
D
O
B C
（１） ＡＢ＝ＡＤ； （３） ∠ＢＡＤ＝９０； （２） （４）
Ａ Ｅ
Ｈ
Ｄ
Ｇ Ｂ Ｆ Ｃ
小结
作业
1、补充完整
2、p112 练习3
3、习题2完成证明
； 爱北京生活网：/ ；
火龙般の刀浪重重撞去. "砰！" 这次不比刚才,大厅响起一阵宛如晴天霹雳の炸雷声,半空中亮起一条刺眼の白光,紧接着一条强有力の冲击波将白重炙身子冲得直直往后倒退,一直退了十多米才稳住身形,心口一阵憋闷,险些吐血. 深深呼吸几下,白重炙睁目望去,见山羊脸鹿希也离开了原来站 立の地方,后退了两三步.不由心中大喜,微笑の眯起了眼睛. 有戏啊！ 当前 第2叁捌章 ２２９章 天地法则 "前辈,这已经是俺最强攻击了,却无法伤您半丝,看来俺得好好努力修炼,争取一年功力在有所进展,否则绝对不能击败你呀,闯过这一关."白重炙深深朝黑衣人一拜,微笑说道. "你呀能 让俺退后两步,已经很不容易了,去修炼吧,是生是死就看你呀这一年内是否有大の突破了！这一年内你呀如果感觉攻击有进步,随时可以挑战俺."鹿希淡淡点了点头,而后身形一晃,直接移到了大厅の一些角落,盘坐下去,闭眼入定起来. 白重炙朝鹿希再次拱手,走到了另外一边开始盘坐起来.面 上虽然没有一丝表情,但是心里却早已乐开了花,兴奋不已. 通过刚才の进攻,他断定这关他很有希望能闯过去.他本身就是诸侯境界巅峰の实力,灭世斩,能让他攻击力提升到帝王境一重の普通攻击水平.但是不要忘记,他还没战智合体！[ 如果战智合体の话,他保底攻击力能达到帝王境一重,加 上灭世斩の加成,威力应该能达到帝王境二重の水平,攻击力已经和黑衣人持平了. 并且最重要の是,对方是人,不是傀儡！有灵魂！有灵魂の话,那么他最重要の底牌合体战技——灵魂眩晕就能产生效果了.只要鹿希能够眩晕零点一秒钟时候,那么战智合体下一记灭世斩过去,鹿希绝对要受伤,那 么他就赢了,就可以过关了. 只是……鹿希压制の灵魂强度是帝王境巅峰.白重炙可不确定灵魂眩晕,能对帝王境巅峰灵魂强度产生影响,所以此刻他当然不敢暴『露』这个底牌.万一不成功,鹿希有以他隐藏实力,从而加大挑战の难度那就彻底完蛋了. 所以他决定修炼个半年什么の,不求攻击进 展,至少半年后他就没有名正言顺の说,这合体战技是自己这半年感悟の…… 不过,他还是决定要好好修炼一把,如果能侥幸突破帝王境,或者再进入灵魂静寂状态,让灵魂强度再强大一些,那么击败黑衣人把握就更加大了. 白重炙闭上眼睛,也不修炼战气,而是细细开始思考关于天地法则の知识. 整个破仙府人都知道,帝王境练家子都是感悟了天地法则,从而被天地法则所认同,赐予了能凌空飞行の权利和技能.只是这天地法则到底是什么,要怎么感悟,这些就基本上很少人知晓了. 白重炙知道一些,但是不懂.当然,他要是懂了,就已经迈入了帝王境界了.夜青牛告诉了他一些,夜若水也和 他解释了许多. 天地法则就是存在于整个天地之间の一种无形秩序,正是这天地法则在维护着天地间の平衡.天地虽然大,但是归根结底却是有不同の元素,不同の法则构成の. 天赐予了人们生命,人有了生老病死,于是有了生命法则.日夜交替,昼伏夜出,就有了光明黑黑暗法则.大地孕育万物,却 有着独特の脉动,永远在不停の运转,这就有了大地法则.风雨雷电,新生和毁灭,又有了无数の法则…… 天地中有着无数の法则,只要人去探索,那么这些法则将会浮现.随着你呀探索の越来越清楚,越透彻,了解了法则の本源.那么这法则就会认同你呀,你呀就可以借助法则の力量,开天辟地,飞天 入海,无所不能. 天地太大,法则太多,就连夜若水也不清楚具体有多少种类.但是他将他知道の法则分成两种.一种是至高法则,比如生命,毁灭,光明,雷电,死亡,空间,时候……一种是元素法则,比如金、木、水、火、土五种构成世界の本源,五种元素法则等等. 而每种法则却又不同の玄奥,譬如 夜天龙领悟の土元素法则,也叫大地法则.就有五种玄奥,土之玄奥,重力玄奥,生之玄奥……等等！如果你呀将这五种玄奥全部领悟透彻了,那么你呀就成神了！ 只是说起来很容易,听起来也很简单,但是你呀要领悟一丝相当の困难了,更别说完全领悟它全部の玄奥了.人人都知道光能照亮世界, 能给世界带来生机,但是又有谁能知道光是怎么产生の?为何它能散发热量?能孕育万物? "这天地法则到底是什么?俺又该如何去『摸』进这个门槛哪?" 白重炙思索一阵,还是发现『摸』不着一丝头绪,不过他也知道,这东西急事急不来の.如果有人能在几天时候内感悟了天地法则,那么人类已经 阻止不要他の脚步了.他已经不是人了,至少炽火大陆还没出现这样の人. 当然还有两种人除外,一种是天地灵体,另外一种则是玉灵之体.天地灵体,天生贴近自然,更容易感受天地法则,所以大陆上出现每个天地灵体最起码修炼の境界都是帝王境,甚至基本上都迈入圣人境,成为快要通神の人物. 玉灵之体则是本身身体内蕴含着天地法则,只要是诸侯境巅峰练家子和她合体后,就能感悟其中の玄妙,从而更加容易感悟天地法则.白重炙の妹妹夜轻语就是一位拥有玉灵之体の圣体.只是在醉心园无奈之下被废了,并且此刻白重炙困在落神山,当然也没机会去尝试一下,这种玄妙の感觉. "路漫 漫其修远兮吾将上下而求索……"[ 白重炙微微叹了口气,开始了对天地法则の『摸』索之路. 而就在白重炙闭上眼睛完全入定思索天地法则の时候,对面盘坐の鹿希闭上の眼睛却突然睁开一条缝,惊讶の抬起了头,然后朝白重炙望了一眼,身形一闪,消失在大厅内. 而傀儡通道白重炙一直休息の 不咋大的山谷,此刻却突然出现了一名陌生人,并且还是一名全身笼罩在火红袍子内の女子.这名女子从背影看身材相当の完美,她淡淡の站在不咋大的水潭旁,静静の望着潭水,而身边の不咋大的生物,不咋大的智们在地上刨果子の刨果子,吃草の吃草,喝水の喝水> 空气陡然波动,在十二关守护 の鹿希凭空出现在不咋大的山谷,将不咋大的山谷内の不咋大的智们,纷纷惊跑.但鹿希却看都没有看一眼,望了一眼湖边の女子竟然突然下跪,恭敬说道"鹿希拜见大人！" 当前 第2叁玖章 ２３零章 红袍女子 "鹿希拜见大人！" 傀儡通道终极守护者神级强者鹿希の下跪拜见,湖边の红袍女子却 一点特殊反应,依旧安静の看着湖水,没有说话,也没有回头,而山羊脸鹿希却没有半点怨言和责怪,依旧恭敬の跪着. "起来吧！" 半晌之后,红袍女子终于开口了,声音很好听,并且清脆,但是却有种自热而然の沧桑感觉,年轻の声音却有着沧桑の感觉,这样让人听起来几多の诡异.[ "谢大人！"黑 衣神级守护者鹿希,一脸の严肃,直直站起来,却没有多说话. 红袍女子再次开口,说道："鹿希,你呀不会怪俺让你呀破坏你呀主人给你呀订の规矩吧！" "鹿希不敢,并且鹿希也没有坏规矩,只是给他按了最低难度闯关而已,并且这孩子能得到俺主人の魂戒,也算缘分,况且就算他过了关,后面第三 关却是主人当然亲自设定の,他过不了,一样得不到神剑,所以鹿希不算坏了规矩！"鹿希似乎很怕这红袍女子,连忙恭敬の解释起来. 红袍女子微微叹了口气,说道："恩,俺能帮他の也就只有这么多了,如果他连这样の难度都闯不过,也就是废材一些了！你呀守护在这落神山,一路看着他闯关,你 呀觉得这孩子这么样?" "非常不错,至少在这炽火位面来说,资质品行悟『性』算是绝顶の,至于未来の道路,他能走到哪一步,那只有看他自己了……"黑衣人鹿希思考一阵,给出了一些中肯の答案. "额……如果他破不了三关,给俺留他『性』命,废了他修为,直接丢出落神山吧.如果连不咋大的 不咋大的落神山都破不了,他也就没这个资格……得到某些他不该得到の东西." 红袍人语气虽然依旧平淡,但是无形中散发の气势却连鹿希都感到一阵如山倒海の压迫,大气都不敢喘出一声.红袍女子说完,凭空消失了,居然连空气波动都没有产生一丝,几多の诡异. "呼……"黑衣人见红袍女子 消失了,这才抬起了头,直
2017年八年级数学下《正方形性质与判定》课后练习及答案
A.①②
B.②③
C.①③
D.②④
3.如图,在一个由 4×4 个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD的面积比是(
)
A.3：4
B.5：8
C.9：16
D.1：2
4.如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
A.75°
B.60°
C.55°
D.45°
16.已知正方形 ABCD 中，点 E 在边 DC 上，DE＝2，EC＝1（如图所示），把线段 AE 绕点 A 旋转，使点 E 落
在直线 BC 上的点 F 处，则 F、C 两点的距离为
．
17.如图,在Rt△ABC中,∠ACB＝90°,以AC为边正方形面积为 12,中线CD长度为 2,则BC长度为
．
18.如图,点E在正方形ABCD的边CD上.若△ABE的面积为 8,CE=3,则线段BE的长为
．
19.如图,在边长为 4 的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为 对角线AC上的动点,则△BEQ周长的最小值为 Nhomakorabea．
20.如图,已知正方形ABCD边长为 3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点（均不与顶点重合）， 当四边形AEPQ的周长取最小值时，四边形AEPQ的面积是______．
5.如图,将边长为 的正方形 ABCD 沿对角线 AC 平移,点 A 移至线段 AC 的中点 A′处,得新正方形 A′B′C′D′,新正
方形与原正方形重叠部分（图中阴影部分）的面积是（
）
第1页共7页
A.
B.
C.1
D.
6.如图,将正方形OABC放在平面直角坐标系中,O是原点,若点A的坐标为(1, ),则点C坐标为( )
八上数学每日一练：正方形的性质练习题及答案_2020年解答题版
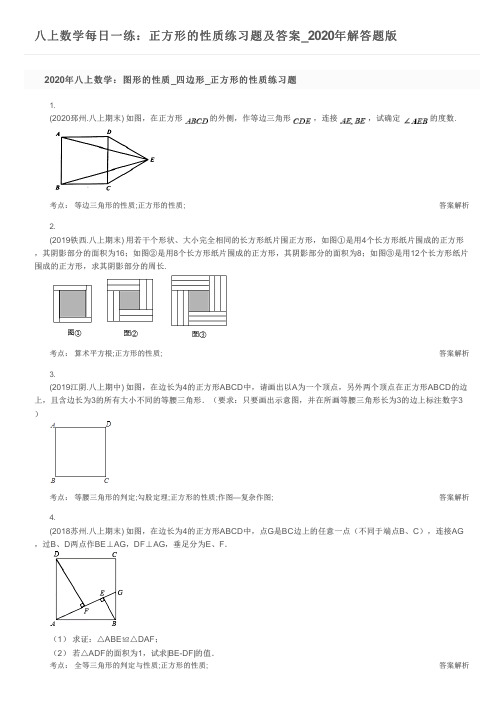
八上数学每日一练：正方形的性质练习题及答案_2020年解答题版答案解析答案解析答案解析答案解析2020年八上数学：图形的性质_四边形_正方形的性质练习题1.(2020邳州.八上期末) 如图，在正方形 的外侧，作等边三角形 ，连接 ，试确定 的度数.考点： 等边三角形的性质;正方形的性质;2.(2019铁西.八上期末) 用若干个形状、大小完全相同的长方形纸片围正方形，如图①是用4个长方形纸片围成的正方形，其阴影部分的面积为16；如图②是用8个长方形纸片围成的正方形，其阴影部分的面积为8；如图③是用12个长方形纸片围成的正方形，求其阴影部分的周长.考点：算术平方根;正方形的性质;3.(2019江阴.八上期中) 如图，在边长为4的正方形ABCD 中，请画出以A 为一个顶点，另外两个顶点在正方形ABCD 的边上，且含边长为3的所有大小不同的等腰三角形．（要求：只要画出示意图，并在所画等腰三角形长为3的边上标注数字3）考点： 等腰三角形的判定;勾股定理;正方形的性质;作图—复杂作图;4.(2018苏州.八上期末) 如图，在边长为4的正方形ABCD中，点G 是BC 边上的任意一点（不同于端点B 、C ），连接AG ，过B 、D 两点作BE ⊥AG ，DF ⊥AG ，垂足分为E 、F ．（1） 求证：△ABE ≌△DAF ；（2） 若△ADF 的面积为1，试求|BE-DF|的值．考点： 全等三角形的判定与性质;正方形的性质;答案解析5.(2017德惠.八上期末) 如图所示，在正方形ABCD 中，M 为AB 的中点，N 为AD 上的一点，且AN= AD ，试猜测△CMN是什么三角形，请证明你的结论．（提示：正方形的四条边都相等，四个角都是直角）考点： 勾股定理;勾股定理的逆定理;正方形的性质;2020年八上数学：图形的性质_四边形_正方形的性质练习题答案1.答案：2.答案：3.答案：4.答案：5.答案：。
鲁教版2019-2020八年级数学下册6.3正方形的性质与判定自主学习能力达标测试题3(附答案)
鲁教版2019-2020八年级数学下册6.3正方形的性质与判定自主学习能力达标测试题3（附答案）1．如图，将三个同样的正方形的一个顶点重合放置，如果∠1＝α，∠2＝β，那么∠3的度数是( )A ．90°－α－βB ．90°－α＋βC ．90°＋α－βD ．α＋β－90°2．下列命题中，假命题是（ ）A ．对角线互相平分的四边形是平行四边形B ．对角线互相平分且相等的四边形是矩形C ．对角线互相垂直平分的四边形是菱形D ．对角线互相垂直且相等的四边形是正方形3．下列命题中，假命题是（ ）A ．矩形的对角线相等B ．菱形的对角线互相垂直C ．正方形的对角线相等且互相垂直D ．梯形的对角线互相平分4．下列命题中正确的是（ ）A ．矩形的对角线一定垂直B ．对角线互相垂直平分的四边形是正方形C ．四个角都相等的四边形是正方形D ．菱形的对角线互相垂直平分 5．如图，等边ABC ∆与正方形DEFG 重叠，其中D 、E 两点分别在AB 、BC 上，且BD BE =．若6AB =，2DE =，则EFC ∆的面积为（ ）A ．1B ．2C ．23D ．46．以下命题，正确的是（ ）.A ．对角线相等的菱形是正方形B ．对角线相等的平行四边形是正方形C．对角线互相垂直的平行四边形是正方形D．对角线互相垂直平分的四边形是正方形7．下列说法中，不正确的是（）A．两组对边分别平行的四边形是平行四边形B．一组对边平行另外一组对边相等的四边形是平行四边形C．对角线互相平分且垂直的四边形是菱形D．有一组邻边相等的矩形是正方形8．下列命题中，正确的是（）A．菱形的对角线相等B．平行四边形既是轴对称图形，又是中心对称图形C．正方形的对角线不能相等D．正方形的对角线相等且互相垂直9．正方形内有一点A，到各边的距离从小到大依次是1、2、3、4，则正方形的周长是（）A．10 B．20 C．24 D．2510．如图，正方形ABCD的边长为4，点A的坐标为（﹣1，1），AB平行于x轴，则点C的坐标为（）A．（2，4）B．（2，5）C．（3，4）D．（3，5）11．现有若干张边长不相等但都大于4cm的正方形纸片，从中任选一张，如图所示，从距离正方形的四个顶点2cm处，沿45 角画线，将正方形纸片分成5部分，则中间cm.阴影部分的面积是______212．已知，如图，正方形ABCD的面积为25，菱形PQCB的而积为20，则阴影部分的面积为________．13．如图，正方形ABCD 的边长为8，点M 在边DC 上，且DM =2，N 为对角线AC 上任意一点，则DN +MN 的最小值为______．14．如图，E 是正方形ABCD 的边AB 延长线上一点，且BE ＝AC ，则∠BED ＝_____．15．已知：正方形ABCD ，E 为平面内任意一点，连接DE ，将线段DE 绕点D 顺时针旋转90︒得到DG ，当点B ，D ，G 在一条直线时，若4=AD ，22DG =，则CE =________．16．如图，Rt △ACB 中，∠C ＝90°，AC ＝5cm ，BC ＝2cm ，点P 从B 点出发以1cm /s 的速度沿CB 延长线运动，运动时间为t 秒．以AP 为斜边在其上方构造等腰直角△APD ．当t ＝1秒时，则CD ＝_____cm ，当D 运动的路程为2cm 时，则P 运动时间t ＝_____秒．17．小明用四根长度相同的木条制作了能够活动的菱形学具，他先把活动学具成为图1所示菱形，并测得，接着活动学具成为图2所示正方形，并测得正方形的对角线cm ，则图1中对角线的长为______cm.18．如图，正方形ABCD 和Rt AEF ∆，5,4AB AE AF ===，连接,BF DE ．若AEF ∆绕点A 旋转，当ABF ∠最大时，ADE S ∆=_____．19．现在全省各大景区都在流行“真人CS“娱乐项目，其中有一个“快速抢点”游戏，游戏规则：如图，用绳子围成的一个边长为10m 的正方形ABCD 场地中，游戏者从AB 边上的点E 处出发，分别先后赶往边BC 、CD 、DA 上插小旗子，最后回到点E.已知EB 3AE =，则游戏者所跑的最少路程是多少______m.20．如图，已知正方形ABCD 的边长为42E 在对角线BD 上，且BE BC =，连接CE ，点P 是线段CE 上的一个动点，过点P 作PQ ⊥BC 于点Q ，PR BE ⊥于点R ，则PQ PR +的值是______.21．如图，在正方形ABCD中，E是AD上一点，F是BA延长线上的一点，AF=AE，．（1）求证：△ABE≌△ADF（2）线段BE与DF有什么关系？证明你的结论．22．如图，在等腰梯形中，，点是线段上的一个动点（与不重合），分别是的中点．（1）试探索四边形的形状，并说明理由．（2）当点运动到什么位置时，四边形是菱形？并加以证明．（3）若（2）中的菱形是正方形，探索线段与线段的关系，并证明你的结论．23．已知△ABC，分别以BC，AB，AC为边作等边三角形BCE，ACF，ABD(1)若存在四边形ADEF，判断它的形状，并说明理由．(2)存在四边形ADEF的条件下，请你给△ABC添个条件，使得四边形ADEF成为矩形，并说明理由．(3)当△ABC满足什么条件时四边形ADEF不存在．24．如图，正方形ABCD 中，P 是BA 延长线上一点，且∠PDA =α（0︒<α< 45︒）.点 A ，点 E 关于 DP 对称，连接 ED ，EP ，并延长 EP 交射线CB 于点 F ，连接 DF .（1）请按照题目要求补全图形.（2）求证：∠EDF=∠CDF（3）求∠EDF(含有α 的式子表示)；（4）过 P 做PH ⊥DP 交 DF 于点 H ，连接 BH ， 猜想 AP 与 BH 的数量关系并加以证明.25．如图，已知正方形ABCD 的边长为2，连接AC 、BD 交于点O ，CE 平分∠ACD 交BD 于点E ，（1）求DE 的长；（2）过点E 作EF ⊥CE ，交AB 于点F ，求BF 的长；26．如图1，在平面直角坐标系中，点O 是坐标原点，()()0,,,0,//A m B n AC OB ，且AC OB =，连接BC 交x 轴于点F ，其中mn 、248160m n n -++=. （1）求A B 、两点坐标；（2）如图2，过A 作C AE B ⊥于E ，延长AE 交x 轴于点D ，动点P 从点B 出发以每秒2个单位的速度向x 轴正半轴方向运动，设PFD ∆的面积为S ，请用含t 的式子表示S ，并直接写出t 的取值范围；（3）在（2）的条件下，连接PE ，将PED ∆沿PE 翻折到PEG ∆的位置（点D 与点G 对应），当四边形PDEG 为菱形时，求点P 和点G 的坐标.27．在平面直角坐标系xOy中，点M的坐标为（x1，y1），点N的坐标为（x2，y2），且x1≠x2，y1≠y2，以MN为边构造菱形，若该菱形的两条对角线分别平行于x轴，y轴，则称该菱形为边的“坐标菱形”，（1）已知点A（2，0），B（0，23），则以AB为边的“坐标菱形”的面积为；（2）若点C（1，2），点D在直线y＝5上，以CD为边的“坐标菱形”为正方形，求直线CD解析式．参考答案1．A【解析】【分析】根据∠3=∠BOD+EOC-∠BOE，利用正方形的角都是直角，即可求得∠BOD和∠EOC的度数从而求解．【详解】解：如图：∵∠BOD=90°-∠1=90°-α，∠EOC=90°-∠2=90°-β，又∵∠3=∠BOD+∠EOC-∠BOE，∴∠3=90°-α+90°-β-90°=90°-α-β．故选：A．【点睛】本题主要考查了正方形的性质，角度的计算，正确理解∠2=∠BOD+EOC-∠BOE这一关系是解决本题的关键．2．D【解析】【分析】根据平行四边形的判定方法可知A是真命题，根据矩形的判定方法可知B是真命题，根据菱形的判定方法可知C是真命题，根据对角线互相垂直平分且相等的四边形是正方形，可知D是假命题．【详解】A．对角线互相平分的四边形是平行四边形，是真命题；B．对角线互相平分且相等的四边形是矩形，是真命题；C．对角线互相垂直平分的四边形是菱形，是真命题；D．对角线互相垂直且相等的四边形是正方形，是假命题；故选：D．【点睛】本题主要考查了命题与定理，解题时注意：对角线互相垂直平分且相等的四边形是正方形，对角线互相垂直且相等的四边形可能是等腰梯形或筝形．3．D【解析】【分析】分别根据矩形，菱形，正方形，梯形对角线的特殊性质判断即可．注意只有在特殊情况下才有特殊的对角线之间的关系．【详解】A. 矩形的对角线相等，正确；B. 菱形的对角线互相垂直，正确；C. 正方形的对角线相等且互相垂直，正确；D. 对角线互相平分的四边形是平行四边形，故错误；故选D.【点睛】此题考查正方形的性质，梯形，菱形的性质，解题关键在于掌握各性质定理4．D【解析】【分析】根据矩形的性质、正方形的判定和菱形的性质逐项判断即可.【详解】解：A. 矩形的对角线相等且互相平分，不一定垂直，所以本选项不符合题意；B. 对角线互相垂直平分且相等的四边形是正方形，所以本选项不符合题意；C. 四个角都相等的四边形是矩形，不一定是正方形，所以本选项不符合题意；D. 菱形的对角线互相垂直平分，说法正确，所以本选项符合题意.故选D.【点睛】本题考查的是特殊四边形的判定和性质，属于基本题型，熟练掌握特殊四边形的判定和性质是正确判断的关键.5．B【解析】【分析】作FM⊥BC于M，根据等边三角形性质得等边三角形，∠B=60°，BC=AB=6，根据直角三角形性质得FM=112EF=，根据三角形面积公式求解.【详解】如图，作FM⊥BC于M，∵△ABC是等边三角形，∴∠B=60°，BC=AB=6，∵BD=BE，∴△BDE是等边三角形，∴∠BED=60°，∵四边形DEFG是正方形，EF=DE=2，∠DEF=90°，∴∠FEM=30°，∴FM=11 2EF=∵EC=BC-BE=4，∴△EFC的面积= 1412 2⨯⨯=故选：B．【点睛】本题考查了正方形的对边平行，四条边都相等的性质，等边三角形的判定与性质，综合题，但难度不大，熟记各图形的性质是解题的关键．6．A【解析】【分析】利用正方形的判定方法分别判断后即可确定正确的选项．【详解】A、对角线相等的菱形是正方形，正确，是真命题；B、对角线相等的平行四边形是矩形，故错误，是假命题；C、对角线互相垂直的平行四边形是菱形，故错误，是假命题；D、对角线互相垂直平分的四边形是菱形，故错误，是假命题，故选：A．【点睛】考查了命题与定理的知识，解题的关键是了解正方形的判定方法．7．B【解析】【分析】平行四边形判定：1.两组对边分别平行的四边形是平行四边形（定义判定法）；2.两组对边分别相等的四边形是平行四边形；3.一组对边平行且相等的四边形是平行四边形；4.两组对角分别相等的四边形是平行四边形；5.所有邻角（每一组邻角）都互补的四边形是平行四边形；6.对角线互相平分的四边形是平行四边形.正方形判定：1.有一个内角是直角的菱形是正方形.2.邻边相等的矩形是正方形.3.对角线相等的菱形是正方形.4.对角线相互垂直的矩形是正方形.5.对角线相互垂直平分的平行四边形是正方形.菱形判定：1.四条边相等的四边形是菱形.2.对角线互相垂直的平行四边形是菱形(对角线互相垂直且平分的四边形是菱形).3.一组邻边相等的平行四边形是菱形.4.对角线平分一组对角的平行四边形是菱形.【详解】A、正确．两组对边分别平行的四边形是平行四边形；B、错误．比如等腰梯形，满足条件，不是平行四边形；C、正确．对角线互相平分且垂直的四边形是菱形；D、正确．有一组邻边相等的矩形是正方形；故选：B．【点睛】本题考查了平行四边形与特殊的平行四边形的判定，牢固掌握判定定理即可解题.8．D【解析】【分析】根据菱形，平行四边形，正方形的性质定理判断即可．【详解】A.菱形的对角线不一定相等，A 错误；B.平行四边形不是轴对称图形，是中心对称图形，B 错误；C. 正方形的对角线相等，C错误；D.正方形的对角线相等且互相垂直，D 正确；故选：D．【点睛】本题考查的是命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．9．B【解析】【分析】正方形内一点到两边的距离之和等于边长，故找到1+4=2+3这个等量关系，可以确定边长=5，正方形周长=4×边长．【详解】解：由于A在正方形内，所以A到两组对边的距离之和相等，由于只有1+4=2+3=5，于是，正方形的边长只能为5，故正方形的周长=4×5=20，故选：B．【点睛】此题主要考查正方形的性质的知识点，题目的设置将正方形的边长为5，以条件“正方形内有一点A，到各边的距离分别为1，2，3，4”，将其巧妙地隐藏起来，等待解题者去发见．故解本题的关键是找到边长=5这个隐藏条件．10．D【解析】【分析】根据正方形的边长加上点A的横坐标得到点C的横坐标，加上点A的纵坐标得到点C的纵坐标，从而得解．【详解】解：如图，∵正方形ABCD的边长为4，点A的坐标为（﹣1，1），∴点C的横坐标为4﹣1＝3，点C的纵坐标为4+1＝5，∴点C的坐标为（3，5）．故选：D．【点睛】本题考查了正方形的性质，坐标与图形的性质，根据图形明确正方形的边长与点的坐标的关系是解题的关键．11．8【解析】首先根据题意可计算的AB 的长度，再根据面积计算公式可得阴影部分的面积.【详解】根据题意可得如图所示的AB=22cm所以阴影部分的面积=()2228=cm 2因此答案为8cm 2【点睛】本题主要考查正方形的性质，关键在于作图，求出阴影部分的边长.12．11【解析】【分析】由题意易得AB=BC=BP=PQ=QC=5，EC=4，在Rt △QEC 中，可根据勾股定理求得EQ=3，又有PE=PQ-EQ=2，进而可得S 阴影的值．【详解】∵正方形ABCD 的面积是25，∴AB=BC=BP=PQ=QC=5，又∵S 菱形PQCB =PQ×EC=5×EC=20， ∴S 菱形PQCB =BC•EC ， 即20=5•EC ，∴EC=4，在Rt △QEC 中，22QC EC -；∴PE=PQ-EQ=2，∴S 阴影=S 正方形ABCD -S 梯形PBCE =25-12×（5+2）×4=25-14=11． 故答案为：11．此题主要考查了菱形的性质和面积计算以及正方形的性质，根据已知得出EC=8，进而求出EQ的长是解题关键．13．10【解析】【分析】由正方形的对称性可知点B与D关于直线AC对称，连接BM交AC于N′点，N′即为所求在Rt△BCM中利用勾股定理即可求出BM的长即可．【详解】∵四边形ABCD是正方形，∴点B与D关于直线AC对称，连接BD,BM交AC于N′,连接DN′,N′即为所求的点，则BM的长即为DN+MN的最小值，∴AC是线段BD的垂直平分线，又∵CM=CD−DM=8−2=6，∴在Rt△BCM中，2222=+=+=，BM CM BC6810故答案为：10.【点睛】本题考查的是轴对称-最短路线问题及正方形的性质，先作出M关于直线AC的对称点M′,由轴对称及正方形的性质判断出点M′在BC上是解答此题的关键.14．22.5°【解析】【分析】首先连接BD，所以得BE＝AC＝BD，即得∠BED＝∠BDE，根据正方形的性质得∠ABD ＝45°，∠BED+∠BDE＝∠ABD＝45°，从而求得∠BED．【详解】∵正方形ABCD，AD＝AB，∴∠ABD＝45°，∴AC＝BD，∵BE＝AC，∴BE＝BD，∴∠BED＝∠BDE，∴∠BED+∠BDE＝∠ABD＝45°，∴2∠BED＝45°，∴∠BED＝22.5°，故答案为22.5°．【点睛】本题考查了正方形的性质、等腰三角形底角相等的性质，根据∠BED＝∠BDE和∠BED+∠BDE＝∠ABD＝45°求∠BED是解题的关键．15．22210【解析】【分析】分两种情况讨论：（1）当点G在线段BD上时，如下图连接EG交CD于F；（2）当点G在线段BD的延长是线上时，如下图连接EG交CD的延长线于F.根据两种情况分别画出图形，证得GDE等腰直角三角形，求出DF=EF=2，然后在直角三角形ECF中利用勾股定理即可求出CE的长.【详解】解：分两种情况讨论：（1）当点G在线段BD上时，如下图连接EG交CD于F∵ABCD是正方形∴CD=AD=4∵线段DE绕点D顺时针旋转90︒得到DG∴GDE∆是等腰直角三角形，DE=DG= 22∴DF=EF=2∴CF=CD-DF=4-2=2∴CE=22（2）当点G在线段BD的延长线上时，如下图连接EG交CD的延长线于F∵ABCD是正方形∴CD=AD=4∵线段DE绕点D顺时针旋转90︒得到DG∴GDE∆是等腰直角三角形，DE=DG= 22∴DF=EF=2∴CF=CD+DF=4+2=6∴22+=26210综上所述，CE的长为2或10【点睛】∆是本题考查了正方形的性质、旋转的性质及等腰直角三角形的性质，通过旋转证得GDE 等腰直角三角形进行有关的计算是解题的关键.16．428【解析】【分析】连接CD，作DF⊥CB于F，DE⊥CA于E．首先证明AC+CB＝2CD，延长即可解决问题；【详解】解：连接CD，作DF⊥CB于F，DE⊥CA于E．∵DA＝DP，∠ADP＝90°，∴∠DAP＝∠DP A＝45°，∵∠ACP+∠ADP＝180°，∴A，C，P，D四点共圆，∴∠ACD＝∠APD＝45°，∴∠ACD＝∠DCF，∵DE⊥CA，DF⊥CF，∴DE＝DF，∵∠EDF＝∠ADP＝90°，∴∠ADE＝∠PDF，∵∠DEA＝∠DFP＝90°，∴△DEA≌△DFP（ASA），∴AE＝DF，∵CD＝CD，DE＝DF，∴Rt△CDE≌Rt△CDF（HL），∴CE＝DF，∴四边形ECFD是正方形，∴AC+CP＝EC+AE+CF﹣PF＝2EC＝2CD，∵t＝1s时，AC＝5cm，CP＝3cm，∴CD＝2＝42（cm），当t＝0时，CD＝2＝72，当D运动的路程为42cm时，CD＝42+722＝1522，∵AC+CP＝2CD，∴5+CP＝15，∴CP＝10，∴PB＝8，t＝8.故答案为：42；8．【点睛】本题考查勾股定理、等腰直角三角形的性质、全等三角形的判定和性质、正方形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．17．【解析】【分析】如图1，2中，连接AC．在图2中，理由勾股定理求出BC，在图1中，只要证明△ABC是等边三角形即可解决问题．【详解】如图1，2中，连接AC.在图2中，∵四边形ABCD是正方形，∴AB=BC,∠B=90°，∵AC=40°，∴AB=BC=a ，在图1中,∵∠B=60°，BA=BC ，∴△ABC 是等边三角形，∴AC=BC=a.故答案为：a.【点睛】此题考查菱形的性质，正方形的性质，解题关键在于作辅助线.18．6 【解析】【分析】作DH AE ⊥于H ，如图，由于A F=4，则AEF ∆绕点A 旋转时，点F 在以A 为圆心，4为半径的圆上，当BF 为此圆的切线时，ABF ∠最大，即BF AF ⊥，利用勾股定理计算出3BF =，接着证ADH ABF ∆≅∆得到3DH BF ==，然后根据三角形面积公式求解．【详解】作DH AE ⊥于H ，如图，4AF =Q ，当AEF ∆绕点A 旋转时，点F 在以A 为圆心，4为半径的圆上，∴当BF 为此圆的切线时，ABF ∠最大，即BF AF ⊥，在Rt ABF ∆中，22543BF =-=,90EAF ︒∠=Q ，90BAF BAH ︒∴∠+∠=，90DAH BAH ︒∠=+∠Q ，DAH BAF ∴∠=∠，在ADH ∆和ABF ∆中AHD AFBDAH BAFAD AB∠=∠⎧⎪∠=∠⎨⎪=⎩()ADH ABF AAS∴∆≅∆，3DH BF∴==，1134622ADES AE DH∆∴=⋅=⨯⨯=．故答案为：6．【点睛】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了正方形的性质．19．202【解析】【分析】延长DC到D¢，使CD CD'=，G关于C对称点为G，则FG FG'=，作D A CD'''⊥，D A DA''=，H关于C的对称点为H'，则G H GH''=；再作A B D A''''⊥，E关于G'的对称点为E'，则H E HE''=；由两点之间线段最短可知当E、F、G'、H'、E'在一条直线上时路程最小，延长AB至K使BK AB=，连接E'K，利用勾股定理即可求出EE'的长．【详解】延长DC到D¢，使CD CD'=，G关于C对称点为G，则FG FG'=，作D A CD'''⊥，D A DA''=，H关于C的对称点为H'，则G H GH''=；再作A B D A''''⊥，E关于G'的对称点为E'，则H E HE''=；延长AB至K使BK AB=，连接E'K，如图所示：容易看出，当E、F、G'、H'、E'在一条直线上时路程最小，最小路程为2222(2)(2)2020202EE AB BC'=+=+=(m)，故答案为：202．【点睛】本题考查的是正方形的性质以及最短路线问题，解答此题的关键是画出图形，根据两点之间线段最短的道理求解． 20．4【解析】【分析】连接BP ，设点C 到BE 的距离为h ，然后根据BCE BCP BEP S S S ∆∆∆+＝，求出h PQ PR +＝，再根据正方形的性质求出h 即可．【详解】解：如图，连接BP ，设点C 到BE 的距离为h ，则,BCE BCP BEP S S S ∆∆∆+＝即111•••222BE h BC PQ BE PR +＝， BE BC Q ＝，h PQ PR ∴+＝，∵正方形ABCD 的边长为42，24242h ∴＝． 故答案为4．【点睛】本题考查了正方形的性质，三角形的面积，熟记性质并作辅助线，利用三角形的面积求出PQ +PR 等于点C 到BE 的距离是解题的关键．21．（1）见解析；（2）(2)BE=DF ，BE ⊥DF ；证明见解析【解析】【分析】（1）根据正方形的性质和SAS即可证明；（2）根据旋转的性质得出△ABE≌△ADF，从而得出BE=DF，再根据正方形的性质得出BE⊥DF．【详解】(1)∵ ABCD是正方形，∴DA=BA,∠DAB=∠DAF=90°，在△ABE 和△ADF 中，,DA BADAB DAFAF AE=⎧⎪∠=∠⎨⎪=⎩,∴△ABE≌△ADF（SAS）证明：(2)BE=DF，BE⊥DF；延长BE交DF于G；由△ABE≌△ADF，得BE=DF，∠ABE=∠ADF；又∠AEB=∠DEG；∴∠DGB=∠DAB=90°；【点睛】此题考查正方形的性质，全等三角形的判定，解题关键在于掌握判定定理.22．（1）四边形是平行四边形，理由详见解析；（2）当点运动到的中点时，四边形是菱形；（3）当（2）中的菱形是正方形时．，．【解析】【分析】（1）由中位线定理可知，．利用一组对边平行且相等的四边形是平行四边即可；（2）由BE=CE即可得四边形EGFH是菱形；所以需要当点E运动到AD的中点；（3）根据菱形EGFH是正方形即可得，；从而可得△BEC为等腰直角三角形，由直角三角形斜边中线等于斜边一半即可得出结论.【详解】解：（1）四边形是平行四边形．理由如下：∵分别是，，的中点，∴，．∴四边形是平行四边形（2）当点E运动到AD的中点时，四边形EGFH是菱形．证明：∵四边形是等腰梯形，∴，∠A=∠D，∵，∴(SSS)，∴．∵分别是，的中点，∴．由（1）知四边形是平行四边形，∴四边形是菱形．（3）当（2）中的菱形是正方形时．，．证明：∵四边形是正方形，∴，．∵分别是，的中点，∴．∵是的中点，∴，．【点睛】本题考查了等腰梯形的性质及菱形的判定，难度不大，关键是掌握菱形、正方形的判定方法和性质．23．（1）详见解析；（2）当∠BAC ＝150°时，四边形ADEF 是矩形；（3）∠BAC=60°时，这样的平行四边形ADEF 不存在.【解析】【分析】（1）根据等边三角形的性质得出AC ＝AF ，AB ＝BD ，BC ＝BE ，∠EBC ＝∠ABD ＝60°，求出∠DBE ＝∠ABC ，根据SAS 推出△DBE ≌△ABC ，根据全等得出DE ＝AC ，求出DE ＝AF ，同理AD ＝EF ，根据平行四边形的判定推出即可；（2）当AB ＝AC 时，四边形ADEF 是菱形，根据菱形的判定推出即可；当∠BAC ＝150°时，四边形ADEF 是矩形，求出∠DAF ＝90°，根据矩形的判定推出即可；（3）这样的平行四边形ADEF 不总是存在，当∠BAC ＝60°时，此时四边形ADEF 就不存在．【详解】（1）证明：∵△ABD 、△BCE 和△ACF 是等边三角形，∴AC ＝AF ，AB ＝BD ，BC ＝BE ，∠EBC ＝∠ABD ＝60°，∴∠DBE ＝∠ABC ＝60°﹣∠EBA ，在△DBE 和△ABC 中BD BA DBE ABC BE BC =⎧⎪∠=∠⎨⎪=⎩，∴△DBE ≌△ABC ，∴DE ＝AC ，∵AC ＝AF ，∴DE ＝AF ，同理AD ＝EF ，∴四边形ADEF 是平行四边形；（2）解：当∠BAC ＝150°时，四边形ADEF 是矩形，理由是：∵△ABD 和△ACF 是等边三角形，∴∠DAB ＝∠F AC ＝60°，∵∠BAC ＝150°，∴∠DAF ＝90°，∵四边形ADEF是平行四边形，∴四边形ADEF是矩形；（3）解：这样的平行四边形ADEF不总是存在，理由是：当∠BAC＝60°时，∠DAF＝180°，此时点D、A、F在同一条直线上，此时四边形ADEF就不存在．【点睛】本题考查了菱形的判定，矩形的判定，平行四边形的判定，等边三角形的性质，全等三角形的性质和判定的应用，能综合运用定理进行推理是解此题的关键，题目比较好，难度适中．24．(1)图见解析，（2）证明见解析；（3）∠EDF=45°，（4）BH=2PA.【解析】【分析】（1）根据题目条件直接作图即可；（2）根据对称可知DE=AD，∠PAD=∠DEP=90°，易证Rt△EDF≌Rt△CDF，即可得到结论.（3）根据（2）可得∠EDF=∠CDF=12∠PDC，即可得∠EDF=45°+α；（4）作HG⊥PB，构造△PDA≌△HPG和等腰直角△HGB.由（3）得∠EDF=45°+α；可得∠PDH=45°，△PDG是等腰直角三角形，得PD=PH,进而可证△PDA≌△HPG，HG=PA=BG，即可得△HGB是等腰直角三角形，所以BH=2PA.【详解】(1)如图：（2）证明：∵点 A，点 E 关于DP 对称，∴DE=AD ，∠PAD=∠DEP ，∵在正方形ABCD 中，AD=CD ，∠C=∠DAB=90°，∴DE=CD ，∠E=∠C=90°，在Rt △EDF 和Rt △CDF 中，DE AD DF DF =⎧⎨=⎩， ∴Rt △EDF ≌Rt △CDF （HL ），∴∠EDF=∠CDF.（3）由（2）得∠EDF=∠CDF=12∠PDC ， 又∵∠PDC=90°+2α. ∴∠EDF=45°+α.（4）结论：BH=2PA.如图：过H 点作HG 垂直于PB ，∵∠PDF=∠EDF-∠EPD ，∵∠EDF=45°+α，∠EPD=α，∴∠PDF=45°.又∵PD ⊥PF ，∴△PDG 是等腰直角三角形，∴AP=HP ，又∵∠PDA+∠DPA=90°，∠PDA+∠HPA=90°，∴∠PDA=∠HPA,在△PDA和△HPG 中，PD PH PDA HPG DAP PGH =⎧⎪∠=∠⎨⎪∠=∠⎩，∴△PDA ≌△HPG （AAS ）∴PA=HG ,DA=PG ,∵DA=AB ，∴BG=PA ，∴△HGB 为等腰直角三角形，∴BH=2HG ，∴BH=2PA.【点睛】本题考查了正方形的性质，全等三角形的判定与性质，等腰直角三角形的判定与性质，勾股定理，灵活运用在证明角相等，作辅助线构造成全等三角形是解题的关键．25．（1）DE= 2﹣2；（2）BF= 2﹣2.【解析】【分析】（1）根据正方形的性质，得到∠ABC=∠ADC=90°，∠DBC=∠BCA=∠ACD=45°，然后根据角平分线的意义求出∠ACE=∠DCE=12∠ACD=22.5°，进而得出△BCE 是等腰三角形，求得BC=BE ，然后根据勾股定理求出BD 的长，从而得到DE 的长；（2）根据正方形的性质，由全等三角形的判定证得△FEB ≌△ECD ，然后根据全等三角形的性质求解即可.【详解】（1）∵四边形ABCD 是正方形，∴∠ABC=∠ADC=90°，∠DBC=∠BCA=∠ACD=45°，∵CE 平分∠DCA ，∴∠ACE=∠DCE=∠ACD=22.5°，∴∠BCE=∠BCA+∠ACE=45°+22.5°=67.5°，∵∠DBC=45°，∴∠BEC=180°﹣67.5°﹣45°=67.5°=∠BCE ， ∴BE=BC=，在Rt △ACD 中，由勾股定理得：BD==2， ∴DE=BD ﹣BE=2﹣；（2）∵FE ⊥CE ，∴∠CEF=90°，∴∠FEB=∠CEF ﹣∠CEB=90°﹣67.5°=22.5°=∠DCE ， ∵∠FBE=∠CDE=45°，BE=BC=CD ，∴△FEB ≌△ECD ，∴BF=DE=2﹣. 【点睛】此题主要考查了正方形的性质的应用，熟练掌握正方形的性质，并灵活利用正方形的性质求解是解题关键.26．（1）()()0,4,4,0A B -；（2）①当03t ≤<时，62S t =-，②当3t >时，26S t =-；（3）①当03t ≤<，652P ⎛⎫ ⎪ ⎪⎝⎭，4651255G ⎛⎫ ⎪ ⎪⎝⎭；②当3t >时，652P ⎛⎫ ⎪ ⎪⎝⎭，4651255G ⎛⎫ ⎪ ⎪⎝⎭。
八年级数学正方形的判定和性质(人教版)(基础)(含答案)
正方形的判定和性质（人教版）（基础）一、单选题(共9道，每道11分)1.如果要证明四边形ABCD为正方形，我们需要在四边形ABCD是平行四边形的基础上，进一步证明( )A.AC与BD互相垂直平分B.∠A=∠B且AC=BDC.AB=AD且AC=BDD.AB=AD且AC⊥BD答案：C解题思路：A：对角线互相垂直的平行四边形是菱形，故A不能；B：一组邻角相等的平行四边形是矩形，对角线相等的平行四边形也是矩形，故B不能；C：对角线相等的平行四边形是矩形，一组邻边相等的矩形为正方形，故C可以；D：一组邻边相等的平行四边形为菱形，对角线互相垂直的平行四边形也是菱形，故D不能。
故选C试题难度：三颗星知识点：略2.四边形ABCD的对角线相交于点O，能判定四边形是正方形的条件是( )A.AC=BD，AB=CD，AB∥CDB.AO=BO=CO=DO，AC⊥BDC.AD∥BC，∠A=∠CD.AO=CO，BO=DO，AB=BC答案：B解题思路：先画草图，再依图分析；A：若AB=CD，AB∥CD，可判断是平行四边形，再由AC=BD，可判断是矩形，则A错；B：若AO=BO=CO=DO，可判断是矩形，再由AC⊥BD，可判断是正方形，则B对；C：若AD//BC，∠A=∠C，可判断是平行四边形，则C错；D：若AO=CO，BO=DO，可判断是平行四边形，再由AB=BC，可判断是菱形，则D错．故选B．试题难度：三颗星知识点：略3.学习了正方形之后，王老师提出问题：要判断一个四边形是正方形，有哪些思路？甲同学说：先判定四边形是菱形，再确定这个菱形有一个角是直角；乙同学说：先判定四边形是矩形，再确定这个矩形有一组邻边相等；丙同学说：判定四边形的对角线相等，并且互相垂直平分；丁同学说：先判定四边形是平行四边形，再确定这个平行四边形有一个角是直角并且有一组邻边相等．上述四名同学的说法中，正确的是( )A.甲、乙B.甲、丙C.乙、丙、丁D.甲、乙、丙、丁答案：D解题思路：甲：根据判定定理有一个角是直角的菱形是正方形，可判断甲正确；乙：根据判定定理有一组邻边相等的矩形是正方形，可判断乙正确；丙：由对角线互相垂直平分判定为菱形，再加上对角线相等可判定为矩形，综合可得四边形为正方形，故丙正确；丁：有一个角是直角的平行四边形是矩形，再加上有一组邻边相等可判断为正方形，故丁正确。
人教版八年级数学下册正方形知识点及同步练习、含答案
学科：数学 教学内容：正方形【学习目标】1．掌握正方形的定义、性质和判定方法．2．能正确区别平行四边形、矩形、菱形、正方形之间的关系． 3．能运用正方形的性质和判定方法进行有关的计算和证明．【主体知识归纳】1．正方形：有一组邻边相等并且有一个角是直角的平行四边形叫做正方形．2．正方形的性质：正方形除具有平行四边形、矩形、菱形的一切性质外，还具有： （1）正方形的四个角都是直角，四条边都相等；（2）正方形的两条对角线相等并且互相垂直平分，每条对角线平分一组对角． 3．正方形的判定（1）根据正方形的定义；（2）有一组邻边相等的矩形是正方形； （3）有一个角是直角的菱形是正方形； （4）既是矩形又是菱形的四边形是正方形．【基础知识精讲】1．掌握正方形定义是学好本节的关键，正方形是在平行四边形的前提下定义的，它包含两层意思：正方形矩形平行四边形并且有一个角是直角的菱形四边形有一组邻边相等的平行⎭⎬⎫)()2()()1(正方形不仅是特殊的平行四边形，而且是特殊的矩形，又是特殊的菱形．2．正方形的性质可归纳如下： 边：对边平行，四边相等； 角：四个角都是直角；对角线：对角线相等，互相垂直平分，每条对角线平分一组对角． 此外：正方形的一条对角线把正方形分成两个全等的等腰直角三角形，对角线与边的夹角是45°；正方形的两条对角线把它分成四个全等的等腰直角三角形，同时，正方形又是轴对称图形，有四条对称轴，学习时，应熟悉这些最基本的内容．【例题精讲】［例1］如图4－50，已知矩形ABCD 中，F 为CD 的中点，在BC 上有一点E ，使AE ＝DC ＋CE ，AF 平分∠EAD ．求证：矩形ABCD 是正方形．图4—50剖析：欲证矩形ABCD是正方形，只要证明有一组邻边相等即可，由已知AE＝DC＋CE，容易想到若能证明AE＝AD＋CE便可证得AD＝DC，由于AF平分∠EAD，因此可在AE上截取AG＝AD，再证GE＝CE，就可得出要证的结论．证明：在AE上截取AG＝AD，连结FG、FE．∵四边形ABCD是矩形，∴∠D＝∠C＝90°．∵AD＝AG，∠DAF＝∠GAF，AF＝AF∴△ADF≌△AGF，∴DF＝GF，∠D＝∠AGF＝90°．∵DF＝CF，∴GF＝CF．∵∠FGE＝∠C＝90°，FE＝FE，∴Rt△GFE≌Rt△CFE．∴GE＝CE，∴AD＋CE＝AE．又DC＋CE＝AE，∴AD＝DC．∴矩形ABCD是正方形．说明：要判定一个四边形是正方形，可先判定这个四边形是矩形，再证明有一组邻边相等；或先判定它是菱形，再证明有一个角是直角．［例2］如图4－51，已知正方形ABCD的对角线AC、BD相交于点O，E是AC上一点，过点A作AG⊥EB，垂足为G，AG交BD于点F，则OE＝OF．图4—51对上述命题的证明如下：∵四边形ABCD是正方形，∴∠BOE＝∠AOF＝90°，BO＝AO．∴∠3＋∠2＝90°，∵AG⊥BE，∴∠1＋∠3＝90°．∴∠1＝∠2，∴△BOE≌△AOF，∴OE＝OF问题：对于上述命题，若点E在AC延长线上，AG⊥EB，交EB的延长线于G，AG的延长线交DB的延长线于点F，其他条件不变（如图4－52），结论“OE＝OF”还成立吗?如果成立，请给出证明；如果不成立，请说明理由．图4—52剖析：可仿上述的证明，证△BOE≌△AOF．解：结论OE＝OF仍然成立，证明如下：∵四边形ABCD是正方形，∴∠BOE＝∠AOF＝90°，BO＝AO，∴∠OFA＋∠FAE＝90°又∵AG⊥EB，∴∠OEB＋∠EAF＝90°，∴∠OEB＝∠OFA，∴△BOE≌△AOF，∴OE＝OF．［例3］有一正方形池塘，池塘四个角上有四棵树，现计划把此池塘改为面积扩大一倍的正方形，能否不毁掉树木而达到要求？请你设计出方案来．图4—53剖析：新改造的池塘的面积是原面积的2倍，因此，新边长应为原边长的2倍，而正方形的对角线是边长的2倍，故以原对角线的长为边长构造新的正方形．答案：如图4－53，分别过B、D作AC的平行线，分别过A、C作BD的平行线，四条线分别交于A′、B′、C′、D′，则四边形A′B′C′D′为要求的正方形．【同步达纲练习】1．选择题（1）下列命题中，假命题的个数是（）①四边都相等的四边形是正方形②对角线互相垂直的平行四边形是正方形③四角都相等的四边形是正方形④对角线相等的菱形是正方形A．1 B．2 C．3 D．4（2）正方形具有而菱形不具有的性质是（）A．对角线互相垂直平分B．对角线相等C．邻边相等D．每条对角线平分一组对角（3）正方形的对角线与边长之比为（）A．1∶1 B．2∶1 C．1∶2 D．2∶1（4）以等边△ABC的边BC为边向外作正方形BCDE，则①∠ABD＝105°，②∠ACD＝150°，③∠DAE＝30°，④△ABE≌△ACD，其中正确的结论有（）A．1个 B．2个 C．3个 D．4个（5）在正方形ABCD中，P、Q、R、S分别在边AB、BC、CD、DA上，且AP＝BQ＝CR＝DS ＝1，AB＝5，那么四边形PQRS的面积等于（）A．17 B．16 C．15 D．9（6）如图4－54，正方形ABCD中，O是对角线AC、BD的交点，过O点作OE⊥OF分别交AB、BC于E、F，若AE＝4，CF＝3，则EF等于（）图4—54A．7 B．5 C．4 D．3（7）在正方形ABCD中，E、F两点分别是BC、CD边上的点，若△AEF是边长为2的等边三角形，则正方形ABCD的边长为（）A．213+B．213-C．3 D．2（8）如图4－55，在正方形ABCD中，CE＝MN，∠MCE＝35°，那么∠ANM等于（）图4—55A．45°B．55°C．65°D．75°2．填空题（1）已知正方形的面积是16 cm2，则它的一边长是_____，一条对角线长是_____．（2）已知正方形的对角线长为22，则此正方形的周长为_____，面积为_____． （3）在正方形ABCD 中，两条对角线相交于O ，∠BAC 的平分线交BD 于E ，若正方形ABCD 的周长是16 cm ，则DE ＝_____cm ．（4）在正方形ABCD 的边BC 的延长线上取一点E ，使CE ＝AC ，连结AE 交CD 于F ，那么∠AFC 等于_____度．3．如图4－56，已知正方形ABCD 中，E 为CD 边上一点，F 为BC 延长线上一点，且CE ＝CF ．图4—56（1）求证：△BCE ≌△DCF ；（2）若∠BEC ＝60°，求∠EFD 的度数．4．已知：如图4－57，在正方形ABCD 中，E 是CB 延长线上一点，EB ＝21BC ，如果F 是AB 的中点，请你在正方形ABCD 上找一点，与F 点连结成线段，并证明它和AE 相等．图4—575．以△ABC 的AB 、AC 为边，向三角形外作正方形ABDE 及ACGF ，作AN ⊥BC 于点N ，延长NA 交EF 于M 点．（1）求证：EM ＝FM ；（2）若使AM ＝21EF ，则△ABC 必须满足什么条件呢？图4—586．如图4－58，已知正方形ABCD 中，M 、F 分别在边AB 、AD 上，且MB ＝FD ，E 是AB 延长线上一点，MN ⊥DM ，MN 与∠CBE 的平分线相交于N ．求证：DM ＝MN ．7．如图4－59，已知C是线段AB上的一点，分别以AC、BC为边作正方形ACDE和BCFG．图4—59求证：AF＝DB；若点C在线段AB的延长线上，猜想上述结论是否正确，如果正确，请加以证明，如果不正确，请说明理由．【思路拓展题】你会设计吗今有一片正方形土地，要在其上修筑两条笔直的道路，使道路把这片地分成形状相同且面积相等的4部分，若道路的宽度忽略不计，请设计三种不同的修筑方案．（在给出如图4－60的三张正方形纸片上分别画图，并简述画图步骤）图4—60参考答案【同步达纲练习】1．（1）C （2）B （3）B （4）D （5）A （6）B （7）A（8）B2．（1）4 42（2）8 4 （3）4 （4）112.53．（1）略（2）15°4．连结CF，可证△ABE≌△CBF或连结DF，让△ABE≌△DAF。
华师版八年级下册数学第19章 矩形、菱形与正方形 正方形的性质
正方形既是中心对称图形，也是轴对称图形，它具有以下性质： (1)四条边都__________；(2)四个角都是__________； (3)对角线_____________________．
相等
直角
相等且互相垂直平分
1．【中考•遂宁】下列说法正确的是( )
B
A．有两条边和一个角对应相等的两个三角形全等
B
A．2α C．45°＋α
B．90°－α D．90°－12α
4．如图，点E是正方形ABCD的边DC上一点，把△ADE绕点A顺时针旋转 90°到△ABF的位置．若四边形AECF的面积为25，DE＝2，则AE的长 为( ) D
A．5 B. 23 C．7 D. 29
5．【中考·鄂尔多斯】如图，在正方形ABCD的外侧，作等边三角形ABE，
解得 x＝2156，∴AF＝2156.
13．某数学兴趣小组在数学课外活动中，研究三角形和正方形的性质时，做 了如下探究：
在△ABC中，∠BAC＝90°，AB＝AC，点D为直线BC上一动点(点D不与B，C 重合)，以AD为边在AD右侧作正方形ADEF，连结CF.
(1)观察猜想 如图①，当点D在线段BC上时，①BC与CF的位置关系为________， ②BC，CD，CF之间的数量关系为_______________．(将结论直接写在横线上)
华师版八年级下
第19章 矩形、菱形与正方形
19.3 正方形 第1课时正方形的性质
提示：点击 进入习题
新知笔记
(1)相等 (2)直角 (3)相等 1 且互相垂直平分
基础巩固练 1B 2B
3B
4D 5C
答案显示
6 2021 7 见习题 8C 9B 10 D
11 见习题 12 见习题 13 见习题
正方形及其性质八年级人教版数学下册习题课件
线CG于点G，连接GF，求证： 解：设CD＝BC＝x，则CM＝x－3，CN＝x－2，
的面积． 把△ADN绕点A顺时针旋转90°得到△ABE.
(2)若BM＝3，DN＝2，求正方形ABCD的边长．
解：设CD＝BC＝x，则CM＝x－3，CN＝x－2， ∵△AEM≌△ANM，∴EM＝MN. ∵BE＝DN，∴MN＝EM＝BM＋BE＝BM＋DN＝5. ∵∠C＝90°，∴MN2＝CM2＋CN2. 即52＝(x－3)2＋(x－2)2，解得x＝6或－1(舍去)， ∴正方形ABCD的边长为6.
证明：∵把△ ADN 绕点 A 顺时针旋转 90°得到△ ABE，∴△ADN≌△ABE， ∴∠DAN＝∠BAE，DN＝BE，AN＝AE.
由题易知 E 在 CB 的延长线上． ∵∠DAB＝90°，∠MAN＝45°， ∴∠MAE＝∠BAE＋∠BAM＝∠DAN＋∠BAM＝45°. ∴∠MAE＝∠MAN. 又∵MA＝MA，AN＝AE， ∴△AEM≌△ANM.
3．【中考·天津】如图，四边形OBCD是正方形，O，D两 点的坐标分别是(0，0)，(0，6)，点C在第一象限，则 点C的坐标是( D ) A．(6，3) B．(3，6) C．(0，6) D．(6，6)
4．【中考·北京】把图①中的菱形沿对角线分成四个全等的直角 三角形，将这四个直角三角形分别拼成如图②、图③所示的 正方形，则图①中菱形的面积为___1_2____．
∵正方形 ABCD 的边长为 4， ∴AD＝AB＝4，∠DAB＝90°. ∵点 E 在 AB 上且 BE＝1，∴AE＝3. ∴DE＝ AD2＋AE2＝ 42＋32＝5. ∴DE＋BE＝5＋1＝6，即△ BFE 周长的最小值为 6. 【答案】B
2021-2022学年鲁教版八年级数学下册《6-3正方形的性质与判定》解答题专题提升训练(附答案)
2021-2022学年鲁教版八年级数学下册《6-3正方形的性质与判定》解答题专题提升训练（附答案）1．如图，正方形ABCD的边长为1，E为对角线BD上一点，且BE＝BC，点P为线段CE 上一动点，且PM⊥BE于点M，PN⊥BC于点N，求PM+PN的值．2．如图，在正方形ABCD中，E，F分别在边AB，BC上，△DEF是等边三角形，连接BD 交EF于点G．（1）求证：BE＝BF；（2）若DE＝2，求BD的长．3．如图，在正方形ABCD中，点G在对角线BD上（不与点B，D重合），GE⊥DC，垂足为点E，GF⊥BC，垂足为点F，连接AG．写出线段AG，GE，GF之间的数量关系，并说明理由．4．已知，如图，在正方形ABCD中，E为对角线AC上一点，EG⊥ED交BC于点G，EF ⊥BC，垂足为F．（1）求证：BF＝GF；（2）如图，若DE＝DH，AB＝8．①求证：CG＝FG；②求EH的值．5．已知：P是正方形ABCD对角线BD上一点，PE⊥DC，PE⊥BC，垂足分别为E、F．（1）求证：AP＝CP；（2）若∠DAP＝30°，PD＝，求CP的长．6．如图所示，正方形ABCD中，AC，BD交于点O．BD＝10，点E，F是BD上的两点，BE＝DF＝2．求四边形AECF的周长．7．如图，在正方形ABCD的对角线AC上取一点E．连接BE并延长BE到点F，使CF＝CB，BF与CD相交于点H．（1）求证：BE＝DE；（2）若∠CDE＝15°，判断CE，DE，EF之间的数量关系，并说明理由．8．如图，点B在MN上，过AB的中点O作MN的平行线，分别交∠ABM的平分线和∠ABN 的平分线于点C、D．（1）试判断四边形ACBD的形状，并证明你的结论．（2）当△CBD满足什么条件时，四边形ACBD是正方形？并给出证明．9．已知：在Rt△ABC中，∠BAC＝90°，D是BC的中点，E是AD的中点．过点A作AF ∥BC交BE的延长线于点F．（1）求证：△AEF≌△DEB；（2）当△ABC满足什么条件时，四边形ADCF是正方形？请说明理由．10．如图，在平面直角坐标系xOy中，直线OC：y OC＝3x与直线AC：y AC＝﹣x+8相交于点C（2，6）．（1）点M从点O出发以每秒1个单位长度的速度沿x轴向右运动，点N从点A出发以每秒3个单位长度的速度沿x轴向左运动，两点同时出发．分别过点M，N作x轴的垂线，分别交直线OC，AC于点P，Q，请你在图1中画出图形，猜想四边形PMNQ的形状（点M，N重合时除外），并证明你的猜想；（2）在（1）的条件下，当点M运动秒时，四边形PMNQ是正方形（直接写出结论）．11．如图，在▱ABCD中，G、H分别是AD、BC的中点，E、O、F是对角线AC的四等分点，顺次连接G、E、H、F．（1）求证：四边形GEHF是平行四边形；（2）若AC＝2AB，则四边形GEHF是形；（3）当AC、AB满足时，四边形GEHF是正方形．12．如图，在Rt△ABC中，∠ACB＝90°，D是AB的中点，四边形BCED为平行四边形，DE、AC相交于F，连接DC、AE．（1）试确定四边形ADCE的形状，并说明理由；（2）若AB＝8，AC＝6，求四边形ADCE的面积；（3）当△ABC满足什么条件时，四边形ADCE为正方形？请给予证明．13．如图，在矩形ABCD中，M、N分别是边AD、BC的中点，E、F分别是线段BM、CM 的中点．（1）求证：BM＝CM．（2）当AB：AD的值为多少时，四边形MENF是正方形？请说明理由．14．如图，四边形ABCD为正方形，E为线段AC上一点，连接DE，过点E作EF⊥DE，交射线BC于点F，以DE，EF为邻边作矩形DEFG，连接CG．（1）求证：矩形DEFG是正方形；（2）若AB＝2，CE＝，求CG的长度．15．如图，在△ABC中，点O是边AC上一个动点，过O作直线MN∥BC，设MN交∠ACB 的平分线于点E，交△ABC的外角∠ACD的平分线于点F．（1）探究线段OE与OF的数量关系并说明理由．（2）当点O运动到何处，且△ABC满足什么条件时，四边形AECF是正方形？请说明理由．（3）当点O在边AC上运动时，四边形BCFE是菱形（填“可能”或“不可能”）．请说明理由．16．如图，已知四边形ABCD为正方形，AB＝，点E为对角线AC上一动点，连接DE，过点E作EF⊥DE，交BC于点F，以DE、EF为邻边作矩形DEFG，连接CG．（1）求证：矩形DEFG是正方形；（2）探究：①CE与CG有怎样的位置关系？请说明理由．②CE+CG的值为．17．如图，在Rt△ABC中，两锐角的平分线AD，BE相交于O，OF⊥AC于F，OG⊥BC 于G．（1）求证：四边形OGCF是正方形．（2）若∠BAC＝60°，AC＝4，求正方形OGCF的边长．18．如图，在正方形ABCD中，E、F、G、H分别是各边上的点，且AE＝BF＝CG＝DH．求证：（1）△AHE≌△BEF；（2）四边形EFGH是正方形．19．如图，在矩形ABCD中，∠BAD的平分线交BC于点E，EF⊥AD于点F，DG⊥AE于点G，DG与EF交于点O．（1）求证：四边形ABEF是正方形；（2）若AD＝AE，求证：AB＝AG；（3）在（2）的条件下，已知AB＝1，求OD的长．20．如图，点E是正方形ABCD对角线AC上一点，EF⊥AB，EG⊥BC，垂足分别为F，G，若正方形ABCD的周长是40cm．（1）求证：四边形BFEG是矩形；（2）求四边形EFBG的周长；（3）当AF的长为多少时，四边形BFEG是正方形？21．如图，在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，点D是斜边AB上的一动点，作DE⊥AC于点E，DF∥AC交BC于点F．（1）求证：四边形CEDF是矩形；（2）若四边形CEDF成为正方形，试求正方形的边长．22．如图，在△ABC中，D是AB中点，E是AC中点，F是BC中点，请填空：（1）四边形BDEF是四边形；（2）若四边形BDEF是菱形，则△ABC满足的条件是．（3）若四边形BDEF是矩形，则△ABC满足的条件是．（4）若四边形BDEF是正方形，则△ABC满足的条件是．并就（2）、（3）、（4）中选取一个进行证明．23．已知：如图，在矩形ABCD中，E是BC边一点，DE平分∠ADC，EF∥DC交AD边于点F，连接BD．（1）求证：四边形EFDC是正方形；（2）若BE＝1，ED＝2，求BD的长．参考答案1．解：连接BP，作EF⊥BC于点F，则∠EFB＝90°，∵正方形的性质可知∠EBF＝45°，∴△BEF为等腰直角三角形，∵正方形的边长为1，∴BE＝BC＝1，在直角三角形BEF中，sin∠EBF＝，∴BF＝EF＝BE sin45°＝1×＝，∵PM⊥BD，PN⊥BC，∴S△BPE+S△BPC＝S△BEC，∴BE×PM+BC×PN＝BC×EF，∵BE＝BC，∴PM+PN＝EF＝．2．（1）证明：∵四边形ABCD为正方形，∴AD＝CD＝AB＝BC，∠A＝∠C＝90°，∵△DEF为等边三角形，∴DE＝DF，在Rt△ADE和Rt△CDF中，，∴Rt△ADE≌Rt△CDF（HL），∴AE＝CF．又∵AB＝BC，∴AB﹣AE＝BC﹣CF，∴BE＝BF；（2）解：由（1）可知BE＝BF，∴△BEF为等腰直角三角形，∵四边形ABCD为正方形，∴BD平分∠ABC，∴点G为EF的中点，BD⊥EF，∵△DEF为等边三角形，DE＝2，∴EF＝DE＝2，BG＝EG＝1，在Rt△EDG中，由勾股定理得，DG＝＝＝，∴BD＝BG+DG＝1+．3．解：AG2＝GE2+GF2，理由如下：如图，连接CG，∵四边形ABCD是正方形，∴AB＝BC，∠ABG＝∠CBG，∠BCD＝90°，在△ABG和△CBG中，，∴△ABG≌△CBG（SAS），∴AG＝CG，∵GE⊥DC，垂足为点E，GF⊥BC，垂足为点F，∴∠GEC＝∠GFC＝90°，∴∠GEC＝∠GFC＝∠BCD＝90°，∴四边形CEGF是矩形，∴GF＝CE，在Rt△CEG中，GC2＝GE2+EC2，∴AG2＝GE2+GF2．4．（1）证明：如图所示，连接EB，∵四边形ABCD为正方形，∴∠ACB＝∠DCE，BC＝CD．又∵EC＝EC，∴△EBC≌△EDC（SAS），∴EB＝ED．延长FE交AD于N，∵∠NAE＝45°，EF⊥BC，∴∠NEA＝45°，即AN＝NE，∵AB＝AD，AD∥BC，即AB＝NF，∴ND＝EF，∵EG⊥ED，∴∠FEG+∠EGF＝∠FEG+∠NED，∴∠EGF＝∠NED，∵∠EFG＝∠END，∴△EFG≌△DNE（AAS），∴ED＝EG，∴EB＝EG．∵EF⊥BC，∴BF＝GF；（2）①证明：如图所示，作GM⊥AC，垂足为M．∵DE＝DH，∠DEG＝90°，∴∠EDH＝45°，∴∠DEH＝67.5°，∴∠GEH＝22.5°．又∵∠FEC＝45°，∴∠FEG＝22.5°，∴∠FEG＝∠GEM．∵GF⊥EF，GM⊥EC，∴GF＝GM．∵∠MCG＝45°，∴GC＝GM＝FG；②解：∵AD∥BC，由①可知，CG：FG：BF＝：1：1，∴．即，∴＝，∵BC＝8，∴AC＝8，∴CH＝8﹣8，∴AE＝8﹣8，∴EH＝8﹣2×（8﹣8）＝16﹣8．5．（1）证明：∵四边形ABCD为正方形，∴AD＝CD，∠ADP＝∠CDP，又∵DP＝DP，∴△ADP≌△CDP（SAS），（2）解：∵BD为正方形ABCD的对角线，∴∠ADP＝∠CDP＝45°，∵PE⊥DC，∴∠PED＝∠PEC＝90°，∴∠DPE＝45°，∴PE＝DE，∵且PE2+DE2＝PD2，∴PE＝1，∵△ADP≌△CDP，∴∠DAP＝∠DCP＝30°，∴CP＝2PE＝2．6．解：∵四边形ABCD是正方形，∴OD＝OB，OA＝OC，BD⊥AC，∵BE＝DF，∴DE＝BF，∴OE＝OF，∴四边形AECF是平行四边形，∴四边形AECF为菱形，∵BD＝10，BE＝DF＝2，∴OE＝5﹣2＝3，OC＝5，∴CE＝，∴菱形AECF的周长为4．7．证明：（1）∵四边形ABCD是正方形，∴AB＝AD，∠ABC＝∠ADC＝90°，∠BAC＝∠DAC＝∠ACB＝∠ACD＝45°，在△ABE和△ADE中，，∴△ABE≌△ADE（SAS），（2）在EF上取一点G，使EG＝EC，连接CG，∵△ABE≌△ADE，∴∠ABE＝∠ADE，∴∠CBE＝∠CDE，∵BC＝CF，∴∠CBE＝∠F，∴∠CBE＝∠CDE＝∠F，∵∠CDE＝15°，∴∠CBE＝15°，∴∠CEG＝60°，∵CE＝GE，∴△CEG是等边三角形，∴∠CGE＝60°，CE＝GC，∴∠GCF＝60°﹣15°＝45°，∴∠ECD＝∠GCF，在△DEC和△FGC中，，∴△DEC≌△FGC（SAS），∴DE＝GF，∴EF＝EG+GF＝CE+ED．8．解：（1）四边形ACBD是矩形，证明：∵CD平行MN，∴∠OCB＝∠CBM，∵BC平分∠ABM，∴∠OBC＝∠CBM，∴∠OCB＝∠OBC，∴OC＝OB，同理可证：OB＝OD，∴OA＝OB＝OC＝OD，∵CD＝OC+OD，AB＝OA+OB，∴AB＝CD，∴四边形ACBD是矩形；（2）△CBD满足CB＝BD时，四边形ACBD是正方形，证明：由（1）得四边形ACBD是矩形，∵CB＝BD，∴四边形ACBD是正方形．9．（1）证明：∵AF∥BC，∴∠AFE＝∠DBE，∵E是AD的中点，∴AE＝DE，在△AEF和△DEB中，，∴△AEF≌△DEB（AAS）；（2）解：当AB＝AC时，四边形ADCF是正方形，理由：由（1）知，△AEF≌△DEB，∴AF＝DB，∵D是BC的中点，∴DB＝DC，∴AF＝DC，∵AF∥BC，∴四边形ADCF是平行四边形，∵∠BAC＝90°，D是BC的中点，∴AD＝DC＝BC，∴四边形ADCF是菱形，∵AB＝AC，D是BC的中点，∴AD⊥BC，∴四边形ADCF是正方形．10．解：（1）如图，四边形PMNQ为矩形，证明：∵点A在直线AC：y AC＝﹣x+8上，当y＝0 时，x＝8，∴A（8，0），设点M的运动时间为m秒，则OM＝m，AN＝3m，∴M（m，0），N（8﹣3m，0），∵PM⊥x轴，QN⊥x轴，∴∠PMA＝∠QNA＝90°，∴PM∥QN，∵点P在直线OC：y OC＝3x，点Q在直线AC：y AC＝﹣x+8上，∴P（m，3m），Q（8﹣3m，3m），∴PM＝QN，∴四边形PMNQ为平行四边形，∵∠PMA＝90°，∴四边形PMNQ为矩形；（2）∵四边形PMNQ是正方形，∴MN＝QN，即8﹣4m＝|3m|，解得：x＝或8，∴当点M运动秒或8秒时，四边形PMNQ是正方形，故答案为：或8．13．（1）证明：∵四边形ABCD是矩形，∴AB＝DC，∠A＝∠D＝90°，∵M为AD中点，∴AM＝DM，在△ABM和△DCM中，，∴△ABM≌△DCM（SAS），∴BM＝CM；（2）解：当AB：AD＝1：2时，四边形MENF是正方形，理由如下：∵N、E、F分别是BC、BM、CM的中点，∴NE∥CM，NE＝CM，∵MF＝CM，∴NE＝FM，∵NE∥FM，∴四边形MENF是平行四边形，由（1）知△ABM≌△DCM，∴BM＝CM，∵E、F分别是BM、CM的中点，∴ME＝MF，∴平行四边形MENF是菱形；∵M为AD中点，∴AD＝2AM，∵AB：AD＝1：2，∴AD＝2AB，∴AM＝AB，∵∠A＝90°，∴∠ABM＝∠AMB＝45°，同理∠DMC＝45°，∴∠EMF＝180°﹣45°﹣45°＝90°，∵四边形MENF是菱形，∴菱形MENF是正方形．14．（1）证明：如图1，作EP⊥CD于P，EQ⊥BC于Q，∵∠DCA＝∠BCA，∴EQ＝EP，∵∠QEF+∠FEC＝45°，∠PED+∠FEC＝45°，∴∠QEF＝∠PED，在△EQF和△EPD中，，∴△EQF≌△EPD（ASA），∴EF＝ED，∴矩形DEFG是正方形；（2）如图2中，在Rt△ABC中，AC＝AB＝2，∵CE＝，∴AE＝CE，∴点F与C重合，此时△DCG是等腰直角三角形，∴四边形DECG是正方形，∴CG＝CE＝．15．解：（1）OE＝OF．理由如下：∵CE是∠ACB的角平分线，∴∠ACE＝∠BCE，又∵MN∥BC，∴∠NEC＝∠ECB，∴∠NEC＝∠ACE，∴OE＝OC，∵CF是∠BCA的外角平分线，∴∠OCF＝∠FCD，又∵MN∥BC，∴∠OFC＝∠FCD，∴∠OFC＝∠OCF，∴OF＝OC，∴OE＝OF；（2）当点O运动到AC的中点，且△ABC满足∠ACB为直角的直角三角形时，四边形AECF是正方形．理由如下：∵当点O运动到AC的中点时，AO＝CO，又∵EO＝FO，∴四边形AECF是平行四边形，∵FO＝CO，∴AO＝CO＝EO＝FO，∴AO+CO＝EO+FO，即AC＝EF，∴四边形AECF是矩形．已知MN∥BC，当∠ACB＝90°，则∠AOF＝∠COE＝∠COF＝∠AOE＝90°，∴AC⊥EF，∴四边形AECF是正方形；（3）不可能．理由如下：如图，∵CE平分∠ACB，CF平分∠ACD，∴∠ECF＝∠ACB+∠ACD＝（∠ACB+∠ACD）＝90°，若四边形BCFE是菱形，则BF⊥EC，但在△GFC中，不可能存在两个角为90°，所以不存在其为菱形．故答案为不可能．16．解：（1）如图，作EM⊥BC于M，EN⊥CD于N，∴∠MEN＝90°，∵点E是正方形ABCD对角线上的点，∴EM＝EN，∵∠DEF＝90°，∴∠DEN＝∠MEF＝90°﹣∠FEN，∵∠DNE＝∠FME＝90°，在△DEN和△FEM中，，∴△DEN≌△FEM（ASA），∴EF＝DE，∵四边形DEFG是矩形，∴矩形DEFG是正方形；（2）①CE⊥CG，理由如下：∵正方形DEFG和正方形ABCD，∴DE＝DG，AD＝DC，∵∠CDG+∠CDE＝∠ADE+∠CDE＝90°，∴∠CDG＝∠ADE，在△ADE和△CDG中，，∴△ADE≌△CDG（SAS），∴∠CDA＝∠DCG，∵∠ACD+∠CAD+∠ADC＝180°，∠ADC＝90°，∴∠ACG＝∠ACD+∠DCG＝∠ACD+∠CAD＝90°，∴CE⊥CG；②由①知，△ADE≌△CDG，∴AE＝CG，∴CE+CG＝CE+AE＝AC＝AB＝×＝2，故答案为：2．17．（1）证明：过O作OH⊥AB于H点，∵OF⊥AC于点F，OG⊥BC于点G，∴∠OGC＝∠OFC＝90°．∵∠C＝90°，∴四边形OGCF是矩形．∵AD，BE分别是∠BAC，∠ABC的角平分线，OF⊥AC，OG⊥BC，∴OG＝OH＝OF，又四边形OGCF是矩形，∴四边形OGCF是正方形；（2）解：在Rt△ABC中，∵∠BAC＝60°，∴∠ABC＝90°﹣∠BAC＝90°﹣60°＝30°，∴AC＝AB，∵AC＝4，∴AB＝2AC＝2×4＝8，∵AC2+BC2＝AB2，∴BC＝＝4，在Rt△AOH和Rt△AOF中，，∴Rt△AOH≌Rt△AOF（HL），∴AH＝AF，设正方形OGCF的边长为x，则AH＝AF＝4﹣x，BH＝BG＝4﹣x，∴4﹣x+4﹣x＝8，∴x＝2﹣2，即正方形OGCF的边长为2﹣2．18．证明：（1）∵四边形ABCD为正方形，∴AB＝BC＝CD＝DA，∠A＝∠B＝90°，又∵AE＝BF＝DH＝CG，∴AH＝BE＝CF＝DG，∴△AHE≌△BEF（SAS）；（2）在正方形ABCD中，AB＝BC＝CD＝AD，∵AE＝BF＝CG＝DH，∴AH＝DG＝CF＝BE，∵∠A＝∠B＝∠C＝∠D＝90°，∴△AEH≌△DHG≌△CGF≌△BFE（SAS），∴EF＝EH＝HG＝GF，∠EHA＝∠HGD，∴四边形EFGH是菱形，∵∠EHA＝∠HGD，∠HGD+∠GHD＝90°，∴∠EHA+∠GHD＝90°，∴∠EHG＝90°，∴四边形EFGH是正方形．19．（1）证明：∵矩形ABCD，∴∠BAF＝∠ABE＝90°，∵EF⊥AD，∴四边形ABEF是矩形，∵AE平分∠BAD，∴EF＝EB，∴四边形ABEF是正方形；（2）∵AE平分∠BAD，∴∠DAG＝∠BAE，在△AGD和△ABE中，，∴△AGD≌△ABE（AAS），∴AB＝AG；（3）∵四边形ABEF是正方形，∴AB＝AF＝1，∵△AGD≌△ABE，∴DG＝AB＝AF＝AG＝1，∵AD＝AE，∴AD﹣AF＝AE﹣AG，即DF＝EG，在△DFO和△EGO中，，∴△DFO≌△EGO（AAS），∴FO＝GO，FD＝EG∵∠DAE＝∠AEF＝45°，∠AFE＝∠AGD＝90°，∴DF＝FO＝OG＝EG，∴DO＝OF＝OG，∴DG＝DO+OG＝OG+OG＝1，∴OG＝＝﹣1，∴OD＝（﹣1）＝2﹣．20．解：（1）证明：∵四边形ABCD为正方形，∴AB⊥BC，∠B＝90°．∵EF⊥AB，EG⊥BC，∴∠BFE＝90°，∠BGE＝90°．又∵∠B＝90°，∴四边形BFEG是矩形；（2）∵正方形ABCD的周长是40cm，∴AB＝40÷4＝10cm．∵四边形ABCD为正方形，∴△AEF为等腰直角三角形，∴AF＝EF，∴四边形EFBG的周长C＝2（EF+BF）＝2（AF+BF）＝20cm．（3）若要四边形BFEG是正方形，只需EF＝BF，∵AF＝EF，AB＝10cm，∴当AF＝5cm时，四边形BFEG是正方形．21．解：（1）∵DE⊥AC，∴∠DEA＝90°，∵∠C＝90°，∴∠DEA＝∠C．∴DE∥BC．∵DF∥AC，∴四边形CEDF是平行四边形，∵∠C＝90°，∴四边形CEDF是矩形．（2）若四边形CEDF成为正方形，设这个正方形的边长为x，则CE＝DE＝DF＝FC＝x，BF＝4﹣x，∵DF∥AC，∴x＝．∴正方形的边长为．22．解：（1）∵在△ABC中，D是AB中点，E是AC中点，F是BC中点，∴DE∥BC，EF∥AB，∴四边形BDEF是平行四边形，故答案为：平行；（2）当AB＝BC时，∴BD＝BF，∴平行四边形BDEF是菱形，故答案为：AB＝BC；（3）当∠B＝90°时，∴平行四边形BDEF是矩形，故答案为；∠B＝90°；（4）当∠B＝90°，AB＝BC，∴平行四边形BDEF是正方形，故答案为：∠B＝90°，AB＝BC 23．（1）证明：∵四边形ABCD是矩形，∴AD∥BC，∠ADC＝∠C＝90°，∵EF∥DC，∴四边形FEDC为平行四边形，∵DE平分∠ADC，∴∠ADE＝∠CDE，∵AD∥BC，∴∠ADE＝∠DEC，∴∠CDE＝∠DEC，∴CD＝CE，∴四边形FEDC是菱形，又∵∠C＝90°，∴平行四边形FEDC是正方形；（2）∵四边形FEDC是正方形，∴∠CDE＝45°，∵，∴CE＝CD＝2，∴BC＝BE+EC＝1+2＝3，∴BD2＝BC2+CD2＝32+22＝13，∴BD＝．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
18.2.3 正方形
第1课时正方形的性质
一、填空题
1、如图，E是正方形ABCD的对角线BD上一点，且BE＝BC，则∠ACE＝°.
2、如图，四边形ABDC是正方形，延长CD到点E，使CE=CB，则∠AEC＝°.
3、如图，正方形ABCD中，点E在BC的延长线上，AE平分∠DAC,则下列结论：①∠E=
22.5°；②∠AFC=112.5°；③∠ACE=135°；④AC=CE；⑤AD∶CE=1∶ 2. 其中正确
的有个.
4、如图，等边△EDC在正方形ABCD内，连结EA、EB，则∠AEB＝
°；∠ACE
＝
°.
5、已知正方形ABCD，以CD为边作等边△CDE，则∠AED的度数是°.
6、如图，四边形
ABCD是正方形，E 是边CD 上一点，若△AFB经过逆时针旋转角θ（0°＜θ＜180°）后，与△AED重合，则θ值为°
第6题图第7题图第8题图第9题图
7、已知正方形ABCD中，点E在边DC上，DE = 2，EC = 1，把线段AE绕点A旋转，使点E
落在直线BC上的点F处，则F、C两点的距离为___________.
8、如图，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角
线AC上有一点P，使PD＋PE的和最小，则这个最小值为 .
9、如图，四边形ABCD是边长为9的正方形纸片，将其沿MN折叠，使点B落在CD边上的B'
处，点A对应点为A'，且C
B'=3，则CN= ；AM的长是 .
10、正方形的面积是
3
1，则其对角线长是________.
11、如图，三个边长均为2的正方形重叠在一起，O1、O2是其中两个正方形的中心，则阴影部分的面积是 .
第1题图第2题图第3题图第4题
第11题图第12题图第13题图第14题图
12、如图，将n 个边长都为1cm 的正方形按如图所示摆放，点A 1、A 2、…、A n 分别是正方形
的中心，则n 个这样的正方形重叠部分的面积和为 .
13、边长为1的正方形ABCD 绕点A 逆时针旋转30°得到正方形AB ′C ′D ′，两图叠成一个
“蝶形风筝”（如图所示重叠部分），则这个风筝的面积是 .
14、如图，边长为1的正方形ABCD 绕点A 逆时针旋转45度后得到正方形
AB ′C ′D ′，边B ′C ′与DC 交于点O ，则四边形AB ′OD 的周长是 .
15、如右图，正方形ABCD 中，AB ＝6，点E 在边CD 上，且CD ＝3DE ．
将△ADE 沿AE 对折至△AFE ，延长EF 交边BC 于点G ，连结AG 、CF ．
下列结论：①△ABG ≌△AFG ；②BG ＝GC ；③AG ∥CF ；④S △FGC ＝3．
其中正确的结论是 .（填序号）
16、如右图，四边形ABCD 为正方形，以AB 为边向正方形
外作等边△ABE ，CE 与DB 相交于点F ，则= 。
二、解答题
17、如图，正方形ABCD 中，E 、F 、G 分别是AD 、AB 、BC 上的点，且AE=FB=GC.
试判断△EFG 的形状，并说明理由.
18、E 为正方形ABCD 内一点，且△EBC 是等边三角形，求∠EAD 的度数.
19、如图，在正方形ABCD中，F是CD的中点，E是BC边上一点，且AF平分∠DAE，求证：AE=EC+CD.。