第三章___控制图-(通用图+选控图)
控制图分类

x~—R
正态分布
平均值与标准差 控制图
(—σ )
x —S
正态分布
个别值与移动极 差控制图Fra bibliotekx—Rm
正态分布
不良数控制图 计 件 值
np
二项分布
计 数
计 件 值 不良率控制图 p 二项分布
计 数 值 控 制 图 计 点 值
缺点数控制图
c
泊松分布
单位缺点数控制 图
u
泊松分布
多品质通用图 其他 短制程控制图
1.控制的对象为不良率、良品率、废品率、交货延迟 率、缺勤率、差错率等。 2.需要注意的是,当p控制图显示异常后,难以找到 异常的原因,因此使用p控制图时,应选择重要的检 查项目,作为判断不良品依据。 3.样本数可以不同,也可以相同。 用于控制一部机器,一个零件,一定的长度,一定的 面积或任何一定单位中所出现的不合格数目。如: 1.布匹上的疵点数; 2.铸件上的砂眼数; 3.机器设备的不合格数; 4.电子设备的焊接不良数; 5.每页印刷的错误数。 控制对象为产品的缺点数量,每个样本大小一定。 1.当上述一定的单位,也即样品的大小保持不变时, 可以应用c控制图,而当样本的大小变化时则应注意 为平均每单位的不合格数后再使用u控制图。例如: 在制造厚度2㎜的钢板的生产过程中,一批样品是2㎜ 的,下一批样品是3㎜的,这时可换算为平均每平方 米的不合格数,然后再对它进行控制。 2.样本大小不固定,测量单位数量(如单位面积、单 位长度)的缺点数来控制产品的质量。 1.适用于生产的产品很多,或每个产品需要控制的特 性很多时。 2.上下限为3σ 。 3.同时将多个产品多个控制特性数据在一份图表中显 示并通过图形可以方便知道每组数据的检验时间。 1.适用于品种多,产品少的制造过程。 2.适用条件为相同操作人员,机器设备。 3.每种产品有近似的相同的σ 。 4.样本大小最好相同。
控制图控制图
控制图1、概念控制图又叫做管制图,是用于分析和判断工序是否处于稳定状态所使用的带有控制界限的一种工序管理图。
控制图是一种对过程质量加以测定、记录从而进行控制管理的一种用科学方法设计的图,图上有中心线(CL )、上控制线(UCL )、下控制线(LCL ),并有按时间顺序抽取的样本计量值的描点序列。
控制图主要用于:过程分析及过程控制。
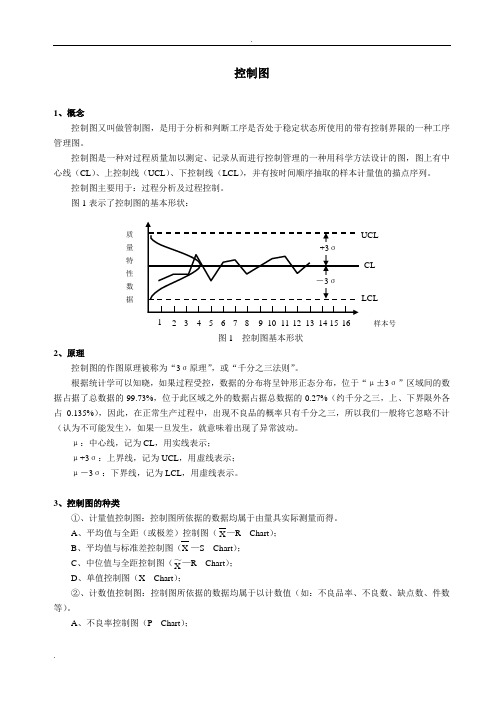
图1表示了控制图的基本形状:2、原理控制图的作图原理被称为“3σ原理”,或“千分之三法则”。
根据统计学可以知晓,如果过程受控,数据的分布将呈钟形正态分布,位于“μ±3σ”区域间的数据占据了总数据的99.73%,位于此区域之外的数据占据总数据的0.27%(约千分之三,上、下界限外各占0.135%),因此,在正常生产过程中,出现不良品的概率只有千分之三,所以我们一般将它忽略不计(认为不可能发生),如果一旦发生,就意味着出现了异常波动。
μ:中心线,记为CL ,用实线表示; μ+3σ:上界线,记为UCL ,用虚线表示; μ-3σ:下界线,记为LCL ,用虚线表示。
3、控制图的种类①、计量值控制图:控制图所依据的数据均属于由量具实际测量而得。
A R Chart ); B S Chart );C Chart );D 、单值控制图(X Chart );②、计数值控制图:控制图所依据的数据均属于以计数值(如:不良品率、不良数、缺点数、件数等)。
A 、不良率控制图(P Chart );质 量 特 性 数 据B、不良数控制图(Pn Chart);C、缺点数控制图(C Chart);D、单位缺点数控制图(U Chart)。
4、控制图的用途根据控制图在实际生产过程中的运用,可以将其分为分析用控制图、控制用控制图:①、分析用控制图(先有数据,后有控制界限):用于制程品质分析用,如:决定方针、制程解析、制程能力研究、制程管制之准备。
分析用控制图的主要目的是:(1)分析生产过程是否处于稳态。
控制图PPT

03 控制图的结构
04 控制图的功能
05 控制图的作用
二、什么是控制图?
二、什么是控制图?
二、什么是控制图?
• 2.3控制图结构
中间一条实线为中心线; 上、下两条虚线分别为 上控制界限和下控制界限; 并有按时间先后排列的 统计数值的描点序列。
控制界限不能驾驭过程,仅仅反应当前过程的状态。
2.92
2.65
2.82
151107
2.83
2.88
2.78
2.73
六、控制图的制作示例
x
xR
计量控制图常数 表
xR
x
当n=4时,A2=0.729;D4=2.282;D3=0
R
R
R
R
控制限 UCL CL LCL
极差UCL 极差CL 极差LCL
计算值 2.818 2.541 2.265 0.865 0.379
7
四、控制图的判稳与判异
①1个点落在A区外
②连续9点落在中心线同一侧
③连续6点递增或递减
④连续14点中相邻点交替上下
⑤连续3点中有2点落在中心线 同一侧的B区以外
⑥连续5点中有4点落在中心线 同一侧的C区以外
⑦连续15点落在中心线两侧C区 内
⑧连续8点落在中心线两侧且无 一在C区内
四、控制图的判稳与判异
二、什么是控制图?
二、什么是控制图?
三、控制图的分类
Contents
01 按数值质量特性分类
02 按控制图用途分类
三、控制图的分类
三、控制图的分类
x x ~x
三、控制图的分类
• 3.2按控制图的用途分类:
分析用控制图
控制用控制图
控制图

与均值-极差控制图类似,这种控制图也是用于观察连续数据的均值和变异性(标准差) 的变化情况。如果点子在控制限内随机分布,且无异常点,说明过程处于控制状态;如果 点子超出控制限或出现异常点,说明过程可能失控。
3. 单值-移动极差控制图
这种控制图用于观察单个数据值和连续数据的变化情况。如果点子在控制限内随机分布, 且无异常点,说明过程处于控制状态;如果点子超出控制限或出现异常点,说明过程可能 失控。
4. 观察控制图
观察控制图上的点 子分布情况,判断 过程是否处于控制 状态。
5. 采取行动
如果发现异常点或 过程失控,采取适 当的措施解决问题 并防止问题再次发 生。
控制图的局限性
1. 数据必须是连续的
控制图只能用于观察连续的数据,对于离散的数据或非连续的数 据,需要采用其他方法进行分析。
2. 需要足够的样本数量
控制图原理
控制图基于中心极限定理和概率统计原理。中心极限定理表明,当样本量足够大时,任何随机变量的 取值都会围绕一个中心值波动,且这个波动是有限的。因此,我们可以通过控制图的上下限来判断过 程是否处于控制状态。
控制图的原理是通过对过程进行多次抽样,计算统计量(如均值、中位数、极差等),并将这些统计 量绘制在图上。通过观察图的走势,我们可以判断过程是否受控,并发现异常情况。如果过程受控, 则说明过程的质量稳定;如果过程失控,则说明过程的质量存在问题。
平均数与标准差控制图
总结词
平均数与标准差控制图是一种常用的统计 控制图,用于监控一组数据的平均值和标 准差。
VS
详细描述
平均数与标准差控制图由两个图表组成: 一个图表显示平均数,另一个图表显示标 准差。这种控制图适用于需要了解数据分 布情况的应用场景,如科学研究、质量控 制和金融分析等。
第三章 控制图

19
3.2 过程波动
3.2 过程波动
3.2 过程波动
过程控制的三种显示型态 过程控制的三种显示型态
(a) 正常型 Frequency LSL=Lower specification limit USL =Upper specification limit (b)共同原因变异 )
(c).特殊原因变异 特殊原因变异
α/2 =0.135
以 X 控制图控制过程前,需决定抽样时间(h)与样本大小(n) 。 故每隔h时间随机抽取n个样本,再将样本统计量 X 描绘控制 图上,即假设检验过程均值是否为 X ,若点出界则表示拒绝H0, 显示过程平均值发生偏差。 H0: µ= X H1: µ ≠ X
3
3.1 统计过程控制
SPC的特点: ——全系统,全过程,全员参加,人人有责。
——强调用科学方法(统计技术,控制图理论) 来保证全过程的预防。 ——不仅用于生产过程,而且可用于服务过程和 一切管理过程。
4
3.1 统计过程控制
SPC发展的三个阶段
SPC——科学地区分生产过程中产品质量的偶然波动和异 常波动,从而对过程的异常及时报警,以便采取措施, 消除异常,恢复过程的稳定。 SPD——统计过程诊断,张公绪提出的选控控制图和两种 质量诊断理论,开辟了统计质量诊断的新方向。 SPA——统计过程调整,过程诊断后要加以措施进行调整 三者之间的关系: 循环不已 不断改进 与时俱进 SPC SPD SPA
Drop to Drop Variation + Wind 油滴之间的变化加上风的作用 Drop to Drop Variation + Wind + the Variation of Steering 油滴之间的变化加上风的作用,以及 方向盘控制的变化 11
控制图

43 40
39 39 40
41 38
39 36 43
43 42
43 40 42
样本組 22
X1 39
X2 39
X3 39
X4 40
X5 45
23
24 25
31
40 46
33
40 44
35
40 41
39
41 41
35
42 39
样本組
1
2
3
4
5
6
7
8
各组平均数
40.4
39.8
41
40.4
41.2
41.2
第三节 常规控制图的分类
数据 名稱 均值-极差控制图 均值-标准差控制图 计量值 中位数-极差控制图 控制名称 X—R控制图 X —S控制图 Me—R控制图
单值-移动极差控制图
X—Re控制图
第三节 常规控制图的分类
数据 名稱 不合格品率控制图 计件值 不合格品数控制图 控制名称 p控制图 np控制图
41.2 39.6
极差
样本组 各组平均数
5
10 39
3
11 41
4
12 40.6
3
13 38.8
4
14 37.4
2
15 41.2
6
16
8
17
45.6 40.6
极差
5
5
5
5
4
9
5
7
样本组
18
19
20
21
22
23
24
25
各组平均数
39.2
39.6
40.4
40.4
常用控制图

SPCSPC(Statistical Process Control,统计过程控制或统计制程控制)目录∙ 1 什么是SPC∙ 2 SPC起源与发展∙ 3 3σ原理简介∙ 4 SPC技术原理∙ 5 SPC控制图及计算∙ 6 SPC控制图(管制图)的实施∙7 SPC控制图(管制图)异常的判断及处理∙8 制程能力指数(参数)CPK∙9 SPC的发展特点∙10 SPC对企业带来的好处什么是SPCSPC即英文“Statistical Process Control”之缩写,意为“统计制程控制” SPC或称统计过程控制。
SPC主要是指应用统计分析技术对生产过程进行实时监控,科学的区分出生产过程中产品质量的随机波动与异常波动,从而对生产过程的异常趋势提出预警,以便生产管理人员及时采取措施,消除异常,恢复过程的稳定,从而达到提高和控制质量的目的。
在生产过程中,产品的加工尺寸的波动是不可避免的。
它是由人、机器、材料、方法和环境等基本因素的波动影响所致。
波动分为两种:正常波动和异常波动。
正常波动是偶然性原因(不可避免因素)造成的。
它对产品质量影响较小,在技术上难以消除,在经济上也不值得消除。
异常波动是由系统原因(异常因素)造成的。
它对产品质量影响很大,但能够采取措施避免和消除。
过程控制的目的就是消除、避免异常波动,使过程处于正常波动状态。
SPC起源与发展1. 1924年休哈特博士在贝尔实验室发明了品质控制图。
2. 1939年休哈特博士与戴明博士合写了《品质观点的统计方法》。
3.二战后美英将品质控制图方法引进制造业,并应用于生产过程。
4. 1950年,戴明到日本演讲,介绍了SQC的技术与观念。
5.SQC是在发生问题后才去解决问题,是一种浪费,所以发展出了SPC。
6.美国汽车制造商福特、通用汽车公司等对SPC很重视,所以SPC得以广泛应用。
7.ISO9000(2000)体系亦注重过程控制和统计技术的应用(如8.1,8.2.3)。
控制图
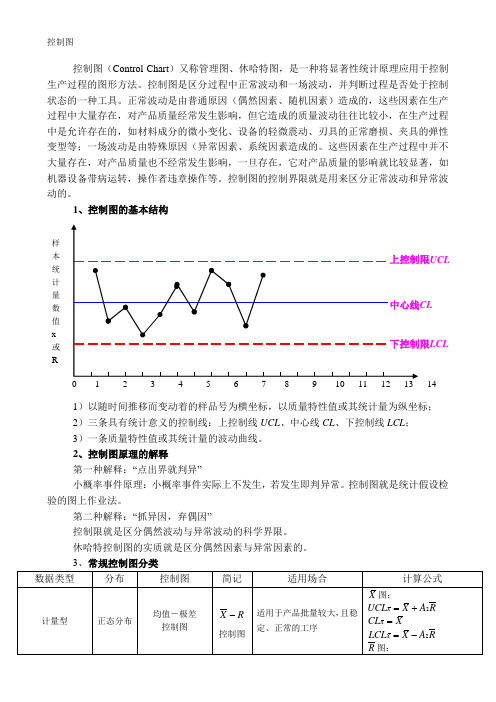
控制图控制图(Control Chart )又称管理图、休哈特图,是一种将显著性统计原理应用于控制生产过程的图形方法。
控制图是区分过程中正常波动和一场波动,并判断过程是否处于控制状态的一种工具。
正常波动是由普通原因(偶然因素、随机因素)造成的,这些因素在生产过程中大量存在,对产品质量经常发生影响,但它造成的质量波动往往比较小,在生产过程中是允许存在的,如材料成分的微小变化、设备的轻微震动、刃具的正常磨损、夹具的弹性变型等;一场波动是由特殊原因(异常因素、系统因素造成的。
这些因素在生产过程中并不大量存在,对产品质量也不经常发生影响,一旦存在,它对产品质量的影响就比较显著,如机器设备带病运转,操作者违章操作等。
控制图的控制界限就是用来区分正常波动和异常波动的。
1、控制图的基本结构1)以随时间推移而变动着的样品号为横坐标,以质量特性值或其统计量为纵坐标; 2)三条具有统计意义的控制线:上控制线UCL 、中心线CL 、下控制线LCL ; 3)一条质量特性值或其统计量的波动曲线。
2、控制图原理的解释 第一种解释:“点出界就判异”小概率事件原理:小概率事件实际上不发生,若发生即判异常。
控制图就是统计假设检验的图上作业法。
第二种解释:“抓异因,弃偶因”控制限就是区分偶然波动与异常波动的科学界限。
休哈特控制图的实质就是区分偶然因素与异常因素的。
UCLLCL样本统计量数值x 或R14 15 16 17 18按用途分类1)分析用控制图——用于质量和过程分析,研究工序或设备状态;或者确定某一“未知的”工序是否处于控制状态;2)控制用控制图——用于实际的生产质量控制,可及时的发现生产异常情况;或者确定某一“已知的”工序是否处于控制状态。
4、R X -图的绘制1)确定控制对象(统计量)一般应选择技术上最重要的、能以数字表示的、容易测定并对过程易采取措施的、大家理解并同意的关键质量特性进行控制。
2)选择控制图对于计量数据而言,R X -控制图是最常用最基本的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
-
-
-
-
-
-
-
-
-
-
-1.9 -1.9
例
• • • • •
步骤1 计算样本平均不合格品率 步骤2 选择参数n的选择范围 50~105 步骤3 计算直接打点表 步骤4 应用直接打点表在通用图上描点 步骤5 观察判断。 通用图判异的准则:
UCLT=3 CLT = 0
LCLT=—3
§5
通用控制图
现场标杆数据= μ + kб
• 二、直接打点法 在通用图上画出7条直线 (k=0,±1,±2,±3) 将图分成8个区域。 (现场标杆数据—μ ) k= —————————— б
直接打点法
• 如果在现场数据中找 出与此对应的七个数 据(称之为现场标杆 数据),则在现场测 得所控制质量指标的 数据后,将它与这七 个现场标杆数据相比 较,便立刻知道应在 通用图上哪个区域中 描点。————
第三章
质量管理旧七种工具 第七种:控制图
第三章
• §1 • • • • • 统计过程控制 (Statistical Process Control) §2 控制图 §3 计量值控制图(6种) §4 计数值控制图(4种) §5 通用控制图(简介) * §6 两种质量诊断(简介)
注意:
• • • • • • • 1、X图上的点是一个分布,而非测量值; 2、控制界限~规格线; 3、合理分组; 容差图 4、经济性; 5、偏移大~小样本,偏移小~大样本; 6、一般不用大样本,而加警戒线和非随机原则; 7、n>10 不能用R图,应用S图。
上工序
本工序
产 品
(上影)
+
(分质量) =(总质量)
3、两种质量诊断理论的思路
• 诊断—— 将表征与标 准对照的 对比过程。 条件——
对 比 方 法 、 过 程 。
比 较 标 准 ;
事 物 表 征 的 测 量 参 数 ;
对比
分质量~总质量
可看出上道工序的影响
差别越大,上影越大 差别越小,上影越小
偶然因素、欲控异因、非控异因
分质量(工序固有质量)
•§6 两种质量诊断理论 (简介)
• (一) 两种质量诊断理论 • (二) 两种控制图的诊断 • (三) 两种过程能力法
工序1
工序2
•工序3 •工序4
»工序5
16
上下工序是相连的、相关的、相互影响的
• б 为常数:
yi - ŷ i ycsi = ———— б0
特例: 本工序质量 指标实测值的总体 的平均值受到非控
系统因素的影响,
y 'csi = yi - ŷ
i
但其标准偏差却保 持稳定。
•
5、区分偶因~异因
(X~RS) 图
^ ^
cs cs cs
UCL=μy
XCS
YCS
+ 3бy ≈ μy + 3бy = y +2.66R ^ CL=μy ≈ μy = y ^ LCL=μy - 3бy ≈ μy - 3бy = y -2.66R
•过滤
^i 常数:y’CSi= yi - y 样本充分大时,y’CS~N(0, б 2 0)
yi-μi yi-y^ i 非常数:yCSi = ——— ≈ ——
бi 样本充分大时,yCS~N(0, 1)
据经验: 本例Y的б是常数
бi
脱
色
31
Y
n=50 n-2=48
ra(n-2)
= 0.01(48)
r
YCS ( 7) - 0.344 1.6715
RSCS ( 8) 2.016
50 总计
77.50
91.30
10.20
4.50
92.634
- 1.334 - 1.072
1.744 57.107
平均
- 0.02144
1.165449
(一)?正态分布 工序1质量——过滤液透光度X 工序2质量——脱色液透光度Y (二)检查Y的标准差б
— 3.10
— 4.920
RS(X)
4 μ: 异 异 异
4 RS: 异 异 正
4
(三) 两种过程能力指数的诊断
• 1、综合过程能力指数 (总过程能力指数) Tt CPt= —— 6бt Tt——总质量的 规格公差 бt——全控图得出 • 2、固有过程能力指数 (分过程能力指数) TP CPP= —— 6бP TP——分质量的 规格公差 бP——选控图得出
•注意:
①如过程不合格品率很小,必须选样本量充分大。? ②实际工作中,样本量不可能无限制的增大。? 大? ③若图上的点超出下控制界限, 小? 表明过程不合格品率异常低,好状态? ④要求下控制界限为正,一般为0。 ⑤样本量不等时,控制界限?不能仅以pi的描点距离判断点是否接近 中心线? ⑥控制界限~样本大小有关?
• 4、选控的过程
正态分布,Y——本工序质量指标 X——上工序质量指标 上影: μ= F(X) б= G(X)
样本足够大时, 近似地Ycs~ N(0,1)分布 μi = 0 бi = 1
将Y标准变换——Ycs
将Y标准变换——Ycs
yi-μi yi- F(X i ) yi- μi^ yi- ŷ
i
Ycsi=——— = ——————≈————= —— ^ бi G(X i ) б^ б i i
±√ /n nmax<2n, nmin>n/2
样本距中心线 的标准化距离:
di=
pi-P
√P(1-P)/ni
· ·
⑦简化凹凸型控制界限成直线:用样本的平均值求控制界限。
§5
通用控制图
1
• 一、标准变换~通用控制图 随机变量的平均值 0,方差
*
以标准偏差б为单位, 各随机变量到分布中心μ的相对距离。 随机变量- μ б
• 3、比较d、dr 质量提高的最大幅度(绝对值) d d=CPP— CPt 质量提高的最大幅度(相对值) dr
d CPP— CPt бP dr= —— = ———— = 1— —— CPP CPP бt
一般地, бP ≤ б t CPt ≤ CPP
^
Scs
6、选控过程举例
例:药厂抗生素车间:
过滤工序(X:过滤液透光度) 脱色工序(Y:脱色液透光度)
数据表
编号 ( 1) 1 2 X ( 2) 76.80 72.30 Y ( 3) 92.10 92.90 RS(X) ( 4) 4.50 RS(Y) ( 5) 0.80
Ŷ
( 6) 92.444 91.229
• nPT图控制界限 ±3 变换后的随机变量nPT (随机变量-μ) = ———————— б D-nP = ——————— =K √nP(1-P )
DK,n=np+K√np(1-p )
(K=-3,-2,-1,0,1,2,3)
D3,55=6.4 =55×0.0389+3√55×0.0389(1-0.0389)
cs cs SCS
cs
cs
cs
^
cs
cs
cs
cs
cs
SCS
• 5 、区分偶因~异因 UCL=μR cs+ 3бR cs≈ =3.27R
S S SCS
μR +3 бR
Scs Scs
^
^
Scs
Rscs
μR = R ^ 3б LCL=μR - 3бR ≈ μR R
^
S Scs Scs Scs Scs
CL=μR cs ≈ = —
CUL= yCS+2.66 RSCS = 3.079 CL= yCS= — 0.02144 LCL= yCS— 2.66RSCS = — 3. 1215
• 7、两种控制图诊断的典型情况
1、诊断基本单元——三图诊断系统 2、三八表——8种典型情况 3、两种控制图诊断——典型实例
三图诊断系统
上工序
休图上
• 分质量
是工序的 固有质量, 正常情况下应与
• 总质量
包含了 上工序影响和 本工序影响的
• 标准值
一致。
• 综合质量,
反映在本工序完成后的
• 测量值上。
• 4、两种质量诊断的方法
(1)用控制图诊断 总质量——全控图(休哈特图) 分质量——选控图(张公绪)
(2)用过程能力指数诊断: 总质量——总过程能力指数Cpt 分质量——分过程能力指数Cpp
• 2、两种质量
用户可感知 的 最终质量
(1)工序综合质量(总质量) 不但包括第n道工序的加工质量, 而且综合了所有以上各道工序的加工质量。 该工 (2)工序固有质量(分质量) 序质 某工序本身的加工质量,不包括上 量 (以前)工序的影响。
分质量(本工序的质量) 总质量 上工序的影响(上影)
半 成 品
UCL=μ+3б CL=μ LCL=μ- 3б
(UCL—μ) ( μ +3 б — μ) UCLT = —————— = ———————— б б
CLT=(CL—μ) / б= ( μ— μ)/ б (LCL—μ) ( μ —3 б — μ) LCLT = —————— = ———————— б б
徒发警报 漏发警报
4
5
6 7 8
徒发警报
正常 正常 异常
正常 正常 正常
分质量异常,上影正常,总质量正常
分质量、上影、总质量均正常
漏发警报
X(X)
X (Y) 87.1 78.3 69.4 67.8 4 4 RS(Y) 12.5 10.9 3.3 — 7.7 84.3
