光通过单轴晶体时的双折射现象
光的双折射现象理论解释与实验探究

光的双折射现象理论解释与实验探究光的双折射是光线在晶体中传播时所表现出的一种非常有趣的现象。
在晶体中,光线被分成两束,分别按照不同速度传播和折射,产生出两束方向不同的光线。
这种现象可以通过理论解释和实验来探究。
首先,理论解释方面,我们需要了解晶体的结构和光的传播机制。
晶体由大量的晶格构成,其中每个晶格都具有相同的结构单元。
光的传播是通过光子在晶格之间进行散射来实现的。
当光传播方向与晶格中的原子或分子排列方向一致时,光子会与晶格产生相互作用,导致光传播速度减慢。
而当光传播方向与晶格排列方向垂直时,光子则不与晶格相互作用,速度维持不变。
基于这个理论,我们可以解释为什么光在经过晶体时会出现双折射现象。
当光线射入晶体时,它会与晶格中的原子或分子相互作用,导致光线被分成两束,其中一束传播速度变慢,另一束传播速度保持不变。
这导致光线的传播方向发生改变,从而使得光线呈现出双折射现象。
为了进一步验证这个理论,我们可以进行实验探究。
实验所需材料包括晶体样品(如方解石)和光源(如激光器或白光源)。
首先,将晶体样品固定在光路上,并确保光线垂直入射到晶体表面。
然后,通过调整光源和观察屏的位置,我们可以观察到晶体中传播出的两束光线。
这两束光线的方向和强度可以用调整观察屏上的位置和观察角度来观察和测量。
实验结果将验证理论解释,并提供更多关于光的双折射现象的信息。
例如,我们可以测量两束光线的入射角和折射角,以确定双折射的程度。
我们还可以调整晶体样品的厚度和方向,观察和比较不同条件下的双折射效应。
除了理论解释和实验探究,光的双折射现象还具有广泛的应用。
例如,在光学仪器和光纤通信中,双折射现象被用于控制和调节光的传播方向和速度。
通过利用晶体的双折射特性,我们可以设计出各种光学器件和系统,提高光学设备和通信网络的性能。
总的来说,光的双折射现象是光传播过程中的一种重要现象,通过理论解释和实验探究可以更好地理解和应用这一现象。
通过深入研究光的双折射现象,我们可以为光学科学和技术的发展提供新的思路和解决方案,推动光学领域的进步和创新。
作图法分析光波在两个单轴晶体分界面上的双反射和双折射

作图法分析光波在两个单轴晶体分界面上的双反射和双折射宋哲;于伟行;张琳;李琳;吴晶;丁一【摘要】通过几何作图法,分析了光轴取向任意时,光波在两个单轴晶体分界面上的双反射和双折射.考虑到入射光波、反射光波、折射光波在界面上相位相等和晶体折射率面的定义,采用斯涅尔作图法,直接在图上得到了两条反射光波和两条折射光波.根据晶体的光学各向异性,进一步讨论了各光波对应的光线方向和振动方向,并通过几何分析,给出了各反射光波、折射光波、反射光线和折射光线位置的一般表达式.斯涅尔作图法简单直观,可以直接获得光波的方向,结果具有普遍性.【期刊名称】《大学物理》【年(卷),期】2017(036)010【总页数】5页(P16-20)【关键词】晶体光学;双反射;双折射;折射率面;相位【作者】宋哲;于伟行;张琳;李琳;吴晶;丁一【作者单位】辽宁师范大学物理与电子技术学院,辽宁大连 116029;中国科学院空间激光通信及检验技术重点实验室,上海201800;辽宁师范大学物理与电子技术学院,辽宁大连 116029;辽宁师范大学物理与电子技术学院,辽宁大连 116029;辽宁师范大学物理与电子技术学院,辽宁大连 116029;辽宁师范大学物理与电子技术学院,辽宁大连 116029;辽宁师范大学物理与电子技术学院,辽宁大连 116029【正文语种】中文【中图分类】O435.1光学各向异性是晶体的主要物理性质之一,双折射现象是其重要表现.利用晶体的双折射效应可以设计出各种晶体光学器件,其中有许多是由多块光轴取向不同的晶体级联构成的,如渥拉斯顿棱镜、偏振分光镜、波片、光开关[1]、光互连网络[2,3]、光桥接器[4,5]、偏振干涉滤波器[6]等.在设计器件时,光波在晶体界面上的反射和折射问题是必须要考虑的.人们采用不同方法对光波在各向同性介质与单轴晶体分界面上的双折射和双反射进行了大量研究,如:光轴取垂直入射面和在入射面内两种特殊方向情况下,光波从各向同性介质入射到单轴晶体时晶体上表面的双折射和光波从单轴晶体入射到各向同性介质时晶体下表面的双反射[7-11];光轴取向任意时,光波在单轴晶体上表面的双折射[12-17]和单轴晶体下表面的双反射[12,16,18-20].由于晶体级联时多采用各向同性介质胶合的方式,所以对光波在两个单轴晶体分界面上的双折射和双反射研究得不多[21-25].但在对器件质量要求较高的场合,晶体之间可以通过光胶工艺直接级联,此外,液晶之间[26]、各向异性薄膜之间[27]可以直接级联,因此,研究光波在两个晶体分界面上的双反射和双折射是有必要的.本研究小组对单轴晶体的双折射问题进行了系列研究,本文在前期工作基础上,利用各光波在界面上相位相等的条件和晶体的折射率面定义,通过作图来分析光轴取向任意时光波在两个单轴晶体分界面上的双折射和双反射.首先建立晶体界面与法线的直角坐标系xyz,选取两个晶体的分界面为xy面,界面的法线为z轴,z>0为晶体a,z<0为晶体b,假设xz面是入射面(即入射光波与界面法线组成的面),则x轴为入射面与界面的交线,如图1所示.x1ax2ax3a组成晶体a的主轴坐标系,x1bx2bx3b组成晶体b的主轴坐标系.令晶体a的光轴x3a (ca)轴与z轴的夹角为φa,0<φa<π,x3a轴与z轴组成的面为晶体a的主截面Ⅰ,其与入射面的夹角为δa(即x3a轴在界面上的投影与x轴之间的夹角),0<δa<2π,x1a垂直于主截面Ⅰ,并在界面xy内,x2a在主截面Ⅰ内.令晶体b的光轴x3b(cb)轴与z轴的夹角为φb,0<φb<π,x3b轴与z轴组成的面为晶体b的主截面Ⅱ,其与入射面的夹角为δb(即x3b轴在界面上投影与x轴之间的夹角),0<δb<2π,x1b轴垂直于主截面Ⅱ,并在界面xy内,x2b轴在主截面Ⅱ内. 根据入射光波、反射光波、折射光波在界面上相位相等的条件和晶体折射率面定义,可以通过斯涅尔作图法来分析光波在两个单轴晶体分界面上的双反射和双折射.单轴晶体的折射率面是个双层面,一个是球面,代表寻常光(o光)的折射率面,定义为矢径r=noko,ko是晶体中o光波法线ko的单位矢量,no是o光的主折射率;另一个是旋转椭球面,代表非寻常光(e光)的折射率面,定义为矢径r=ne(θ)ke,ke是晶体中e光波法线ke的单位矢量,ne(θ)是e光沿ke方向的折射率(说明e光折射率是随传输方向而变化的),θ是ke与光轴的夹角,两个面在光轴处相切.在图1所示的情况下,两个单轴晶体中,球面在入射面上的中心截面是圆面Σ1a和Σ1b,半径分别为noa和nob,noa和nob分别是o光在晶体a和晶体b中的主折射率;椭球面在入射面上的中心截面是椭圆面Σ2a和Σ2b,长、短半轴分别为、nea和、neb,其中长轴方向分别平行于光轴x3a和x3b在入射面内的投影和,他们与x轴的夹角分别为βa和βb角,长轴的长度是e光沿和方向传输时的折射率和,设短轴方向分别为和,其长度是e光沿和方向传输时的折射率,等于e光在晶体a和晶体b中的主折射率nea和neb,如图2所示,图中Σ1a、Σ2a和Σ1b、Σ2b只画出晶体a和晶体b中部分.根据单轴晶体折射率面方程可以得到Σ1a、Σ2a和Σ1b、Σ2b的方程:+=1==其中θca和θcb分别是与晶体a光轴x3a的夹角和与晶体b光轴x3b的夹角.根据文献[17]和[20]的方法可求得:在图1所示坐标系下,当一束o光波ko1以θ1角从晶体a入射到晶体b时,在分界面上将发生双反射和双折射.由各光波在界面上相位相等的条件可得:nobsin θ2ook=neb(θkoecb)sin θ2oek其中是o光光波反射角,nea(θkoeca)为e光反射光波方向的折射率,θkoeca是与光轴ca的夹角,为e光光波反射角,θ2ook为o光光波折射角,neb(θkoecb)为e光折射光波koe2方向的折射率,θkoecb是koe2与光轴cb的夹角,θ2oek为e光光波折射角.根据晶体折射率面定义可知,任一矢径在x轴上的投影即为沿该方向传输的光波的相位.设入射o光波ko1交折射率面Σ1a于P点,作PA垂直于x轴,交x轴于A,则OA=noasin θ1.在x轴上取OB=OA,过B点作x轴的垂线,分别交Σ1a于C,交Σ2a于D,交Σ1b于E,交Σ2b于F,则OC即是o光反射光波方向,OD是e光反射光波方向,OE是o光折射光波koo2方向,OF是e光折射光波koe2方向,如图2所示.由式(11)可得o光的光波反射角和光波折射角,分别为:e光的光波反射角和光波折射角可以利用图2通过几何关系来求得,分别为:cot =cot θ2oek=式(12)—式(15)确定了o光反射光波和折射光波koo2的方向,e光反射光波和折射光波koe2的方向,他们都在入射面内.o光的光线方向与光波方向是一致的,所以o光入射光线to1、反射光线、折射光线too2分别与入射光波ko1、反射光波、折射光波koo2的方向平行,均在入射面内,但振动方向与光轴有关,他们的振动方向是不同的,入射光的振动方向垂直于光轴ca与入射光波ko1组成的面,反射光的振动方向垂直于光轴ca与反射光波组成的面,折射光的振动方向垂直于光轴cb与折射光波koo2组成的面.e光的光线方向与光波方向之间存在离散角,并与光轴取向有关,一般不在入射面内,且不共面,振动方向也不同.e光反射光线在光轴ca与反射光波组成的面内,与反射光波的离散角为根据几何关系可得:将式(17)代入式(16)可以得到反射光线的位置:为负值,表示在远离光轴一侧;为正值,表示在与光轴之间.振动方向在该面内,并垂直于.e光折射光线toe2在光轴cb与折射光波koe2组成的面内,与折射光波koe2的离散角αoe2为同理由式(18)和式(19)得到折射光线的位置.振动方向在该面内,垂直于koe2.利用各矢量之间的几何关系还可以求出e光的光线反射角和光线折射角θ2oet:在图1坐标系下,当一束e光波ke1以θ1角从晶体a入射到晶体b时,在界面上也将发生双反射和双折射.根据各光波在界面上相位相等的条件,有:nea(θk1ca)sin θ1= noasin =nea(θkeeca)sin =nobsin θ2eok=neb(θkeecb)sin θ2eek其中nea(θk1ca)为e光入射光波方向的折射率,θk1ca是e光入射光波与光轴ca的夹角:是o光光波反射角,nea(θkeeca)为e光反射光波方向的折射率,θkeeca是与光轴ca的夹角,为e光光波反射角,θ2eok为o光光波折射角,neb(θkeecb)为e 光折射光波kee2方向的折射率,θkeecb是kee2与光轴cb的夹角,θ2e ek为e 光光波折射角.设入射e光波ke1交折射率面Σ2a于P′点,作P′A′垂直于x轴,交x轴于A′,则OA′=nea(θk1ca)sin θ1.在x轴上取OB′=OA′,过B′点作x轴的垂线,分别交Σ1a于C′,交Σ2a于D′,交Σ1b于E′,交Σ2b于F′,则OC′即是o 光反射光波方向,OD′是e光反射光波方向,OE′是o光折射光波keo2方向,OF′是e光折射光波kee2方向,如图2所示.由式(22)可得o光的光波反射角和光波折射角,分别为:e光的光波反射角和光波折射角可以利用图2通过几何关系来求得,分别为:cot =式(25)—式(28)确定了o光反射光波和折射光波keo2的方向,e光反射光波和折射光波kee2的方向,他们都在入射面内,但e光的光线也是不在入射面内,且不共面,他们的振动方向也是不同的.o光反射光线和折射光线teo2分别与反射光波和折射光波keo2的方向平行,均在入射面内,反射光的振动方向垂直于光轴ca 与反射光波组成的面,折射光的振动方向垂直于光轴cb与折射光波keo2组成的面.e光入射光线te1在光轴ca与入射光波ke1组成的面内,与入射光波ke1的离散角αe1为:振动方向在该面内,垂直于ke1,由式(24)和式(29)可得到入射光线的位置.e光反射光线在光轴ca与反射光波组成的面内,与反射光波的离散角为:cos θkeeca=sin sin φacos δa+cos cos φa振动方向在该面内,垂直于,由式(30)和式(31)可得到反射光线的位置.e光折射光线tee2在光轴cb与折射光波kee2组成的面内,与折射光波kee2的离散角αee2为:cos θkeecb=sin θ2eeksin φbcos δb-cos θ2eekcos φb振动方向在该面内,垂直于kee2,由式(32)和式(33)可得到折射光线的位置.同样,根据几何关系可以求出e光光线入射角θ1et、光线反射角和光线折射角θ2eet:本文根据晶体折射率面的定义和各光波在界面上相位相等的条件,利用斯涅尔作图法,分析了光轴取向任意时,光波在两个单轴晶体分界面上的双反射与双折射情况.通过几何作图,在图中直接获得了反射光波和折射光波的方向.再根据晶体的光学各向异性,讨论了各光波对应的光线方向和振动方向,根据光轴、光波、光线等各矢量的几何关系,确定了反射光线和折射光线的位置,并给出光波反射角、光波折射角、光线反射角、光线折射角、光波与光线之间离散角的一般表达式,该结果具有普遍性,能够为分析光波在晶体中的传播路径和利用晶体设计光学器件提供理论依据.【相关文献】[1] Mendlovic D, Leibner B, Cohen N. Multistage optical system for broadcasting and switching information [J]. Appl Opt,1999, 38(29):6103-6110.[2] Wang N, Yin Y, Qian J, et al. Compact soild-state optical multi-stage network [J]. Intern J of Optoelectronics. 1996, 10(3):223-229.[3] Song Zhe, Liu Liren, Liu De’an, et al. Packagable free-space optical crossbar network based on bypass-exchange switch [J]. Optik, 2003, 114(11):491-496.[4] Smutny B, Kaempfner H, Muehlnikel G, et al. 5.6Gbps optical intersatellite communication link [J]. SPIE, 2009, 7199:719906-1.[5] 侯培培,周煜,职亚楠,等.晶体双折射自由空间2×4 90°光学桥接器[J].光学学报,2010,30(12):3413-3418.[6] 周煜,刘立人,张娟,等.Solc型双折射滤波器离轴消光比的研究[J].光学学报,2003,23(2):159-163.[7] Yariv A, Yeh P. Optical waves in crystals[M]. New York:John Wiley & Sons, 1984:121-154.[8] 蒋民华.晶体物理[M].济南:山东科学技术出版社,1980:258-271.[9] Avendano-Alejo Maximino, Stavroudis O N. Huygen’s principle and rays in uniaxial anisotropic media. I. Crystal axis normal to refracting surface [J]. J Opt Soc Am A, 2002, 19(8):1669-1673.[10] Ren Haixia, Liu Liren, Song Zhe, et al. Double refraction and reflection of sequential interfaces in a crystal and application to integration of 1×N optical switch [J]. J Mod Opt, 2003, 50(14):2231-2242.[11] 宋哲,刘立人,周煜,等.非常偏振光在单轴晶体表面的反射-透射研究[J].光学学报,2004,24(12):1701-1704.[12] Beyerle G, McDermid I S. Ray-tracing formulas for refraction and internal reflection in uniaxial crystals [J]. Appl Opt, 1998, 37( 34):7947-7953.[13] Stamnes J J, Dhavalan V. Double refraction of a Gaussian beam into a uniaxial crystal [J]. J Opt Soc Am A, 2012, 29(4):486-497.[14] Cojocaru E. Direction cosines and vectorial relations for extraordinary-wave propagation in uniaxial media [J]. Appl Opt, 1997, 36(1):302-306.[15] Liang Quanting. Simple ray tracing formulas for uniaxial optical crystals [J].Appl Opt, 1990, 29(7):1008-1010.[16] Ren Haixia, Liu Liren, Liu De’an, et al. Double refraction and reflection of sequentialcrystal interfaces with arbitrary orientation of the optic axis and application to optimum design [J]. J Mod Opt, 2005, 52(4):529-539.[17] 宋哲,郝林岗,吴宁,等.光轴取向任意时单轴晶体界面上的双折射[J].辽宁师范大学学报,2013,36(3):335-339.[18] 熊平凡.光在单轴晶体内表面上的反射[J].大学物理,2000,19(4):29-31.[19] 胡树基.再论光在单轴晶体内表面上的反射[J].杭州师范学院学报,2002,1 (3):67-70.[20] 宋哲,郝林岗,吴宁,等.光轴取向任意时单轴晶体内表面上的双反射[J].辽宁师范大学学报,2013,36(2):168-173.[21] Stamnes J J, Sherman G C. Reflection and refraction of an arbitrary wave at a plane interface separating two uniaxial crystals [J]. J Opt Soc Am, 1977, 67:683-695.[22] McClain S C, Hillman L W, Chipman R A. Polarization ray tracting in anisotropic optically active media. I. Algorithms [J]. J Opt Soc Am A, 1993, 10(11):2371-2382.[23] 胡树基.光轴任意取向的单轴晶体间光的传播[J].首都师范大学学报,2002,23(4):31-34.[24] 许丽萍.光在两单轴晶体分界面的反射和透射系数[J].大学物理,2000,19(12):13-16.[25] 裴芳芳,陈西园.光在两单轴晶体间界面的反射和透射[J].光学技术,2009,35(5):745-750.[26] Yu H F, Kwok H S. Comparison of extended Jones matrices for twisted nematic liquid crystal displays at oblique angles of incidence [J]. J Opt Soc Am, 1999, 16(11):2772-2780.[27] 胡树基.光轴任意取向的单轴晶体薄膜间的“菲涅耳公式”[J].光学仪器,2002,24(4-5):55-58.。
晶体的双折射现象讲解

正晶体
v0 ve
负晶体
v0 ve
几点说明:
1、以上讨论的是自然光入射情形,双折射总是存在的;
2、若入射的光是线偏振光,当偏振方向垂直入射面,则 在晶体中只能引起o光的次波波面,折射光只有o光;
3、若入射的光是线偏振光,当偏振方向在入射面内,则 在晶体中只能引起e光的次波波面,折射光只有e光;
单轴晶体中的波面——惠更斯假设
e光:
o
no
c
o
e
ne
c
e
n0 ,ne称为晶体的主折射率
正晶体 : ne> no (ve< vo)
负晶体 : ne< no (ve > vo)
光轴 vet
vot 子波源
光轴
vot vet
子波源
正晶体 (vo > ve)
负晶体 (vo < ve )
位相差 作为补偿,目的是使 与入,的总和等于o
或 。
入 附 补 0或
(2、巴俾涅补偿器
由两块光轴互相垂直的楔形石英组成,上楔中o光进入下 楔,变为e光;……
2
[(n0
ne )d1
(ne
n0 )d2 ]
2
(n0
ne )(d1
光光
方解石 晶体
纸面
光光
方解石 晶体
纸面
光光
方解石 晶体
纸面
光光
方解石 晶体
纸面
光光
方解石 晶体
纸面
光光
方解石 晶体
纸面
光 光
方解石 晶体
1、放玻璃板时看到一个字。
玻璃是各向同性介质。 光射到各向同性介质的表面时它将按折射定 律向某一方向折射,这是一般常见的折射现象。
光通过单轴晶体时的双折射现象ppt课件
3、o光和e光的振动方向 o 光和 e光都是线偏振光,其振动方向如何?
o 光轴
e 光轴
o 光主截面
e 光主截面
用检偏器检验知
o 光的振动垂直 o光的主截面 e 光的振动在 e 光的主截面内
光轴在入射面内时, 两条光线的主截面就是入射面 o光的振动垂直入射面 两光偏振方向垂直 e光的振动在入射面内
4、o光和e光的主折射率(仅讨论单轴晶体) 光轴 o光的主折射率 两个主折射率
注意:在晶体内光轴是一个方向 实验上怎么操作呢?令入射表面垂直光轴,光线沿光轴方向入射,光线在晶体内 部传播不发生双折射。
光轴方向
空气
方解石 不发生双折射
方解石晶体的光轴(方向)
两钝隅连线方向为 光轴方向
101°52′
78°8′
78°8′
三个角度均为 101°52′的顶点 称为钝隅
单轴晶体 单轴晶体(uniaxis crystal) 只有一个光轴方向: 方解石 (冰洲石)、石英(quartz)、红宝石 人工拉制单轴晶体、ADP(磷酸二氢氨)、铌酸锂(LiNiO3) 方解石晶体的演示 双轴晶体(biaxis crystal)
方解石 晶体
纸面
双 折 射
光 光
当方解石晶体旋转时,o 光不动,e 光围绕o 光旋转
方解石 晶体
纸面
双 折 射
光 光
当方解石晶体旋转时,o 光不动,e 光围绕o 光旋转
方解石 晶体
纸面
双 折 射
光 光
当方解石晶体旋转时,o 光不动,e 光围绕o 光旋转
方解石 晶体
纸面
双 折 射
光 光
当方解石晶体旋转时,o 光不动,e 光围绕o 光旋转
方解石晶体实物照 片 纸面
光的双折射解析

o光:双折射的两束折射光中,一束遵循折射定律,传播速度v o沿各个方向都相同,折射率n o=si n i/si n t o=c/v o=常量,称作寻常光,记为o光。
e光:通常不遵循折射定律,折射方向通常在入射面之外,传播速度随传播方向而改变,si n i/si n t e≠常量,称作非寻常光,记为e光o光和e光都是传播光线在双折射晶体内部定义的,双折射晶体外没有o光和e光光轴:晶体中的一个方向,光沿此方向传播不发生双折射,且折射光遵循折射定律光轴仅代表一个特殊的方向,凡平行于此方向的直线均为光轴只有一个光轴方向的晶体称作单轴晶体,有两个光轴方向的晶体称作双轴晶体在单轴晶体内,光线的传播方向与晶体光轴构成的平面称作该光线的主平面o主平面:光轴+o光线e主平面:光轴+e光线主截面:光轴+晶体表面法线。
入射面:入射光+晶体表面在入射点处的法线o光和e光都是线偏振光o光的电矢量垂直于o主平面,振动方向始终与光轴垂直。
e光的电矢量平行于e主平面,振动方向平行于e主平面通常e光不在入射面内,即e光和o光不共面。
只有当光轴在入射面内(也即入射光在主截面内)时,入射面、主截面、o主平面和e主平面四个面重合,此时o光和e光都在入射面内。
若入射光与光轴重合,则不再发生双折射。
若入射光与光轴共面但不重合,则有折射角t e≠t o,sin t e≠si n t o,发生双折射在双折射晶体中,o光沿各个方向传播的速度相同,o光的波面为半径为球面,o光的传播方向始终垂直于波面。
e光沿各个方向的传播速度不同,e光的波面为椭球面,传播方向仅在椭球的长短轴处垂直于波面。
o光和e光沿光轴方向的传播速度相同,沿垂直于光轴的方向传播速度相差最大n e称作晶体的主折射率。
n o为恒量,n e定义为e光沿垂直于光轴方向的折射率,其数学表达式中的v e也为同一方向的传播速度n e=cv e n o=cv o正晶体和负晶体:满足v o>v e→n o<n e的称作正晶体,e光波面在o光波面之内,椭球面内切于球面,切点为长轴(2v o t)的顶点,长轴方向即光轴,短轴(2v e t)。
光的偏振和双折射

或
将各方向的 E 投影到二个任意互相垂直的方向 上,由于在所有可能的方向上 E 完全相等,所以在
任二个互相垂直的方向上光矢量的分量的和相等。 自然光也可以表示为:
Leabharlann 传播方向 图中:“︱”表示 在板面内的分振动 E “●”表示 E 垂直板面的分振动
二个相互垂直的光振动,光强各占一半
tgib n2 n1
12
ib
n2
布儒斯特定律:当自然光以布儒斯特 角 ib 入射到二介质界面时,反射光为 完全偏振光,振动方向⊥入射面
三. 应用
1. 测量不透明介质的折射率 让光线入射到不透明的介质上,改变入射角i 并测反 射光线的偏振化程度,当反射光线为完全偏振光时, 入 射角 ib 即为布儒斯特角,即:
4
2. 偏振化方向: 偏振片允许通过的光振动的方向。
偏振片 自然光I0
线偏振光I
1 2
偏振化方向
I
I0
※不是只有一个振动方向 的光可以通过偏振片,其他方 向振动的光在偏振化方向的分 量均可以通过偏振片。
偏振片 自然光I0
线偏振光I
1 2
偏振化方向
I
I0
※自然光不是只有2个方 向的振动,在 0~2p 内有无数 个振动方向。
光
的
大学物理波动光学章节,布儒斯特定律 双折射现象

e光
e 光的 主平面
Байду номын сангаас
(e 光振动在e 光主平面内)
e 光:
ne
c ( e 光主折射率) ve
光轴
光轴 v o t
v e t
正晶体
vo ve no ne
负晶体
光轴
vo ve no ne
光轴
v o t
v e t
( 过光轴截面 )
( 过光轴截面 )
ve
vo
( 垂直光轴截面 )
ve
vo
( 垂直光轴截面 )
二. 单轴晶体中的波面 ( 惠更斯作图法(ve>vo) )
1.自然光垂直入射
光轴垂直晶体表面
光轴平行晶体表面
光轴平行入射面
2.自然光斜入射
三. 晶体偏振器
1. 尼科耳棱镜 2. 渥拉斯顿棱镜
(1.5159) no (1.6584) n(1.55) ne
光轴
光轴
(o光振动垂直o 光主平面)
光轴在入射面时,o 光主平面和e 光主平面重合,此时o 光振动和e 光 振动相互垂直。一般情况下,两个主平面夹角很小,故可认为o 光振 动和e 光振动仍然相互垂直。
5. 正晶体、负晶体 o 光:
no c ( o 光折射率) vo
v o t
·
· o光
o 光的 主平面
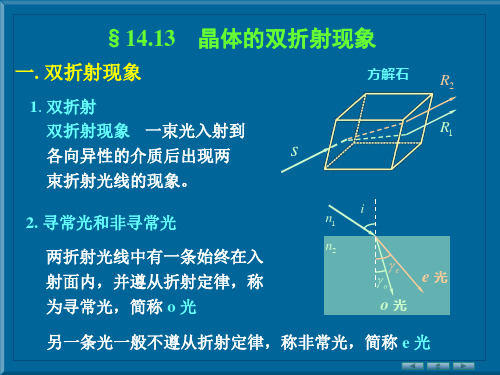
§14.13 晶体的双折射现象
一. 双折射现象
1.双折射
方解石
R2 R1
双折射现象
一束光入射
到各向异性的介质后出现 两束折射光线的现象。
s
2. 寻常光和非寻常光
晶体的双折射现象(精)
方解石
光轴
o光
e光
o光
e光
3. 光轴平行晶体表面,自然光垂直入射
o光
e光
e光
o光
此时,o, e 光传播方向相同,但传播速度不同。从晶体出 射后,二者产生相位差。
三. 晶体偏振器 1. 尼科耳棱镜 2. 渥拉斯顿棱镜
no (1.658) n(1.55) ne (1.486)
光轴
v o t
v e t
( 平行光轴截面 )
( 平行光轴截面 )
ve
vo
( 垂直光轴截面 )
ve
vo
( 垂直光轴截面 )
二. 单轴晶体中的波面 ( 惠更斯作图法(ve>vo) )
1. 光轴平行入射面,自然光斜入射负晶体中 B
光轴
A
光轴
B'
方解石
o光 e光
2. 光轴平行入射面,自然光垂直入射负晶体中
光轴
o光
负晶体 no ne
加拿大树胶
o光 e光
e光 o光
o光 ie,o e光
e光
e
上述两种棱镜得到的偏振光 质量非常好,但棱镜本身价 格很高,因而使用较少。
o
o光
3. 波晶片 (光轴平行于表面且厚度均匀的晶体) 自然光垂直入射波晶片后, o 光, e 光传播速度不同, 产生的相位不同 。 出射 o 光 e 光的相差为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
非常光( 非常光 extraordinary light e光): 光 (1) 是振动面平行于自己的主平面的线偏振光 是振动面平行于自己的主平面的线偏振光; (2) 一般不符合折射定律 在垂直于光轴的方向 一般不符合折射定律,在垂直于光轴的方向 传播时符合折射定律. 传播时符合折射定律 (3) 沿不同的方向折射率不同 传播速度不同 沿不同的方向折射率不同, 传播速度不同. 沿光轴的方向折射率和速度与O光相同 沿光轴的方向折射率和速度与 光相同. 光相同 光和e光的主平面相互平行时 两光的振动面互相垂直. 当o光和 光的主平面相互平行时 两光的振动面互相垂直 光和 光的主平面相互平行时,两光的振动面互相垂直 对于e光 沿垂直于光轴的方向的折射率称为主折射率,记为 记为n 对于 光, 沿垂直于光轴的方向的折射率称为主折射率 记为 e.
o
e
晶体主 截面 O
晶体绕入射光方向旋转时两束光的相对光强不断变化 O’ 入射光 振动面
o e
晶体主 截面 O
晶体绕入射光方向旋转时两束光的相对光强不断变化 O’ 入射光 振动面
o
e
O
晶体主 截面
晶体绕入射光方向旋转时两束光的相对光强不断变化 O’ 入射光 振动面
o
e
O
晶体主 截面
晶体绕入射光方向旋转时两束光的相对光强不断变化 O’ 入射光 振动面
方解石晶体实 物照片 纸面 方解石晶体 CaCO3
折射现 双 折射现 象
1、双折射现象 用眼睛观看发光点, 会看到两个像点,透 过方解石晶体,纸面 上的字成了的双字
O光和e光
自然光进入各向异性晶体中,光线怎样传播?
两束折射光
▲ 服从折射定律寻常光线
ordinary ray— O光 extra —e光
方解石 晶体
纸面 双 折 射
光 光
当方解石晶体旋转时,o 光不动,e 光围绕o 光旋转
方解石 晶体
纸面 双 折 射
光 光
当方解石晶体旋转时,o 光不动,e 光围绕o 光旋转
方解石 晶体
纸面 双 折 射
光 光
当方解石晶体旋转时,o 光不动,e 光围绕o 光旋转
方解石 晶体
纸面 双 折 射
光 光
当方解石晶体旋转时,o 光不动,e 光围绕o 光旋转
方解石 晶体
纸面 双 折 射
光 光
当方解石晶体旋转时,o 光不动,e 光围绕o 光旋转
方解石 晶体
纸面 双 折 射
光 光
当方解石晶体旋转时,o 光不动,e 光围绕o 光旋转
方解石 晶体
纸面 双 折 射
光 光
当方解石晶体旋转时,o 光不动,e 光围绕o 光旋转
方解石 晶体
纸面 双 折 射
光 光
当方解石晶体旋转时,o 光不动,e 光围绕o 光旋转
▲ 不服从折射定律异常光线
不服从折射定律指的是 折射光线一般不在入射面内; 不遵守折射定律,折射率(传播速度)和入射光线在晶体内 的方向有关。 O光、 e光仅在晶体内部有意义
寻常光( 寻常光( ordinary light O光): 光
(1) 是振动面垂直与自己的主平面的线偏振光 是振动面垂直与自己的主平面的线偏振光; (2) 符合折射定律和反射定律 符合折射定律和反射定律; (3) 沿各个方向折射率相同 传播速度相同 沿各个方向折射率相同, 传播速度相同.
光学 光学
光轴
晶体
返回
三、 o光和e光的相对光强 晶体的 主截面 入射光的 振动方向 入射光的 振动面
O’ Ae θ Ao B O A O B θ
B’ 设入射光强为I,振幅为A 1、自然光入射发生双折射 O’ I
Ie = Io =
2
2、线偏振光垂直入射发生双折射
Ao = A sin θ
Ae = A cosθ
▲
在晶体中
Io no tg 2θ = I e ne (α )
o光完全消失 e光强度最大 o光强度最大 e光完全消失
θ = 90
扩大入射光束使两束光相互重叠,由于
e
I o + I e = I (sin 2 θ + cos 2 θ ) = I
o
无论晶体怎样转动, 重叠部分光强度不变
晶体绕入射光方向旋转时两束光的相对光强不断变化 O’ 入射光 e 振动面
o
晶体主 截面 O
o
e
O
晶体主 截面
晶体绕入射光方向旋转时两束光的相对光强不断变化 O’ 入射光 振动面
o
e
O
晶体主 截面
晶体绕入射光方向旋转时两束光的相对光强不断变化 O’ 入射光 振动面
o e
晶体主 截面 O
晶体绕入射光方向旋转时两束光的相对光强不断变化 O’ 入射光 振动面
o
e
晶体主 截面 O
晶体绕入射光方向旋转时两束光的相对光强不断变化 O’ 入射光 振动面
方解石 晶体
纸面 双 折 射
光 光
3、O光和e光偏振态 均是偏振光 振动方向垂直(条件见后)
用检偏器检验O光和e光
问题:(1) e (1) e光在晶体内的传播方向? (2) o光e光的振动方向 ?
二、光轴与主截面 1、光轴(特殊方向) 晶体轴 实验中改变入射光的方向,发现在晶体中存在特殊方向, 光在晶体中沿这个方向传播时不发生双折射,该特殊方向称 为晶体的光轴 注意:在晶体内光轴是一个方向 实验上怎么操作呢?令入射表面垂直光轴,光线沿光轴方向 入射,光线在晶体内部传播不发生双折射。 光轴方向 空气 方解石 不发生双折射
c no = vo
vo:o光在晶体中的传播速度 c e光的主折射率 ne = ve ve:e光在晶体中垂直于光轴 方向的传播速度 e 光在晶体中的传播速度与 ve:与光 传播方向有关,ve取垂直于 轴垂直 光轴的特殊方向 ne>no( ve< vo ):正晶体,如石英 ` ne<no ( ve > vo ) :负晶体,如方解石
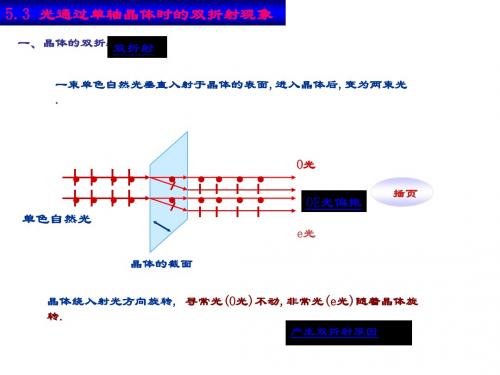
5.3 光通过单轴晶体时的双折射现象 一、晶体的双折射现象 双折射 一束单色自然光垂直入射于晶体的表面, 一束单色自然光垂直入射于晶体的表面,进入晶 体后,变为两束光. 体后,变为两束光.
• • • • • • • •
单色自然光
• •
• • • • • • • •
O光
OE光偏振
插页
e光
晶体的截面
(O光 不动, 晶体绕入射光方向旋转, 寻常光(O 晶体绕入射光方向旋转, 寻常光(O光)不动,非常光 随着晶体旋转. (e光)随着晶体旋转. 产生双折射原因
晶体绕入射光方向旋转时两束光的相对光强不断变化 O’ 入射光 振动面
e
o
晶体主 截面 O
晶体绕入射光方向旋转时两束光的相对光强不断变化 O’ 入射光 振动面
e
o
晶体主 截面 O
晶体绕入射光方向旋转时两束光的相对光强不断变化 O’ 入射光 振动面
o
e
晶体主 截面 O
晶体绕入射光方向旋转时两束光的相对光强不断变化 O’ 入射光 振动面
方解石 晶体
纸面 双 折 射
光 光
当方解石晶体旋转时,o 光不动,e 光围绕o 光旋转
方解石 晶体
纸面 双 折 射
光 光
当方解石晶体旋转时,o 光不动,e 光围绕o 光旋转
方解石 晶体
纸面 双 折 射
光 光
当方解石晶体旋转时,o 光不动,e 光围绕o 光旋转
方解石 晶体
纸面 双 折 射
光 光
当方解石晶体旋转时,o 光不动,e 光围绕o 光旋转
e
o
晶体主 截面 O
小
故
事
偏振光的最普遍的来源之一是从电介媒 质反射这一个无所不在的过程。来自窗玻璃、 纸张或秃头上的反光,电话机面盘上、弹子 球或者书皮封套上的光泽,一般都是部分偏 振的。 这个效应是马吕斯在1808年开始研究的。 巴黎科学院悬赏征求双折射的数学理论,马 吕斯就着手研究这个问题。一天傍晚,他站 在家中的窗户旁边研究方解石晶体。当时夕 阳西照,夕阳的象从离他家不远的卢森堡宫 的窗户上反射到他这里来。
当方解石晶体旋转时,o 光不动,e 光围绕o 光旋转
方解石 晶体
纸面 双 折 射
光 光
当方解石晶体旋转时,o 光不动,e 光围绕o 光旋转
方解石 晶体
纸面 双 折 射
光 光
当方解石晶体旋转时,o 光不动,e 光围绕o 光旋转
方解石 晶体
纸面 双 折 射
光 光
当方解石晶体旋转时,o 光不动,e 光围绕o 光旋转
2、主截面 晶体的主截面:单轴晶体中包含晶体光轴和一条给定光线的 平面 e光主截面: 过e光线和晶体光轴的平面 光轴 O 光的 主截面 o e 方解石 e光的 主截面 o光主截面: 过o光线和晶体光轴的平面 给定一束入射光
一般情况下, o光和e光的主截面不重合,但夹角很小 光轴在入射面内的特殊情况下实验和理论都指出:o光和e 光的主截面和晶体的主截面重合—我们讨论的情况
e o
晶体主 截面 O
晶体绕入射光方向旋转时两束光的相对光强不断变化 O’ 入射光 振动面
e
o
晶体主 截面 O
晶体绕入射光方向旋转时两束光的相对光强不断变化 O’ 入射光 振动面
e
o
晶体主 截面 O
晶体绕入射光方向旋转时两束光的相对光强不断变化 O’ 射光方向旋转时两束光的相对光强不断变化 O’ 入射光 振动面
他拿起了晶体,通过它观察反射来的阳光。使他感到意 外的是当转动方解石时,双象中的一个象消失了。太阳下 山之后,夜里他继续用从水面上和玻璃面上反射回来的烛 光来核实他的观察。 用一支蜡烛和一片玻璃试一试,把玻璃放在θP≈56°时效 应最显著。但在近掠射时, 两个象都很明亮,无论怎样转 动晶体,哪个象都不会消失。 马吕斯显然很幸运,站在对着 宫殿窗户的一个好角度上。
