大学物理_2运动与力
大学物理基础教程答案1-2力-2

r α x = ±h tan θ = ±h tan ωt X ωt dx 2 2 h v= = ±hsec ωt ⋅ ω = ±hω / cos ωt dt π 0 0 2π t= 当α = 60 , ωt = θ = 30 , 60 6 3 2π v = ±5×10 / cos2 300 = ±698(m⋅ s−1 ) 60 2 sin ωt −2 & = ±2hω & a=x |α=600 = ±84.4(m⋅ s ) 3 4 cos ωt
r
r vθ
ωt
r v
r v
o
r
& = rωtan ωt, && = rω2 tan2 ωt + rω2tg2ωt Qr r & θ = ω, && = 0, θ && ∴ar = 2rω tan ωt, a0 = 2rθ = 2rω2 tan ωt
2 2
sinωt a = a + a = 2hω 2 cos ωt 注意: ωr = vθ ≠ v
&& = 2, && = 2 && + && = 2 2 (m/ s2 ) (3) Qx y ∴a = x y dv 16 t − 8 t = 2s aτ = = = 2 (m⋅ s-2 ) dt 2 8 t 2 − 8 t + 4
∴an = a − a = 2 (m/ s )
2 2 τ 2
9
一质点沿一圆周按下述规律运动: 式中s 2-10 一质点沿一圆周按下述规律运动:s=t3+2t2,式中s是沿圆周测 得的路程,以米为单位, 以秒为单位,如果当t=2 t=2秒时质点的加 得的路程,以米为单位,t 以秒为单位,如果当t=2秒时质点的加 求圆的半径。 速度为 16 2 米/秒2,求圆的半径。
大学物理第二章第二部分

变力问题的处理方法(1)力随时间变化:F =f (t )在直角坐标系下,以x方向为例,由牛顿第二定律:()x dv m f t dt=且:t =t 0时,v x =v 0 ;x =x 0则:1()x dv f t dt m =直接积分得:1()()x x v dv f t dt mv t c===+∫∫其中c由初条件确定。
由速度求积分可得到运动学方程:2()x x v dt x t c ==+∫其中c 2由初条件确定。
例:飞机着陆时受到的阻力为F=-ct(c为常数)且t=0时,v=v 0。
求:飞机着陆时的速度。
解:根据牛顿第二定律:-ct =m dv / dt212c v dv tdt mc t c m==−=−+∫∫当t =0时,v =v 0,代入得:v 0=c 1202c v v t m=−(2)力随速度变化:F=f(v)直角坐标系中,x 方向f (v )=m dv ⁄dt 经过移项可得:()dv dt m f v =等式两边同时积分得:01()()m t t dt dv m dv f v f v −===∫∫∫具体给出f(v)的函数试就可进行积分运算例:质量为m的物体以速度v 0投入粘性流体中,受到阻力f=-cv (c为常数)而减速,若物体不受其它力,求:物体的运动速度。
解:根据牛顿第二定律:dv cv m dt−=移项变换:-c/m dt =dv/v 1ln c dv dt m vc t v c m−=−=+∫∫积分得由初条件定c 1:当t =0时,v =v 0∴0=lnv 0+c 1∴c 1=-lnv 00ln c t mc v t m v v v e −−==(3)力随位移变化:F =f (x)直角坐标系中,x方向:()dv dx dv dv f x m m mv dt dt dx dx===经过移项可得:f (x )dx =mv dv等式两边同时积分得:2201()()2f x dx mvdv m v v ==−∫∫例:光滑的桌面上一质量为M,长为L的匀质链条,有极小一段被推出桌子边缘。
大学物理2-1质点系的内力和外力 质心 质心运动定理
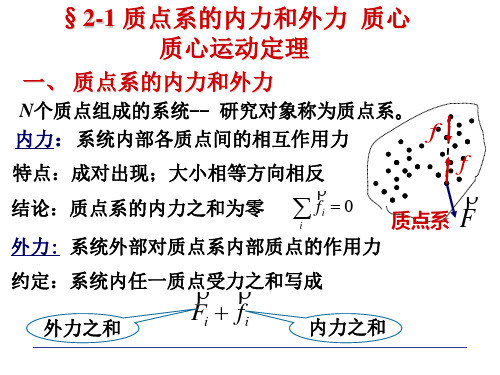
M mi
mN y c mi
rc mi ri / M
xc mi xi / M yc mi yi / M zc mi zi / M
m1
rN
ri
r2 m2 x
rc
r1
O
z
对于质量连续分布的物体
rc
rdm rdm m dm
y c rc dm
由牛顿第二定律得
dv m a m
n n n
d v1 m1a1 m1 F1 f12 f13 f1n dt d v2 m2 a2 m2 F2 f 21 f 23 f 2 n dt
n
dt
Fn f n1 f n 2
f nn 1
对于内力
f12 f 21 0,, f in f ni 0,
mi ai F i Fi Fi ac mi ai M mi ac mi 质心运 动定理 Fi Mac
yc
ydl
m
0
R sin Rd m
2 R 2 R R m
2
2
例
确定半径为R的均质半球的质心位置。
解:建立如图所示坐标 已知薄圆盘的质心位于圆心,取 厚度为dy的薄圆盘为质量微元。
y dy
R
d m dV R y d y
2 2
例题2-1求腰长为a等腰直角三角形均匀薄板的质心位置。 解:建立图示坐标, 在离原点x处取宽度为dx的面积元, 由于面积元的高度为2y,所以其面积为2ydx=2xdx。设 薄板每单位面积的质量为 则此面积元的质量
(自然科学基础物理)运动和力

运动和力是自然科学基础物理中非常重要的概念,它们是描述物体运动状态和相互作用的基础。
下面简单介绍一下这两个概念:
1. 运动:在物理学中,运动是指物体在空间中的位置随时间而变化的过程。
运动可以是直线运动、曲线运动、往复运动等不同形式。
运动的描述需要考虑物体的速度、加速度以及路径等因素。
2. 力:力是导致物体产生运动或形变的原因,是物体之间相互作用的结果。
根据牛顿运动定律,力可以改变物体的运动状态,包括使物体加速、减速或改变方向等。
常见的力包括重力、弹力、摩擦力、张力等。
在描述物体的运动时,物体所受的所有外力之和会影响物体的加速度,即根据牛顿第二定律(F=ma),物体的加速度与作用在物体上的合力成正比,与物体的质量成反比。
力还可以分为接触力和非接触力。
接触力是通过物体之间的直接接触而产生的力,如摩擦力、支持力等;非接触力则是通过距离作用于物体之间,如引力、静电力等。
通过研究运动和力的关系,可以深入理解物体的运动规律和相互作用原理,为解释自然现象、设计工程应用等提供基础。
物理学中的运动
和力是许多其他物理学领域的基础,对于理解自然界的规律和推动科学技术发展具有重要意义。
大学物理2牛顿运动定律

解:分析受力:mg B R ma
v dv tK d v K ( v v ) T 运动方程变为: 0 d t 0 vT v m dt m
d v mg B Kv 加速度 a dt m mg B 极限速度为:vT K
B R
m
mg
vT v K ln t vT m
x
g sin a2 arc tg g cos
例题2-3 一重物m用绳悬起,绳的另一端系在天花板上,
绳长l=0.5m,重物经推动后,在一水平面内作匀速率圆 周运动,转速n=1r/s。这种装置叫做圆锥摆。求这时绳 和竖直方向所成的角度。
2 2Biblioteka 解: T sin m r m l sin T cos mg 角速度: 2n T 拉力:T m 2l 4 2 n 2 ml
1.电磁力
电磁力:存在于静止电荷之间的电性力以及 存在于运动电荷之间的磁性力,本质上相互联系, 总称为电磁力。 分子或原子都是由电荷系统组成,它们之间 的作用力本质上是电磁力。例如:物体间的弹力、 摩擦力,气体的压力、浮力、粘滞阻力。
2.强力
强力:亚微观领域,存在于核子、介子和超 子之间的、把原子内的一些质子和中子紧紧束缚 在一起的一种力。 15 15
F
N 1
i
i
3、矢量性:具体运算时应写成分量式
dv x Fx ma x m dt 直角坐标系中: F ma m dv y y y dt
dvz Fz maz m dt
dv 自然坐标系中: F m dt
F
n
m
v
2
4、惯性的量度: 质量
三. 牛顿第三定律
大学物理第二章牛顿第二定律

二、牛顿第一定律(惯性定律)
任何物体如果没有力作用在它上面,都将保持静止得或作匀速直线 运动得状态。
牛顿第一定律得意义: 1、定义了惯性参考系
2、定性了物体得惯性与力:保持运动状态与改变运动状态
三、牛顿第二定律
定义质点动量:Pm主F 要 d内dPt容:ddt某有mv时关刻系m质: dd点vt F受v得ddm合dtdPt力为Fddm,t则合0力与动F量得m变a化率
Fr FN (mg F sin ) (2、3-4) 将(2、3-3)式 代入(2、3-4)式,得
F cos (mg F sin ) 0
所以 F
mg
sin cos
(2、3-5)
由(2、3-5)式可知:只有当
f ( ) sin cos
为最大时,拉力才为最小,故对函数 f ( ) 求导数,则有
第三定律就是牛顿在惠更斯、雷恩、沃 利 斯弹等性人物研体究得碰碰撞撞得定时律候,得在基力础学上得建体立系得中。, 就是从牛顿定律中推出得,但从定律发现得过 程瞧,牛顿第二、第三运动定律就是从碰撞定 律、动量守恒定律得研究中逐步行成得。
六、几种常见得力与基本得自然力
❖ (一)、几种常见得力
❖ 1、重力 ——由于地球吸引而使物体受到得力叫做重力。 重力得作用使液体有天然形状--球状。
❖ 2、惯性(参考)系 (1)、惯性系定义—— 在研究物体相对运动时,选取得参考系 就是牛顿运动定律适用得参考系,这样得系统称为惯性(参考) 系; (2)、惯性系属性—— 凡就是相对于某一已知得惯性系,作匀 速直线运动得参考系也都就是惯性参考系。
?
匀速直
线运动
S
S
S系
仅凭观测球得上 抛与下落,不能 觉察车相对地面 得运动。
大学物理-第二章-牛顿定律(运动定律)

二 弹性力:(压力、支持力、张力、弹簧弹性力等)
物体在受力形变时,有恢复原状的趋势, 这种抵抗外 力, 力图恢复原状的的力就是弹性力.
在弹性限度内弹性力遵从胡克定律
FP
FT
F FT
FT (l) FT (l)
F kx
al
l
FT (l l) FT (l l)
害处: 消耗大量有用的能量, 使机器运转部分发热等. 减少摩擦的主要方法:
化滑动摩擦为滚动摩擦, 化干摩擦为湿摩擦. 摩擦的必要性:
人行走, 车辆启动与制动, 机器转动(皮带轮), 弦乐器演奏等.
失重状态下悬浮在飞船舱内的宇航员, 因几乎受 不到摩擦力将遇到许多问题. 若他去拧紧螺丝钉, 自 己会向相反的方向旋转, 所以必须先将自己固定才行.
1、关于力的概念
1)力是物体与物体间的相互作用,这种作用可使物体产生形 变,可使物体获得加速度。
2)物体之间的四种基本相互作用;
两种长程作用电引磁力作作用用 两种短程作用弱 强相 相互 互作 作用 用
7
3)力的叠加原理 若一个物体同时受到几个力作用,则合力产生的加速
度,等于这些力单独存在时所产生的加速度之矢量和。 力的叠加原理的成立,不能自动地导致运动的叠加。 牛顿第二定律给出了力、质量、加速度三者间瞬 时的定量关系
17
讨论:胖子和瘦子拔河,两人彼此之间施与的力 是一对作用力和反作用力(绳子质量可略),大小 相等,方向相反,那么他们的输赢与什么有关?
50kg
胜负的关键在于脚下的摩擦力.
18
扩展:
四种基本相互作用
力的种类 相互作用的粒子 力的强度 力程
万有引力 一切质点
大学物理第2章 牛顿运动定律

推论:当你不去追求一个美眉,这个美眉就会待在那里不动。 2、第二定律(F=ma,物体的加速度,与施加在该物体上的外力成正比); 推论:当你强烈地追求一个美眉,这个美眉也会有强烈的反应。 评述:这个显然也是错误的!如果你是一只蛤蟆,那么公主是不会动心的。 你的鲜花送得越勤,电话费花得越多,可能对方越是反感,还可能肥了不费力 气的对手。更可能的情况是,当多个人同时在追求一个美眉时,该美眉反而无 动于衷,心想:机会多着呢,再挑一挑。所以,紧了绷,轻了松,火候要拿捏 得好。
mgR 2 F r2
R2 dv mg 2 m 由牛顿第二定律得: r dt 2 dv dv dr dv gR 又 v dr vdv 2 dt dr dt dr r
当r0 = R 时,v = v0,作定积分,得:
v gR 2 R r 2 dr v0 vdv r
故有
k
例题2-4 不计空气阻力和其他作用力,竖直上抛物体的初速 v0最小应取多大,才不再返回地球?
分析:初始条件,r R 时的速度为 v0 只要求出速率方程 v v ( r ) “不会返回地球”的数学表示式为: 当
r 时, v 0
结论:用牛顿运动定律求出加速度后,问 题变成已知加速度和初始条件求速度方程或运动 方程的第二类运动学问题。 解∶地球半径为R,地面引力 = 重力= mg, 物体距地心 r 处引力为F,则有:
说明
1)定义力
2)力的瞬时作用规律
3)矢量性
4)说明了质量的实质 : 物体惯性大小的量度
5)适用条件:质点、宏观、低速、惯性系
在直角坐标系中,牛顿第二定律的分量式为
d ( mv x ) Fx dt
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
dt
g sin dv dv d v dv dt d dt R d
o R
T v m
mg
v
vdv gR sin d
v0
0
得:1 2
(v 2
v02
)
gR(cos
1)
v( )=[ v02 -2gR(1 - cos ) ]1/2
g
y
N地M
x
Mg
MNaM0m
四、匀速转动非惯性系中的惯性力
设S'系相对惯性系S 匀速转动
物体 S: S'
令 则
m 在 S' 中静止
fafsFsFm0m0 anm2ramo
2
(r )
r^
m
2
r
m
m 2r0 ─ 惯性离心力
m 2r
S ' 中向心力与惯性离心力平衡,m静止
二、非惯性系
S
E
a
a
在 E 参考系, 运动符合牛顿定律,在 S 则不然
非惯性系中的如何研究运动的动力学规律?
任务:
寻求一普遍物理方法, 以使用统一的动力学规律,
引入 惯性力
研究惯性系和非惯性系中 的力学问题。
如何求得?
三、平动非惯性系中惯性力
惯性a系FaFma(a0m a
Sin
巴黎, 49,T 31小时52分
北京, 40,T 37小时15分
这是在地球上验证地球转动的著名的实验。
▲落体偏东; ▲河岸冲刷,双轨磨损(北半球右,南半球左); ▲大气环流,赤道附近的信风(北半球东北,
南半球东南)。
*§2.7 潮汐 (1)为什么潮汐受太阳影响比月亮影响弱一些呢?
v
fc
只有相对转动参考系运动时才出现
*与转动角速度一次方成正比
当角速度较小时,科氏力比离心力更重要
*科氏力方向垂直相对速度
该力不会改变相对速度的大小
*科氏力在地球上的表现
▲ 傅科摆
摆长67m, 摆锤28kg,摆平面转动
顶视 1
摆 Fc
2
2 Fc
傅
地球
科
3 1
摆 摆平面转动周期 T 24小时
S
线运动
S
S系
仅凭观测球的上 抛和下落,不能 觉察车相对地面 的运动。
匀速直
匀速直
S
线运动
S
线运动
S系
匀速直
匀速直
S
线运动
S
线运动
S系
力学相对性原理数学表述:
m m , F F ,
a
a
因此
F
ma
F
ma
对于不同的惯性系,力学的基本规律— 牛顿方程的形式相同。 或者说:牛顿方程具有伽利略变换协变对称 性。
微分方程组 代数方程组
1 f1 f2
m1 m2 N1
f1
F
2
N2
【例】已知:m1,m2 ; 1,2 求:使m2抽出的最小的F
1 f1 f2
m1 m2 N1
f1
F
2
N2
解:设m2尚未抽出,m1,m2 相对静止,
f1为静摩擦力
对m1,m2: F - (m1+m2 )g2 = (m1+m2 )a
对m1:
m1a = f1 <= m1g1 a <= g1
F - (m1+m2 )g2 <= (m1+m2 )g1
使m2抽出的最小的
F= (m1+m2 )(1+2)g
二、微分方程(组)型
一般F为变力 , 除求a外,还求v,r . 需要积分
【例】 轻绳系球m, v=0 = v0 求: v(), T()
M
以地面为参考系对M列方程
N Mm sin Ma0 ①
以M为参考系对m 列方程 (非)
ma0 cos mg sin mamM
ma 0
NMm
m
y x
a0
② mg M
NmM ma0 sin mg cos 0 ③
amM
(M m)sin M msin2
以最简单的情况来直观地说明科里奥利力的起因
质点沿径向以 v匀速运动
地面参考系
m
r^
取平面极坐标 t=0 时位置为极轴
极点在圆心 v
vr^
r^
a
r
2^r
2v^
o
极轴
例. 水桶以 旋转,水对桶静止 。求水面形状?
z
ω
N
解:任选水面一小质元,在切线
z rθ· θ m
第一定律: 定义了“惯性系”(inertial frame) 定性给出了“力”与“惯性”的概念
惯性系: 牛顿第一定律成立的参考系。 力:改变物体运动状态的原因(并非维持物 体运动状态的原因)。
二、牛顿第二定律
运动的改变(指动量变化)和引起运动所施加的
运动力(指外力)成正比,且发生在所施加的运动力
的方向上
2mv^
转动参考系
质点相对转动参考系匀速运动
F
m
2rr^
2mv^
0
^ v
o
极轴
离心力
与物体速度有 关的科氏力
指向物体运动的右方 一般,用矢量表示 fc
2mv
v
fc
fi
m 2rr^
fc
2mv
科里奥利力的特征
*与相对速度成正比
z0
方向静止,
mg sin mr 2 cos 0
mg O
r tan r 2 为z(r)曲线的斜率
g
mr2
由导数关系知 dz r 2
dr g
mg
积分
z dz r dr r 2
g
z
z0
r
2 2
2g
z0
0
由牛顿第二定律
F
m 2r^r
向对方
F12 F21
作用的 相互性
自学: SI单位和量纲
自学: Δ§2.2 常见的几种力 Δ§2.3 基本的自然力
力的基本类型: 四种
◆万有引力定律:
fG
G
m1m2 r2
引力 质量
r m2
定律对两个质点得出。
m1
由叠加可证: 可用于
球与质点; 两球之间。
r M
m
M1
M2
r
◆实验:地面上同一地点一切自由落体 加速度相同。
(2)为什么潮汐同时在向月和背月侧发生?
自由降落“大升降机”中的引潮力:
引力 不均匀 D
惯性力 均匀
A
C
B
D 引潮力
A
C
B
E
E
加速度
引力和惯性力
引潮力=引力+惯性力
引潮力是被惯性力抵消后的“残余的力”。
地球自转引起的惯性离心力顾及在海水视重中,
只考虑在引力场中地球的平动。
忽略海水相对地球的流动引起的效应。
惯性力: 非惯性系中的附加力 作用:使非惯性系中可用牛顿第二定律。
其大小∝惯性质量 (因而所产生的加速度与质量无关)
性质:既虚拟又真实。 “虚拟”(牛顿力学观点): 无相互性。 “真实” : 同真实力一样产生加速度。
二战中的小故事:
美Tinosa号潜艇携带16枚鱼雷,在太平洋离 敌舰4000码斜向攻击,发射4枚,使敌舰停航。
第二章 运动与力
§2.1 牛顿运动定律 Δ§2.2 常见的几种力 Δ§2.3 基本的自然力
§2.4 牛顿定律应用举例 §2.5 非惯性系与惯性力 §2.6 科里奥利力 *§2.7 潮汐
Isaac Newton(1642-1727)
§2.1 牛顿运动定律
一、牛顿第一定律——惯性定律
任何物体都保持其静止或沿一条直线做匀速运动状 态,除非有力加于其上迫使它改变这种状态。
有关惯性离心力的几个问题:
▲ 失重:在绕地球旋转的飞船中观察,引力被 惯性离心力完全抵消,出现失重 飞船中是真正能验证惯性定律的地方
▲ 重力和纬度的关系: 思考 ● 重力是物体所受的
地球的引力吗?
● 重力加速度 g 和地球
纬度 的关系式为:
ω
· r m
F引 PF0O来自P Rg
g0 (1
4、地面系(实验室系):坐标轴固定在地面 上—赤道处自转向心加速度~3.410-2m/s2
对于描述力学规律来说,所有的惯性参考系都 是等效的。 或者说:相对某惯性系作匀速直线运动的参考 系,其内部发生的力学过程,不受系统整体的 匀速直线运动的影响。
—力学相对性原理,
或伽利略相对性原理。
?
匀速直
§2.5非惯性系和惯性力 一、惯性系与伽利略相对性原理
总能找到特殊的物体群(参考系),在这个 参考系中牛顿第一定律成立。这个参考系称为 惯性系。
牛顿第一、二定律只在惯性系中成立。 在非惯性系中通过引入“惯性力”,牛顿第
一、二定律才形式上成立。
实用的惯性系:
1、FK4系:以1535颗恒星平均静止位形作为 基准—目前最好。 2、太阳系:太阳中心为原点,坐标轴指向恒 星—绕银河中心的向心加速度~1.810-10m/s2 3、地心系:地心为原点,坐标轴指向恒星— 绕太阳的向心加速度~610-3m/s2(g的10-3)
