泊松 (Poisson, Simeon-Denis)
第3讲 第三章泊松过程(1)

g N (u ) E e
iuN t
e
t eiu 1
二. 时间间隔的分布与到达时间(等待时间) N(t) T4 一个样本:跃度 T3 为1 的阶梯函数 T2 T1 W1 W2 W3 W4 … t
Wn为第n个事件到达的时间(等待时间). Tn为第n个事件与第n-1个事件出现的时间间隔.
§3.2 泊松过程的性质 一.有限维分布、特征函数、布数字特征 N(t)的有限维分布:
对任意 0<t1 t2 , tn ,
N(t)的有限维分布为:
P X t1 k1 , X t2 k2 , , X t n k n
P X t1 k1 , X t2 X t1 k2 k1 ,, X t n X t n 1 k n k n 1
t1
k1 !
k1
e
t1
k
i i 2
n
t
ti 1
k1 ki 1
1
ki 1 !
e (ti ti 1 )
N(t)的特征函数: N (t ) ~ t
g N (u ) E e
iuN t
e
t eiu 1
0
s
t
显然,计数过程应满足: (1) N( 0)=0; (2) N( t ) 取非负整数值;
(3) 如果s < t,则N( s )≤N( t );
(4) 对于s < t, N(t) -N(s)表示时间间隔(s, t]内事 件出现的次数.
定义3.2 若计数过程{N(t),t≥0}满足下述条件: (1) N(0)=0;
泊松 (Poisson, Simeon-Denis)

泊松(Poisson, Simeon-Denis)(1781—1840)“泊松是第一个沿着复平面上的路径实行积分的人.”──克兰“我建立了描述随机现象的一种概率分布.”──泊松法国数学家.1781 年6月21日生于法国卢瓦雷省的皮蒂维耶,1840年4月25日卒于法国索镇.泊松是法国数学家、物理学家和力学家.1781年6月21日生于皮蒂维耶;1840年4月25日卒于巴黎附近的索镇.1798年入巴黎综合工科学校深造.在毕业时,因优秀的研究论文而被指定为讲师.受到P.-S.拉普拉斯、J.-L.拉格朗日的赏识.1800年毕业后留校任教,1802年任副教授,1806年接替J.-B.-J.傅里叶任该校教授.1808年任法国经度局天文学家,1809年任巴黎理学院力学教授.1812年当选为巴黎科学院院士.泊松的父亲是退役军人,退役后在村里作小职员,法国革命爆发时任村长.泊松最初奉父命学医,但他对医学并无兴趣,不久便转向数学.于1798年进入巴黎综合工科学校,成为拉格朗日、拉普拉斯的得意门生.在毕业时由于其学业优异,又得到拉普拉斯的大力推荐,故留校任辅导教师,1802年任巴黎理学院教授.1812年当选为法国科学院院士.1816年应聘为索邦大学教授.1826年被选为彼得堡科学院名誉院士.1837年被封为男爵.著名数学家阿贝尔说:“泊松知道怎样做到举止非常高贵.”泊松是法国第一流的分析学家.年仅18岁就发表了一篇关于有限差分的论文,受到了勒让德的好评.他一生成果累累,发表论文300多篇,对数学和物理学都作出了杰出贡献.泊松一生从事数学研究和教学,他的主要工作是将数学应用于力学和物理学中.他第一个用冲量分量形式写分析力学,使用后称为泊松括号的运算符号;他所著《力学教程》在很长时期内被作为标准教科书.在天体力学方面,他推广了拉格朗日和拉普拉斯有关行星轨道稳定性的研究,还计算出球体和椭球体之间的引力.他用行星内部质量分布表示重力的公式对20世纪通过人造卫星轨道确定地球形状的计算仍有实用价值.他独立地获得轴对称重刚体定点转动微分方程的积分,即通常称为拉格朗日(工作在泊松前,发表在后)的可积情况.他在1831年发表的《弹性固体和流体的平衡和运动一般方程研究报告》一文中第一个完整地给出说明粘性流体的物理性质的方程,即本构关系.在这以前,I.牛顿在《自然哲学的数学原理》(1687)一书中曾对此给出简单的说明,A.-L.柯西 1823年写出用分量形式表达的本构关系,但缺静压力项.泊松在数学方面贡献很多.最突出的是1837年在《关于判断的概率之研究》一文中提出描述随机现象的一种常用分布,在概率论中现称泊松分布.这一分布在公用事业、放射性现象等许多方面都有应用.他还研究过定积分、傅里叶级数、数学物理方程等.除泊松分布外,还有许多数学名词是以他名字命名的,如泊松积分、泊松求和公式、泊松方程、泊松定理,等等.在数学物理方面:泊松解决了许多热传导方面的问题,他使用了按三角级数、勒让德多项式、拉普拉斯曲面调和函数的展开式,关于热传导的许多成果都包含在其专著《热的数学理论》之中.他解决了许多静电学和静磁学的问题;奠定了偏向理论的基础;研究了膛外弹道学和水力学的问题;提出了弹性理论方程的一般积分法,引入了泊松常数.他还用变分法解决过弹性理论的问题.在数学方面:美国数学史家克兰(Kline)指出:“泊松是第一个沿着复平面上的路径实行积分的人.”在他1817年的出版物中对序列收敛的条件就有了正确的概念,现在一般把这个条件归功于柯西.泊松对发散级数作了深入的探讨,并奠定了“发散级数求积”的理论基础,引进了一种今天看来就是可和性的概念.把任意函数表为三角级数和球函数时,他广泛地使用了发散级数,用发散级数解出过微分方程,并导出了用发散级数作计算怎样会导致错误的例子.他还把许多含有参数的积分化为含参数的幂级数.他关于定积分的一系列论文以及在傅里叶级方面取得的成果,为后来的狄利克雷和黎曼的研究铺平了道路.泊松也是19世纪概率统计领域里的卓越人物.他改进了概率论的运用方法,特别是用于统计方面的方法,建立了描述随机现象的一种概率分布──泊松分布.他推广了“大数定律”,并导出了在概率论与数理方程中有重要应用的泊松积分.他是从法庭审判问题出发研究概率论的,1837年出版了他的专著《关于刑事案件和民事案件审判概率的研究》.泊松就三个变数的二次型建立起特征值理论;并给出新颖的消元法;研究过曲面的曲率问题和积分方程.泊松一生对摆的研究极感兴趣,他的科学生涯就是从研究微分方程及其在摆的运动和声学理论中的应用开始的.直到晚年,他仍用大部分时间和精力从事摆的研究.他为什么对摆如此着迷?有一个传说,泊松小时候由于身体孱弱,他的母亲曾把他托给一个保姆照料,保姆一离开他时,就把泊松放在一个摇篮式的布袋里,并将布袋挂在棚顶的钉子上,吊着他摆来摆去.这个保姆认为,这样不但可以使孩子身上不被弄脏,而且还有益于孩子的健康.泊松后来风趣地说:吊着我摆来摆去不但是我孩提时的体育锻炼,并且使我在孩提时就熟悉了摆. 在数学中以他的姓名命名的有:泊松定理、泊松公式、泊松方程、泊松分布、泊松过程、泊松积分、泊松级数、泊松变换、泊松代数、泊松比、泊松流、泊松核、泊松括号、泊松稳定性、泊松积分表示、泊松求和法……等.泊松的主要著作还有《毛细管作用新理论》和《热学的数学理论》等.。
泊松分布的概念及表和查表方法
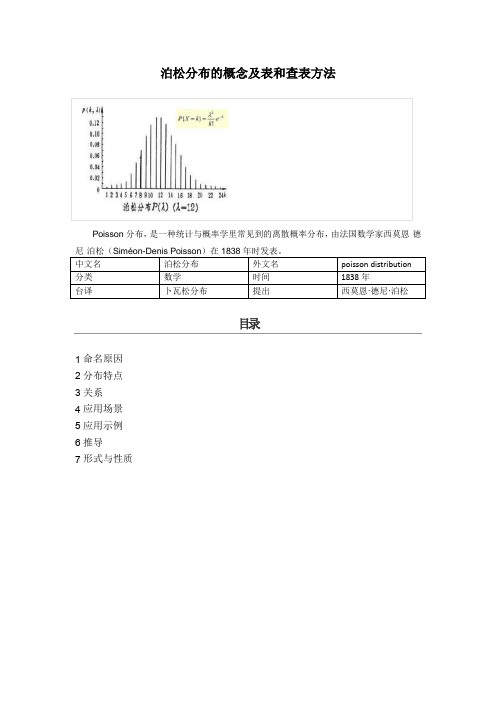
泊松分布的概念及表和查表方法目录1命名原因2分布特点3关系4应用场景5应用示例6推导7形式与性质命名原因泊松分布实例泊松分布(Poisson distribution),台译卜瓦松分布(法语:loi de Poisson,英语:Poisson distribution,译名有泊松分布、普阿松分布、卜瓦松分布、布瓦松分布、布阿松分布、波以松分布、卜氏分配等),是一种统计与概率学里常见到的离散机率分布(discrete probability distribution)。
泊松分布是以18~19 世纪的法国数学家西莫恩·德尼·泊松(Siméon-Denis Poisson)命名的,他在1838年时发表。
这个分布在更早些时候由贝努里家族的一个人描述过。
分布特点泊松分布的概率函数为:泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。
泊松分布适合于描述单位时间内随机事件发生的次数。
泊松分布的期望和方差均为特征函数为关系泊松分布与二项分布泊松分布当二项分布的n很大而p很小时,泊松分布可作为二项分布的近似,其中λ为np。
通常当n≧20,p≦0.05时,就可以用泊松公式近似得计算。
事实上,泊松分布正是由二项分布推导而来的,具体推导过程参见本词条相关部分。
应用场景在实际事例中,当一个随机事件,例如某电话交换台收到的呼叫、来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等,以固定的平均瞬时速率λ(或称密度)随机且独立地出现时,那么这个事件在单位时间(面积或体积)内出现的次数或个数就近似地服从泊松分布P(λ)。
因此,泊松分布在管理科学、运筹学以及自然科学的某些问题中都占有重要的地位(在早期学界认为人类行为是服从泊松分布,2005年在nature上发表的文章揭示了人类行为具有高度非均匀性)。
应用示例泊松分布适合于描述单位时间(或空间)内随机事件发生的次数。
泊松怎么读

泊松怎么读
泊松读bósōng。
泊松(Simeon-Denis Poisson 1781~1840)法国数学家、几何学家和物理学家。
泊松的科学生涯开始于研究微分方程及其在摆的运动和声学理论中的应用。
他工作的特色是应用数学方法研究各类物理问题,并由此得到数学上的发现。
他对积分理论、行星运动理论、热物理、弹性理论、电磁理论、位势理论和概率论都有重要贡献。
科学贡献
菲涅尔提出光的衍射有衍射但因为波长小所以不明显并做出了说明,泊松指出,根据菲涅耳的理论,应当能看到一种非常奇怪的现象:如果在光束的传播路径上,放置一块不透明的圆板。
由于光在圆板边缘的衍射,在离圆板一定距离的地方,圆板阴影的中央应当出现一个亮斑,在当时来说,这简直是不可思议的,所以泊松宣称,他已驳倒了波动理论。
菲涅耳和阿拉果接受了这个挑战,立即用实验检验了这个理论预言,非常精彩地证实了这个理论的结论,影子中心的确出现了一个亮斑。
后人戏剧性地称这个亮点为泊松亮斑。
材料力学中的名人

照相法、数字散斑面内相关法(DSCM)等。
罗伯特·胡克Robert Hooke
英国物理学家、天文学家。1635年7月18
日生于威特岛的弗雷施瓦特。1662年起
直到逝世一直担任皇家学会实验管理员。
1663年胡克获得了牛津大学文学学士学
位,并被选为皇家学会会员。1665年胡
理问题,并由此得到数学上的发现。他对
积分理论、行星运动理论、热物理、弹性
理论、电磁理论、位势理论和概率论都有
重要贡献。
材料力学方面的贡献
泊松比(Poisson ratio):材料在单向受拉或受
压时,横向正应变与轴向正应变的绝对值的
比值。
• 泊松比µ作为基本的弹性常数,可以由体积
模量K和剪切模量G的比值来确定,满足如下
细胞。用自己制造的显微镜观察植物组织,
于1665年发现了植物细胞(实际上看到的是
细胞壁),并命名为“cell”,至今仍被使用。
光学贡献
在光学方面,胡克是光的波动说的支持
者。1655年,胡克提出了光的波动说,他认
为光的传播与水波的传播相似。1672年胡克
进一步提出了光波是横波的概念。在光学研
究中,胡克更主要的工作是进行了大量的光
导出弹性体的运动方程,发现在弹性介质中可
以传播纵波和横波,并且从理论上推演出各向
同性弹性杆在受到纵向拉伸时,横向收缩应
变与纵向伸长应变之比是一常数,其值为四
分之一。
常用材料弹性模量&泊松比
泊松比的测试方法
1.1 机械方法
运用机械方法测定材料泊松比一般属于接触式测量。
弹性泊松比的测试已经标准化。ASTM规定采用两对引
泊松过程的定义

泊松过程的定义泊松过程(Poisson Process)是一种随机过程,它表示了在固定时间段内发生的不同类型事件的概率分布。
泊松过程由泊松分布发展而来,它是一种概率分布,其中包含一个无限的平均特征。
泊松过程是一种重要的概率过程,在许多领域都有应用,例如通讯、生物学、信号处理等等。
泊松过程的定义是描述一个不断发生的随机事件的概率分布,即它是一种持续的随机过程,表示在给定的时间段内,某种类型的事件在某个时间段内会发生多少次。
这种过程的性质是:在一个给定的时间段内,随机事件的发生次数是一个服从泊松分布的随机变量。
泊松过程的定义一般可以描述为:设定一个时间段Δt,若在Δt内某种类型的事件发生m次,则该事件的发生概率满足泊松分布:P(m) = (λΔt)^me-λΔt/ m!,其中λ 是发生次数的平均数,Δt 是时间段,m 是发生次数。
泊松过程的定义还包括“独立性”的要求,即在一定的时间段内,发生的每一次事件都是相互独立的。
此外,泊松过程还有一个重要的性质——“不确定性”,即在一定时间段内,发生的每一次事件是不确定的,也就是说,我们不能准确预测每次发生的次数。
泊松过程是一种重要的概率过程,在一定的时间段内,对某种事件的发生次数的预测,可以使用泊松分布来实现。
泊松过程的应用可以追溯到19世纪,由法国数学家和物理学家泊松(Simeon Denis Poisson)发现,并且受到广泛的应用。
泊松过程的定义和性质是概率论中的重要概念,它主要用于描述在一定的时间段内,某种类型的事件发生的概率分布。
它可以用来描述不同类型事件发生的概率,从而可以模拟不同类型事件的发生情况。
同时,它可以用来研究一定时间段内,某种类型事件发生的概率,从而帮助我们更好地预测未来事件的发生情况。
泊松方程推导
泊松方程推导泊松方程(Poisson's Equation)是数学中的一种偏微分方程,描述了标量场在无源情况下的分布。
它在物理学、工程学和其他领域中有着广泛的应用,尤其在电场和重力场的研究中起着重要的作用。
泊松方程是由法国数学家西蒙·泊松(Siméon Denis Poisson)于19世纪初提出的,它描述了一个标量函数在空间中的分布情况。
泊松方程可以用来解决各种物理问题,如电场分布、热传导等。
它的一般形式可以表示为:∇²φ = -ρ/ε₀其中,φ是待求的标量场,ρ是源项,ε₀是真空介电常数。
这个方程描述了标量场的拉普拉斯算子(Laplacian)与源项之间的关系。
泊松方程的解可以通过数值计算或解析解得到。
在一些简单的情况下,可以通过分离变量法、格林函数法等方法求解。
然而,在实际问题中,往往需要借助计算机进行数值求解。
泊松方程的数值求解方法包括有限差分法、有限元法等。
其中,有限差分法是一种常用的数值求解方法。
它将空间离散化为网格,并通过近似计算网格点上的函数值和导数值。
有限差分法的核心思想是将微分方程转化为代数方程,通过求解代数方程组得到解。
在有限差分法中,泊松方程的离散形式可以表示为:φᵢ₊₁ⱼ + φᵢ₋₁ⱼ + φᵢⱼ₊₁ + φᵢⱼ₋₁ - 4φᵢⱼ = -ρᵢⱼ/ε₀其中,i和j分别表示网格点的索引,φᵢⱼ表示网格点上的函数值,ρᵢⱼ表示源项的值。
通过求解代数方程组,可以得到网格点上的函数值,从而得到整个空间中的标量场分布。
泊松方程的求解涉及到边界条件的选择。
边界条件是指在边界上给定的条件,用于确定解的唯一性。
常见的边界条件有:第一类边界条件(Dirichlet边界条件)和第二类边界条件(Neumann边界条件)。
第一类边界条件是指在边界上给定函数值,第二类边界条件是指在边界上给定导数值。
根据具体问题的要求和边界条件的给定,可以选择合适的边界条件进行求解。
泊松亮斑和牛顿环展板
常奇怪的现象:当在光束的传播路径上放置一块不透明的圆板,
由于光在圆板边缘的衍射,在离圆板一定距离的光屏上,圆板阴
影的中央应当出现一个亮斑,在当时来说,是不可思议的,所以
泊松宣称,他已驳倒了波动理论。对此,彩地证实了这个结论,后人也
Simeon-Denis Poisson (1781~1840)
戏剧性地称这个亮点为泊松亮斑。
法国数学家、物理学家
牛顿环
英国物理学家托马斯·杨和法国物理学家菲涅尔于1801 年提出干涉理论,并利用干涉观念成功解释了牛顿环。
用一个曲率半径很大的凸透 镜的凸面和一平面玻璃接触,在
白光照射下的牛顿环
日光下或用白光照射时,可以看到接触点为一暗点,其周
围为一些明暗相间的彩色圆环;而用单色光照射时,则表
泊松亮斑
Augustin - Jean Fresnel (1788~1827) 法国物理学家
1818年,在法国物理学家阿拉果与安 培的鼓励和支持下,菲涅尔向科学院提交应 征论文,指出光是具有衍射特性的横波,而 由于波长过小所以衍射现象不明显。但是菲 涅尔的波动理论遭到了粒子论者的反对。
泊松亮斑
泊松通过计算指出,根据菲涅耳的理论,应当能看到一种非
现为一些明暗相间的单色圆圈。这些圆圈的距离不等,随
离中心点的距离的增加而逐渐变窄。本质是由球面上和平
光在牛顿环装置中的传播路径 面 上 反 射 的 光 线 相 互 干 涉 而 形 成 的 干 涉 条 纹 。
虽然牛顿在1675年首先观察到这一现象,并做了精确的定量测定,可以说已经 走到了光的波动说的边缘,但由于过分偏爱微粒说,始终无法正确解释这个现象。 直到19世纪初,英国科学家托马斯·杨才用光的波动说圆满地解释了牛顿环实验。开 启了光的波动说的。
泊松过程
泊松过程
泊松过程是由法国著名数学家泊松(Poisson, Simeon-Denis)(1781—1840)证明的。
1943年C.帕尔姆在电话业务问题的研究中运用了这一过程,后来辛钦于50年代在服务系统的研究中又进一步发展了它。
它是一种累计随机事件发生次数的最基本的独立增量过程。
例如随着时间增长累计某电话交换台收到的呼唤次数的过程。
一般地来说,一个泊松过程是在每个有界的时间区间或在某个空间(例如:一个欧几里得平面或三维的欧几里得空间)中的每一个有界的区域,赋予一个随机的事件数,使得在一个时间区间或空间区域内的事件数,和另一个互斥(不重叠)的时间区间或空间区域内的事件数,这两个随机变数是独立的。
在每一个时间区间或空间区域内的事件数是一个随机变数,遵循泊松分布。
(技术上而言,更精确地来说,每一个具有有限测度的集合,都被赋予一个泊松分布的随机变数。
)泊松过程是莱维过程(Lévy pro cess)中最有名的过程之一。
时间齐次的泊松过程也是时间齐次的连续时间Markov过程的例子。
一个时间齐次、一维的泊松过程是一个纯出生过程,是一个出生——死亡过程的最简单例子。
对泊松过程,通常可取它的每个样本函数都是跃度为1的左(或右)连续阶梯函数。
可以证明,样本函数具有这一性质的、随机连续的独立增量过程必是泊松过程,因而泊松过程是描写随机事件累计发生次数的基本数学模型之一。
直观上,只要随机事件在不相交时间区间是独立发生的,而且在充分小的区间上最多只发生一次,它们的累
计次数就是一个泊松过程。
poisson分布定义
poisson分布定义
泊松分布,由法国数学家和物理学家Simeon-Denis Poisson在19世纪发现的一种特殊的概率分布,它主要用于描述在一个确定时间或空间内发生某些类型的事件的次数。
其定义是:当每个单位时间内的事件发生概率相同时,事件的出现频率,也就是单位时间内事件出现的次数,是一个泊松分布。
泊松分布具有很多特点,比如概率分布的中心参数、事件出现的平均概率等。
此外,泊松分布也可以定义为:一个随机变量X的概率分布函数,其概率密度函数为f(x)=λexp(-λx),其中,λ是一个常数,表示每个单位时间内的事件发生概率,也就
是单位时间内事件出现的次数。
在该分布下,我们可以利用泊松函数
P(x)来计算任意一个数值x的概率,其中P(x)是x次试验中事件出
现的概率。
这种概率分布通常用于预测一段时间内事件发生的次数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
泊松(Poisson, Simeon-Denis)
(1781—1840)
“泊松是第一个沿着复平面上的路径实行积分的人.”──克兰“我建立了描述随机现象的一种概率分布.”──泊松
法国数学家.1781 年6月21日生于法国卢瓦雷省的皮蒂维耶,1840年4月25日卒于法国索镇.泊松是法国数学家、物理学家和力学家.1781年6月21日生于皮蒂维耶;1840年4月25日卒于巴黎附近的索镇.
1798年入巴黎综合工科学校深造.在毕业时,因优秀的研究论文而被指定为讲师.受到P.-S.拉普拉斯、J.-L.拉格朗日的赏识.1800年毕业后留校任教,1802年任副教授,1806年接替J.-B.-J.傅里叶任该校教授.1808年任法国经度局天文学家,1809年任巴黎理学院力学教授.1812年当选为巴黎科学院院士.
泊松的父亲是退役军人,退役后在村里作小职员,法国革命爆发时任村长.泊松最初奉父命学医,但他对医学并无兴趣,不久便转向数学.于1798年进入巴黎综合工科学校,成为拉格朗日、拉普拉斯的得意门生.在毕业时由于其学业优异,又得到拉普拉斯的大力推荐,故留校任辅导教师,1802年任巴黎理学院教授.1812年当选为法国科学院院士.1816年应聘为索邦大学教授.1826年被选为彼得堡科学院名誉院士.1837年被封为男爵.著名数学家阿贝尔说:“泊松知道怎样做到举止非常高贵.”
泊松是法国第一流的分析学家.年仅18岁就发表了一篇关于有限差分的论文,受到了勒让德的好评.他一生成果累累,发表论文300多篇,对数学和物理学都作出了杰出贡献.
泊松一生从事数学研究和教学,他的主要工作是将数学应用于力学和物理学中.他第一个用冲量分量形式写分析力学,使用后称为泊松括号的运算符号;
他所著《力学教程》在很长时期内被作为标准教科书.在天体力学方面,他推广了拉格朗日和拉普拉斯有关行星轨道稳定性的研究,还计算出球体和椭球体之间的引力.他用行星内部质量分布表示重力的公式对20世纪通过人造卫星轨道确定地球形状的计算仍有实用价值.他独立地获得轴对称重刚体定点转动微分方程的积分,即通常称为拉格朗日(工作在泊松前,发表在后)的可积情况.他在1831年发表的《弹性固体和流体的平衡和运动一般方程研究报告》一文中第一个完整地给出说明粘性流体的物理性质的方程,即本构关系.在这以前,I.牛顿在《自然哲学的数学原理》(1687)一书中曾对此给出简单的说明,A.-L.柯西 1823年写出用分量形式表达的本构关系,但缺静压力项.
泊松在数学方面贡献很多.最突出的是1837年在《关于判断的概率之研究》一文中提出描述随机现象的一种常用分布,在概率论中现称泊松分布.这一分布在公用事业、放射性现象等许多方面都有应用.他还研究过定积分、傅里叶级数、数学物理方程等.除泊松分布外,还有许多数学名词是以他名字命名的,如泊松积分、泊松求和公式、泊松方程、泊松定理,等等.
在数学物理方面:泊松解决了许多热传导方面的问题,他使用了按三角级数、勒让德多项式、拉普拉斯曲面调和函数的展开式,关于热传导的许多成果都包含在其专著《热的数学理论》之中.他解决了许多静电学和静磁学的问题;奠定了偏向理论的基础;研究了膛外弹道学和水力学的问题;提出了弹性理论方程的一般积分法,引入了泊松常数.他还用变分法解决过弹性理论的问题.
在数学方面:美国数学史家克兰(Kline)指出:“泊松是第一个沿着复平面上的路径实行积分的人.”在他1817年的出版物中对序列收敛的条件就有了正确的概念,现在一般把这个条件归功于柯西.泊松对发散级数作了深入的探讨,并奠定了“发散级数求积”的理论基础,引进了一种今天看来就是可和性的概念.把任意函数表为三角级数和球函数时,他广泛地使用了发散级数,用发散级数解出过微分方程,并导出了用发散级数作计算怎样会导致错误的例子.他还把许多含有参数的积分化为含参数的幂级数.他关于定积分的一系列论文以及在傅里叶级方面取得的成果,为后来的狄利克雷和黎曼的研究铺平了道路.
泊松也是19世纪概率统计领域里的卓越人物.他改进了概率论的运用方法,特别是用于统计方面的方法,建立了描述随机现象的一种概率分布──泊松分布.他推广了“大数定律”,并导出了在概率论与数理方程中有重要应用的泊松积分.他是从法庭审判问题出发研究概率论的,1837年出版了他的专著《关于刑事案件和民事案件审判概率的研究》.
泊松就三个变数的二次型建立起特征值理论;并给出新颖的消元法;研究过曲面的曲率问题和积分方程.
泊松一生对摆的研究极感兴趣,他的科学生涯就是从研究微分方程及其在摆的运动和声学理论中的应用开始的.直到晚年,他仍用大部分时间和精力从事摆的研究.他为什么对摆如此着迷?有一个传说,泊松小时候由于身体孱弱,他
的母亲曾把他托给一个保姆照料,保姆一离开他时,就把泊松放在一个摇篮式的布袋里,并将布袋挂在棚顶的钉子上,吊着他摆来摆去.这个保姆认为,这样不但可以使孩子身上不被弄脏,而且还有益于孩子的健康.泊松后来风趣地说:吊着我摆来摆去不但是我孩提时的体育锻炼,并且使我在孩提时就熟悉了摆. 在数学中以他的姓名命名的有:泊松定理、泊松公式、泊松方程、泊松分布、泊松过程、泊松积分、泊松级数、泊松变换、泊松代数、泊松比、泊松流、泊松核、泊松括号、泊松稳定性、泊松积分表示、泊松求和法……等.
泊松的主要著作还有《毛细管作用新理论》和《热学的数学理论》等.。
