稳态第五章2
稳态第五章 作业含答案

1、两台发电机容量均为100MW ,耗量特性分别为:211110.20.002G G F P P =++ (t/h )222230.10.002G G F P P =++ (t/h )两台发电机同时供一个负荷L P ,试求:1)当系统负荷L P =65MW 时,120G P MW =,245G P MW =分配负荷是不是最优方案?2)当L P =160MW 时,两发电机间的最优分配方案是多少?解:1)⎪⎪⎩⎪⎪⎨⎧+==+==22221111004.01.0004.02.0G G G G P dP dF P dP dF λλ(1分), 当120G P MW =,245G P MW =代入上式令212128.045*004.01.028.020*004.02.0λλλλ=⇒⎭⎬⎫=+==+=,所以是最优分配。
2)当L P =160MW 时5.92,5.67160004.01.0*004.02.02121211==⇒⎭⎬⎫=++=+=G G G G G G P P P P P P λ2、三个火电厂并列运行,各发电厂的耗量特性F (t/h )及功率约束条件如下:(10分)21114.00.300.00070G G F P P =++ 100MW 1G P≤≤200MW 1T 22223.50.320.00040G G F P P =++ 120MW 2G P≤≤250MW 23333.50.300.00045G G F P P =++ 150MW 3G P ≤≤300MW 当总负荷为700MW 和400MW 时,试分别确定发电厂间功率的经济分配(不计网损影响) 解:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+==+==+==3333222211110009.03.0008.032.00014.03.0G G G G G G P dP dF P dP dF P dP dF λλλ 令321λλλ==⎩⎨⎧+=++=+32210009.03.00008.032.00008.032.00014.03.0G G G G P P P P MW P MW P MW P P P P G G G G G G 274,250,176700321321===⇒=++3、某系统的综合负荷单位调节功率为Hz MW /500,系统负荷增大1000MW 时,调频厂经二次调频增发的500MW ,系统频率变化为0.2Hz ,求系统的发电机的单位调节功率? 答:4、 A 、B 两系统中,A 、B 两系统的容量分别是3000MW 、2000MW ,25*=G A K ,6.1*=LA K ,20*=G B K ,4.1*=LB K ,MW PLA 200=∆时,求 (1) 系统A 、B 的机组都参加一次调频后系统频率的变化值;(2) 若A 、B 两系统的机组都参加一次调频,且B 系统部分机组参加二次调频增发50MW 时,求统频率偏移以及联络线上流动的功率。
第5章稳态作业参考答案

1.张先生是某电网公司的总经理,该公司的线路 阻抗很小,可以忽略不计,且发电机组耗量特性 均为二次曲线。有一天他去视察调度部门,看到 一张有关发电机的输出功率与生产总成本递增变 化规律的报表:
为什么?
第五章作业一
解:
i
Fi P Gi
Fi i P Gi
F F1 F2 F3 Fi
第五章作业三
解:AB 两系统各自的系统单位调节功率为
k A kGA kDA 270 21 291( MW / Hz ) kB kGB kDB 480 39 519( MW / Hz )
(1)两系统均只参与一次调频
PLA Pab PGA K A f 由 P P P K f 得到 ab GB B LB 0 Pab 0 291f f 0.1852Hz Pab 53.89MW 150 Pab 0 519f
P 1 162.58 MW G P 2 284.52 MW G G P 3 252.90 MW
第五章作业二
dF1 PG1 0 d PG1 PG1 170.79MW dF P 3 G3 0 PG 2 250MW d PG 3 PG 3 273.91MW P P 700 250 G1 G 3
第五章作业二
min f PGi F1 PG1 F2 PG 2 F3 PG 3 PG1 PG 2 PG 3 700 100 P 200 G1 s.t. 120 PG 2 250 150 PG 3 300 C F P 1 F P 2 F P 3 P 1 P 2 P 3 700 G G G G G G
第五章对流扩散问题(一维稳态对流扩散问题)
第五章 对流扩散问题———一维稳态对流扩散问题
a P P a E E a W W
中心节点系数
相邻节点系数
aP aE , a W aP aE a W (Fe Fw )
考虑到连续方程
Fe-Fw=0
满足相邻系 数之和准则
a P aE a W
扩散项和以前的处理方法一样,即有:
(u) e e (u) w w e ( E P ) ( x ) e w ( P E ) ( x ) w
而控制容积界面上的变量值取其相应上风侧网格 节点上的值。即:
第五章 对流扩散问题———一维稳态对流扩散问题
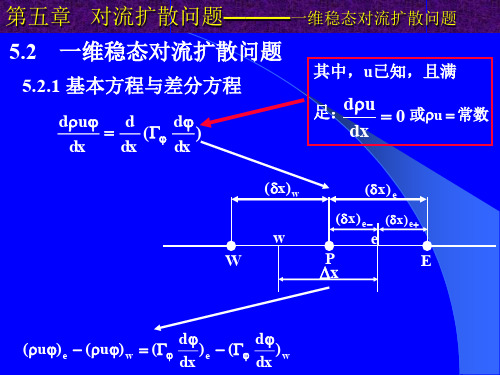
第五章 对流扩散问题———一维稳态对流扩散问题 5.2 一维稳态对流扩散问题
5.2.1 基本方程与差分方程
du d d ( ) dx dx dx
(x)w
其中,u已知,且满
d u 足: 0 或u 常数 dx
( x ) e
( x ) e ( x ) e
w W
e P x
a P P a E E a W W
aE 1 4 1 2 4 aW 1 3 2 a P 1 3 4 4 2
2P E 3W
De Dw 1 Fe Fw 4
E 200, W 100
E 100 W 200
2 P 0.25E 1.75 W
De D w 1 Fe Fw 1.5
E 200, W 100
E 100 W 200
P 187.5
P 112.5
某问题 结果合理
第五章 对流扩散问题———一维稳态对流扩散问题
电力系统稳态分析讲解第五章

( i 1,2, , n)
C PGi
C Fi ( PGi )
i 1 n
dFi ( PGi ) dPGi
( i 1,2, , n)
24
不等式约束的处理
功率上下限约束
PGi min PGi PGi max
先不考虑该约束条件进行经济分配计算,若发现 越限,越限的发电厂按极限分配负荷,其余发 电厂再按经济分配。 节点电压及无功功率约束 Vi min Vi Vi max
F F1 ( PT 1 ( t ))dt
0
这是一个求泛函极值问题,一般应用变分法求解。
27
§5.2电力系统中有功功率的最优分配
5、水、火发电厂间的负荷经济分配
变分法求解,分段处理 等式约束: H 2. k
P
W
k t
PT 1.k PLD.k 0
( PH 2. k )t k K 2 0
弧炉、轧钢机、电力机车等冲击性负荷
调频器 频率的二次调整,由调频发电厂的机组承担
(3)变动周期最大,变化幅度最大:气象、生产、生活规律, 可预测。
根据预测负 荷,按等耗 量微增率准 则在各机组 间进行最优 负荷分配
频率的三次调整,电力系统的经济运行调 度(发电计划)
6
§5.1电力系统中有功功率的平衡
dF1 ( PG 1 ) 0 dPG 1 dF2 ( PG 2 ) 0 dPG 2 PG 1 PG 2 PLD 0
等耗量微增率
1 2
21
物理意义:
dF dF2 假如两台机组微增率不等: 1 ,并且总输出功率不变, dP 1 dP 2 G G 调整负荷分配,机组 减少P,机组2增加P,节约的燃料消耗为: 1
第五章 基于稳态模型的异步电动机调速系统(电力拖动自动控制系统)

2.异步电动机三相原始模型的非独立性
图6-2 二极直流电动机的物理模型 F—励磁绕组 A—电枢绕组 C—补偿绕组
2.异步电动机三相原始模型的非独立性
图6-3 三相坐标系和两相坐标系物理模型
2.异步电动机三相原始模型的非独立性
图6-4 静止两相正交坐标系和旋转正交坐标系的物理模型
2.异步电动机三相原始模型的非独立性
2.计算转子磁链的电压模型
图6-32 磁电动机的仿真
图6-18 按转子磁链定向的异步电动机动态结构图
2.三相异步电动机的仿真
图6-19 异步电动机矢量变换及等效直流电动机模型
2.三相异步电动机的仿真
图6-20 矢量控制系统原理结构图
2.三相异步电动机的仿真
图6-21
简化后的等效直流调速系统
2.三相异步电动机的仿真
图6-22 电流闭环控制后的系统结构图
(2)在mt坐标系上计算转子磁链的电流模型
图6-30 在mt坐标系上计算转子磁链的电流模型
2.计算转子磁链的电压模型
1)用定子电流转矩分量i*和转子磁链ψ*计算转差频率给定信号ω*,
即 2)定子电流励磁分量给定信号i*和转子磁链给定信号ψ*之间的关 系是靠
2.计算转子磁链的电压模型
图6-31 计算转子磁链的电压模型
第五章
第一节
1.系统结构 2.起动过程 3.加载过程 第二节1.磁链方程 2.电压方程 3.转矩方程
4.运动方程
第三节1.异步电动机三相原始模型的非线性强耦合性 2.异步电动机三相原始模型的非独立性
图5-42 按恒值控 制的=f()特性
图5-43 定子电压补偿恒/ 控制的电压-频率特性
1. dq坐标系中的状态方程
稳态分析讲义之高等电力系统稳态分析第五章电力系统复杂故障分析

一、复杂故障计算
严格地讲电力系统的短路故障或其他复杂的故 障都伴随着复杂的电磁和机电暂态过程。在整 个故障期间电力系统各部分的电流和电压是随 时间变化比其中不仅包括幅值随时间变化的工 频周期分量,同时还有随时间衰减的非周期分 员以及其他频率的周期分量。所以,完整的短 路电流及复杂故障计算要求解微分方程和代数 方程组。
当xk1=xk2=1时,利用xk3=-1/2和xk3= 3 / 2 , 构成两个不同的特征向量,就是克拉克 法的变换矩阵。
二、序分量原理
序分量法有如下的结论:
三相对称元件序导纳(阻抗)在所有序分量法 坐标下显然都是相同的,都等于其相导纳 (阻抗)矩阵的特征值。只不过,其称呼将随 序分量称呼的变化而变化。
相分量法能够轻松地处理任意的复杂故障, 程序实现也极其方便。
二、复杂故障计算的方法
不对称网络系统计算
随着电力工业的飞速发展,三相参数不对称 的元件不断出现,电力系统三相参数不对称 的问题越来越突出。由于参数的三相不对称, 元件不能实现在序分量坐标空间解耦,也就 不能形成独立的序网,因而序分量的序网连 接的故障处理方法也就不能继续使用了。
一、系统对称性分析: 轮换矩阵(循环对称矩阵)的特点
由于轮换元件的导纳参数矩阵都是轮换矩阵, 而轮换矩阵之间的四则运算结果仍然是轮换 矩阵,所以与轮换节点相关的自导纳和互导 纳矩阵都是轮换矩阵。
对于任意的轮换矩阵,恒有:
其中
一、系统对称性分析:
三相对称元件
如果各端三相电压之间发生任意交换,各电 压值对应的电流值能够始终不变。则称该元 件具有三相对称性。并称此元件为三相对称 元件。
二、序分量原理
可以求得
由于有重根,其特征向量只有两组,而 重根对应的组有两个自由基:
第五章正弦稳态电路的分析

正弦电流电路
激励和响应均为同频率的正弦量的线性电路 (正弦稳态电路)称为正弦电路或交流电路。
研究正弦电路的意义
1.正弦稳态电路在电力系统和电子技术领域 占有十分重要的地位。
优 ①正弦函数是周期函数,其加、减、求导、 点 积分运算后仍是同频率的正弦函数。
②正弦信号容易产生、传送和使用。
返 回 上 页 下 页
j
F | F | e | F |
j
极坐标式
返 回 上 页 下 页
几种表示法的关系:
Im
F a jb
F | F | e | F |
j
b |F|
F
O
| F | a b b 或 θ arctan( ) a
2 2
a
Re
a | F | cos b | F | sin
O
F Re
返 回
上 页
下 页
特殊旋转因子
jF
Im
F
Re
jF
π jπ π π 2 , e cos( ) jsin( ) j 2 2 2
O
F
π j π π π 2 , e cos( ) jsin( ) j 2 2 2
π , e
w 2π f 2π T (3) 初相位
单位: rad/s ,弧度/秒
反映正弦量的计时起点,常用角度表示。
返 回 上 页 下 页
注意 同一个正弦量,计时起点不同,初相
位不同。
i
=0
一般规定:| |< 。
O
=/2
wt
=-/2
返 回
上 页
05第五章 稳态工况法
5.3.2 简易稳态工况法排放限值
表 5-2 和表 5-3 中规定的最低限值为各地方城市开始实施本检测方法时的最低要求;最高限值为经 过检测与维护制度,该车种应最终达到的限值标准。各地方城市可在最低限值与最高限值之间根据各自 情况调整本地区的限值标准,也可根据车辆年度类型划分不同限值。 对于 2000 年 7 月 1 日以前生产的第一类轻型汽车和 2001 年 10 月 1 日以前生产的第二类轻型汽 车,参考的稳态工况法排放限值见表 5-2。 -6 -6 其中 CO 的单位为%、HC 的单位为 10 、NO 的单位为 10 。
地方点燃式发动机在用汽车简易工况法排放标准,按国家有关法律规定,由省级人民政府批准、发 布。省级人民政府可委托其环境保护行政主管部门制订地方排放标准。在确定当地在用点燃式发动机汽
- 64 -
机动车排气污染物检测培训教材
车简易工况法排放限值时,应遵循以下原则和方法,也可参考采用表 5-2 和表 5-3 中的参考排放限值。 (1)基本原则 ① 遵循“新车新标准,老车老标准”的原则。根据车型在新车进行型式核准时所达到的排放标准水 平,同时考虑车辆在正常使用和维修保养情况下排放控制系统的正常劣化,来确定该车型的在用汽车排 气污染物排放限值。 ② 确定的排放限值应能有效地检测出高排放的车辆。 推荐的城市控制高排放车辆的比例为 10—25%。 ③ 在确定排放限值时,应根据当地实际情况,坚持“初始放松,逐步加严”的原则。 (2)排放限值的确定方法 ① 地方城市环境保护主管部门可根据需要建立在用汽车排放检测中心站,负责确定和调整地方排气 污染物排放限值,同时负责对检测数据的统计分析以及对其它检测站的监督管理等。 ② 在用汽车排放检测中心站应选用通过国家环境保护行政主管部门核准的检测设备和仪器。 ③ 根据国家不同阶段的新生产机动车排放标准,对地方在用车分布情况进行调查,对不同排放水平 类型的在用车进行排放检测,原则上每种排放水平类型车辆的抽测数量应不低于 100 辆,同时应考虑不 同排放水平车型的占有比例。 ④ 对检测数据进行统计分析,根据地方对高排放车辆的监管比例,确定地方在用汽车排放限值。 (3)达标要求 ① 采用简易工况法进行排放检测时,如果检测污染物有一项超过规定的限值,则认为受检车辆排放 不合格。 ② 对于单一气体燃料汽车,仅按燃用气体燃料进行排放检测;对于两用燃料汽车,要求对两种燃料 分别进行排放检测。 ③ 对于排放超高或超低的车辆,检测时允许使用快速通过的检测方式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 电力系统的有功功率和频率调整第二节 电力系统中的有功功率的最优分配(发电计划,解决三次调整)三、最优分配负荷时的目标函数和约束条件z 一个时间断面下的经济功率分配z 耗量特性:发电设备输入与输出的关系。
– 比耗量:耗量特性曲线上某一点纵坐标和横坐标的比值,即单位时间内输入能量与输出功率之比称比耗量μ 。
显然,比耗量实际是原点和耗量特性曲线上某一点连线的斜率, μ =F/P 或μ =W/P。
– 发电效率:当耗量特性纵横坐标单位相同时,比耗量的倒数就是发电设备的效率η 。
– 耗量微增率:耗量特性曲线上某一点切线的斜率称耗量微增率λ 。
耗量微增率是单位时间内输入能量微增量与输出功率微增量的比值,即dP dF P F //=ΔΔ=λ或dP dW P W //=ΔΔ=λ – 对于一台机组,比耗量曲线和耗量微增率曲线的交点是单台发电机效率最高的点。
–若耗量特性曲线为二次曲线F = aP2 + bP + C –则μ=aP+b+c/P, λ=2aP+b。
–若耗量特性曲线为F = aP2 + bP–则μ=aP+b, λ=2aP+b。
–若耗量特性曲线为一次曲线F = bP –则μ=λ=b。
z 目标函数和约束条件 – 问题的提出:负荷最优分配的目的在于:确定电网中每台机组的有功功率输出,在满足负荷需求、系统安全的同时,使单位时间内的能源消耗最少。
– 优化问题的通用模型d u x g 0d u x f d u x C ≤=),,(),,(..),,(t s Min式中C 为目标函数,f 为等式约束,g 为不等式约束– 最优分配负荷时的目标函数和约束条件• 目标函数:∑=Σ=+++=ni Gi i Gn n G G P F P F P F P F F 12211)()()()(" – 其中:表示发电机i 的耗量曲线)(Gi i P F • 等式约束(不计网损)011=Δ−−Σ==∑∑P P P ni Li n i Gi • 不等式约束(发电有功、无功,节点电压幅值)Gimax Gi GiminP P P ≤≤ Gimax Gi GiminQ Q Q ≤≤imax i imin U U U ≤≤• 系统中发电设备消耗的能源可能受限制。
例如,水电厂一昼夜间消耗的水量受约束于水库调度。
出现这种情况时,目标函数就不应再是单位时间内消耗的能源,而应是一段时间内消耗的能源,即应为 ∑∫==Σ=m i i Gi i dt P F F 10)(τ• 而等约束条件除式(5—2)外,还应增加∫=τ0)(定值dt P W Gi j • 这里的F i ,可理解为单位时间内火力发电设备的燃料消耗;为单位时间内水力发电设备的水量消耗;τ为时间段长,例如24h。
而这里设i=1,2,…,m 为火力发电设备,j =(m 十1),(m 十2),…,n 为水力发电设备。
W j 四、最优分配负荷的等耗量微增率准则z 公式推导:¾ 问题的简化• 略去不等式约束• 仅有两台机组¾ 推导:• 目标函数)()(),(221121G G G G P F P F P P C C +==• 约束条件0),(2121=−+=LD G G G G P P P P P f• 拉格朗日函数)()()(),(),(2122112121*LD G G G G G G G G P P P P F P F P P f P P C C −+−+=−=λλ• 原问题变成求拉格朗日函数的最小值,将有约束极值问题转化为无约束极值问题,λ称为拉格朗日乘数。
当然,天下没有白吃的午餐,去掉了一个等式约束,但增加了一个变量λ • 极值条件: ;0;0;0*2*1*=∂∂=∂∂=∂∂λC P C P C G G • 展开: ⎪⎪⎪⎭⎪⎪⎪⎬⎫==∂∂−∂∂=∂∂−∂∂0),(0),(),(0),(),(21221221121121G G G G G G G G G G G G G G P P f P P P f P P P C P P P f P P P C λλ• 解出:⎪⎪⎪⎭⎪⎪⎪⎬⎫==−=−0),(0)(0)(21222111G G G G G G P P f dP P dF dP P dF λλ • 由于 111)(G G dP P dF ,222)(G G dP P dF 分别为发电设备1、2各自承担• 有功功率负荷PG1、PG2时的耗量微增率λ1、 λ2,可以得到: λ1= λ2= λ,这就是等耗量微增率准则,它表示为使总耗量最小,应该按相等的耗量微增率在发电设备或发电厂之间分配负荷。
¾ 物理意义:•对于这个简单问题,可以用作图法求解。
设上图中线段OO’的长度等于负荷功率PLD。
在线段的上、下两方分别以O和O’为原点做出机组1和2的燃料消耗特性曲线1和2,前者的横坐标PG1自左向右,后者的横坐标PG2自右向左。
•显然,在横坐标上任取一点A,都有OA十AO’=OO’,即 PG1 +PG1= PLD 。
因此,横坐标上的每一点都表示一种可行的(满足约束条件的)功率分配方案。
•如过A点作垂线分别交于两机组耗量特性曲线的B1和B2点,则B1B2=B1A+AB1=F1(PG1)+F2(PG2)=C就代表了总的燃料消耗量。
•由此可见,只要在OO’上找到一点,通过它所作垂线与两耗量特性曲线的交点距离为最短,则该点所对应的负荷分配方案就是最优的.•图中的点A’ 就是这样的点,通过A’点所作垂线与两特性曲线的交点为B1’和B2’。
在耗量特性曲线具有凸性的情况下,曲线1在B1’点的切线与曲线2在B2’点的切线相互平行。
耗量曲线在某点的斜率即是该点的耗量微增率。
由此可得结论:负荷在两台机组间分配时,如它们的燃料消耗微增率相等.¾ 公式推广(多发电设备或发电厂):),,,(),,,(2121*Gn G G Gn G G P P P f P P P C C ""λ−=• 推出 ⎪⎪⎭⎪⎪⎬⎫=−==−∑==0),,2,1(0)(1LD n i i Gi GiGi i P Pn i dP P dF "λ • 结论: λ1= λ2= …= λn =λ¾ 对于不等式约束,可以使用kuhn-Tucker 条件解决。
¾ 关于电压和无功的约束,与有功功率负荷分配没有直接关系,省略。
¾ 对于发电设备有功输出功率的约束,当发生越限时。
将发电设备有功输出功率固定在边界上。
z 计算步骤:五、等耗量微增率准则的推广运用z 公式推导:¾ 问题的简化• 略去不等式约束• 仅有一台火力发电单元和一台水力发电单元¾ 推导:• 目标函数∫=Στ011)]([dt t P F F T • 约束条件2022)]([K dt t P W H =∫τ 021=−+LD H T P P P• K2为水力发电设备2在0到τ时间内 规定消耗的水量。
将0到τ时间分成t 个时段: k t k k k T k t P F F Δ=∑==⋅⋅Σ111)(2122)(K t P Wk t k k k H k =Δ∑==⋅⋅ 021=−+⋅⋅⋅k LD k H k T P P P• 建立拉格朗日函数])([][)(21222121111*K t P W t P P P t P F C k t k k k H k k tk k LD k H k T k k t k k k T k −Δ+Δ−+−Δ=∑∑∑==⋅⋅==⋅⋅==⋅⋅γλ• 其中λ1、λ2……λt 和γ2 都是拉格朗日乘数,其中γ2 是由于引入水电厂的约束条件而新增加的。
• 极值条件;0;0;0;02**2*1*=∂∂=∂∂=∂∂=∂∂⋅⋅γλC C P C P C k k H k T• 展开 ⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫=−Δ==−+==−==−∑==⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅0)(),,2,1(0),,2,1(0)(),,2,1(0)(2122212222111K t P W t k P P P t k dP P dW t k dP P dF t k k k k H k LD k H k T k k H k H k k kT k T k """λγλ • 一共(3t+1)个独立方程,变量也是(3t+1)个,可以求解。
• 第一、二式合并,可得 ),,2,1()()(2222111t k dP P dW dP P dF k k H k H k kT k T k "===⋅⋅⋅⋅⋅⋅λγ• 略去下标k,得到 λγ==2222111)()(H H T T dP P dW dP P dF• 式中,111)(T T dP P dF 为火力发电厂的燃料耗量微增率 • 111)(T T dP P dF 为水力发电厂的水耗量微增率 • 上式可改为:λλγλ==221H T• 由上式可见,只要将水力发电的水耗量微增率乘以某一个待定的拉格朗日乘数γ2 ,就可将指导火力发电设备(厂)之间负荷最优分配的等耗量微增率准则推广运用于火力发电设备(厂)与水力发电设备(厂)之间负荷的最优分配。
为此,需确定拉格朗日乘数γ2 。
这乘数为 )()()()(22112221112H T H H T T P dW P dF dP P dW dP P dF ==γ • 式中分子、分母上的dPT1、dPH2之所以可相约,是由于问题仅涉及增减同样大小有功功率时火力或水力发电设备燃料或水耗量增减的多少。
由式可见,如F1的单位为t/h,W2的单位为,则γ2的单位为 h m /33/m t•因此,这个拉格朗日乘数γ2实际上可看作是一个换算系数.•既然γ2可看作换算系数,水力发电设备(厂)在一定时间内可消耗的水量越多,单位重量燃料可折换的水量就愈大, γ2从而γ2λH2也就愈小,按等耗量微增率准则水力发电设备(厂)应分配的负荷也就愈大;反之,水力发电设备(厂)应分配的负荷愈小。
六、网络损耗的修正:网络上不同地点上的发电机在发电时,对网损的影响不同,也就是说这些发电机即使有相同的发电功,它们对负荷的贡献也是不一样的。
例如:率假设G1、G2煤耗曲线相同,P1>P2,如果不考虑网损修正,果考虑网损,则(P1+P2)/2<G1<P1、P2<G2<(P1+P2)/2其实,在电力市场中电力交易软件也要对各机组的报价进行网损折算,原理一样。
则G1=G2=(P1+P2)/2最好,但是如时最为节省。
