传热学-第二章-稳态热传导
传热学(第二章)
(2-32)
热阻
R=
1 1 1 ( 4πλ r r2 1
(2-33)
由球坐标系一般形式的导热微分方程
1 T 1 T 1 T T (λr2 + 2 2 (λ ) + 2 (λ sin θ ) + Φ = ρcp r2 r r) r sin θ r sin θ θ θ τ
2 1
λ1
第二章
导热基本定律及稳态导热
2-3 通过平壁,圆筒壁,球壳和其他变截面物体的导热 通过平壁,圆筒壁,
1 T 1 T T T (λr + 2 (λ ) + (λ ) + Φ = ρcp τ r r r) r z z d dt 简化变为 dr (r dr ) = 0 (2-25)
⒉ 通过圆筒壁的导热 由导热微分方程式(2—12)
⒉ 通过圆筒壁的导热 根据热阻的定义,通过整个圆筒壁的导热热阻为 (2-29) 29) 与分析多层平壁—样,运用串联热阻叠加的原则,可得通过图2-9所示的多层圆筒壁的 导热热流量 2πl(t1 t4 ) Φ= (2-30) ln( d2 / d1) / λ1 + ln( d3 / d2 ) / λ2 + ln( d4 / d3) / λ3 ⒊ 通过球壳的导热 导热系数为常数,无内热源的空心球壁.内,外半径为r1,r2,其内外表面均匀 恒定温度为t1,t2,球壁内的温度仅沿半径变化,等温面是同心球面. 由傅立叶定律得: dt 各同心球面上的热流率q不相等,而热流量Φ相等. Φ = 4πr2λ dr dr Φ 2 = 4πλdt r
的热传导微分方程:
T(r,τ ) τ ρc 当 λ = const 时, 2T(r,τ ) + Φ = p T(r,τ ) λ λ τ [λT(r,τ )] + g(r,τ ) = ρcp
工程热力学与传热学第二章稳态热传导基本概念

2. 常温边界
系统边界温度恒定,即 (T = T_b)
3. 周期性边界
系统边界温度呈周期性变化, 即 (T(x, y, z, t) = T(x + L, y,
z, t))
求解方法
有限差分法
将导热微分方程转化为差 分方程,通过迭代求解温 度分布。
有限元法
将导热微分方程转化为变 分形式,利用有限元离散 化求解温度分布。
在稳态热传导过程中,导热系数和热 阻共同决定了物体内部温度分布的特 性。
当材料的导热系数越大,其对应的热 阻就越小,表示热量传递越容易;反 之,导热系数越小,热阻越大,热量 传递越困难。
04 稳态热传导的实例分析
一维稳态热传导
总结词
一维稳态热传导是热传导在单一方向上的情况,常见于细长物体或薄层材料。
三维稳态热传导
要点一
总结词
三维稳态热传导涉及三个方向的热量传递,常见于球体或 立方体。
要点二
详细描述
在三维稳态热传导中,热量在三个相互垂直的方向上传递 ,常见于球体或立方体等三维物体。三维稳态热传导的温 度分布在不同方向上都是稳定的,其数学模型比一维和二 维情况更为复杂,需要考虑三个方向的热量传递。三维稳 态热传导在解决实际问题时具有重要意义,如地球内部的 热量传递、建筑物的散热分析等。
稳态热传导的重要性
01
02
03
工程应用广泛
稳态热传导在许多工程领 域都有广泛应用,如建筑、 机械、航空航天等。
基础理论支撑
稳态热传导是传热学的基 础理论之一,对于理解更 复杂的传热过程和现象至 关重要。
节能减排
通过掌握稳态热传导规律, 有助于优化能源利用,实 现节能减排。
稳态热传导的应用场景
《传热学》第二章热传导

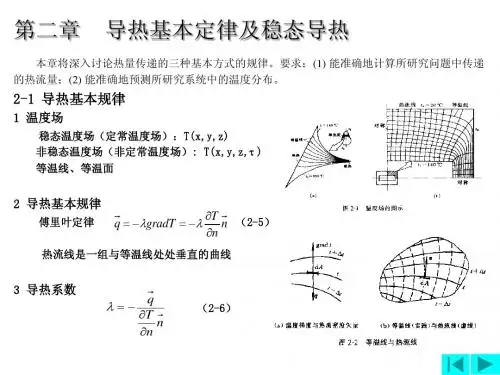
第二章热传导一、名词解释1.温度场:某一瞬间物体内各点温度分布的总称。
一般来说,它是空间坐标和时间坐标的函数。
2.等温面(线):由物体内温度相同的点所连成的面(或线)。
3.温度梯度:在等温面法线方向上最大温度变化率。
4.热导率:物性参数,热流密度矢量与温度降度的比值,数值上等于1 K/m的温度梯度作用下产生的热流密度。
热导率是材料固有的热物理性质,表示物质导热能力的大小。
5.导温系数:材料传播温度变化能力大小的指标。
6.稳态导热:物体中各点温度不随时间而改变的导热过程。
7.非稳态导热:物体中各点温度随时间而改变的导热过程。
8.傅里叶定律:在各向同性均质的导热物体中,通过某导热面积的热流密度正比于该导热面法向温度变化率。
9.保温(隔热)材料:λ≤0.12 W/(m·K)(平均温度不高于350℃时)的材料。
10.肋效率:肋片实际散热量与肋片最大可能散热量之比。
11.接触热阻:材料表面由于存在一定的粗糙度使相接触的表面之间存在间隙,给导热过程带来额外热阻。
12.定解条件(单值性条件):使微分方程获得适合某一特定问题解的附加条件,包括初始条件和边界条件。
二、填空题1.导热基本定律是_____定律,可表述为。
(傅立叶,)2.非稳态导热时,物体内的_____场和热流量随_____而变化。
(温度,时间)3.导温系数的表达式为_____,单位是_____,其物理意义为_____。
(a=λ/cρ,m2/s,材料传播温度变化能力的指标)4.肋效率的定义为_______。
(肋片实际散热量与肋片最大可能散热量之比。
)5.按照导热机理,水的气、液、固三种状态中_______态下的导热系数最小。
(气)6.一般,材料的导热系数与_____和_____有关。
(种类,温度)7.保温材料是指_____的材料.(λ≤0.12 W/(m·K)(平均温度不高于350℃时))8.已知材料的导热系数与温度的关系为λ=λ0(1+bt),当材料两侧壁温分别为t1、t2时,其平均导热系数可取下的导热系数。
传热学-学习课件-2-5 具有内热源的一维稳态导热

主讲老师:王舫 适用专业:能源与动力工程专业
传热学 Heat Transfer
第二章 稳态热传导
2-1 导热基本定律 2-2 导热问题的数学描写 2-3 典型一维稳态导热问题的分析解 2-4 通过肋片的导热 2-5 具有内热源的一维导热问题 2-6 多维稳态导热的求解
三、通过含内热源实心圆柱体的导热
①数学描写
一维,稳态,有均匀内热源,导热系数λ为 常数,外侧为第一类边界
②求解
1 r
d dr
r
dt dr
Φ
0;
r 0, dt 0; dr
r rw , t tw
t
Φ
r
rw
传热学 Heat Transfer
2
tw
d 2t dx2
Φ
/
0
x 0, dt 0 dx
x , t tw
例 题2-9
传热学 Heat Transfer
已知:
1 14 mm
2 6 mm &=1.5 107 W/m3
1 35 W m K 2 100 W m K
h 3 500 W m2 K tf 150 ℃
利用两个边界得出圆柱体内的温度分为:
Φ
t tw 4
rw2 r 2
由傅里叶定律可得出壁面处的热流量:
r
2 w
l
Φ
由能量守恒法则,可直接得到上式。
t1 r
rw
传热学 Heat Transfer
Thanks
传热学 Heat Transfer
传热学课件第 二 章 稳 态 热传导

d2t d x2
m 2 t t f
1
通过肋壁的导热
一、等截面直肋的导热
4.求解:
4>.引入过余温度:<1>式变为 <4> 5>.解微分方程得温度场 <4>式为一个二阶线性齐次常微分方程,它的通解为: =C1emx+C2e-mx <5> 将边界条件<2>、<3>代入<5>即得肋片沿H方向的温度分布:
通过圆筒壁的导热
一、已知第一类边界条件
据傳里叶定律并整理后可得热流量的表达式: 1 ln d2 2l d1 式中的分母即为长度为l的圆筒壁的导热热阻。 单位为:℃/W 实际工程多采用单位管长的热流量ql来计算热流量:
t w1 t w 2
ql
Q l
t w1 t w 2
d ln d2 2 1 1
通过平壁的导热
二、已知第三类边界条件:
q
q
t f 1 t f 2
1 1 h1 h2
也可写作:q=k(tf1-tf2) (请牢记K的物理意义!) 对于冷热流体通过多层平壁的导热,可写作:
t f 1 t f 2
1 h1
i 1
n
i 1 i h2
若已知传热面积A,则热流量为:
e m x H e m x H 0 e mH e mH
d 2 m 2 d x2
or :
0
或写作:
0
ch mx H ch mH
expmx H exp mx H expmH exp mH
1
h21d x 0
传热学

华北电力大学
传热学 Heat Transfer
2、温度梯度
• 定义:沿等温面法线方向上的温度增量与法向 距离比值的极限。温度梯度表示为:
t t grad t n lim n n 0 n n
式中,n
是等温面法线方向上的单位矢量。
华北电力大学
传热学 Heat Transfer
华北电力大学
传热学 Heat Transfer
沿x 轴方向导入与导出微元体净热量
Φx Φx dx
同理可得:
t dxdydz x x
沿 y 轴方向导入与导出微元体净热量
Φy Φy dy
t dxdydz y y
t ( ) Φ 0 x x
华北电力大学
传热学 Heat Transfer
三、其它坐标系中的导热微分方程式
1. 圆柱坐标系(r, , z)
x r cos ; y r sin ; z z
t 1 t 1 t t c (r ) 2 ( ) ( ) r r r r z z
(3)微元体内热源生成的热量
ΦV Φdxdydz
5. 导热微分方程的基本形式
t t t t c ( ) ( ) ( ) Φ x x y y z z
非稳态项
华北电力大学
三个坐标方向净导入的热量
内热源项
传热学 Heat Transfer
传热学 Heat Transfer
利用两个边界条件
t
x 0, t t1 x , t t2
c2 t1 t 2 t1 c1
t1 t 2
传热学 第2章 稳态导热
t t t t c Φ x x y y z z
3、常物性且稳态:
2t 2t 2t Φ a 2 2 2 0 x y z c
如果边界面上的热流密度保持为常数,则 q | w 常数 当边界上的热流密度为零时,称为绝热边界条件
t t qw 0 0 n w n w
18
(3)第三类边界条件 给出了物体在边界上与和它直接接触的流体之 间的换热状况。 根据能量守恒,有:
返回
2.1.1 各类物体的导热机理
气体:气体分子不规则热运动时相互碰撞的结果,高温的气体分子运 动的动能更大 固体:自由电子和晶格振动 对于导电固体,自由电子的运动在导热中起着重要的作用,电的良导 体也是热的良导体 对于非导电固体,导热是通过晶格结构的振动,即原子、分子在其平 衡位置附近的振动来实现的
返回
2.2.2 定解条件
导热微分方程式是能量守恒定律在导热过程中的应用,是一切导热 过程的共性,是通用表达式。 完整数学描述:导热微分方程 + 定解条件 定解条件包括初始条件和边界条件两大类,稳态问题无初始条件 初始条件:初始时刻的状态表示为: =0,t =f (x,y,z)
边界条件: 给出了物体在边界上与外界环境之间在换热上的联系或相互作用
2、推导基本方法:傅里叶定律 + 能量守恒定律 在导热体中取一微元体
进入微元体的总能量+微元体内热源产生的能量-离开微元体的总能量= 微元体内储存能的增加
11
Ein Eg Eout Es
d 时间段内:
Ein Φx Φy Φz d Eiout Φxdx Φy dy Φz dz d
传热学第2章-1
t f (x, y, z, )
2. 等温线,等温面
1) 定义:同一瞬间温度相等的各点连成的线或面称为 等温线(Isotherm)或等温面(Isothermal surface)。
5/41
2)特点:
传热学 Heat Transfer 第5版
(1)等温线(面)不能相交(同一点不可能有两个温度);
(1768-1830)
9/41
传热学 Heat Transfer 第5版
1. 导热基本定律的文字表达
在导热现象中,单位时间内通过给定截面的热量, 正比于垂直于该截面方向上的温度变化率和截面面 积,方向与温度梯度相反。
2. 导热基本定律的数学表达
q gradt t n
A
Φ
c
a c
称为热扩散率(Thermal diffusivity)
或导温系数,单位:m2/s,是物性参数;
2.λ=constant 并且t x 2
2t y 2
2t z 2
)
a2t
Laplace算子
28/41
传热学 Heat Transfer 第5版
4/41
传热学 Heat Transfer 第5版
按温度场随空间与时间的变化特性,可以区分为:
稳态温度场 t f (x, y, z) 非稳态温度场
t f (x, y, z, )
一维温度场 二维温度场 三维温度场
t f (x)
t f (x, )
t f (x, y)
t f (x, y, )
传热学 Heat Transfer 第5版
代入能量平衡式, (1)+(2)=(3) 得导热微分方程的基本形式
传热学第二章稳态热传导
h h
t f t f ( )
五、 热扩散系数 (thermal diffusivity)
a
物体导热能力 c 物体蓄热能力
从导热方程看:
a
t
温度变化快 扯平能力强
故,a 是评价温度变化速度的一个指标
2.3 通过平壁及圆筒壁的一维稳态导热
一、通过单层平壁的导热
0 , 则 2. Φ
t a 2 t
2
3. 稳态:
Φ a t 0 c
,则
0 4. 稳态且 Φ
t 0
2
三、其它正交坐标
1、柱坐标: (cylinder coordinate)
x r cos ; y r sin ; z z
2 t 1 t 1 2 t 2 t t a 2 2 2 2 r r r z c r
p
各类物质导热系数的范围
导热机理
气体:分子热运动 t
金属 非金属
固体:自由电子和晶格振动
t 晶格振动 阻碍自由电子运动
液体的导热机理不清
固体> 液体 > 气 ; 取决于物质的种类和温度
热绝缘(保温)材料 insulation material:<0.2W/(mK) (50
(2)固体的热导率
(a) 金属的热导率
金属 12~418W (m K)
纯金属的导热:依靠自由电子的迁移和晶格振动; 金属导热与导电机理一致,良导体也是良导热体。
银 铜 金 铝
T
10K:Cu 12000 W (m K) 15K : Cu 7000 W (m K)
传热学
2.气体辐射对波长有选择性。
3.气体辐射在整个容器内进行
七、固体表面的换热情况 1. 固体表面与固体相接触——单纯导热。
2. 固体表面与液体相接触——对流换热。
2. 固体表面与气体相接触——复合换热。
第九章
传热过程与换热器
一、传热过程 ——热流体通过固体壁面将热量传递 给冷流体。 1.平壁
i 1 1 h1 λi h2 i t f1 t f 2 Φ do 1 1 1 ln hi d i l 2l di hod o l
W
四、影响对流换热的因素
1.流动原因——强迫对流、自然对流。
2.流动状态——层流、紊流。
3.流体物性——、、、、v 、Cp等。 4.流体相变——凝结、沸腾。 5.壁面形状
五、四个准则数
ul ul 惯性力 1)雷诺数 Re 粘性力
2)普朗特数
Pr a c p 动量扩散率 c p 热量扩散率
K fi
1 1 1 hi h0 0
A0 肋化系数 Ai
; 肋壁效率 0 查表。
*加装肋片的目的和注意事项
二、换热器 1.对数平均温差
t ' t" 顺流、逆流: t m t ' ln t "
叉流、复杂流: t m t m逆 温差修正系数 f P、R t 2 "t 2 ' t1 't1 " P ;R t1 't 2 ' t 2 "t 2 '
第五章
对流换热
一、热对流与对流换热的定义与机理 二、速度边界层和热边界层
1.速度边界层——从速度为零的壁面到速度达 到主流速度的99%的流体薄层。 2.热边界层——从壁面过余温度(t-tw)为零, 到流体过余温度为来流过余温度的99 % 的 流体薄层 3.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
t 1 t 1 t t ( r ) 2 ( ) ( ) qv r r r r z z
球坐标系 (r, ,F)
t r 1 t q r 1 t q r sin qr
x r sin cos ; y sin r sin ; z cos r
a.必须有温差;
b.物体直接接触;
c.依靠分子、原子及自由电子等微观粒子热运动 而传递热量;
2.热对流:由于流体的宏观运动引起的流体各部分间 发生位移,冷热掺混所导致的热量传递现象。 3.热辐射:物体通过电磁波的形式传递能量的方式称为 辐射,因热的原因发出辐射能的现象称为热辐射。
§2-1 导热基本定律
黄铜 109w/m K 黄铜:70%Cu, 30%Zn
金属的加工过程也会造成晶格的缺陷
合金的导热:依靠自由电子的迁移和晶格的振动;且 主要依靠后者
T
温度升高、晶格振动加强、导热增强
(2) 非金属的导热系数: 非金属的导热:依靠晶格的振动传递热量
T
0.025~3W (m C)
非稳态,常物性,无内热源:
稳态,常物性,有内热源:
稳态,常物性,无内热源:
圆柱坐标系 (r, F, z)
t r 1 t q r t q z z qr
x r cos ; y r sin ; z z
c
t 1 t t q gradt t i j k r z r
一、导热微分方程式 (Heat Diffusion Equation)
理论基础:傅里叶定律 + 热力学第一定律
在导热体中任取一平行六面体微 元
单位时间内,由内热源产生的能量
单位时间内,微元体热力学能净增量
热力学第一定律:
z
Q U W W 0, Q U
导入热量-导出热量+内热源发热量=系统热力学能的增量
定义:导热是由温度不同的两物体,或者同一物体中温度不同的两部分之 间,直接接触时由微观粒子的热运动而引起的能量转移过程。 本章的论述重点是建立在这一微观现象基础上的宏观现象,对导热的微观 机理的研究超出了本书的研究范围。
温度场(Temperature field)
某 时 刻 , 空 间 所 有 点 温 度 分 布 的 集 合 , 又 叫 温 度 分 布 ( temperature distribution)。温度场是时间和空间的函数,即:
(2)第二类边界条件
给定物体边界上热流密度的分布及变化规律称为第二类 边界条件。 由傅里叶定律:
t q n w
n:壁面法线方向
第二类边界条件相当于已知任何时刻物体边界法向温度梯度值
稳态导热: q f (r )
非稳态导热:
t q0 绝热边界面(特例): n w
q
t q f ( r , ) n w
☺ 温度是标量,但温度梯度是矢量,指向温度增加最快的方向; 热流密度是矢量,方向正好与温度梯度相反。
二、导热基本定律
1822 年,法国数学家傅里叶( FOURIER )在实验研究的基础 上,发现导热基本规律 —— 傅利叶定律 导热基本定律一般性表述:单位时间内通过给定截面的导热热
流量,正比于该截面的法向温度变化率(温度梯度),方向与 温升方向相反。
热流量的形式:
三、导热系数 (Thermal conductivity)
导热系数表征物质导热能力大小(需实验测定) 稳态法(傅里叶定律)
非稳态法
影响导热系数的因素:物质的种类、温度、湿度、压力、密度等
金属 非金属; 固相 液相 气相
不同材料的导热系数 有些天然材料(石英石、木材)和人造材料(复合板), 其密度和导热系数沿各方向不同,属于非均各向异性材料
导热微分方程式不适用范围——非傅里叶导热过程: 极短时间、产生极大的热流密度的热量传递现象,如激光加 工过程 极低温度(接近于0K)时的导热问题
二、定解条件
定解条件(几何,物性,初始,边界) 导热问题完整的数学描述 导热微分方程 导热微分方程描写物体的温度随时间和空间变化的关系,没有 涉及具体、特定的导热过程;是针对普适情况的通用表达式。 对特定的导热过程:需要得到满足该过程的补充说明条件,即 单值性条件:获得唯一解的补充条件。
稳态温度场:温度的空间分布不随时间而改变(Steady temperature field)
非 稳 态 温 度 场 : 温 度 的 空 间 分 布 随 时 间 而 改 变 (Transient/unsteady temperature field)
等温面与等温线
等温面(isothermal surface) :某一时刻、温度场中所有温度相同的 点连接起来所构成的面
思考:每两条相邻等温线间温差相等时,其疏密可直观反映热流密度的大小?
温度梯度:空间点r处,等温面法线方向上的温度变化率
垂直于等温面(线) 指向温度升高的方向
——各坐标轴上温度变化率与单位向量乘积的矢量叠加
热流密度:单位时间,单位面积上传递的热量。 总是通过等温面上某点指向温度降低的方向。
- T =e (Tw4 Te4) w n w
补充2. 界面处(不考虑接触热阻):同时满足,温度、热流密度连续条件:
T w =T w
- T n =-
w
F
导入微元体的热量Qout: t F x dydz dx x x x
F z
t dxdy z z
F z dz
t F z dydx dz (3) z z z
均匀但各向异性材料——空心砖 细观上非均匀各向异性,但宏观上均匀且各项同性——多 孔结构介质
压制复合木板 (非均各向异性)
空心砖 (均匀各向异性)
多孔结构材料
不同物质导热系数的差异 1、气体的导热系数 气体导热:由于分子的热运动和相互碰撞传递能量
气体 0.006~0.6 W (mK)
Qin Qout Qs U (1)
x 轴方向:
d 时间内、经 x 表面导入的热量Fx:
傅里叶定律
F x
t dydz x x
d 时间内、经 x+dx 表面导出的热量Fx+dx :
泰勒级数:
导入微元体的热量Qin:
x dx t F x dydz x x t t F y dxdz (2) F y dy F y dxdz dy y y y y y
基本规律:
液体 0.07~0.7 W (mK )
T
p
McLaughlin, E., “Theory of the Thermal Conductivity of Fluids,” in R. P. Tye, Ed., Thermal Conductivity, Vol. 2, Academic Press, London, 1969.
第二章
稳态热传导
Steady Heat Conduction
第二章 稳态热传导
主要内容:
1.(掌握)导热的基本定律——傅里叶定律
2.(重点掌握)导热问题的数学描述来自3.(掌握)典型一维导热问题的分析解
4.(掌握)通过肋片的导热
5.(掌握)具有内热源的一维导热问题
6.(了解)多维稳态导热问题的求解
1. 导热:指同一物体各部分或温度不同的两物体间直 接接触时,依靠分子、原子及自由电子等微观粒子热 运动而进行的热量传递的现象。
t 1 t 1 t q gradt t i j k r r sin r
t 1 1 t 1 t 2 t c 2 ( r ) 2 ( sin ) 2 2 ( ) qv r r r r sin r sin
微元体内热源生成热量
(4)
Qin Qout Qs U (1)
导热微分方程一般性表达式:
笛卡尔坐标系内,三维非稳态导热微分方程的一般形式
热扩散系数(thermal diffusivity)
导热系数为常数
a
[m2/s] cp
热扩散系数a反映了导热过程中材料的导热能力( )与沿途物质储热 能力( cp )之间的关系。 a值大,即 值大或( cp) 值小,说明物体的某一部分一旦获得热量, 该热量能在整个物体中很快扩散。 a 表征物体被加热或冷却时,物体内各部分温度趋向于均匀一致的能力, 在同样加热条件下,物体的热扩散率越大,物体内部各处的温度差别越 小。 a反应导热过程动态特性,研究非稳态导热重要物理量。
1、几何条件:给定导热体的几何形状和大小
如:平壁或圆筒壁;厚度、直径等
2、物理条件:给定导热体的物理特征
如:物性参数 、cp 和 的数值,是否随温度变化; 有无内热源、大小和分布;是否各向同性 3、时间条件:说明导热过程随着时间变化的特点
稳态导热过程不需要时间条件 — 与时间无关 对非稳态导热过程必须给出过程开始时刻导热体内的 温度分布
时间条件又称为初始条件(Initial conditions)
4、边界条件(Boundary Condition)
给出导热体边界上温度或传热情况的条件称为边界条件 边界条件一般可分为三类:第一类、第二类、第三类边界条件
(1)第一类边界条件
规定了边界上温度值称为第一类边界条件
稳态导热: tw = f (r) 非稳态导热:>0, tw = f (r,) 例: x 0, t tw1 x , t tw2
