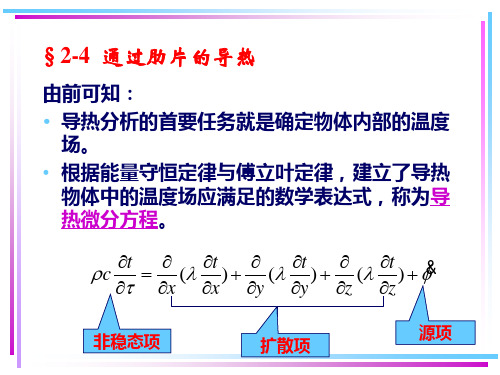
第二章 稳态导热-1
合集下载
传热学-第二章 导热基本定律及稳态导热第一讲-动力工程
大多数液体（分子量M不变）： T
液体的热导率随压力p的升高而增大 p
2-3 导热微分方程式及单值性条件
理论解析的基本思路
简化
物理问题
数学模型
求解
热流量
温度场
导热定律
控制方程 定解条件
q -grad T [W m2 ]
建立导热体内的温度分布计算模型是导热理论 的首要任务
理论基础：傅里叶定律 + 热力学第一定律
导入与导出微元体净热量：
qx dxdydz d
x
[J]
d 时间内、沿 y 轴方向
导入与导出微元体净热量：
qy dxdydz d
y
[J]
d 时间内、沿 z 轴方向导
入与导出微元体净热量：
qz dxdydz d
z
[J]
D. 导入与导出净热量:
[] ( qx qy qz )dxdydzd
[J]
dQx qx dydz d [J]
B. d 时间内、沿 x 轴方向、
经 x+dx 表面处dydz导出的热量：
dQxdx qxdx dydz d [J]
qxdx
qx
qx x
dx
C. d 时间内、沿 x 轴方向导入与导出微元体净热量：
dQx
dQxdx
qx x
dxdydz d
[J]
d 时间内、沿 x 轴方向
2、推导过程 在导热体中取一微元体，能量平衡分析 热力学第一定律：
Q U W
W 0, Q U
d 时间内微元体中：
[导入与导出净热量] + [内热源发热量] = [热力学能的增加]
数学模型建立基本思路 能量平衡分析
(1)导入与导出微元体的净热量
液体的热导率随压力p的升高而增大 p
2-3 导热微分方程式及单值性条件
理论解析的基本思路
简化
物理问题
数学模型
求解
热流量
温度场
导热定律
控制方程 定解条件
q -grad T [W m2 ]
建立导热体内的温度分布计算模型是导热理论 的首要任务
理论基础：傅里叶定律 + 热力学第一定律
导入与导出微元体净热量：
qx dxdydz d
x
[J]
d 时间内、沿 y 轴方向
导入与导出微元体净热量：
qy dxdydz d
y
[J]
d 时间内、沿 z 轴方向导
入与导出微元体净热量：
qz dxdydz d
z
[J]
D. 导入与导出净热量:
[] ( qx qy qz )dxdydzd
[J]
dQx qx dydz d [J]
B. d 时间内、沿 x 轴方向、
经 x+dx 表面处dydz导出的热量：
dQxdx qxdx dydz d [J]
qxdx
qx
qx x
dx
C. d 时间内、沿 x 轴方向导入与导出微元体净热量：
dQx
dQxdx
qx x
dxdydz d
[J]
d 时间内、沿 x 轴方向
2、推导过程 在导热体中取一微元体，能量平衡分析 热力学第一定律：
Q U W
W 0, Q U
d 时间内微元体中：
[导入与导出净热量] + [内热源发热量] = [热力学能的增加]
数学模型建立基本思路 能量平衡分析
(1)导入与导出微元体的净热量
第二章--稳态导热-肋片-1
l
Φc
δ
0
Φx
Φx+dx
x
肋厚（ｙ）方向：沿肋厚 方向的导热热阻一般远小 于它与环境的换热热阻。
dx λ 1/h
把沿ｙ方向的散热视为负的内热源。
于是我们可以把通过肋片的导热问题 视为沿肋片方向上的一维导热问题。
t1
t
假设 1 ）导热系数 λ 及表面传热系数 h 均为常 数； 2 ）肋片宽度远大于肋片的厚度，不考虑温 度沿该方向的变化； 3 ）表面上的换热热阻 1/h ，远大于肋片的 导热热阻 δ/λ ，即肋片上沿肋厚方向上的温度 均匀不变；
（1）当热流量不变时，接触热阻 rc 较大时，必然 在界面上产生较大温差 （2）当温差不变时，热流量必然随着接触热阻 rc 的增大而下降 （3）即使接触热阻 rc 不是很大，若热流量很大， 界面上的温差是不容忽视的
例：
q 6 105 W m 2 rc 2.64 104 m 2 K W tc q rc 158.4 C
hP h2(l ) mH H H Ac l
l
P 2l
Φc
H AL 肋片的纵剖面积
2h 3 2 h 3 mH H 2 H2 H AL
1 2
δ
0
Φx
Φx+dx
x
dx H
可见， f
3 h 与参量 2 H AL
三角形肋片
2.其他形状 肋片的效率
为了减轻肋片重量、节省材料，并保持散热量 基本不变，需要采用变截面肋片，其中包括环肋及 三角形直肋、针肋等。 对于变截面肋片来讲，由于从导热微分方程求
得的肋片散热量计算公式相当复杂。其计算式可参
见相关文献。教材表2-1给出四种计算式。
Φc
δ
0
Φx
Φx+dx
x
肋厚（ｙ）方向：沿肋厚 方向的导热热阻一般远小 于它与环境的换热热阻。
dx λ 1/h
把沿ｙ方向的散热视为负的内热源。
于是我们可以把通过肋片的导热问题 视为沿肋片方向上的一维导热问题。
t1
t
假设 1 ）导热系数 λ 及表面传热系数 h 均为常 数； 2 ）肋片宽度远大于肋片的厚度，不考虑温 度沿该方向的变化； 3 ）表面上的换热热阻 1/h ，远大于肋片的 导热热阻 δ/λ ，即肋片上沿肋厚方向上的温度 均匀不变；
（1）当热流量不变时，接触热阻 rc 较大时，必然 在界面上产生较大温差 （2）当温差不变时，热流量必然随着接触热阻 rc 的增大而下降 （3）即使接触热阻 rc 不是很大，若热流量很大， 界面上的温差是不容忽视的
例：
q 6 105 W m 2 rc 2.64 104 m 2 K W tc q rc 158.4 C
hP h2(l ) mH H H Ac l
l
P 2l
Φc
H AL 肋片的纵剖面积
2h 3 2 h 3 mH H 2 H2 H AL
1 2
δ
0
Φx
Φx+dx
x
dx H
可见， f
3 h 与参量 2 H AL
三角形肋片
2.其他形状 肋片的效率
为了减轻肋片重量、节省材料，并保持散热量 基本不变，需要采用变截面肋片，其中包括环肋及 三角形直肋、针肋等。 对于变截面肋片来讲，由于从导热微分方程求
得的肋片散热量计算公式相当复杂。其计算式可参
见相关文献。教材表2-1给出四种计算式。
传热学
等温线
华北电力大学
传热学 Heat Transfer
2、温度梯度
• 定义：沿等温面法线方向上的温度增量与法向 距离比值的极限。温度梯度表示为：
t t grad t n lim n n 0 n n
式中，n
是等温面法线方向上的单位矢量。
华北电力大学
传热学 Heat Transfer
华北电力大学
传热学 Heat Transfer
沿x 轴方向导入与导出微元体净热量
Φx Φx dx
同理可得：
t dxdydz x x
沿 y 轴方向导入与导出微元体净热量
Φy Φy dy
t dxdydz y y
t ( ) Φ 0 x x
华北电力大学
传热学 Heat Transfer
三、其它坐标系中的导热微分方程式
1. 圆柱坐标系（r, , z）
x r cos ; y r sin ; z z
t 1 t 1 t t c (r ) 2 ( ) ( ) r r r r z z
（3）微元体内热源生成的热量
ΦV Φdxdydz
5. 导热微分方程的基本形式
t t t t c ( ) ( ) ( ) Φ x x y y z z
非稳态项
华北电力大学
三个坐标方向净导入的热量
内热源项
传热学 Heat Transfer
传热学 Heat Transfer
利用两个边界条件
t
x 0, t t1 x , t t2
c2 t1 t 2 t1 c1
t1 t 2
华北电力大学
传热学 Heat Transfer
2、温度梯度
• 定义：沿等温面法线方向上的温度增量与法向 距离比值的极限。温度梯度表示为：
t t grad t n lim n n 0 n n
式中，n
是等温面法线方向上的单位矢量。
华北电力大学
传热学 Heat Transfer
华北电力大学
传热学 Heat Transfer
沿x 轴方向导入与导出微元体净热量
Φx Φx dx
同理可得：
t dxdydz x x
沿 y 轴方向导入与导出微元体净热量
Φy Φy dy
t dxdydz y y
t ( ) Φ 0 x x
华北电力大学
传热学 Heat Transfer
三、其它坐标系中的导热微分方程式
1. 圆柱坐标系（r, , z）
x r cos ; y r sin ; z z
t 1 t 1 t t c (r ) 2 ( ) ( ) r r r r z z
（3）微元体内热源生成的热量
ΦV Φdxdydz
5. 导热微分方程的基本形式
t t t t c ( ) ( ) ( ) Φ x x y y z z
非稳态项
华北电力大学
三个坐标方向净导入的热量
内热源项
传热学 Heat Transfer
传热学 Heat Transfer
利用两个边界条件
t
x 0, t t1 x , t t2
c2 t1 t 2 t1 c1
t1 t 2
传热学 第2章 稳态导热
t t t t c Φ x x y y z z
3、常物性且稳态:
2t 2t 2t Φ a 2 2 2 0 x y z c
如果边界面上的热流密度保持为常数，则 q | w 常数 当边界上的热流密度为零时，称为绝热边界条件
t t qw 0 0 n w n w
18
（3）第三类边界条件 给出了物体在边界上与和它直接接触的流体之 间的换热状况。 根据能量守恒，有：
返回
2.1.1 各类物体的导热机理
气体：气体分子不规则热运动时相互碰撞的结果，高温的气体分子运 动的动能更大 固体：自由电子和晶格振动 对于导电固体，自由电子的运动在导热中起着重要的作用，电的良导 体也是热的良导体 对于非导电固体，导热是通过晶格结构的振动，即原子、分子在其平 衡位置附近的振动来实现的
返回
2.2.2 定解条件
导热微分方程式是能量守恒定律在导热过程中的应用，是一切导热 过程的共性，是通用表达式。 完整数学描述：导热微分方程 + 定解条件 定解条件包括初始条件和边界条件两大类，稳态问题无初始条件 初始条件：初始时刻的状态表示为： =0，t =f (x,y,z)
边界条件： 给出了物体在边界上与外界环境之间在换热上的联系或相互作用
2、推导基本方法：傅里叶定律 + 能量守恒定律 在导热体中取一微元体
进入微元体的总能量+微元体内热源产生的能量-离开微元体的总能量= 微元体内储存能的增加
11
Ein Eg Eout Es
d 时间段内：
Ein Φx Φy Φz d Eiout Φxdx Φy dy Φz dz d
传热学第2章-1
t f (x, y, z)
t f (x, y, z, )
2. 等温线，等温面
1) 定义：同一瞬间温度相等的各点连成的线或面称为 等温线(Isotherm)或等温面(Isothermal surface)。
5/41
2）特点：
传热学 Heat Transfer 第5版
(1)等温线(面)不能相交(同一点不可能有两个温度)；
(1768-1830)
9/41
传热学 Heat Transfer 第5版
1. 导热基本定律的文字表达
在导热现象中，单位时间内通过给定截面的热量， 正比于垂直于该截面方向上的温度变化率和截面面 积，方向与温度梯度相反。
2. 导热基本定律的数学表达
q gradt t n
A
Φ
c
a c
称为热扩散率(Thermal diffusivity)
或导温系数，单位：m2/s，是物性参数；
2.λ=constant 并且t x 2
2t y 2
2t z 2
)
a2t
Laplace算子
28/41
传热学 Heat Transfer 第5版
4/41
传热学 Heat Transfer 第5版
按温度场随空间与时间的变化特性，可以区分为：
稳态温度场 t f (x, y, z) 非稳态温度场
t f (x, y, z, )
一维温度场 二维温度场 三维温度场
t f (x)
t f (x, )
t f (x, y)
t f (x, y, )
传热学 Heat Transfer 第5版
代入能量平衡式， （1）＋（2）＝（3） 得导热微分方程的基本形式
t f (x, y, z, )
2. 等温线，等温面
1) 定义：同一瞬间温度相等的各点连成的线或面称为 等温线(Isotherm)或等温面(Isothermal surface)。
5/41
2）特点：
传热学 Heat Transfer 第5版
(1)等温线(面)不能相交(同一点不可能有两个温度)；
(1768-1830)
9/41
传热学 Heat Transfer 第5版
1. 导热基本定律的文字表达
在导热现象中，单位时间内通过给定截面的热量， 正比于垂直于该截面方向上的温度变化率和截面面 积，方向与温度梯度相反。
2. 导热基本定律的数学表达
q gradt t n
A
Φ
c
a c
称为热扩散率(Thermal diffusivity)
或导温系数，单位：m2/s，是物性参数；
2.λ=constant 并且t x 2
2t y 2
2t z 2
)
a2t
Laplace算子
28/41
传热学 Heat Transfer 第5版
4/41
传热学 Heat Transfer 第5版
按温度场随空间与时间的变化特性，可以区分为：
稳态温度场 t f (x, y, z) 非稳态温度场
t f (x, y, z, )
一维温度场 二维温度场 三维温度场
t f (x)
t f (x, )
t f (x, y)
t f (x, y, )
传热学 Heat Transfer 第5版
代入能量平衡式， （1）＋（2）＝（3） 得导热微分方程的基本形式
高等传热学_第二章_稳态导热
2-1 一维稳态导热
通过长圆筒壁（图2-2）的导热由傅里叶定律直接积分的方法。 若已知圆筒壁的内外壁面温度分别为t1和t2。注意到，圆筒壁的导
热面积在径向上是变化的，但单位长度上的总热流量ql（单位为 W/m）仍应是常量（不随r变化）。由傅里叶定律可得
分离变量并积分
ql
dt 2 r dr
x 0, x ,
并整理得到
t 0 t 0
（2-1-20）
代入以上得到的通解式(2-1-19)，可以确定其中的两个任意常数，
qV t x( x) 2
（2-1-21）
2-1 一维稳态导热
如果给定两个表面的温度分别为t1和t2，即
t t1 x , t t 2 代入以上得到的通解式(2-1-19)，可以确定其中的两个任意常数， 并整理得到
2-1 一维稳态导热
图2-1通过大平壁的导热
2-1 一维稳态导热
2-1-1 无内热源的一维导热 求解导热问题的一般思路是首先从导热微分方程和相应的定解条
件出发，解得温度场。 对于如图2-1所示的大平壁的稳态导热，已知两表面的温度分别为 t1和t2。导热微分方程简化为
其通解为
d 2t 0 2 dx
t
qv 2 r C1 ln r C2 4
（2-1-25）
2-1 一维稳态导热
r＝0处温度应该有界，即 t
r 0
，可以作为一个边界条件，
由此可得C1＝0。如果给定另一个边界条件是第一类边界条件， 即r＝R，t＝t1。代入通解可得
t t1
qv 2 2 (R r ) 4
种换热设备中，常在换热表面上增添一些肋， 以增大换热表面，达到减小换热热阻的目的。
第二章导热基本定律及稳态导热
d 边界条件：第一类
o x
控制
根据上面的条件可得：
方程
c t x( x t)Φ ddx2
t
2
0
第一类边条：
边界 条件
t
x
t1
x 0,
x
,
t t1 t t2
t2
o
直接积分，得：
ddxtc1 tc1xc2
带入边界条件：
c1
t2
t1
c2 t1
线性
t
t2t1
xt1
分布
dt
t2t1
带入Fourier 定律
4 、保温材料热量转移机理 ( 高效保温材料 ) 高温时：
（ 1 ）蜂窝固体结构的导热 （ 2 ）穿过微小气孔的导热
更高温度时： （ 1 ）蜂窝固体结构的导热 （ 2 ）穿过微小气孔的导热和辐射
5 、超级保温材料
采取的方法： （ 1 ）夹层中抽真空（减少通过导热而造成
热损失） （ 2 ）采用多层间隔结构（ 1cm 达十几层）
由此可见ɑ物理意义： ① ɑ越大，表示物体受热时，其内部各点温 度扯平的能力越大。 ② ɑ越大，表示物体中温度变化传播的越快。 所以，ɑ也是材料传播温度变化能力大小的指 标，亦称导温系数。
2 、导热微分方程的适用范围 1 ）适用于 q 不很高，而作用时间长。同时 傅立叶定律也适用该条件。 2 ）若时间极短，而且热流密度极大时，则 不适用。 3 ）若属极底温度（ -273 ℃ ）时的导热不 适用。
§2-3 通过平壁，圆筒壁，球壳和 其它变截面物体的导热
本节将针对一维、稳态、常物性、无内热源 情况，考察平板和圆柱内的导热。
直角坐标系：
c t x( x t) y( y t) z( z t) Φ
o x
控制
根据上面的条件可得：
方程
c t x( x t)Φ ddx2
t
2
0
第一类边条：
边界 条件
t
x
t1
x 0,
x
,
t t1 t t2
t2
o
直接积分，得：
ddxtc1 tc1xc2
带入边界条件：
c1
t2
t1
c2 t1
线性
t
t2t1
xt1
分布
dt
t2t1
带入Fourier 定律
4 、保温材料热量转移机理 ( 高效保温材料 ) 高温时：
（ 1 ）蜂窝固体结构的导热 （ 2 ）穿过微小气孔的导热
更高温度时： （ 1 ）蜂窝固体结构的导热 （ 2 ）穿过微小气孔的导热和辐射
5 、超级保温材料
采取的方法： （ 1 ）夹层中抽真空（减少通过导热而造成
热损失） （ 2 ）采用多层间隔结构（ 1cm 达十几层）
由此可见ɑ物理意义： ① ɑ越大，表示物体受热时，其内部各点温 度扯平的能力越大。 ② ɑ越大，表示物体中温度变化传播的越快。 所以，ɑ也是材料传播温度变化能力大小的指 标，亦称导温系数。
2 、导热微分方程的适用范围 1 ）适用于 q 不很高，而作用时间长。同时 傅立叶定律也适用该条件。 2 ）若时间极短，而且热流密度极大时，则 不适用。 3 ）若属极底温度（ -273 ℃ ）时的导热不 适用。
§2-3 通过平壁，圆筒壁，球壳和 其它变截面物体的导热
本节将针对一维、稳态、常物性、无内热源 情况，考察平板和圆柱内的导热。
直角坐标系：
c t x( x t) y( y t) z( z t) Φ
传热学第二章--稳态导热精选全文
t
无内热源，λ为常数，并已知平 t1
壁的壁厚为，两个表面温度分别 维持均匀而恒定的温度t1和t2
t2
c t ( t ) Φ x x
d 2t dx2
0
o
x 0,
x ,
t t
t1 t2
x
直接积分，得：
dt dx
c1
t c1x c2
2024/11/6
35
带入边界条件：
c1
t2
t1
c t
1 r2
r 2
r
t r
1
r 2 sin
sin
t
r2
1
sin 2
t
Φ
2024/11/6
26
6 定解条件 导热微分方程式的理论基础：傅里叶定律+能 量守恒。 它描写物体的温度随时间和空间变化的关系； 没有涉及具体、特定的导热过程。通用表达式。
完整数学描述：导热微分方程 + 单值性条件
4
2 等温面与等温线
①定义
等温面：温度场中同一瞬间同温度各点连成的 面。 等温线：在二维情况下等温面为一等温曲线。
t+Δt t
t-Δt
2024/11/6
5
②特点
t+Δt t
t-Δt
a) 温度不同的等温面或等温线彼此不能相交
b)在连续的温度场中，等温面或等温线不会中
止，它们或者是物体中完全封闭的曲面（曲
它反映了物质微观粒子传递热量的特性。
不同物质的导热性能不同：
固体 液体 气体
金属 非金属
金属 12~418 W (m C) 非金属 0.025 ~ 3W/(mC)
合金 纯金属
第二章--稳态热传导(导热理论基础)
具有稳态温度场的导热过程我们常称之为稳态导热；具有非稳态温 度场的导热过程我们常称之为非稳态导热。
2021/3/10
2
导热理论基础
二、傅里叶（J.Fourier）定律：
1.基本概念：
2>.等温面与等温线：（温度场习惯上用等温面图或等温线图来表 示，如图2-1）
等温线
a.等温面：同一时刻温度场中所有 温度相同的点构成的面。
第二章 稳态热传导（导热理论 基础）
一、概述 二、傅里叶（J.Fourier）定律 三、导热系数 四、导热微分方程 五、导热微分方程的单值性条件 六、解决一具体导热问题的一般步骤
2021/3/10
1
导热理论基础
一、概述：
一般我们认为：导热是发生在物体中的宏观现象，故将物质看作是 连续介质。
导热基础理论的主要任务：
3
导热理论基础
二、傅里叶（J.Fourier）定律：
1.基本概念：
3>.温度梯度gradt:两等温面间的温差△t与其法线方向
的距离△n比值的极限。在单位距离内温度沿法线方
向上的变化值最大、最显著，此时的温度变化率称
之为温度梯度。即： gr a lid m n ttn n n t
n 0
t+△t t t-△t
2.傅里叶（J.Fourier）定律：
在导热现象中，单位时间内通过给定面积的传热量，正比例于该处 垂直导热方向的截面面积及此处的温度梯度，其数学表达式为：
q g A g rrW a a / W m 2 d dtt
几点问题：
1>.负号表示热量传递指向温度降低的方向，与温度梯度方向相反。
2>.温度梯度是引起物体内热量传递的根本原因。
2021/3/10
2
导热理论基础
二、傅里叶（J.Fourier）定律：
1.基本概念：
2>.等温面与等温线：（温度场习惯上用等温面图或等温线图来表 示，如图2-1）
等温线
a.等温面：同一时刻温度场中所有 温度相同的点构成的面。
第二章 稳态热传导（导热理论 基础）
一、概述 二、傅里叶（J.Fourier）定律 三、导热系数 四、导热微分方程 五、导热微分方程的单值性条件 六、解决一具体导热问题的一般步骤
2021/3/10
1
导热理论基础
一、概述：
一般我们认为：导热是发生在物体中的宏观现象，故将物质看作是 连续介质。
导热基础理论的主要任务：
3
导热理论基础
二、傅里叶（J.Fourier）定律：
1.基本概念：
3>.温度梯度gradt:两等温面间的温差△t与其法线方向
的距离△n比值的极限。在单位距离内温度沿法线方
向上的变化值最大、最显著，此时的温度变化率称
之为温度梯度。即： gr a lid m n ttn n n t
n 0
t+△t t t-△t
2.傅里叶（J.Fourier）定律：
在导热现象中，单位时间内通过给定面积的传热量，正比例于该处 垂直导热方向的截面面积及此处的温度梯度，其数学表达式为：
q g A g rrW a a / W m 2 d dtt
几点问题：
1>.负号表示热量传递指向温度降低的方向，与温度梯度方向相反。
2>.温度梯度是引起物体内热量传递的根本原因。
第二章-导热理论基础-1
一般而言：
λ固 > λ 液 > λ 气 λ 金属 > λ 非金属
一定温度范围内， ∝ f (t ) ，可写成：λ = λ0 ⋅ (1 + bt ) λ 即，导热系数是温度的线性函数。 由于热能的传输在固体中体现为自由电子的迁移和晶格振动 波，于是 λ固 = λe + λl
晶格分量 电子分量 对于金属： e λ
∂t qx = −λ ⋅ ∂x ∂t q y = −λ ⋅ 或 ∂y ∂t q z = − λ ⋅ ∂z
2-1-6 导热系数
q qx =− 定义： λ = − gradt ∂t ∂x
物理意义： 物体中单位时间、单位温降通过单位面积的导
W 热量；为表征物质导热能力的系数。 m ⋅ ℃
如果初始时刻物体各部分的温度相同，可以把初始条件改 写为： t τ =0 = t0 = const
（4）边界条件 ）
①第一类边界条件 已知任何时刻物体边界的温度值 第一类边界条件—已知任何时刻物体边界的温度值 第一类边界条件
tw = const t s = tw = tw = f (τ )
dτ 时间内，微元体内部产生的能量为：
& E g = qv ⋅ dx ⋅ dy ⋅ dz ⋅ dτ
dτ 时间内，微元体贮存能的变化量为：
∂t dE = ρc p ⋅ dxdydzdτ ∂τ
根据能量守恒： 可得
Ein + E g − Eout = dE
∂t ∂q x ∂q y ∂q z = ρc p ∂x + ∂y + ∂z + qv & ∂τ
∂t −λ ∂x
= h t f − t (0 , τ )
λ固 > λ 液 > λ 气 λ 金属 > λ 非金属
一定温度范围内， ∝ f (t ) ，可写成：λ = λ0 ⋅ (1 + bt ) λ 即，导热系数是温度的线性函数。 由于热能的传输在固体中体现为自由电子的迁移和晶格振动 波，于是 λ固 = λe + λl
晶格分量 电子分量 对于金属： e λ
∂t qx = −λ ⋅ ∂x ∂t q y = −λ ⋅ 或 ∂y ∂t q z = − λ ⋅ ∂z
2-1-6 导热系数
q qx =− 定义： λ = − gradt ∂t ∂x
物理意义： 物体中单位时间、单位温降通过单位面积的导
W 热量；为表征物质导热能力的系数。 m ⋅ ℃
如果初始时刻物体各部分的温度相同，可以把初始条件改 写为： t τ =0 = t0 = const
（4）边界条件 ）
①第一类边界条件 已知任何时刻物体边界的温度值 第一类边界条件—已知任何时刻物体边界的温度值 第一类边界条件
tw = const t s = tw = tw = f (τ )
dτ 时间内，微元体内部产生的能量为：
& E g = qv ⋅ dx ⋅ dy ⋅ dz ⋅ dτ
dτ 时间内，微元体贮存能的变化量为：
∂t dE = ρc p ⋅ dxdydzdτ ∂τ
根据能量守恒： 可得
Ein + E g − Eout = dE
∂t ∂q x ∂q y ∂q z = ρc p ∂x + ∂y + ∂z + qv & ∂τ
∂t −λ ∂x
= h t f − t (0 , τ )
《传热学》第2章-稳态导热
第一类边界条件： x 0 , t t w1 积分得:
控制方程
边界条件
x , t tw 2
t
dt 1 2 0 ( 1 bt ) c1 0 ( t bt ) c1 x c2 tw1 dx 2
代入边界条件，得:
1 1 2 2 ( t bt ) c 0 c , ( t bt 1 2 0 w2 w 2 ) c1 c 2 0 w1 2 w1 2 1 2 c ( t bt 2 0 w1 w1 ) 2 t w1 t w 2 1 c [ 1 b( t w1 t w 2 )] 0 1 2
tw 2 tw3
2
tw3 tw4
3
tw1 tw4 tw1 tw4 3 相加可得： q R ,1 R ,2 R ,3 R ,i
i 1
例2-1：有一锅炉炉墙，三层，内层为230mm的耐火 砖层，中间为50mm厚的保温层，外层为240mm的 红砖层，导热系数分别为1.10 W/(m.K) ，0.072 W/(m.K) ，0.58W/(m.K)，已知炉墙内外表面温度 为500℃与50℃，求炉墙的导热热流密度和红砖墙的 最高温度。
第二章 稳态导热
Steady-State Conduction —— One Dimension
主要内容
掌握稳态导热。
§2-1 §2-2 §2-3 §2-4 §2-5 §2-6
通过平壁的导热 通过复合平壁的导热 通过圆筒壁的导热 具有内热源的平壁导热 通过肋片的导热 通过接触面的导热
对各层直接应用单层大平壁的热量计算式 tw1 tw 2 tw1 tw 2 第一层平壁 : q1 , 变换 : q1 R ,1 t w1 t w 2 1 R ,1
控制方程
边界条件
x , t tw 2
t
dt 1 2 0 ( 1 bt ) c1 0 ( t bt ) c1 x c2 tw1 dx 2
代入边界条件，得:
1 1 2 2 ( t bt ) c 0 c , ( t bt 1 2 0 w2 w 2 ) c1 c 2 0 w1 2 w1 2 1 2 c ( t bt 2 0 w1 w1 ) 2 t w1 t w 2 1 c [ 1 b( t w1 t w 2 )] 0 1 2
tw 2 tw3
2
tw3 tw4
3
tw1 tw4 tw1 tw4 3 相加可得： q R ,1 R ,2 R ,3 R ,i
i 1
例2-1：有一锅炉炉墙，三层，内层为230mm的耐火 砖层，中间为50mm厚的保温层，外层为240mm的 红砖层，导热系数分别为1.10 W/(m.K) ，0.072 W/(m.K) ，0.58W/(m.K)，已知炉墙内外表面温度 为500℃与50℃，求炉墙的导热热流密度和红砖墙的 最高温度。
第二章 稳态导热
Steady-State Conduction —— One Dimension
主要内容
掌握稳态导热。
§2-1 §2-2 §2-3 §2-4 §2-5 §2-6
通过平壁的导热 通过复合平壁的导热 通过圆筒壁的导热 具有内热源的平壁导热 通过肋片的导热 通过接触面的导热
对各层直接应用单层大平壁的热量计算式 tw1 tw 2 tw1 tw 2 第一层平壁 : q1 , 变换 : q1 R ,1 t w1 t w 2 1 R ,1
传热学-清华大学 (2)
b2 bq当§2-2 通过复合平壁的导热工程上会遇到这样一类平壁：无论沿宽度还是厚度方向，都是由不同材料组合而成——复合平壁在复合平壁中，由于不同材料的导热系数不同，严格地说复合平壁的温度场是二维或三维的。
如：空斗墙、空斗填充墙、空心板墙、夹心板墙若B、C、D材料的导热系数相差较大时，应按二维或三维温度场计算。
准确的方法是数值求解。
作为近似的简便计算，可按上述第一种方法、根据串、并联热阻方法计算总热阻后，再加以修正自学例题2-3= tc wln( 2t t w =∴h1h2h1h21r1h1h2λλins q l（1）增加温差（（2）减小热阻：在一些换热设备中，在换热面上加装肋片是增大换热量的重要手段如：钢片式暖气片；汽车水箱及家用冰箱、空调的散热片等肋壁：直肋、环肋；等截面、变截面电子器件冷却微细板翅结构1、等截面直肋的稳态导热严格地说，肋片中的温度场是三维l的。
其温度分布取决于内部x、y、z三个方向的导热热阻以及表面与流体之间的对流换热热阻。
求解三维、二维问题较复杂；将问题进行简化：（1）λ大、δ<<H，认为温度沿厚度变化很小；（2）宽度l >>δ，认为肋片温度只沿高度方向变化简化为一维温度场dx dtAΦx λ−=ldt d Φ=hUdx Φcdt稳态条件下肋片表面的散热量(th m A d AΦ⋅=−=θλθλl（2）上述分析近似认为肋片温度场为一维。
当Bi=hδ/λ≤0.05 时，误差小于1%。
对于短而厚的肋片，二维温度场，上述算式不适用；实际上，肋片表面上表面传热系数h 不是均匀一致的—数值计算l（3）敷设肋片不一定就能强化传热，只有满足一定的条件才能增加散热量。
设计肋片时要注意这一点。
（参考《传热学》俞佐平等编）当m数值一定时，随着肋片高度肋片散热量的计算方法：设计肋片：选择形状、计算；考虑质量、制造的难易程度、价格、空间位置的限制等（2）计算出理想情况下的散热量Φ0=hUH (t 0-t ∞)（1）由图线或计算公式得到ηf（3）由式Φ= ηf Φ0计算出实际散热量Φ§2-5 通过接触面的导热实际固体表面不是理想平整的，所以两固体表面直接接触的界面容易出现点接触，或者只是部分的而不是完全的和平整的面接触——给导热带来额外的热阻（Thermal contact resistance）——接触热阻当界面上的空隙中充满导热系数远小于固体的气体时，接触热阻的影响更突出当两固体壁具有温差时，接合处的热传递机理为接触点间的固体导热和间隙中的空气导热，对流和辐射的影响一般不大。
传热学-第2章
第二章 稳态热传导 12
在导热体中取一微元体 热力学第一定律：
Q U W
W 0, Q U
d 时间内微元体中： [导入与导出净热量]+ [内热源发热量] = [热力学能的增加]
1、导入与导出微元体的净热量 d 时间内、沿 x 轴方向、经 x 表面导入的热量：
dQx qx dydz d
t t1
n i
x
i 1
t tn1
t1 t2 t3 t4
热阻：
r1
1 , , rn n 1 n
第二章 稳态热传导
三层平壁的稳态导热
30
q
t1 t n 1
由热阻分析法：
ri
i 1
n
t1 t n 1
i i 1 i
n
问：现在已经知道了q，如何计算其中第 i 层的右侧壁温？
第一章复习
(1) 导热
傅里叶定律：
(2) 对流换热 牛顿冷却公式： (3) 热辐射
斯忒藩－玻耳兹曼定律 ：
dt Φ A dx
Aht
A T 4
(4) 传热过程
(t f 1 t f 2 ) (t f 1 t f 2 ) Φ 1 1 Rh1 R Rh 2 Ah1 A Ah2
多层、第三类边条
tf1
q
tf1 tf 2 1 n i 1 h1 i 1 i h2
h1 t2 t3
h2 tf2
W 单位： 2 m
传热系数？ tf1
？
t1 t2 t3 t2
？ tf2
32
三层平壁的稳态导热
第二章 稳态热传导
一台锅炉的炉墙由三层材料叠合而成.最里面的是耐火黏土砖,厚 115MM;中间是B级硅藻土砖,厚125MM;最外层为石棉板,厚 70MM.已知炉墙内外表面温度分别为485℃ 和60 ℃ , 试求每平方 米炉墙的热损失及耐火黏土砖和硅藻土砖分界面上的温度。 解：各层的导热系数可根据估计的平均温度从手册中查出。第一 次估计的平均温度不一定正确，待算得分界面温度时，如发现不 对，可重新假定每层的平均温度。经几次试算，逐步逼近，可得 合理的数值。这里列出的是几次试算后的结果： W 3 0.116 /(m K ) W 1 1.12W /(m K ) 2 0.116 /(m K )
在导热体中取一微元体 热力学第一定律：
Q U W
W 0, Q U
d 时间内微元体中： [导入与导出净热量]+ [内热源发热量] = [热力学能的增加]
1、导入与导出微元体的净热量 d 时间内、沿 x 轴方向、经 x 表面导入的热量：
dQx qx dydz d
t t1
n i
x
i 1
t tn1
t1 t2 t3 t4
热阻：
r1
1 , , rn n 1 n
第二章 稳态热传导
三层平壁的稳态导热
30
q
t1 t n 1
由热阻分析法：
ri
i 1
n
t1 t n 1
i i 1 i
n
问：现在已经知道了q，如何计算其中第 i 层的右侧壁温？
第一章复习
(1) 导热
傅里叶定律：
(2) 对流换热 牛顿冷却公式： (3) 热辐射
斯忒藩－玻耳兹曼定律 ：
dt Φ A dx
Aht
A T 4
(4) 传热过程
(t f 1 t f 2 ) (t f 1 t f 2 ) Φ 1 1 Rh1 R Rh 2 Ah1 A Ah2
多层、第三类边条
tf1
q
tf1 tf 2 1 n i 1 h1 i 1 i h2
h1 t2 t3
h2 tf2
W 单位： 2 m
传热系数？ tf1
？
t1 t2 t3 t2
？ tf2
32
三层平壁的稳态导热
第二章 稳态热传导
一台锅炉的炉墙由三层材料叠合而成.最里面的是耐火黏土砖,厚 115MM;中间是B级硅藻土砖,厚125MM;最外层为石棉板,厚 70MM.已知炉墙内外表面温度分别为485℃ 和60 ℃ , 试求每平方 米炉墙的热损失及耐火黏土砖和硅藻土砖分界面上的温度。 解：各层的导热系数可根据估计的平均温度从手册中查出。第一 次估计的平均温度不一定正确，待算得分界面温度时，如发现不 对，可重新假定每层的平均温度。经几次试算，逐步逼近，可得 合理的数值。这里列出的是几次试算后的结果： W 3 0.116 /(m K ) W 1 1.12W /(m K ) 2 0.116 /(m K )
2-1 第二章 导热基本定律及稳态导热
q
q
qx
t x
;
qy
t y
;
qz
t z
q q cos
§2-1 导热基本定律
长江大学机械工程学院
School of Mechanical Engineering
3. 意义: 已知物体内部的温度分布后，由该定律可求
得各点的热流密度或热流量。
例1：已知右图平板中的温度分 布可以表示成如下的形式： t = C1 x2 + C2
冷面
冷面
流体
热面 流体
§2-1 导热基本定律
2. 导热系数的相对大小和典型数据
长江大学机械工程学院
School of Mechanical Engineering
金 属 非 金 属
固 相 液 相 气 相
20℃时： 纯 铜 399 W (m C )
碳 钢 36.7 W (m C )
能准确的计算所研究问题中传递的热流。
要解决的问题：
温度分布如何描述和表示？
温度的分布和导热的热流存在什么关系？ 如何得到导热体内部的温度分布？
长江大学机械工程学院
School of Mechanical Engineering
本章内容结构
§2-1 导热基本定律
§2-2 导热问题的数学描述
回答问题1和2 回答问题3 具 体 稳 态 导 热 问 题
§2-1 导热基本定律
长江大学机械工程学院
School of Mechanical Engineering
三、热导率（ Thermal conductivity ）
1.定义
q grad t
传热学-第二章导热基本定律及稳态传热
1、导入微元体的净热量
d 时间X方向流入与流出微元体的热流量
dQx
- dQxdx
- qx x
dxdydz d
( t ) dxdydz d
x x
d 时间Y方向流入与流出微元体的热流量
dQy
- dQydy
- q y y
dy dxdz d
y
( t ) dxdydz d
y
2.4 导热微分方程及定解条件
影响热导率的因素：物质的种类、材料成分、温度、压力及 密度等。
2.3 导热系数
2.3.1 气体导热系数
气体导热——由于分子的无规则热运动以及分子间 的相互碰撞
1 3
vlcv
v 3RT M
V 气体分子运动的均方根 m/s L 气体分子两次碰撞之间的平均自由程 m
Cv气体的定容比热 J/kg·℃
2.3 导热系数
2.4 导热微分方程及定解条件
建立数学模型的目的：
求解温度场 t f x, y, z,
步骤： 1）根据物体的形状选择坐标系, 选取物体中的 微元体作为研究对象； 2）根据能量守恒, 建立微元体的热平衡方程式； 3）根据傅里叶定律及已知条件, 对热平衡方程式 进行归纳、整理，最后得出导热微分方程式。
通过某一微元面积dA的热流：
dA q
d
q dA
t
n
dA
t
dydz
t
dxdz
t
பைடு நூலகம்
dxdy
n
x
y
z
2.2导热的基本定律
例：判断各边界面的热流方向
2.3 导热系数
由傅里叶定律可得，导热系数数学定义的具体形式为：
q t n
d 时间X方向流入与流出微元体的热流量
dQx
- dQxdx
- qx x
dxdydz d
( t ) dxdydz d
x x
d 时间Y方向流入与流出微元体的热流量
dQy
- dQydy
- q y y
dy dxdz d
y
( t ) dxdydz d
y
2.4 导热微分方程及定解条件
影响热导率的因素：物质的种类、材料成分、温度、压力及 密度等。
2.3 导热系数
2.3.1 气体导热系数
气体导热——由于分子的无规则热运动以及分子间 的相互碰撞
1 3
vlcv
v 3RT M
V 气体分子运动的均方根 m/s L 气体分子两次碰撞之间的平均自由程 m
Cv气体的定容比热 J/kg·℃
2.3 导热系数
2.4 导热微分方程及定解条件
建立数学模型的目的：
求解温度场 t f x, y, z,
步骤： 1）根据物体的形状选择坐标系, 选取物体中的 微元体作为研究对象； 2）根据能量守恒, 建立微元体的热平衡方程式； 3）根据傅里叶定律及已知条件, 对热平衡方程式 进行归纳、整理，最后得出导热微分方程式。
通过某一微元面积dA的热流：
dA q
d
q dA
t
n
dA
t
dydz
t
dxdz
t
பைடு நூலகம்
dxdy
n
x
y
z
2.2导热的基本定律
例：判断各边界面的热流方向
2.3 导热系数
由傅里叶定律可得，导热系数数学定义的具体形式为：
q t n
高等传热学Chap2
ρcp
∂t ∂t ∂t ∂t ∂ ∂t ∂ ∂t ∂ ∂t + u + v + w = λ + λ + λ + Φ + Φv ∂x ∂y ∂z ∂x ∂x ∂y ∂y ∂z ∂z ∂τ
d dt λ + Φv = 0 dx dx
§2-1 一维稳态导热
自变量变换关系： 自变量变换关系：
ξ=lnr 和 η=1/r
定义无因次温度： 定义无因次温度：
Θ=(t−t2)/(t1−t2)
定义无因次坐标： 定义无因次坐标： X=x/L=(ξ−ξ1)/(ξ2−ξ1) =(η−η1)/(η2−η1) 三种情况下温度分布统一表达式： 三种情况下温度分布统一表达式：
对于Φv=常数的情形，导热方程变为
Φv 1 d dt r = − r dr dr λ
连续积分两次得温度分布的通解 通解为： 通解
t=−
Φv 2 r + c1 ln r + c2 4λ
r = r0 , −λ dt = h tw − t f dr r = r0
对于半径为r0的长圆柱，第三类边界条件可写为
§2-1 一维稳态导热
圆柱表面温度 表面温度为： tw=tf+Φvr0/2h 表面温度 中心温度为： 中心温度 tc=tf+Φvr0/2h+Φvr02/4λ
r t − tw Θ= =1− tc − t w r 0
2
因此有无因次温度：
即温度呈抛物线分布 抛物线分布。 抛物线分布 对于内、外半径分别为r1和r2的圆筒壁，当为第一类边界条 件时，即r=r1时t=tw1，r=r2时t=tw2，温度分布 温度分布为 温度分布
∂t ∂t ∂t ∂t ∂ ∂t ∂ ∂t ∂ ∂t + u + v + w = λ + λ + λ + Φ + Φv ∂x ∂y ∂z ∂x ∂x ∂y ∂y ∂z ∂z ∂τ
d dt λ + Φv = 0 dx dx
§2-1 一维稳态导热
自变量变换关系： 自变量变换关系：
ξ=lnr 和 η=1/r
定义无因次温度： 定义无因次温度：
Θ=(t−t2)/(t1−t2)
定义无因次坐标： 定义无因次坐标： X=x/L=(ξ−ξ1)/(ξ2−ξ1) =(η−η1)/(η2−η1) 三种情况下温度分布统一表达式： 三种情况下温度分布统一表达式：
对于Φv=常数的情形，导热方程变为
Φv 1 d dt r = − r dr dr λ
连续积分两次得温度分布的通解 通解为： 通解
t=−
Φv 2 r + c1 ln r + c2 4λ
r = r0 , −λ dt = h tw − t f dr r = r0
对于半径为r0的长圆柱，第三类边界条件可写为
§2-1 一维稳态导热
圆柱表面温度 表面温度为： tw=tf+Φvr0/2h 表面温度 中心温度为： 中心温度 tc=tf+Φvr0/2h+Φvr02/4λ
r t − tw Θ= =1− tc − t w r 0
2
因此有无因次温度：
即温度呈抛物线分布 抛物线分布。 抛物线分布 对于内、外半径分别为r1和r2的圆筒壁，当为第一类边界条 件时，即r=r1时t=tw1，r=r2时t=tw2，温度分布 温度分布为 温度分布
2第二章 一维稳态导热
t 0
t f (x, y,z,)
一、温度场和温度梯度
2.等温线（面）：同一瞬间温度场中温度相同的点连成的 线（面）称为等温线（面）。
等温线（面）有如下特点：
①不可能相交；
②对连续介质，等温线（面）只可 能在物体边界中断或完全封闭；
③沿等温线（面）无热量传递；
t+Δt
④由等温线（面）的疏密可直观反
t1 t2
x
t
t2
t1
x
t1
代入一维Fourier定律
线性分布 q dt
dx
可得一维大平板的热流密度：
q
(t1
t2
)
与x无关
一维大平板的热流量：
A
(t1
t2
)
与x无关
3.平壁导热的热阻
传递过程中的转移量
过程的动力 过程的阻力
t t
(A) R
R是导热热阻：
R A
对单位面积的面积热阻为：RA
• 傅立叶定律给出了导热系数的定义 :单位 温度梯度下物体内所产生的热流密度 。
q /gradt [W/（m·℃ ）]
•它表示物体导热本领的大小。
•导热系数的影响因素：是物性参数。 ——物质结构：物质的种类、材料成分； ——物质的状态：温度、 湿度、压力、 密度等。
0(1bT)
保温材料 （绝热材料）
【例题】管道结垢问题（续）
【解】 （ 1）干净表面时管壁的热阻
为
R1
ln(r2 / r1)
t
映出不同区域温度梯度（或热流密度）
t-Δt
的相对大小。
一、温度场和温度梯度
3.温度梯度：系统中某一点所在的等温 面与相邻等温面之间的温差与其法线 间的距离之比的极限为该点的温度梯 度，记为gradt。
传热学试题01
第二章 稳态导热本章重点：具备利用导热微分方程式建立不同边界条件下稳态导热问题的数学模型的能力第一节 通过平壁的导热1-1 第一类边界条件 研究的问题：（1）几何条件：设有一单层平壁，厚度为δ，其宽度、高度远大于其厚度（宽度、高度是厚度的10倍以上）。
这时可认为沿高度与宽度两个方向的温度变化率很小，温度只沿厚度方向发生变化。
（属一维导热问题）（2）物理条件：无内热源，材料的导热系数λ为常数。
（3） 边界条件：假设平壁两侧表面分别保持均匀稳定的温度1w t 和2w t ，21w w t t >。
（为第一类边界条件，同时说明过程是稳态的）求：平壁的温度分布及通过平壁的热流密度值。
方法1 导热微分方程：采用直角坐标系，这是一个常物性、无内热源、一维稳态导热问题（温度只在 x 方向变化）。
导热微分方程式为：022=dxtd （2-1）边界条件为：10w x t t == ， 2w x t t ==δ （2-2）对式（2-1）连续积分两次，得其通解： 21c x c t += （2-3）这里1c 、2c 为常数，由边界条件确定 ，解得：⎪⎩⎪⎨⎧=-=11221ww w t c t t c δ （2-4）最后得单层平壁内的温度分布为： x t t t t w w w δ211--= （2-5）由于δ 、1w t 、2w t 均为定值。
所以温度分布成线性关系，即温度分布曲线的斜率是常数（温度梯度），const t t dx dt w w =-=δ12 （2-6）热流密度为：)(21w w t t dx dt q -=-=δλλ2/m W （2-7） 若表面积为 A, 在此条件下 , 通过平壁的导热热流量则为 :t A qA ∆==Φδλ W （2-8）考虑导热系数随温度变化的情况：对于导热系数随温度线形变化，即)1(0bt +=λλ，此时导热微分方程为：0=⎪⎭⎫⎝⎛dx dt dx d λ 解这个方程，最后得：⎥⎦⎤⎢⎣⎡++-+⎪⎭⎫ ⎝⎛+=+)(211212121121122w w w w w w t t b x t t bt t bt t δ 或 x tt t t b b t b t w w w w w δ12211)(21122-⎥⎦⎤⎢⎣⎡+++⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+说明：壁内温度不再是直线规律，而是按曲线变化。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
t ln(d 2 / d1 ) R 2l
W
虽然是稳态情况，但 热流密度 q 与半径 r 成反比！
根据热阻的定义，通过整个圆筒壁的导热热阻为：
25
单位长度圆筒壁的热流量：
t w1 t w 2 Φ t w1 t w 2 ql r2 1 L R l ln 2 r1
2
2
t1 b<0 t2 0 δ
λ =λ 0(1+bt) b>0
d t 当b 0时 : 0 (下凹) 2 dx d 2t 当b 0时 : 0 (直线) 2 dx 2 d t 当b 0时 : 0 (上凹) 2 dx
2
x
7
温度分布曲线的凹向取决于系 数b的正负。 当b>0，λ=λ0(1+bt)，随着t增大，b<0 λ增大，即高温区的导热系数大 于低温区。Q=-λA(dt/dx)，所以 高温区的温度梯度dt/dx较小， 而形成上凸的温度分布。
t t t t c ( ) ( ) ( ) Φ x x y y z z
t1 t2
根据上面的条件可得：
t 0 ( ) x x
控制 方程
d 2t dx 2
0
3
x
dt 0 2 dx x 0, t t1 x , t t2
1、通过单层圆筒壁的导热 稳态导热 t 柱坐标
0
t 1 t 1 t t c ( r ) 2 ( ) ( ) r r r r z z
圆筒壁就是圆管的壁面。当管子的壁面相对于 管长而言非常小，且管子的内外壁面又保持均匀的 温度时，通过管壁的导热就是圆柱坐标系上的一维 导热问题。
t1 t 4 1 1 1 r3 r2 ln r1 ln r2 ln r4 r3 21l 22l 23l t1 t n 1 通式为： n 1 ri 1 ln ri i 1 2i l
28
3 通过球壁的导热 1 / r 1 / r2 t t 2 (t1 t 2 ) 温度分布：
27
t2 t3 t3 t4 t1 t2 d2 d3 d4 1 1 1 n n n 21l d1 22l d 2 23l d3
t1 t4 2 l (t1 t4 ) 3 3 1 1 di 1 1 di 1 ln ln 2 l i 1 i di di i 1 i
d dt 0 (1 bt) 0 dx dx
b 2 0 (t t ) c1 x c2 2
最后可求得其温度分布
t w1 t w2 b 2 b 2 t t (t w1 t w1 ) 2 2 b 1 2 (t w1 t w2 ) x
2
完整的数学描写
直接积分，得：
dt c1 t c1 x c2 dx t2 t1 c1 带入边界条件： c2 t1
t
t2 t1
x t1
4
t2 t1 线性 t x t1 分布 带入Fourier 定律 d t t t 2 1 dx
x t2 Δt
t1
t
12
【例】 有一砖砌墙壁，厚为 0.25m 。已知内外壁面
的温度分别为 25℃和 30℃。试计算墙壁内的温度 分布和通过的热流密度。
解：由平壁导热的温度分布
t
t2 t1
x t1
代入已知数据可以得出墙壁内 t=25+20x的温度分布表达式。
从附录查得红砖的λ=0.87W/(m℃),于是可以 计算出通过墙壁的热流密度 q (t1 t2 ) 17.4W / m2
ln(r r1 ) t t1 (t1 t2 ) ln(r2 r1 )
dt t1 t2 q dr r ln(r2 r1 )
求导
t1 t2 1 dt dr ln(r2 r1 ) r
2 W m
2 l (t1 t2 ) Φ 2 rlq ln(r2 r1 )
t1 t2 0 δ
λ =λ 0(1+bt) b>0
x
当b<0，λ=λ0(1+bt)，随着t增大，λ减小，高温区的温度梯度 dt/dx较大。
8
2) 多层平壁的一维稳态导热
多层平壁：由几层不同材料组成 例：房屋的墙壁 — 白灰内层、 水泥沙浆层、红砖（青砖） 主体层等组成 假设各层之间接触良好， 可以近似地认为接合面上 各处的温度相等
6
b t t w1 1 t t w1 2 x b t w2 t w1 1 t t w2 w1 2
二次曲线方程
2
d t b dt b dt 2 dx 1 bt dx 0 dx
13
例 一锅炉炉墙采用密度为 300kg/m3 的水泥珍珠岩制 作，壁厚 = 100 mm，已知内壁温度t1=500℃，外壁 温度 t2=50℃，求炉墙单位面积、单位时间的热损失。 [解] 材料的平均温度为： t = (t1 + t2)/2 = (500 + 50)/2 = 275 ℃ 查得：
{}W/(mk) 0.0651 0.000105 {t}C
W m
r2 Rl ln — 单位长度圆筒壁的导热 热阻 m C W 2 r1 1
26
2、通过多层圆筒壁的导热 由不同材料构成的多层圆筒壁 带有保温层的热力管道、嵌套的金属管道和结垢、 积灰的输送管道等 由不同材料制作的圆筒同心紧密结合而构成多层圆 筒壁 ，如果管子的壁厚远小于管子的长度，且管 壁内外边界条件均匀一致，那么在管子的径向方向 构成一维稳态导热问题。
15
【例】 由三层材料组成的加热炉炉墙。第一层为耐火
砖。第二层为硅藻土绝热层，第三层为红砖，各层的 厚 度 及 导 热 系 数 分 别 为 1 ＝ 240mm ， 1=1.04W/(m℃)， 2＝50mm, 2=0.15W/(m℃)， 3 ＝ 115mm, 3=0.63W/(m℃) 。炉墙内侧耐火砖的 表 面 温 度 为 1000℃ 。 炉 墙 外 侧 红 砖 的 表 面 温 度 为 60℃。试计算硅藻土层的平均温度及通过炉墙的导热 热流密度。
9 2015-4-29
q
t1 t 2
1
t 2 t3
1
2
t3 t 4
t1
t2 t3
2
3
3
q t4
由和分比关系
q
1
1
＋ 2
t1 t 4
2
＋
3
3
t1
r1
t2 r2
t3
r3
t4
推广到n层壁的情况:
q t1 t n 1
i i 1 i
n
10
层间分界面温度
q t1 t 2
1
t 2 t3
1
2
t3 t 4
t1
2
3
t2 t3
3
q
1 t2 t1 q 1 3 t3 t 4 q 3 2 t3 t 2 q 2
t4
11
3）接触热阻： 实际的两个固体表面之间不可能完全接触，只能是 局部的、甚至存在点接触，如图所示。只有在界面 上那些真正接触的点上，温度才是相等的。 当未接触的空隙中充满空气或其它气体时，由于气 体的热导率远远小于固体 ,就会对两个固体间的导热 过程产生附加热阻Rc，称之为接触热阻。 由于接触热阻的存在，使导热过程中两个接触表面 之间出现温差tc。
解：
已知 1＝0.24m, 1=1.04W/(m℃) 2＝0.05m, 2=0.15W/(m℃)
3＝0.115m, 3=0.63W/(m℃)
t1=1000℃ t2=60℃
16
1 2 3 1 2 3 1 t2 t1 q 700℃ 1 2 t3 t2 q 289℃ 2
获得两个系数
t2 t1 c1 ; ln(r2 r1 )
ln r1 c2 t1 (t2 t1 ) ln(r2 r1 )
23
将系数带入第二次积分结果
t2 t1 t t1 ln( r r1 ) ln( r2 r1 )
t1 r1
t2
显然，温度呈对数曲线分布
r r2
24
下面来看一下圆筒壁内部的热流密度和热流分布情况
18
如果采用单层玻璃窗，则散热损失为
10 Φ' 3333 .3W 0.003
是双层玻璃窗散热损失的 35 倍，可见采用双层玻璃 窗可以大大减少散热损失，节约能源。
19
第三类边界条件下的一维大平壁稳态导热 P30
通过复合平壁的导热 P32----- 自学，注意处理 方法
20
二、 通过圆筒壁的导热
t w1 t w 4 t w1 t w 4 Φ δ3 δ1 δ2 R λ1 R λ 2 R λ 3 Aλ1 Aλ2 Aλ3
15 5 94.3W 0.003 0.005 0.003 2 0.5 2 0.025 2 0.5
可见，单层玻璃的导热热阻为0.003 K/W，而空气 夹层的导热热阻为0.1 K/W，是玻璃的33.3倍。
1
§2 一维稳态导热
1 通过平壁的导热
条件：平壁、一维稳态导热(x方向) 长和宽 ≥ 10 厚度 内容：热流量计算、温度分布。
1)温度分布 已知平壁的壁厚为，两个表面温度： 分别维持均匀而恒定的温度t1和t2，即 边界条件：
x 0 : t t1 x : t t2
2
W
虽然是稳态情况，但 热流密度 q 与半径 r 成反比！
根据热阻的定义，通过整个圆筒壁的导热热阻为：
25
单位长度圆筒壁的热流量：
t w1 t w 2 Φ t w1 t w 2 ql r2 1 L R l ln 2 r1
2
2
t1 b<0 t2 0 δ
λ =λ 0(1+bt) b>0
d t 当b 0时 : 0 (下凹) 2 dx d 2t 当b 0时 : 0 (直线) 2 dx 2 d t 当b 0时 : 0 (上凹) 2 dx
2
x
7
温度分布曲线的凹向取决于系 数b的正负。 当b>0，λ=λ0(1+bt)，随着t增大，b<0 λ增大，即高温区的导热系数大 于低温区。Q=-λA(dt/dx)，所以 高温区的温度梯度dt/dx较小， 而形成上凸的温度分布。
t t t t c ( ) ( ) ( ) Φ x x y y z z
t1 t2
根据上面的条件可得：
t 0 ( ) x x
控制 方程
d 2t dx 2
0
3
x
dt 0 2 dx x 0, t t1 x , t t2
1、通过单层圆筒壁的导热 稳态导热 t 柱坐标
0
t 1 t 1 t t c ( r ) 2 ( ) ( ) r r r r z z
圆筒壁就是圆管的壁面。当管子的壁面相对于 管长而言非常小，且管子的内外壁面又保持均匀的 温度时，通过管壁的导热就是圆柱坐标系上的一维 导热问题。
t1 t 4 1 1 1 r3 r2 ln r1 ln r2 ln r4 r3 21l 22l 23l t1 t n 1 通式为： n 1 ri 1 ln ri i 1 2i l
28
3 通过球壁的导热 1 / r 1 / r2 t t 2 (t1 t 2 ) 温度分布：
27
t2 t3 t3 t4 t1 t2 d2 d3 d4 1 1 1 n n n 21l d1 22l d 2 23l d3
t1 t4 2 l (t1 t4 ) 3 3 1 1 di 1 1 di 1 ln ln 2 l i 1 i di di i 1 i
d dt 0 (1 bt) 0 dx dx
b 2 0 (t t ) c1 x c2 2
最后可求得其温度分布
t w1 t w2 b 2 b 2 t t (t w1 t w1 ) 2 2 b 1 2 (t w1 t w2 ) x
2
完整的数学描写
直接积分，得：
dt c1 t c1 x c2 dx t2 t1 c1 带入边界条件： c2 t1
t
t2 t1
x t1
4
t2 t1 线性 t x t1 分布 带入Fourier 定律 d t t t 2 1 dx
x t2 Δt
t1
t
12
【例】 有一砖砌墙壁，厚为 0.25m 。已知内外壁面
的温度分别为 25℃和 30℃。试计算墙壁内的温度 分布和通过的热流密度。
解：由平壁导热的温度分布
t
t2 t1
x t1
代入已知数据可以得出墙壁内 t=25+20x的温度分布表达式。
从附录查得红砖的λ=0.87W/(m℃),于是可以 计算出通过墙壁的热流密度 q (t1 t2 ) 17.4W / m2
ln(r r1 ) t t1 (t1 t2 ) ln(r2 r1 )
dt t1 t2 q dr r ln(r2 r1 )
求导
t1 t2 1 dt dr ln(r2 r1 ) r
2 W m
2 l (t1 t2 ) Φ 2 rlq ln(r2 r1 )
t1 t2 0 δ
λ =λ 0(1+bt) b>0
x
当b<0，λ=λ0(1+bt)，随着t增大，λ减小，高温区的温度梯度 dt/dx较大。
8
2) 多层平壁的一维稳态导热
多层平壁：由几层不同材料组成 例：房屋的墙壁 — 白灰内层、 水泥沙浆层、红砖（青砖） 主体层等组成 假设各层之间接触良好， 可以近似地认为接合面上 各处的温度相等
6
b t t w1 1 t t w1 2 x b t w2 t w1 1 t t w2 w1 2
二次曲线方程
2
d t b dt b dt 2 dx 1 bt dx 0 dx
13
例 一锅炉炉墙采用密度为 300kg/m3 的水泥珍珠岩制 作，壁厚 = 100 mm，已知内壁温度t1=500℃，外壁 温度 t2=50℃，求炉墙单位面积、单位时间的热损失。 [解] 材料的平均温度为： t = (t1 + t2)/2 = (500 + 50)/2 = 275 ℃ 查得：
{}W/(mk) 0.0651 0.000105 {t}C
W m
r2 Rl ln — 单位长度圆筒壁的导热 热阻 m C W 2 r1 1
26
2、通过多层圆筒壁的导热 由不同材料构成的多层圆筒壁 带有保温层的热力管道、嵌套的金属管道和结垢、 积灰的输送管道等 由不同材料制作的圆筒同心紧密结合而构成多层圆 筒壁 ，如果管子的壁厚远小于管子的长度，且管 壁内外边界条件均匀一致，那么在管子的径向方向 构成一维稳态导热问题。
15
【例】 由三层材料组成的加热炉炉墙。第一层为耐火
砖。第二层为硅藻土绝热层，第三层为红砖，各层的 厚 度 及 导 热 系 数 分 别 为 1 ＝ 240mm ， 1=1.04W/(m℃)， 2＝50mm, 2=0.15W/(m℃)， 3 ＝ 115mm, 3=0.63W/(m℃) 。炉墙内侧耐火砖的 表 面 温 度 为 1000℃ 。 炉 墙 外 侧 红 砖 的 表 面 温 度 为 60℃。试计算硅藻土层的平均温度及通过炉墙的导热 热流密度。
9 2015-4-29
q
t1 t 2
1
t 2 t3
1
2
t3 t 4
t1
t2 t3
2
3
3
q t4
由和分比关系
q
1
1
＋ 2
t1 t 4
2
＋
3
3
t1
r1
t2 r2
t3
r3
t4
推广到n层壁的情况:
q t1 t n 1
i i 1 i
n
10
层间分界面温度
q t1 t 2
1
t 2 t3
1
2
t3 t 4
t1
2
3
t2 t3
3
q
1 t2 t1 q 1 3 t3 t 4 q 3 2 t3 t 2 q 2
t4
11
3）接触热阻： 实际的两个固体表面之间不可能完全接触，只能是 局部的、甚至存在点接触，如图所示。只有在界面 上那些真正接触的点上，温度才是相等的。 当未接触的空隙中充满空气或其它气体时，由于气 体的热导率远远小于固体 ,就会对两个固体间的导热 过程产生附加热阻Rc，称之为接触热阻。 由于接触热阻的存在，使导热过程中两个接触表面 之间出现温差tc。
解：
已知 1＝0.24m, 1=1.04W/(m℃) 2＝0.05m, 2=0.15W/(m℃)
3＝0.115m, 3=0.63W/(m℃)
t1=1000℃ t2=60℃
16
1 2 3 1 2 3 1 t2 t1 q 700℃ 1 2 t3 t2 q 289℃ 2
获得两个系数
t2 t1 c1 ; ln(r2 r1 )
ln r1 c2 t1 (t2 t1 ) ln(r2 r1 )
23
将系数带入第二次积分结果
t2 t1 t t1 ln( r r1 ) ln( r2 r1 )
t1 r1
t2
显然，温度呈对数曲线分布
r r2
24
下面来看一下圆筒壁内部的热流密度和热流分布情况
18
如果采用单层玻璃窗，则散热损失为
10 Φ' 3333 .3W 0.003
是双层玻璃窗散热损失的 35 倍，可见采用双层玻璃 窗可以大大减少散热损失，节约能源。
19
第三类边界条件下的一维大平壁稳态导热 P30
通过复合平壁的导热 P32----- 自学，注意处理 方法
20
二、 通过圆筒壁的导热
t w1 t w 4 t w1 t w 4 Φ δ3 δ1 δ2 R λ1 R λ 2 R λ 3 Aλ1 Aλ2 Aλ3
15 5 94.3W 0.003 0.005 0.003 2 0.5 2 0.025 2 0.5
可见，单层玻璃的导热热阻为0.003 K/W，而空气 夹层的导热热阻为0.1 K/W，是玻璃的33.3倍。
1
§2 一维稳态导热
1 通过平壁的导热
条件：平壁、一维稳态导热(x方向) 长和宽 ≥ 10 厚度 内容：热流量计算、温度分布。
1)温度分布 已知平壁的壁厚为，两个表面温度： 分别维持均匀而恒定的温度t1和t2，即 边界条件：
x 0 : t t1 x : t t2
2