ansys教程22 热-应力耦合分析实例
ANSYS耦合场分析_热应力

例如: 如果结构网格包括在热模型中不存在的圆角 时,许多节点将落在热模型的外面。如果圆角足 够大而且热模型足够细致,圆角区域的载荷将不 能写出。
10-15
基本过程
在热-应力分析中,由温度求解得到的节点温度 将在结构分析中用作体载荷。 当在顺序求解使用手工方法时将热节点温度施加到结构单元上有两种选项。选择 的原则在于结构模型和热模型是否有相似的网格划分:
如果热和结构的单元有相同 的节点号码. . .
1
• 热模型自动转换为结构模型,使用 ETCHG 命令(见相应单元表格)。 • 温度可以直接从热分析结果文件读出 并使用LDREAD 命令施加到结构模型 上。
10-3
直接方法 - 例题
在第七章对流部分中,介绍了FLUID66和FLUID116热—流单元。该单元具有 热和压力自由度,因此是直接耦合场单元。
ANSYS有一些其他的耦合单元,具有结构,热,电,磁等自由度。绝大多数 的实际问题只涉及到少数几个物理场的耦合。这里提供了几个涉及到热现象 的直接耦合场分析。
• 不同场之间使用统一的单位制。例如,在热-电分析中,如果电瓦单位使 用瓦(焦耳/秒),热单位就不能使用Btu/s。
• 由于需要迭代计算,热耦合场单元不能使用子结构。
10-6
直接方法 - 加载, 求解, 后处理
在直接方法的加载,求解,后处理中注意以下方面: • 如果对带有温度自由度的耦合场单元选择 瞬态 分析类型的话: – 瞬态温度效果可以在所有耦合场单元中使用。 – 瞬态电效果(电容,电感)不能包括在热-电分析中(除非只是TEMP和VOLT自由度 被 激活)。 – 带有磁向量势自由度的耦合场单元可以用来对瞬态磁场问题建模(如,SOLID62). 带 有标量势自由度的单元只能模拟静态现象(SOLID5)。 • 学习每种单元的自由度和允许的载荷。耦合场单元允许的相同位置(节点,单元面等)施加多 种类型的载荷 (D, F, SF, BF) 。 • 耦合场分析可以使高度非线性的。考虑使用Predictor 和 Line Search 功能改善收敛性。 • 考虑使用Multi-Plots功能将不同场的结果同时输出到多个窗口中。
Ansys 应力分析ppt课件

实体单元
网格划分
FEA 模型
Ansys 应力分析
应力分析 - 前处理
...网格划分
• 网格划分的三个步骤:
• 定义单元属性 • 指定网格控制 • 生成网格
• 单元属性 是网格划分前必须建立的有限单元模型
属性。它们包括:
• 单元类型 • 实常数 • 材料性质
Ansys 应力分析
应力分析 - 前处理
应力分析 - 前处理
B. 几何模型
• 典型的实体模型是由体、面、线和关键点组成的 。
• 体 由面围成,用来描述实体物体。 • 面 由线围成,用来描述物体的表面或者块、壳等。 • 线 由关键点组成,用来描述物体的边。 • 关键点 是三维空间的位置, 用来描述物体的顶点。
体
面
线和关键点
Ansys 应力分析
• 在弹出的对话框中,选择 No defeaturing * (缺省值) ,按下 OK (默
认其他选项)。 • 在第二个对话框中选择想要的文件并
点击OK.
• 或使用 IGESIN 命令:
• /aux15 • ioptn,iges,nodefeat • igesin, • finish
* 关于 No Defeaturing 及 Defeaturing 方法及其他选项将在后面论述
• 求解
• 施加载荷 • 求解
• 后处理
• 结果评价 • 检查结果的正确性
Ansys 应力分析
前处理 求解 后处理
应力分析
...应力分析步骤
• 注意!ANSYS 的主菜单也是按照前处理、求解、 后处理来组织的
Ansys 应力分析
应力分析
...应力分析步骤
• 前处理器 (在ANSYS中称为 PREP7) 提供了对程序 的主要输入
热分析(ansys教程)

1. 对流边界条件:需要提供对流 系数、流体温度和表面传热系数 等信息。
3. 初始条件:确保初始温度等初 始条件设置合理,不会导致求解 过程不稳定。
求解收敛问题
•·
1. 迭代方法:选择合适的迭代方 法,如共轭梯度法、牛顿-拉夫森 法等。
2. 松弛因子调整:根据求解过程, 适时调整松弛因子,以提高求解 收敛速度。
稳态热分析的步骤
建立模型
使用ANSYS的几何建模工具创建分析对象 的几何模型。
后处理
使用ANSYS的后处理功能,查看和分析结 果,如温度云图、等温线等。
网格化
对模型进行网格化,以便进行数值计算。 ANSYS提供了多种网格化工具和选项,可 以根据需要进行选择。
求解
运行求解器以获得温度分布和其他热分析 结果。
电子设备散热分析
研究电子设备在工作状态下的散热性能,提高设备可靠性和 使用寿命。
06 热分析的常见问题与解决 方案
网格划分问题
网格划分是热分析中重要 的一步,如果处理不当, 可能导致求解精度和稳定 性问题。
•·
1. 网格无关性:确保随着 网格数量的增加,解的收 敛性得到改善,且解不再 发生大的变化。
03 稳态热分析
稳态热分析的基本原理
01
稳态热分析是用于确定物体在稳定热载荷作用下的温度分布。在稳态条件下, 物体的温度场不随时间变化,热平衡状态被建立,流入和流出物体的热量相等 。
02
稳态热分析基于能量守恒原理,即流入物体的热量等于流出物体的热量加上物 体内部热量的变化。
03
稳态热分析通常用于研究物体的长期热行为,例如散热器的性能、电子设备的 热设计等。
热分析的基本原理基于能量守恒定律,即物体内部的能量变化应满足能量守恒关系。
ansys磁热耦合实例

ANSYS磁热耦合实例简介磁热耦合是一种将磁场和热场相互作用考虑在内的仿真方法。
ANSYS是一款广泛应用于工程领域的仿真软件,提供了强大的磁场和热场仿真功能。
本文将通过一个实例来介绍如何在ANSYS中进行磁热耦合仿真。
实例背景假设我们需要设计一个电机,其中的线圈将在工作过程中产生磁场,并在电流通过时发热。
为了确保电机的正常运行,我们需要对磁场和热场进行耦合仿真,以评估线圈的性能和温度分布。
步骤一:建立几何模型首先,在ANSYS中建立电机的几何模型。
可以使用ANSYS提供的几何建模工具,或者导入其他CAD软件生成的几何模型。
步骤二:设置材料属性根据电机的实际情况,设置线圈和其他部件的材料属性。
材料属性包括磁导率、热导率、比热容等。
步骤三:设置边界条件根据电机的工作条件,设置边界条件。
例如,设置线圈的电流密度和温度,设置外部磁场的大小和方向。
步骤四:设置求解器选择合适的求解器来求解磁场和热场方程。
ANSYS提供了多种求解器,可以根据实际情况选择。
步骤五:进行仿真计算使用ANSYS的仿真计算功能,对磁场和热场进行耦合仿真计算。
根据设置的边界条件和材料属性,求解磁场和热场的分布情况。
步骤六:分析结果根据仿真计算得到的结果,分析线圈的磁场分布和温度分布。
评估线圈的性能和温度是否满足设计要求。
实例详解建立几何模型在ANSYS中,我们可以使用几何建模工具来创建电机的几何模型。
可以绘制线圈、转子、定子等部件,并设置其尺寸和形状。
设置材料属性在ANSYS中,可以为线圈和其他部件设置材料属性。
通过设置磁导率、热导率、比热容等参数,来描述材料的磁性和热性能。
设置边界条件在ANSYS中,可以设置线圈的电流密度和温度,以及外部磁场的大小和方向。
这些边界条件将影响磁场和热场的分布情况。
设置求解器在ANSYS中,可以选择适合的求解器来求解磁场和热场方程。
根据问题的复杂程度和求解速度的要求,选择合适的求解器。
进行仿真计算使用ANSYS的仿真计算功能,对磁场和热场进行耦合仿真计算。
ANSYS热应力分析经典例题

ANSYS热应力分析例题实例1——圆简内部热应力分折:有一无限长圆筒,其核截面结构如图13—1所示,简内壁温度为200℃,外壁温度为20℃,圆筒材料参数如表13.1所示,求圆筒内的温度场、应力场分布。
该问题属于轴对称问题。
由于圆筒无限长,忽略圆筒端部的热损失。
沿圆筒纵截面取宽度为10M的如图1 3—2所示的矩形截面作为几何模型。
在求解过程中采用间接求解法和直接求解法两种方法进行求解。
间接法是先选择热分析单元,对圆筒进行热分析,然后将热分析单元转化为相应的结构单元,对圆筒进行结构分析;直接法是采用热应力藕合单元,对圆筒进行热力藕合分析。
/filname,exercise1-jianjie/title,thermal stresses in a long/prep7 $Et,1,plane55Keyopt,1,3,1 $Mp,kxx,1,70Rectng,0.1,0.15,0,0.01 $Lsel,s,,,1,3,2Lesize, all,,,20 $Lsel,s,,,2,4,2Lesize,all,,,5 $Amesh,1 $Finish/solu $Antype,staticLsel,s,,,4 $Nsll,s,1 $d,all,temp,200lsel,s,,,2 $nsll,s,1 $d,all,temp,20allsel $outpr,basic,allsolve $finish/post1 $Set,last/plopts,info,onPlnsol,temp $Finish/prep7 $Etchg,ttsKeyopt,1,3,1 $Keyopt,1,6,1Mp,ex,1,220e9 $Mp,alpx,,1,3e-6 $Mp,prxy,1,0.28Lsel,s,,,4 $Nsll,s,1 $Cp,8,ux,allLsel,s,,,2 $Nsll,s,1 $Cp,9,ux,allAllsel $Finish/solu $Antype,staticD,all,uy,0 $Ldread,temp,,,,,,rthAllsel $Solve $Finish/post1/title,radial stress contoursPlnsol,s,x/title,axial stress contoursPlnsol,s,y/title,circular stress contoursPlnsol,s,z/title,equvialent stress contoursPlnsol,s,eqv $finish/filname,exercise1-zhijie/title,thermal stresses in a long/prep7 $Et,1,plane13Keyopt,1,1,4 $Keyopt,1,3,1Mp,ex,1,220e9 $Mp,alpx,,1,3e-6 $Mp,prxy,1,0.28MP,KXX,1,70Rectng,0.1,0.15,0,0.01 $Lsel,s,,,1,3,2Lesize, all,,,20 $Lsel,s,,,2,4,2Lesize,all,,,5 $Amesh,1Lsel,s,,,4 $Nsll,s,1 $Cp,8,ux,allLsel,s,,,2 $Nsll,s,1 $Cp,9,ux,allALLSEL $Finish/solu $Antype,staticLsel,s,,,4 $Nsll,s,1 $d,all,temp,200lsel,s,,,2 $nsll,s,1 $d,all,temp,20allsel $outpr,basic,allsolve $finish/post1 $Set,last/plopts,info,onPlnsol,temp/title,radial stress contoursPlnsol,s,x/title,axial stress contoursPlnsol,s,y/title,circular stress contoursPlnsol,s,z/title,equvialent stress contoursPlnsol,s,eqv $finish318页实例2——冷却栅管的热应力分析图中为一冷却栅管的轴对称结构示意图,其中管内为热流体,温度为200℃,压力为10Mp,对流系数为11 0W/(m2•℃);管外为空气,温度为25℃,对流系数为30w/(mz.℃)。
基于ANSYS的发动机气门热一应力耦合分析

l
一
i l i
…
…
{
l 、 一
图 2有限元 网格 划分图
} 斗 ~ + ~ } ÷ … } 卜卜 卜 卜 H~ }
1 _ 3载荷与边界 条件 的施加 f 1 忾 门材料参数 的选择 。 本 文以工作条件 比较恶劣 的排 气 门( 盘部 有 凹槽 ) 为研究 对象 , 根 据对气 门材料 的分析 , 取气 门材料 为 2 1 - 4 N钢 , 图 5气 门盘部表 面沿径向应 力分布 图 该气门材料的性能参数为 : 密度 7 8 3 3 k s , 弹性模量 2 1 0 G P a , 比热 图5 为气 门盘部沿 径向应力分布 图 , x轴为径 向方 向, Y轴 为等效 4 4 8 J / ( k g ・ K ) , 热传 导系数 2 5 . 9 6 , 泊松 比 0 . 3 。 应力 。由图可知 : 在 凹槽边缘 部分应力 变化非 常明显 ; 在接 近气 门盘部 f 2 1 边界条 件的选择 。 本文对气 门的 1 , 4 进行分析 , 需要对 其施 加对 边缘 的位置 , 应力 发生 了一 次明显 的突变 , 这是 因为在该位 置受 到落座 称 约束 。 假设气 门盘部在落座 时处于理想 的弹 胜状态 , 气 门落 座时受到 力 的作用 ; 在气 门盘部边缘位 置 , 应 力达到最小 。 气 门座圈对 它的作用 ,所 以要 对气 门和气 门座 圈之间施 加 Y方 向 ( 轴 向) 的约 束 , 在气 门锁夹 槽和 锁夹位 置 , 因为气 门锁 夹是 将气 门弹 簧座 和气 门杆锁住 ,使气 门能够沿 Y方 向上下运 动 ,所 以要 对接触 面施加 x、 z 方 向( 径向) 的约束 。 对气 门进行 热一 应力耦 合分析 的 时候 , 在热 分析 的过程 中 , 需 要对 r丁… f Ⅲ … r T … rr ~ _ r 气 门施加温度 边界 条件 , 由于气 门工 作时 , 气 门各 个部 分 温度不 同 , 所 眦 上 I … 上 l … L } … ~ } … 1 i { … ~ L ; ~ L』 } ~ _ L i ~ 以需要对 气门施加非线 性温度载荷 , 如图 3 所 示。
ansys 热 结构耦合分析

第21章热-结构耦合分析热-结构耦合问题是结构分析中通常遇到的一类耦合分析问题。
由于结构温度场的分布不均会引起结构的热应力,或者结构部件在高温环境中工作,材料受到温度的影响会发生性能的改变,这些都是进行结构分析时需要考虑的因素。
为此需要先进行相应的热分析,然后在进行结构分析。
热分析用于计算一个系统或部件的温度分布及其它热物理参数,如热量的获取或损失、热梯度、热流密度(热通量)等。
本章主要介绍在ANSYS中进行稳态、瞬态热分析的基本过程,并讲解如何完整的进行热-结构耦合分析。
21.1 热-结构耦合分析简介热-结构耦合分析是指求解温度场对结构中应力、应变和位移等物理量影响的分析类型。
对于热-结构耦合分析,在ANSYS中通常采用顺序耦合分析方法,即先进行热分析求得结构的温度场,然后再进行结构分析。
且将前面得到的温度场作为体载荷加到结构中,求解结构的应力分布。
为此,首先需要了解热分析的基本知识,然后再学习耦合分析方法。
21.1.1 热分析基本知识ANSYS热分析基于能量守恒原理的热平衡方程,用有限元法计算各节点的温度,并导出其它热物理参数。
ANSYS热分析包括热传导、热对流及热辐射三种热传递方式。
此外,还可以分析相变、有内热源、接触热阻等问题。
热传导可以定义为完全接触的两个物体之间或一个物体的不同部分之间由于温度梯度而引起的内能的交换。
热对流是指固体的表面和与它周围接触的流体之间,由于温差的存在引起的热量的交换。
热辐射指物体发射电磁能,并被其它物体吸收转变为热的热量交换过程。
如果系统的净热流率为0,即流入系统的热量加上系统自身产生的热量等于流出系统的热量:q流入+q生成-q流出=0,则系统处于热稳态。
在稳态热分析中任一节点的温度不随时间变化。
瞬态传热过程是指一个系统的加热或冷却过程。
在这个过程中系统的温度、热流率、热边界条件以及系统内能随时间都有明显变化。
ANSYS热分析的边界条件或初始条件可分为七种:温度、热流率、热流密度、对流、辐射、绝热、生热。
ansys热分析实例教程
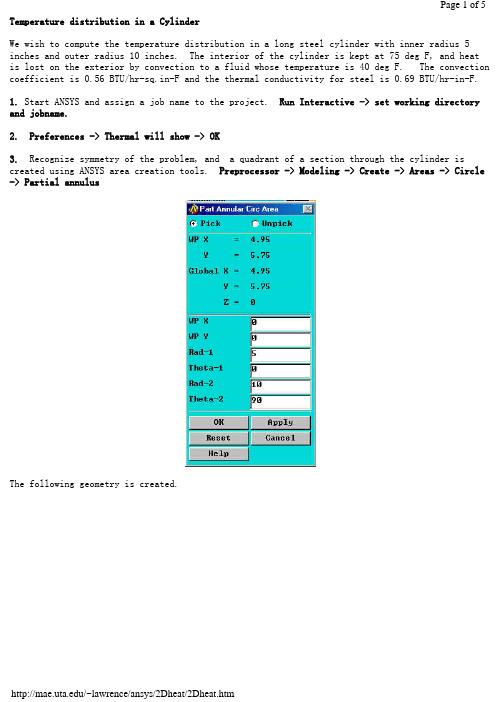
Temperature distribution in a CylinderWe wish to compute the temperature distribution in a long steel cylinder with inner radius 5 inches and outer radius 10 inches. The interior of the cylinder is kept at 75 deg F, and heatis lost on the exterior by convection to a fluid whose temperature is 40 deg F. The convection coefficient is 0.56 BTU/hr-sq.in-F and the thermal conductivity for steel is 0.69 BTU/hr-in-F.1. Start ANSYS and assign a job name to the project. Run Interactive -> set working directory and jobname.2. Preferences -> Thermal will show -> OK3. Recognize symmetry of the problem, and a quadrant of a section through the cylinder is created using ANSYS area creation tools. Preprocessor -> Modeling -> Create -> Areas -> Circle -> Partial annulusThe following geometry is created.4. Preprocessor -> Element Type -> Add/Edit/Delete -> Add -> Thermal Solid -> Solid 8 node 77 -> OK -> Close5. Preprocessor -> Material Props -> Isotropic -> Material Number 1 -> OKEX = 3.E7 (psi)DENS = 7.36E-4 (lb sec^2/in^4)ALPHAX = 6.5E-6PRXY = 0.3KXX = 0.69 (BTU/hr-in-F)6. Mesh the area and refine using methods discussed in previous examples.7. Preprocessor -> Loads -> Apply -> Temperatures -> NodesSelect the nodes on the interior and set the temperature to 75.8. Preprocessor -> Loads -> Apply -> Convection -> LinesSelect the lines defining the outer surface and set the convection coefficient to 0.56 and the fluid temp to 40.9. Preprocessor -> Loads -> Apply -> Heat Flux -> LinesTo account for symmetry, select the vertical and horizontal lines of symmetry and set the heat flux to zero.10. Solution -> Solve current LS11. General Postprocessor -> Plot Results -> Nodal Solution -> TemperaturesThe temperature on the interior is 75 F and on the outside wall it is found to be 45. These results can be checked using results from heat transfer theory.BackThermal Stress of a Cylinder using Axisymmetric ElementsA steel cylinder with inner radius 5 inches and outer radius 10 inches is 40 inches long and has spherical end caps. The interior of the cylinder is kept at 75 deg F, and heat is lost on the exterior by convection to a fluid whose temperature is 40 deg F. The convection coefficient is 0.56 BTU/hr-sq.in-F. Calculate the stresses in the cylinder caused by the temperature distribution.The problem is solved in two steps. First, the geometry is created, the preference set to'thermal', and the heat transfer problem is modeled and solved. The results of the heat transfer analysis are saved in a file 'jobname.RTH' (Results THermal analysis) when you issue a save jobname.db command.Next the heat transfer boundary conditions and loads are removed from the mesh, the preference is changed to 'structural', the element type is changed from 'thermal' to 'structural', and the temperatures saved in 'jobname.RTH' are recalled and applied as loads.1. Start ANSYS and assign a job name to the project. Run Interactive -> set working directory and jobname.2. Preferences -> Thermal will show -> OK3. A quadrant of a section through the cylinder is created using ANSYS area creation tools.4. Preprocessor -> Element Type -> Add/Edit/Delete -> Add -> Solid 8 node 77 -> OK ->Options -> K3 Axisymmetric -> OK5. Preprocessor -> Material Props -> Isotropic -> Material Number 1 -> OKEX = 3.E7 (psi)DENS = 7.36E-4 (lb sec^2/in^4)ALPHAX = 6.5E-6PRXY = 0.3KXX = 0.69 (BTU/hr-in-F)6. Mesh the area using methods discussed in previous examples.7. Preprocessor -> Loads -> Apply -> Temperatures -> NodesSelect the nodes on the interior and set the temperature to 75.8. Preprocessor -> Loads -> Apply -> Convection -> LinesSelect the lines defining the outer surface and set the coefficient to 0.56 and the fluid temp to 40.9. Preprocessor -> Loads -> Apply -> Heat Flux -> LinesSelect the vertical and horizontal lines of symmetry and set the heat flux to zero.10. Solution -> Solve current LS11. General Postprocessor -> Plot Results -> Nodal Solution -> TemperatureThe temperature on the interior is 75 F and on the outside wall it is found to be 43.12. File -> Save Jobname.db13. Preprocessor -> Loads -> Delete -> Delete All -> Delete All Opts.14. Preferences -> Structural will show, Thermal will NOT show.15. Preprocessor -> Element Type -> Switch Element Type -> OK (This changes the element to structural)16. Preprocessor -> Loads -> Apply -> Displacements -> Nodes(Fix nodes on vertical and horizontal lines of symmetry from crossing the lines of symmetry.)17. Preprocessor -> Loads -> Apply -> Temperature -> From Thermal AnalysisSelect Jobname.RTH (If it isn't present, look for the default 'file.RTH' in the root directory)18. Solution -> Solve Current LS19. General Postprocessor -> Plot Results -> Element Solution - von Mises StressThe von Mises stress is seen to be a maximum in the end cap on the interior of the cylinder and would govern a yield-based design decision.Back。
