小学奥数容斥原理专题训练
小学奥数总复习第七讲《容斥原理》练习
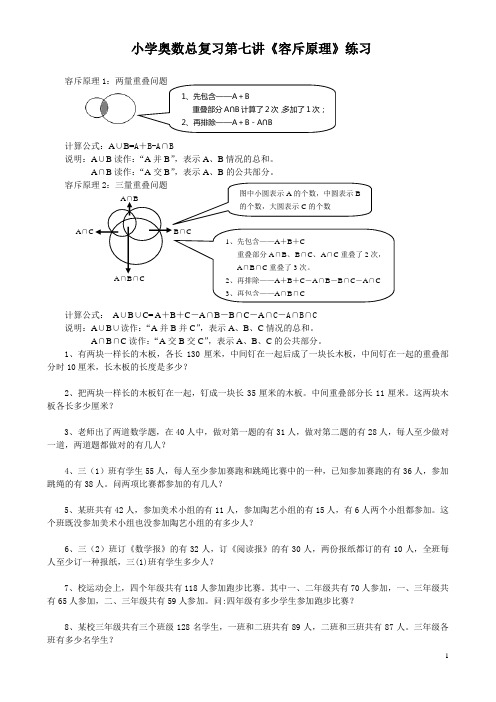
1、先包含——A +B 重叠部分A ∩B 计算了2次,多加了1次;2、再排除——A +B -A ∩B小学奥数总复习第七讲《容斥原理》练习容斥原理1:两量重叠问题计算公式:A ∪B=A +B-A ∩B说明:A ∪B 读作:“A 并B ”,表示A 、B 情况的总和。
A ∩B 读作:“A 交B ”,表示A 、B 的公共部分。
容斥原理2:三量重叠问题计算公式: A ∪B ∪C= A +B +C -A ∩B -B ∩C -A ∩C -A ∩B ∩C说明:A ∪B ∪读作:“A 并B 并C ”,表示A 、B 、C 情况的总和。
A ∩B ∩C 读作:“A 交B 交C ”,表示A 、B 、C 的公共部分。
1、有两块一样长的木板,各长130厘米,中间钉在一起后成了一块长木板,中间钉在一起的重叠部分时10厘米,长木板的长度是多少?2、把两块一样长的木板钉在一起,钉成一块长35厘米的木板。
中间重叠部分长11厘米。
这两块木板各长多少厘米?3、老师出了两道数学题,在40人中,做对第一题的有31人,做对第二题的有28人,每人至少做对一道,两道题都做对的有几人?4、三(1)班有学生55人,每人至少参加赛跑和跳绳比赛中的一种,已知参加赛跑的有36人,参加跳绳的有38人。
问两项比赛都参加的有几人?5、某班共有42人,参加美术小组的有11人,参加陶艺小组的有15人,有6人两个小组都参加。
这个班既没参加美术小组也没参加陶艺小组的有多少人?6、三(2)班订《数学报》的有32人,订《阅读报》的有30人,两份报纸都订的有10人,全班每人至少订一种报纸,三(1)班有学生多少人?7、校运动会上,四个年级共有118人参加跑步比赛。
其中一、二年级共有70人参加,一、三年级共有65人参加,二、三年级共有59人参加。
问:四年级有多少学生参加跑步比赛?8、某校三年级共有三个班级128名学生,一班和二班共有89人,二班和三班共有87人。
三年级各班有多少名学生?A ∩C A ∩B ∩C B ∩C A ∩B 图中小圆表示A 的个数,中圆表示B 的个数,大圆表示C 的个数 1、先包含——A +B +C 重叠部分A ∩B 、 B ∩C 、 A ∩C 重叠了2次, A ∩B ∩C 重叠了3次。
小学奥数之容斥原理

五.容斥原理问题1.有100种赤贫.其中含钙的有68种,含铁的有43种,那么,同时含钙和铁的食品种类的最大值和最小值分别是( )A 43,25B 32,25 C32,15 D 43,11解:根据容斥原理最小值68+43-100=11最大值就是含铁的有43种2.在多元智能大赛的决赛中只有三道题.已知:(1)某校25名学生参加竞赛,每个学生至少解出一道题;(2)在所有没有解出第一题的学生中,解出第二题的人数是解出第三题的人数的2倍:(3)只解出第一题的学生比余下的学生中解出第一题的人数多1人;(4)只解出一道题的学生中,有一半没有解出第一题,那么只解出第二题的学生人数是( )A,5 B,6 C,7 D,8解:根据“每个人至少答出三题中的一道题”可知答题情况分为7类:只答第1题,只答第2题,只答第3题,只答第1、2题,只答第1、3题,只答2、3题,答1、2、3题。
分别设各类的人数为a1、a2、a3、a12、a13、a23、a123由(1)知:a1+a2+a3+a12+a13+a23+a123=25…①由(2)知:a2+a23=(a3+ a23)×2……②由(3)知:a12+a13+a123=a1-1……③由(4)知:a1=a2+a3……④再由②得a23=a2-a3×2……⑤再由③④得a12+a13+a123=a2+a3-1⑥然后将④⑤⑥代入①中,整理得到a2×4+a3=26由于a2、a3均表示人数,可以求出它们的整数解:当a2=6、5、4、3、2、1时,a3=2、6、10、14、18、22又根据a23=a2-a3×2……⑤可知:a2>a3因此,符合条件的只有a2=6,a3=2。
然后可以推出a1=8,a12+a13+a123=7,a23=2,总人数=8+6+2+7+2=25,检验所有条件均符。
故只解出第二题的学生人数a2=6人。
3.一次考试共有5道试题。
做对第1、2、3、、4、5题的分别占参加考试人数的95%、80%、79%、74%、85%。
小学奥数计数之容斥原理练习【三篇】

【导语】天⾼鸟飞,海阔鱼跃,学习这舞台,秀出你独特的精彩⽤好分秒时间,积累点滴知识,解决疑难问题,学会举⼀反三。
以下是为⼤家整理的《⼩学奥数计数之容斥原理练习【三篇】》供您查阅。
【第⼀篇】1.⼀个班有45个⼩学⽣,统计借课外书的情况是:全班学⽣都借有语⽂或数学课外书.借语⽂课外书的有39⼈,借数学课外书的有32⼈.语⽂、数学两种课外书都借的有⼈. 3.在1~100的⾃然数中,是5的倍数或是7的倍数的数有个. 4.某区100个外语教师懂英语或俄语,其中懂英语的75⼈,既懂英语⼜懂俄语的20⼈,那么懂俄语的教师为⼈. 5.六⼀班有学⽣46⼈,其中会骑⾃⾏车的17⼈,会游泳的14⼈,既会骑车⼜会游泳的4⼈,问两样都不会的有⼈. 6.在1⾄10000中不能被5或7整除的数共有个. 7.在1⾄10000之间既不是完全平⽅数,也不是完全⽴⽅数的整数有个. 8.某班共有30名男⽣,其中20⼈参加⾜球队,12⼈参加蓝球队,10⼈参加排球队.已知没⼀个⼈同时参加3个队,且每⼈⾄少参加⼀个队,有6⼈既参加⾜球队⼜参加蓝球队,有2⼈既参加蓝球队⼜参加排球队,那么既参加⾜球队⼜参加排球队的有⼈. 9.分母是1001的最简真分数有个. 10.在100个学⽣中,⾳乐爱好者有56⼈,体育爱好者有75⼈,那么既爱好⾳乐,⼜爱好体育的⼈最少有⼈,最多有⼈.【第⼆篇】[ 例1 ] 洗好的8块⼿帕夹在绳⼦上晾⼲,同⼀个夹⼦夹住相邻的两块⼿帕的两边,这样⼀共要多少个夹⼦? 分析:两块⼿帕有⼀边重叠,⽤3个夹⼦。
三块⼿帕有两边重叠,⽤4个夹⼦,我们发现夹⼦数总⽐⼿帕数多1,因此8块⼿帕就要⽤9个夹⼦。
[ 例2 ] 把图画每两张重叠在⼀起钉在墙上,现在有5张画要多少个图钉呢? 分析:每排两张画要6个图钉,每排三张画要8个图钉,每排四张画要10个图钉。
可以看出,图画每增加⼀张,图钉就要增加2颗,那么5张画要12个图钉。
1.有两块⽊板,⼀块长72厘⽶,另⼀块长56厘⽶,如果把两块⽊板重叠后钉成⼀块⽊板,重叠部分是20厘⽶。
小学奥数7-7-4 容斥原理之数论问题.专项练习及答案解析

1. 了解容斥原理二量重叠和三量重叠的内容;2. 掌握容斥原理的在组合计数等各个方面的应用.一、两量重叠问题 在一些计数问题中,经常遇到有关集合元素个数的计算.求两个集合并集的元素的个数,不能简单地把两个集合的元素个数相加,而要从两个集合个数之和中减去重复计算的元素个数,即减去交集的元素个数,用式子可表示成:A B A B A B =+-(其中符号“”读作“并”,相当于中文“和”或者“或”的意思;符号“”读作“交”,相当于中文“且”的意思.)则称这一公式为包含与排除原理,简称容斥原理.图示如下:A 表示小圆部分,B 表示大圆部分,C 表示大圆与小圆的公共部分,记为:A B ,即阴影面积.图示如下:A 表示小圆部分,B 表示大圆部分,C 表示大圆与小圆的公共部分,记为:A B ,即阴影面积.包含与排除原理告诉我们,要计算两个集合A B 、的并集A B 的元素的个数,可分以下两步进行:第一步:分别计算集合A B 、的元素个数,然后加起来,即先求A B +(意思是把A B 、的一切元素都“包含”进来,加在一起);第二步:从上面的和中减去交集的元素个数,即减去C A B =(意思是“排除”了重复计算的元素个数).二、三量重叠问题A 类、B 类与C 类元素个数的总和A =类元素的个数B +类元素个数C +类元素个数-知识要点教学目标1.先包含——A B +重叠部分A B 计算了2次,多加了1次;2.再排除——A B A B +-把多加了1次的重叠部分A B 减去.7-7-4 容斥原理之数论问题既是A 类又是B 类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数.用符号表示为:A B C A B C A B B C A C A B C =++---+.图示如下:在解答有关包含排除问题时,我们常常利用圆圈图(韦恩图)来帮助分析思考.【例 1】 在1~100的全部自然数中,不是3的倍数也不是5的倍数的数有多少个?A B【考点】容斥原理之数论问题 【难度】2星 【题型】解答【解析】 如图,用长方形表示1~100的全部自然数,A 圆表示1~100中3的倍数,B 圆表示1~100中5的倍数,长方形内两圆外的部分表示既不是3的倍数也不是5的倍数的数.由1003331÷=可知,1~100中3的倍数有33个;由100520÷=可知,1~100中5的倍数有20个;由10035610÷⨯=()可知,1~100既是3的倍数又是5的倍数的数有6个.由包含排除法,3或5的倍数有:3320647+-=(个).从而不是3的倍数也不是5的倍数的数有1004753-=(个).【答案】53【巩固】 在自然数1100~中,能被3或5中任一个整除的数有多少个?【考点】容斥原理之数论问题 【难度】2星 【题型】解答【解析】 1003331÷=,100520÷=,10035610÷⨯=().根据包含排除法,能被3或5中任一个整除的数有3320647+-=(个).【答案】47【巩固】 在前100个自然数中,能被2或3整除的数有多少个?【考点】容斥原理之数论问题 【难度】2星 【题型】解答【解析】 如图所示,A 圆内是前100个自然数中所有能被2整除的数,B 圆内是前100个自然数中所有能被3整除的数,C 为前100个自然数中既能被2整除也能被3整除的数.例题精讲 图中小圆表示A 的元素的个数,中圆表示B 的元素的个数,大圆表示C 的元素的个数.1.先包含:A B C ++ 重叠部分A B 、B C 、C A 重叠了2次,多加了1次. 2.再排除:A B C A B B C A C ++--- 重叠部分A B C 重叠了3次,但是在进行A B C ++- A B B C A C --计算时都被减掉了. 3.再包含:A B C A B B C A C A B C ++---+.前100个自然数中能被2整除的数有:100250÷=(个).由1003331÷=知,前100个自然数中能被3整除的数有:33个.由10023164÷⨯=()知,前100个自然数中既能被2整除也能被3整除的数有16个.所以A 中有50个数,B 中有33个数,C 中有16个数.因为A ,B 都包含C ,根据包含排除法得到,能被2或3整除的数有:50331667+-=(个).【答案】67【例 2】 在从1至1000的自然数中,既不能被5除尽,又不能被7除尽的数有多少个?【考点】容斥原理之数论问题 【难度】2星 【题型】解答【解析】 1~1000之间,5的倍数有10005⎡⎤⎢⎥⎣⎦=200个,7的倍数有10007⎡⎤⎢⎥⎣⎦=142个,因为既是5的倍数,又是7的倍数的数一定是35的倍数,所以这样的数有100035⎡⎤⎢⎥⎣⎦=28个.所以既不能被5除尽,又不能被7除尽的数有1000-200-142+-28=686个.【答案】686【巩固】 求在1至100的自然数中能被3或7整除的数的个数.【考点】容斥原理之数论问题 【难度】2星 【题型】解答【解析】 记 A :1~100中3的倍数,1003331÷=,有33个;B :1~100中7的倍数,1007142÷=,有14个;A B :1~100中3和7的公倍数,即21的倍数,10021416÷=,有4个.依据公式,1~100中3的倍数或7的倍数共有3314443+-=个,则能被3或7整除的数的个数为43个.【答案】43【例 3】 以105为分母的最简真分数共有多少个?它们的和为多少?【考点】容斥原理之数论问题 【难度】4星 【题型】解答【解析】 以105为分母的最简真分数的分子与105互质,105=3×5×7,所以也是求1到105不是3、5、7倍数的数有多少个,3的倍数有35个,5的倍数有21个,7的倍数有15个,15的倍数有7个,21的倍数有5个,35的倍数有3个,105的倍数有1个,所以105以内与105互质的数有105-35-21-15+7+5+3-1=48个,显然如果n与105互质,那么(105-n )与n 互质,所以以105为分母的48个最简真分数可两个两个凑成1,所以它们的和为24.【答案】48个,和24【巩固】 分母是385的最简真分数有多少个?并求这些真分数的和.【考点】容斥原理之数论问题 【难度】4星 【题型】解答【解析】 385=5×7×11,不超过385的正整数中被5整除的数有77个;被7整除的数有55个;被11整除的数有35个;被77整除的数有5个;被35整除的数有11个;被55整除的数有7个;被385整除的数有1个;最简真分数的分子可以有385-77-55-35+5+11+7-1=240.对于某个分数a/385如果是最简真分数的话,那么(385-a )/385也是最简真分数,所以最简真分数可以每两个凑成整数1,所以这些真分数的和为120.【答案】240个,120个【例 4】 在1至2008这2008个自然数中,恰好是3、5、7中两个数的倍数的数共有个.【考点】容斥原理之数论问题 【难度】3星 【题型】填空【关键词】西城实验【解析】 1到2008这2008个自然数中,3和5的倍数有200813315⎡⎤=⎢⎥⎣⎦个,3和7的倍数有20089521⎡⎤=⎢⎥⎣⎦个,5和7的倍数有20085735⎡⎤=⎢⎥⎣⎦个,3、5和7的倍数有200819105⎡⎤=⎢⎥⎣⎦个.所以,恰好是3、5、7中两个数的倍数的共有1331995195719228-+-+-=个.【答案】228个【例 5】 求1到100内有____个数不能被2、3、7中的任何一个整除。
小学数学奥林匹克辅导及练习容斥原理(二)(含答案)-.doc

容斥原理(二)【例题分析】例1. 有25人参加跳远达标赛,每人跳三次,每人至少有一次达到优秀。
第一次达到优秀的有10人,第二次达到优秀的有13人,第三次达到优秀的有15人,三次都达到优秀的只有1人。
只有两次达到优秀的有多少人?分析与解:“每人至少有一次达到优秀”说明没有三次都没达到优秀的。
要求只有两次达到优秀的人数,就是求重叠两层的部分(图中阴影部分)。
(人)答:只有两次达到优秀的有11人。
例2. 在一个炎热的夏日,几个小朋友去冷饮店,每人至少要了一样冷饮,其中有6人要了冰棍,6人要了汽水,4人要了雪碧,只要冰棍和汽水的有3人,只要冰棍和雪碧的没有,只要汽水和雪碧的有1人;三样都要的有1人。
问:共有几个小朋友去了冷饮店?分析与解:根据题意画图。
方法一:(人)方法二:(人)答:共有10个小朋友去了冷饮店。
例3. 有28人参加田径运动会,每人至少参加两项比赛。
已知有8人没参加跑的项目,参加投掷项目的人数与参加跑和跳两项的人数都是17人。
问:只参加跑和投掷两项的有多少人?分析与解:“每人至少参加两项比赛”说明没有不参加的,也没有参加一项比赛的,我们可以在下图中参加一项的区域用0表示。
(人)答:只参加跑和投掷两项的有3人。
例4. 某校六年级二班有49人参加了数学、英语、语文学习小组,其中数学有30人参加,英语有20人参加,语文小组有10人。
老师告诉同学既参加数学小组又参加语文小组的有3人,既参加数学又参加英语和既参加英语又参加语文的人数均为质数,而三种全参加的只有1人,求既参加英语又参加数学小组的人数。
分析与解:根据已知条件画出图。
三圆盖住的总体为49人,假设既参加数学又参加英语的有x人,既参加语文又参加英语的有y人,可以列出这样的方程:整理后得:由于x、y均为质数,因而这两个质数中必有一个偶质数2,另一个质数为7。
答:既参加英语又参加数学小组的为2人或7人。
例5. 某班同学参加升学考试,得满分的人数如下:数学20人,语文20人,英语20人,数学、英语两科满分者8人,数学、语文两科满分者7人,语文、英语两科满分者9人,三科都没得满分者3人。
小学数学六年级奥数《容斥原理(1)》练习题(含答案)

小学数学六年级奥数《容斥原理(1)》练习题(含答案)一、填空题1.一个班有45个小学生,统计借课外书的情况是:全班学生都借有语文或数学课外书.借语文课外书的有39人,借数学课外书的有32人.语文、数学两种课外书都借的有 人.2.有长8厘米,宽6厘米的长方形与边长为5厘米的正方形,如图,放在桌面上(阴影是图形的重叠部分),那么这两个图形盖住桌面的面积是 平方厘米.3.在1~100的自然数中,是5的倍数或是7的倍数的数有 个.4.某区100个外语教师懂英语或俄语,其中懂英语的75人,既懂英语又懂俄语的20人,那么懂俄语的教师为 人.5.六一班有学生46人,其中会骑自行车的17人,会游泳的14人,既会骑车又会游泳的4人,问两样都不会的有 人.6.在1至10000中不能被5或7整除的数共有 个.7.在1至10000之间既不是完全平方数,也不是完全立方数的整数有 个.8.某班共有30名男生,其中20人参加足球队,12人参加蓝球队,10人参加排球队.已知没一个人同时参加3个队,且每人至少参加一个队,有6人既参加足球队又参加蓝球队,有2人既参加蓝球队又参加排球队,那么既参加足球队又参加排球队的有 人.9.分母是1001的最简真分数有 个.10.在100个学生中,音乐爱好者有56人,体育爱好者有75人,那么既爱好音乐,又爱好体育的人最少有 人,最多有 人.二、解答题11.某进修班有50人,开甲、乙、丙三门进修课、选修甲这门课的有38人,选修乙这门课有的35人,选修丙这门课的有31人,兼选甲、乙两门课的有29人,兼选甲、丙两门课的有28人,兼选乙、丙两门课的有26人,甲、乙、丙三科均选的有24人.问三科均未选的人数?12.求小于1001且与1001互质的所有自然数的和.13.如图所示,A 、B 、C 分别代表面积为8、9、11的三张不同形状的纸片,它们重叠放在一起盖住的面积是18,且A 与B ,B 与C ,C 与A 公共部分的面积分别是5、3、4,求A 、B 、C 三个图形公共部分(阴影部分)的面积.614.分母是385的最简真分数有多少个,并求这些真分数的和.———————————————答 案——————————————————————1. 26从图中可以看出全班45人,借语文或数学课外读物的共39+32=71(人),超过全班人数71-45=26(人),这26人都借了语文、数学两种课外书。
六年级奥数思维训练题集(八)容斥原理

专题七容斥原理姓名:例1、五年级二班40名同学,其中有25人没参加数学小组,有18人参加航模小组,有10人两个小组都参加.那么只参加了一个小组的学生有多少人?例2、渔乡小学举行长跑和游泳比赛,共305人参加。
有150名男生和90名女生参加长跑比赛,有120名男生和70名女生参加游泳比赛,有110名男生两项比赛都参加了。
请问:只参加游泳而没参加长跑的女生有多少人?例3、在1至1000的自然数中,不能被5或7整除的数有多少个?例4、如图所示,A、B、C分别代表面积为8、9、11的三张不同形状的纸片,它们重叠放在一起盖住的面积是18,且A与B,B与C,C与A公共部分的面积分别是5、3、4,求A、B、C三个图形公共部分(阴影部分)的面积。
1、李老师出了两道题,全班40 人中,第一题有30 人做对,第2 题有12 人未做对,两题都做对的有20 人。
第1 题不对、第2 题对的有几个人?两题都不对的有几个人?2、某校参加数学竞赛的有120 名男生、80 名女生,参加语文竞赛的有120 名女生、80 名男生.已知该校共有260 名学生参加竞赛,其中75 名男生两科竞赛都参加了,那么只参加数学竞赛而没有参加语文竞赛的女生有多少人?3、在1到1000的自然数中,能被3或5整除的数共有多少个?不能被3或5整除的数共有多少个?4、如图,桌面上放有两本书,A的面积是56,B的面积是48,桌面面积是200,书本未覆盖部分面积是116,求两本书重叠部分的面积。
)AB5、有一根长为180 厘米的绳子,从一端开始每隔3 厘米作一记号,每隔4 厘米也作一记号,然后将标有记号的地方剪断.问绳子共被剪成了多少段?1、在1到2004的所有自然数中,既不是2的倍数,也不是3、5的倍数的数有多少个?2、如图,已知甲、乙、丙3个圆的面积均为30,甲与乙、乙与丙、甲与丙重合部分的面积分别为6,8,5,而3个圆覆盖的总面积为73.求阴影部分的面积.3、某个班的全体学生在进行了短跑、游泳、投掷三个项目的测试后,有4名学生在这三个项目上都没有达到优秀,其余每人至少有一项达到了优秀,达到了优秀的这部分学生情况如下表:这个班的学生共有多少人?4、有2008盏亮着的电灯,各有一个拉线开关控制着,现按其顺序编号为1,2,3,…,2008,然后将编号为2的倍数的灯线拉一下,再将编号为3的倍数的灯线拉一下,最后将编号为5的倍数的灯线拉一下,三次拉完后,亮着的灯有多少盏?投掷1565621817投掷短跑游泳游泳投掷投掷游泳短跑短跑游泳短跑。
奥数训练专题容斥原理

容斥原理1、某班学生手中分别拿红、黄、蓝三种颜色的小旗,手中有红旗的共有34人,手中有黄旗的共有26人,手中有蓝旗的共有18人.其中手中有红、黄、蓝三种小旗的有6人.而手中只有红、黄两种小旗的有9人,手中只有黄、蓝两种小旗的有4人,手中只有红、蓝两种小旗的有3人,那么这个班共有多少人?2、某班有42人,其中26人爱打篮球,17人爱打排球,19人爱踢足球,9人既爱打篮球又爱踢足球,4人既爱打排球又爱踢足球,没有一个人三种球都爱好,也没有一个人三种球都不爱好.问:既爱打篮球又爱打排球的有几人?3、四年级一班有46名学生参加3项课外活动.其中有24人参加了数学小组,20人参加了语文小组,参加文艺小组的人数是既参加数学小组也参加文艺小组人数的3.5倍,又是3项活动都参加人数的7倍,既参加文艺小组也参加语文小组的人数相当于3项都参加的人数的2倍,既参加数学小组又参加语文小组的有10人.求参加文艺小组的人数.〔6级〕4、五年级三班学生参加课外兴趣小组,每人至少参加一项.其中有25人参加自然兴趣小组,35人参加美术兴趣小组,27人参加语文兴趣小组,参加语文同时又参加美术兴趣小组的有12人,参加自然同时又参加美术兴趣小组的有8人,参加自然同时又参加语文兴趣小组的有9人,语文、美术、自然3科兴趣小组都参加的有4人.求这个班的学生人数.〔6级〕5、光明小学组织棋类比赛,分成围棋、中国象棋和国际象棋三个组进展,参加围棋比赛的有42人,参加中国象棋比赛的有55人,参加国际象棋比赛的有33人,同时参加了围棋和中国象棋比赛的有18人,同时参加了围棋和国际象棋比赛的有10人,同时参加了中国象棋和国际象棋比赛的有9人,其中三种棋赛都参加的有5人,问参加棋类比赛的共有多少人?〔6级〕6、新年联欢会上,共有90人参加了跳舞、合唱、演奏三种节目的演出.如果只参加跳舞的人数三倍于只参加合唱的人数;同时参加三种节目的人比只参加合唱的人少7人;只参加演奏的比同时参加演奏、跳舞但没有参加合唱的人多4人;50人没有参加演奏;10人同时参加了跳舞和合唱但没有参加演奏;40人参加了合唱;那么,同时参加了演奏、合唱但没有参加跳舞的有多少人?7、五年级三班有46名学生参加三项课外活动,其中24人参加了绘画小组,20人参加了合唱小组,参加朗读小组的人数是既参加绘画小组又参加朗读小组人数的倍,又是三项活动都参加人数的7倍,既参加朗读小组又参加合唱小组的人数相当于三项都参加人数的2倍,既参加绘画小组又参加合唱小组的有10人,求参加朗读小组的人数.8、六年级100名同学,每人至少爱好体育、文艺和科学三项中的一项.其中,爱好体育的55人,爱好文艺的56人,爱好科学的51人,三项都爱好的15人,只爱好体育和科学的4人,只爱好体育和文艺的17人.问:有多少人只爱好科学和文艺两项?只爱好体育的有多少人?9、在某个风和日丽的日子,10个同学相约去野餐,每个人都带了吃的,其中6个人带了汉堡,6个人带了鸡腿,4个人带了芝士蛋糕,有3个人既带了汉堡又带了鸡腿,1个人既带了鸡腿又带了芝士蛋糕.2个人既带了汉堡又带了芝土蛋糕.问:三种都带了的有几人?只带了一种的有几个?9、盛夏的一天,有10个同学去冷饮店,向效劳员交了一份需要冷饮的统计表:要可乐、雪碧、橙汁的各有5人;可乐、雪碧都要的有3人;可乐、橙汁都要的有2人;雪碧、橙汁都要的有2人;三样都要的只有1人,证明其中一定有1人这三种饮料都没有要.10、全班有25个学生,其中17人会骑自行车,13人会游泳,8人会滑冰,这三个运动工程没有人全会,至少会这三项运动之一的学生数学成绩都及格了,但又都不是优秀.假设全班有6个人数学不及格,那么,数学成绩优秀的有几个学生?有几个人既会游泳,又会滑冰?11、在一个自助果园里,只摘山莓者两倍于只摘李子者;摘了草莓、山莓和李子的人数比只摘李子的人数多3个;只摘草莓者比摘了山莓和草莓但没有摘李子者多4人;50个人没有摘草莓;11个人摘了山莓和李子但没有摘草莓;总共有60100,你能答复以下问题吗?①有人摘了山莓;②有人同时摘了三种水果;③有人只摘了山莓;④有人摘了李子和草莓,而没有摘山莓;⑤有人只摘了草莓.12、五年级一班共有36人,每人参加一个兴趣小组,共有A、B、C、D、E五个小组,假设参加A组的有15人,参加B组的人数仅次于A组,参加C组、D组的人数一样,参加E组的人数最少,只有4人.那么,参加B组的有多少人?13、五一班有28位同学,每人至少参加数学、语文、自然课外小组中的一个.其中仅参加数学与语文小组的人数等于仅参加数学小组的人数,没有同学仅参加语文或仅参加自然小组,恰有6个同学参加数学与自然小组但不参加语文小组,仅参加语文与自然小组的人数是3个小组全参加的人数的5倍,并且知道3个小组全参加的人数是一个不为0的偶数,那么仅参加数学和语文小组的人有多少人?14、某学校派出假设干名学生参加体育竞技比赛,比赛一共只有三个工程,参加长跑、跳高、标枪三个工程的人数分别为10、15、20人,长跑、跳高、标枪每一项的的参加选手中人中都有五分之一的人还参加了别的比赛工程,求这所学校一共派出多少人参加比赛?图形中的重叠问题1、 把长38厘米和53厘米的两根铁条焊接成一根铁条.焊接局部长4厘米,焊接后这根铁条有多长?2、把长23厘米和37厘米的两根铁条焊接成一根铁条.焊接局部长3厘米,焊接后这根铁条有多长?3、两张长4厘米,宽2厘米的长方形纸摆放成如下图形状.把它放在桌面上,覆盖面积有多少平方厘米?4、 如图,一张长8厘米,宽6厘米,另一个正方形边长为6厘米,它们中间重叠的局部是一个边长为4厘米的正方形,求这个组合图形的面积.5、一个长方形长12厘米,宽8厘米,另一个长方形长10厘米,宽6厘米,它们中间重叠的局部是一个边长4厘米的正方形,求这个组合图形的面积.图32厘米4厘米图36、三个面积均为50平方厘米的圆纸片放在桌面上(如图),三个纸片共同重叠的面积是10平方厘米.三个纸片盖住桌面的总面积是100厘米.问:图中阴影局部面积之和是多少?7、如图,三角形纸板、正方形纸板、圆形纸板的面积相等,都等于60平方厘米.阴影局部的面积总和是40平方厘米,3张板盖住的总面积是100平方厘米,3张纸板重叠局部的面积是多少平方厘米?8、如下图,A 、B 、C 分别是面积为12、28、16的三张不同形状的纸片,它们重叠在一起,露在外面的总面积为38.假设A 与B 、B 与C 的公共局部的面积分别为8、7,A 、B 、C 这三张纸片的公共局部为3.求A 与C 公共局部的面积是多少?容斥原理在数论问题中的应用1、 在1~100的全部自然数中,不是3的倍数也不是5的倍数的数有多少个?2、 在自然数1100~中,能被3或5中任一个整除的数有多少个?3、 在前100个自然数中,能被2或3整除的数有多少个?4、 在从1至1000的自然数中,既不能被5除尽,又不能被7除尽的数有多少个5、求在1至100的自然数中能被3或7整除的数的个数.5、 以105为分母的最简真分数共有多少个?它们的和为多少? CB A107、分母是385的最简真分数有多少个?并求这些真分数的和.8、在1至2021这2021个自然数中,恰好是3、5、7中两个数的倍数的数共有个.9、在从1到1998的自然数中,能被2整除,但不能被3或7整除的数有多少个?10、50名同学面向教师站成一行.教师先让大家从左至右按1,2,3,…,49,50依次报数;再让报数是4的倍数的同学向后转,接着又让报数是6的倍数的同学向后转.问:现在面向教师的同学还有多少名11、有2000盏亮着的电灯,各有一个拉线开关控制着,现按其顺序编号为1,2,3, (2000)然后将编号为2的倍数的灯线拉一下,再将编号为3的倍数的灯线拉一下,最后将编号为5的倍数的灯线拉一下,三次拉完后,亮着的灯有多少盏?12、写有1到100编号的灯100盏,亮着排成一排,每一次把编号是3的倍数的灯拉一次开关,第二次把编号是5的倍数的灯拉一次开关,那么亮着的灯还有多少盏?13、在游艺会上,有100名同学抽到了标签分别为1至100的奖券.按奖券标签号发放奖品的规那么如下:〔1〕标签号为2的倍数,奖2支铅笔;〔2〕标签号为3的倍数,奖3支铅笔;〔3〕标签号既是2的倍数,又是3的倍数可重复领奖;〔4〕其他标签号均奖1支铅笔.那么游艺会为该项活动准备的奖品铅笔共有多少支14、在一根长木棍上,有三种刻度线,第一种刻度线将木棍分成十等份;第二种将木棍分成十二等份;第三种将木棍分成十五等份;如果沿每条刻度线将木棍锯断,那么木棍总共被锯成________段.15、一根101厘米长的木棒,从同一端开场,第一次每隔2厘米画一个刻度,第二次每隔3厘米画一个刻度,第三次每隔5厘米画一个刻度,如果按刻度把木棒截断,那么可以截出段.16、一根1.8米长的木棍,从左端开场每隔2厘米画一个刻度,涂完后再从左端开场每隔3厘米画一个刻度,再从左端每隔5厘米画一个刻度,再从左端每隔7厘米画一个刻度,涂过按刻度把木棍截断,一共可以截成多少段小木棍?容斥原理中的最值问题1、将1~13这13个数字分别填入如下图的由四个大小一样的圆分割成的13个区域中,然后把每个圆内的7个数相加,最后把四个圆的和相加,问:和最大是多少?2、如图,5条同样长的线段拼成了一个五角星.如果每条线段上恰有1994个点被染成红色,那么在这个五角星上红色点最少有多少个3、某班共有学生48人,其中27人会游泳,33人会骑自行车,40人会打乒乓球.那么,这个班至少有多少学生这三项运动都会?4、某班有50名学生,参加语文竞赛的有28人,参加数学竞赛的有23人,参加英语竞赛的有20人,每人最多参加两科,那么参加两科的最多有人.5、60人中有23的人会打乒乓球,34的人会打羽毛球,45的人会打排球,这三项运动都会的人有22人,问:这三项运动都不会的最多有多少人?6、图书室有100本书,借阅图书者需在图书上签名.这100本书中有甲、乙、丙签名的分别有33,44和55本,其中同时有甲、乙签名的图书为29本,同时有甲、丙签名的图书为25本,同时有乙、丙签名的图书为36本.问这批图书中最少有多少本没有被甲、乙、丙中的任何一人借阅过7、甲、乙、丙都在读同-一本故事书,书中有100个故事.每个人都从某一个故事开场,按顺序往后读.甲读了75个故事,乙读了60个故事,丙读了52个故事.那么甲、乙、丙3人共同读过的故事最少有多少个8、在阳光明媚的一天下午,甲、乙、丙、丁四人给100盆花浇水,甲浇了30盆,乙浇了75盆,丙浇了80盆,丁浇了90盆,请问恰好被3个人浇过的花最少有多少盆?恰好被1个人浇过的花最多有多少盆?9、甲、乙、丙同时给100盆花浇水.甲浇了78盆,乙浇了68盆,丙浇了58盆,那么3人都浇过的花最少有多少盆。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学奥数容斥原理专题训练
姓名:
1.现有50名学生都做物理、化学实验,如果物理实验做正确的有40人,化学实验做正确的有31人,两种实验都错的有4人,则两种实验都做对的有多少人?
2.某服装厂生产的一批衬衫大号和小号各占一半。
其中25%是白色的,75%是蓝色的。
如果这批衬衫共有100件,其中大号白色衬衫有10件,小号蓝色衬衫有多少件?
3.一些学生接受调查,这些学生中准备参加会计师考试的有63人,准备参加英语考试的有89人,准备参加计算机考试的有47人,三种都准备参加的有24人,只准备参加两种考试的有46人,不参加其中任何一种考试的有15人。
请问有多少学生接受调查?
4.六一班参加无线电小组和航模小组的共26人,其中参加无线电小组的比参加航模小组的多3人,两组都参加的有5人,请问参加航模小组的有几人?
5.某班统计考试成绩,数学得90分上的有25人;语文得90分以上的有21人;两科中至少有一科在90分以上的有38人。
问两科都在90分以上的有多少人?
6.某班同学中有39人打篮球,37人跑步,25人既打篮球又跑步,问全班参加篮球、跑步这两项体育活动的总人数是多少?
7.有28人参加田径运动会,每人至少参加两项比赛。
已知有8人没参加跑的项目,参加投掷项目的人数与参加跑和跳两项的人数都是17人。
问:只参加跑和投掷两项的有多少人?
8.某车间有工人100人,其中有5个人只能干电工工作,有77人能干车工工作,86人能干焊工工作,既能干车工工作又能干焊工工作的有多少人?
9.某次语文竞赛共有五道题(满分不是100分),丁一只做对了(1)、(3)、(4)三题得了25分;于山只做对了(2)、(4)三题,得了16分;王水只做对了(2)、(3)、(5)三题,得了
28分,张灿只做对了(1)、(5)三题,得了21分,李明五个题都对了他得了多少分?
10.某大学有外语教师120名,其中教英语的有50名,教日语的有45名,教法语的有40名,有15名既教英语又教日语,有10名既教英语又教法语,有8名既教日语又教法语,有4名教英语、日语和法语三门课,则不教三门课的外语教师有多少名?
小学奥数容斥原理专题训练(答案)
1.现有50名学生都做物理、化学实验,如果物理实验做正确的有40人,化学实验做正确的有31人,两种实验都错的有4人,则两种实验都做对的有多少人?
40+31+4-50=25(人)
答:则两种实验都做对的有25人。
2.某服装厂生产的一批衬衫大号和小号各占一半。
其中25%是白色的,75%是蓝色的。
如果这批衬衫共有100件,其中大号白色衬衫有10件,小号蓝色衬衫有多少件?
100×25%-10=15(件)
100×50%-15=35(件)
答:小号蓝色衬衫35件。
3.一些学生接受调查,这些学生中准备参加会计师考试的有63人,准备参加英语考试的有89人,准备参加计算机考试的有47人,三种都准备参加的有24人,只准备参加两种考试的有46人,不参加其中任何一种考试的有15人。
请问有多少学生接受调查?
63+89+47-46-24×2+15=120(名)
答:120名学生接受调查。
4.六一班参加无线电小组和航模小组的共26人,其中参加无线电小组的比参加航模小组的多3人,两组都参加的有5人,请问参加航模小组的有几人?
(26+5-3)÷2=14(人)
答:参加航模小组的有14人。
5.某班统计考试成绩,数学得90分上的有25人;语文得90分以上的有21人;两科中至少有一科在90分以上的有38人。
问两科都在90分以上的有多少人?
(25+21-38)÷2=4(人)
答:两科都在90分以上的有4人
6.某班同学中有39人打篮球,37人跑步,25人既打篮球又跑步,问全班参加篮球、跑步这两项体育活动的总人数是多少?
39+37-25=51(人)
答:全班参加篮球、跑步这两项体育活动的总人数是51人。
7.有28人参加田径运动会,每人至少参加两项比赛。
已知有8人没参加跑的项目,参加投掷项目的人数与参加跑和跳两项的人数都是17人。
问:只参加跑和投掷两项的有多少人?
28-17-8=3(人)
答:只参加跑和投掷两项的有3人。
8.某车间有工人100人,其中有5个人只能干电工工作,有77人能干车工工作,86人能干焊工工作,既能干车工工作又能干焊工工作的有多少人?
86+77-(100-5)=68(人)
答:既能干车工工作又能干焊工工作的有68人。
9.某次语文竞赛共有五道题(满分不是100分),丁一只做对了(1)、(3)、(4)三题得了25分;于山只做对了(2)、(4)三题,得了16分;王水只做对了(2)、(3)、(5)三题,得了28分,张灿只做对了(1)、(5)三题,得了21分,李明五个题都对了他得了多少分?
解析:丁一、于山、王水、张灿四人作对的题目10题,且这10题正好是两张考卷,所以将四人的分数相加再除以2即可得出一张考卷的总分。
(25+16+28+21)÷2=45(分)
答:李明五个题都对了他得了45分。
10.某大学有外语教师120名,其中教英语的有50名,教日语的有45名,教法语的有40名,有15名既教英语又教日语,有10名既教英语又教法语,有8名既教日语又教法语,有4名教英语、日语和法语三门课,则不教三门课的外语教师有多少名?
50+45+40-15-10-8+4=106(人) 120-106=14(人)
答:不教三门课的外语教师有14名。
