多项式练习题及标准答案
高等代数竞赛练习题

高等代数竞赛练习题一. 多项式. 计算题:1. 设,12)(234++++=x x x x x f ,122)(23+++=x x x x g 求))(),((x g x f . 答案:辗转相除法求.1))(),((2++=x x x g x f2. 设u x tx x x f +++=23)(及1)1()(23+++=x t x x g 的最大公因式是一个二次多项式,求u t ,. 3. 设)(x f 与)(x g 是有理系数多项式且1))(),((=x g x f ,令)()1()()1()(233x g x x x x f x x -+-+-=ϕ,)()()()1()(22x g x x x f x x -+-=ψ,求))(),((x x ψϕ.4. 设)(),(21x f x f 是首项系数为1的次数3≤的互异多项式,设)()(|13243124x f x x f x x +++,求)(),(21x f x f 的最大公因式.证明题:5. 设一元多项式)(),(),(x h x g x f ,其中1))(),((=x h x f ,且)(x f 与)(x g 被)(x h 除所得余式相等,6. 设数域F 上的多项式)(),(),(x h x g x f ,证明存在:][)(x P x p ∈使得)(|)(x p x f ,且))()((|)(x h x p x g +当且仅当h g f |),(.7. 设][)(),(),(x x h x g x f R ∈,且满足以下等式:0)()2()()1()()1(2=-+-++x g x x f x x h x ,0)()2()()1()()1(2=+++++x g x x f x x h x ,证明: )(|1),(|122x g x x f x ++.8. 证明: 任给非负整数n ,都有))1((|11222++++++n n x xx x .9. 设][)(1110x a x a x a x a x f n n n n Z ∈++++=-- ,证明:若0,a a n 为奇数,且)1(f 及)1(-f 中至少有一个为奇数,则)(x f 无有理根.10. 设)(),(),(x h x g x f 是实系数多项式,满足222xh xg f+=,证明:0===h g f .11. 设p 是素数,a 是整数,1)(++=px ax x f p,且)1(|2+a p ,证明)(x f 没有有理根.12. 证明:如果n 次多项式()f x 满足()()',f x f x 则()f x 有n 重根.13. 设A 是复数域C 上的一个n 阶方阵,()x f 是复数域C 上的一个次数大于0的多项式,()x g 是矩阵A 的最小多项式.试证明:⑴.若()()()()x g x f x d ,=,则秩=)(A d 秩)(A f . ⑵.)(A f 可逆当且仅当()x f 与()x g 互素.二. 行列式. 计算题:1. 计算n 阶行列式x y y y y zx y y y z z x y y z z z x y zzzzx.2. 计算n阶行列式2cos100012cos 100012cos 012cos n D αααα=,其中k απ≠.3. 计算n 阶行列式nn n n nn y x y x y x y x y x y x y x y x y x D ++++++++++++=1112122212121114. 计算n 阶行列式nD 222232222222221=5. 设0132110432340122310112210a a a a a a a a a a a a a a a a a a a a a a a a a D n n n n n n n n n n n ----------=,称为循环行列式,求其行列式.6. 若3≥n ,求行列式nn n n n n n αααααααααααααααααααααααααααα2sin )sin()sin()sin()sin(2sin )sin()sin()sin()sin(2sin )sin()sin()sin()sin(2sin 321332313232212131211++++++++++++.证明题:7. ∑=+=+++++++++=n j i ij nn n n n n A x A xa x a x a xa x a x a xa x a x a D 1,212221211211 .8. 证明当βα≠时,,1000001000100011βαβαβααββαβααββααββα--=+++++=++n n n D9. 设nij a D =,ij A 为ij a 的代数余子式,证明∑=-=nj i j i ij nn nn n n nn x x A D y y y x a a a x a a a x a a a 1,21212222211112111.10. 若n 阶方阵A 与B 只是第j 列不同,证明:B A B A n+=+-12.三. 矩阵与线性方程组. 计算题1. 问b a ,取何值时方程组1231231234324ax x x x bx x x bx x ++=⎧⎪++=⎨⎪++=⎩有解?有解时求解.2. 若1102510101113010002X ⎛⎫⎛⎫⎛⎫⎪= ⎪ ⎪ ⎪⎝⎭⎝⎭⎪⎝⎭,求X . 3. 设⎪⎪⎪⎭⎫ ⎝⎛---=111111111A ,矩阵B 满足*12A B A B -=+,求矩阵B . 4. 设)4,,4(),2,1,(),1,,1(),1,1,1(2321-==-=-=t t t βααα,若β可由321,,ααα线性表出且表示法不唯一,求t 及β的表示法.5. 若n 阶方阵A 的各行元素之和均为零,且1)(-=n A r ,求线性方程组0=AX 的通解.6. 设A 的伴随阵为⎪⎪⎪⎪⎪⎭⎫⎝⎛-=8030010100100001*A ,且E XA AXA 311+=--.求X 7, (1) 设n 阶方阵A ,且A A =2,证明:A E 2-可逆. (2) 设n 阶方阵A ,且3)(2A E A A =-,证明A E -可逆.(3) 设n 阶方阵B A ,满足AB B A =+,证明A E -可逆,且BA AB =. 8. 设B A ,为数域F 上的两个n 阶方阵,k 是一个正整数,若0,01=≠+k kBB ,A 可逆,且BA AB =,证明:B A -可逆,并求1)(--B A .证明题9. 设A 是一实矩阵,证明:1) 齐次线性方程组0=AX 与0=AX A T同解. 2) )()(A A r A r T=,3) 方程组B A AX A TT =有解.其中B 是一个s 维列向量.10. 设A 是一n 阶方阵,*A 为A 的伴随矩阵且011≠A ,证明: 0=AX 有无穷多个解当且仅当0*=X A 有非零解.11. 设A 是数域P 上的一个n m ⨯矩阵,记),,,(21n A ααα =,设β是一个列向量,记),,,,(21βαααn A =为方程组β=AX 的增广矩阵,令),,,(21βααn A =,已知方程组β=AX 有解,证明:方程组β=AX 的任一解的第一个分量为零当且仅当)()(1A r A r <.12. 设向量组m ααα,,,21 线性无关,而向量组m αααβ,,,,21 线性相关,且0≠β,证明:向量组m αααβ,,,,21 中有且仅有一个向量)1(m j j ≤≤α可由其前面的向量121,,,,-j αααβ 线性表出.13. 设n m ⨯矩阵A ,β=AX 是非齐次线性方程组,有解0γ,s ηηη,,,21 是导出组0=AX 的一个基础解系,证明: (1) s ηγηγηγγ+++020100,,,, 是β=AX 的线性无关的解.(2) β=AX 的任一解可表示为s ηγηγηγγ+++020100,,,, 的一个线性组合. 14. (1) 设A 是n 阶方阵,满足A A =2,则存在可逆矩阵P ,使得⎪⎪⎭⎫⎝⎛=-0001rE AP P . 设A 是n 阶方阵,满足E A =2,则存在可逆矩阵P ,使得⎪⎪⎭⎫⎝⎛-=--r n rE E AP P 001. 设A 是n 阶方阵,满足02=A ,则存在可逆矩阵P ,使得⎪⎪⎭⎫⎝⎛=-000001rE AP P . 15. 设B A ,都是n 阶方阵,A A =2,BA AB B B ==,2,证明存在可逆阵G ,使得BG G AG G 11,--同时为对角阵.16. 设A 是一个n 阶可逆矩阵,证明:存在对角元为1的下三角阵L 和上三角阵T ,使得LT A =当且仅当A 的各阶顺序主子式均非零,且上述分解唯一.17. 设F 是一个数域, nm F ∈ααα,,,21 ,s r m =),,,(21ααα ,且m ααα,,,21 中任意s 个向量均线性无关,证明: 1) 若02211=+++m m k k k ααα ,则或者021====m k k k 或者至少存在1+s 个系数全不为零.2) 若m s <,则m ααα,,,21 中任一向量均可由其余向量线性表出.四.二次型部分. 计算题:1. t 取何值时,二次型323121232221321222)(),,(x x x x x x x x x t x x x f -++++=正定. 2. 化二次型23323121321262),,(x x x x x x x x x x f ++-=为标准形3. 用正交线性替换化二次型323121232221844552x x x x x x x x x f --+++=为标准形.4. 设实对称阵,⎪⎪⎪⎭⎫ ⎝⎛--=510810228211A ,(1) 求A 的特征根及相应的线性无关的特征向量. (2) 求正交阵Q ,使得AQ Q T是对角阵. 5. 设A 是n 阶可逆实矩阵,求⎪⎪⎭⎫⎝⎛=00T A A B 的正负惯性指数. 6. 用正交线性替换化实二次型323121232221321222),,(x x x x x bx x ax x x x x f +++++=为标准形.证明题:7. 假设AX X f T =是一个实二次型,若有n 维实向量21,X X 使得0,02211<>AX X AX X TT ,证明:存在n 维实向量0X ,使得000=AX X T.8. 下列关于n 阶实对称阵A 的命题等价. (1) A 是正定阵.(2) 存在主对角线元素全等于1的上三角矩阵B ,使得DB B A T=,其中D 是正定对角阵. (3) 存在主对角线元素全为正的上三角阵C ,使得C C A T=.9. 设AX X X f T=)(是实二次型,若A 的前1-n 个顺序主子式11,,-n P P 非零,求证:经过可逆线性变换f 可化为下标准形212212211n n n y P P y P P y P f -+++= ,其中A P n =. 10. (1) 设A 是n 阶半正定阵,求证:对于任意的自然数1>k ,必存在同阶半正定阵B ,使kB A =. (2) 设A 是n 阶正定阵,求证:对于任意的自然数1>k ,必存在同阶正定阵B ,使kB A =. 11. . (1) 设A 是n 阶正定阵,B 是n 阶实对称阵,则存在可逆阵P ,使得E AP P T=,⎪⎪⎪⎪⎪⎭⎫⎝⎛=n T BP P λλλ21,其中i λ是B A 1-的特征值.(2) 设B A ,是n 阶实对称阵,则存在正交阵Q ,使得BQ Q AQ Q TT ,是对角阵⇔BA AB =.五. 线性空间和线性变换部分 计算题:1. 设B A ,均为n 阶方阵s B r r A r ==)(,)(,k B A r =⎪⎪⎭⎫ ⎝⎛,设满足0=AX 与0=BX 的n 阶方阵X 组成的解空间分别为21,V V ,求21V V +的维数.2. 已知232212,1,1x x f x f x f +=+=-=是3][x F 的一组基,线性变换σ满足232211,,2x x f x f x f ++==+=σσσ.(1) 求基2,,1x x 到321,,f f f 基的过渡矩阵. (2) 求σ在321,,f f f 基下的矩阵. (3) 求2321x x f ++=在σ下的像.3. 设n 维线性空间V ,线性变换σ,n ααα,,,21 线性无关,i i βσα=,n i ,,2,1 =,设矩阵A 与B 的列向量分别是向量n ααα,,,21 与n n βββββ++-1211,,, 在V 的基n εεε,,,21 下的坐标,求σ在基n εεε,,,21 下的矩阵.4. 已知线性空间3R 的线性变换σ为TTb ac b a ),,0(),,(=σ,其中nTc b a R ∈),,(,(1) 选取3R 的一组基,求σ在基下的矩阵.(2) 求)ker(),(3σσR 及)ker()(3σσ R 的各一组基.5. 设矩阵⎪⎪⎪⎭⎫ ⎝⎛---=5334111y xA ,已知A 有3个线性无关的特征向量,2=λ是A 的二重特征值,求可逆矩阵P ,使得AP P 1-为对角阵.6. 设矩阵A 是n 阶可对角化矩阵,特征值为n λλλ,,,21 ,求矩阵的⎪⎪⎭⎫⎝⎛A A A A22的特征值. 7. 设⎪⎪⎭⎫⎝⎛-=0110A ,AX X :σ是2R 的一个线性变换,求σ的不变子空间. 8. 设σ是n 维线性空间V 的一个线性变换,取V ∈α,设W 是含α的V 最小σ不变子空间,求W 的维数与一组基.证明题:9. 设nn F⨯是n 阶矩阵组成的线性空间,设},,0|{1nF X AX X V ∈==},,|{n s F X X AX X V ∈==证明21V V F n ⊕=当且仅当A A =2.10. 设nn FA ⨯∈,][)(),(x F x g x f ∈,且1))(),((=x g x f ,令21,,W W W 分别为齐次线性方程组0)()(=X A g A f ,0)(=X A f 与0)(=X B f 的解空间,证明21W W W ⊕=.11. 设)(x f 是数域F 上的一个二次多项式,有互异特征值F ∈21,λλ,V 是F 上的二维线性空间,σ是V 的一个线性变换,满足2,1,=≠i id i λσ,但0)(=σf ,证明: (1)21,λλ是σ的特征值, (2) 21λλV V V ⊕=. 12. 设n 维线性空间V 中的线性变换σ满足等式22E σσ+=,1{2}V Vασαα=∈=-,2{}V V ασαα=∈=,证明:12V V V =⊕.13. 设数域F 上n 阶矩阵A 的特征值n λλλ,,,21 全在F 中,则存在可逆矩阵P ,使得AP P 1-是上三角阵, 14. 设σ是2R 的一个线性变换,在标准基下的矩阵是⎪⎪⎭⎫⎝⎛-=2211A (1) 证明σ的不变子空间只能为2R 与}0{,(2) 若τ是2C 的一个线性变换,在标准基下的矩阵是A ,证明τ有一维不变子空间. 15. 令σ是数域P 上线性空间V 的一个线性变换,且满足σσ=2,证明: (1) ()()10{|}V σζσζζ-=-∈. (2) ())(01V V σσ⊕=-.首届中国大学生数学竞赛赛区竞赛试卷-高等题目. 1 设nn ⨯C是n n ⨯复矩阵全体在通常的运算下所构成的复数域C 上的线性空间,⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛----=--121100020001000a a a a F n n n .(1) 假设⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=nn n n n n a a a a a a a a a A212222111211,若AF FA =,证明:E a F a F a F a A n n n n 112121111++++=--- . (2) 求nn ⨯C的子空间}|{)(XF FX X F C nn =∈=⨯C的维数.证明: 设A 的列向量组为),,,(21n A ααα =,E a F a Fa F a M n n n n 112121111++++=--- ,证明A 与M 的各列对应相等.设n e e e ,,,21 为n 维单位列向量.证明:)(i i i Ae Me α==.记Tn n a a a ),,(11,---=- β则),,,,(32βn e e e F =,而且n n n e Fe e F e Fe e F e Fe =====--111321221,, . (*)则11121211111)(e E a F a Fa F a Me n n n n ++++=--- 1111122111111111211211111Ae e a e a e a e a Ee a Fe a e F a e F a n n n n n n n n ==++++=++++=-----α .211112Ae AFe FAe FMe MFe Me =====.3121212123Ae e AF Ae F Me F e MF Me =====.如此下去,就有A M =.(2) 由(1), },,,,{)(12-=n F F F E span F C ,设0112210=++++--n n F x F x F x E x ,两边同乘1e ,利用(*)得:11122101)(00e F x F x F x E x e n n --++++== 1111221110e F x e F x Fe x e x n n --++++=n n e x e x e x e x 1322110-++++=由于n e e e ,,,21 线性无关,则01210=====-n x x x x ,故12,,,,-n F F F E 线性无关,为)(F C 的基,从而n F C =)(dim .2. 假设V 是复数域C 上n 维数线性空间)0(>n ,g f ,是V 上的线性变换,若f gf fg =-,证明:f 的特征都是0,且g f ,有公共特征向量.证明: 假设0λ是f 的特征值,W 是相应的特征子空间,即})(|{0ηληη=∈=f V W ,于是W 在f 下是不变的.先证明: 00=λ,任取非零向量W ∈η,记m 为使得)(,),(),(,2ηηηηm g g g 线性相关的最小的正整数,则当10-≤≤m i 时, )(,),(),(,2ηηηηi g g g 线性无关, 10-≤≤m i 令)}(,),(),(,{2ηηηηi i g g g span W =,其中}0{0=W ,因此)1(dim m i i W i ≤≤=,并且 ===++21m m m W W W ,显然1)(+⊆i i W W g ,特别的, m W 在g 下是不变的.再证明: m W 在f 下是不变的.事实上由ηλη0)(=f ,知道ηληληηη00)()()()(+=+=g f gf fg . ηληληληληληληληηη002000002)(2)())(())(()()()(++=+++=+=g g g g g fg gfg fg)())(()()()(1111ηηηηη----+=+=k k k k k fg fg g fg gfg fg ,用归纳法可以证明)(ηk fg 可表示为)(,),(),(,2ηηηηk g g g 的线性组合,且)(ηk g 前的系数为0λ.m W 在f 下是不变的.mW f |在基)(,),(),(,12ηηηη-m g g g 下的矩阵是个上三角阵,且对角线元素都是0λ.故mW f |的迹为0λm . f gf fg =-在m W 上仍成立,而gf fg -的迹为零,故00=λm ,从而00=λ.任取W ∈η,由于0)(=ηf ,则0)()()(=+=ηηηf gf fg 故W g ∈η,因此W 在g 下是不变的.从而W 中存在g 的特征向量,这也是g f ,的公共特征向量.。
多项式乘多项式试题精选(二)附标准答案
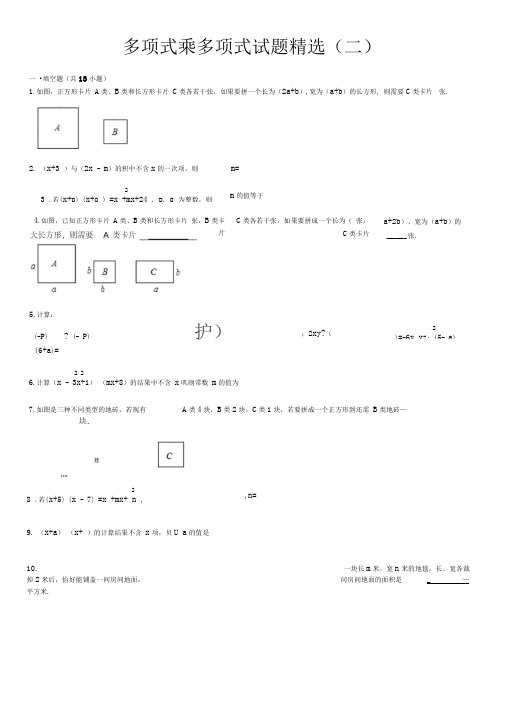
多项式乘多项式试题精选(二)一 •填空题(共13小题)1.如图,正方形卡片 A 类、B 类和长方形卡片 C 类各若干张,如果要拼一个长为(2a+b ),宽为(a+b )的长方形, 则需要C 类卡片 张.(6+a )=2 26.计算(x - 3x+1) (mx+8)的结果中不含 x 叽则常数 m 的值为7.如图是三种不同类型的地砖,若现有A 类4块,B 类2块,C 类1块,若要拼成一个正方形到还需 B 类地砖—28 .若(x+5) (x - 7) =x +mx+ n ,9. (x+a ) (x+ )的计算结果不含 x 项,贝U a 的值是10.一块长m 米,宽n 米的地毯,长、宽各裁掉2米后,恰好能铺盖一间房间地面,问房间地面的面积是_—平方米.2. (x+3 )与(2x - m )的积中不含x 的一次项,则m= 23 .若(x+p ) (x+q ) =x +mx+24 , p , q 为整数,则 m 的值等于4.如图,已知正方形卡片 A 类、B 类和长方形卡片 张,B 类卡片5.计算:(-P )? (- P )护)C 类各若干张,如果要拼成一个长为( 张,C 类卡片;2xy?(a+2b )、宽为(a+b )的______ 张.2)=-6x yz; (5- a ),n=二•解答题(共17小题)2 214 .若(x +2nx+3 ) (x - 5x+m )中不含奇次项,求 m 、n 的值. 15. 化简下列各式:2 2(1) (3x+2y ) ( 9x - 6xy+4y );2(2) (2x - 3) (4x +6xy+9 ); (3) ( m -) ( m2+ m+ );2 3 46 92 2 2 2(4) (a+b ) (a 2- ab+b 2) (a - b ) (a+ab+b 2) •16. 计算:(1) (2x - 3) (x - 5);2 3、/ 2 3、 (2) (a - b ) (a +b )17 .计算:(1)-( 2a - b ) +[a -( 3a+4b )]2 2(2) (a+b ) (a - ab+b )18. (x+7) (x - 6)-( x - 2) ( x+1)19. 计算:(3a+1) (2a- 3)-( 6a - 5) (a - 4).2 220 .计算:(a - b ) (a +ab+b )21 .若(x 2+px -4) (x 2- 3x+q )的积中不含x 项与x 3项,3(1) 求p 、q 的值;22-1 2012 2014(2)求代数式(-2p q ) + (3pq ) +p q 的值.2 2-4 (- xy +3x y ),其中 x= - 2, y=3 .23223.若(x - 1) (x +mx+ n ) =x - 6x +11x -6,求 m , n 的值. 24.如图,有多个长方形和正方形的卡片,图甲是选取了2块不同的卡片,拼成的一个图形,借助图中阴影部分面2积的不同表示可以用来验证等式a (a+b ) =a +ab 成立.(1)根据图乙,利用面积的不同表示方法,写出一个代数恒等式___________ ;(2)试写出一个与(1)中代数恒等式类似的等式,并用上述拼图的方法说明它的正确性.22.先化简,再求值:/ 22、 5 ( 3x y - xy )abb甲乙25.小明想把一长为60cm,宽为40cm的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形纸片的四个角各剪去一个相同的小正方形.(1)若设小正方形的边长为xcm ,求图中阴影部分的面积;(2)当x=5时,求这个盒子的体积.26. (x - 1) (x - 2) = (x+3) (x - 4) +20.c2 -227.若(x - 3) (x+m ) =x +nx - 15,求.的值.8 口十528•小明在进行两个多项式的乘法运算时(其中的一个多项式是 结果得到(2a - b ),请你帮小明算算,另一个多项式是多少? 29.有足够多的长方形和正方形的卡片如图.如果选取1号、2号、3号卡片分别为1张、2张、3张,可拼成一个长方形(不重叠无缝隙) •请画出这个长方形的草图,并运用拼图前后面积之间的关系说明这个长方形的代数意义.2 3 230.( 1)填空:(a - 1) ( a+1) = ______________ (a - 1) (a +a+1) = ______________ (a - 1) (a +a +a+1) = _____________(2) 你发现规律了吗?请你用你发现的规律填空: __________ (a - 1) (a n +a n -1+ ••+a 2+a+1) =(3) ________________________________________________________________________ 根据上述规律,请你求 42012+42011+4201°+ --+4+1的值. __________________________________________________________________________ .b - 1),把乘以(b - 1)"错看成除以(b - 1)多项式乘单项式试题精选(二)参考答案与试题解析•填空题(共13小题)考点:多项式乘多项式.分析:根据长方形的面积等于长乘以宽列式,再根据多项式的乘法法则计算,然后结合卡片的面积即可作出判断.2 2解答: 解:长为2a+b ,宽为a+b 的矩形面积为(2a+b )( a+b )=2a +3ab+b ,A 图形面积为a 2,B 图形面积为b 2,C 图形面积为ab ,则可知需要A 类卡片2张,B 类卡片1张,C 类卡片3张. 故答案为:3 •点评:此题主要考查了多项式乘多项式,掌握多项式乘以多项式的法则是本题的关键.注意不要漏项,漏字母, 有同类项的合并同类项.2. (x+3 )与(2x - m )的积中不含x 的一次项,贝U m= 6 考点:i 多项式乘多项式.专题:1 计算题.分析:: 先求出(x+3 )与(2x m )的积,再令 x 的一次项为0即可得到关于 m 的一兀一次方程,求出 m 的值即 可.解答:/2解:•••( x+3) ( 2x - m ) =2x + (6- m ) x - 3m , 6 - m=0,解得 m=6 . 故答案为:6.点评: 本题考查的是多项式乘以多项式的法则,即先用一个多项式的每一项乘另外一个多项式的每一项,再把所 得的积相加.23.若(x+p ) (x+q ) =x +mx+24 , p , q 为整数,则 m 的值等于 10, 11, 14, 25考点:多项式乘多项式.分析:根据多项式的乘法法则,可得一个多项式,根据多项式相等,可得对应项相等,由P?q-24, p , q 为整数,可得p , q 的值,再根据p+q-m ,可得m 的值.解答: 解:T( x+p ) ( x+q ) -x +mx+24 ,••• p -24, q-1; p-12, q-2; p-8, q-3; p-6, q-4, •••当 p-24, q-1 时,m-p+q-25 ,当 p-12 , q-2 时,m-p+q-14 , 当 p-8, q-3 时,m-p+q-11 , 当 p-6 , q-4 时,m-p+q-10 , 故答案为:10, 11, 14, 25.点评:本题考察了多项式,先根据多项式的乘法法则计算,分类讨论p , q 是解题关键.4.如图,已知正方形卡片 A 类、B 类和长方形卡片 C 类各若干张,如果要拼成一个长为(a+2b )、宽为(a+b )的大长方形,则需要 A 类卡片 1张,B 类卡片 2张,C 类卡片 3张.1如图,正方形卡片 A 类、B 类和长方形卡片 C 类各若干张,如果要拼一个长为( 2a+b ),宽为(a+b )的长方形,则需要C 类卡片 3张.考点:多项式乘多项式.分析:根据边长组成图形•数出需要A类卡片1张,B类卡片2张,C类卡片3张.解答:解:如图,要拼成一个长为(a+2b)、宽为(a+b)的大长方形,则需要A类卡片1张,B类卡片2张,C 类卡片3张.点评:本题主要考查了多项式乘多项式,解题的关键是根据边长组成图形.5•计算:(—P)? (— p) = — p ;)兀_g a b ;2xy? ( - 3xz ) = - 6x yz; (5- a) (6+a)= -2卜;2a —a+30考点:多项式乘多项式;同底数幕的乘法;幕的乘方与积的乘方;单项式乘单项式.分析:根据同底数幕的乘法、积的乘方和幕的乘方、单项式除以单项式法则、多项式乘以多项式法则求出每个式子的值即可.解答:解:(-p) 2? (—p) 3= (—p) 5=—p5,(—a b) = ( ——) ? (a ) b = ——a b ,2 2 3c 2•—6x yz 吃xy= - 3xz,2••• 2xy? (—3xz) = —6x yz,2 2 2(5—a) ( 6+a) =30+5a —6a—a =30 - a—a = —a—a+30,故答案为:-p5,—丄a6b3,—3xz,—a—a+30.8点评:本题考查了同底数幕的乘法、积的乘方和幕的乘方、单项式除以单项式法则、多项式乘以多项式法则的应用.6.计算(x2—3x+1) (mx+8)的结果中不含x2叽则常数m的值为」._3_考点:多项式乘多项式. 分析:把式子展开,找到所有x2项的所有系数,令其为0,可求出m的值.2 4 2 2解答:解:•( x2—3x+1 ) ( mx+8 ) =mx4+8x2—3mx2—24x+mx+8 . 又••结果中不含x2的项,• 8—3m=0 ,解得m=—.3故答案为:£点评:本题主要考查了多项式乘多项式的运算,注意当要求多项式中不含有哪一项时,应让这一项的系数为0.7.如图是三种不同类型的地砖,若现有A类4块,B类2块,C类1块,若要拼成一个正方形到还需B类地砖一2块.考点:多项式乘多项式.分析:分别计算出4块A的面积和2块B的面积、1块C的面积,再计算这三种类型的砖的总面积,用完全平方公式化简后,即可得出少了哪种类型的地砖.2解答:解:4块A的面积为:4>m>m=4m ;2块B的面积为:2 Xm>n=2mn ;21块C的面积为n>h=n ;那么这三种类型的砖的总面积应该是:2 2 2 2 24m +2mn+n =4m +4mn+n - 2mn= (2m+n) - 2mn,因此,少2块B型地砖,故答案为:2.点评:本题考查了完全平方公式的几何意义,立意较新颖,注意面积的不同求解是解题的关键,对此类问题要深入理解.2考点:\ \ ・/ ・・・,、・・?・・・— ? ・・• 多项式乘多项式.分析:已知等式左边利用多项式乘以多项式法则计算,利用多项式相等的条件即可求出m与n的值.解答:2 2解: (x+5) (x - 7) =x - 2x - 35=x +mx+n, 贝U m= - 2, n= - 35.故答案为:-2, - 35.点评:此题考查了多项式乘以多项式,熟练掌握运算法则是解本题的关键.9.(x+a) (x+—)的计算结果不含x项,则a的值是-—5 5~考点:多项式乘多项式.分析:多项式乘多项式法则,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加,依据法则运算,展开式不含关于字母x的一次项,那么一次项的系数为0,就可求a的值.解答:解:•••( x+a) (x+ :)5=/+ (計£)又•••不含关于字母x的一次项,•応二0,解得a= .5点评:本题考查了多项式乘多项式法则,相乘后不含哪一项,就让这一项的系数等于0,难度适中.10. 一块长m米,宽n米的地毯,长、宽各裁掉2米后,恰好能铺盖一间房间地面,问房间地面的面积是—皿2) (n - 2)或(mn - 2m - 2n+4) 平方米.考点:多项式乘多项式.分析:根据题意得出算式是(m-2) ( n- 2),即可得出答案.解答:解:根据题意得出房间地面的面积是( m - 2) (n- 2);(m- 2) (n- 2) =mn - 2m - 2n+4.故答案为:(m- 2) (n - 2)或(mn - 2m - 2n+4)点评:本题考查了多项式乘多项式的应用,关键是能根据题意得出算式,题目比较好,难度适中.211.若(x+m ) (x+n) =x - 7x+m n,则—m—n 的值为7 .考点:多项式乘多项式.专题:计算题.分析:按照多项式的乘法法则展开运算后解答:解:•••( x+m) (x+n) =x + (m+n) x+mn=x - 7x+mn ,m+n= —7,/•- m —n=7 ,故答案为:7.点评:本题考查了多项式的乘法,解题的关键是牢记多项式乘以多项式的乘法法则,属于基础题,比较简单.12 .若(x2+mx+8 ) (x2—3x+n )的展开式中不含x3和x2项,贝V mn的值是3考点:i 多项式乘多项式.专题:1 计算题.分析:利用多项式乘以多项式法则计算得到结果,根据展开式中不含x2和x3项列出关于m与n的方程组,求出方程组的解即可得到m与n的值.解答:1】解 :原式=x + ( m —3) x + ( n - 3m+8) x + ( mn - 24) x+8n , (x +mx —8) (x —3x+n)2 3fm ~ 3=0根据展开式中不含x2和x3项得:,3nr1-8=0解得:严J L n=l• mn=3,故答案为:3.点评:此题考查了多项式乘以多项式,熟练掌握运算法则是解本题的关键.2 2 313.已知x、y、a都是实数,且|x|=1 —a, y = (1 —a) (a—1 —a ),贝V x+y+a +1 的值为2考点:代数式求值;绝对值;多项式乘多项式.专题:计算题.分析:根据绝对值非负数,平方数非负数的性质可得 1 —a=0,从而得到a的值,然后代入求出x、y的值,再把a、x、y的值代入代数式进行计算即可求解.解答:解:T |x|=1 - a%,2••• a—1 包),—a 切,2a—1 —a 包),2 2又y = (1 —a) ( a—1 —a )为,1 —a=0,解得a=1,••• |x|=1 —1=0,x=0 ,2 2y = (1 —a) (—1 —a ) =0,3• x+y+a +1=0+0+1+1=2 .故答案为:2.点评:本题主要考查了代数式求值问题,把y2的多项式整理,然后根据非负数的性质求出a的值是解题的关键, 也是解决本题的突破口,本题灵活性较强.二•解答题(共17小题)2 214 .若(x +2nx+3 ) (x —5x+m )中不含奇次项,求m、n的值.考点:多项式乘多项式.分析:把式子展开,让x4的系数,x2的系数为0,得到m, n的值.2 2解答:解:(x +2nx+3 ) ( x - 5x+m)4 3 2 3=x - 5x +mx +2nx - 10nx +2mnx+3x - 15x+3m4 3 2=x + (2n - 5) x + ( m - 10n+3) x + (2mn - 15) x+3m ,•••结果中不含奇次项,/• 2n - 5=0, 2mn - 15=0, 解得m=3 , n=§.2点评:本题主要考查了多项式乘多项式的运算,注意当要求多项式中不含有哪一项时,应让这一项的系数为o.15.化简下列各式:2 2(1)(3x+2y) ( 9x - 6xy+4y );2(2)(2x - 3) (4x +6xy+9 );(3)(丄m-丄)(丄m2+ m+ );2 3 4 6 92 2 2 2(4)(a+b) (a - ab+b ) (a- b) (a +ab+b ).考点:多项式乘多项式.分析:根据立方和与立方差公式解答即可.解答:解:(1) ( 3x+2y) (9x2- 6xy+4y2)3 3=(3x) + (2y)3 3=27x +8y ;2(2)(2x - 3) (4x +6xy+9 )3 ^3=(2x) - 3=8x3- 27;(3)(2m - 2)(2m2+gm+2)2 3 4 6 9寺^27;2 2 2 2(4)(a+b) (a2- ab+b2) (a- b) (a +ab+b2)3 3、/ 3 」3、=(a +b ) (a - b )6 .6=a - b .点评:本题考查了立方和与立方差公式,熟练记忆公式是解题的关键.16.计算:(1)(2x - 3) (x - 5);2 3 2 3、(2)(a - b ) (a +b )考点:多项式乘多项式.a+b) ( m+n) =am+an+bm+bn,计算即可;分析:(1)根据多项式乘以多项式的法则,可表示为((2)根据平方差公式计算即可.17.计算:(1)-( 2a- b) +[a -( 3a+4b)]2 2(2) (a+b) (a - ab+b )考点:2多项式乘多项式;整式的加减.专题:1 计算题.分析:(1)先去小括号,再去大括号,最后按照整式加减混合运算规则进行计算即可;(2)根据多项式乘以多项式的法则,可表示为( a+b) ( m+n)=am+an+bm+bn,计算即可.解答:/ 解: (1)原式=—2a+b+[a —3a—4b],=—2a+b+a —3a—4b,=—4a—3b;3 2 2 2 2 3(2)原式=a —a b+ab +a b—ab +b ,3 3点评:本题主要考查多项式乘以多项式的法则.注意不要漏项,漏字母,有冋类项的合并冋类项.18. (x+7) (x- 6) — ( x—2) ( x+1)考点:多项式乘多项式.分析:依据多项式乘多项式法则运算.解答:f 解: (x+7) (x —6) — ( x —2) ( x+1)2 2=x —6x+7x —42 —x —x+2x+2=2x —40.点评:;本题考查了多项式乘多项式法则,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加.关键是不能漏项.丿19.计算:(3a+1) (2a—3) — ( 6a— 5) (a— 4).考点:多项式乘多项式.分析:根据整式混合运算的顺序和法则分别进行计算,再把所得结果合并即可.解答:解:(3a+1) (2a—3) + (6a—5) ( a—4)2 2=6a —9a+2a —3+6a —24a—5a+202=12a —36a+17.点评:此题考查了整式的混合运算,在计算时要注意混合运算的顺序和法则以及运算结果的符号,是一道基础题.2 220.计算:(a—b) (a +ab+b )考点:多项式乘多项式;单项式乘单项式.专题:计算题.分析:根据多项式乘以多项式的法则和单项式乘单项式的法则进行计算即可.解答:解:原式=a +a b+ab —a b —ab —b3 .3=a —b .点评:本题主要考查对多项式乘以多项式的法则和单项式乘单项式的法则得理解和掌握,能熟练地运用法则进行计算是解此题的关键.2 1 2—3x+q)的积中不含x项与x3项,21.若(x +px — .) (x■_:I(1)求p、q的值;2 2 -1 2012 2014(2)求代数式(-2p q) + (3pq) +p q 的值.考点:多项式乘多项式.分析:(1)形开式子,找出x项与x3令其系数等于0求解.(2)把p, q的值入求解.解军答: 2 2 4 3 " 2口•解:(1) ( x +px —-) (x —3x+q ) =x + ( p —3) x + (9 —3p—) x + (qp+1 ) x+q,•••积中不含x项与x3项,••• P—3=0, qp+1=0-p=3, q=-_32、2,、-1 2012 2014(2) (- 2 3P q ) + ( 3pq )+p q212I=[-2X3 >(— ) ] + :;.i 亠.]0 0=36 - —+93442=44 —.3点评: 本题主要考查了多项式乘多项式,解题的关键是正确求出2 2 2 222.先化简,再求值:5 ( 3x y - xy ) - 4 (- xy +3x y ),其中 x= - 2, y=3 .考点:整式的加减一化简求值;合并同类项;多项式乘多项式.专题:计算题.分析:根据单项式乘多项式的法则展开,再合并同类项,把x y 的值代入求出即可.2 2 2 2解答: 解:原式=15x y - 5xy +4xy - 12x y2 2=3x y - xy ,当 x= - 2, y=3 时,原式=3 X ( - 2)2X3-( - 2) X32=36+18 =54 .点评:本题考查了对整式的加减,合并同类项,单项式乘多项式等知识点的理解和掌握,注意展开时不要漏乘, 同时要注意结果的符号,代入- 2时应用括号.23223.若(x - 1) (x +mx+ n ) =x - 6x +11x -6,求 m , n 的值.考点:多项式乘多项式. 专题:计算题.232分析: 把(x - 1) (x +mx+ n )展开后,每项的系数与 x - 6x +11x - 6中的项的系数对应,可求得 m 、n 的值.解答:解:•••( x - 1) (x2+mx+n )3 2=x + (m - 1) x + (n - m ) x - n 3^2=x - 6x +11x - 6m - 1= - 6, - n= - 6,解得 m= - 5, n=6.点评:本题主要考查了多项式乘多项式的法则,注意不要漏项,漏字母,有同类项的合并同类项.根据对应项系数相等列式求解 m 、n 是解题的关键.24.如图,有多个长方形和正方形的卡片,图甲是选取了2块不同的卡片,拼成的一个图形,借助图中阴影部分面 积的不同表示可以用来验证等式 a (a+b ) =a 2+ab 成立.(1) 根据图乙,利用面积的不同表示方法,写出一个代数恒等式(a+2b ) (a+b ) =a 2+3ab+2b 2;(2) 试写出一个与(1)中代数恒等式类似的等式,并用上述拼图的方法说明它的正确性..I .. 2>3p ,q 的值甲乙解答:解:()观察图乙得知:长方形的长为:,宽为,2 2•••面积为:(a+2b) (a+b) =a +3ab+2b ;(2)如图所示:恒等式是,(a+b)( a+b)=a3 4 5+2ab+b2.2 2答:恒等式是a+b) (a+b) =a +2ab+b •考点:;多项式乘多项式;代数式求值.分析:(1)剩余部分的面积即是边长为60 - 2x, 40 - 2x的长方形的面积;(2)利用长方体的体积公式先表示出长方形的体积,再把x=5,代入即可.解答:彳/]/解: (1) ( 60- 2x) (40 - 2x) =4x2- 200x+2400 , 答:阴影部分的面积为(4x2- 200x+2400) cm2;2 2(2) 当x=5 时,4x - 200x+2400=1500 (cm ),3这个盒子的体积为:1500^5=7500 (cm ),答:这个盒子的体积为7500cm3.点评:此题主要考查用代数式表示正方形、矩形的面积和体积,需熟记公式,且认真观察图形,得出等量关系.26. (x - 1) (x - 2) = (x+3) (x - 4) +20.考点:多项式乘多项式;解一兀一次方程.分析:将方程的两边利用多项式的乘法展开后整理成方程的- 「般形式求解即可.解答:解:原方程变形为:x - 3x+2=x - x - 12+20整理得:-2x - 6=0,解得:x= - 3.点评:本题考查了多项式乘多项式及解一兀二次方程的知识,解题的关键是利用多项式的乘法对方程进行化简.考点:多项式乘多项式.分析:首先把)(x - 3) (x+m)利用多项式的乘法公式展开,然后根据多项式相等的条件:对应项的系数相同即可得到m、n的值,从而求解.点评:本题主要考查对多项式乘多项式的理解和掌握,能表示各部分的面积是解此题的关键.25.小明想把一长为60cm,宽为40cm的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形纸片的四个角各剪去一个相同的小正方形.4 若设小正方形的边长为xcm,求图中阴影部分的面积;5 当x=5时,求这个盒子的体积.考点:2多项式乘多项式.专题:1 计算题.分析:(1)根据图形是一个长方形求出长和宽,相乘即可;(2)正方形的面积是2个长方形的面积加上2个正方形的面积,代入求出即可.27•若(x- 3)2(x+m) =x +nx - 15, 8n+5 的值.解答:解:(x - 3) (x+m)2=x + ( m - 3) x- 3m2=x +nx - 15,则二一-[-3m=- 15解得:严ILn=2n£-m2 2£-5g_Hl ='心三点评:本题考查了多项式的乘法法则以及多项式相等的条件,理解多项式的乘法法则是关键.28•小明在进行两个多项式的乘法运算时(其中的一个多项式是b- 1),把乘以(b- 1)”错看成除以(b- 1)结果得到(2a- b),请你帮小明算算,另一个多项式是多少?考点:多项式乘多项式.分析:根据被除式=商>除式,所求多项式是(2a- b)( b - 1),根据多项式乘多项式的法则计算即可.解答:解:设所求的多项式是M,则M= (2a-b) (b- 1)2=2ab - 2a- b +b.点评:本题考查了多项式乘多项式法则,根据被除式、除式、握运算法则也很重要.商三者之间的关系列出等式是解题的关键,熟练掌29.有足够多的长方形和正方形的卡片如图.如果选取1号、2号、3号卡片分别为1张、2张、3张,可拼成一个长方形(不重叠无缝隙).请画出这个长方形的草图,并运用拼图前后面积之间的关系说明这个长方形的代数意义.考点:多项式乘多项式.分析:先根据题意画出图形,然后求出长方形的长和宽,长为a+2b,宽为a+b,从而求出长方形的面积.解答:解:如图:2 23 3 2 430. (1)填空:(a- 1) (a+1) = a - 1 (a- 1) (a +a+1) = a - 1 ( a- 1) (a +a +a+1) = a - 1 (2) 你发现规律了吗?请你用你发现的规律填空:(a- 1) (a n+a n 1 + ・・+a2+a+1) = a n+1- 12012 2011 2010(3)根据上述规律,请你求 4 +4 +4 +-+4+1的值.: J13- 1).考点:多项式乘多项式.专题:规律型.分析: (1)根据平方差公式和立方差公式可得前2个式子的结果, 利用多项式乘以多项式的方法可得出第3个式子的结果;(2)从而总结出规律是:(a - 1)(玄“+玄“1+ ・・+a 2+a+1) =a “「1;(3) 根据上述结论计算下列式子即可.解答: 解:根据题意:(1)(a - 1) (a+1) =a 2- 1;23(a - 1) ( a+a+1) =a - 1; (a - 1) ( a +a +a+1) =a - 1;n n -1 n - 22、 n+1. (2) (a - 1) (a +a +a + --+a +a+1) =a - 1 • / c 、士口I 、丨 L / J 丄匚 / \ A 2012 2011 2010 999897(3) 根据以上分析(1) 4+4 +4 + --+4+12 +2 +2 +-+2+1 ,1 z 、 , 2012 2011 2010 、=—(4 - 1) (4 +4 +4+-+4+1 ),3_____ 3主要考查了学生的分析、总结、归纳能力,规律型的习题一般是从所给的数据和运算方法进行分析,从特 殊值的规律上总结出一般性的规律.211. 若(x+m ) (x+n ) =x - 7x+mn ,则- m - n 的值为 ______________________ .12 .若(x 2+mx+8 ) (x 2- 3x+n )的展开式中不含 x 3和x 2项,贝V mn 的值是 __________________________ .22313.已知 x 、y 、a 都是实数,且 |x|=1 - a , y = (1 - a ) (a - 1 - a ),则 x+y+a +1 的值为 _____________________ .12013=—(4-1).3故答案为:(1) a 2- 1, a 3 - 1, a 4- 11; (2) a n+1 -- 1; ( 3) _ (42013- 1) 点评:。
多项式练习题参考答案.doc

多项式练习题参考答案一、填空题1.f(x) = X4 -4x3 -l,g(x) = x2 -3x-l.则y(x)被g(x)除所得的商式为亍—X —2 ,余式为-7x - 3 .2 • f(x),g(x),u(x),v(x)e P[x],若“(x)f (x) + v(x)g(x) = 2,则(f(x),g(x))= _L(w(x),v(x))=—・L 13. f (x) = a n x n+■■■ + a l x + a0 e P[x]且*0,/(x) I g(x), (/(x),g(x)) = —/(x).a n4.尸+2,(x —1)(X +3),0,2X +4,X3 —1 中是本原多项式的为尸+2,(x —l)(x +3), .r3 -1.5.多项式/(x) = [4(5x-4)2000X2-2X-1]2°01(8 X3-11X2 + 2) 2002的所有系数之和= 1_ (取X = 1得到),常数项=-22。
2 (取》=0得到).6.能被任一多项式整除的式项式是零多项式;能整除任意多项式的多项式一定是零次多项式.7.多项式f⑴除以ax-b(a^O)的余式为/(-).a8.设2%3— %2 + 3x — 5 =。
(尤一2)3 + Z?(x — 2)2 + c(x — 2) + 6?,则ci,b,c,d的值为2, 9, 23,13 .9.f⑴=营+ 4x4 +X3-10X2-4X +8在有理数上的标准分解式是(x-l)2(x + 2)3.10.x2 +3x + 2|x4 +mx2- px+ 2 ,贝ll m = -6 , p = 3二、判断说明题(先判断正确与错误,再简述理由)1.若心)f(x) + v(x)g(x)=』3),则必为/(X)与g(x)的最大公因式.错.如/(x) = x-l,g(x) = x + l,w(x) = x + l,v(x) = -x ,贝!J d(x) = -x-l,但/(x)与g(x)互素.2.若p(x) I /(x)g(x),p(x)在P 上不可约,且p(x) I [/(x) + g(x)],则p(x) I /(x)且p(x) I g(x).对.由p(x)I /(x)g(x),p(x)在P 上不可约可得p(x)I /(x)或p(x)I g(x).若p(x) I /(x),又p(x) I [/(x) + g(x)],因此p(x)l[/(x) + g(x)]-/(x),即p(x)lg(x).3.设p(x),f(x)为P上的多项式,且p(x)不可约.若p(x)为f'(x)的*重因式, 则p(x)必为/(X)的)+ 1重因式.错.如/(x) = (x2+2)5+5, x2 +2是广⑴在Q上的4重因式,但尸+2不是了(x)的因式.4.有理系数多项式/(%)在Q上可约,则f(x)有有理根.错.如f(x)=x4-4 = (x2+2)(x2-2)在Q上可约,但f(x)没有有理根.5.若"是整系数多项式f(x)的根,p,q为互素的整数,则⑴.P对.由里是整系数多项式f(x)的根可得px-q为f(x)的因式,艮口Pf (%) = (px-q)g(x),且g(x)是整系数的,取x = l可得(p-q)|f ⑴.6.奇数次实系数多项式在实数域上一定有实根,因此在实数域上一定可约. 错.一次实系数多项式有实根但不可约.7.若f(x)|/z(x)且g(x)|/z(x),则f(x)g(x)|/z(x).错.缺f(x),g(x)互素.8.若g(x) + f(x)则(f(x),g(x)) = l.错.如 %2 -1 / %3 -1,但(x2 - l,x3 -1) = x-19.数域P上的任意一个不可约多项式p(x)在复数域内没有重根.正确.10.多项式f(x)有重根当且仅当f(x)有重因式.与所考虑的范围有关,在复数域上正确,在其它数域上有重因式未必有重根.三、计算题1.设f (x) = x4 -x3 -x2 +2x-l,g(x) = X3— 2x + l,求(f (x),g(x))以及w(x),v(x),使w(x)f(x) +v(x)g(x) = (f(x),g(x)).解:利用辗转相除法得/■(x) = g(x)0i (x) + * (x) = g(x)(x T) + -X, g(x) = ^(x)^2(x) + ^(x)= (x2 - x)(x +1) - X +1, r^x) = r2 (x)q3 (x) = (-x + l)(-x).因此(f (x), g ⑴)=x — 1.又r(X)= g(X)- * (x)02 (x) = g (x) - (f (x) - g(X)01 (x))02 (x) =-<112(x)f (x) + (1 + 01 (x)02 (x)) .g (x)) = -r(x) = q, (x)/(x) - (1 + (x)^2 (x))g (x) .2所以i/(x) = q2 (x) = x + l,v(x) = —1 —0(x)02(x)= —l-(x — l)(x + l) = -x2.2./(x) = x5 - x3 + 4x2 - 3x + 2(1)判断f(x)在R上有无重因式?如果有,求出所有的重因式及重数;(2)求f(x)在R上的标准分解式.解:(1) f,(x) = 5x4-3x2+8x-3.运用辗转相除法可得:(f(x),f'(x)) = x2—x + 1.r —x + 1为f (x)在R上二重因式.(2)由⑴可得/Xx)在R上的标准分解式为/(x) = (x2 - x + l)2(x + 2).解法2: f(x)的可能有理根为±1,±2,经检验-2为f(x)的有理根,由综合除法可得-210-14-32-2 4 -6 4 -21-23-210因此有f(x) = (x4- 2W + 3x2 — 2% +1)(》+2)=(若 _ * +1)2 (x + 2).若一》+1 为f(x)在R上二重因式.f(x)在R上的标准分解式为f(x) = (x2-x + l)2(x + 2).3.已知f (x) = x3 +6x2 + 3px + 8 ,试确定p的值,使/'(x)有重根,并求其根.解:若f (x)有重根,则/(x) = (x — a)2(x-幻=x3~(2a + b)x2 +(a2 + 2ab)x-a2b.因此有2Q + b =—6, Q = —2,a2 + 2ab = 3p,解得,b = -2,或<a2b = -8. p = 4.当p = 4时-2为f (x)的3重根;当p = -5时1为f⑴的2重根,-8为单根.解法2:若f(x)有重根,贝I] (f (%),广⑴)丰1.f\x) = 3x2 +12x + 3p =3(x2 +4i + p).f(X)= ! f '(x)(x + 2) + (2p - 8)x + (8 - 2p)=(x2 + 4x + p)(x + 2) + (2p — 8)(x -1),'(-Y)= (x-l)(x + 5) + (p + 5) •当p = 4 时,f (x) = (x + 2)3, 一2 为f(x)的 3 重根;当p = —5 时,(y(w,广⑴) =x-1,1 为/(x)的2 重根,此时/(x) = (x-l)2(x + 8),-8 为单根.4.已知1 -z•是多项式X4-4X3+5X2-2X-2的一个根,求其所有的根.解:由实系数多项式虚根成对性,1 +,也是¥ —4F +5亍_2》一2的根./(x) = x4 -4x3 +5x2 - 2x-2 = (x2 -2x + 2)(x2 -2x-l).因此f(x)的所有根为l-i,l + z,l + V2,l-V2.5.当a,。
整式的加减测试题多项式加减的进阶练习

整式的加减测试题多项式加减的进阶练习整式的加减是初中数学中的一个重要概念,也是代数运算中的基本操作之一。
通过多项式的加减运算,我们可以对代数式进行合并和简化,从而更好地解决实际问题。
本文将为读者提供一系列有关整式加减的测试题和多项式加减的进阶练习,帮助读者加深对该知识点的理解和运用能力。
一、整式的加减测试题1. 计算下列各题,并将结果写成最简形式:(1) 3x + 5y - 2x - 3y(2) 2a^2 - 4ab + 3ab^2 - 5a^2b(3) 7x^3 - 4x^2 + 9x^3 - 2x^22. 根据题意转化成代数式,并计算:(1) 已知一个长方形的宽度为x,长度为2x+3,求其周长。
(2) 某商店原价x元的商品,打八折后再进行一次半价促销,最终售价为多少?二、多项式加减的进阶练习1. 合并下列各题中的同类项,并写出结果:(1) 3x^3 - 4x^2 + 2x - 5x^3 + 7x^2 + 3x(2) 2a^2b - 5ab^2 - 3a^2b^2 + 4ab^2 - a^2 + 2ab2. 计算下列各题,并将结果写成标准形式:(1) (4x^2 - 3x^3 + x) + (-2x^2 + 5x^3 - 3x)(2) (3a^2 - 2ab - 5b^2) - (a^2 + 4ab - 2b^2)3. 解决下列题目并给出答案:(1) 一个长方形的长度是宽度的5倍,周长为60cm,求长和宽分别是多少?(2) 一辆汽车从A地到B地的直线距离为200km,来回共行驶8次,一次比一次多行驶20km,求汽车来回一次的距离及汽车最初的直线距离。
结语:通过对整式的加减测试题和多项式加减的进阶练习,我们可以更好地理解和掌握这个数学概念。
整式的加减是代数运算中的基本技能,对于解决实际问题和数学建模非常重要。
希望读者通过本文的练习,能够提升自己的数学能力,并在今后的学习中能够灵活运用整式的加减。
线性代数第4,5章综合练习题和答案

第4,5章 综合练习题 一、填空题1.已知211A 121112⎡⎤⎢⎥=⎢⎥⎣⎦,100B 01000a ⎡⎤⎢⎥=⎢⎥⎣⎦且A 与B 相似,则_______________a =.2.设可逆阵A 的一个特征值是2,且-4detA =,则A 的伴随阵*A 的一个特征值为__________.3.设A 与B 相似,B 与112⎡⎤⎢⎥-⎢⎥⎣⎦相似,则A 的特征值是_______.4.已知211A 121112⎡⎤⎢⎥=⎢⎥⎣⎦有二重特征值1,则A 的另一个特征值是______.5.二元二次型()112122x 13f (x ,x )x x 52x ⎛⎫⎡⎤= ⎪⎢⎥⎣⎦⎝⎭的矩阵是_______. 6.若矩阵A 的一个特征值为0,则A =7. 二次型()2221231231223,,3524f x x x x x x x x x x =++++的矩阵A =8.设A 为3阶矩阵,其特征值分别为1,2,-1,则A = , 2A 的特征值是__________,1A -的特征值分别为 , *A 的特征值分别为 ,.9.已知矩阵20000101A x ⎛⎫ ⎪= ⎪⎝⎭与20000001B y ⎛⎫⎪= ⎪-⎝⎭相似,则x = , y =10. 已知三阶矩阵11020421A x -⎛⎫⎪= ⎪⎝⎭的特征值为1、2、3,则x =11. 设向量组:(),0,1,11T=α ()T 1,0,12=α ,则与21,αα 等价的正交向量组为___________.12. ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=300020001A 的特征值为:_______, 2A 的特征值为:_______.13. 用配方法把二次型32312123222162252x x x x x x x x x +++++化成标准形为 .二、单项选择题1. 设12,αα都是n 阶矩阵A 的属于不同特征值的特征向量,则( ) (A) 02T 1=αα; (B) 12T 1=αα ; (C) 线性相关与21αα ;(D) 线性无关与21αα2. 设n 阶矩阵A 与B 相似,则( )(A) (A)(B)r r =; (B)A 与B 和同一个对角矩阵相似; (C) B E A E -=-λλ; (D) A 与B 的特征向量相同. 3. 设A 为n 阶可逆矩阵,与A 有相同特征值的是( ) (A) -1A ; (B) TA ; (C) *A ; (D) 2A . 4.以下四个矩阵,正定的是( )(A) 1-10-120003⎡⎤⎢⎥⎢⎥⎣⎦ ;(B)120210002⎡⎤⎢⎥⎢⎥⎣⎦ ;(C)120240001⎡⎤⎢⎥⎢⎥⎣⎦; (D)200012023⎡⎤⎢⎥⎢⎥⎣⎦.5.A 与B 都是n 阶矩阵,且都可逆,则( )(A) 必存在可逆n 阶矩阵P ,使B AP P =-1; (B) 必存在可逆n 阶矩阵C ,使TC AC B =; (C) 必存在可逆n 阶矩阵P 与Q ,使B PAQ =; (D) A 与B 都与同一个对角矩阵相似.6. 设4-52A 5-736-94⎡⎤⎢⎥=⎢⎥⎣⎦,则A 的属于特征值00λ=的特征向量是( )(A) T )2,1,1(1=α ; (B) T )3,2,1(2=α ;(C) T)1,0,1(3=α ; (D) T )1,1,1(4=α .7. 二次型2123222132162-6-2)x ,x ,x (f x x x x x +-=是( ) (A)正定的; (B)负定的; (C) 半正定的; (D) 半负定的.8. 设001A 010100⎡⎤⎢⎥=⎢⎥⎣⎦,则以下四个向量中是A 的特征向量者是( )(A) T )1,0,1(; (B) T )1,1,1(-; (C) T )2,0,0( ; (D) T)2,1,0(.9. 设A 为n 阶实对称阵,B 为n 阶可逆阵,Q 为n 阶正交阵,则矩阵 ( )与A 有相同的特征值(A )1T-B Q AQB ; (B) ()11TT --BQ AQB ; (C )T T B Q AQB ; (D) T T BQ AQB10. 设矩阵A 与B 相似,则必有( )(A)A 、B 都不可逆 ; (B)A 、B 有相同的特征值 ; (C )A 、B 均与同一个对角矩阵相似 ; (D)矩阵A E λ-与B E λ-相等 11. 设A 是三阶矩阵,10λ=,21λ=,31λ=-是A 的三个特征值,对应的特征向量分别为123,,ααα,则使得1100000001P AP --⎛⎫⎪= ⎪⎝⎭成立的P 是( )(A )(123,,ααα) (B)(132,,ααα) (C)(321,,ααα) (D)(312,,ααα) 12. A 与B 是两个相似的n 阶矩阵,则( )(A)存在非奇异矩阵P ,使1P AP B -= (B)存在对角矩阵D ,使A 与B 都相似与D (C)0AB = (D)E A E B λλ-=-13.如果( ),则矩阵A 与B 相似(A)A B = (B)()()r A r B = (C)A 与B 有相同的特征多项式 (D)n 阶矩阵A 与B 有相同的特征值,且n 个特征值各不相同 14.A 是n 阶正定矩阵的充分必要条件是( )(A)0A > (B)存在n 阶矩阵C ,使TA C C = (C)负惯性指数为零 (D)各阶顺序主子式均为正数 15. 若矩阵A 与B 相似,则下列结论不成立的为( )A. A B =B. ()()r A r B =C. A 与B 有相同的特征值D. A B = 16. 若A 为设n 阶矩阵,则下列结论正确的是( )A. A 的任n 个特征向量线性无关B. A 的属于不同特征值的特征向量线性无关C. A 的属于不同特征值的特征向量正交D. A 的任n 个特征向量线性相关17. 若n 阶方阵A 与B 的特征值完全相同,且A 与B 都有n 个线性无关的特征向量,则( )A. A B =B. A B ≠ 但0A B -=C. A 相似于BD. A 与B 不一定相似,但A B =18.设矩阵a b A b a -⎛⎫=⎪⎝⎭,其中0a b >>,221a b +=,则A 为( ) A. 正定矩阵 B. 初等矩阵 C. 正交矩阵 D. 以上都不对 19. 下列各矩阵中,不是正交矩阵的为( )(A)⎛⎫ ⎪ ⎪⎝⎭;(B)cos sin sin cos θθθθ-⎛⎫ ⎪⎝⎭;(C )1001⎛⎫ ⎪⎝⎭;(D)11222⎛⎫⎪-⎝⎭ 20. 设矩阵A 与B 相似,则必有( )(A)A 、B 同时可逆或不可逆 ; (B)A 、B 有相同的特征向量 ; (C )A 、B 均与同一个对角矩阵相似 ; (D)矩阵E A λ-与E B λ-相等21. 设三阶方阵A 的特征值分别为 -1,0,2.则下列结论正确的是( )。
整式的乘除测试题(3套)及答案

第一章整式的乘除单元测试卷(一)一、精心选一选(每小题3分,共21分)43 31•多项式xy 2x y 9xy 8的次数是A. 3B. 4C. 5D. 62•下列计算正确的是 ()A. 2x 26x 412x 84 mB . y3mmyy C .x y 2 x 22 , 2y D. 4a 2a33.计算a ba b 的结果是()A. b 2 a 2B.2 ,2a bC. a 22ab b 2D.a 2 2ab b 224. 3a 5a1与 2a 2 3a 4的和为()A. 5a 22a 3 2小B. a 8a3 C.2a3a 52小D. a 8a55.下列结果正确的是()21 A.-1 B. 9 50C.53.7 01D. 2 31398m^n26.右 a b8 6a b,那么m 22n 的值是()A. 10B. 52C. 20D. 327•要使式子9x 225y 2成为一个完全平方式,则需加上( )二、耐心填一填(第1~4题每空1分,第5、6题每空2分,共28分)班级 ____ 姓名 ______ 学号 ________ 得分 ________A. 15xyB. 15xyC. 30xyD. 30xy1•在代数式3xy 2 ,个,多项式有一2m ,6a个。
2a 3 , 12 , 4x yz1 2xy 2 , 中,单项式有 5 3ab2•单项式 5x 2y 4z 的系数是,次数是 。
,413•多项式3ab ab 有项,它们分别是。
54•⑴ x 2 x 5。
34⑵y 3。
23⑶2a b。
⑷x 5y24。
93⑸a a。
⑹ 10 5 2 40z 1 2 635.⑴ mnmn。
⑵x 5 x 5。
3 5⑶(2a b )25 。
⑷ 12x 3小 2y3xy 。
/、m32m6•⑴ aa a。
⑵ 22a 8a242…。
20062 220051 ⑶ x y x y x y。
⑷3。
3三、精心做一做(每题5分,共15分)1. 4x 2 y 5xy 7x5x 2 y 4xy x2 2 32. 2a 23a 2 2a 1 4a 32 ^343.2x y 6x y 8xy 2xy1. X 1 2x 1 x 22. 2x 3y 5 2x 3y 5四、计算题(每题6分,共12分)1五、化简再求值:XX 2y x 12 2x,其中X -,y 25。
2021年七上数学同步练习-数与式_整式_多项式的项和次数-单选题专训及答案

的次数是
25.答 案 : D 26.答 案 : A 27.答 案 : D 28.答 案 : A 29.答 案 : C 30.答 案 : D
2、
(2019沭阳.七上期末) 多项式1+2xy-3xy2的次数及最高次项的系数分别是( )
A . 3,-3 B . 2,-3 C . 5,-3 D . 2,3
3、
(2020莘.七上期末) 多项式2x3-8x2+x-1与多项式3x3+2mx2-5x+3的和不含有二次项,则m为取值为( )
A . 2 B . -2 C . -4 D . 4
20、
(2020岑溪.七上期中) 下列四个说法,其中正确的是( ) A . 单项式x3的系数是3 B . 单项式﹣2ab的次数是2 C . 多项式a2+2a﹣1的常数项是1 D . 多项式x2﹣y2的次数是4
21、
(2020港南.七上期中) 下列说法错误的是( )
A . 多项式
是三次三项式 B .
8、 (2019重庆.七上期末) 若多项式5x2y|m|
(m+1)y2﹣3是三次三项式,则m等于( )
A . ﹣1 B . 0 C . 1 D . 2
9、
(2020西安.七上期末) 已知关于x的多项式(2mx2+5x2+3x+1)-(6x2+3x)化简后不含x2项,则m的值是( )
A . 0 B . 0.5 C . 3 D . -2.5
6、
(2019南山.七上期末) 下列结论中,正确的是
A . 单项式
的系数是3,次数是2 B . 单项式m的次数是1,没有系数 C . 单项式
系数是 ,次数是4 D . 多项式
上海中学七年级数学上册第二单元《整式加减》-解答题专项经典练习题

一、解答题1.若关于x ,y 的多项式my 3+3nx 2y +2y 3-x 2y +y 不含三次项,求2m +3n 的值. 解析:-3. 【分析】先合并同类项,根据已知得出m+2=0,3n-1=0,求出m 、n 的值后代入进行计算即可. 【详解】my 3+3nx 2y +2y 3-x 2y +y =(m +2)y 3+(3n -1)x 2y +y , ∵此多项式不含三次项, ∴m +2=0,3n -1=0, ∴m =-2,n =13, ∴2m +3n =2×(-2)+3×13=-4+1=-3. 【点睛】本题考查了合并同类项和解一元一次方程的应用,关键是求出m 、n 的值. 2.已知22332A x y xy =+-,2222B xy y x =--. (1)求23A B -.(2)若|23|1x -=,29y =,且||x y y x -=-,求23A B -的值.解析:(1)2212127x y xy +-;(2)114或99.【分析】(1)把22332A x y xy =+-,2222B xy y x =--代入23A B -计算即可;(2)根据|23|1x -=,29y =,且||x y y x -=-求出x 和y 的值,然后代入(1)中化简的结果计算即可. 【详解】 解:(1)()()2222232332322A B x y xy xy y x-=+----2222664366x y xy xy y x =+--++ 2212127x y xy =+-;(2)由题意可知:231x -=±,3=±y , ∴2x =或1,3=±y ,由于||x y y x -=-, ∴2x =,3y =或1x =,3y =. 当2x =,3y =时,23114A B -=. 当1x =,3y =时,2399A B -=. 所以,23A B -的值为114或99. 【点睛】本题考查了整式的加减运算,绝对值的意义,以及分类讨论的数学思想,熟练掌握整式的加减运算法则是解(1)的关键,分类讨论是解(2)的关键.3.如图,将面积为2a 的小正方形和面积为2b 的大正方形放在同一水平面上(0b a >>)(1)用a 、b 表示阴影部分的面积;(2)计算当3a =,5b =时,阴影部分的面积. 解析:(1)22111222a ab b ++;(2)492【分析】(1)阴影部分为两个直角三角形,根据面积公式即可计算得到答案; (2)将3a =,5b =代入求值即可. 【详解】 (1)()21122a ab b ⨯++, 22111222a ab b =++; (2)当3a =,5b =时,原式221113355222=⨯+⨯⨯+⨯492=. 【点睛】此题考察列式计算,根据图形边长正确列式表示图形的面积即可.4.为鼓励居民节约用电,某市采用价格调控手段达到省电目的,该市电费收费标准如下表(按月结算): 每月用电量度 电价/(元/度) 不超过150度的部分0.50元/度 超过150度且不超过250度的部分 0.65元/度 超过250度的部分0.80元/度(2)设某月的用电量为x 度(0300x <≤),试写出不同电量区间应缴交的电费.解析:(1)该居民12月份应缴电费94.5元;(2)0.5,01500.6522.5,1502500.860,250300x x x x x x <≤⎧⎪-<≤⎨⎪-<≤⎩【分析】(1)根据用电量类型分别进行计算即可;(2)分三种情况进行讨论,当x 不超过150度时,x 超过150度,但不超过时250度时和x 超过250度时,再分别代入计算即可. 【详解】解:(1)由题意,得150×0.50+(180-150)×0.65=94.5(元) 答:该居民12月应缴交电费94.5元;(2)若某户的用电量为x 度,则当x≤150时,应付电费:0.50x 元; 当150<x≤250时,应付电费:0.65(x -150)+75=0.65x 22.5-(元); 当250<x <300,应付电费:0.80(x -250)+140=0.8x 60-(元).∴不同电量区间应缴交的电费为:0.5,01500.6522.5,1502500.860,250300x x x x x x <≤⎧⎪-<≤⎨⎪-<≤⎩.【点睛】本题考查了列代数式,读懂题目信息,理解阶梯电价的收费方法和电费的计算方法是解题的关键.5.窗户的形状如图所示(图中长度单位:cm ),其中上部是半圆形,下部是边长相同的四个小正方形. 已知下部小正方形的边长是acm. (1)计算窗户的面积(计算结果保留π). (2)计算窗户的外框的总长(计算结果保留π).(3)安装一种普通合金材料的窗户单价是175元/平方米,当a=50cm 时,请你帮助计算这个窗户安装这种材料的费用(π≈3.14,窗户面积精确到0.1).解析:(1)2214a +a 2π;(2)6a a π+;(3)245. 【分析】(1)根据图示,窗户的面积等于4个小正方形的面积加上半径是a 的半圆的面积; (2)根据图示,窗户外框的总长就是用3条长度是2acm 的边的长度加上半径是acm 的半圆的长度;(3)根据窗户的总面积,代入求值即可. 【详解】解:(1)窗户的面积为:()()222214a a 422a a a cm ππ⎛⎫⨯+=+ ⎪⎝⎭(2)窗户的外框的总长为:()()132a 262a a a cm ππ⨯+⨯=+ (3)当a=50cm ,即:a=0.5m 时, 窗户的总面积为:()2220.540.5128m ππ⎛⎫⨯+=+ ⎪⎝⎭取π≈3.14,原式=1+0.3925≈1.4(m 2) 安装窗户的费用为:1.4×175=245(元). 【点睛】本题考查的知识点是求组合图形的面积与周长,将已知图形分解为所熟悉的简单图形是解此题的关键. 6.化简并求值:已知2232A a b ab abc =-+,小明错将“2A B -”看成“2A B +”,算得结果22434C a b ab abc =-+. (1)计算B 的表达式;(2)小强说正确结果的大小与c 的取值无关,对吗?请说明理由. (3)若18a =,15b = ,求正确结果的代数式的值. 解析:(1)2222a b ab abc -++;(2)小强的说法对,正确结果的取值与c 无关,理由见解析;(3)0. 【分析】(1)由2A+B=C 得B=C-2A ,将C 、A 代入根据整式的乘法计算可得B ;(2)将A 、B 代入2A-B ,根据整式的加减运算法则进行化简,由化简后的代数式中无字母c 可知其值与c 无关;(3)将a 、b 的值代入计算即可. 【详解】解:(1)∵2A B C +=,∴2B C A =-. B 22224342(32)a b ab abc a b ab abc =-+--+2222434642a b ab abc a b ab abc =-+-+- 2222a b ab abc =-++;(2)222222(32)(22)A B a b ab abc a b ab abc -=-+--++222264222a b ab abc a b ab abc =-++-- 2285a b ab =-.因正确结果中不含c ,所以小强的说法对,正确结果的取值与c 无关;(3)将18a =, 15b =代入(2)中的代数式,得: 22221111858()5()8585a b ab -=⨯⨯-⨯⨯0= .【点睛】本题主要考查整式的乘法,熟练掌握整式的乘法法则是解题的关键. 7.求多项式的值222232424a b ab a b ab --+-,其中1a =-,2b =-. 解析:24a b --,-2. 【分析】原式合并同类项后代入字母的值计算即可. 【详解】解:原式24a b =--, 当1a =-,2b =-时, 原式2=-. 【点睛】本题考查了整式的化简求值,正确的将原式合并同类项是解决此题的关键.8.日历上的规律:下图是2020年元月的日历,图中的阴影区域是在日历中选取的一块九宫格.(1)九宫格中,四个角上的四个数之和与九宫格中央这个数有什么关系?(2)请你自选一块九宫格进行计算,观察四个角上的四个数之和与九宫格中央那个数是否还有这种关系. (3)试说明原理.解析:(1)四个角上的四个数之和等于九宫格中央这个数的4倍;(2)四个角上的四个数之和等于九宫格中央这个数的4倍,选取九宫格见解析;(3)见解析. 【分析】(1)求出四个角上的四个数之和与九宫格中央这个数,从而验证它们的关系. (2)选择如下图的九宫格,验证他们的关系即可. (3)设九宫格中央这个数为a ,列等式进行验证即可. 【详解】(1)四个角上的四个数之和等于九宫格中央这个数的4倍. 理由如下:6228202828414+++=+=⨯.(2)如图,9112325174+++=⨯,所以四个角上的四个数之和等于九宫格中央这个数的4倍.(选取的九宫格不唯一).(3)设九宫格中央这个数为a ,那么左上角的数为71a --,右上角的数为71a -+,左下角的数为71a +-,右下角的数为71a ++,四个数的和为(71)(71)(71)(71)4a a a a a --+-+++-+++=. 即四个角上的四个数之和等于九宫格中央这个数的4倍. 【点睛】本题考查了整式的加减应用,掌握整式的加减运算法则是解题的关键.9.将一个长方形纸片连续对折,对折的次数越多,折痕的条数也就越多,如第一次对折后,有1条折痕,第2次对折后,共有3条折痕. (1)第3次对折后共有多少条折痕?第4次对折后呢? (2)对折多少次后折痕会超过100条?(3)请找出折痕条数与对折次数的对应规律,写出对折n 次后,折痕有多少条? 解析:(1)第3次对折后共有7条折痕,第4次对折后有15条折痕;(2)对折7次后折痕会超过100条;(3)对折n 次后,折痕有21n -条. 【分析】(1)动手操作即可得出第3次、第4次对折后的折痕条数;(2)在(1)的基础上,归纳类推出一般规律,再结合67264,2128==即可得出答案;(3)由题(2)已求得. 【详解】(1)动手操作可知,第3次对折后的折痕条数为7条, 第4次对折后的折痕条数为15条;(2)观察可知,第1次对折后的折痕条数为1121=-条, 第2次对折后的折痕条数为2321=-条, 第3次对折后的折痕条数为3721=-条, 第4次对折后的折痕条数为41521=-条, 归纳类推得:第n 次对折后的折痕条数为21n -条,因为67264,2128==,所以对折7次后折痕会超过100条;(3)由(2)已得:对折n 次后的折痕条数为21n -条. 【点睛】本题考查了有理数乘方的应用,依据题意,根据前4次对折后的结果,正确归纳类推出一般规律是解题关键. 10.用代数式表示:(1)比x 的平方的5倍少2的数; (2)x 的相反数与y 的倒数的和; (3)x 与y 的差的平方;(4)某商品的原价是a 元,提价15%后的价格;(5)有一个三位数,个位数字比十位数字少4,百位数字是个位数字的2倍,设x 表示十位上的数字,用代数式表示这个三位数.解析:(1)5x 2-2;(2)-x +1y;(3)(x -y )2;(4)(1+15%)a ;(5)200(x -4)+10x +(x -4).【分析】(1)明确是x 的平方的5倍与2的差;(2)先求出x 的相反数与y 的倒数,然后相加即可; (3)注意是先做差后平方;(4)注意是提价后的价格而非所提的价格; (5)注意正确表示百位,十位,个位上的数. 【详解】 (1)5x 2-2;(2)-x +1y;(3)(x -y )2; (4)(1+15%)a ; (5)200(x -4)+10x +(x -4) . 【点睛】本题考查了列代数式,能够根据运算顺序正确书写,同时注意数位的意义,注意“多,少,积,差”等关键字的把握.11.一种商品每件成本a 元,原来按成本增加22%定出价格. (1)请问每件售价多少元?(2)现在由于库存积压减价,按售价的85%出售,请问每件还能盈利多少元? 解析:(1)每件售价1.22a 元;(2)每件盈利0.037a 元. 【分析】(1)根据每件成本a 元,原来按成本增加22%定出价格,列出代数式,再进行整理即可; (2)用原价的85%减去成本a 元,列出代数式,即可得出答案. 【详解】(1)根据题意,得: (1+22%)a =1.22a (元), 答:每件售价1.22a 元; (2)根据题意,得: 1.22a ×85%-a =0.037a (元). 答:每件盈利0.037a 元. 【点睛】本题考查了列代数式,解决问题的关键是读懂题意,找到所求的量的等量关系,注意把列出的式子进行整理.12.数学课上,老师出示了这样一道题目:“当1,22a b ==-时,求多项式3233233733631061a a b a a b a b a a b +++----的值”.解完这道题后,张恒同学指出:“1,22a b ==-是多余的条件”师生讨论后,一致认为这种说法是正确的,老师及时给予表扬,同学们对张恒同学敢于提出自己的见解投去了赞赏的目光. (1)请你说明正确的理由;(2)受此启发,老师又出示了一道题目,“无论x 取任何值,多项式2233x mx nx x -++-+的值都不变,求系数m 、n 的值”.请你解决这个问题.解析:(1)见解析;(2)3n =,1m =. 【分析】(1)将原式进行合并同类项,然后进一步证明即可;(2)将原式进行合并同类项,根据“无论x 取任何值,多项式值不变”进一步求解即可. 【详解】(1)3233233733631061a a b a a b a b a a b +++---- =3332233731033661a a a a b a b a b a b +-+-+-- =1-,∴该多项式的值与a 、b 的取值无关, ∴1,22a b ==-是多余的条件. (2)2233x mx nx x -++-+ =2233x nx mx x -++-+ =2(3n)(1)3x m x -++-+ ∵无论x 取任何值,多项式值不变, ∴30n -+=,10m -=, ∴3n =,1m =. 【点睛】本题主要考查了多项式运算中的无关类问题,熟练掌握相关方法是解题关键.13.国庆期间,广场上设置了一个庆祝国庆70周年的造型(如图所示).造型平面呈轴对称,其正中间为一个半径为b的半圆,摆放花草,其余部分为展板.求:(1)展板的面积是.(用含a,b的代数式表示)(2)若a=0.5米,b=2米,求展板的面积.(3)在(2)的条件下,已知摆放花草部分造价为450元/平方米,展板部分造价为80元/平方米,求制作整个造型的造价(π取3).解析:(1)12ab平方米;(2)12 (平方米);(3)3660元.【分析】(1)利用分割法求解即可.(2)把a,b的值代入(1)中代数式求值即可.(3)分别求出摆放花草部分造价,展板部分造价即可解决问题.【详解】(1)由题意:展板的面积=12a•b (平方米).故答案为:12ab (平方米).(2)当a=0.5米,b=2米时,展板的面积=12×0.5×2=12(平方米).(3)制作整个造型的造价=12×8012π×4×450=3660(元).【点睛】本题考查轴对称图形,矩形的性质,圆的面积等知识,解题的关键是熟练掌握基本知识.14.生活中,有人喜欢把传送的便条折成形状,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为26cm,宽为cmx,分别回答下列问题:(1)为了保证能折成图④的形状(即纸条两端均超出点P),试求P的取值范围.(2)如果不但要折成图④的形状,而且为了美观,希望纸条两端超出点P的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点M与点P的距离(用P表示)解析:(1) x<5.2(2) 13-1.5x 【详解】分析:(1)按图中方式折叠后可得到除去两端,纸条使用的长度为5x ,那么纸条使用的长度应大于0,小于纸条总长度. (2)是轴对称图形,那么AM=AP+x .解答:解:(1)由折纸过程可知0<5x <26,∴0<x <5.2.(2)∵图④为轴对称图形,∴AM=2652x-+x=13-1.5x , 即点M 与点A 的距离是(13-1.5x )cm .点评:本题考查学生的动手操作能力,难点是得到纸条除去两端使用的纸条的长度. 15.已知2223,Ax xy y B x xy()1若()2230x y ++-=,求2A B -的值()2若2A B -的值与y 的值无关,求x 的值解析:(1)-9;(2)x=-1 【分析】(1)根据去括号,合并同类项,可得答案;(2)根据多项式的值与y 无关,可得y 的系数等于零,根据解方程,可得答案. 【详解】(1)A-2B=(2x 2+xy+3y )-2(x 2-xy ) =2x 2+xy+3y-2x 2+2xy =3xy+3y .∵(x+2)2+|y-3|=0, ∴x=-2,y=3. A-2B=3×(-2)×3+3×3 =-18+9 =-9.(2)∵A-2B 的值与y 的值无关, 即(3x+3)y 与y 的值无关, ∴3x+3=0. 解得x=-1. 【点睛】此题考查整式的加减,解题关键在于掌握去括号,括号前是正数去括号不变号,括号前是负数去括号都变号.16.已知A=3a 2b ﹣2ab 2+abc ,小明同学错将“2A ﹣B”看成“2A+B”,算得结果为4a 2b ﹣3ab 2+4abc . (1)计算B 的表达式; (2)求出2A ﹣B 的结果;(3)小强同学说(2)中的结果的大小与c的取值无关,对吗?若a=18,b=15,求(2)中式子的值.解析:(1)﹣2a2b+ab2+2abc;(2) 8a2b﹣5ab2;(3)对,0.【分析】(1)根据B=4a2b﹣3ab2+4abc-2A列出关系式,去括号合并即可得到B;(2)把A与B代入2A-B中,去括号合并即可得到结果;(3)把a与b的值代入计算即可求出值.【详解】解:(1)∵2A+B=4a2b﹣3ab2+4abc,∴B=4a2b﹣3ab2+4abc-2A=4a2b-3ab2+4abc-2(3a2b-2ab2+abc)=4a2b-3ab2+4abc-6a2b+4ab2-2abc=-2a2b+ab2+2abc;(2)2A-B=2(3a2b-2ab2+abc)-(-2a2b+ab2+2abc)=6a2b-4ab2+2abc+2a2b-ab2-2abc=8a2b-5ab2;(3)对,由(2)化简的结果可知与c无关,将a=18,b=15代入,得8a2b-5ab2=8×218⎛⎫⎪⎝⎭×15-5×18×21()5=0.【点睛】本题考查了整式的加减,整式加减的运算法则:一般地,几个整式相加减,如果有括号先去括号,然后再合并同类项.17.已知多项式2x2+4xy﹣3y2+x2+kxy+5y2,当k为何值时,它与多项式3x2+6xy+2y2是相等的多项式.解析:k=2.【分析】根据两个多项式是相同的多项式,可以直接列等式根据各项前对应系数相等直接列式计算.【详解】解:2x2+4xy﹣3y2+x2+kxy+5y2,=3x2+(4+k)xy+2y2,因为它与多项式3x2+6xy+2y2是相等的多项式,所以4+k=6,解得:k=2.【点睛】本题考查了带系数多项式与已知多项式相等求未知系数,掌握多项式的概念是解决此题的关键.18.历史上的数学巨人欧拉最先把关于x的多项式用记号f(x)的形式来表示,把x等于某数a时的多项式的值用f(a)来表示,例如x=﹣1时,多项式f(x)=x2+3x﹣5的值记为f(﹣1),则f(﹣1)=﹣7.已知f(x)=ax5+bx3+3x+c,且f(0)=﹣1(1)c=_____.(2)若f(1)=2,求a+b的值;(3)若f(2)=9,求f(﹣2)的值.解析:(1)-1;(2)0;(3)-11.【解析】分析:(1)把x=0,代入f(x)=ax5+bx3+3x+c,即可解决问题;(2)把x=1,代入f(x)=ax5+bx3+3x+c,即可解决问题;(3)把x=2,代入f(x)=ax5+bx3+3x+c,利用整体代入的思想即可解决问题;详解:(1)∵f(x)=ax5+bx3+3x+c,且f(0)=-1,∴c=-1,故答案为-1.(2)∵f(1)=2,c=-1∴a+b+3-1=2,∴a+b=0(3)∵f(2)=9,c=-1,∴32a+8b+6-1=9,∴32a+8b=4,∴f(-2)=-32a-8b-6-1=-4-6-1=-11.点睛:本题考查的多项式代数式求值,解题的关键是理解题意,灵活运用所学知识解决问题.19.已知多项式-13x2y m+1+12xy2-3x3+6是六次四项式,单项式3x2n y2的次数与这个多项式的次数相同,求m2+n2的值.解析:13【解析】试题分析:根据多项式次数的定义,可得2+m+1=6,从而可求出m的值,根据单项式的次数的定义结合题意可得2n+2=6,求解即可得到n的值,把m,n的值代入到m2+n2中,计算即可得到求解.试题根据题意得2+m+1=6,2n+2=6解得:m=3, n=2,所以m2+n2=13.点睛:此题考查多项式,解题的关键是弄清多项式的次数是多项式中次数最高的项的次数,还要弄清有几项.20.已知有理数a和b满足多项式A,且A=(a﹣1)x5+x|b+2|﹣2x2+bx+b(b≠﹣2)是关于x 的二次三项式,求(a﹣b)2的值.解析:16或25【解析】试题分析:根据有理数a和b满足多项式A.A=(a﹣1)x5+x|b+2|﹣2x2+bx+b是关于x的二次三项式,求得a、b的值,然后分别代入计算可得.试题解:∵有理数a和b满足多项式A.A=(a﹣1)x5+x|b+2|﹣2x2+bx+b是关于x的二次三项式,∴a﹣1=0,解得:a=1.(1)当|b+2|=2时,解得:b=0或b=4.①当b=0时,此时A不是二次三项式;②当b=﹣4时,此时A是关于x的二次三项式.(2)当|b+2|=1时,解得:b=﹣1(舍)或b=﹣3.(3)当|b+2|=0时,解得:b=﹣2(舍)∴a=1,b=﹣4或a=1,b=﹣3.当a=1,b=﹣4时,(a﹣b)2=25;当a=1,b=﹣3时,(a﹣b)2=16.点睛:本题考查了多项式的知识,解题的关键是根据题意求得a、b的值,题目中重点渗透了分类讨论思想.21.已知多项式﹣3x2+mx+nx2﹣x+3的值与x无关,求(2m﹣n)2017的值.解析:-1【分析】先把多项式进行合并同类项得(n-3)x2+(m-1)x+3,由于关于字母x的二次多项式-3x2+mx+nx2-x+3的值与x无关,即不含x的项,所以n-3=0,m-1=0,然后解出m、n,代入计算(2m-n)2017的值即可.【详解】合并同类项得(n﹣3)x2+(m﹣1)x+3,根据题意得n﹣3=0,m﹣1=0,解得m=1,n=3,所以(2m﹣n)2017=(﹣1)2017=﹣1.【点睛】考查了多项式及相关概念:几个单项式的和叫做多项式,每个单项式叫做多项式的项,其中不含字母的项叫做常数项.多项式中次数最高的项的次数叫做多项式的次数.22.若1+2+3+…+n=m,求(ab n)•(a2b n﹣1)…(a n﹣1b2)•(a n b)的值.解析:a m b m【解析】试题分析:根据单项式的乘法法则,同底数幂相乘,底数不变,指数相加的性质,(ab n)•(a2b n﹣1)…(a n﹣1b2)•(a n b)=a1+2+…n b n+n﹣1+…+1=a m b m.解:∵1+2+3+…+n=m,∴(ab n)•(a2b n﹣1)…(a n﹣1b2)•(a n b),=a1+2+...n b n+n﹣1+ (1)=a m b m考点:单项式乘单项式;同底数幂的乘法.点评:本题考查单项式的乘法法则和同底数幂的乘法的性质.23.国庆期间,王老师计划组织朋友去晋西北游览两日.经了解,现有甲、乙两家旅行社针对组团两日游的游客报价均为每人500元,且提供的服务完全相同.甲旅行社表示,每人都按八五折收费;乙旅行社表示,若人数不超过20人,每人都按九折收费,超过20人,则超出部分每人按八折收费.假设组团参加甲、乙两家旅行社两日游的人数均为x 人. (1)请列式表示甲、乙两家旅行社收取组团两日游的总费用;(2)若王老师组团参加两日游的人数共有30人,请你通过计算,在甲、乙两家旅行社中,帮助王老师选择收取总费用较少的一家.解析:(1)甲旅行社收取组团两日游的总费用为425x 元;若人数不超过20人时,乙旅行社收取组团两日游的总费用为450x 元;若人数超过20人时,乙旅行社收取组团两日游的总费用为(4001000x +)元;(2)王老师应选择甲旅行社.【分析】(1)根据总费用等于人数乘以打折后的单价,易得甲旅行社的费用=500 x×0.85,对于乙家旅行社的总费用,应分类讨论:当0≤x≤20时,乙旅行社的费用=500 x×0.9;当x >20时,乙旅行社的费用=500×20×0.9+500(x-20)×0.8;(2)把x=30分别代入(1)中对应关系计算甲旅行社的费用和乙旅行社的费用的值,然后比较大小即可.【详解】(1)甲旅行社收取组团两日游的总费用为:5000.85425x x ⨯=元若人数不超过20人时,乙旅行社收取组团两日游的总费用为:5000.9450x x ⨯=元 若人数超过20人时,乙旅行社收取组团两日游的总费用为:()500(20)0.8500200.94001000-⨯+⨯⨯=+x x 元(2)因为王老师组团参加两日游的人数共有30人,所以甲旅行社收取组团两日游的总费用为:4253012750⨯=元乙旅行社收取组团两日游的总费用为40030100013000⨯+=元1275013000<,王老师应选择甲旅行社.【点睛】本题考查了代数式,能根据具体情境列代数式并求代数式的值是关键.24.将正整数1,2,3,4,5,……排列成如图所示的数阵:(1)十字框中五个数的和与框正中心的数11有什么关系?(2)若将十字框上下、左右平移,可框住另外五个数,这五个数的和与框正中心的数还有这种规律吗?请说明理由;(3)十字框中五个数的和能等于180吗?若能,请写出这五个数;若不能,请说明理由; (4)十字框中五个数的和能等于2020吗?若能,请写出这五个数;若不能,请说明理由.解析:(1)十字框中五个数的和是正中心数的5倍;(2)十字框中五个数的和是正中心数的5倍,理由见解析;(3)不能,理由见解析;(4)这五个数是404,403,405,397,411.【分析】(1)把框住的数相加即可求解;(2)设中心的数为a ,则其余4个数分别为1a -,1a +,7a -,7a +,相加即可得到规律;(3)由(2)得五个数的和为5a ,令5a=180,根据解得情况即可求解;(4)由(2)得五个数的和为5a ,令5a=2020,根据解得情况即可求解;【详解】解:(1)十字框中五个数的和是正中心数的5倍.∵十字框中五个数的和41011121855511=++++==⨯,∴十字框中五个数的和是正中心数的5倍.(2)五个数的和与框正中心的数还有这种规律.设中心的数为a ,则其余4个数分别为1a -,1a +,7a -,7a +.11775a a a a a a +-+++-++=,∴十字框中五个数的和是正中心数的5倍.(3)十字框中五个数的和不能等于180.∵当5180a =时,解得36a =,36751÷=,36在数阵中位于第6排的第1个数,其前面无数字,∴十字框中五个数的和不能等于180.(4)十字框中五个数的和能等于2020.∵当52020a =时,解得404a =,4047575÷=,404在数阵中位于第58排的第5个数,∴十字框中五个数的和能等于2020,这五个数是404,403,405,397,411.【点睛】此题主要考查一元一次方程的应用,解题的关键是设中心的数为a ,求出十字框中五个数的和为5a.25.已知A =2a 2+3ab ﹣2a ﹣1,B =﹣a 2+1223ab + (1)当a =﹣1,b =﹣2时,求4A ﹣(3A ﹣2B )的值;(2)若(1)中式子的值与a 的取值无关,求b 的值.解析:(1)4ab ﹣2a+13;(2)b=12 【分析】(1)将a=﹣1,b=﹣2代入A=2a 2+3ab ﹣2a ﹣1,B=﹣a 2+12ab+23,求出A 、B 的值,再计算4A ﹣(3A ﹣2B )的值即可;(2)把(1)结果变形,根据结果与a 的值无关求出b 的值即可.【详解】(1)4A ﹣(3A ﹣2B )=4A ﹣3A+2B=A+2B ,∵A=2a 2+3ab ﹣2a ﹣1,B=﹣a 2+12ab+23, ∴A+2B=2a 2+3ab ﹣2a ﹣1+2(﹣a 2+12ab+23) =2a 2+3ab ﹣2a ﹣1﹣2a 2+ab+43 =4ab ﹣2a+13; (2)因为4ab ﹣2a+13 =(4b ﹣2)a+13, 又因为4ab ﹣2a+13的值与a 的取值无关, 所以4b ﹣2=0,所以b=12. 【点睛】本题考查了整式的加减、化简求值,熟练掌握运算法则是解答本题的关键.26.学习了整式的加减运算后,张老师给同学们布置了一道课堂练习题“当2a =-,2018b =,求222221(324)2(23)2()12a b ab a a b a ab a b -+--++-的值”.小明做完后对同桌说:“老师给的条件2018b =是多余的,这道题不给b 的值,照样可以求出结果来”.同桌不相信他的话.亲爱的同学们,你相信小明的说法吗?解析:-21【分析】首先化简代数式,通过去括号、合并同类项,得出结论即含有b 的代数式相加为0,即可说明.【详解】解()()222221324223212a b ab a a b a ab a b ⎛⎫-+--++- ⎪⎝⎭=222223244621a b ab a a b a ab a b -+-+++-=101a -当2a =-时原式=()1021⨯--=-21.【点睛】考查整式的化简求值,熟练掌握去括号法则以及合并同类项法则是解题的关键. 27.已知230x y ++-=,求152423x y xy --+的值. 解析:-24.【分析】首先根据绝对值的非负性求出x ,y ,然后代入代数式求值.【详解】解:∵230x y ++-=,∴x+2=0,y-3=0,∴x=-2,y=3, ∴152423x y xy --+ ()()552342323=-⨯--⨯+⨯-⨯ ()5524=-+-24=-.【点睛】本题考查了代数式求值,利用非负数的和为零得出x 、y 的值是解题关键.28.已知31A B x ,且3223A x x ,求代数式B .解析:2322x x -++【分析】将A 代入A-B=x 3+1中计算即可求出B .【详解】解:∵A-B=x3+1,且A=-2x3+2x+3,∴B=A-(x3+1)=-2x3+2x+3-x3-1=-3x3+2x+2.【点睛】本题考查了整式的加减,涉及的知识有:去括号法则,以及合并同类项法则,熟练掌握法则是解题的关键.29.观察下列式子:0×2+1=12……①1×3+1=22……②2×4+1=32……③3×5+1=42……④……(1)第⑤个式子____,第⑩个式子_____;(2)请用含n(n为正整数)的式子表示上述的规律,并证明.解析:(1)4×6+1=52,9×11+1=102;(2)(n﹣1)(n+1)+1=n2;证明见解析.【分析】(1)根据已知等式中的规律即可得;(2)根据整数的平方等于前一个整数与后一个整数乘积与1的和可得,利用整理的运算法则即可验证.【详解】(1)第⑤个式子为4×6+1=52,第⑩个式子9×11+1=102;故答案为4×6+1=52,9×11+1=102;(2)第n个式子为(n﹣1)(n+1)+1=n2,证明:左边=n2﹣1+1=n2,右边=n2,∴左边=右边,即(n﹣1)(n+1)+1=n2.【点睛】本题主要考查数字的变化规律,解题的关键是根据已知等式得出(n﹣1)(n+1)+1=n2的规律,并熟练加以运用.30.已知多项式2x2+25x3+x﹣5x4﹣13.(1)请指出该多项式的次数,并写出它的二次项和常数项;(2)把这个多项式按x的指数从大到小的顺序重新排列.解析:(1)该多项式的次数是4,它的二次项是2x2,常数项是﹣13;(2)﹣5x4+25x3+2x2+x﹣13.【分析】(1)根据多项式的次数、项等定义解答即可;(2)按x得降幂排列多项式即可.【详解】解:(1)该多项式的次数是4,它的二次项是2x2,常数项是﹣13;(2)这个多项式按x 的指数从大到小的顺序为:432215253x x x x -+++-. 【点睛】本题考查的是多项式的概念及应用.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单项式乘多项式练习题一.解答题(共18小题)1.先化简,再求值:2(a2b+ab2)﹣2(a2b﹣1)﹣ab2﹣2,其中a=﹣2,b=2.2.计算:(1)6x2•3xy (2)(4a﹣b2)(﹣2b)3.(3x2y﹣2x+1)(﹣2xy)4.计算:(1)(﹣12a2b2c)•(﹣abc2)2= _________ ;(2)(3a2b﹣4ab2﹣5ab﹣1)•(﹣2ab2)= _________ .5.计算:﹣6a•(﹣﹣a+2)6.﹣3x•(2x2﹣x+4)7.先化简,再求值3a(2a2﹣4a+3)﹣2a2(3a+4),其中a=﹣2 8.(﹣a2b)(b2﹣a+)9.一条防洪堤坝,其横断面是梯形,上底宽a米,下底宽(a+2b)米,坝高米.(1)求防洪堤坝的横断面积;(2)如果防洪堤坝长100米,那么这段防洪堤坝的体积是多少立方米?10.2ab(5ab+3a2b)11.计算:.12.计算:2x(x2﹣x+3)13.(﹣4a3+12a2b﹣7a3b3)(﹣4a2)= _________ .14.计算:xy2(3x2y﹣xy2+y)15.(﹣2ab)(3a2﹣2ab﹣4b2)16.计算:(﹣2a2b)3(3b2﹣4a+6)17.某同学在计算一个多项式乘以﹣3x2时,因抄错运算符号,算成了加上﹣3x2,得到的结果是x2﹣4x+1,那么正确的计算结果是多少?18.对任意有理数x、y定义运算如下:x△y=ax+by+cxy,这里a、b、c是给定的数,等式右边是通常数的加法及乘法运算,如当a=1,b=2,c=3时,l△3=1×l+2×3+3×1×3=16,现已知所定义的新运算满足条件,1△2=3,2△3=4,并且有一个不为零的数d使得对任意有理数x△d=x,求a、b、c、d的值.多项式 一、填空题 1.计算:_____________)(32=+y x xy x .2.计算:)164(4)164(24242++-++a a a a a =________.3.若3k (2k-5)+2k (1-3k )=52,则k=____ ___.4.如果x+y=-4,x-y=8,那么代数式的值是 cm 。
5.当x=3,y=1时,代数式(x +y )(x -y )+y 2的值是__________.6.若是同类项,则 .7.计算:(x+7)(x-3)=__________,(2a-1)(-2a-1)=__________.8.将一个长为x ,宽为y 的长方形的长减少1,宽增加1,则面积增加________.二、选择题1. 化简)1()1(a a a a --+的结果是( )A .2a ;B . 22a ;C .0 ;D .a a 222-.2.下列计算中正确的是 ( )A.()aa a a +=+236222 ; B.()x x y x xy +=+23222; C.a a a +=10919 ; D.()a a =336.3. 一个长方体的长、宽、高分别是x x -342、和x ,它的体积等于 ( )A.x x -3234;B.x 2 ;C.x x -3268;D.x x -268.4. 计算:ab b a ab 3)46(22•-的结果是( )A.23321218b a b a -;B.2331218b a ab -;C.22321218b a b a -;D.23221218b a b a -. 5.若且,,则的值为( )A .B .1C .D .6.下列各式计算正确的是( )A .(x+5)(x-5)=x 2-10x+25B .(2x+3)(x-3)=2x 2-9C .(3x+2)(3x-1)=9x 2+3x-2D .(x-1)(x+7)=x 2-6x-77.已知(x+3)(x-2)=x 2+ax+b ,则a 、b 的值分别是( )A .a=-1,b=-6B .a=1,b=-6C .a=-1,b=6D .a=1,b=68.计算(a-b )(a 2+ab+b 2)的结果是( )A .a 3-b 3B .a 3-3a 2b+3ab 2-b 3C .a 3+b 3D .a 3-2a 2b+2ab 2-b3 三、解答题1.计算: (1) )2(222ab b a ab -•; (2))12()3161(23xy y x x -•-; (3))13()4(32-+•-b a ab a ; (4) )84)(21(323xy y y x +-; (5))()(a b b b a a ---; (6) )1(2)12(322--+-x x x x x .2.先化简,再求值:)22(32)231(2x x x x ----,其中2=x 3.某同学在计算一个多项式乘以-3x 2时,因抄错符号,算成了加上-3x 2,得到的答案是x 2-0.5x+1,那么正确的计算结果是多少?4.已知:(),,A ab B ab a b C a b ab =-=+=-222323,且a b 、 异号,a 是绝对值最小的负整数,b =12,求3A ·B-21A ·C 的值. 5.若(x 2+mx+8)(x 2-3x+n )的展开式中不含x 3和x 2项,求m 和n 的值参考答案与试题解析一.解答题(共18小题)1.先化简,再求值:2(a 2b+ab 2)﹣2(a 2b ﹣1)﹣ab 2﹣2,其中a=﹣2,b=2.=(2a2b﹣2a2b)+(2ab2﹣ab2)+(2﹣2)=0+ab2=ab2当a=﹣2,b=2时,原式=(﹣2)×22=﹣2×4=﹣8.点评:本题是一道整式的加减化简求值的题,考查了单项式乘以多项式的法则,合并同类项的法则和方法.2.计算:(1)6x2•3xy(2)(4a﹣b2)(﹣2b)考点:单项式乘单项式;单项式乘多项式.分析:(1)根据单项式乘单项式的法则计算;(2)根据单项式乘多项式的法则计算.解答:解:(1)6x2•3xy=18x3y;(2)(4a﹣b2)(﹣2b)=﹣8ab+2b3.点评:本题考查了单项式与单项式相乘、单项式与多项式相乘,熟练掌握运算法则是解题的关键.3.(3x2y﹣2x+1)(﹣2xy)考点:单项式乘多项式.分析:根据单项式乘多项式的法则,用单项式乘多项式的每一项,再把所得的积相加,计算即可.解答:解:(3x2y﹣2x+1)(﹣2xy)=﹣6x3y2+4x2y﹣2xy.点评:本题考查单项式乘多项式的法则,熟练掌握运算法则是解题的关键,本题一定要注意符号的运算.4.计算:(1)(﹣12a2b2c)•(﹣abc2)2= ﹣a4b4c5;(2)(3a2b﹣4ab2﹣5ab﹣1)•(﹣2ab2)= ﹣6a3b3+8a2b4+10a2b3+2ab2.考点:单项式乘多项式;单项式乘单项式.分析:(1)先根据积的乘方,等于把积中的每一个因式分别乘方,再把所得的幂相乘;单项式乘单项式,把他们的系数,相同字母的幂分别相乘,其余字母连同他的指数不变,作为积的因式的法则计算;(2)根据单项式乘多项式,先用单项式去乘多项式的每一项,再把所得的积相加的法则计算即可.解答:解:(1)(﹣12a2b2c)•(﹣abc2)2,=(﹣12a2b2c)•,=﹣;故答案为:﹣a4b4c5;(2)(3a2b﹣4ab2﹣5ab﹣1)•(﹣2ab2),=3a2b•(﹣2ab2)﹣4ab2•(﹣2ab2)﹣5ab•(﹣2ab2)﹣1•(﹣2ab2),=﹣6a3b3+8a2b4+10a2b3+2ab2.故答案为:﹣6a3b3+8a2b4+10a2b3+2ab2.点评:本题考查了单项式与单项式相乘,单项式与多项式相乘,熟练掌握运算法则是解题的关键,计算时要注意运算符号的处理.5.计算:﹣6a•(﹣﹣a+2)考点:单项式乘多项式.分析:根据单项式乘以多项式,用单项式去乘多项式的每一项,再把所得的积相加,计算即可.解答:解:﹣6a•(﹣﹣a+2)=3a3+2a2﹣12a.点评:本题主要考查单项式与多项式相乘,熟练掌握运算法则是解题的关键,计算时要注意运算符号.6.﹣3x•(2x2﹣x+4)考点:单项式乘多项式.分析:根据单项式与多项式相乘,用单项式去乘多项式的每一项,再把所得的积相加,计算即可.解答:解:﹣3x•(2x2﹣x+4),=﹣3x•2x2﹣3x•(﹣x)﹣3x•4,=﹣6x3+3x2﹣12x.点评:本题主要考查单项式与多项式相乘的运算法则,熟练掌握运算法则是解题的关键,计算时要注意运算符号.7.先化简,再求值3a(2a2﹣4a+3)﹣2a2(3a+4),其中a=﹣2考点:单项式乘多项式.分析:首先根据单项式与多项式相乘的法则去掉括号,然后合并同类项,最后代入已知的数值计算即可.解答:解:3a(2a2﹣4a+3)﹣2a2(3a+4)=6a3﹣12a2+9a﹣6a3﹣8a2=﹣20a2+9a,当a=﹣2时,原式=﹣20×4﹣9×2=﹣98.点评:本题考查了整式的化简.整式的加减运算实际上就是去括号、合并同类项,这是各地中考的常考点.8.计算:(﹣a2b)(b2﹣a+)考点:单项式乘多项式.专题:计算题.分析:此题直接利用单项式乘以多项式,先把单项式乘以多项式的每一项,再把所得的积相加,利用法则计算即可.解答:解:(﹣a2b)(b2﹣a+),=(﹣a2b)•b2+(﹣a2b)(﹣a)+(﹣a2b)•,=﹣a2b3+a3b﹣a2b.点评:本题考查单项式乘以多项式的运算,熟练掌握运算法则是解题的关键.9.一条防洪堤坝,其横断面是梯形,上底宽a米,下底宽(a+2b)米,坝高米.(1)求防洪堤坝的横断面积;(2)如果防洪堤坝长100米,那么这段防洪堤坝的体积是多少立方米?考点:单项式乘多项式.专题:应用题.分析:(1)根据梯形的面积公式,然后利用单项式乘多项式的法则计算;(2)防洪堤坝的体积=梯形面积×坝长.解答:解:(1)防洪堤坝的横断面积S=[a+(a+2b)]× a=a(2a+2b)=a2+ab.故防洪堤坝的横断面积为(a2+ab)平方米;(2)堤坝的体积V=Sh=(a2+ab)×100=50a2+50ab.故这段防洪堤坝的体积是(50a2+50ab)立方米.点评:本题主要考查了梯形的面积公式及堤坝的体积=梯形面积×长度,熟练掌握单项式乘多项式的运算法则是解题的关键.10.2ab(5ab+3a2b)考点:单项式乘多项式.分析:根据单项式与多项式相乘,先用单项式乘多项式的每一项,再把所得的积相加计算即可.解答:解:2ab(5ab+3a2b)=10a2b2+6a3b2;故答案为:10a2b2+6a3b2.点评:本题考查了单项式与多项式相乘,熟练掌握运算法则是解题的关键,计算时要注意符号的处理.11.计算:.考点:单项式乘多项式.分析:先根据积的乘方的性质计算乘方,再根据单项式与多项式相乘的法则计算即可.解答:解:(﹣xy2)2(3xy﹣4xy2+1)=x2y4(3xy﹣4xy2+1)=x3y5﹣x3y6+x2y4.点评:本题考查了积的乘方的性质,单项式与多项式相乘的法则,熟练掌握运算法则是解题的关键,计算时要注意运算顺序及符号的处理.12.计算:2x(x2﹣x+3)考点:单项式乘多项式.专题:计算题.分析:根据单项式与多项式相乘,先用单项式乘多项式的每一项,再把所得的积相加计算即可.解答:解:2x(x2﹣x+3)13.(﹣4a3+12a2b﹣7a3b3)(﹣4a2)= 16a5﹣48a4b+28a5b3.14.计算:xy2(3x2y﹣xy2+y)15.(﹣2ab)(3a2﹣2ab﹣4b2)号的处理.16.计算:(﹣2a2b)3(3b2﹣4a+6)考点:单项式乘多项式.分析:首先利用积的乘方求得(﹣2a2b)3的值,然后根据单项式与多项式相乘的运算法则:先用单项式乘多项式的每一项,再把所得的积相加计算即可.解答:解:(﹣2a2b)3(3b2﹣4a+6)=﹣8a6b3•(3b2﹣4a+6)=﹣24a6b5+32a7b3﹣48a6b3.点评:本题考查了单项式与多项式相乘.此题比较简单,熟练掌握运算法则是解题的关键,计算时要注意符号的处理.17.某同学在计算一个多项式乘以﹣3x2时,因抄错运算符号,算成了加上﹣3x2,得到的结果是x2﹣4x+1,那么正确的计算结果是多少?考点:单项式乘多项式.专题:应用题.分析:用错误结果减去已知多项式,得出原式,再乘以﹣3x2得出正确结果.解答:解:这个多项式是(x2﹣4x+1)﹣(﹣3x2)=4x2﹣4x+1,(3分)正确的计算结果是:(4x2﹣4x+1)•(﹣3x2)=﹣12x4+12x3﹣3x2.(3分)点评:本题利用新颖的题目考查了单项式与多项式相乘,熟练掌握运算法则是解题的关键,计算时要注意符号的处理.18.对任意有理数x、y定义运算如下:x△y=ax+by+cxy,这里a、b、c是给定的数,等式右边是通常数的加法及乘法运算,如当a=1,b=2,c=3时,l△3=1×l+2×3+3×1×3=16,现已知所定义的新运算满足条件,1△2=3,2△3=4,并且有一个不为零的数d使得对任意有理数x△d=x,求a、b、c、d的值.考点:单项式乘多项式.专题:新定义.分析:由x△d=x,得ax+bd+cdx=x,即(a+cd﹣1)x+bd=0,得①,由1△2=3,得a+2b+2c=3②,2△3=4,得2a+3b+6c=4③,解以上方程组成的方程组即可求得a、b、c、d的值.解答:解:∵x△d=x,∴ax+bd+cdx=x,∴(a+cd﹣1)x+bd=0,∵有一个不为零的数d使得对任意有理数x△d=x,则有①,∵1△2=3,∴a+2b+2c=3②,∵2△3=4,∴2a+3b+6c=4③,又∵d≠0,∴b=0,∴有方程组解得.故a的值为5、b的值为0、c的值为﹣1、d的值为4.点评:本题是新定义题,考查了定义新运算,解方程组.解题关键是由一个不为零的数d使得对任意有理数x△d=x,得出方程(a+cd﹣1)x+bd=0,得到方程组,求出b的值.多项式参考答案一填空1.y x y x 3233+2. 646-a ;3.-4.4.-325.-26.:37.x 2+4x-21;1-4a 28.x-y-1二选择1.B ;2.B ;3.C4.A.5.C 6.C 7.B 8.A三解答1.(1) 322342b a b a -; (2)23442y x y x +-; (3)a b a b a 4124422+--; (4) 543342y x y x --; (5)22b a -; (6) x x x 3423+-.2.x x 38232+-,314. 3. 23431512x x x -+-.4.解:由题意得11,2a b =-=,原式=32231621a b a b --,当11,2a b =-=时,原式=118. 5.m=3,n=1。
