最新人教版七年级数学绝对值 ppt
合集下载
1.2.4《绝对值》课件-2024-2025学年人教版(2024)数学 七年级上册

-5.25
(3)绝对值等于5.25的负数是______;
2或-2
(4)绝对值等于2的数是_______。
【点睛】注意绝对值等于某个正数的数有两个,他们互为相反数,解题时不要遗
漏负值。
课堂练习
3. 如果| a |+| b-1 |=0,那么a = 0 ,b = 1
。
4. 已知x =30,y =-4,则| x | - 3 | y |= 18 。
B
-10
10
O
0
10
A
10
-10与10在数轴上所表示的点到原点的距离是 10个单位长度 ,它们
的 符号 不同。我们把这个距离10叫做+10和-10的 绝对值 。
新知探究
定义
距离不能是负数,所以任何
数的绝对值一定是非负数
( |a| ≥ 0)
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,
记作|a|.
1. 求下列各数的绝对值.
12, - 3 , -7.5 , 0
5
解: | 12 | =12;
|- 3 |= 3
5
5
正数的绝对值等于它本身
负数的绝对值等于它的相反数
| -7.5 | = 7.5;
| 0 | = 0。
0的绝对值是0
随堂检测
2. 填一填:
0
(1)绝对值等于0的数是___;
5.25
(2)绝对值等于5.25的正数是_____;
(5) 绝对值等于同一个正数的数有两个,且这两个数互为相反数.(
√
)
新知探究
我们知道,互为相反数的两
个数(除0之外)只有符号不同,
这两个数的相同部分在数轴上表
示什么?
(3)绝对值等于5.25的负数是______;
2或-2
(4)绝对值等于2的数是_______。
【点睛】注意绝对值等于某个正数的数有两个,他们互为相反数,解题时不要遗
漏负值。
课堂练习
3. 如果| a |+| b-1 |=0,那么a = 0 ,b = 1
。
4. 已知x =30,y =-4,则| x | - 3 | y |= 18 。
B
-10
10
O
0
10
A
10
-10与10在数轴上所表示的点到原点的距离是 10个单位长度 ,它们
的 符号 不同。我们把这个距离10叫做+10和-10的 绝对值 。
新知探究
定义
距离不能是负数,所以任何
数的绝对值一定是非负数
( |a| ≥ 0)
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,
记作|a|.
1. 求下列各数的绝对值.
12, - 3 , -7.5 , 0
5
解: | 12 | =12;
|- 3 |= 3
5
5
正数的绝对值等于它本身
负数的绝对值等于它的相反数
| -7.5 | = 7.5;
| 0 | = 0。
0的绝对值是0
随堂检测
2. 填一填:
0
(1)绝对值等于0的数是___;
5.25
(2)绝对值等于5.25的正数是_____;
(5) 绝对值等于同一个正数的数有两个,且这两个数互为相反数.(
√
)
新知探究
我们知道,互为相反数的两
个数(除0之外)只有符号不同,
这两个数的相同部分在数轴上表
示什么?
人教版七年级数学上册1.2.4《绝对值》课件 (13张PPT)

人民教育出版社七年级上册
1.2.4(1) 绝对值
1、数轴三要素
2、什么是互为相反数
谁离乒乓球网架远呢?
20 20
-20 -15 -10 -5 5 10 0 15 20 -20与+20在数轴上所表示的点到原点的距离都是 20个单位,距离20是-20和20的绝对值.
-20的绝对值表示-20的点到原点的距离,它的绝对值是20. -3的绝对值表示什么呢?它的绝对值是多少呢?
数轴原点表示的是0,0绝对值是0
绝对值性质:对于任意一个有理数a都有, 1、当a>0 时, |a|= _____ a ;
0 ; 2、当a=0 时, |a|= _____
3、当a<0 时, |a|= _____. -a
绝对值的代 数意义
1.填空:
1.7 |-1.7|_____ ; -4 ; -|-4|=____
-7 7
绝 对 值 发 生 器
7 7
、数轴原点右边表示的是什么数?该数的绝对值与这个数有什 么关系?
数轴原点右边表示的是正数,正数的绝对值是它本身
、数轴原点左边表示的是什么数?该数的绝对值与这个数有 什么关系?
数轴原点左边表示的是负数,负数的绝对值是它的相反数
、数轴原点表示的是什么数?该数的绝对值是多少?
1、绝对值的几何意义及表示方法 2、绝对值的代数意义 (1)一个正数的绝对值是它本身;
(2)零的绝对值是零;
(3)一个负数的绝对值是它的相反数;
1、必做题:习题1.2 第5、8题 2、选做题:绝对值评测训练
2的绝对值表示什么呢?它的绝对值是多少呢? 2 3 的绝对值表示什么呢?它的绝对值是多少呢?
2 3
-3 -2 -1
0
1.2.4(1) 绝对值
1、数轴三要素
2、什么是互为相反数
谁离乒乓球网架远呢?
20 20
-20 -15 -10 -5 5 10 0 15 20 -20与+20在数轴上所表示的点到原点的距离都是 20个单位,距离20是-20和20的绝对值.
-20的绝对值表示-20的点到原点的距离,它的绝对值是20. -3的绝对值表示什么呢?它的绝对值是多少呢?
数轴原点表示的是0,0绝对值是0
绝对值性质:对于任意一个有理数a都有, 1、当a>0 时, |a|= _____ a ;
0 ; 2、当a=0 时, |a|= _____
3、当a<0 时, |a|= _____. -a
绝对值的代 数意义
1.填空:
1.7 |-1.7|_____ ; -4 ; -|-4|=____
-7 7
绝 对 值 发 生 器
7 7
、数轴原点右边表示的是什么数?该数的绝对值与这个数有什 么关系?
数轴原点右边表示的是正数,正数的绝对值是它本身
、数轴原点左边表示的是什么数?该数的绝对值与这个数有 什么关系?
数轴原点左边表示的是负数,负数的绝对值是它的相反数
、数轴原点表示的是什么数?该数的绝对值是多少?
1、绝对值的几何意义及表示方法 2、绝对值的代数意义 (1)一个正数的绝对值是它本身;
(2)零的绝对值是零;
(3)一个负数的绝对值是它的相反数;
1、必做题:习题1.2 第5、8题 2、选做题:绝对值评测训练
2的绝对值表示什么呢?它的绝对值是多少呢? 2 3 的绝对值表示什么呢?它的绝对值是多少呢?
2 3
-3 -2 -1
0
新人教版七年级上册数学1.2.4绝对值——绝对值的定义及性质优质课件

| b-1 | 0,又 | a-2 |+| b-1 |=0 ,所以a -2 =0 ,
b-1=0.
解:根据题意可知:a-2=0,b-1=0 ,
所以:a=2 ,b=1.
第二十一页,共二十五页。
总结
若几个非负数的和为0,则这几个数都为0.
知3-讲
第二十二页,共二十五页。
1 绝对值最小的数是______0__;绝对值最小的负整数
第七页,共二十五页。
1 (中考·连云港)数轴上表示-2的点与原点的距离是
____2____.
知1-练
第八页,共二十五页。
知识点 2 绝对值的求法
1.几何定义:一般地,数轴上表示数a的点与原点的距
离叫做数a的绝对值,记作 a .
2.代数定义:一个正数的绝对值是它本身;一个负数
的绝对值是它的相反数;0的绝对值是0;任意一个
所以x 的相反数为-4,y 的相反数为2.
第十九页,共二十五页。
总结
知3-讲
本题运用了巧用非负性技巧,考查了非负数的性质,
该性质可巧记为“0+0=0”,可以推广为:如果几个非 负数的和为0,那么这几个非负数均为0.
第二十页,共二十五页。
知3-练
例 5
已知
a-2 + b-,1 求=0a、b的值.
导引:因为 | a-2 | 和 | b-1 | 都是非负数,所以 | a-2 | 0 ,
=
__2._5__,-
2
=
2 (中考·东营)
-
1 3的相反数是(
A. 1 B.- 1 C.3
3
3
)B
D.-3
第十六页,共二十五页。
知2-练
知识点 3 绝对值的性质
1.2.4 绝对值 课件 人教版七年级数学上册 (27)

【示范题1】-|-2|的值为 ( )
A.-2
B.2
C.- 1
D.1
2
2
【教你解题】
【想一想】 有没有绝对值最大的有理数?有没有绝对值最小的有理数? 提示:没有绝对值最大的有理数;有绝对值最小的有理数,是0.
【备选例题】求下列各数的绝对值.
(1)3.2.(2) 1. (3)1 4 . (4)0.
3
5
【解析】(1)|3.2|=3.2.(2) | 1 | 1 .
33
(3) |1 4 | 1(44.)|0|=0.
55
【微点拨】正确理解绝对值的三个方面 1.若一个数的绝对值是正数,则这样的数有两个,它们互为相反 数. 2.只有0的绝对值是0,0是绝对值最小的有理数. 3.任何有理数的绝对值都不能是负数.
【思维诊断】(打“√”或“×”) 1.一个有理数的绝对值必是正数. ( × ) 2.绝对值最小的有理数是0. ( √ ) 3.如果两个数不相等,那么这两个数的绝对值也不相等.( × ) 4.如果两个数的绝对值相等,那么这两个数也相等. ( × ) 5.负数没有绝对值. ( × )
知识点一 求有理数的绝对值
【方法一点通】 求有理数绝对值的步骤 1.先判断有理数是正数、负数、还是0. 2.再根据正数、负数、0的绝对值的意义,化去绝对值符号,确定 最后结果.
知识点二 绝对值的性质及应用
【示范题2】某工厂生产一批零件,根据零件质量要求:零件的
长度可以有0.2厘米的误差,现抽查5个零件,检查数据记录如表
ቤተ መጻሕፍቲ ባይዱ
(超过规定长度的厘米数记为正数,不足规定长度的厘米数记为
负数):
零件号数
1
2
3
4
新版人教版七年级数学上册《绝对值》课件(17张)
创设情境
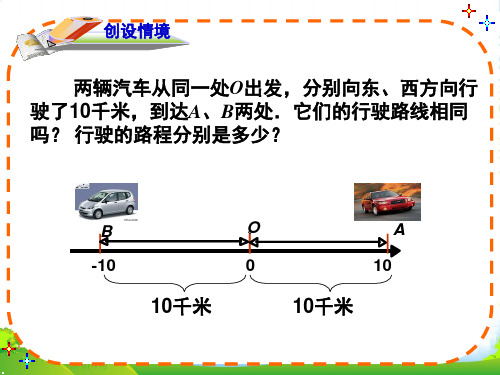
两辆汽车从同一处O出发,分别向东、西方向行 驶了10千米,到达A、B两处.它们的行驶路线相同 吗? 行驶的路程分别是多少?
B
O
A
-10
0
10
10千米
10千米
做游戏
请两位同学分别站在老师的左右两边,两位同学 同时向东、西相反的方向走1米,把这两位同学所 站位置用数轴上的点表示出来.
距
距
离
离
是1
学生活动 2.互为相反数的两个数的绝对值有什么关系?
一对相反数虽然分别在原点两边,但它们 到原点的距离是相等的.所以互为相反数的两 个数的绝对值相等.
7 图1.2-7
学生活动
你能把14个气温从低到高排列吗?能把这14个数 用数轴上的点表示出来吗?观察这些点在数轴上的位 置,思考它们与温度的高低之间的关系,你觉得两个 有理数可以比较大小吗?
(B )
A.可以是负数 B.不可能是负数
C.必是正数
D.可以是正数也可以是负数
温馨提示: 认真完成作业是巩固知识的有效方法!!
12、首先是教师品格的陶冶,行为的教育,然后才是专门知识和技能的训练。 13、在教师手里操着幼年人的命运,便操着民族和人类的命运。2022/5/52022/5/5May 5, 2022 14、孩子在快乐的时候,他学习任何东西都比较容易。 15、人自身有一种力量,用许多方式按照本人意愿控制和影响这种力量,一旦他这样做,就会影响到对他的教育和对他发生作用的环境。
练习2:|-13 |的相反数是 ;若|a|=2,则a=±2 .
练习3:绝对值小于3.5的整数是-3,-2,-1,0,1,2,3 . 练习4:已知:x342y0,则x= -3 ,y= 2 .
课堂练习
两辆汽车从同一处O出发,分别向东、西方向行 驶了10千米,到达A、B两处.它们的行驶路线相同 吗? 行驶的路程分别是多少?
B
O
A
-10
0
10
10千米
10千米
做游戏
请两位同学分别站在老师的左右两边,两位同学 同时向东、西相反的方向走1米,把这两位同学所 站位置用数轴上的点表示出来.
距
距
离
离
是1
学生活动 2.互为相反数的两个数的绝对值有什么关系?
一对相反数虽然分别在原点两边,但它们 到原点的距离是相等的.所以互为相反数的两 个数的绝对值相等.
7 图1.2-7
学生活动
你能把14个气温从低到高排列吗?能把这14个数 用数轴上的点表示出来吗?观察这些点在数轴上的位 置,思考它们与温度的高低之间的关系,你觉得两个 有理数可以比较大小吗?
(B )
A.可以是负数 B.不可能是负数
C.必是正数
D.可以是正数也可以是负数
温馨提示: 认真完成作业是巩固知识的有效方法!!
12、首先是教师品格的陶冶,行为的教育,然后才是专门知识和技能的训练。 13、在教师手里操着幼年人的命运,便操着民族和人类的命运。2022/5/52022/5/5May 5, 2022 14、孩子在快乐的时候,他学习任何东西都比较容易。 15、人自身有一种力量,用许多方式按照本人意愿控制和影响这种力量,一旦他这样做,就会影响到对他的教育和对他发生作用的环境。
练习2:|-13 |的相反数是 ;若|a|=2,则a=±2 .
练习3:绝对值小于3.5的整数是-3,-2,-1,0,1,2,3 . 练习4:已知:x342y0,则x= -3 ,y= 2 .
课堂练习
人教版2024-2025学年七年级数学上册1.2.4 绝对值(课件)

易错提醒:注意绝对值等于某个正数的数有两个,它们互为 相反数,解题时不要遗漏负值.
归纳总结 绝对值的性质
(1)任何有理数都有绝对值,且只有一个. (2)由绝对值的几何定义可知,数的绝对值是两点间的距离,因此,任 何一个数的绝对值都是非负数;在数轴上,一个数离原点的越近,绝 对值越小,离原点越远,绝对值越大. (3)互为相反数的两个数的绝对值相等. (4)绝对值相等的两个数相等或互为相反数.
若|x|=5,则x的值是( C )
A. 5
B. -5
C. ±5
1
D.
5
解析:|x|=5,即数x到原点的距离是5,而到原点 的距离是5的数有5和-5,所以x的值是5和-5.
素养考点 3 利用绝对值求字母的值
例3 已知|x–4|+|y–3|=0,求x+y的值.
分析:一个数的绝对值总是大于或等于0,即为非负数, 如果两个非负数的和为0,那么这两个数同时为0.
第一章 有理数
1.2 有理数及其大小比较 1.2.4 绝对值
1.理解绝对值的概念及其几何意义. 2.会求一个数(不涉及字母)的绝对值. 3.会求绝对值已知的数. 4.了解绝对值的非负性,并能用其非负性解决相关问题.
两辆汽车从同一处O出发分别向东、西方向行驶10km,到 达A、B两处.
B 10 O 10 A
例1 求下列各数的绝对值. 12, - 3 , -7.5, 0.
5
解: |12|=12; 正数的绝对值等于它本身.
-3 3;
55
负数的绝对值等于它的相反数.
|-7.5|=7.5;
|0|=0.
0的绝对值是0.
方法总结 求一个数的绝对值的步骤
判断下列说法是否正确.
人教版七年级数学上册1.2.4《绝对值》 课件(共23张ppt)

课堂小结
3.不论有理数a取何值,它的绝对值总是正数或0(非负数), 即对任意有理数a,总有|a|≥0.
4.互为相反数的两个数的绝对值相等. 5.数轴上的数的排列规律是: 在数轴上表示有理数,它们从左到右的顺序,就是从 小到大的顺序,即左边的数小于右边的数.
课件PPT部编版课件统编版部编版人 教版七 年级数 学上册1.2.4《 绝对值 》 课件(共23张ppt)课件优质课课件免 费课件PPT
课件PPT部编版课件统编版部编版人 教版七 年级数 学上册1.2.4《 绝对值 》 课件(共23张ppt)课件优质课课件免 费课件PPT
课堂小结
6.有理数大小比较法则: (1)正数大于0,0大于负数,正数大于负数; (2)两个负数,绝对值大的反而小.
课件PPT部编版课件统编版部编版人 教版七 年级数 学上册1.2.4《 绝对值 》 课件(共23张ppt)课件优质课课件免 费课件PPT
21 21
77
又∵
8 <3 21 7
,即
- 8 <-3
21
7
,
∴
- 8 >- 3
21
7
.
(3)化简,得:-(-0.3)=0.3,-
1 3
=
1 3
.
1 ∵0.3< 3 ,
∴-(-0.3)<
-1 3
.
课堂练习
1.比较大小:
(1)-2_<__5,
-7 2
_>__
+
3 8
,
-0.01_>__-1;
4 (2)- 5
合作探究
一个正数的绝对值是什么?0的绝对值是什么?负数呢?
归纳:一个正数的绝对值是它本身;一个负数的绝对值是它的相反 数;0的绝对值是0.
绝对值PPT课件

-6 -5 -4 -3 -2
│4│=4
0 1 2 3 4
B
5 6
-1
-5的绝对值应该记作│-5︱=? 4的绝对值应该记作 │4︱ =? 0的绝对值应该如何表示呢? │0︱ =?
练习:
-6 -5 -4 -3 -2
-1
0
1
2
3
4
5
6
1.表示+7的点与原点的距离是 7 , 即+7的绝对值是 7 ,记作 7 7 ; 表示2.8的点与原点的距离是 2.8 , 即2.8的绝对值是 2.8 ,记作 2.8 2.8 ; 2.表示0的点与原点的距离是 0 , 即0的绝对值是 0 ,记作 0 0 ;
0 0
7 7
1、(1)正数的绝对值是它的本身;
(2)0的绝对值是0;
(3)负数的绝对值是它的相反数。
2、非负性 由绝对值的定义可知绝对值 具有非负性,即|a|≥0。
练习:
1、判断下列各题: (1)负数没有绝对值。 × (2)有些数的绝对值有两个。× (3)正数和零的绝对值是它的本身。√ (4)负数和零的绝对值是它的相反数。√ √ (5)任何有理数的绝对值一定不是负数。
答:记为-8的足球质量好一些。
因为 │-20│= 20, │-8│ = 8, │+10│=10, │+12│=12, │-11│=11;
所以│-8│ < │+10│ < │-11│ < │+12│ < │-20│
也就是说记为-8的足球与规定的质量相差比较小, 因此其质量比较好。
思考:
1.计算:|–(+3.6)| + |–(–1.2)| – |–[+(–4)]| 2.已知 |x–2| + |y–3| + |z–4| = 0, 求x+y–z的值。
│4│=4
0 1 2 3 4
B
5 6
-1
-5的绝对值应该记作│-5︱=? 4的绝对值应该记作 │4︱ =? 0的绝对值应该如何表示呢? │0︱ =?
练习:
-6 -5 -4 -3 -2
-1
0
1
2
3
4
5
6
1.表示+7的点与原点的距离是 7 , 即+7的绝对值是 7 ,记作 7 7 ; 表示2.8的点与原点的距离是 2.8 , 即2.8的绝对值是 2.8 ,记作 2.8 2.8 ; 2.表示0的点与原点的距离是 0 , 即0的绝对值是 0 ,记作 0 0 ;
0 0
7 7
1、(1)正数的绝对值是它的本身;
(2)0的绝对值是0;
(3)负数的绝对值是它的相反数。
2、非负性 由绝对值的定义可知绝对值 具有非负性,即|a|≥0。
练习:
1、判断下列各题: (1)负数没有绝对值。 × (2)有些数的绝对值有两个。× (3)正数和零的绝对值是它的本身。√ (4)负数和零的绝对值是它的相反数。√ √ (5)任何有理数的绝对值一定不是负数。
答:记为-8的足球质量好一些。
因为 │-20│= 20, │-8│ = 8, │+10│=10, │+12│=12, │-11│=11;
所以│-8│ < │+10│ < │-11│ < │+12│ < │-20│
也就是说记为-8的足球与规定的质量相差比较小, 因此其质量比较好。
思考:
1.计算:|–(+3.6)| + |–(–1.2)| – |–[+(–4)]| 2.已知 |x–2| + |y–3| + |z–4| = 0, 求x+y–z的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
-
9
回顾与小结
本节课里你学到了什么???
(1)绝对值的几何意义及代数意义。 (2)如何求一个数的绝对值。
:教材P15第4、10题。
-
10
练习1 化简
(1)|-0.1|=____; (2) |-101|=____; (3)| 3 |=______; (4) |-8|=_____;
100
(5) |+6|=____ ; (6) |0| ______;
(7) -|-7.5|=_____; (8 -|+8|=_____;
(9)如果|x|=2,则x=______
|8|=8, |-8|=8.
-
4
活动3:练一练,想一想
完成下列表格
数a 4 3 1.5 0
—1.5 —3 —4
数a的绝对值|a| |4|= 4 |3|= 3 |1.5|= 1.5 |0|= 0
|—1.5|= 1.5 |—3|= 3
|—4|=4
—1.5 O 1.5
-4 -3 -2 -1 0 1 2 3 4
1.2.4
-
1
活动1:想一想
问题1:小明的家与两个商店在同一直线上, 其中商店A在小明家东边1km处,商店B在小 明家西边2km。
(1)怎样用数轴表示两个商店与小明家的位置关系?
(2)如果小明要 买笔记本,你认为小明应该选择去哪个商 店呢?
B
2km
O 1km A
-2
-1
0
1
2
活动2:绝对值概念的学习和理解
-
7
练习2
(1)绝对值是3的数有几个?各是什 么?
(2)绝对值是0的数有几个?各是什 么?
(3)绝对值是-2的数是否存在?若 存在,请说出来?
-
8
练习3 判断
( 1 ) |-1.4|>0 ( 2 ) |-0.3|=|0.3| ( 3 ) 有理数的绝对值一定是正数。 ( 4 ) 绝对值最小的数是0。 ( 5 ) 如果数a的绝对值等于a,那么a一定为正数。 ( 6 ) 一个数的绝对值越大,表示它的点在数轴上越 靠 右。 ( 7) 一个数的绝对值越大,表示它的点在数轴上离原 点越远 ( 8 ) 若a=b,则|a|=|b| ( 9 ) 若|a|=|b|,则a=b。
-
5
1、一个正数的绝对值是它本身;一个负数的绝对值是 它的相反数是负数时,|a|=__-a; (3)当a=0时,|a|=___0。
a (a 0) | a| a (a 0)
0 (a 0)
2.互为相反数的两个数的绝对值相等
-
6
一般地,数轴上表示数a的点与原点 的距离叫做数a的绝对值,记作|a|。
B
O
A
-2
0
1
想一想:
根据上面的数轴表示,你能求出-2和1的绝对值吗?
-
3
思考:-8与8是相反数,把它们在数轴 上表示出来,那么它们的方向又有什么 关系?到原点的距离又有什么关系?
8
-8
8
0
8
-8与8虽然符号不同,但它们在数轴上所表示 的点到原点的距离都是是8个单位长度,我们把这 个距离8叫做+8和-8的绝对值。记为:
