云模型实现图形-MATLAB程序
云模型实现图形-MATLAB程序
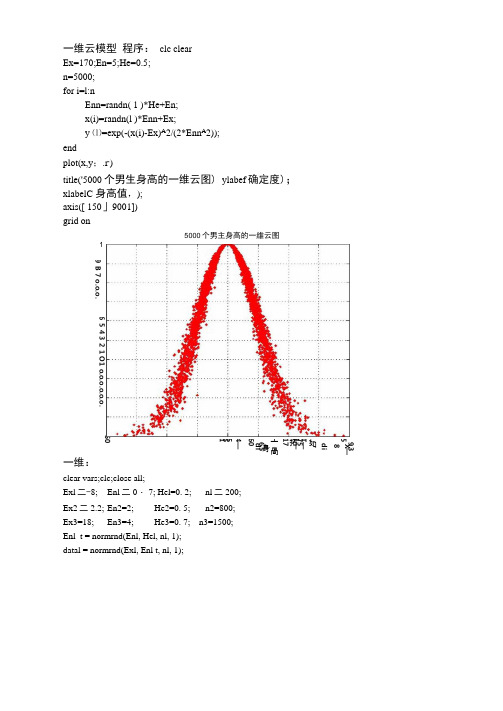
一维云模型 程序: clc clearEx=170;En=5;He=0.5;n=5000;for i=l:nEnn=randn( 1 )*He+En;x(i)=randn(l )*Enn+Ex;y ⑴=exp(-(x(i)-Ex)A 2/(2*Enn A 2));endplot(x,y ;.r ,)title('5000个男生身高的一维云图) ylabef 确定度);xlabelC 身高值,);axis([ 150」9001])grid on一维:clear vars;clc;close all;Exl 二-8; Enl 二0・ 7; Hel=0. 2;nl 二200; Ex2二2.2; En2=2;He2=0. 5; n2=800; Ex3=18; En3=4; He3=0. 7; n3=1500;Enl_t = normrnd(Enl, Hel, nl, 1);datal = normrnd(Exl, Enl t, nl, 1);150 6 5 4 3 2 1 O1 o.o.o.o.o.o.93 X — 5 8 di如T — 75 1—拓 17亠咼 身65 di 60 4— 5 5 1 5000个男主身高的一維云图9 B 7 o.o.o.mul = exp(-0. 5*((datal-Exl). /Enl_t). 2);En2_t = normrnd (En2, He2, n2, 1);data2 = normrnd (Ex2, En2_t, n2,1);mu2 = exp(-0. 5*((data2-Ex2). /En2_t)・ ~2);En3_t = normrnd (En3, He3, n3, 1);data3 = normrnd(Ex3, En3_t, n3,1);mu3 = exp(-0. 5*((data3-Ex3). /En3_t). 2);figure(l);plot (data!, mul, I b‘,data2, mu2,' *r‘, data3, mu3,' +k'); axis equal;二维云模型程序:clcclearEx l = 170;Enl=5;He 1=0.5;Ex2=65 ;En2=3 ;He2=0.2; n=5000;for i=I:nEnn 1 =randn( 1 )*He 1 +En 1; x l(i)=randn( 1 )*Enn 1 +Ex 1;Enn2=randn( 1 )*He2+En2; x2(i)=randn( 1 )*Enn2+Ex2;y(i)=exp(-(x 1 (i)-Ex 1 )A2/(2*Enn 1 A2)-(x2(i)-Ex2)A2/(2*Enn2A2)); end plot3(xl,x2,y,'f)title('5OOO个男生身高体jg的二维云图')axis([ 148,190.50,80 A I])grid on结果:5ooyi-男生身高体重的二维云图50 160多个一维clear vars;clc;close all;Exl二0; Enl=0.103; Hel二0.013; nl=5000;Ex2二0.309; En2=0.064; He2=0.008; n2=5000;Ex3二0・ 5; En3二0・ 039; He3=0. 005; n3=5000;Ex4=0.691; En4=0.064; He4=0.008; n4=5000;Ex5=l; En5二0.103; He5=0.013; n5=5000:Enl_t = normrnd(Enl, Hel, nl, 1);datal = normrnd(Exl, Enl_t, nl,1);mul = exp(-0. 5*((datal-Exl). /Enl_t). 2);En2_t = normrnd (En2, He2, n2, 1);data2 = normrnd(Ex2, En2_t, n2, 1);mu2 = exp(-0. 5*((data2-Ex2). /En2_t). *2);En3_t = normrnd (En3, He3, n3, 1);data3 = normrnd(Ex3, En3_t, n3,1);mu3 = exp(-0. 5*((data3-Ex3). /En3_t). 2);En4_t = normrnd(En4, He4, n4, 1);data4 = normrnd(Ex4, En4_t, n4,1);mu4 = exp(-0. 5*((data4-Ex4)・/En4_t)・ 2);En5_t = normrnd (En5, He5, n5, 1);data5 = normrnd (Ex5, En5_t, n5, 1);mu5 = exp (一0・ 5* ((data5-Ex5)・/En5_t)・2);figure(l);plot (datal, mul,'・ r*, data2, mu2,'・r , data3, mu3,'・r , data4, mu4,'・ r*, data5, mu5,'・ r* ); titleC评价集')ylabelC 隶属度');axis([-0. 4, 1. 4, 0, 1])grid on评价集04 02 0 0.2 0.4 0.6 0.8 1 1.2 1.4一维Ex二1100;En二84. 926;He 二0. 1;n二1000;X=zeros (1, n);Y=zeros (1, n);X(1 :n) =normrnd(En, He, 1, n):for i=l:nEnl二X(l, i);X(l, i)=normrnd(Ex, Enl, 1):Y(l, i)=exp((-(X(l, i)-Ex)"2)/(2*En「2));plot(X, Y,'. ',' MarkerEdgeCo1or,‘ k', ' markersize*, 4); title C强等级','fontsize', 16);grid on;end强等级逆发生器代码X1=X;Y1=Y;i=l;while i<=(n-flag)lfYl(l,i)>0.9999Y1(:J)=[];Xl(:,i)=[];flag=flag+l;End;Ex=mean(Xl);En2=zeros⑴m);for i=l:m;Enl(lJ)=abs(Xl(l/i).Ex)/sqrt(.2*log(Yl(l/i))); End;En二mean(Enl);He=O;for i=l:m;He=He+(Enl(lJ)-En)A2;He=sqrt(He/(m-l));End;XI =X;Y1=Y;i=l;while i<=(n-flag)ifYl(lj)>0.9999Y1(:J)=[J;X1(:J)=[];flag=flag+l;elsei=i+l;m=m +1;endendEx=mean(Xl)En l=zeros(l z m);for i= l:mEnl(l,i)=abs(Xl(l/i)-Ex)/sqrt(-2*log(Yl(l/i))); endEn二mea n(Enl);He=0;for i=l:mHe=He+(Enl(l /i)-En)A 2; endHe=sqrt(He/(m-l))Enl_t = normrnd(Enl, Hel, nl, 1); datal = normrnd(Exl, Enl_t, nl, 1); mul = exp(-0. 5*((datal-Exl). /Enl_t). 2);En2_t = normrnd (En2, He2, n2, 1);data2 = normrnd(Ex2, En2_t, n2, 1);mu2 = exp(-0. 5*((data2-Ex2). /En2_t). *2);En3_t = normrnd (En3, He3, n3, 1);data3 = normrnd(Ex3, En3_t, n3,1);mu3 = exp(-0. 5*((data3-Ex3)・/En3_t). 2);En4_t = normrnd(En4, He4, n4, 1);data4 = normrnd (Ex4, En4_t, n4, 1); mu4 = exp(-0. 5*((data4-Ex4). /En4_t)・~2); En5_t = normrnd (En5, He5, n5, 1);data5 = normrnd(Ex5, En5_t, n5,1);mu5 = exp (一0・ 5*((data5~Ex5)・/En5_t)・ 2);En6_t = normrnd (En6, He6, n6, 1);data6 = normrnd(Ex6, En6_t, n6,1);mu6 = exp(-0. 5*((data6-Ex6)・/En6_t). 2);En7_t = normrnd (En7, He7, n7, 1);data? = normrnd (Ex7, En7_t, n7, 1);mu7 = exp(-0. 5*((data7-Ex7). /En7_t)・ ~2);En8_t = normrnd (En8, He8, n8, 1); dataS = normrnd (Ex8, En8_t, n& 1);clear vars;clc;close all;Enl 二0.150; Hel=0. 050; Exl=0. 457; Ex2二0・454; Ex3二0・435; Ex4二0. 415; Ex5=0. 414; Ex6 二0.410;Ex7 二0.410; Ex8=0. 500;En2=0. 156 En3=0. 229 En4=0. 177 En5=0. 298 En6=0. 242 En7=0. 188 En8=0. 039 He2=0. 056 He3=0. 067 He4=0. 071 He5=0. 099 He6=0.061 He7=0.061 He8=0.005 nl=4000; n2=4000;n3=4000;n4=4000;n5=4000;n6=4000;n7=4000;n8=5000;mu8 = exp(-0. 5*((data8-Ex8). /En8_t). *2);figure(l);plot (datal, mul,'・ r*, data2, mu2,'・ r , data3, mu3,'・ r , data4, mu4,'・ r*, data5, mu5,'・ r* ,data6, mu6,'・:r' , data7, mu7,'・ r*, data8, mu8,'・ r ):titleC 评价集')ylabel ('隶属度');axis([-0. 4, 1. 4, 0, 1])grid onclear vars;clc;close all;Enl_t = normrnd(Enl, Hel, nl, 1); datal = normrnd(Exl, Enl_t, nl, 1); mul = exp(-0. 5*((datal-Exl). /Enl_t). 2);En2_t = normrnd (En2, He2, n2, 1);data2 = normrnd (Ex2, En2_t, n2,1); mu2 = exp(-0. 5*((data2-Ex2). /En2_t)・ 2);En3_t = normrnd (En3, He3, n3, 1);data3 = normrnd(Ex3, En3_t, n3,1); mu3 = exp (-0. 5* ((data3-Ex3). /En3_t). 2);En4_t = normrnd(En4, He4, n4, 1);data4 = normrnd (Ex4, En4_t, n4, 1); mu4 = exp(-0. 5*((data4-Ex4). /En4_t)・ ~2);En5_t = normrnd (En5, He5, n5, 1);data5 = normrnd (Ex5, En5_t, n5, 1);mu5 = exp (一0. 5* ((data5-Ex5)・/En5_t)・ 2);figure(l);plot (datal, mul,'・ r , data2, mu2,'・ r , data3, mu3,'・ x , data4, mu4,'・, data5, mu5,'・ r* );titleC 评价集')ylabel(,隶属度');axis([-0. 4, 1. 4, 0, 1])grid on Exl 二0.716;Ex2=0. 545;Ex3二0・534; Ex4二0.Enl 二0.123; Hel=0. 045; nl=4000; En2=0. 140; He2=0. 052 En3=0. 233; He3=0. 085 En 仁0.202; He4=0. 063 En5=0. 064; n2=4000; n3=4000; n4=4000; He5=0. 008; n5二6000;。
matlab 程序 2d有限元方法

matlab 程序2d有限元方法全文共四篇示例,供读者参考第一篇示例:有限元方法是一种数值计算方法,旨在解决工程结构、力学和热力学等领域的复杂问题。
这种方法通过将一个连续的问题离散化为无限多的小单元,然后通过求解每个小单元的方程来逼近整个问题的解。
有限元方法在解决非线性、非定常、多物理场耦合等复杂问题上表现出色,因此在工程领域得到了广泛应用。
2D有限元方法是指在二维平面上建立有限元模型,然后求解其方程得到问题的解。
在MATLAB中,构建2D有限元模型的步骤大致分为三个阶段:几何建模、网格剖分和有限元分析。
首先是几何建模阶段,即对求解问题的几何形状进行建模。
这一步通常通过MATLAB中的绘图函数绘制图形,定义节点和单元信息。
这个阶段的难点在于如何准确表达问题的几何形状和边界条件,因为这将直接影响到后续的网格划分和求解结果的准确性。
接着是网格剖分阶段,即将几何形状离散化为小单元。
在MATLAB中,可以利用自带的网格生成函数或者第三方的网格生成工具箱来生成有限元网格。
网格的质量和密度对求解结果的准确性有很大影响,因此在网格剖分时需要谨慎选择参数和方法。
最后是有限元分析阶段,即对离散化后的有限元模型进行求解。
在MATLAB中,可以利用现成的有限元求解函数来求解线性或非线性方程。
在求解过程中,需要考虑边界条件的处理、材料参数的输入和求解精度的控制等因素,以保证求解的准确性和稳定性。
在实际应用中,2D有限元方法常用于解决板、壳结构的弯曲、扭转、振动等问题,以及流体动力学、电磁场等问题。
MATLAB提供了丰富的工具箱和函数库,使得有限元方法的实现更加简单和高效。
通过合理的建模、网格剖分和求解方法,我们可以快速地解决复杂的工程问题,提高工程设计的效率和精度。
2D有限元方法结合MATLAB工具的应用为工程领域提供了一种高效、准确和可靠的计算方法。
通过不断学习和实践,我们可以更好地利用有限元方法解决实际工程问题,推动工程技术的发展和进步。
matlab数学建模100例

matlab数学建模100例Matlab是一种强大的数学建模工具,广泛应用于科学研究、工程设计和数据分析等领域。
在这篇文章中,我们将介绍100个使用Matlab进行数学建模的例子,帮助读者更好地理解和应用这个工具。
1. 线性回归模型:使用Matlab拟合一组数据点,得到最佳拟合直线。
2. 多项式拟合:使用Matlab拟合一组数据点,得到最佳拟合多项式。
3. 非线性回归模型:使用Matlab拟合一组数据点,得到最佳拟合曲线。
4. 插值模型:使用Matlab根据已知数据点,估计未知数据点的值。
5. 数值积分:使用Matlab计算函数的定积分。
6. 微分方程求解:使用Matlab求解常微分方程。
7. 矩阵运算:使用Matlab进行矩阵的加减乘除运算。
8. 线性规划:使用Matlab求解线性规划问题。
9. 非线性规划:使用Matlab求解非线性规划问题。
10. 整数规划:使用Matlab求解整数规划问题。
11. 图论问题:使用Matlab解决图论问题,如最短路径、最小生成树等。
12. 网络流问题:使用Matlab解决网络流问题,如最大流、最小费用流等。
13. 动态规划:使用Matlab解决动态规划问题。
14. 遗传算法:使用Matlab实现遗传算法,求解优化问题。
15. 神经网络:使用Matlab实现神经网络,进行模式识别和预测等任务。
16. 支持向量机:使用Matlab实现支持向量机,进行分类和回归等任务。
17. 聚类分析:使用Matlab进行聚类分析,将数据点分成不同的类别。
18. 主成分分析:使用Matlab进行主成分分析,降低数据的维度。
19. 时间序列分析:使用Matlab进行时间序列分析,预测未来的趋势。
20. 图像处理:使用Matlab对图像进行处理,如滤波、边缘检测等。
21. 信号处理:使用Matlab对信号进行处理,如滤波、频谱分析等。
22. 控制系统设计:使用Matlab设计控制系统,如PID控制器等。
(完整版)云模型matlab程序

1.绘制云图Ex=18En=2He=0.2hold onfor i=1:1000Enn=randn(1)*He+En;x(i)=randn(1)*Enn+Ex;y(i)=exp(-(x(i)-Ex)^2/(2*Enn^2)); plot(x(i),y(i),'*')endEx=48.7En=9.1He=0.39hold onfor i=1:1000Enn=randn(1)*He+En;x(i)=randn(1)*Enn+Ex;y(i)=exp(-(x(i)-Ex)^2/(2*Enn^2)); plot(x(i),y(i),'*')end2.求期望、熵及超熵X1=[51.93 52.51 54.70 43.14 43.85 44.48 44.61 52.08];Y1=[0.91169241573 0.921875 0.96032303371 0.75737359551 0.76983848315 0.7808988764 0.78318117978 0.9143258427];m=8;Ex=mean(X1)En1=zeros(1,m);for i=1:mEn1(1,i)=abs(X1(1,i)-Ex)/sqrt(-2*log(Y1(1,i)));endEn=mean(En1);He=0;for i=1:mHe=He+(En1(1,i)-En)^2;endEn=mean(En1)He=sqrt(He/(m-1))3.平顶山so2环境:X1=[0.013 0.04 0.054 0.065 0.07 0.067 0.058 0.055 0.045];Y1=[0.175675676 0.540540541 0.72972973 0.8783783780.945945946 0.905405405 0.783783784 0.743243243 0.608108108]; m=9;Ex=mean(X1)En1=zeros(1,m);for i=1:mEn1(1,i)=abs(X1(1,i)-Ex)/sqrt(-2*log(Y1(1,i)));endEn=mean(En1);He=0;for i=1:mHe=He+(En1(1,i)-En)^2;endEn=mean(En1)He=sqrt(He/(m-1))1.绘制正向云图Ex=18En=2He=0.2hold onfor i=1:1000Enn=randn(1)*He+En;x(i)=randn(1)*Enn+Ex;y(i)=exp(-(x(i)-Ex)^2/(2*Enn^2));plot(x(i),y(i),'*')endEx=48.7En=9.1He=0.39hold onfor i=1:1000Enn=randn(1)*He+En;x(i)=randn(1)*Enn+Ex;y(i)=exp(-(x(i)-Ex)^2/(2*Enn^2));plot(x(i),y(i),'*')end2.逆向云发生器中需要剔除隶属度大于0. 9999 的云滴,剩下个云滴。
matlab图形操作

matlab图形操作本⽂对matlab中利⽤图形句柄对图⽚属性进⾏设置的操作进⾏简单的总结说明:(1)对图窗和坐标轴属性进⾏整体设置可以通过gcf和gca语句获取当前图窗句柄和坐标轴句柄,通过该句柄可以对图窗和坐标轴的各项属性进⾏操作。
图窗和坐标轴分别包含如下属性:% 图窗属性... ...Children: [1×1 Axes] Color: [0.9400 0.9400 0.9400]Colormap: [256×3 double] CurrentAxes: [1×1 Axes]... ...InnerPosition: [680 558 560 420] PaperUnits: 'centimeters'OuterPosition: [672 550 576 514] Position: [680 558 560 420]Units: 'pixels'% 坐标轴属性... ...Box: 'on' BoxStyle: 'back'Children: [1×1 Line] Color: [1 1 1]FontAngle: 'normal' FontName: 'Helvetica'FontSize: 10 FontSizeMode: 'auto'FontSmoothing: 'on' FontUnits: 'points'FontWeight: 'normal' GridColor: [0.1500 0.1500 0.1500]GridLineStyle: '-' Legend: [0×0 GraphicsPlaceholder]LineWidth: 0.5000 OuterPosition: [0 0 1 1]Parent: [1×1 Figure] Position: [0.1300 0.1100 0.7750 0.8150]Title: [1×1 Text] TitleFontWeight: 'normal'Units: 'normalized' UserData: []View: [0 90] Visible: 'on'... ...XAxis: [1×1 NumericRuler] XAxisLocation: 'bottom'XColor: [0.1500 0.1500 0.1500] XColorMode: 'auto'XDir: 'normal' XGrid: 'off'XLabel: [1×1 Text] XLim: [0 100]XScale: 'linear' XTick: [0 10 20 30 40 50 60 70 80 90 100]XTickLabel: {11×1 cell} XTickLabelRotation: 0YAxis: [1×1 NumericRuler] YColor: [0.1500 0.1500 0.1500]YGrid: 'off' YLabel: [1×1 Text]YLim: [0 100] YScale: 'linear'YTick: [0 10 20 30 40 50 60 70 80 90 100] YTickLabel: {11×1 cell}YTickLabelRotation: 0 ZLabel: [1×1 Text]ZLim: [-1 1] ZScale: 'linear'ZTick: [-1 0 1] ZTickLabel: ''ZTickLabelRotation: 0... ...上⾯仅仅是展⽰了图窗和坐标轴部分重要且常⽤的属性,它们的全部属性可通过查matlab的帮助⽂档或直接在matlab的命令⾏上输⼊gcf、gca或通过如下图所⽰的属性窗⼝进⾏查询和设置。
matlab加工自由曲面程序代码

一、引言Matlab是一种高级技术计算语言和交互环境,被广泛用于工程、科学和数学领域的计算与模拟。
在Matlab中,加工自由曲面是一项常见的任务,例如创建和修改三维曲面模型。
本文将介绍如何使用Matlab 编写程序代码来加工自由曲面,以实现对曲面的精确控制和调整。
二、准备工作在编写程序代码之前,首先需要明确自由曲面的定义和参数化方法。
自由曲面通常由参数方程或控制点构成,对于不同的曲面类型,需要选择合适的参数化方法。
还需要了解Matlab中与曲面加工相关的函数和工具,以便在编写程序时能够调用这些资源。
三、编写程序代码1. 定义自由曲面在Matlab中,可以使用符号变量和代数表达式定义自由曲面的参数方程。
对于二次曲面,可以使用二次多项式表示其参数方程。
具体代码如下:syms u vx = a*u^2 + b*v^2 + c*u*v + d*u + e*v + f;y = g*u^2 + h*v^2 + i*u*v + j*u + k*v + l;z = m*u^2 + n*v^2 + o*u*v + p*u + q*v + r;其中a-r为曲面的系数,u和v为曲面的参数。
2. 控制曲面形状通过调整曲面的参数和系数,可以控制曲面的形状。
可以通过改变系数a-r的值来实现对曲面的放大缩小、旋转、偏移等操作。
具体代码如下:a = 1;b = 1;c = 0;d = 0;e = 0;f = 0;g = 1; h = 1; i = 0; j = 0; k = 0; l = 0;m = 1; n = 1; o = 0; p = 0; q = 0; r = 0;这里以简单的二次曲面为例,通过调整系数的数值来控制曲面的形状。
3. 曲面绘制和可视化在定义和控制曲面之后,可以使用Matlab中的绘图函数将曲面绘制出来。
可以使用surf函数创建曲面图形,并通过设置图形属性来进行可视化调整。
具体代码如下:[u, v] = meshgrid(-2:0.1:2);x = a*u.^2 + b*v.^2 + c*u.*v + d*u + e*v + f;y = g*u.^2 + h*v.^2 + i*u.*v + j*u + k*v + l;z = m*u.^2 + n*v.^2 + o*u.*v + p*u + q*v + r;surf(x, y, z);四、应用实例在实际应用中,自由曲面加工可以用于创建各种复杂的曲面模型。
利用Matlab绘制云模型

利用Matlab绘制云模型许大亮【摘要】The cloud model is an uncertainty model for transformation between qualitative concept and quantitative descrip-tion, then it can express qualitative concept and process quantitative calculation. The development of cloud model is from one-dimension to two-dimension and even multidimensional model at present.As a result, it is used to represent more compli-cated natural language concept. This paper mainly introduces the one-dimension and two-dimension normal cloud generator implementation algorithm.In addition, the Matlab implements cloud generator algorithm and draws the graphs of two different dimension cloud models.%云模型是定性概念与定量描述的不确定性转换模型,可以用来表示定性概念并进行定量计算。
目前云模型由一维发展到二维甚至多维,这样就可以利用它表示更加复杂的自然语言概念。
介绍了一维和二维云模型的正向云发生器,并用Matlab语言实现了云模型算法,绘制了两种不同维数云模型的图形。
【期刊名称】《科技创新与生产力》【年(卷),期】2016(000)001【总页数】3页(P108-110)【关键词】云模型;不确定性;正向云发生器;Matlab【作者】许大亮【作者单位】安徽理工大学测绘学院,安徽淮南 232001【正文语种】中文【中图分类】G202E-mail:*****************。
基于MATLAB平台的凝聚相爆炸模型的分析与程序实现_王颖

本文重点是研究爆炸的预防控制措施, 因此将凝 聚相爆
炸( CPE) 模型用 于模 拟评 价与 分析 烟花 爆竹 爆炸 事故 的后 果严重度、危险等级、灾害影响和破坏范围。
爆炸具有多种破坏形式, 如冲击波破坏, 热辐射危害, 一 次、二次碎片破坏, 爆炸产物毒气危害, 以及由爆炸引 起的火 灾等。其中 , 最危险、破坏力最强、破坏区域最大的是 冲击波
大当量爆炸提供了理论依据。
1. 2 冲击波伤害模型
在安全分析以及安全评价中, 通常把冲击波超压所破 坏
的范围进行人员伤害分区和财产损失分 区, 即有: 死亡区, 重 伤区, 财产损失区, 轻伤区和安 全区[ 4] 。为了数据的 精确性,
本文重点讨论死亡区和重伤区。
在死亡区中, 人员如缺少 防护, 则被 认为 将无例 外地 蒙
Q1/ 3/ R= Q01/ 3/ R0
(1)
则在不同距离上的超压是相同的。式中, R 为爆炸测 量点到
爆炸点的距离; R0 为 1 000 kg 的 TNT 爆 炸测 量点 到爆 炸点
的距离; Q 为某次炸药的 TNT 当量; Q 0 为 1 000 kg TNT。 爆炸相似律为我们 从小当量 爆炸所 获得 的结果 换算 到
( 5)
综上可以得出
WTNT= 1. 8 W f
( 6)
式中, WTNT 为 爆 源的 TNT 当 量, kg ; E 为 爆 源 的 总能 量, J; QTNT为 TNT 爆热, 可取为 4. 52 MJ/ kg; Wf 为爆源的质量, kg。
如果认为该圆周内 没有死亡 的人数 正好 等于圆 周外 死
润滑油必须使用钢丝绳专用润滑脂这种润滑脂具有渗透性防锈性和抗磨性如半年或运行10万次视使用环境频率而增减在清理维护中不应用清洗剂一类的液体对钢丝绳进行清洗否则会影响绳芯中的油脂含量及油脂成分进而影响到钢丝绳的正常使用在清理维护钢丝绳时应使用毛刷棉纱压缩空气等对钢丝绳的表面进行清理在钢丝绳清理干净后要用钢丝绳润滑脂及时对钢丝绳表面进行适量涂油处理过量的润滑会使钢丝绳与曳引轮之间的摩擦力得不到保证钢丝绳表面油脂应薄而均匀定期检查钢丝绳张力绳槽磨损情况发现磨损及时调整gb8903电梯用钢丝绳
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一维云模型程序:clcclearEx=170;En=5;He=0.5;n=5000;for i=1:nEnn=randn(1)*He+En;x(i)=randn(1)*Enn+Ex;y(i)=exp(-(x(i)-Ex)^2/(2*Enn^2)); endplot(x,y,'.r')title('5000个男生身高的一维云图') ylabel('确定度');xlabel('身高值');axis([150,190,0,1])grid on一维:clear vars;clc;close all;Ex1=-8; En1=0.7; He1=0.2; n1=200; Ex2=2.2; En2=2; He2=0.5; n2=800; Ex3=18; En3=4; He3=0.7; n3=1500; En1_t = normrnd(En1,He1,n1,1);data1 = normrnd(Ex1,En1_t,n1,1);mu1 = exp(-0.5*((data1-Ex1)./En1_t).^2);En2_t = normrnd(En2,He2,n2,1);data2 = normrnd(Ex2,En2_t,n2,1);mu2 = exp(-0.5*((data2-Ex2)./En2_t).^2);En3_t = normrnd(En3,He3,n3,1);data3 = normrnd(Ex3,En3_t,n3,1);mu3 = exp(-0.5*((data3-Ex3)./En3_t).^2);figure(1);plot(data1,mu1,'.b',data2,mu2,'*r',data3,mu3,'+k'); axis equal;二维云模型程序:clcclearEx1=170;En1=5;He1=0.5;Ex2=65;En2=3;He2=0.2;n=5000;for i=1:nEnn1=randn(1)*He1+En1;x1(i)=randn(1)*Enn1+Ex1;Enn2=randn(1)*He2+En2;x2(i)=randn(1)*Enn2+Ex2;y(i)=exp(-(x1(i)-Ex1)^2/(2*Enn1^2)-(x2(i)-Ex2)^2/(2*Enn2^2)); endplot3(x1,x2,y,'.r')title('5000个男生身高体重的二维云图')axis([148,190,50,80,0,1])grid on结果:多个一维clear vars;clc;close all;Ex1=0; En1=0.103; He1=0.013; n1=5000;Ex2=0.309; En2=0.064; He2=0.008; n2=5000;Ex3=0.5; En3=0.039; He3=0.005; n3=5000;Ex4=0.691; En4=0.064; He4=0.008; n4=5000;Ex5=1; En5=0.103; He5=0.013; n5=5000;En1_t = normrnd(En1,He1,n1,1);data1 = normrnd(Ex1,En1_t,n1,1);mu1 = exp(-0.5*((data1-Ex1)./En1_t).^2);En2_t = normrnd(En2,He2,n2,1);data2 = normrnd(Ex2,En2_t,n2,1);mu2 = exp(-0.5*((data2-Ex2)./En2_t).^2);En3_t = normrnd(En3,He3,n3,1);data3 = normrnd(Ex3,En3_t,n3,1);mu3 = exp(-0.5*((data3-Ex3)./En3_t).^2);En4_t = normrnd(En4,He4,n4,1);data4 = normrnd(Ex4,En4_t,n4,1);mu4 = exp(-0.5*((data4-Ex4)./En4_t).^2);En5_t = normrnd(En5,He5,n5,1);data5 = normrnd(Ex5,En5_t,n5,1);mu5 = exp(-0.5*((data5-Ex5)./En5_t).^2);figure(1);plot(data1,mu1,'.r',data2,mu2,'.r',data3,mu3,'.r',data4,mu4,'.r',data5,mu5,'.r' );title('评价集')ylabel('隶属度');axis([-0.4,1.4,0,1])grid on一维Ex=1100;En=84.926;He=0.1;n=1000;X=zeros(1,n);Y=zeros(1,n);X(1:n)=normrnd(En,He,1,n);for i=1:nEn1=X(1,i);X(1,i)=normrnd(Ex,En1,1);Y(1,i)=exp((-(X(1,i)-Ex)^2)/(2*En1^2));plot(X,Y,'.','MarkerEdgeColor','k','markersize',4); title('强等级','fontsize',16);grid on;end逆发生器代码X1=X ;Y1=Y;i=1;while i<=(n-flag)If Y1(1,i)>0.9999Y1(:,i)=[ ] ;X1(:,i)=[ ] ;flag=flag+1;End;Ex=mean(X1) ;En1=zeros(1,m) ;for i=1:m ;En1(1,i)=abs(X1(1,i)-Ex)/sqrt(-2*log(Y1(1,i))) ; End ;En=mean(En1) ;He=0 ;for i=1:m ;He=He+(En1(1,i)-En)^2 ;He=sqrt(He/(m-1)) ;End ;X1 =X;Y1=Y;i=1;while i<=(n-flag)if Y1(1,i)>0.9999Y1(:,i)=[];X1(:,i)=[];flag=flag+1;elsei=i+1;m=m +1;endendEx=mean(X1)En1=zeros(1,m);for i= l:mEn1(1,i)=abs(X1(1,i)-Ex)/sqrt(-2 *log(Y1(1,i))); endEn=mean(En1);He=0;for i=l:mHe=He+(En1(1,i)-En)^2;endHe=sqrt(He/(m-1))clear vars;clc;close all;Ex1=0.457; En1=0.150; He1=0.050; n1=4000; Ex2=0.454; En2=0.156; He2=0.056; n2=4000;Ex3=0.435; En3=0.229; He3=0.067; n3=4000;Ex4=0.415; En4=0.177; He4=0.071; n4=4000;Ex5=0.414; En5=0.298; He5=0.099; n5=4000; Ex6=0.410; En6=0.242; He6=0.061; n6=4000;Ex7=0.410; En7=0.188; He7=0.061; n7=4000;Ex8=0.500; En8=0.039; He8=0.005; n8=5000;En1_t = normrnd(En1,He1,n1,1);data1 = normrnd(Ex1,En1_t,n1,1);mu1 = exp(-0.5*((data1-Ex1)./En1_t).^2);En2_t = normrnd(En2,He2,n2,1);data2 = normrnd(Ex2,En2_t,n2,1);mu2 = exp(-0.5*((data2-Ex2)./En2_t).^2);En3_t = normrnd(En3,He3,n3,1);data3 = normrnd(Ex3,En3_t,n3,1);mu3 = exp(-0.5*((data3-Ex3)./En3_t).^2);En4_t = normrnd(En4,He4,n4,1);data4 = normrnd(Ex4,En4_t,n4,1);mu4 = exp(-0.5*((data4-Ex4)./En4_t).^2);En5_t = normrnd(En5,He5,n5,1);data5 = normrnd(Ex5,En5_t,n5,1);mu5 = exp(-0.5*((data5-Ex5)./En5_t).^2);En6_t = normrnd(En6,He6,n6,1);data6 = normrnd(Ex6,En6_t,n6,1);mu6 = exp(-0.5*((data6-Ex6)./En6_t).^2);En7_t = normrnd(En7,He7,n7,1);data7 = normrnd(Ex7,En7_t,n7,1);mu7 = exp(-0.5*((data7-Ex7)./En7_t).^2);En8_t = normrnd(En8,He8,n8,1);data8 = normrnd(Ex8,En8_t,n8,1);mu8 = exp(-0.5*((data8-Ex8)./En8_t).^2);figure(1);plot(data1,mu1,'.r',data2,mu2,'.r',data3,mu3,'.r',data4,mu4,'.r',data5,mu5,'.r' ,data6,mu6,'.r',data7,mu7,'.r',data8,mu8,'.r');title('评价集')ylabel('隶属度');axis([-0.4,1.4,0,1])grid onclear vars;clc;close all;Ex1=0.716; En1=0.123; He1=0.045; n1=4000;Ex2=0.545; En2=0.140; He2=0.052; n2=4000;Ex3=0.534; En3=0.233; He3=0.085; n3=4000;Ex4=0.461; En4=0.202; He4=0.063; n4=4000;Ex5=0.691; En5=0.064; He5=0.008; n5=6000;En1_t = normrnd(En1,He1,n1,1);data1 = normrnd(Ex1,En1_t,n1,1);mu1 = exp(-0.5*((data1-Ex1)./En1_t).^2);En2_t = normrnd(En2,He2,n2,1);data2 = normrnd(Ex2,En2_t,n2,1);mu2 = exp(-0.5*((data2-Ex2)./En2_t).^2);En3_t = normrnd(En3,He3,n3,1);data3 = normrnd(Ex3,En3_t,n3,1);mu3 = exp(-0.5*((data3-Ex3)./En3_t).^2);En4_t = normrnd(En4,He4,n4,1);data4 = normrnd(Ex4,En4_t,n4,1);mu4 = exp(-0.5*((data4-Ex4)./En4_t).^2);En5_t = normrnd(En5,He5,n5,1);data5 = normrnd(Ex5,En5_t,n5,1);mu5 = exp(-0.5*((data5-Ex5)./En5_t).^2);figure(1);plot(data1,mu1,'.r',data2,mu2,'.r',data3,mu3,'.r',data4,mu4,'.r',data5,mu5,'.r' );title('评价集')ylabel('隶属度');axis([-0.4,1.4,0,1]) grid on。
