地下水动力学第一章PPT课件
地下水动力学 课后思考题及其参考答案ppt课件

精选课件PPT
26
(13)画出间歇性河流对潜水的补给过程的横断面示意 流网图,并说明间歇性河流变化规律对潜水含水层动 态的影响。
P68。
(14)某水源地附近一口泉的流量发生衰减,可能原因 有哪些?
补给量减少或者排泄量增大!
精选课件PPT
27
第十章 孔隙水
在地壳下部深约1535km处地温高达400以上压力也非常大这里的水不可能以普通液态气态水形式存在均是以非自由态第一章地球上的水及其循环3地球上水的循环按其循环途径长短循环速度的快慢以及涉及层圈的范围可分为水文循环地质循环
绪言 第一章 地球上的水及其循环
(1)从大气圈到地壳上半部属于浅部层圈水,其中分布有大气水 、地表水、地下水以及生物体中的水,这些水以 自由态H2O分子 形式存在, 液态 为主,也呈现 固态 与 气态 存在。
精选课件PPT
12
(2)请对以下陈述作出辨析
>>潜水面如果不是流线,则流线可能向下穿越潜水面,也可 能向上穿越潜水面;
正确。
>>地下水总是从高处往低处流; 错误,地下水总是从能量高的地方流向能量低的地方。
>>含水层孔隙度越大,则渗透系数越大; 错误,粘土的孔隙度很大,但其渗透系数很小。
>>当有入渗补给或蒸发排泄时,潜水面可以看作一个流面。 P39中。
P57中。 (4)由深循环地下水补给的、温度较高的泉水中,阳离子通 常以Na+为主,这是由于( d )的结果。 a.溶滤作用;b.脱硫酸作用;c.浓缩作用;d.脱碳酸作用
P57中。
精选课件PPT
20
(5)在某含水层的局部地区,沿着地下水流动方向,SO42-浓度显著下 降,HCO3-浓度则显著升高,试回答以下问题: (A)什么样的化学作用可能引起这种变化?
地下水动力学(第一章 渗流理论基础-2-专)

∂2H ∂2ψ ∂2H ∂2ψ −K = ; −K =− 2 ∂x∂y ∂y2 ∂y∂x ∂x
二、流网及其性质
流网:在渗流场内,取一组流线和一组等势线 组成的网格。 流网的性质: 流网的性质: 1. 在各向同性介质中,流线与等势线处处垂直, 故流网为正交网格。 证明:等水头线和流线的梯度为:
gradH = ∇H = ∂H ∂H i+ j ∂x ∂y
一般地下水流都为Darcy流。 思考题
§1—3 岩层透水特征分类和渗透系数张量 一、岩层透水特征分类 据岩层透水性随空间坐标的变化情况,将岩层 分为均质的和非均质的两类。 均质岩层:在渗流场中,所有点都具有相同的 渗透系数。 非均质岩层:在渗流场中,不同点具有不同的 渗透系数。 非均质岩层有两种类型:一类透水性是渐变的, 另一类透水性是突变的。 均质、非均质:指 与空间坐标的关系 与空间坐标的关系, 均质、非均质 指K与空间坐标的关系,即不同位 是否相同; 置K是否相同; 是否相同
K1M1 + K2M2 M1 + M2 Kp − Kv = − M1 M2 M1 + M2 + K1 K2 M1M2 = >0 (K1M1 + K2M2 )(M1 + M2 )
(K1 − K2 )
2
安建工 地下水动力学 第一章(xiu)

渗流场(flow field)由固体骨架和岩石空隙中的水两
部分组成。渗流只发生在岩石空隙中。
多孔介质概念与特性
我们把孔隙岩层称为多孔介质(porous media).
•多孔介质特性:
彼此连通的网络,几何形态及连通情况异
常复杂,难以用精确的方法来描述。
由固体骨架和孔隙组成,孔隙通道是不连
续的。
nd 32
2
J
K
nd 32
渗透系数的表达式
裂隙介质(概化为走向和缝宽相同的平行板)
k nB 12 K k
2
nB 12
2
v KJ
nB 12
2
J
K
nB 12
2
六、渗流分类
1. 按运动要素(v,p,H)是否随时间变化,分:稳定流与非稳定流 2. 按地下水质点运动状态的混杂程度,分:
微分形式:
五、渗透系数(hydraulic conductivity)
是重要的水文地质参数,它表征在一般正常条
件下对某种流体而言岩层的渗透能力
(permeability)
v=KJ;
当J=1时,K=v
K在数值上是当J=1时的渗透流速,量钢[L/T];
常用单位cm/s;m/d。
渗透系数与哪些因素有关呢?
: 比重;:动力粘滞性系数;
K k
渗透率k:反映介质几何特性,量纲[L2];
常用单位:cm2; 石油地质中用达西: 1 达西=9.8697*10-9cm2.
渗透系数的表达式
多孔介质(概化为等径的平行毛细管束):
地下水动力学第一章ppt课件

因此,无论是固体骨架,还是空隙空间,微观上讲都不是连续函数
2020年2月9日星期日
普通水流与渗流
颗粒 孔隙
图1-1-0b 在一般管道中的普通水流
图1-1-3a 地下水实际流线
共同点:1.总体流向取决于水头差 2.流量取决于水头差及沿程损耗
承压含水层压强与水头
图1-1-4b 承压含水层的压强与水头
2020年2月9日星期日
水力坡度
大小等于dH/dn ,方向沿着等水头线
的法线方向指向水头降低的方向的矢量
定义为水力坡度,记为J。
JgradHdH dn
Jx H x Jy H y Jz H z
2020年2月9日星期日
2020年2月9日星期日
渗透系数的表达式
多孔介质(概化为等径的平行毛细管束):
k nd 2 32
K k nd 2 32
v KJ nd 2 J 32
K nd 2 • 32
2020年2月9日星期日
渗透系数的表达式
裂隙介质(概化为走向和缝宽相同的平行板)
v=KJ; 当J=1时,K=v K在数值上是当J=1时的渗透流速,量钢[L/T];
常用单位cm/s;m/d。 渗透系数与哪些因素有关呢?
2020年2月9日星期日
影响渗透系数大小的因素
K= f (孔隙大小、多少、液体性质) ➢ 岩层空隙性质(孔隙大小、多少) ➢ 由流体的物理性质决定,与γ成正比,与
渗透流速——假想渗流的速度,是假想
的平均流速。实际流速在REV上的平均
地下水动力学

1,地下水动力学:研究地下水在孔隙岩石,裂隙岩石和岩溶(喀斯特)岩石中运动规律的科学第一章渗流理论基础2,多孔介质:在地下水动力学中,把具有孔隙的岩石称为多孔介质3有效空隙:互相连通的,不为结合水所占据的那一部分空隙4,有效孔隙度:有效孔隙体积与多孔介质总体积之比5,贮水率:又称释水率面积为一个单位,厚度为一个单位,当水头降低一个单位时所能释放出的水量贮水系数(释水系数)=贮水率乘以含水层厚度表示面积为一个单位,厚度为含水层全厚度的含水层主体中,当水头改变一个单位时弹性释放或贮存的水量贮水率与贮水系数相互关系:1,都是表示含水层弹性释水能力的参数2,对于承压含水层,只要水头不降低到隔水底板以下,水头降低只会引起弹性释水,可用贮水系数表示这种释水能力3,对于潜水含水层,当水头下降时可引起两部分水的排出(1,在上部潜水面下降引起重力排水,用给水度表示重力排水的能力2,在下部饱水部则引起弹性释水,用贮水率表示这一部分的释水能力)弹性释水和重力排水的不同点:1,影响范围不同(弹性释水影响整个承压含水层,重力释水影响潜水含水层和包气带)2,和时间有关(1 弹性释水瞬时完成不随时时间变化 2 重力释水存在滞后效应是时间的函数)3 两只大小不同(弹性释水系数多在0.001-0.00005之间重力排水参数在0.1-0.01之间)7 渗流:假设这种假想水流运动时,在任意岩石体积内所受的阻力等于真是水流所受的阻力,通过任意断面的流量及任一点的压力或水头均和实际水流相同,这种假想水流称为渗流渗流与实际水流相比相同点:阻力相同水头相同流量相同8 渗流速度:代表渗流在过水断面上的平均流速,时一种假想流速实际平均流速:在空隙中的不同地点,地下水运动的方向和速度可能不同平均速度称为实际平均速度测压管水头:H_z=z+p/r水位:一般用在野外,基准面相同(黄海水位标高)水头:基准面可任意选定水位是一种特殊的水头9 地下水头:书十页10,水力坡度:把大小等于坡度值,方向沿着等水头面的法线指向水头降低方向的矢量称为水力坡度p1111,地下水运动特征的分类p11运动要素:表征渗流运动的物理量,主要有渗流量Q,渗流速度V ,压强P,水头H等按运动要素和时间的关系分为:(1)稳定流:运动要素不随时间变化;(2)非稳定流:运动要素随时间变化按地下水运动方向和空间坐标的关系:一维运动,二维运动,三维运动12,层流:流速较小时,液体质点做有条不紊的线性运动,彼此不相掺混紊流:流速较大时,液体质点的运动轨迹曲折混乱,互相掺混13,Dacry在此处键入公式。
地下水动力学基础.ppt

-- 每降低一个单位压强,单位体积的地层压缩“挤”出水的体积
对于各向异性介质,当所选座标方向与介质主渗方向平行时
一般三维问题的基本微分方程
x
(K xx
H x
)
y
(K
yy
H y
)
z
(K zz
H z
) W
SS
H t
地下水流动基本微分方程 -柱坐标描述方式
作变换:x r cos , y r sin
折射定律及应用
tgq1 = K 1 tgq2 K 2
多用于简化越流问题(90度折射)
-忽 简略 化弱 准透 三水 维层 流弹
性 ( 压
密 ) 释 水 情 况
等效推行储水系数,包括 部分弱透水层的压密释水
多层含水层越流系统的近似微分方程式--准三维流 忽略含水层中垂直分量,忽略夹层水平分量与释水
以两层为例,上层潜水H1、中间弱透水层、下层承压水H2组成的 越流系统。含水层内主要为水平流动分量,弱透水层内主要为垂直流动分量
潜水:
x
K
(
H1
B)
H1 x
y
K (H1
B)
H1 y
W1
+
K' m'
(H2
-
H1)
Sy
H1 t
承压水:
承压水:
x
T3
H3 x
y
T3
H3 y
W3
K2
H 2 z
Z 承压顶板
S3
地下水动力学简介
第一章 渗流理论基础§1-1 渗流的基本概念一、渗流及连续介质假说1 多孔介质(porous medium)与连续介质(continuous medium)多孔介质很难给出其精确定义,在地下水动力学中,把具有孔隙的岩石称为多孔介质。
它包括孔隙介质和裂隙介质。
一般来说,具有以下特点的物质就称为多孔介质。
(1)该物体为多相体:固体相-骨架,流体相-空隙;(2)固体相的分布遍及整个多相体所占据的区域;(3)空隙空间具有连通性。
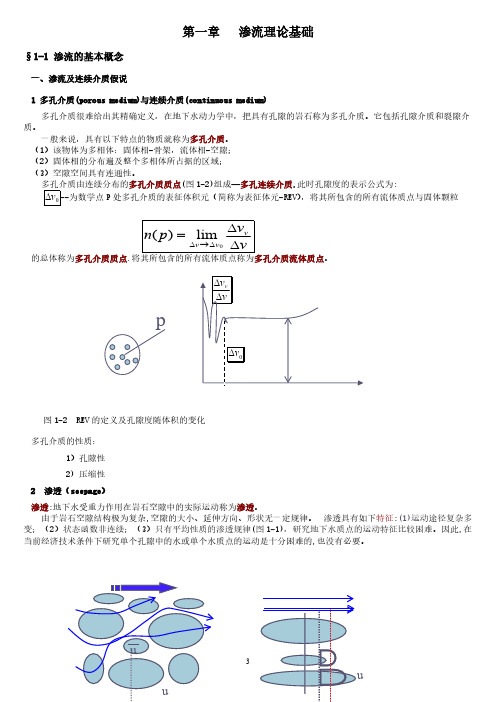
多孔介质由连续分布的多孔介质质点(图1-2)组成—多孔连续介质.此时孔隙度的表示公式为:--为数学点P 处多孔介质的表征体积元(简称为表征体元-REV ),将其所包含的所有流体质点与固体颗粒0v ∆的总体称为多孔介质质点.将其所包含的所有流体质点称为多孔介质流体质点。
图1-2 REV 的定义及孔隙度随体积的变化多孔介质的性质:1)孔隙性2) 压缩性2 渗透(seepage )渗透:地下水受重力作用在岩石空隙中的实际运动称为渗透。
由于岩石空隙结构极为复杂,空隙的大小、延伸方向、形状无一定规律。
渗透具有如下特征:(1)运动途径复杂多变;(2)状态函数非连续;(3)只有平均性质的渗透规律(图1-1),研究地下水质点的运动特征比较困难。
因此,在当前经济技术条件下研究单个孔隙中的水或单个水质点的运动是十分困难的,也没有必要。
vv p n v v v ∆∆=∆→∆0lim)(图1-2岩石中地下水的渗透针对这种极为复杂的地下水运功,在地下水动力学中一般可采用两种研究方法。
1) 研究微观情况下的运动,即研究地下水在以孔隙介质中的骨架为边界孔隙或裂隙中的运动。
由于空隙介质的结构具有随机性,所以用统计平均方法来确定地下水运动的宏观规律性;2) 从宏观角度出发,采用试验及数学分析方法,对大量微观运动进行宏观研究得出各种运动条件下地下水运动的基本规律。
3 渗流(seepage flow)前面已经提到,要研究实际的渗透十分困难,因此,我们用一种假想水流来代替真实水流,这种假想水流是在连续介质的基础上通过概化得出的:(1)假定水流充满整个含水层空间(既包括空隙所占据的空间,也包括颗粒/骨架所占据的空间);(2)只考虑水流运动的总体方向,不考虑水流实际运动途径的复杂变化.将通过上述概化后所得到的假想水流—渗流。
地下水动力学1.4
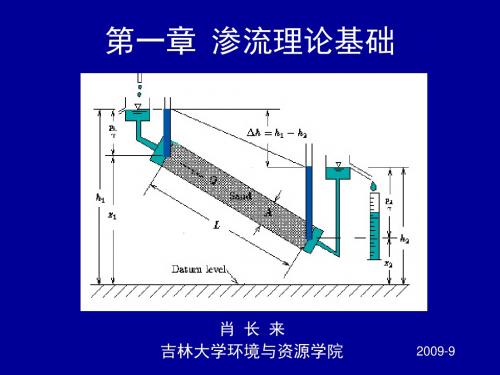
图1-27 某地的流网图
图1-28 叠加抽水井的流网图
(1-33a)
图1-17 流线
(1-33b)
•
• •
M和M’是任意流线上任选的两点。因此,上式对流线上的 任一点都是正确的,可以把它看成是流线的方程,用它来 描述流线。 上面的流线方程无论对各向同性和各向异性介质都是适用 的。 在各向异性介质中,如果选取的坐标轴(直角坐标系)的方 向分别与渗透系数的主方向一致,则上式变为:
(1)在各向同性介质中,流线与等水头线处处垂 直,流网为正交网格。 由(1-38)式,得:
(1-40)
消去K,得:
(1-41)
等水头线 流线 式中i,j——单位矢量。
(1-42) (1-43)
在非均质各向同性介质中,上式亦成立。 (2)在均质各向同性介质中,流网中每一网格的边长比为 常数。
(1-44)
(4) 流函数的特性
① 对于一给定的流线,流函数是常数。不同的流线有 不同的常数值。流函数决定于流线。Y=c ② 在平面运动中,两流线之间的单宽流量等于和这两 条流线相应的流函数之差。q=Y2 - Y1
③ 在均质各向同性介质中,流函数满足Laplace方程; 而在其他情况下,流函数均不满足该方程。
1.4.2 流函数方程
(1) 流线的方程
根据上述定义,没有水流穿越流线。如下图,在任一流 线上取任意两点M(x, y)和M' (x+dx, y+dy)。M点的渗流速度 矢量为v,它与它的两个分量Vx,Vy构成一个三角形MAB。自 M' 点作垂线Mb,并延长至a。 当M与M' 无限逼近时,弧线 MM’ 可用切线Ma来代替,故有 Mb= dx,ab=dy。因为 MAB≈Mab,有以下等式 成立---流线方程 :
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
V
V0
2. 若P点取孔隙中心且V只取小于孔隙体积时孔隙率n=1;
3. 当V取值由一个颗粒或一个孔隙逐渐放大时,n值会因随机划进的颗粒或孔 隙体积而产生明显的波动,但随着V取值再增大,n值波动逐渐减小。
4. 当V取至某个体积时,孔隙率趋于某一平均值n,此时的V称为典型体元 (REV),记为V0
5. 若再增大V使其大于V0,则有可能将P点外围的非均质区也划进来平均,此 时n值可能又产生明显的变化。
实验条件:均匀介质,一维流动,稳定流, 层流。
是否适用:非均匀介质,二维或三维流动, 非稳定流,层流条件?
2020年12月3日星期四
三、变水头达西实验
非稳定流达西实验(实验一):
水自上部加入,用溢水管保持稳定水位 ,下部用管口出流,可通过它测定渗流 量,用两根测压管来测量水头值。
达西定理:
Q KAH1H2 KAH
JgradHdH dn
Jx H x Jy H y Jz H z
2020年12月3日星期四
§1.2 渗流基本定律--达西定律
一、达西定律
法国水力学家 H.Darcy通过大量稳 定流实验得出:
2020年12月3日星期四
二、达西实验条件
稳定达西实验:得出渗透流速与水力坡度成 正比即线性渗流定律,说明此时地下水的流 动状态呈层流。
l
l
H1 H, H2 0, z 0
实验结果:
在非稳定流条件下,地下水运动 仍满足线性渗流定律
2020年12月3日星期四
变水头达西实验原理
达西定律:
QKA H 1H 2KA H
l
l
dVQ(t)dtKH(t) Adt l
dVAdH
KH(t) l
Ad t AdHK l
dt
dH H
积分有:
tK
H dH
dt
理想渗流等效简化原则: 理想渗流通过某断面的流量应等于通过该内孔
隙面积的实际流量:质量等效。 理想渗流通过某岩层所受到的阻力与实际渗流
所受到的阻力相等:能量等效。
2020年12月3日星期四
概化后的理想渗流
颗粒 孔隙
图1-1-0b 在一般管道中的普通水流
颗粒
孔隙
图 1-1A -3a 地 下 水 实 际 流 线
渗透流速与实际流速关系
vA uA v Q
v
u
Av A
un
e
v neu
2020Байду номын сангаас12月3日星期四
渗透流速与实际流速关系
2020年12月3日星期四
三、水头与水力坡度
总水头 Hz pu2
2g
u2《z p
2g
Hp
测压水; 头Hp
H
某砾石含水层中,u = 1.65cm/s
u2 1.652 0.000c1m 4 2g 2980
一、典型体元
(Representative elementary volume)
在水力学中引进质点的概念,把水看成连续介质, 则可用连续函数描述运动要素。
为了把渗流场概化为多孔介质连续体,用连续函 数描述,引进典型体元的概念。
什么是典型体元呢?现以孔隙度为例来讨论。
2020年12月3日星期四
典型体元(REV)的提出
2020年12月3日星期四
潜水含水层压强与水头
图1-1-4a 潜水含水层的压强与水头
2020年12月3日星期四
承压含水层压强与水头
图1-1-4b 承压含水层的压强与水头
2020年12月3日星期四
水力坡度
大小等于dH/dn ,方向沿着等水头线
的法线方向指向水头降低的方向的矢量
定义为水力坡度,记为J。
n Vv V
n(p) limVv V0 V
P1 P2
2020年12月3日星期四
典型体元(REV)概念的引入
v
n(p) limVv
颗粒
VV0 V
1
V=1个 孔 隙 的 体 积
孔隙
K1
非均质介质
n
均质介质
K2
图1-1-1a 多孔介质空隙度计算
0 V=1个 颗 粒 的 体 积
1. 若P点取颗粒中心且V只取小于颗粒体积时孔隙率n=0;
区别:水在管道中运动取决于管道大小、形状及 粗糙度;渗流运动取决于空隙大小、形状、连 通性。
2020年12月3日星期四
渗流特点
– 通道是曲折的,质点运动轨迹弯曲; – 流速是缓慢的,多数为层流; – 水流仅在空隙中运动,在整个多孔介质
中不连续; – 通常是非稳定的; – 通常为缓变流。
2020年12月3日星期四
典型体元的定义
把V0称为典型体元。 引进REV后就可以把多孔介质处理为连
续体,这样多孔介质就处处有孔隙度了。 REV究竟有多大? REV相对于单个孔隙是相当大的,但相
对于渗流场又是非常小的。
2020年12月3日星期四
理想渗流
在REV的基础上,引入理想渗流的概念:地下 水充满整个含水层或含水系统(包括空隙和固 体骨架),渗流充满整个渗流场。
0l
H H 0
K t ln H 0
l
H
t
l K
ln
H0
彼此连通的网络,几何形态及连通情况异 常复杂,难以用精确的方法来描述。 由固体骨架和孔隙组成,孔隙通道是不连 续的。
因此,无论是固体骨架,还是空隙空间,微观上讲都不是连续函数
2020年12月3日星期四
普通水流与渗流
颗粒 孔隙
图1-1-0b 在一般管道中的普通水流
图1-1-3a 地下水实际流线
共同点:1.总体流向取决于水头差 2.流量取决于水头差及沿程损耗
第一章 地下水运动基本概念
重要知识点: 渗流、典型体元(REV) 地下水质点实际流速、空隙平均流速,达西流速
及其关系 达西定律基本式,微分式,推广式及应用条件 渗透系数及其影响因素 渗流分类 均质、非均质,各向同性、各向异性区别 流网绘制
2020年12月3日星期四
§1.1 渗流基本概念
地下水在岩石空隙中的运动称为渗流(seepage flow/ groundwater flow)。发生渗流的区域称为渗流场。
渗流场(flow field)由固体骨架和岩石空隙中的水两部 分组成。渗流只发生在岩石空隙中。
2020年12月3日星期四
多孔介质概念与特性
我们把孔隙岩层称为多孔介质(porous media). •多孔介质特性:
颗粒 孔隙
B 2020年12月3日星期四
二、地下水实际流速、渗透流速
地下水实际流速—质点流速在以P点为中 心REV体积上的平均值称为地下水在P点 的实际流速。
渗透流速——假想渗流的速度,是假想
的平均流速。实际流速在REV上的平均
值。
v(P) 1 V0
V0v u'dVv
2020年12月3日星期四
