混凝土第5章 受弯构件正截面受力性能
合集下载
第5章 受弯构件的斜截面承载力
第5章 受弯构件的斜截面承载力5．1概述上一章讲了钢筋混凝土受弯构件在主要承受弯矩的区段内，会产生垂直裂缝，如果正截面受弯承载力不够，将沿垂直裂缝发生正截面受弯破坏。
钢筋混凝土受弯构件在弯矩和剪力共同作用下，当正截面受弯承载力得到保证时，则有能产生斜截面破坏。
斜截面破坏包括斜截面受剪破坏和斜截面受弯破坏两方面。
因此为了保证受弯构件的承载力，除了进行正截面受弯承载力计算外，还必须进行斜截面受剪承载力计算，同时斜截面受弯承载力则是通过对纵向钢筋和箍筋的构造要求来满足的。
钢筋混凝土受弯构件在出现裂缝前的应力状态，由于它是两种不同材料组成的非均质体，因而材料力学公式不能完全适用。
但是当作用的荷载较小，构件内的应力也较小，其拉应力还未超过混凝土的抗拉极限强度、亦即处于裂缝出现以前的I a 阶段状态时，则构件与均质弹性体相似，应力-应变基本成线性关系，此时其应力可近似按一般材料力学公式来进行分析。
在计算时可将纵向钢筋截面按其重心处钢筋的拉应变取与同一高度处混凝土纤维拉应变相等的原则，由虎克定律换算成等效的混凝土截面，得出一个换算截面，则截面上任意一点的正应力和剪应力分别按下式计算，其应力分布见图5-1。
图5-1 钢筋混凝土简支梁开裂前的应力状态（a ）开裂前的主应力轨迹线；（b ）换算截面；（c ）正应力σ图；（d ）剪应力τ图正应力 0I My =σ （5-1） 剪应力 0bI VS =τ （5-2） 式中 I 0——换算截面惯性矩。
由于受弯构件纵向钢筋的配筋率一般不超过2%，所以按换算截面面积计算所得的正应力和剪应力值与按素混凝土的截面计算所得的应力值相差不大。
根据材料力学原理，受弯构件正截面上任意一点在正应力σ和剪应力τ共同作用下，在该点所产生的主应力，可按下式计算主拉应力 2242τσσσ++=tp （5-3）主压应力 2242τσσσcp +-= （5-4） 主应力的作用方向与构件纵向轴线的夹角α可由下式求得：στα22-=tg （5-5）在中和轴附近，正应力很小，剪应力大，主拉应力方向大致为45°。
混凝土受弯构件正截面承载力计算
h0—有效高度。 1.最大配筋率及界限相对受压区高度
r As f y As a1 fcbx x a1 fc
bh0 bh0 f y bh0 f y h0 f y
令
x
h0
则
r
a1 fc
fy
令b为 = r max时的相对受压区高度，即
rmax
b
a1
f
fc
y
= r max时的破坏形态为受压区边缘混凝土达到极限压
c fc e0 e ecu
n
2
1 60
(
fcu,k
50)
2.0
各系数查表4-3
e0 0.002 0.5( fcu,k 50)105 0.002
ecu 0.0033 0.5( fcu,k 50)105 0.0033
4.钢筋应力—应变关系的假定（本构关系）
Ese e e y fy e ey
4.3钢筋混凝土受弯构件正截面试验研究
一、受弯构件正截面破坏过程
受弯构件正截面破坏分为三个阶段 • 第一阶段：裂缝开裂前 • 第二阶段：从开裂到钢筋屈服 • 第三阶段：从钢筋屈服到梁破坏
（1）第I阶段
当荷载比较小时，混凝土基本处 于弹性阶段，截面上应力分布为三 角形，荷载-挠度曲线或弯矩-曲率 曲线基本接近直线。截面抗弯刚度 较大，挠度和截面曲率很小，钢筋 的应力也很小，且都于弯矩近似成 正比。
My
Mu
Failure”，破坏前
可吸收较大的应变
能。
0
f
2．超筋梁(Over reinforced)破坏
钢筋配置过多，将发生这种破坏。 破坏特征：破坏时钢筋没有达到屈服强度，破坏是由 于压区混凝土被压碎引起，没有明显预兆，为脆性破 坏。
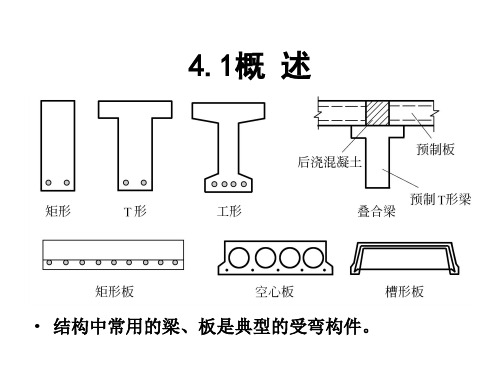
r As f y As a1 fcbx x a1 fc
bh0 bh0 f y bh0 f y h0 f y
令
x
h0
则
r
a1 fc
fy
令b为 = r max时的相对受压区高度，即
rmax
b
a1
f
fc
y
= r max时的破坏形态为受压区边缘混凝土达到极限压
c fc e0 e ecu
n
2
1 60
(
fcu,k
50)
2.0
各系数查表4-3
e0 0.002 0.5( fcu,k 50)105 0.002
ecu 0.0033 0.5( fcu,k 50)105 0.0033
4.钢筋应力—应变关系的假定（本构关系）
Ese e e y fy e ey
4.3钢筋混凝土受弯构件正截面试验研究
一、受弯构件正截面破坏过程
受弯构件正截面破坏分为三个阶段 • 第一阶段：裂缝开裂前 • 第二阶段：从开裂到钢筋屈服 • 第三阶段：从钢筋屈服到梁破坏
（1）第I阶段
当荷载比较小时，混凝土基本处 于弹性阶段，截面上应力分布为三 角形，荷载-挠度曲线或弯矩-曲率 曲线基本接近直线。截面抗弯刚度 较大，挠度和截面曲率很小，钢筋 的应力也很小，且都于弯矩近似成 正比。
My
Mu
Failure”，破坏前
可吸收较大的应变
能。
0
f
2．超筋梁(Over reinforced)破坏
钢筋配置过多，将发生这种破坏。 破坏特征：破坏时钢筋没有达到屈服强度，破坏是由 于压区混凝土被压碎引起，没有明显预兆，为脆性破 坏。
混凝土结构设计原理-受弯构件正截面承载力
受弯构件正截面承载力计算
第一阶段：构件未开裂，弹性工作阶段。 第二阶段：带裂缝工作阶段。 第三阶段：钢筋塑流阶段。
受弯构件正截面承载力计算
阶段Ia — 抗裂计算依据； 阶段II — 变形、裂缝宽度计算依据； 阶段IIIa — 承载力计算依据。
受弯构件正截面承载力计算
二 钢筋混凝土梁正截面的破坏形式
受弯构件正截面承载力计算
钢筋的布置 Construction of reinforced bars
梁腹板高度hw>450mm时，要求在梁两侧沿高度每隔200mm设置一根纵 向构造钢筋，以减小梁腹部的裂缝宽度，直径≥10mm。
1. 为保证耐久性、防火性以及钢筋与混凝土的粘结性能，钢筋的混凝 土保护层厚度一般不小于25mm，与环境类别有关；
HRB335 钢筋 HRB400 钢筋
b s,max b s,max
最大配筋率ρmax
b max b
1 f c
fy
受弯构件正截面承载力计算
最小配筋率ρmin
最小配筋率规定了少筋和适筋的界限
min
As ft 0.45 bh fy
且同时不应小于0.2%
受弯构件正截面承载力计算
2.
3.
矩形截面梁高宽比h/b=2.0~3.5；T形截面梁高宽比h/b=2.5~4.0；
梁的高度h通常取为1/10~ 1/15梁跨，由250mm以50mm为模数增大; 梁宽为120、150、180、200、220、250、300……
受弯构件正截面承载力计算
三 受弯构件的力学特性
P
A B
M
P C D A
少筋梁：一裂即坏，裂缝很宽，脆性破坏，截面过大不经济，设计时应避免。 适筋梁：受拉钢筋屈服，混凝土达抗压极限强度，充分利用材料，作为设计依据 超筋梁：压区混凝土的压碎，受拉钢筋未屈服，脆性破坏，设计时应避免。
混凝土结构设计原理-05章-受弯构件的斜截面承载力
第5章 受弯构件的斜截面承载力
第5章 受弯构件的斜截面承载力
主要内容
● ● ● ●
重点
斜裂缝、剪跨比及斜截面受剪破坏形态 简支梁斜截面受剪机理 斜截面受剪承载力计算公式及设计计算 保证斜截面受剪承载力的构造措施
● 斜裂缝、剪跨比及斜截面受剪破坏形态 ● 简支梁斜截面受剪机理 ● 斜截面受剪承载力的设计计算 ● 保证斜截面受剪承载力的构造措施
图形。 材料抵抗弯矩图：按实际配置的受力钢筋计算的各个
正截面受弯承载力 Mu 所绘制的图形。
5.5 保证斜截面受弯承载力的构造措施
第5章 受弯构件的斜截面承载力
对承受均布荷载的单筋矩形截面简支梁：
Mu
As
fsd (h0
fsd As ) 2 fcdb
每根纵筋所承担的
M ui可近似按钢筋面积分配， M ui
5.4 斜截面受剪承载力计算
第5章 受弯构件的斜截面承载力
公式的适用范围 ■ 截面的最小尺寸（上限值） 为防止斜压破坏，要求：
0Vd (0.51 103 ) fcu,k bh0
否则，应加大截面尺寸或提高混凝土强度等级。 ■ 构造配箍条件（下限值）
0Vd (0.5 103 ) 2 f tdbh0
而略有降低。 T形截面梁的受剪承载力高于矩形截面梁。
5.4 斜截面受剪承载力计算
第5章 受弯构件的斜截面承载力
2. 斜截面受剪承载力计算公式
由于抗剪机理和影响因素的复杂性，目前各国规范的斜
截面受剪承载力计算公式均为半理论半经验的实用公式。
《公路桥规》中的斜截面受剪承载力计算公式以剪压破
坏为建立依据，假定梁的斜截面受剪承载力Vu由剪压区混凝 土的抗剪能力Vc、与斜裂缝相交的箍筋的抗剪能力Vsv 和与斜 裂缝相交的弯起钢筋的抗剪能力Vsb 三部分所组成。
第5章 受弯构件的斜截面承载力
主要内容
● ● ● ●
重点
斜裂缝、剪跨比及斜截面受剪破坏形态 简支梁斜截面受剪机理 斜截面受剪承载力计算公式及设计计算 保证斜截面受剪承载力的构造措施
● 斜裂缝、剪跨比及斜截面受剪破坏形态 ● 简支梁斜截面受剪机理 ● 斜截面受剪承载力的设计计算 ● 保证斜截面受剪承载力的构造措施
图形。 材料抵抗弯矩图：按实际配置的受力钢筋计算的各个
正截面受弯承载力 Mu 所绘制的图形。
5.5 保证斜截面受弯承载力的构造措施
第5章 受弯构件的斜截面承载力
对承受均布荷载的单筋矩形截面简支梁：
Mu
As
fsd (h0
fsd As ) 2 fcdb
每根纵筋所承担的
M ui可近似按钢筋面积分配， M ui
5.4 斜截面受剪承载力计算
第5章 受弯构件的斜截面承载力
公式的适用范围 ■ 截面的最小尺寸（上限值） 为防止斜压破坏，要求：
0Vd (0.51 103 ) fcu,k bh0
否则，应加大截面尺寸或提高混凝土强度等级。 ■ 构造配箍条件（下限值）
0Vd (0.5 103 ) 2 f tdbh0
而略有降低。 T形截面梁的受剪承载力高于矩形截面梁。
5.4 斜截面受剪承载力计算
第5章 受弯构件的斜截面承载力
2. 斜截面受剪承载力计算公式
由于抗剪机理和影响因素的复杂性，目前各国规范的斜
截面受剪承载力计算公式均为半理论半经验的实用公式。
《公路桥规》中的斜截面受剪承载力计算公式以剪压破
坏为建立依据，假定梁的斜截面受剪承载力Vu由剪压区混凝 土的抗剪能力Vc、与斜裂缝相交的箍筋的抗剪能力Vsv 和与斜 裂缝相交的弯起钢筋的抗剪能力Vsb 三部分所组成。
钢筋混凝土受弯构件正截面承载力计算
为保证钢筋混凝土结构的耐久性、防火性以及钢
筋与混凝土的粘结性能，钢筋的混凝土保护层厚
５度、一配般筋不率小于2A 5msm% ； ....4...2()
bh0
用下述公式表示
As bh0
%
公式中各符号含义：
As为受拉钢筋截面面积； b为梁宽；h0为梁的有效 高度，h0=h-as；as为所有受拉钢筋重心到梁底面 的距离，单排钢筋as= 35mm ，双排钢筋as= 55~60mm 。
M/ M u
Mu
1.0
0.8 My
0.6
II
0.4
III III a II a
M cr I a
I
0
f cr
fy
fu f
加载过程中弯矩－曲率关系
说明：
对于配筋合适的梁，在III
阶段，其承载力基本保持不 变而变形可以很大，在完全
M/ M u
Mu
1.0
破坏以前具有很好的变形能 力，破坏预兆明显，我们把
0.8 My
通常采用两点对称集中加荷，加载点位于梁跨度 的1/3处，如下图所示。这样，在两个对称集中荷载间 的区段(称“纯弯段”)上，不仅可以基本上排除剪力的 影响(忽略自重)，同时也有利于在这一较长的区段上(L ／3)布置仪表，以观察粱受荷后变形和裂缝出现与开 展的情况。在“纯弯段”内，沿梁高两侧布置多排测 点，用仪表量测梁的纵向变形。
梁破坏时的极限弯矩Mu小于在正常情况下的开
裂弯矩Mcr。梁配筋率越小， Mcr -Mu的差值越大； 越大(但仍在少筋梁范围内)， Mcr -Mu的差值越小。
当Mcr -Mu =0时，它就是少筋梁与适筋梁的界限。这
时的配筋率就是适筋梁最小配筋率的理论值min。
混凝土
2、建筑结构的极限状态有_____________________和___________________。
3、结构上的作用按其随时间的变异可分为_________、__________、_________。
4、永久荷载的分项系数是这样取的：当其效应对结构不利时，由可变荷载控制的效应组合取_________，由永久荷载控制的效应组合取__________：对结构有利时，一般取______，对结构的倾覆、滑移或漂流验算可以取_______________。
（一）.章
一、填空题
1、在混凝土中配置受力钢筋的主要作用是提高结构或构件的_____和_____。
2、结构或构件的破坏类型有_____与_____。
二、选择题
1、与素混凝土梁相比，钢筋混凝土梁承载能力（）。
A.相同B.提高许多C.有所提高
2.与素混凝土梁相比，钢筋混凝土梁抵抗开裂的能力（）。
A.提高不多B.提高许多C.完全相同
8、我国《建筑结构可靠度设计统一标准》规定，对于一般工业与民用建筑构件，在延性破坏时可靠度指标β取_________，脆性破坏时β取_________。
二、选择题
1、若用S表示结构或构件截面上的荷载效应，用R表示结构或构件截面的抗力，结构或构件截面处于极限状态时，对应于（）式。
A.R＞S B.R＝S C.R＜S D.R≤S
Ａ．徐变使混凝土压应力减小
Ｂ．混凝土及钢筋的压应力均不变
Ｃ．徐变使混凝土压应力减小，钢筋压应力增大
Ｄ．徐变使混凝土压应力增大，钢筋压应力减小
７.热轧钢筋冷弯后（）。
A.可提高抗拉强度和抗压强度B.只能提高抗拉强度
C.可塑性提高，强度提高不多D.只能提高抗压强度
8.下列拿一下说法不正确（）。
3、结构上的作用按其随时间的变异可分为_________、__________、_________。
4、永久荷载的分项系数是这样取的：当其效应对结构不利时，由可变荷载控制的效应组合取_________，由永久荷载控制的效应组合取__________：对结构有利时，一般取______，对结构的倾覆、滑移或漂流验算可以取_______________。
（一）.章
一、填空题
1、在混凝土中配置受力钢筋的主要作用是提高结构或构件的_____和_____。
2、结构或构件的破坏类型有_____与_____。
二、选择题
1、与素混凝土梁相比，钢筋混凝土梁承载能力（）。
A.相同B.提高许多C.有所提高
2.与素混凝土梁相比，钢筋混凝土梁抵抗开裂的能力（）。
A.提高不多B.提高许多C.完全相同
8、我国《建筑结构可靠度设计统一标准》规定，对于一般工业与民用建筑构件，在延性破坏时可靠度指标β取_________，脆性破坏时β取_________。
二、选择题
1、若用S表示结构或构件截面上的荷载效应，用R表示结构或构件截面的抗力，结构或构件截面处于极限状态时，对应于（）式。
A.R＞S B.R＝S C.R＜S D.R≤S
Ａ．徐变使混凝土压应力减小
Ｂ．混凝土及钢筋的压应力均不变
Ｃ．徐变使混凝土压应力减小，钢筋压应力增大
Ｄ．徐变使混凝土压应力增大，钢筋压应力减小
７.热轧钢筋冷弯后（）。
A.可提高抗拉强度和抗压强度B.只能提高抗拉强度
C.可塑性提高，强度提高不多D.只能提高抗压强度
8.下列拿一下说法不正确（）。
《建筑结构》第五课习题答案
第五章受弯构件正截面承载力计算《建筑结构》第五章习题：共用条件：一类环境使用，结构安全等级为二级。
5-25 一钢筋混凝土矩形梁截面尺寸200mm×500mm，弯矩设计值M=120kN·M。
混凝土强度等级C25，试计算其纵向受力钢筋截面面积：①当选用HPB235级钢筋时；②改用HRB400级钢筋时；最后画出相应配筋截面图。
解：依题意查得参数：γ0=1，fc=11.9N/mm2，ft=1.27N/mm2，c=25mm，21fy=210N/mm，ξb=0.614；as=65mm。
h0=500-65=435mm ○M120?106先按单筋矩形截面计算，?s???0.266 22?1fcbh011.9?200?435??1??2?s?1??2?0.266?0.32??b?0.614As=M/[fyh0（1-0.5ξ）]=1560.65mm2，选5?20，As=1571mm2＞?min=0.45 ftbh/fy=0.45×1.27×200×500*210=272mm22＞0.02bh=0.002×200×500=200mm,22 fy=360N/mm，ξb=0.517；as=40mm，h0=500-40=460mm ○M120?106先按单筋矩形截面计算，?s???0.238?1fcbh0211.9?200?4602??1??2?s?1??2?0.238?0.28??b?0.517As=M/[fyh0（1-0.5ξ）]=120×106/[360×460×（1-0.5×0.28）]=842.6 1mm2，选3#20，As=941mm2，或4#18，As=1018mm2＞?min=272 mm21 ○2 ○5-26 某大楼中间走廊单跨简支板，计算跨度2.18m，承受均布荷载设计值g ＋q=6kN/m2（包括自重），混凝土强度等级C20，HPB235级钢筋。
混凝土结构及砌体结构-第五章受弯构件斜截面承载力计算
Asv 1.75 V Vcs f t bh0 f yv h0 1.0 s
注意：
1.5 3
17
2.公式的适用范围 （1）、上限值－－最小截面尺寸和最大配箍率：
hw 当 4 时，V 0.25 c f cbh0 b hw 当 6 时，V 0.2 c f c bh0 b hw 当4 6 时，按线性内插法取用 b
250 300 350 500
150 200
24
3.弯起钢筋的要求
1.画出弯矩图和正截面受弯承载力图； 2.根据各根钢筋面积大小按比例分配受弯承载力图，
弯起的钢筋画在外面； 3.找出要弯起钢筋的充分利用点和不需要点； 4.从充分利用点向外延伸0.5h0，作为弯起点，并 找出弯起钢筋与中和轴的交点。如该点在不需要点 的外面，可以，否则再向外延伸； 5.验算是否满足斜截面受剪承载力要求和其它构造 要求。
las≥15d（光面）
37
（2）中间支座直线锚固：
0.7la ≥l a
l ≥0.a7la
38
（3）中间支座的弯折锚固：
≥0.4la ≥0.4la
15d
39
（4）节点或支座范围外的搭接：
ll
40
5.4.5
箍筋的构造要求
单肢箍n=1
双肢箍n=2
四肢箍n=4
41
梁受扭或承受动荷载时，不得使用开口箍筋
45
46
19
－斜截面上弯起钢筋与构件纵向轴线的夹角。
2. 斜截面承载力计算步骤
⑴ 确定计算截面及其剪力设计值； ⑵ 验算截面尺寸是否足够； ⑶ 验算是否可以按构造配筋；
⑷ 当不能按构造配箍筋时，计算腹筋用量；
⑸ 验算箍筋间距、直径和最小配箍率是否 满足要求。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
M
s
s
t0
tb= tu
b
C xn=xc
r
T
c
sAs
为了计算方便用矩形应力 分布代替原来的应力分布
ft
tu
t c
s
h xcr xcr h0 xcr
t c
Ec c
s Ess
t ft
t o t0 2t0
ft 0.5Ec tu
五、受弯构件正截面受力分析
2. 弹性阶段的受力分析 ct
X 0
五、受弯构件正截面受力分析
3. 开裂阶段的受力分析
压区混凝土处于弹塑性阶段，但0 <ct< cu
(以混凝土强度等级不大于C50的钢筋混凝土受弯构件为例 )
M
fcbn
h0
(1
1 3
0 ct
)
1
n
1
1 2
1 12
0
t c
1
1 3
0 t c
2
xn= nh y0 y h0 h 0
c 0
n
o
0
0 0.002 0.5 fcu 50105
0 0.002时，取0 0.002
c cu
cu 0.0033 fcu 50105
cu 0.0033时，取cu 0.0033
五、受弯构件正截面受力分析
1. 基本假定
混凝土受拉时的应力-应变关系
t ft
t=Ect
t
o t0
P
L/3
L/3
L
P 超筋
III
II 少筋 I O
适筋
III
II 少筋 I O
适筋
四、受弯构件的试验研究
2. 试验结果
结论二
•在适筋和超筋破坏之间存在一种平衡破坏。其破坏特征是钢 筋屈服的同时，混凝土压碎，是区分适筋破坏和超筋破坏的 定量指标
平衡破坏（界限破坏，界 限配筋率）
四、受弯构件的试验研究
五、受弯构件正截面受力分析
3. 开裂阶段的受力分析
压区混凝土处于弹性阶段
M较小时， c可以认为 是按线性分布，忽略拉
区混凝土的作用
ct
ct
A
s
b
X 0
xn=n
c
h0
h0 h
y
M
s
cb
yc C xn
sAs
c
Ec c
Ec
t c
y
n h0
t c
y
n h0
0.5
t c
bn
h0
s As
Ess As
Es
四、受弯构件的试验研究
2. 试验结果
当配筋适中时——适筋梁的破 坏过程
P
L/3
L/3
L
ct
ct
ct
ct
(ct=cu) ct
MI
Mcr
MII
My
(Mu) MIII
sAs tb<ft
sAs tb=ft(tb =tu)
s<y
sAs
s= fyAs
y
fyAs s>y
四、受弯构件的试验研究
2. 试验结果
适筋破坏
As
s
cb b
s
As h0
1 n
1
1 2
1 12
0 t c
1
1 3
0 t c
2
(s fy )
ct c0
M
fc
yc
C
xn
Ts=sAs
五、受弯构件正截面受力分析
4. 破坏阶段的受力分析
t c
cu。当fcu
50Mpa时，
n 2,0 0.002,cu 0.0033 As
C
f
cbn
h0
(1
1 3
0 ct
)
xn= nh y0 y h0 h 0
As
s
cb b
ct c0
M
fc
yc
C
xn
Ts=sAs
yc
n h0
1
1 2
1 12
0
t c
1
1 3
0 t c
2
fcbn h0
1
0
3
t c
Es
1 n n
t c
As
fcn2
1
0
3
t c
Es
1 n
t c
(1 n )h0 n h0
t c
As
E
1n n
t c
As
n2 2En 2E 0
五、受弯构件正截面受力分析
3. 开裂阶段的受力分析
压区混凝土处于弹性阶段
A
s
b
ct
xn=n
c
h0
h0 h
y
M
s
tb
ct yc
C xn
sAs
M 0
M
0.5ctbnh02 (1
1 3
n
)
s Ash0 (1
1 3
n
)
2
t c
n h0
0
y
t 2 c
n h0
2 0
y
2
dy
fcb
n
h0
t c
0
t c
2
3
2 0
fcbn h0
t c
0
t2 c
3
2 0
Es
1 n n
t c
As
yc
nh0
fcb
n 0
h0
2
c 0
2 c 2 0
ydy
fcb
n 0
h0
2
c 0
2 c 2 0
dy
xcr 0.5h
五、受弯构件正截面受力分析
2. 弹性阶段的受力分析
ct
ct
M 0
xn=n
c
h0
A
h0 h
M
s
s
t0
tb= tu
b
C xn=xc
r
T
c
sAs
M cr
f
tb(h
xcr
)(
h
xcr 2
2E
ft
As (h0
xcr 3
)
2 xcr 3
)
设h0
0.92h, 令 A
2E
As bh
Mcr 0.292(1 2.5A) ftbh2
当配筋很少时——少筋梁的破 坏过程
cb
cb
P
L/3
L/3
L
Mcr=
MI
My
sAs tb<ft
sAs tb=ft(t b=tu)
四、受弯构件的试验研究
2. 试验结果
少筋破坏
四、受弯构件的试验研究
2. 试验结果
结论一
•适筋梁具有较好的变形能力，超 筋梁和少筋梁的破坏具有突然性， 设计时应予避免。
M 超筋
对适筋梁，达极限状态时，
As
t c
cu
0.0033,s
fy
xn= nh y0 y h0 h 0
s
cb b
X 0
n
1.253s
fy fc
ct c0
Mu
fc
yc
C
xn
Ts=sAs
M 0
M u fy Ash0 (1 0.412n ) fcbh02n (0.798 0.329n )
六、受弯构件正截面简化分析
b
nb 界限受压区相对高度 适筋破坏
h0
nb
xnb h0
cu cu y
y
xb 矩形应力图形的界限受压区高度
b 矩形应力图形的界限受压区相对高度
超筋破坏
b
xnb h0
1xb
h0
1cu cu y
1
1
y
1
1 fy
cu
Es cu
六、受弯构件正截面简化分析
2. 界限受压区高度
fcu 50Mpa时：
b
1
0.8 fy
0.0033Es
b即n nb
b即n nb
b即n nb
平衡破坏 适筋破坏
0 0.002,cu 0.0033
1100.9.86294
1
1
1.0, 1 0.8 0.94, 1 0.74,
fcu
50Mpa fcu 80Mpa
线性插值（《混凝土结构设计 规范》GB50010 ）
六、受弯构件正截面简化分析
2. 界限受压区高度
cu
xnb 界限受压区高度
平衡破坏
xn
fc
1 fc
由C的大小不变
xn=nh
0
yc C
xn=nh
0
yc C
x=1xn
Mu
Mu
C
1
f cbn h0
(1
1 3
0 cu
)
1
f c 1n bh0
sAs
sAs
1
1
1
(1
1 3
0 cu
)
由C的位 置不变
2
2
yc
n h0
(1
1 2
1 12
1 1
0 cu 0
)
0.51nh0 ,
1
1
2 3
0 cu
架立
箍筋
弯矩引起的 垂直裂缝
弯筋
纵筋
三、截面尺寸和配筋构造
1. 梁
c
c
净距30mm 1.5钢筋直径d
净距25mm 钢筋直径d