江苏省苏州市2019届高三上学期期初调研考试数学试题
苏州市2018-2019学年上学期高2019届高三期中调研数学答案

18.(本题满分 16 分) 解: (1)函数的定义域为 R ,因为 f ( x ) 为奇函数,由 f ( x) f ( x) 可知, f (0) 0 , 所以 1 a 0 ,所以 a 1 ; ………………
1 1 e x x f ( x) ,此时 f ( x) 为奇函数. ……………… e x e 1 1 (2)令 e x x t ( t ≥ 0 ) ,所以 e 2 x 2 x t 2 2 e e
1 ,0) e2
5.
12. 256
6. 10
13.
3
21 4
14. a -1 或 a 3 二、解答题(本大题共 6 个小题,共 90 分,请在答题卷区域内作答,解答时应写出文字说明、 证明过程或演算步骤) 15.(本题满分 14 分) 解: (1)因为
1 3 ). ,所以 n ( , 2 2 6
因为 [0, ] ,所以 2
2
(2)由 m / / n ,所以 (2cos 2 3)cos 2sin 2 sin 0 , 所以 2cos(2 ) 3cos 0 ,
所以 2cos( )cos 2sin( )sin 3cos( )cos 3sin( )sin 0 , 因为 、 的终边不在 y 轴上,所以 cos( ),cos 均不为 0, 所以 5cos( )cos sin( )sin 0 , 因为所以 tan( ) tan 5 . ………………12 分 ………………14 分
17. (本题满分 14 分)
解: (1)由 DAO , OC AB , OA OB 1 ,
苏州市2019~2020学年第一学期高三数学上学期期中调研试卷附答案解析

苏州市2019~2020学年第一学期高三上学期期中调研数学试卷(满分160分,考试时间120分钟) 2019.11一、 填空题:本大题共14小题,每小题5分,共70分.1. 已知集合A ={-2,-1,0,1,2},B ={x|x >0},则A∩B=________.2. 已知复数z 满足z2+i=i(i 为虚数单位),则复数z 的实部为________. 3. 已知向量a =(x ,2),b =(2,-1),且a⊥b ,则实数x 的值是________. 4. 函数y =lg (x -1)2-x的定义域为________.5. 在等比数列{a n }中,a 1=1,a 4=8,S n 是{a n }的前n 项和,则S 5=________.6. 已知tan α=2,则sin αcos α+2sin α的值为________.7. “x >2”是“x>1”的________条件.(选填“充分不必要”“必要不充分”“充要”或“既不充分又不必要”)8. 已知函数y =sin 2x 图象上的每个点向左平移φ(0<φ<π2)个单位长度得到函数y =sin(2x +π6)的图象,则φ的值为________.9. 设函数f(x)=⎩⎪⎨⎪⎧e x,x ≥0,2x +1,x <0,则不等式f(x +2)>f(x 2)的解集为________.10. 已知函数f(x)=ln x -mx 的极小值大于0,则实数m 的取值范围是________.11. 在各项都为正数的等差数列{a n }中,已知a 5=3,则a 3a 7的最大值为________.12. 已知菱形ABCD 的棱长为3,E 为棱CD 上一点且满足CE →=2ED →.若AE →·EB →=-6,则cos C =________. 13. 若方程cos(2x -π6)=35在(0,π)上的解为x 1,x 2,则cos(x 1-x 2)=________.14. 已知函数f(x)=3x 2-x 3,g(x)=e x -1-a -ln x .若对于任意x 1∈(0,3),总是存在两个不同的x 2,x 3∈(0,3),使得f(x 1)=g(x 2)=g(x 3),则实数a 的取值范围是________.二、 解答题:本大题共6小题,共90分. 解答时应写出必要的文字说明、证明过程或演算步骤. 15. (本小题满分14分)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,C =120°,c =7,a -b =2. (1) 求a ,b 的值; (2) 求sin(A +C)的值.16. (本小题满分14分)已知向量a =(cos x ,3cos x),b =(cos x ,sin x). (1) 若a∥b ,x ∈[0,π2],求x 的值;(2) 若f(x)=a·b,x∈[0,π2],求f(x)的最大值及相应x的值.17. (本小题满分14分)已知等比数列{a n}满足a2=2,且a2,a3+1,a4成等差数列.(1) 求数列{a n}的通项公式;(2) 设b n=|a n-2n+1|,求数列{b n}的前n项和T n.18. (本小题满分16分)如图所示,某窑洞窗口形状上部是圆弧CD,下部是一个矩形ABCD,圆弧CD所在圆的圆心为O.经测量AB=4m,BC=33m,∠COD=120°,现根据需要把此窑洞窗口形状改造为矩形EFGH,其中E,F在边AB上,G,H在圆弧CD上.设∠OGF=θ,矩形EFGH的面积为S.(1) 求矩形EFGH的面积S关于变量θ的函数关系式;(2) 求cos θ为何值时,矩形EFGH的面积S最大?19. (本小题满分16分)已知函数f(x)=x-1x .(1) 求f(x)的图象在x=1处的切线方程;(2) 求函数F(x)=f(x)-x的极大值;(3) 若af(x)≤ln x对x∈(0,1]恒成立,求实数a的取值范围.20. (本小题满分16分)已知数列{a n}满足(n-1)a n+1=na n-a1,n∈N*.(1) 求证:数列{a n}为等差数列;(2) 设数列{a n}的前n项和为S n.若a2-a1=1,且对任意的正整数n,都有13<1S1+1S2+1S3+…+1S n<43,求整数a1的值;(3) 设数列{b n }满足b n =a n +310.若a 2-a 1=15,且存在正整数s ,t ,使得a s +b t 是整数,求|a 1|的最小值.数学附加题(满分40分,考试时间30分钟)21. 【选做题】 从A ,B ,C 三小题中选做两题,每小题10分,共20分.若多做,则按作答的前两题评分.解答时应写出必要的文字说明、证明过程或演算步骤.A. (选修42:矩阵与变换) 已知二阶矩阵M =⎣⎢⎡⎦⎥⎤a 13b 的特征值λ=-1所对应的一个特征向量为⎣⎢⎡⎦⎥⎤-1 3.(1) 求矩阵M ;(2) 设曲线C 在变换矩阵M 作用下得到的曲线C′的方程为y 2=x ,求曲线C 的方程.B. (选修44:坐标系与参数方程)已知曲线C 的极坐标方程为ρ=2cos α+23sin α(α为参数),直线l 的参数方程为⎩⎪⎨⎪⎧x =1+tcos β,y =tsin β(t为参数,0<β<π2).若曲线C 被直线l 截得的弦长为13,求β的值.C. (选修45:不等式选讲)设正数a ,b ,c 满足a +b +c =1,求证:a b +c +b c +a +c a +b ≥32.【必做题】 第22,23题,每小题10分,共20分.解答时应写出必要的文字说明、证明过程或演算步骤. 22. 某射击小组有甲、乙、丙三名射手,已知甲击中目标的概率是34,甲、丙二人都没有击中目标的概率是112,乙、丙二人都击中目标的概率是14.甲、乙、丙是否击中目标相互独立. (1) 求乙、丙二人各自击中目标的概率;(2) 设乙、丙二人中击中目标的人数为X ,求X 的分布列和数学期望.23. 如图,在直三棱柱ABCA 1B 1C 1中,∠BAC =90°,AB =AC =a ,AA 1=b ,点E ,F 分别在棱BB 1,CC 1上,且BE =13BB 1,C 1F =13CC 1.设λ=b a.(1) 当λ=3时,求异面直线AE 与A 1F 所成角的大小; (2) 当平面AEF⊥平面A 1EF 时,求λ的值.数学参考答案及评分标准1. {1,2}2. -13. 14. (1,2)5. 316. 257. 充分不必要8. π12 9. (-1,2)10. (-∞,-1e ) 11. 9 12. 13 13. -3514. [1,e 2-ln 3-4)15. 解:(1) 由余弦定理cos C =a 2+b 2-c 22ab ,且c =7,C =120°得a 2+b 2+ab =49.(3分)因为a -b =2,所以b 2+2b -15=0.(5分) 因为b >0,所以b =3,a =5. 综上:a =5,b =3.(7分)(2) 由(1)知a =5,b =3,c =7,所以cos B =a 2+c 2-b 22ac =1314.(10分)因为B 为△ABC 的内角,所以sin B =1-cos 2B =3314.(12分)因为sin(A +C)=sin(π-B)=sin B =3314, 所以sin(A +C)的值为3314.(14分)16. 解:(1) 因为a =(cos x ,3cos x),b =(cos x ,sin x),a ∥b , 所以cos xsin x =3cos 2x ,所以cos x(sin x -3cos x)=0,(2分)所以cos x =0或sin x -3cos x =0,即cos x =0或tan x = 3.(4分) 因为x∈⎣⎡⎦⎤0,π2,所以x =π2或x =π3.(6分) (2) 因为a =(cos x ,3cos x),b =(cos x ,sin x), 所以f(x)=a·b =cos 2x +3cos xsin x(8分) =1+cos 2x 2+32sin 2x =sin(2x +π6)+12.(10分) 因为x∈⎣⎡⎦⎤0,π2,所以2x +π6∈⎣⎡⎦⎤π6,7π6, 所以sin(2x +π6)∈⎣⎡⎦⎤-12,1,所以f(x)∈⎣⎡⎦⎤0,32,(12分)所以f(x)的最大值为32,此时x =π6.(14分)17. 解:(1) 设等比数列{a n }的公比为q(不为0),因为a 2 ,a 3+1,a 4成等差数列,所以2(a 3+1)=a 2+a 4.(1分) 因为a 2=2,所以2(2q +1)=2+2q 2,解得q =2或q =0(舍去),所以a 1=a 2q =1,(3分)所以数列{a n }的通项公式为a n =2n -1.(5分)(2) 设c n =a n -2n +1=2n -1-2n +1, 所以c n +1-c n =2n-2(n +1)+1-(2n -1-2n +1)=2n -1-2,所以n≥3,c n +1>c n .(7分)因为c 4=1>0,所以n≥4时,c n >0,即n≥4时,b n =c n =2n -1-2n +1.因为c 1=0,c 2=-1,c 3=-1,所以b 1=0,b 2=1,b 3=1, 所以T 1=0,T 2=1,T 3=2.(10分)当n≥4时,T n =b 1+b 2+b 3+b 4+…+b n =(0+1+1)+b 4+b 5+…+b n =2+(23+24+…+2n -1)-(7+9+…+2n -1)=2+23(1-2n -3)1-2-7+2n -12·(n -3)=2n -n 2+3.(13分)综上,T n=⎩⎪⎨⎪⎧0,n =1,1,n =2,2,n =3,2n-n 2+3,n ≥4.(14分)18. 解:(1) 如图,作OP⊥CD 分别交AB ,GH 于M ,N.由四边形ABCD ,EFGH 是矩形,O 为圆心,∠COD=120°,所以OM⊥AB,ON⊥GH,点P,M,N分别为CD,AB,GH的中点,∠CON=60°. 在Rt△COP中,CP=2,∠COP=60°,所以OC=433,OP=233,所以OM=OP-PM=OP-BC=33.(3分)在Rt△ONG中,∠GON=∠OGF=θ,OG=OC=433,所以GN=433sin θ,ON=433cos θ,所以GH=2GN=833sin θ,GF=MN=ON-OM=433cos θ-33,(6分)所以S=GF·GH=(433cos θ-33)·833sin θ=83(4cos θ-1)sin θ,θ∈(0,π3),所以S关于θ的函数关系式为S=83(4cos θ-1)sin θ,θ∈(0,π3).(8分)(2) S′=83(4cos2θ-4sin2θ-cos θ)=83(8cos2θ-cos θ-4).(10分)因为θ∈(0,π3),所以cos θ∈(12,1),所以S′=0,得cos θ=1+12916∈(12,1).(12分)设θ0∈(0,π3)且cos θ0=1+12916,所以由S′>0,得0<θ<θ0,即S在(0,θ0)上单调递增,由S′<0,得θ0<θ<π3,即S在(θ0,π3)上单调递减,(14分)所以当θ=θ0时,S取得最大值,所以当cos θ=1+12916时,矩形EFGH的面积S最大.(16分)19. 解:(1) 因为f(x)=x-1x,所以f′(x)=12x+12x x,所以f′(1)=1.(2分)因为y=f(x)经过(1,0),所以f(x)的图象在x=1处的切线方程为y=x-1.(4分)(2) 因为F(x)=x-1x-x,x>0,所以F′(x)=12x+12x x-1,F′(x)在(0,+∞)上递减.又F′(1)=0,(5分)所以当x∈(0,1)时,F′(x)>0,即F(x)在x∈(0,1)上递增;当x∈(1,+∞)时,F′(x)<0,即F(x)在x∈(1,+∞)上递减,(7分) 所以在x=1处,F(x)的极大值为F(1)=-1.(8分)(3) 设g(x)=ln x-af(x)=ln x-a(x-1x),x∈(0,1],所以g′(x)=1x -a 2(1x +1x x )=-a (x )2+2x -a2x x.①当a≤0时,g ′(x)>0对x∈(0,1]恒成立,所以g(x)在(0,1]上递增.又g(1)=0,所以∃x 0∈(0,1)时,g(x 0)<0,这与af(x)≤ln x 对x∈(0,1]恒成立矛盾;(10分) ②当a≥1时,设φ(x)=-a(x)2+2x -a ,x ∈(0,1],Δ=4-4a 2≤0,所以φ(x)≤0,x ∈(0,1],所以g′(x)≤0对(0,1]恒成立,所以g(x)在(0,1]上递减.又g(1)=0,所以g(x)≥0对x∈(0,1]恒成立,所以a≥1成立;(12分)③当0<a <1时,设φ(x)=-a(x)2+2x -a ,x ∈(0,1],Δ=4-4a 2>0,解φ(x)=0得两根为x 1,x 2,其中x 2=1+1-a 2a >1,x 1=1-1-a 2a =a1+1-a2∈(0,1),所以0<x 1<1,x 2>1,所以x∈(x 1,1),φ(x)>0,g ′(x)>0,所以g(x)在(x 1,1)上递增.又g(1)=0,所以g(x 1)<0,这与af(x)≤ln x 对x∈(0,1]恒成立矛盾.(15分) 综上:a≥1.(16分)20. (1) 证明:因为(n -1)a n +1=na n -a 1,n ∈N *①, 所以(n -2)a n =(n -1)a n -1-a 1,n ≥2且n∈N *②.①-②,得(n -1)a n +1-2(n -1)a n +(n -1)a n -1=0,n ≥2且n∈N *,(2分) 所以a n +1-2a n +a n -1=0,n ≥2且n∈N *, 所以a n +1-a n =a n -a n -1=…=a 2-a 1, 所以数列{a n }为等差数列.(4分)(2) 解:因为a 2-a 1=1,所以{a n }的公差为1.因为对任意的正整数n ,都有13<1S 1+1S 2+1S 3+…+1S n <43,所以13<1S 1<43,所以34<S 1<3,即34<a 1<3,所以a 1=1或2.(6分)当a 1=1时,a 2=2,S 1=1,S 2=3,所以1S 1+1S 2=1+13=43,这与题意矛盾,所以a 1≠1;(7分)当a 1=2时,a n =n +1,S n =n (n +3)2>0,1S 1=12>13,1S 1+1S 2+1S 3+…+1S n >13恒成立.(8分) 因为1S n =23(1n -1n +3),1S 1+1S 2+1S 3+…+1S n =23(1-14+12-15+13-16+…+1n -2-1n +1+1n -1-1n +2+1n -1n +3)=23(1+12+13-1n +1-1n +2-1n +3)<119<43. 综上,a 1的值为2.(10分)(3) 解:因为a 2-a 1=15,所以{a n }的公差为15,所以a n =a 1+15(n -1),所以b n =a 1+15n +110.(11分)由题意,设存在正整数s ,t ,使得a s +b t =l ,l ∈Z ,则a 1+s 5-15+a 1+t 5+110=l ,即20a 1=2(5l -s -t)+1.因为5l -s -t∈Z ,所以2(5l -s -t)是偶数,所以|20a 1|≥1,所以|a 1|≥120.(14分)当a 1=120时,b 4=1920,所以存在a 1+b 4=1∈Z .综上,|a 1|的最小值为120.(16分)。
(备用答案)江苏省苏州市2019届高三期初调研

江苏省苏州市2019届高三期初调研1. {1} [解析]由交集定义知A ∩B ={1}.2. 4 [解析]因为z 1=2+i ,z 2=a -2i ,所以z 1·z 2=(2+i )(a -2i )=2a +2+(a -4)i ,又z 1z 2是实数,所以a -4=0,即a =4.3. 2 [解析]由题知15(1+2+3+4+a)=2,得a =0,所以方差s 2=15×[(1-2)2+(2-2)2+(3-2)2+(4-2)2+(0-2)2]=2.4. 4 [解析]初始值n =7,S =0,满足条件S<18,S =7,n =6,满足条件S<18,S =13,n =5,满足条件S<18,S =18,n =4,不满足条件S<18,结束循环,输出n =4.5. 35 [解析]记3个黑球为黑1,黑2,黑3,2个白球为白1,白2,从中一次摸出2个,有如下基本事件:(黑1,黑2),(黑1,黑3),(黑1,白1),(黑1,白2),(黑2,黑3),(黑2,白1),(黑2,白2),(黑3,白1),(黑3,白2),(白1,白2),共10个,其中满足条件的有6个,故所求概率P =610=35. 6. -2 [解析]当x<0时,f(-x)=x 2-2×(-x)=-f(x),所以f(x)=-x 2-2x ,故a =-2.7. π3 [解析]由题知f ⎝⎛⎭⎫-5π12=±1,即2×⎝⎛⎭⎫-5π12+φ=k π+π2,k ∈Z ,故φ=k π+4π3,k ∈Z .又0≤φ≤π,所以k =-1,φ=π3.8. 2 [解析]设数列{a n }的公比为q ,则由题知2S 6=S 2+S 4.当q =1时,不符合题意;当q ≠1时,由2×a 1(1-q 6)1-q =a 1(1-q 2)1-q +a 1(1-q 4)1-q ,得2q 6-q 4-q 2=0,即q 2(2q 2+1)(q 2-1)=0,得q 2=1,q =-1,所以a 2+a 4a 6=a 2(1+q 2)a 2q 4=2.9. -1124 [解析]设高为2,3,4对应的三边分别为a ,b ,c ,根据面积相等,得12×2×a=12×3×b =12×4×c ,故a ∶b ∶c =6∶4∶3,不妨设a =6,b =4,c =3,则由余弦定理知最大内角的余弦值为cos A =b 2+c 2-a 22bc =-1124.10.423 [解析]设四棱锥的棱长为a cm ,则由题知a 2+32a =3+1,得a =2,故该四棱锥的体积V =13×2×2×⎝⎛⎭⎫2×322-12=423(cm 3).11. 12 [解析]由AB ∥CD ,知△ABE ∽△CDE ,则AB CD =AEEC =2.又AC =310,所以AE=2EC =210.由tan A =3,A ∈(0,π),得sin A =31010,cos A =1010.在△ABE 中,BE 2=AE 2+AB 2-2AE·AB·cos A =52,所以BE =213,cos ∠ABE =AB 2+BE 2-AE 22AB·BE =21313,所以BE →·CD →=|BE →|·|CD →|·cos ∠ABE =213×3×21313=12.12. 16 [解析]作出函数f(x)=|x 2-6|的图象如图所示,由a>b>0,f(a)=f(b),得a 2-6=6-b 2,0<b<6,即a 2=12-b 2,所以a 2b =12b -b 3.令g(b)=12b -b 3,0<b<6,则g′(b)=12-3b 2,令g′(b)=0,得b =2(负值舍去).当0<b<2时,g′(b)>0,g(b)单调递增;当2<b<6时,g′(b)<0,g(b)单调递减,所以当b =2时,g(b)取得最大值g(2)=16,故a 2b 的最大值为16.(第12题)13. -22 [解析]由题知cos A sin A +cos B sin B +sin C cos C =0,即-sin C cos C =cos A sin B +cos B sin Asin A sin B =sin (A +B )sin A sin B =sin Csin A sin B ,因为sin C ≠0,所以-cos C =cos (A +B)=cos A cos B -sin A sin B=sin A sin B ,所以tan A tan B =12.因为A ,B 为斜三角形ABC 的两个内角,所以tan A>0,tanB>0,所以-tan C =1tan A +1tan B≥21tan A ·1tan B=22,所以tan C ≤-2 2. 14. ⎣⎡⎭⎫41015,+∞ [解析]由题知圆心C(3,2),如图,设点C 到直线3x +y =3的距离为d ,则d =|3×3+2-3|32+12=4105.当MN 为圆C 的直径时,由图知MP =MN =2r ,即CP -r=2r ,CP =3r ,又CP ≥d =4105,所以r ≥41015.(第14题)15. (1) 因为cos α=437,α∈⎝⎛⎭⎫0,π2,所以sin α=1-cos 2α=1-⎝⎛⎭⎫4372=17,所以sin ⎝⎛⎭⎫π4+α=sin π4cos α+cos π4sin α=22×437+22×17=46+214. (2) 因为α∈⎝⎛⎭⎫0,π2,β∈⎝⎛⎭⎫0,π2,所以α+β∈(0,π),所以sin (α+β)>0. 因为cos (α+β)=1114,所以sin (α+β)=1-cos 2(α+β)=1-⎝⎛⎭⎫11142=5314,所以cos β=cos [(α+β)-α]=cos (α+β)cos α+sin (α+β)sin α=1114×437+5314×17=32.因为β∈⎝⎛⎭⎫0,π2,所以β=π6. 16. (1) 如图,连接CE ,交DF 于点G ,连接MG ,(第16题)因为在矩形CDEF 中,DF ∩EC =G , 所以G 为EC 的中点. 又因为M 为AE 的中点,所以MG 为△EAC 的中位线, 所以MG ∥AC ,因为AC ⊄平面DMF ,MG ⊂平面DMF , 所以AC ∥平面DMF.(2) 在矩形CDEF 中,CD ⊥ED , 因为∠ADC =90°,所以CD ⊥AD ,因为AB ∥CD ,所以AB ⊥ED ,AB ⊥AD.因为AD ∩ED =D ,AD ⊂平面ADE ,ED ⊂平面ADE ,所以AB ⊥平面ADE. 因为MD ⊂平面ADE ,所以MD ⊥AB. 因为DE =DA ,M 为AE 中点, 所以MD ⊥AE ,因为AB ∩AE =A ,AB ⊂平面ABE , AE ⊂平面ABE ,所以MD ⊥平面ABE , 因为BE ⊂平面ABE ,所以BE ⊥DM.17. (1) 如图,过点G 作GM ⊥AB 于点M ,连接OH , 因为∠GOB =60°,所以GM =OG·sin 60°=32r. 又∠BOC =θ,所以BC =r sin θ,OB =r cos θ, 所以GF =GM -BC =32r -r sin θ. 由对称性知AB =2OB =2r cos θ, ∠HOA =∠GOB =60°, 所以∠HOG =60°,则△OHG 为等边三角形, 所以GH =OG =r , 所以S 矩形ABCD =AB·BC =(2r cos θ)·r sin θ=2r 2sin θcos θ,S 矩形EFGH =GH·GF =r·⎝⎛⎭⎫32r -r sin θ=32r 2-r 2sin θ,所以f(θ)=S 矩形ABCD +S 矩形EFGH =2r 2sin θcos θ+32r 2-r 2sin θ(0<θ<π3). (2) 由(1)得f(θ)=r 2(2sin θcos θ-sin θ+32), 所以f′(θ)=r 2(2cos 2θ-2sin 2θ-cos θ)=r 2(4cos 2θ-cos θ-2). 令f′(θ)=0,则4cos 2θ-cos θ-2=0, cos θ=1±338.因为θ∈⎝⎛⎭⎫0,π3,即cos θ∈⎝⎛⎭⎫12,1, 所以cos θ=1+338.令θ0∈⎝⎛⎭⎫0,π3,cos θ0=1+338, 则当θ变化时,f(θ),f′(θ)的变化情况如下表:所以f(θ)max =f(θ0).答:当cos θ=1+338时,可使市民活动广场及停车场的占地总面积最大.(第17题)18. (1) 因为离心率e =c a =12,所以a =2c.因为a 2=b 2+c 2,所以b =3c , 所以椭圆C :x 24c 2+y 23c2=1.因为点P ⎝⎛⎭⎫1,32在椭圆上, 所以14c 2+34c 2=1,解得c =1,所以椭圆C :x 24+y 23=1.(2) 设M(x 1,y 1),N(x 2,y 2), 直线l :y =kx +1(k>1),联立⎩⎪⎨⎪⎧x 24+y 23=1,kx -y +1=0,消去y 得(4k 2+3)x 2+8kx -8=0,则⎩⎪⎨⎪⎧x 1+x 2=-8k4k 2+3,x 1·x 2=-84k 2+3,因为k 1=y 1x 1+2,k 2=y 2x 2-2,且k 1=2k 2,所以y 1x 1+2=2y 2x 2-2,即y 21(x 1+2)2=4y 22(x 2-2)2. ① 又因为M(x 1,y 1),N(x 2,y 2)在椭圆上, 所以⎩⎨⎧y 21=34(4-x 21),y 22=34(4-x 22).②将②代入①可得2-x 12+x 1=4(x 2+2)2-x 2,即3x 1x 2+10(x 1+x 2)+12=0, 所以-244k 2+3-80k4k 2+3+12=0,即12k 2-20k +3=0, 解得k =16或k =32.又因为k>1,所以k =32.19. (1) 由题意得a 1=1,a 2=2, a 3=a 1+d =1+d ,a 4=a 2q =2q , a 5=1+2d ,所以S 3=a 1+a 2+a 3=1+2+(1+d)=4+d. 因为S 3=a 4,a 5=a 2+a 3,所以2q =4+d ,1+2d =3+d , 解得d =2,q =3,所以a n =⎩⎪⎨⎪⎧n , n 为奇数,2·3n 2-1, n 为偶数.(2) 1° 当m =2k -1(k ∈N *)时,因为a m a m +1=a m +2,所以(2k -1)·2·3k -1=2k +1, 所以2·3k -1=2k +12k -1=1+22k -1,因为2·3k-1为整数,所以22k -1必为整数,所以2k -1=1,所以k =1,此时2·3k -1≠3,不合题意. 2° 当m =2k (k ∈N *)时,因为a 2k a 2k +1=a 2k +2,所以2·3k -1·(2k +1)=2·3k , 即2k +1=3,所以k =1,即m =2.(3) S 2m =m (1+2m -1)2+2(1-3m )1-3=3m+m 2-1,S 2m -1=S 2m -a 2m =m 2+3m -1-2·3m -1=m 2+3m -1-1,所以S 2mS 2m -1=m 2+3m -1m 2+3m -1-1 =3-2(m 2-1)3m -1+m 2-1≤3.若S 2mS 2m -1为数列{a n }中的项,则只能为a 1,a 2,a 3. ①当S 2mS 2m -1=1时,3-2(m 2-1)3m -1+m 2-1=1,所以3m -1=0,m 无解.②当S 2mS 2m -1=2时,3-2(m 2-1)3m -1+m 2-1=2,所以3m -1+1-m 2=0.当m =1时,等式不成立; 当m =2时,等式成立;当m ≥3时,令f (x )=3x -1+1-x 2=13·3x +1-x 2,所以f ′(x )=ln 33·3x -2x ,f ″(x )=ln 233·3x-2.当x ≥3时,f ″(x )>0,f ′(x )在[3,+∞)上单调递增.又f ′(3)=9ln 3-6>0,所以f ′(x )>0在[3,+∞)上恒成立, 所以f (x )在[3,+∞)上单调递增.因为f (3)=1>0,所以当m ≥3时,方程3m -1+1-m 2=0无解.③当S 2mS 2m -1=3时,3-2(m 2-1)3m -1+m 2-1=3,所以m 2-1=0,即m =1.综上所述,存在正整数m =1或2,使得S 2mS 2m -1恰好为数列中的一项.20. (1) 函数f(x)=x 2是“恒切函数”,设切点为(x 0,y 0),则⎩⎪⎨⎪⎧f (x 0)+kx 0+b =kx 0+b ,f′(x 0)+k =k ,所以⎩⎪⎨⎪⎧f (x 0)=0,f′(x 0)=0.对于函数f(x)=x 2,f′(x)=2x ,设切点为(x 0,y 0),所以⎩⎪⎨⎪⎧x 20=0,2x 0=0,解得x 0=0,所以f(x)=x 2是“恒切函数”. (2) 设切点为(x 0,y 0),因为f′(x)=mx +n ,所以⎩⎪⎨⎪⎧m ln x 0+nx 0=0,m x 0+n =0,解得ln x 0=1,即x 0=e ,所以实数m ,n 满足的关系式为m +e n =0. (3) 设切点为(x 0,y 0), 因为f′(x)=(2e x -x -2)e x ,所以⎩⎪⎨⎪⎧(e x 0-x 0-1)e x 0+m =0,(2e x 0-x 0-2)e x 0=0,所以⎩⎪⎨⎪⎧m =-(e x 0-x 0-1)e x 0,2e x 0=x 0+2.设g(x)=2e x -x -2,令g′(x)=2e x -1=0,得x =-ln 2.当x ∈(-∞,-ln 2)时,g′(x)<0,g(x)单调递减;当x ∈(-ln 2,+∞)时,g′(x)>0,g(x)单调递增,所以g(x)min =g(-ln 2)=ln 2-1<0. ①当x ∈(-∞,-ln 2)时,因为g(-2)=4e 2>0,g(-1)=2e -1<0,所以g(x)在(-∞,-ln 2)上有唯一零点x 0∈(-2,-1). 又m =-(e x 0-x 0-1)e x 0=14x 0(x 0+2),所以m ∈⎝⎛⎭⎫-14,0. ②当x ∈(-ln 2,+∞)时,因为g(0)=0,所以g(x)在(-ln 2,+∞)上有唯一零点0,所以m =0.综上所述,m ∈⎝⎛⎦⎤-14,0.。
江苏省苏州市2019届高三上学期期中学考试试数学
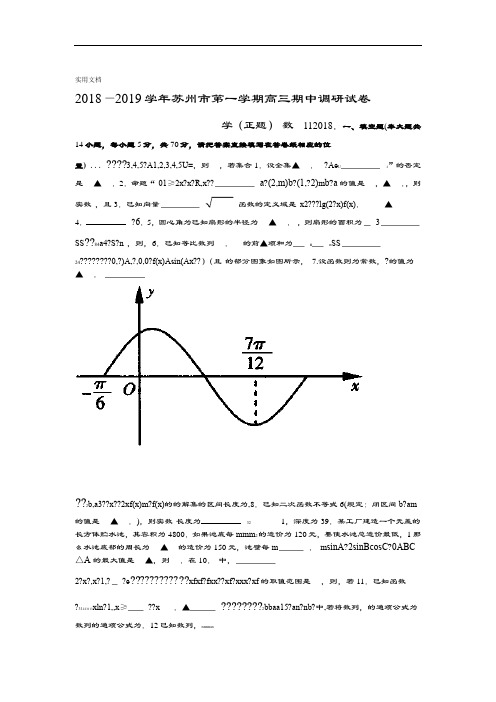
实用文档2018—2019学年苏州市第一学期高三期中调研试卷学(正题)数112018.一、填空题(本大题共14小题,每小题5分,共70分,请把答案直接填写在答卷纸相应的位置) ...????3,4,5?A1,2,3,4,5U=,则,若集合1.设全集▲.?Ae U2”的否定是▲.2.命题“01≥2x?x?R,x??a?(2,m)b?(1,?2)m b?a的值是,▲.,则实数,且3.已知向量函数的定义域是x2???lg(2?x)f(x).▲4.?6.5,圆心角为已知扇形的半径为▲.,则扇形的面积为3 SS??84a4?S?n,则,6.已知等比数列.的前▲项和为n n SS 24????????0,?)A,?,0,0?f(x)Asin(Ax??)(且的部分图象如图所示,7.设函数则为常数,?的值为▲.??2b,a3??x??2xf(x)m?f(x)的的解集的区间长度为,8.已知二次函数不等式6(规定:闭区间b?am 的值是▲.),则实数长度为321,深度为39.某工厂建造一个无盖的长方体贮水池,其容积为4800.如果池底每mmm2的造价为120元,要使水池总造价最低,1那么水池底部的周长为▲的造价为150元,池壁每m.m sinA?2sinBcosC?0ABC △A的最大值是▲,则.在10.中,2?x?,x?1,??e????????????xfxf?fxx??xf?xxx?xf的取值范围是,则,若11.已知函数?31223113xln?1,,x≥??x.▲????????2bbaa15?an?nb?中,若将数列,的通项公式为数列的通项公式为.12已知数列,nnnn n n实用文档??cc.▲,则相同的项按从小到大的顺序排列后看作数列的值为n63?2CB?CD ABCD?BCAD?CD60BCD??AB?若点,中,,. 13.如图,在平面四边形,ruuuuuuur C BCM上的动点,则的最小值为▲.为边DM?AM MBDAa x1,2)?(a?(x)?exf.在14的取值范围是▲.函数上单调递增,则实数分,请在答题卷区域内作答,解答时应写出文字说明、证明90本大题共6个小题,共二、解答题() 过程或演算步骤)分(本题满分1415.????),cos3,2sin2n)?m?(2cos2(sin?,.已知????)f(?m?f(n)?][0,?在,求,且(1)若上的取值范围;26???)tantan(????nm//y?、轴上,求,且的终边不在的值.2()若)分(本题满分1416.????a5?ab nn36?ABA,且的前项和为,已知等差数列.数列项和为的前,??}a{b和的通项公式;)求数列(1nn??c nb?ca?S项和)设(2.,求数列的前6nn3nn1?bB?2.nnnnnnn实用文档17 .(本题满分14分)某湿地公园围了一个半圆形荷花塘如图所示,为了提升荷花池的观赏性,现计划在池塘的中轴AB?2CDBDDDO,CADOC km与点,,段建设架空木栈道,不重合),其中已知线,上设计一个观景台(点y km.设建设的架空木栈道的总长为??y?(rad)?DAO?的取值范围;(1)设,将的函数关系式,并写出表示成(2)试确定观景台的位置,使三段木栈道的总长度最短.18.(本题满分16分)a x?ex)?f(已知是奇函数.x e)求实数的值;(1a2x?2x?f(x2y?e??e)x?[0,??)上的值域;在)求函数(232)?3x0gg(x?1)?(1?x2)(?xg()fx?的解集.(,求不等式3)令实用文档19.(本题满分16分)*Nn?,数列满足的首项为1,定义:若对任意的,则称数列已知数列}{a{a?3a}}a?a{nnn?1nn M数列”.为“??2*M n?S2n2?的,项和满足“求数列数列”,其前为(1)已知等差数列N n?n}{aa{}S n nnn d的取值范围;公差3M数列”,记数列满足为“2)已知公比为正整数的等比数列,且数列不(a?b}{{}b}b{a nn nnn4M数列,求数列的通项公式.为“}a{n20.(本题满分16分)a xln1?x)?ax?f(为常数.,设函数a?2(1,f(1)))f(x处的切线方程;时,求1)当在点(f(x)的两个零点,为函数(2)若.xx?x,x2121a的取值范围;①求实数2的大小关系,并说明理由.与②比较x?x21a实用文档学年第一学期高三期中调研试卷—20192018数学(附加) 2018.11注意事项:1.本试卷共2页.满分40分,考试时间30分钟.2.请在答题卡上的指定位置作答,在本试卷上作答无效.3.答题前,请务必将自己的姓名、学校、考试证号填写在答题卡的规定位置.21.【选做题】本题包括A、B、C、D四小题,请选定其中两题,在答题卡上填涂选作标志,并在相......................应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演.........算步骤.A.(本题满分10分)ADABCEACBCDDAABC的外接圆于点,的外角∠延长的平分线,交已知交△是△的延长线于点FFBFC.,连结,FB?FC;)求证:(1?ADABCAB6?BC的长.外接圆的直径,,(2)若,求是△120??EAC10分)B.(本题满分b?22a????1?1?A?AA已知可逆矩阵的特征值.=的逆矩阵为,求????a?773????C 10分).(本题满分?,2?2cosx???xxOyOC为极点,(的参数方程为以点为参数)在平面直角坐标系,中,圆??2siny??轴的正半轴为极轴建立极坐标系.C的极坐标方程;1()求圆OACAO交于点的中点所在曲线的极坐标方程.(2)过极点作直线与圆,求D分).(本题满分10 axx14???)x?3xg6(x)(fa)?x?xf()g(的取,若存在实数,已知函数使成立,求实数实用文档值范围.分).(本题满分10222?2ABPA?3?BC?ABP?ABCDBC?BCAD//BCAD,,,中,如图,在四棱锥⊥,,PB3?PB.A??CDP (1)求二面角的余弦值;BEPAE PCD//BE (2)若点平面在棱的长.上,且,求线段PECBDA10分)23.(本题满分xcos*的导数,.已知函数是,设Nn?0)x)(x??(f)(fx)(fx01nn?xπππ求的值;(1) )f(?2f()212222πππ*N n? (2) 证明:对于任意都成立.,等式??fnf())(n1n?4442实用文档实用文档实用文档实用文档实用文档实用文档实用文档实用文档。
江苏省苏州市2019届高三上学期期中调研测试数学试卷 PDF版缺答案

AB=2km,设 建设 的架 空 木栈 道 的总 长 为 ykm。 (1)设 ZDA0=ε (rad〉 ,将 y表 示 成 ε的 函数关 系式 ,并 写 出 ε的取 值 范 围
(2)试 确 定 观景 台的位 置 ,使 三段 木 栈 道 的总长 度 最短
.
;
18.(本 题 满分 16分 )
已 知
r(=)=召
'|=一
口 |在 (-1,2)上 单 调 递增 ,则 实数 四的取值 范 围是
▲
^
。
D
=(2∞
s2α
十
3,2sin2α
),"〓
(⒍
叩
,∞
昭
)・
(D若 (2)若
卩=詈
,且 r(α )=″
・ ″ ,求
∫ (α )在
EO,号 ]上 的
上
取 值 范 围
;
″ ∥ 】 ,且 α+`,α 的 终 边 不 在
y轴
,求 tan(α 十 ρ tam的
nB∞
旦
m。
,“ nA+2⒍
ABC中
sC=0,则
A的
最
大
值
是
▲
=十
,J(1,
若 只 伍
11.已 知 函数
r(J)=
▲
召
)=∫
(=2)=r(=3)(助
<奶
(奶
),则
ln¢
品
=l∫
(奶 )的
取
,∞ ≥
1,
值 范 围是
高 三 数学 (正 题
)
第 1页
共 4页
12.已 知 数 列 (四 ″ )的 通 项 公 式 为 色
苏州市2019~2020学年第一学期高三期初调研试卷高三数学(I卷)

2019~2020学年第一学期高三期初调研试卷数学Ⅰ 2019. 9(参考公式:样本数据1x ,2x ,,n x 的方差2211()==−∑ni i s x x n ,其中11==∑ni i x x n .)一、填空题:本大题共14小题,每小题5分,共计70分.不需要写出解答过程,请把答案直接填在答题卡相应位置上......... 1.已知集合{}1,3A =,{}3,9B =,则A B = ▲ .2.如果复数2()3bib R i−∈+的实部与虚部互为相反数,则b 等于 ▲ . 3.下表是某同学五次数学附加题测试的得分情况,则这五次测试得分的方差为 ▲ .4.已知4瓶饮料中有且仅有2瓶是果汁类饮料,从这4瓶饮料中随机取2瓶,则所取2瓶中至少有一瓶是果汁类饮料的概率为 ▲ .5.根据如图所示的伪代码,当输入的a ,b 分别为2,3时, 最后输出的b 的值为 ▲ .6.在平面直角坐标系xOy 中,已知双曲线()222210,0y x a b a b−=>>的两条渐近线方程为2y x =±, 则该双曲线的离心率为 ▲.注 意 事 项考生在答题前请认真阅读本注意事项及各题答题要求1. 本试卷共4页,包含填空题(第1题 − 第14题)、解答题(第15题 − 第20题).本卷满分160分,考试时间为120分钟.考试结束后,请将答题卡交回.2. 答题前,请您务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在答题卡的规定位置.3. 请在答题卡上按照顺序在对应的答题区域内作答,在其他位置作答一律无效.作答必须用0.5毫米黑色墨水的签字笔.请注意字体工整,笔迹清楚.4. 如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.5. 请保持答题卡卡面清洁,不要折叠、破损.一律不准使用胶带纸、修正液、可擦洗的圆珠笔.7.如图,在直三棱柱ABC A B C −111中,若四边形11AAC C 是边长 为4的正方形,且3AB =,5BC =,M 是1AA 的中点,则三 棱锥A MBC −11的体积为 ▲ .8.已知等差数列{}n a 的前n 项和为n S ,若1530S =,71a =,则S 10的值为 ▲ .9.已知()y f x =是定义在R 上的偶函数,当[),x ∈+∞0时,()[)()[)sin ,,,,,,x x f x f x x ⎧∈⎪=⎨−∈+∞⎪⎩0111则(5)6f π−−= ▲ .10.已知在ABC ∆中,AC =1,BC =3.若O 是该三角形内的一点,满足()()0OA OB CA CB +⋅−=,则CO AB ⋅= ▲ .11.已知sin 222cos2αα−=,则2sin sin 2αα+= ▲ .12.已知点A 、B 是圆O :224x y +=上任意两点,且满足23AB =P 是圆C :22(4)(3)4x y +++=上任意一点,则PA PB +的取值范围是 ▲ .13.设实数1a ≥,若不等式||2x x a a −+≥,对任意的实数[1,3]x ∈恒成立,则满足条件的实数a的取值范围是 ▲ . 14.在ABC ∆中,若tan tan 3tan tan A A B C+=,则sin A 的最大值为 ▲ .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(本小题满分14分) 如图,在直三棱柱ABC —A 1B 1C 1中,AB =BC ,点P 是棱AC 的中点.(1)求证:AB 1∥平面PBC 1; (2)求证:平面PBC 1⊥平面AA 1C 1C .▲ ▲ ▲ACB PA 1B 1C 116.(本小题满分14分) 已知函数7()sin()sin()412f x x x ππ=+++.(1)求函数()y f x =的最小正周期和单调递增区间;(2)当[0,]x π∈时,求函数()y f x =的最大值,并写出取得最大值时自变量x 的值.▲ ▲ ▲17.(本小题满分14分) 已知椭圆()2222:10y x C a b a b+=>>的四个顶点恰好是一边长为2,一内角 为60o 的菱形的四个顶点. (1)求椭圆C 的方程;(2)若直线y kx =交椭圆C 于A 、B 两点,在直线:30l x y +−=上存在点P ,使得PAB ∆为等边三角形,求实数k 的值.▲ ▲ ▲18.(本小题满分16分) 某地举行水上运动会,如图,岸边有A ,B 两点,30BAC ∠=.小船从A 点以v 千米/小时的速度沿AC 方向匀速直线行驶,同一时刻运动员出发,经过t 小时与小船相遇.(水流速度忽略不计)(1)若4v =,2AB km =,运动员从B 处出发游泳匀速直线追赶,为保证在1小时内(含1小时)能与小船相遇,试求运动员游泳速度的最小值;(2)若运动员先从A 处沿射线AB 方向在岸边跑步匀速行进m (0)m t <<小时后,再游泳匀速直线追赶小船.已知运动员在岸边跑步的速度为4千米/小时,在水中游泳的速度为2千米/小时,试求小船在能与运动员相遇的条件下v 的最大值.▲ ▲ ▲ABC岸边30o19.(本小题满分16分) 已知函数()e x f x =,()ln g x x =,(1)设2()()h x g x x =−,求函数()h x 的单调增区间;(2)设01x >,求证:存在唯一的0x ,使得函数y =()g x 的图象在点A (00,()x g x )处的切线l 与函数()y f x =的图象也相切;(3)求证:对任意给定的正数a ,总存在正数x ,使得不等式()1|1|f x a x−−<成立. ▲ ▲ ▲20.(本小题满分16分) 等差数列{}n a 的前n 项和为S n ,数列{}n b 满足:b 1=5a 1=5,a 5=b 2=9,当3n ≥ 时,1n n S b +>,且n S ,1n n S b +−,2n S −成等比数列,n *∈N . (1)求数列{}n a ,{}n b 的通项公式;(2)求证:数列{}n b 中的项都在数列{}n a 中;(3)将数列{}n a 、11{}+n n b b 的项按照:当n 为奇数时,a n 放在前面;当n 为偶数时,11+n n b b 放在前面进行“交叉排列”,得到一个新的数列:1a ,121b b ,231b b ,2a ,3a ,341b b ,451b b ,…记这个新数列的前n 和为T n ,试求T n 的表达式.▲ ▲ ▲。
2019届江苏省苏州市高三上学期期初调研考试数学(文)试题(word版)

EDCBA2019届江苏省苏州市高三上学期期初调研考试数学(文)试题(正卷)2018.9注 意 事 项考生在答题前请认真阅读本注意事项及各题答题要求 1.本试卷共4页,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部分.本试卷满分160分,考试时间120分钟. 2.答题前,请您务必将自己的姓名、考试号用0.5毫米黑色墨水的签字笔填写在答题卡的指定位置. 3.答题时,必须用0.5毫米黑色墨水的签字笔填写在答题卡的指定位置,在其它位置作答一律无效. 4.如有作图需要,可用2B 铅笔作答,并请加黑加粗,描写清楚.5. 请保持答题卡卡面清洁,不要折叠、破损.一律不准使用胶带纸、修正液、可擦洗的圆珠笔. 方差公式:2222121[()()()]n s x x x x x x n =-+-++-,其中121()n x x x x n=+++.锥体体积公式:1=3V Sh 锥体(S 为锥体底面面积,h 为锥体的高).一、填空题:本大题共14小题,每小题5分,共70分.不需要写出解答过程,请把答案直接填在答题卡相应位置上......... 1.已知集合{1,0,1}A =-,集合{|0}B x x =>,则AB = ▲ .2.若复数12i z =+,22i z a =-(i 为虚数单位),且12z z 为实数,则实数a = ▲ .3.一组数据1,2,3,4,a 的平均数为2,则该组数据的方差等于 ▲ . 4.如图是某一算法的伪代码,则输出值n 等于 ▲ .5.一只口袋中装有5个大小相同的球,其中3个黑球,2个白球,从中一次 摸出2只球,则摸出1个黑球和1个白球的概率等于 ▲ .6.已知函数222(0)()(0)x x x f x x ax x ⎧-⎪=⎨-+<⎪⎩≥为奇函数,则实数a 的值等于 ▲ .7.已知函数()sin(2)f x x ϕ=+(0ϕπ<≤)的一条对称轴是512x π=-,则ϕ= ▲ .8.已知等比数列{}n a 的前 项和为n S ,若264,,S S S 成等差数列,则246a a a +的值为 ▲ .9.已知△ABC 的三边上高的长度分别为2,3,4,则△ABC 最大内角的余弦值等于 ▲ . 101(cm)的圆形纸片按如图所示的实线裁剪,并按虚线折叠为各棱长均相等的四棱锥,则折叠所成的四棱锥的体积为 ▲ cm 3.11.如图,已知AC 与BD 交于点E ,AB ∥CD ,AC =26AB CD ==,则当tan 3A =时,BE CD ⋅= ▲ .(第4题)(第11题)12.已知函数f (x )=|x 2-6|,若0a b >>,且f (a )=f (b ),则a 2b 的最大值是 ▲ . 13.在斜三角形ABC 中,已知11tan 0tan tan C A B++=,则tan C 的最大值等于 ▲ . 14.已知⊙C 的方程为:222(3)(2)(0)x y r r -+-=>,若直线33x y +=上存在一点P ,在⊙C 总存在不同的两点M ,N ,使得点M 是线段PN 的中点,则⊙C 的半径r 的取值范围是 ▲ .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答,解答时应写出必要的文字说明、证明过程或演算步骤. 15.(本题满分14分)已知πcos (0,)2αα=∈. (1)求πsin()4α+的值;(2)若()11πcos ,(0,)142αββ+=∈,求β的值.16.(本题满分14分)如图,已知矩形CDEF 和直角梯形ABCD ,AB ∥CD ,90ADC ∠=︒,DE =DA , M 为AE 的中点.(1)求证:AC ∥平面DMF ; (2)求证:BE ⊥DM .MFE DCBA (第16题)17.(本题满分14分)如图,有一块半圆形的空地,政府计划在空地上建一个矩形的市民活动广场ABCD 及矩形的停车场EFGH ,剩余的地方进行绿化.其中半圆的圆心为O ,半径为r ,矩形的一边AB 在直径上,点C ,D ,G ,H 在圆周上,E ,F 在边CD 上,且∠BOG =60︒,设BOC θ∠=.(1)记市民活动广场及停车场的占地总面积为()f θ,求()f θ的表达式; (2)当cos θ为何值时,可使市民活动广场及停车场的占地总面积最大.18.(本题满分16分)已知椭圆C :22221(0)x y a b a b +=>>的左、右顶点分别为A ,B ,离心率为12,点P (1,32)为椭圆上一点.(1)求椭圆C 的标准方程;(2)如图,过点(0,1)C 且斜率大于1的直线l 与椭圆交于M ,N 两点,记直线AM 的斜率为1k ,直线BN 的斜率为2k ,若122k k =,求直线l 斜率的值.FEGH C DOBA(第17题)19.(本小题满分16分)已知数列{}n a 的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列,数列{}n a 前n 项和为n S ,且满足34S a =,523a a a =+.(1)求数列{}n a 的通项公式;(2)若12m m m a a a ++=,求正整数m 的值; (3)是否存在正整数m ,使得221mm S S -恰好为数列{}n a 中的一项?若存在,求出所有满足条件的m 值,若不存在,说明理由.20.(本小题满分16分)若对任意的实数k ,b ,函数()y f x kx b =++与直线y kx b =+总相切,则称函数()f x 为“恒切函数”.(1)判断函数2()f x x =是否为“恒切函数”;(2)若函数()ln f x m x nx =+(0m ≠)是“恒切函数”,求实数m ,n 满足的关系式; (3)若函数()(e 1)e x x f x x m =--+是“恒切函数”,求证:104m -<≤.2018~2019学年第一学期期初教学质量调研卷 高三数学(正卷)参考解答与评分标准一、填空题:(每题5分,满分70分) 1.{1}2.43.24.45.356.−2 7.3π 8.2 9.1124-1011.1212.1613.-14.)+∞ 二、解答题(共6小题,满分90分) 15.(本题满分14分) 解:(1)由πcos (0,)2αα=∈,得1sin 7α=,············································· 2分 所以πππsin()sin cos cos sin 444ααα+=+ ·············································· 4分17=+=. ································ 6分 (2)因为π,(0,)2αβ∈,所以(0,π)αβ+∈.又()11cos 14αβ+=,则()sin αβ+== 8分所以()()()sin sin sin cos cos sin βαβααβααβα=+-=+-+ ·············· 10分11111472=-⨯=. ············································· 12分 因为π(0,)2β∈,所以π6β=. ······················································ 14分16.(本题满分14分)证明:(1)连接EC 交DE 于N ,连接MN .∵矩形CDEF ,∴EC ,DF 相互平分,∴N 为EC 中点. ·· 2分 又∵M 为EA 中点,∴MN ∥AC . ··································· 4分 又∵AC ⊄平面DMF ,且MN ⊂平面DMF .∴AC ∥平面DMF . ·················································· 7分 (2)∵矩形CDEF ,∴CD ⊥DE .又∵AB ∥CD ,∴AB ⊥DE . ·························································· 8分 又∵直角梯形ABCD ,AB ∥CD 且90ADC ∠=︒,∴AB ⊥AD . ∵DEAD =D ,∴AB ⊥平面ADE . ··············································· 10分又∵DM ⊂平面ADE ,∴AB ⊥DM .∵AD DE =,M 为AE 的中点,∴AE ⊥DM . ·································· 11分 又∵AB AE A =,∴MD ⊥平面A BE . ·········································· 13分∵BE ⊂平面ABE ,∴BE ⊥MD . ··················································· 14分 17.(本题满分14分)解:(1)∵半圆的半径为r ,BOC θ∠=,∠OBC =90°.∴在直角三角形OBC 中,cos OB r θ=,sin BC r θ=,∴2cos AB r θ=.∴22sin cos ABCD S AB BC r θθ=⋅=矩形. ················································ 2分 又∵∠BOG =60︒,由半圆的对称性可知,∠HOA =60︒,∴∠HOG =60︒. ∴△HOG 为等边三角形,∴HG =r ,HEsin r θ-=sin )r θ.∴2sin )EFGH S EF EH r θ=⋅=-矩形. ·············································· 4分 ∴()ABCD EFGH f S S θ=+=矩形矩形2(2sin cos sin r θθθ-+,其中(0,)3πθ∈. ································································································· 7分(2) ∵222()(2cos 2sin cos )f r θθθθ'=--=22(4cos cos 2)r θθ--. ··········· 9分 令()0f θ'=,即24cos cos 20θθ--=,解得:cos θ=cos θ=(舍去). ·································· 11分令0cos θ=0(0,)3πθ∈. 1︒当0(0,)θθ∈时,()0f θ'>,()f θ单调递增;2︒当0(,)3πθθ∈时,()0f θ'<,()f θ单调递减.∴当0θθ=时,()f θ取得最大值. ···················································· 13分答:当cos θ= · 14分18.(本题满分16分)解:(1)∵椭圆的离心率为12,∴2a c =.又∵222a b c =+,∴b =.∴椭圆的标准方程为:2222143x y c c+=. ··············· 3分ABODC H GEF又∵点P (1,32)为椭圆上一点,∴22914143c c +=,解得:1c =. ··············· 5分∴椭圆的标准方程为:22143x y +=. ················································· 6分 (2)由椭圆的对称性可知直线l 的斜率一定存在,设其方程为1y kx =+. 设1122(,),(,)M x y N x y .联列方程组:221431x y y kx ⎧+=⎪⎨⎪=+⎩,消去y 可得:22(34)880k x kx ++-=. ∴由韦达定理可知:122834k x x k +=-+,122834x x k =-+. ····················· 8分 ∵1112y k x =+,2212yk x =-,且122k k =,∴1212222y y x x =+-. ·················· 10分即221222124(2)(2)y y x x =+-.①又∵1122(,),(,)M x y N x y 在椭圆上, ∴22113(4)4y x =-,22223(4)4y x =-.②将②代入①可得:121224(2)22x x x x -+=+-,即1212310()120x x x x +++=. ······· 12分 ∴22883()10()1203434k k k-+-+=++,即2122030k k -+=. ················· 14分 解得:16k =或32k =.又∵k >1,∴32k =. ······································ 16分 19.(本小题满分16分)解:(1)设奇数项的等差数列公差为d ,偶数项的等比数列公比为q . ∴数列{}n a 的前5项依次为:1,2,1+d ,2q ,1+2d .∵34523S a a a a =⎧⎨=+⎩,∴42123d q d d +=⎧⎨+=+⎩,解得:23d q =⎧⎨=⎩. ···························· 2分∴12()23()nn n n a n -⎧⎪=⎨⎪⋅⎩为奇数为偶数. ······························································ 4分 (2) ∵12m m m a a a ++=.1︒若2m k =(N*k ∈)则22122k k k a a a ++=,∴123(21)23k k k -⋅⨯+=⋅,即213k +=,∴1k =,即2m =. ································································································· 6分2︒若21m k =-(N*k ∈)则21221k k k a a a -+=,∴1(21)2321k k k --⨯⋅=+,∴12122312121k k k k -+⋅==+--. ∵123k -⋅为整数,∴221k -必为整数,∴211k -=,∴1k =,此时0233⋅≠. 不合题意. ················································································· 8分 综上可知:m =2. ········································································ 9分 (3)∵21321242()()m m m S a a a a a a -=++⋅⋅⋅++++⋅⋅⋅+=(121)2m m +-+2(13)13m --=231m m +-. ································· 10分21122122312331m m m m m m S S a m m ---=-=+--⋅=+-. ··························· 11分∴221m m S S -=2123131m m m m -+-+-=2122(1)3331m m m ---+-≤. ······································ 12分 若221mm S S -为数列{}n a 中的项,则只能为123,,a a a . 1︒2211m m S S -=,则2122(1)3131m m m ---=+-,∴130m -=,m 无解. ··················· 13分 2︒2212m m S S -=,则2122(1)3231m m m ---=+-,∴12310m m -+-=. 当1m =时,等式不成立; 当2m =时,等式成立;当3m ≥时,令1221()31313x x f x x x -=+-=⋅+-.∴ln3()323xf x x '=⋅-,2ln 3()323x f x ''=⋅-. 当3x ≥时,()0f x ''>,∴()f x '在[3,)+∞上单调递增. 又∵(3)9ln 360f '=->,∴()0f x '>在[3,)+∞上恒成立, ∴()f x 在[3,)+∞上单调递增.∵(3)10f =>,∴当3m ≥时,方程12310m m -+-=无解. ···················· 14分3︒2213m m S S -=,则2122(1)3331m m m ---=+-,∴210m -=,即1m =. ·············· 15分 综上可知:1m =或2m =. ···························································· 16分 20.(本小题满分16分)解:(1)函数()f x 为“恒切函数”,设切点为00(,)x y .则0000()()f x kx b kx b f x k k ++=+⎧⎨'+=⎩,∴00()0()0f x f x =⎧⎨'=⎩. ······································· 2分对于函数2()f x x =,()2f x x '=.设切点为00(,)x y ,∴20020x x ⎧=⎪⎨=⎪⎩, ······················································· 3分解得:00x =.∴2()f x x =是“恒切函数”. ······································· 4分 (2)若函数()ln f x m x nx =+(0m ≠)是“恒切函数”,设切点为00(,)x y .∵()mf x n x '=+,∴000ln 00m x nx m n x +=⎧⎪⎨+=⎪⎩, ·············································· 5分解得:0ln 1x =,即0x e =. ···························································· 7分 ∴实数m ,n 满足的关系式为:0m ne +=. ······································· 8分 (3) 函数()(1)x x f x e x e m =--+是“恒切函数”,设切点为00(,)x y . ∵()(22)xxf x e x e '=--,∴000000(1)0(22)0x x x x e x e m e x e ⎧--+=⎪⎨--=⎪⎩, ∴0000(1)22x x x m e x e e x ⎧=---⎪⎨=+⎪⎩. ······························································· 10分考查方程22x e x =+的解,设()22x g x e x =--. ∵()21x g x e '=-,令()0g x '=,解得:ln 2x =-. ∴当(,ln 2)x ∈-∞-时,()0g x '<,()g x 单调递减; 当(ln 2,)x ∈-+∞时,()0g x '>,()g x 单调递增.∴min ()(ln 2)ln 210g x g =-=-<. ··················································· 12分1︒当(,ln 2)x ∈-∞-时∵24(2)0g e -=>,2(1)10g e-=-<. ∴()22x g x e x =--在(,ln 2)-∞-上有唯一零点0(2,1)x ∈--.又∵00(1)x x m e x e =---=001(2)4x x +,∴1(,0)4m ∈-. ························ 14分2︒当(ln 2,)x ∈-+∞时∵(0)0g =,∴()22x g x e x =--在(ln 2,)-+∞上有唯一零点0,∴0m =.································································································15分综上可知:14m-<≤.································································16分。
江苏省苏州市2019届高三期期调研数学试卷

End While
5.一只口袋中装有 5 个大小相同的球,其中 3 个黑球, 2 个白球,从中一次
Print n
摸出 2 只球,则摸出 1 个黑球和 1 个白球的概率等于 ▲ .
6.已知函数 f (x)
2
x
2x
( x≥0)
为奇函数,则实数 a 的值等于
2
x ax ( x 0)
▲ M ,N,使得点 M 是线段 PN 的中点,则⊙ C 的半径 r 的取值范 围是 ▲ .
二、解答题:本大题共 6 小题,共计 90 分.请在答.题.卡.指.定.区.域. 内作答,解答时应写出必 要的文字说明、证明过程或演算步骤.
15.(本题满分 14 分)
已知 cos
4 3, 7
(第 11 题 )
12.已知函数 f (x)= |x2- 6|,若 a b 0 ,且 f (a)= f (b),则 a2b 的最大值是
▲ .
13.在斜三角形 ABC 中,已知 1
1 tanC 0 ,则 tanC 的最大值等于
tan A tanB
▲ .
14.已知⊙ C 的方程为: ( x 3)2 ( y 2)2 r 2 (r 0) ,若直线 3x y 3 上存在一点 P,在
2018~2019 学年第一学期期初教学质量调研卷
高三数学(正卷)
2018. 9
注意事项
考生在答题前请认真阅读本注意事项及各题答题要求
1.本试卷共 4 页,包括填空题 (第 1 题~第 14 题)、解答题(第 15 题~第 20 题)两部分. 本 试卷满分 160 分,考试时间 120 分钟.
2.答题前,请您务必将自己的姓名、考试号用 指定位置.
0.5 毫米黑色墨水的签字笔填写在答题卡的
