04动态电路分析-(1)
动态电路分析方法

第四章动态电路分析方法 (66)4.1 一阶电路的分析 (66)4.1.1 一阶电路的零输入响应 (66)4.1.2 一阶电路的零状态响应 (70)4.1.3 一阶电路的完全响应 (74)4.2 二阶电路的分析 (79)4.2.1 LC电路中的自由振荡 (79)4.2.2 二阶电路的零输入响应描述 (81)4.2.3 二阶电路的零输入响应—非振荡情况 (83)4.2.4 二阶电路的零输入响应—振荡情况 (86)习题 (89)第四章动态电路分析方法前面介绍了线性电阻电路的分析方法。
由于电阻元件的伏安特性为代数关系,所以在分析电阻电路时,只需求解一组代数方程,如网孔分析法、节点分析法等。
但在本章所讨论的电路中,除了含有电源和电阻以外,还将含有电容和电感元件。
电容和电感元件的伏安特性为微分或积分关系,故称为动态元件(dynamic element)(参见1.4.3)。
包含动态元件的电路叫做动态电路。
动态电路在任一时刻的响应与激励的全部过去历史有关,这是和电阻性电路完全不同的。
例如,一个动态电路,尽管输入已不再作用了,但仍然可以有输出,因为输入曾经作用过。
因此,动态电路是具有“记忆”(memory)的特点,这完全是由动态元件的性能所决定的。
4.1 一阶电路的分析不论是电阻性电路还是动态电路,各支路电流与各支路电压都受到基尔霍夫定律的约束,只是在动态电路中,来自元件性质的约束,除了电阻元件的欧姆定律,还有电容、电感的电压、电流关系,这些关系已在1.4.3中讨论过,需要微分(或积分)的形式来表示。
因此,线性动态电路不能用线性代数方程,而需用线性微分方程来描述。
用解析方法求解动态电路的问题就是求解微分方程的问题。
在实际工作中经常遇到只包含一个动态元件的线性电路,这种电路是用线性常系数一阶常微分方程来描述的,故称一阶电路或一阶网络(first order network)。
本节讨论这类网络的解法。
以电容元件为例,这类网络可以用图4-1(a)来概括,图中所示的方框部分只有电阻和电源组成电路,可以用戴维南等效电路或诺顿等效电路来代替。
初中物理故障及动态电路分析答案(1)

一、初中物理故障电路分析1、电压表示数为零的情况a 电压表测量的用电器发生短路一灯亮一灯不亮,电流表有示数;b 干路用电器发生断路两灯都不亮,电流表无示数;C 电压表故障或与电压表连线发生断路两灯都亮,电流表有示数2 电压表示数等于电源电压的情况A 电压表测量的用电器发生断路两灯都不亮,电流表无示数B 干路用电器发生短路一灯亮一灯不亮,电流表有示数3 用电压表判断电路故障电压表有示数说明:和电压表接线柱连接的两根线路完好无损电源电压为6V,用电压表测得:Uab=0;Ued=6v;Ucd=0;Uac=6v,灯泡不亮,哪里出现故障?解题思路:先找有示数的,Ued=6v说明从e点到电源正极线路完好,从d点到电源负极线路完好;Uac=6v 说明从a点到电源正极线路完好,从c点到电源负极线路完好,这样将故障锁定在ac之间了,由Uab=0,说明bc之间出现故障,故电阻出现断路。
4 电流表有示数说明和电流表串联的电路是通路;电流表没有示数则有两种情况:1断路 2 电路中电流太小,不足以使电流表指针发生偏转(例如:电压表与电流表串联,见上面2A)1、如图1是测定小灯泡两端的电压和通过小灯泡的电流的电路图。
如果某同学在操作的过程中对两只电表的量程选择是正确的,但不慎将两电表的位置对调了,则闭合开关S后A、电流表、电压表均损坏;B、电流表损坏,电压表示数为零;()C、电流表有示数,电压表示数为零;D、电流表示数为零,电压表有示数。
2、如图2所示,下列说法正确的是()A、电流表的连接是正确的;B、电压表的连接是正确的;C、两表的连接都是错误的;D、电流表将会被烧坏。
3、如图3所示,两只电灯L1和L2并联在电路中,当S1和S2都闭合时,电路中可能出现A、电流表被烧坏;B、电压表被烧坏;()C、两只灯会被烧坏;D、两只灯都能发光。
4、如图4所示,当开关闭合后两灯均不亮,电流表无示数,电压表示数等于电源电压,则电路发生的故障是()A、电源接线接触不良;B、电流表损坏,断路,其他元件完好;C、灯L1发生灯丝烧断;D、灯L2发生短路,其他元件完好。
04动态电路分析 (1)

04动态电路分析 (1)动态电路分析一、是非题1.对于零状态电路,过渡过程的起始瞬间,电容相当于短路,电感相当于开路(不计冲激作用)。
2.换路定律仅用来确定u c(0+)和i L(0+),其他电量的初始值应根据u c(0+)或i L(0+)按欧姆定律及基尔霍夫定律确定。
3.同一个一阶电路的零输入响应、零状态响应和全响应具有相同的时间常数。
4.用短路开关把载流线圈短接,则线圈电阻越大,线圈电流衰减时间越长。
5.全响应中,零状态响应由外加激励引起的,所以零状态响应就是稳态响应。
6.电路的零输入响应就是自由分量,零状态响应就是强制分量。
7.R大于、等于或小于是判断RLC串联电路零输入响应处于非振荡放电、临界放电和振荡放电状态的判别式。
8.电感元件是用电压电流特性来定义的元件。
9.如电感元件的电流不变,无论其电感值为多大,都可等效为短路;如电容元件的电压不变,无论其电容值为多大,都可等效为开路。
10.一个在t=0-时电压为零且电压不跃变的电容在换路时相当于短路;一个在t=0-时电流为零且电流不跃变的电感在换路时相当于开路。
11.由R、L组成的一阶电路,若R越大,其零输入响应衰减得越慢。
12.零输入的RC电路中,只需时间常数τ不变,电容电压从100V放电到50V所需时间与从150V放电到100V所需时间相等。
13.在零输入响应的情况下,电路的时间常数τ是电流或电压由初始值衰减到该值的0.632倍所需的时间。
14.电压为100V的直流电压源,通过100kΩ电阻对10μF电容充电,经过1s,充电电流为0.368mA。
15.在零状态RL串联电路接入恒定电压,如果电源电压不变,增加电阻可以减少稳态电流及缩短过渡过程时间。
16.全响应中,暂态响应仅由元件初始储能产生,稳态响应则由外加激励产生。
17.设某电压可表示为u(t)=ε(t)-ε(t-3)V,则当t=3s时有u(3+)≠u(3-)。
18.RLC串联电路接通直流电压源瞬间,除u C和i L之外,其余元件的电压或电流均能跃变。
动态电路的分析

06
动态电路的应用实例
滤波器设计
滤波器类型
包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器等,用 于实现不同频率信号的通过或抑制。
滤波器设计原则
根据所需的频率特性,选择合适的滤波器类型和元件参数,以满足 信号处理的要求。
滤波器性能指标
包括通带范围、阻带范围、过渡带宽度和群延迟等,用于评估滤波 器的性能。
二阶RLC电路在输入信号作用下,其输出信号同样会产生振荡。通过调整电感L、 电容C和电阻R的值,可以改变振荡的频率和幅度。
高阶电路的响应
高阶电路的分析方法
高阶电路的响应特性通常需要采用数值分析方法进行求解,如拉普拉斯变换、有限元法等。
高阶电路的应用
高阶电路在通信、控制等领域有广泛应用,如滤波器、放处理,改善音质和音效。
电力电子
用于转换和控制系统中的电能 ,实现高效、可靠的电力供应
。
02
动态电路的基本原理
电容与电感
电容
存储电能的一种元件,其特性是电压 与电流的相位差为90度。
电感
存储磁场能量的元件,其特性是电流 与电压的相位差为90度。
电压与电流的瞬态过程
感谢您的观看
频域分析法是一种将时域问题转换为频域 问题进行分析的方法。
通过傅里叶变换将时域中的电压和电流转 换为频域中的复数形式,然后求解电路的 频率响应。
优点
缺点
能够得到电路的频率响应特性,适用于分 析谐波和滤波器等电路。
对于非线性电路和瞬态响应分析较为困难 。
复平面分析法
定义 步骤 优点 缺点
复平面分析法是一种利用复平面上的极点和零点分析电路的方 法。
动态电路的重要性
实际应用
动态电路广泛应用于电子、通信、控制 等领域,如振荡器、滤波器、放大器等 。
原创3:电路的动态分析
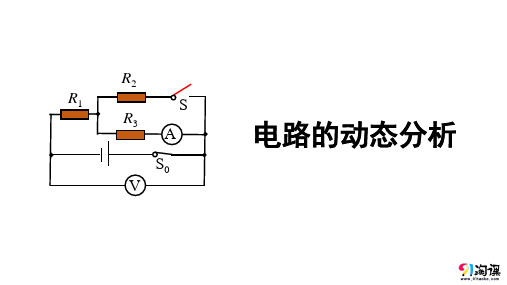
R1
S
R3 A
S0 V
电路的动态分析
1.什么是电路的动态分析问题? 由于断开或闭合开关、滑动变阻器滑片的滑动等造成电路结构发生了变 化,某处电路变化又引起其他电路一系列变化的问题.
L3
P
R L2
L1 S
灯泡亮度如何变化?
R2
R1
S
R3 A
S0 V
电表示数如何变化?
2.电路动态分析的方法 直流电路的动态分析方法: (1)程序法:基本思想是“部分→整体→部分”.思维流程如下:
解析:保持开关S闭合,把滑动变阻器R1的滑片向上滑动,电路中的 总电阻变小,电流变大,电流表A的示数变大,由U=IR3知电压表V 的示数变大,A正确;保持开关S闭合,滑动变阻器R1的滑片不滑动, 则电容器两极板间的电压不变,R2中没有电流通过,B错误;若保持 开关S闭合,拉开电容器两极板之间的距离,电容器的电容变小,两
1.电源负极接地,说明了什么?
审题 2.变阻器的滑片P由a向b移动,它的有效电阻如何变化?
析疑 外电路的总电阻如何变化?整个电路的总电流如何变化?
3.如何判断流过如何判断电压表、电流表示数?
解析:滑动头P自a端向b端滑动的过程中,滑动变阻器的电阻减小,电路
总电阻减小,由闭合电路的欧姆定律可得,干路电流增大,由UR1=IR1可 知R1两端电压即电压表的示数变大,选项A错误;由U=E-Ir可知路端电 压U减小;由UR2=U-UR1可得R2两端的电压减小,又由I2=URR22 可得流过R2
方法提炼
电路稳定时电容器的处理方法
电路稳定后,与电容器串联的电路中没有电流,同 支路的电阻相当于导线,即电阻不起降低电压的作 用,与电容器串联的电阻视为等势体,电容器两端 的电压为与之并联的电阻两端的电压。
第15讲 动态电路的分析(一)

一、关于动态电路的类型的概述在电路中,往往会利用开关来控制电路中电流的产生与终止,并通过滑动变阻器的变化来对电阻进行控制,进而改变电路中的电流以及相应的电压,这种电路一般被称为动态电路。
学生需要明确的是,在动态电路中有两个恒定的量:电压以电阻的值。
在以往的考题中,一类是确定定量后再进行计算,另一类则是分析动态电路中相应数值的变化。
二、关于动态电路题型的解题技巧分析1.化繁为简、化动为静。
画出简化的电路图是解答动态电路题型的基本步骤,通过将原本复综合、动态的电路图简化为一个简单明了的静态电路图,能够让学生更好地对其中的变化要素加以分析。
要做到这一步,首先需要把电流表的存在认为是“短路”。
其次,要把电压表的存在认为是“断路”。
最后,将题干中明确给出或者暗示给出的相关物理量应用到电路简图中,从而更好思考出解题思路。
2.合理应用相关的定律公式。
动态电路相关试题中主要涉及到三个定律,欧姆定律是最常用的,也是解答电学问题需要使用到的最基本的定律,其公式为:I=U/R。
除此之外,动态电路试题中还经常会用到电功计算公式和电功率计算公式。
3.熟悉基本的情况。
由于初中物理属于知识的入门阶段,因此知识点的考查不会太深。
在动态电路相关试题中主要有两种类型的试题,即“开关型”、“滑动变阻器”型试题这两种,学生往往掌握了这两种基本题型的解题思路之后,对于其变形题也能很快得出答案。
三、关于动态电路的题型分析在涉及到动态电路相关内容的考试中,考查的类型主要有以下两种:第一,利用开关的闭合来控制电路,即在电路中接入一个或者一个以上的电阻来改变其连接的方法,从而影响其中电流的流动方向。
例1:现有一个电路,在电源和电压都保持恒定的状态下,如果将开关S闭合之后,会出现以下哪种情况()A.电流表上所显示的值有所增加B.电压表上所显示的值有所增加C.整个电路中的电阻增加D.电路所消耗的功率下降解析:这是最基本、也是最简单的题型。
第一步是根据电路图来观察开关的闭合情况,可以看出,开关之前是断开的,而题干中所涉及到的情况时在闭合之后,因此开关是一个由闭到开的过程。
动态电路分析课件

温度为20℃时,热敏电阻对应的阻值为50Ω,
则总电阻为R总=50Ω+10Ω=60Ω.电源电压U 总=R总I1=60Ω×0.2A=12V
❖ 合作探究
2.环境温度根据什么来求?请写出解答过程
动 由题意可以知道,环境温度可以根据热敏电阻的阻 态 值来求。所以要先求出电流为0.4A时热敏电阻的阻
值,再根据图像得出环境温度。
0.6A).开关,定
值电阻R0(10Ω)、
导线若干。
❖ 合作探究
(1)当环境温度为20℃时.电流表的读数
动 为0.2A,求电源的电压。
态 电 路
(2)电流表的读数为0.4A时,当时环境 温度是多少?
分析: 1.这是什么电路,要求电源电压要知 道哪些条件?怎样得到这些已知条件?
分 析
这是串联电路,要求电源电压要知道对应温 度下的电流值和总电阻。由图像可以知道当
❖ 学习内容二
动
态
电 路
动态电路的计算
分
析
❖学习指导
动 态 电 回顾欧姆定律的公式以及其变形式 路 分 析
❖ 自学检测
1.欧姆定律的公式:I=____ 、 U=___ 、
动 R=_____。
态 电 路 分 析
2.串、并联电路中的电流、电阻、电压 之间的关系: 串联电路中的电流关系是:I=______ 电压关系是U总=________ 电阻之间的关系R总=________。 并联电路中的电流关系是:I总=_____
电 当I2=0.4A时,电路中的总电阻R总=U总/ I2 路 =12V/0.4A=30Ω
分 析
热敏电阻的阻值R=R总-R1=30Ω-10Ω =20Ω
由图像可知道此时环境温度为40℃。
初三物理动态电路专题(1)

初三物理动态电路专题知识精解一动态电路分析方法:(1)确定电路的联接方式:电压表相当于断开的电路,电流表相当于导线。
(2)确定各表测量对象:电压表只抱一个,电流表和谁串联。
(3)电阻的变化情况:变阻器滑片的移动以及断开(或闭合)电键,注意局部短路的情况。
(4)各表的变化情况:在并联中,电压表示数不变,测定值电阻的电流表示数不变;测滑动变阻器的电流表与电阻变化相反;测干路中的电流表与测滑动变阻器的电流表变化情况相同。
在串联电路中,电流表与电阻的变化相反,测定值电阻的电压表与电流表变化相同,测滑动变阻器的电压表与电阻变化相同.记忆方法:动态电路判断前,先看电路串并联,电流表来似导线,电压表来似断电;串联电阻在上升,电流示数减小中,定值电压也减小,滑动电压在上升;并联电阻在增大,电压示数不变化,滑动电流在减小,干路电流跟着跑,定值电流不变化,反向思考靠大家二.定量计算:1。
常考由滑动变阻器引起的电流表、电压表示数变化的范围;解答时采用极端值法---—即:找出滑动变阻器阻值最大和最小时电流表和电压表的示数,以确定电表范围.2。
多开关的不同状态引起的电路变化,主要表现为电路连接方式的改变,从而导致电表示数变化,这类题的解答关键在于用电器连接方式、电表测量范围的判断;通常会有两到三种状态:简单电路、串联或者并联,判断清楚后,每种状态相当于一个简单的电路计算题。
经典例题动态专题类型一:开关的断开或闭合引起电路中电流、电压以及电阻的变化。
例1.如图7所示电路,将开关S闭合,电流表的示数将;电压表的示数将。
(选填“变大”、“变小“或”不变“)针对练习:如图8所示电路中,当开关S 断开时,电阻R 1和R 2是 联,开关S 闭合后,电压表的示数将 (选填”变大“、”变小“或”不变“).例2。
如图9所示电路中,灯泡L 1和L 2是 联,当开关S 断开时,电压表的示数将 ,电流表的示数将 .(选填“变大”、“变小"或“不变”)针对练习:如图10所示电路,灯泡L 1和L 2是 联,开关S 断开时,电压表的示数将 ;电流表的示数A 1的示数将 ;A 的示数将 (选填“变大”、“变小”或“不变”)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
动态电路分析一、是非题1.对于零状态电路,过渡过程的起始瞬间,电容相当于短路,电感相当于开路(不计冲激作用)。
2.换路定律仅用来确定u c(0+)和i L(0+),其他电量的初始值应根据u c(0+)或i L(0+)按欧姆定律及基尔霍夫定律确定。
3.同一个一阶电路的零输入响应、零状态响应和全响应具有相同的时间常数。
4.用短路开关把载流线圈短接,则线圈电阻越大,线圈电流衰减时间越长。
5.全响应中,零状态响应由外加激励引起的,所以零状态响应就是稳态响应。
6.电路的零输入响应就是自由分量,零状态响应就是强制分量。
7.R大于、等于或小于是判断RLC串联电路零输入响应处于非振荡放电、临界放电和振荡放电状态的判别式。
8.电感元件是用电压电流特性来定义的元件。
9.如电感元件的电流不变,无论其电感值为多大,都可等效为短路;如电容元件的电压不变,无论其电容值为多大,都可等效为开路。
10.一个在t=0-时电压为零且电压不跃变的电容在换路时相当于短路;一个在t=0-时电流为零且电流不跃变的电感在换路时相当于开路。
11.由R、L组成的一阶电路,若R越大,其零输入响应衰减得越慢。
12.零输入的RC电路中,只需时间常数τ不变,电容电压从100V放电到50V所需时间与从150V放电到100V所需时间相等。
13.在零输入响应的情况下,电路的时间常数τ是电流或电压由初始值衰减到该值的0.632倍所需的时间。
14.电压为100V的直流电压源,通过100kΩ电阻对10μF电容充电,经过1s,充电电流为0.368mA。
15.在零状态RL串联电路接入恒定电压,如果电源电压不变,增加电阻可以减少稳态电流及缩短过渡过程时间。
16.全响应中,暂态响应仅由元件初始储能产生,稳态响应则由外加激励产生。
17.设某电压可表示为u(t)=ε(t)-ε(t-3)V,则当t=3s时有u(3+)≠u(3-)。
18.RLC串联电路接通直流电压源瞬间,除u C和i L之外,其余元件的电压或电流均能跃变。
19.线性动态电路微分方程的阶次与电路中的储能元件数恒等。
20.当电感元件在某时刻t的电流i(t)=0时,电感元件两端的电压u(t)不一定为零;同样,当u(t)=0时,i(t)不一定为零。
21.非零初始状态的电路,当所有独立源的大小加倍时,全响应也加倍。
答案部分1.答案(+)2.答案(+)3.答案(+)4.答案(-)5.答案(-)6.答案(-)7.答案(+)8.答案(-)9.答案(+)10.答案(+)11.答案(-)12.答案(-)13.答案(-)14.答案(+)15.答案(+)16.答案(-)17.答案(+)18.答案(-)19.答案(-)20.答案(+)21.答案(-)二、单项选择题1.图示电路开关S在闭合前和都无储能,则开关S合上瞬间跃变的量为(A)i (B) i 1 (C)i2 (D)u2.由于电感线圈中储存的能量不能跃变,所以电感线圈在换路时不能跃变的量是(A)电压 (B)电流 (C)电动势3.图示电路在开关S合上前电感L中无电流,合上开关的瞬间u L(0+)的值为(A)0V (B)63.2V (C)∞ (D)100V4.右上图示电路中电流源电流恒定,电路原先已稳定。
在开关S合上后瞬间,电流i(0+)的值为(A)0A (B)1A (C)0.2A (D)0.8A5.线性一阶电路的特征方程是(A)线性代数方程组 (B)一元一次线性代数方程(C)二次代数方程 (D)一阶微分方程6.若R为电阻,L为电感,则R/L的单位为(A)V (B)A (C)s (D)s-17.已知电容C=1F,选择其电压u与电流i为关联参考方向,u的变化规律如图(A)所示,则电流i的变化规律为下图中的哪一个?8.若一阶电路的时间常数为3s,则零输入响应每经过3s后衰减为原来的(A)50% (B)25% (C)13.5% (D)36.8%9.关于一阶动态电路的零输入响应,以下叙述中正确的是(A)RL电路的零输入响应与初始磁场能量成正比(B)零输入响应随着时间增长衰减至零(C)零输入响应的时间常数一般为5τ(D)零输入响应中的电磁能量始终不变10.图示电路中,u C(0+)=0,开关S闭合后描述过渡过程的正确的表达式是:(A)(B)τ=R2C (C)(D)[τ=(R1+R2)C]11.关于一阶动态电路的零状态响应,以下概念中错误的是(A)零状态响应的绝对值均为逐渐增长(B)零状态响应就是零初始状态响应(C)零状态响应中电路的电磁储能逐渐增长(D)零状态响应一般认为在历时5τ后已基本进入稳态12.图示电路中电压源电压恒定,电路原已稳定,断开开关S后,电压表两端电压u v(t)为(A)(B)(C)(D)(150kΩ为电压表内阻)13.图示电路中U S恒定,电路在开关S合上前已稳定。
当开关闭合后,电路的情况为(A)i L衰减为零,i变为(B)i L减小为(C)i L不变,i亦不变(D)i L不变,i变为14.含有两个动态元件的电路(A)一定是二阶电路;(B)有可能是一阶电路;(C)一定是一阶电路;(D)有可能是三阶电路。
15.图示电路中,4A为直流电流源,该电路处于稳态时储存有能量的元件是(A)电容C(B)电感L(C)电容C和电感L(D)电阻R116.图示电路中,若接上电阻R,则换路后过渡过程持续的时间与原来相比(A)缩短(B)增长(C)不变(D)由R的数值决定17.图示电路原已稳定,t=0时断开开关S后,u C到达47.51V的时间为(A)6μs (B)2μs (C)4μs (D)无限长18.图示电路的时间常数τ为(A)1s (B)0.5s (C)s (D)s19.图示电路,电压源电压恒定i L(0-)=0,t=0时闭合开关S后,i(t)为(A)2(1-e-t)A (B)3.6(1-e-16t)A (C)3.6e-t A (D)0.5+0.5e-16t A20.图示电路中U S = 10V不变,电路原已稳定。
在t = 0时开关S闭合,则响应i(t)(A)(B)(C)e 20t A (D)1A23.电容对电阻放电的电路中,在任一瞬时电阻已消耗的能量为(A)(B)(C)(D)24.图示电路中电压源电压恒定,电路已达稳态,开关S闭合后i L(t)的时间常数为(A)(B)(C)(D)1.(A)2.(B)3.(D)4.(A)5.(B)6.(D)7.(C)8.(D)9.(B)10.(A)11.(A)12.(C)13.(C)14.(B)15.(B)16.(A)17.(A)18.(A)19.(D)20(D) 23(D)24(C)1.对于电感电流和电容电压不能跃变的电路,若电路的初始储能为零,则在t=0+时,电容相当于_______;电感相当于_____________________。
2.动态电路中,若电容电压u C(0-)为3V,且电容电压又不跃变,则在t=0+的等效电路中,该电容元件可等效为____________________。
3.图示电路中电压源电压恒定,电路已稳定,u C(0-)=0,t=0时开关S闭合。
则i2(0+)=________,i C(0+)=________,i1(∞)=_____。
4.图示电路中电压源电压恒定,在开关S合上前,u C(0-)=0,i L(0-)=0,t=0时,开关S合上,则i1(0+)=________,u L(0+)=________,i1(∞)=_______,u C(∞)=________。
5.在RC一阶电路中,若电容电压u C(0+)增大A倍,则该电路中____________响应也增大A倍。
6.RLC串联电路中,R、L、C三者关系满足_________________时,称为临界阻尼情况;满足_______________时,称为无阻尼情况。
7.电感为L的电感元件的磁场储能W L=________________。
正弦电流电路中,在选择电压与电流为______________参考方向下,电感元件的电流的相位比其电压超前。
8.由q-u平面中一条曲线所确定的元件称为_________元件;由ψ-i平面中一条曲线所确定的元件称为__________元件。
9.图示电路中电压源电压恒定。
开关断开前电路已稳定,t=0时断开开关S,则u C(0+)=____________,i C(0+)=_________,u C(∞)=________。
10.图示电路处于零状态,t=0时开关S闭合,则t=0+时i(0+)=__________;t=∞时i(∞)=_________。
11.图示电路中电流源电流恒定,开关S在t=0时闭合,闭合前电路为零状态,则i C(0+)为____________。
12.RC电路中,已知R=2MΩ,如果要求时间常数为10s,则C值为_________。
13.图示中电压源电压恒定,电路原已处于稳态,t=0时开关S断开。
则i L(0)=__________,u L(0+)=________________,时间常数+τ=__________________。
14.已知流过50mH电感的电流为i L(t)=A,其中τ=0.1s,则电感电压为u L(t)=_________________。
15.图示电路中U S恒定,电路已稳定。
在开关S断开后u C(0+)=_____,i C(0+)=____________及τ=_____________。
16.RC串联支路处于零状态,t=0时与电压为U S的直流电压源接通。
(1)充电开始时电流为_______________。
(2)t=τ时,电容电压为_____________。
17.图示电路中,电压源电压恒定,电流源电流恒定,电感无初始电流,t=0时开关S闭合,则i L(t)=_______。
18.右上图示电路中,电压源电压恒定,i(0-)=0,t=0时开关S闭合,则t1=0.1s时的电流i(t1)=____A,u L(t)达到5V时的时间t=___s。
19.在直流一阶RL电路中,若i L(∞)=3A,时间常数τ为0.25s,则电感电流在t≥0时的零状态响应表达式为___________________。
20.图示电路中U S不变,电路原已稳定,t=0时开关S闭合。
则i L(0+)=_________;u L(0+)=___________;τ=______。
21.右上图示电路中,U S=10V不变,i L(0-)=2A,试求开关S闭合后i L的零输入响应和零状态响应。
22.左下图示电路中,U和U S都不变。
已知u C(0-)=52V,欲使电路在换路后无过渡过程,则U=___________。
27.右上图示电路中电压源电压恒定,电流源电流恒定。
电路已处于稳态,t=0时合上开关S,则时间常数τ=_________,i L(0+)=________。
